Pulse-shaping based two-photon FRET stoichiometry

Abstract

Förster Resonance Energy Transfer (FRET) based measurements that calculate the stoichiometry of intermolecular interactions in living cells have recently been demonstrated, where the technique utilizes selective one-photon excitation of donor and acceptor fluorophores to isolate the pure FRET signal. Here, we present work towards extending this FRET stoichiometry method to employ two-photon excitation using a pulse-shaping methodology. In pulse-shaping, frequency-dependent phases are applied to a broadband femtosecond laser pulse to tailor the two-photon excitation conditions to preferentially excite donor and acceptor fluorophores. We have also generalized the existing stoichiometry theory to account for additional cross-talk terms that are non-vanishing under two-photon excitation conditions. Using the generalized theory we demonstrate two-photon FRET stoichiometry in live COS-7 cells expressing fluorescent proteins mAmetrine as the donor and tdTomato as the acceptor.

1. Introduction

Förster (or equivalently “fluorescence”) Resonance Energy Transfer (FRET) based microscopy uses nonradiative energy transfer from one molecule (donor) to another (acceptor) to provide information about molecular interactions within biological systems [1,2]. Often referred to as a “spectroscopic ruler”, the FRET efficiency is proportional to 1/r⁶, where r is the intermolecular distance. This results in energy transfer only when the donor and acceptor molecules are within close proximity (1–10 nm) and can therefore provide information on a wide range of molecular interactions [2–6]. Until recently, FRET has been measured in arbitrary units, inhibiting stoichiometric inference of the system of interest [7, 8]. Several approaches have been taken to enable quantitative FRET measurements. These include methods that employ various combinations of multiple excitation wavelengths and detection channels, as well as spectrally-resolved and fluorescence lifetime imaging (FLIM) approaches.

In 2001, Erickson et al. developed a quantitative “three-cube FRET” technique employing spectral filtering to isolate donor and acceptor signals [9]. Hoppe et al. extended that work by demonstrating one-photon FRET stoichiometry in live cells where the fraction of donor and acceptor in complex as well as the ratio of total donor and acceptor molecules were quantified from intensity-based measurements at two excitation wavelengths in two detection channels [10]. Neher et al. considered the use of spectral fingerprinting in the case of single and two excitation wavelengths and the utility of including fluorescence lifetime information to perform FRET stoichiometry [11]. Multiple excitation wavelength methods (ALEX-FRET) have also been applied to single molecule FRET studies [12, 13]. Raicu et al. have used spectrally-resolved one-photon FRET instead of intensity-based imaging to quantify protein interactions [14]. Elder et al. developed a standardized FRET stoichiometry theory that can be used to compare the different results reported in literature [15].

FRET-FLIM techniques offer another approach to measuring FRET efficiencies and obtaining stoichiometric information [16–19]. Compared to intensity-based measurements, FRET-FLIM measurements are less sensitive to fluorophore concentration, photobleaching, and autofluorescence and intrinsically give an estimate of the ratio of complexed to non-complexed donor fluorophores [18]. The technique currently requires longer acquisition times than intensity-based measurements, although rapid advancement in detectors and fluorophores promise an exciting future for this technique [20].

Combining the advantages of two-photon excitation (greater depth penetration, automatic sectioning, reduced photobleaching) [21] with the benefits of FRET has already found wide application [22–28]. However, the nature of two-photon excitation, and the laser sources that are typically employed in two-photon fluorescence studies present some challenges to adapting one-photon FRET stoichiometry approaches to two-photon applications. In particular, intensity-based approaches that rely on multiple excitation wavelengths are problematic: the high cost of femtosecond laser sources makes the use of multiple lasers for multiple excitations prohibitively expensive, and the slow tuning speed of typical femtosecond lasers limits the time resolution that can be achieved. In addition, cross-talk terms that are negligible in one-photon applications may become significant under two-photon excitation conditions. Thus, to date, multiphoton FRET stoichiometry measurements have used either spectrally-resolved or lifetime-resolved approaches. Two-photon spectrally-resolved FRET has been used to study protein-protein interactions [29]. Raicu et al. have also extended their spectrally-resolved approach [30], using the calculated apparent FRET efficiencies to study the sizes and configurations of multiple donors and acceptors as found in interacting membrane proteins. This technique assumes that the acceptor fluorophore is only excited via FRET, and requires that fluorescence spectra be recorded per pixel throughout the experiment. Two-photon FRET-FLIM microscopy has been used for analyzing protein dimerization [31, 32]. This technique is also susceptible to spectral cross-talk, which must be removed from the FRET signal using correction algorithms [32].

In the present work, we demonstrate that intensity-based one-photon FRET stoichiometry approaches can be adapted to two-photon FRET applications using pulse-shaping of a broadband titanium:sapphire oscillator. Such sources generate a broad bandwidth (650 – 1000 nm), and therefore have the potential to excite multiple fluorophores, including many potential donor and acceptor pairs for two-photon FRET studies. Previously, pulse-shaping of a broadband laser has been shown to provide selective two-photon fluorescence excitation [33–36] and has been used to discriminate between autofluorescence and GFP (green fluorescent protein) fluorescence in live cells [33]. The technique has been used to image calcium concentration using a FRET-based calcium sensor [37]. It has also recently been used for three-color multiphoton fluorescence imaging [38]. Pulse-shapers enable rapid switching on the millisecond timescale [38–40] to allow two-photon excitation of specific fluorophores within the laser bandwidth, facilitating rapid acquisition of images with different excitation conditions. The combination of phase-shaping and spectral filtering of the emission has been shown to enhance fluorophore discrimination [33]. Here we apply pulse-shaping of a broadband laser to extend the approach of Hoppe et al. [10], to two-photon FRET stoichiometry.

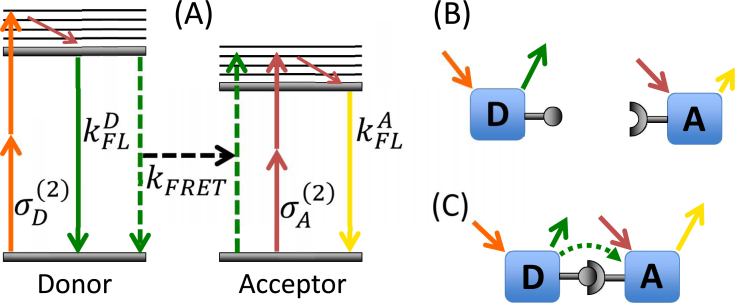
The Hoppe FRET stoichiometry theory [10] makes several assumptions (see Appendix, Eq. (12)) that may no longer be valid when using two-photon excitation. Here we generalize Hoppe’s FRET stoichiometry theory to account for two additional cross-talk terms η and θ (defined in Table 1) that are significant for our implementation of two-photon FRET stoichiometry. These cross-talk terms are likely to be significant for many two-photon FRET studies due to the highly overlapped two-photon cross-sections of S₀ → S_n transitions for many fluorescent proteins that make it difficult to avoid direct acceptor excitation [41]. For the donor and acceptor, we choose the fluorescent proteins mAmetrine and tdTomato respectively, on account of the strong overlap between donor emission and acceptor absorption, their two-photon brightness [41] and because of the ease of genetically encoding fluorescent tags in living cells. For mAmetrine, the S₀ → S₁ transition is used, while for tdTomato, we use the S₀ → S_n transition because of the reported high absorption cross-section [41]. We apply the technique to live COS-7 cells, where we demonstrate that we can directly quantify the ratio of donor and acceptor molecules in complex as well as the molar ratio of acceptor to donor in vitro, and show that this technique can be used to quantify cellular dynamics on biologically relevant time scales. Figure 1 illustrates the two-photon excitation process and fluorescence emission of donor and acceptor in the cases where they are either in complex or free.

Table 1.

Glossary of symbols for FRET stoichiometry. The constants θ and η account for additional cross-talk terms that were negligible in the Hoppe FRET stoichiometry theory.

Symbols	Description
IA	Intensity or image at the acceptor excitation and acceptor emission.
ID	Intensity or image at the donor excitation and donor emission.
IF	Intensity or image at the donor excitation and acceptor emission.
IN	Intensity or image at the acceptor excitation and donor emission.
E	Efficiency calculated from FLIM measurements
R	The molar ratio of acceptor to donor measured by FRET stoichiometry.
fA	Fraction of acceptor in complex as measured by FRET stoichiometry.
fD	Fraction of donor in complex as measured by FRET stoichiometry.
α	Proportionality constant relating acceptor fluorescence at the acceptor excitation to the donor excitation.
β	Proportionality constant relating donor fluorescence detected at the acceptor emission relative to that detected at the donor emission.
θ	Proportionality constant relating donor fluorescence at the acceptor excitation to the donor excitation.
η	Proportionality constant relating acceptor fluorescence detected at the acceptor emission relative to that detected at the donor emission.
γ	Ratio of the extinction coefficient of the acceptor to the donor at the donor excitation.
ξ	Proportionality constant relating the sensitized acceptor emission to the decrease in donor fluorescence due to FRET.

Fig. 1.

(a) The scheme for two-photon FRET is shown, where the donor (mAmetrine) and acceptor (tdTomato) are selectively excited by process ${\sigma }_D^{(2)}$ (orange arrows) and ${\sigma }_A^{(2)}$ (red arrows) respectively, while the emission is split with a dichroic and detected with two PMTs. FRET efficiency is defined as $k_{\mathit{FRET}}/\left(k_{\mathit{FRET}}+k_{\mathit{FL}}^D\right)$ for the donor, where k_FRET is the rate of FRET, while $k_{\mathit{FL}}^D$ (solid green arrow) is the total rate of all other radiative and non-radiative decay of donor excitation. (b) When the donor and acceptor are not associated, no FRET occurs, and a majority of the emission from the donor is collected in the donor channel (green arrow) and a majority of the acceptor emission is collected in the acceptor channel(yellow arrow). (c) When associated in a complex, FRET occurs between the donor and acceptor (dotted green arrow), resulting in increased emission from the acceptor (denoted by a longer yellow arrow) and decreased emission from the donor when excited by the donor pulse-shape (smaller green solid arrow).

Briefly, two pulse-shapes chosen to excite primarily the donor and acceptor fluorophores and two detection conditions corresponding to the donor and acceptor emission afford us four images labeled I_A, I_D, I_F, and I_N, which are defined in Table 1. First, the crosstalk parameters α, β, θ, and η are calculated from images taken of cells expressing only donor or only acceptor (see section 2.1 for sample methods). As with the Hoppe stoichiometry technique, an a priori knowledge of the FRET efficiency E is required, which is experimentally measured for the given choice of proteins using two samples – purely-linked and donor-only in a FRET-FLIM setup. The constants γ, and ξ are then calculated using a known donor-acceptor linked construct (guaranteed FRET). To perform FRET stoichiometry on unknown samples, only three images I_A, I_D, and I_F are collected. The expression describing the fraction of acceptors in complex, f_A, the fraction of donors in complex, f_D, and the molar ratio of acceptor to donor, R, is shown in Eq. (1), where [A_T] and [D_T] are the molar concentrations of acceptor and donor respectively. The parameters α, β, θ, η, γ, and ξ are described in Table 1 with their corresponding mathematical descriptions found in the Appendix.

$$\begin{array}{ll}\hfill f_A& =\gamma \left[\frac{\frac{\eta }{\eta -\beta }{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D}{\frac{\theta \alpha }{\theta -\alpha }{I}_A-\frac{\alpha }{\theta -\alpha }{I}_F}-1\right]\frac{1}{E}\hfill \\ \hfill f_D& =\left[1-\frac{\frac{1}{\eta -\beta }\left(\eta I_D-I_F\right)}{\xi \left(\frac{\eta \theta -\beta \alpha }{(\theta -\alpha )(\eta -\beta )}{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D-\frac{\alpha \theta }{\theta -\alpha }{I}_A\right)+\frac{1}{\eta -\beta }\left(\eta I_D-I_F\right)}\right]\frac{1}{E}\hfill \\ \hfill R& =\frac{f_D}{f_A}=\frac{[A_T]}{[D_T]}\hfill \end{array}$$ (1)

2. Materials and methods

2.1. COS-7 cell culture and transfection

COS-7 cells were grown in Dulbecco’s Modified Eagle Medium (Ref: 11885-084, supplemented with 10% fetal bovine serum-(qualified) and 1% penicillin/streptomycin mixture) at 37°C in 5% CO₂. COS-7 cells were plated on 35-mm tissue culture dishes 24 hours prior to transfection. Three different plasmid DNAs were used for transfection, mAmetrine, td-Tomato, and an mAmetrine-tdTomato linked construct. mAmetrine was inserted in frame into the ptdTomato-N1 vector (Clontech) by an amino acid polypeptide linker (ASGAPVAT) between the NheI and AgeI sites to create the mAmetrine-tdTomato linked construct. Transfections were performed when cells were 50% confluent, where 0.5 μg of plasmid DNA was combined with 100 μL of serum-free media and 3 μL of FuGene. The following construct combinations were used to transfect different plates: mAmetrine, tdTomato, mAmetrine + tdTomato, mAmetrine-tdTomato, mAmetrine-tdTomato + tdTomato, mAmetrine-tdTomato + mAmetrine plasmids (‘−’ denotes the amino acid linker, whereas ‘+’ denotes a mixture). 24 hours after transfection, cells were imaged in Ringer’s Buffer while being maintained at 37°C using a heated stage during data collection.

2.2. Pulse-shaping

The recent development of ultrafast lasers having few-femtosecond pulse durations and octave-spanning bandwidths [42, 43] enables new imaging opportunities. While microscope optics introduce significant dispersion resulting in pulse broadening, pulse-shaping has been demonstrated to successfully compress pulses to their transform limit at the sample [34]. Improvements in static pulse-shaping methods such as prism compressors, grisms, and chirped mirrors as well as dynamic pulse-shaping methods including acousto-optic and spatial light modulator (SLM) based pulse-shapers have made femtosecond coherent control schemes possible [44,45]. For example, SLMs can quickly correct and manipulate the spectral phase of a laser pulse to arbitrary orders of dispersion [46]. Integrated into a 4-f pulse-shaper setup, a grating spatially disperses laser frequencies that are then focused onto a phase-only 640-pixel SLM located at the Fourier plane where the SLM adjusts the spectral phase of the laser pulse. A flat spectral phase at the sample plane results in the constructive interference of all frequencies in the time domain and the shortest pulse duration (transform-limited). We refer the readers to the many excellent review articles that discuss techniques for shaping and characterizing laser pulses [45–48].

Assuming no intermediate resonant levels, the fluorescence signal S from a two-photon excited fluorophore can be written as

$$S\propto g(\omega ){\left|E^{(2)}(\omega )\right|}^2,$$ (2)

where g(ω) is the two-photon excitation spectrum, and |E⁽²⁾(ω)|² is the second harmonic power spectrum of the laser [34, 49, 50]. The second harmonic spectrum is a convolution of the two fundamental fields, each with an amplitude term, |E(ω)|, and a spectral phase term, ϕ(ω) :

$$E^{(2)}(\omega )\propto \underset{-\infty }{\overset{\infty }{\int }}\text{d}{\omega }^{\prime }\left|E({\omega }^{\prime })\right|\left|E(\omega -{\omega }^{\prime })\right|\text{exp}\left\{i\left[\varphi ({\omega }^{\prime })+\varphi (\omega -{\omega }^{\prime })\right]\right\}.$$ (3)

The second harmonic field can be shaped by using the SLM to apply an appropriate spectral phase such that different fundamental frequency combinations constructively and destructively interfere to achieve selective excitation [34]. Techniques for determining the required spectral phase for a given pulse-shape involve using symmetry arguments and can be further refined with optimization algorithms [51–53].

2.3. Imaging

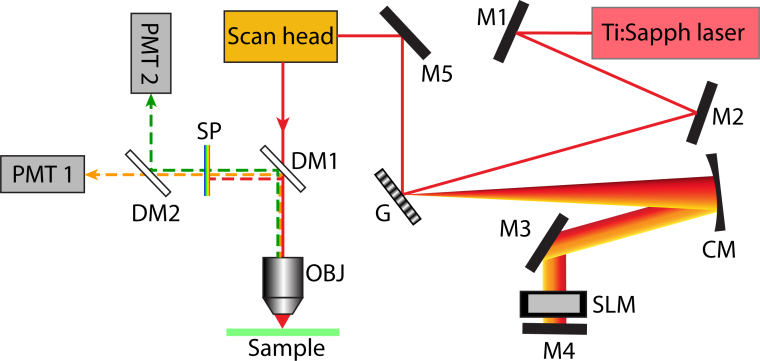
The microscope setup used in this experiment is shown in Fig. 2. Pulses from an 82-MHz titanium:sapphire oscillator (Venteon: Pulse one), having a broad bandwidth (>300-nm) centered at 800 nm, were phase-shaped by a pulse-shaper (MIIPS 640 Box, BioPhotonic Solutions Inc.) equipped with a 640-pixel SLM (PerkinElmer) in a folded 4-f geometry. The phase-shaped beam is sent into the scan head of an upright microscope (Olympus BX51WI modified by Prairie Technologies) equipped with two orthogonally scanning galvo-mounted mirrors for imaging. A water-immersion microscope objective (Olympus UPlanApo 60X, 1.2NA) was used to focus the fundamental pump beam onto the sample and collect epi-fluorescence signal. Excitation power at the sample was approximately 2 mW. The emitted signal was separated from the excitation light with a dichroic mirror (Chroma 660DCXXR), filtered with a short-pass filter (Chroma E650SP), and spectrally split into two PMT channels (corresponding to ${\lambda }_D^{\mathit{em}}$ and ${\lambda }_A^{\mathit{em}}$, see Appendix) using a dichroic (Chroma 550DCXR).

Fig. 2.

Experimental setup: M1–M5: mirrors, G = grating, CM = concave mirror, SLM = spatial light modulator, DM1 = 660DCXXR dichroic mirror (Chroma), DM2 = 550DCXR dichroic mirror (Chroma), OBJ = 60X 1.2 NA water immersion objective (Olympus), SP = E650SP short pass filter (Chroma), Ti:Sapph laser = Titanium:sapphire laser (Venteon Pulse:One, 650 – 1000 nm).

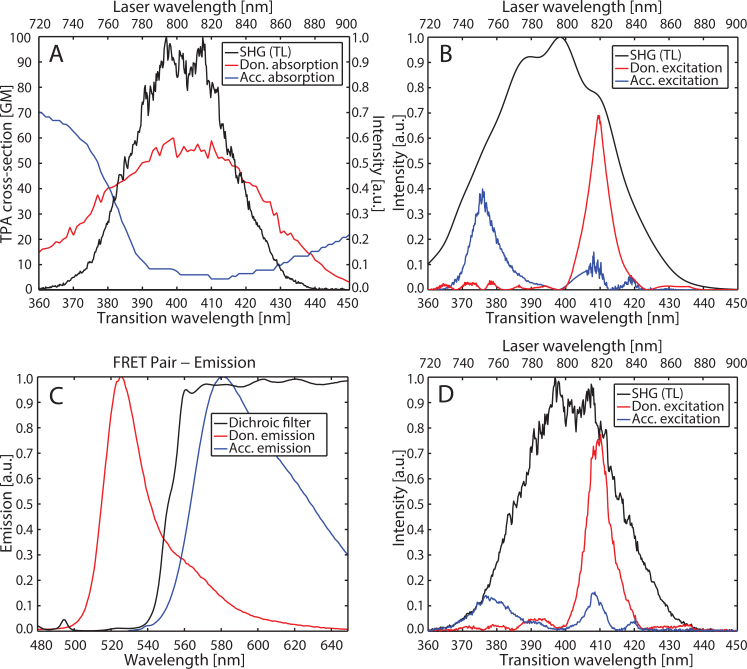
Multiphoton Intrapulse Interference Phase Scan (MIIPS) was used to pre-compensate for dispersion caused by the microscope optics and to achieve a near TL pulse at the sample [34, 51, 52, 54–58]. Then an additional phase mask was added to this compression phase mask to shape pulses for selective excitation. With knowledge of the donor and acceptor two-photon absorption spectra (Fig. 3(A)) [41], pulse-shapes were designed to produce second harmonic spectra that would provide efficient excitation of the donor and acceptor fluorophores [59]. For this particular FRET pair we take advantage of the S₀ → S_n transition of the acceptor, exciting it at shorter wavelengths than the donor [41]. The pulse-shapes were designed using a genetic algorithm (MATLAB Global Optimization Toolbox, Mathworks) by minimizing the difference between a target and the simulated second harmonic spectrum. The target second harmonic spectra were chosen to be a Gaussian of width 8 nm (FWHM) centered at 410 nm for the donor and 375 nm for the acceptor. The spectral amplitude of the laser pulses as measured at the sample position was used in the simulation of the second harmonic spectrum. An initial population of a hundred binary phase masks were generated using a prime number based destructive interference scheme [51, 52]. The algorithm took approximately 2 minutes to converge to the solution for each mask. The genetic algorithm yielded pulse-shapes producing second harmonic spectra for the donor, ${\lambda }_D^{\mathit{ex}}$, and acceptor, ${\lambda }_A^{\mathit{ex}}$, as shown in Fig. 3(B). The simulation approach is significantly faster than a genetic algorithm feedback loop integrated into the experimental system, which can take hours to converge depending on excitation type and initial population [60]. The corresponding experimentally-detected second harmonic spectra are shown in Fig. 3(D). We note that the acceptor excitation is not particularly selective and generates considerable donor excitation. Given the nonzero two-photon cross-section of both donor and acceptor across the second harmonic spectrum of the laser, high selectivity cannot be achieved with this particular FRET pair. Indeed this is likely to be a common occurrence for many two-photon FRET pairs, where S₀ → S_n two-photon transitions of the acceptor may overlap with two-photon donor excitation. The lack of selectivity does not pose a problem for our method, which simply requires two independent excitation conditions that yield different levels of donor and acceptor excitation, each producing high signal-to-noise fluorescence images. Cross-talk terms resulting from low selectivity are accounted for (see Appendix). The SLM response time of 35 ms allows for rapid switching between pulse-shapes. The two excitation conditions and two detection channels generate the three distinct images – I_A, I_D, and I_F, as well as an additional image, I_N ((defined in Table 1), which is not included in our stoichiometric analysis.

Fig. 3.

(A) Two-photon absorption spectra with respect to transition wavelength of donor (mAmetrine, red) and acceptor (tdTomato, blue) adapted from Drobizhev et al. [41], and their overlap with the second harmonic of the transform-limited titanium:sapphire laser pulse (SHG(TL), black). (B) Simulated second harmonic signal for excitation of donor (red) and acceptor (blue) obtained upon applying the binary spectral phase function determined via genetic algorithm. Also shown is the second harmonic spectrum of the transform-limited pulse (black). (C) Emission spectra of donor (red) and acceptor (blue). Also shown is the transmission of the dichroic filter (black) splitting the emission into two PMT channels. (D) Experimental second harmonic spectra for excitation of donor (red) and acceptor (blue) obtained upon applying the binary spectral phase function determined via genetic algorithm. Also shown is the second harmonic spectrum of the transform-limited pulse (black).

2.4. Image processing

Each microscope image comprises 512×512 pixels with a total image size of 223μm×223μm. An image acquisition time of approximately 50 s was a result of the 12-μs pixel dwell time and averaging of 16 exposures. Image processing and analysis was performed in MATLAB. All images were background-subtracted using the average shuttered PMT dark counts and shading-corrected using the intensity profile of the emission from a uniformly-doped autofluorescence slide (Chroma Part No. 92001). After correction for background and shading, corrected images were analyzed with a watershed algorithm and a single binary mask was used to select individual cells from images [61]. Thresholding algorithms were used to choose pixels with intensities in the PMT linear response regime (away from saturation as well as the dark noise floor). The signal over each cell was averaged to extract a single value in order to make the stoichiometry calculation more robust against pixel-to-pixel variations. The numbers are reported per cell.

2.5. Determination of efficiency by fluorescence lifetime

The fluorescence lifetime of fluorescent proteins in cells expressing donor (mAmetrine) and the linked donor-acceptor (mAmetrine-tdTomato) construct were measured with a FLIM microscope configured for time-correlated single photon counting. The FLIM measurements were performed using an Olympus IX-81 microscope with a 60X 1.2NA water immersion objective. A supercontinuum excitation source (Fianium SC 400-6-PP) with a repetition rate of 20 MHz, 100-ps pulse duration and configured with an acousto-optic tunable filter was used for picking the excitation wavelengths at 405 nm and 408 nm. The emission was split into two channels using a 562 nm low-pass dichroic filter. The transmitted light was further filtered by a 593 ± 20 nm band-pass filter to measure the acceptor emission, whereas the reflected light was filtered by a 531 ± 20 nm band-pass filter to measure donor emission. Single photon detection was performed with two Hamamatsu H7422P-40 PMTs.

The donor lifetime was fit to a bi-exponential decay both in the absence as well as presence of FRET. From the average fluorescence lifetime of mAmetrine and of mAmetrine-tdTomato in complex, the FRET efficiency, E, was determined to be 0.29 ± 0.03 inside cells according to the relation [62]

$$E=\left[1-\frac{{\tau }_{\mathit{DA}}}{{\tau }_D}\right],$$ (4)

where τ_D = 3.19 ± 0.03 ns and τ_DA = 2.26 ± 0.07 ns are the experimentally measured fluorescence lifetimes of mAmetrine alone and mAmetrine-tdTomato linked construct, respectively.

2.6. Determination of parameters: α, β, η, θ, γ, ξ

The parameters α and β were calculated according to the equations (for derivation, see Appendix)

$$\alpha =\frac{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}=\frac{I_F}{I_A}$$ (5)

$$\beta =\frac{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{I_F}{I_D}$$ (6)

from cells expressing only acceptor and donor respectively. This step is identical to previously published work [10]. The α and β values for our system were found to be 0.33 ± 0.02 and 0.25 ± 0.01 as determined from measurements of 23 acceptor only and 42 donor only cells respectively. In a similar manner, η and θ are determined from cells expressing only acceptor and only donor respectively, given by the relations:

$$\eta =\frac{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{I_A}{I_N}$$ (7)

$$\theta =\frac{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}{F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{I_D}{I_N}.$$ (8)

The η and θ values were found to be 5.9 ± 0.6 and 2.2 ± 0.3 as determined from measurements of 23 acceptor-only and 42 donor-only cells respectively. γ and ξ are constants of the system that are experimentally measured using cells expressing the donor-acceptor linked construct (see section 2.1). In this case, since f_A = f_D = 1 by design, by inverting Eq. (1), we obtain

$$\gamma =E{\left[\frac{\frac{\eta }{\eta -\beta }{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D}{\frac{\theta \alpha }{\theta -\alpha }{I}_A-\frac{\alpha }{\theta -\alpha }{I}_F}-1\right]}^{-1}$$ (9)

and

$$\xi =\frac{E\left(\frac{\eta I_D-I_F}{\eta -\beta }\right)}{(1-E)\left(\frac{\eta \theta -\beta \alpha }{(\theta -\alpha )(\eta -\beta )}{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D-\frac{\alpha \theta }{\theta -\alpha }{I}_A\right)}.$$ (10)

The γ and ξ values were found to be 0.3 ± 0.1 and 1.0 ± 0.1 determined from measurements of 59 cells expressing the linked construct.

3. Two-photon FRET stoichiometry results

To demonstrate two-photon FRET stoichiometry we imaged COS-7 cells expressing either linked construct, free donor and acceptor, linked construct + acceptor and linked construct + donor, computing an average f_A, f_D and R for each cell in the different cases. Typical cell images for the different transfections are shown in Figs. 4 – 7 color coded according to the average stoichiometry of each cell. The stoichiometry results are reported in Table 2, where averages over the indicated number of cells are given for the different expression conditions. We show results from the generalized FRET stoichiometry theory described in the appendix (indicated with a G) as well as the original FRET stoichiometry theory which does not account for the additional cross-talk terms η and θ.

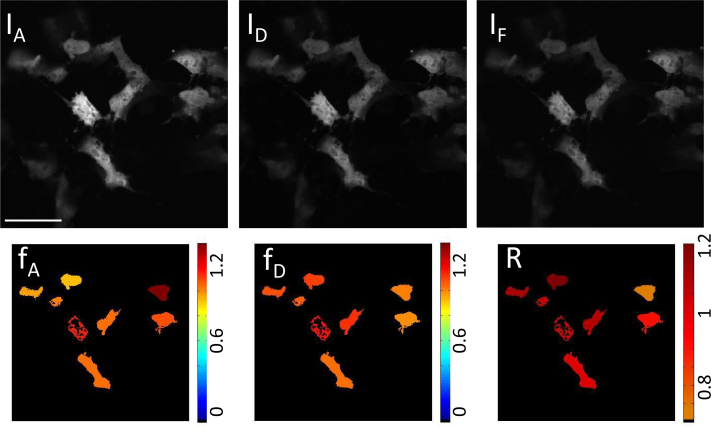
Fig. 4.

Top: Raw microscope images from channels I_A, I_D, and I_F for cells expressing linked construct mAmetrine-tdTomato. Bottom: Color coded cells after analysis for the cells expressing linked construct mAmetrine-tdTomato giving the ratio of acceptor in construct (f_A, expected value = 1), ratio of donor in construct (f_D, expected value = 1), and absolute concentration ratio (R, expected value = 1). Scale bar insert:55 μm

Fig. 7.

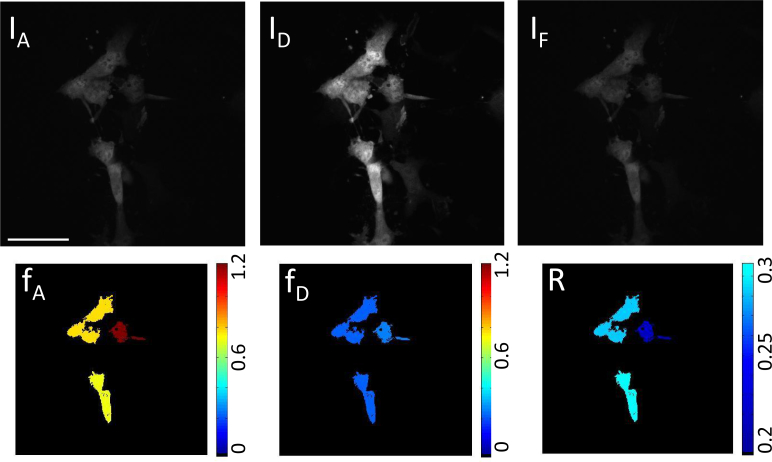
Top: Raw microscope images from channels I_A, I_D, and I_F for cells expressing linked construct mAmetrine-tdTomato plus excess tdTomato. Bottom: Color coded cells after analysis for cells expressing linked construct mAmetrine-tdTomato plus excess td-Tomato giving the ratio of acceptor in construct (f_A, expected value < 1), ratio of donor in construct (f_D, expected value = 1), and absolute concentration ratio (R, expected value > 1). Scale bar insert: 55 μm

Table 2.

Average FRET stoichiometry values for cell expression of combinations of linked and unlinked molecules. The results determined using the generalized (G) stoichiometry theory and the original stoichiometry theory are compared to illustrate points of differentiation. The expected values for the given transfection type are given in parentheses. The number of individual cells used to calculate the average and standard deviation (SD) for each transfection type are noted in row 2.

	linked construct	free donor and acceptor	linked construct + acceptor	linked construct + donor
Number of cells	59	42	17	18
fD ± SD(G)	1.0 ± 0.2(1)	0.0 ± 0.1(0)	0.8 ± 0.3(1)	0.2 ± 0.1
fA ± SD(G)	1.0 ± 0.3(1)	0.1 ± 0.1(0)	0.2 ± 0.1	0.8 ± 0.3(1)
fD ± SD	1.0 ± 0.2(1)	−0.2 ± 0.1(0)	0.5 ± 0.3(1)	0.0 ± 0.1
fA ± SD	1.0 ± 0.2(1)	−0.3 ± 0.2(0)	0.2 ± 0.1	0.0 ± 0.3(1)

4. Discussion

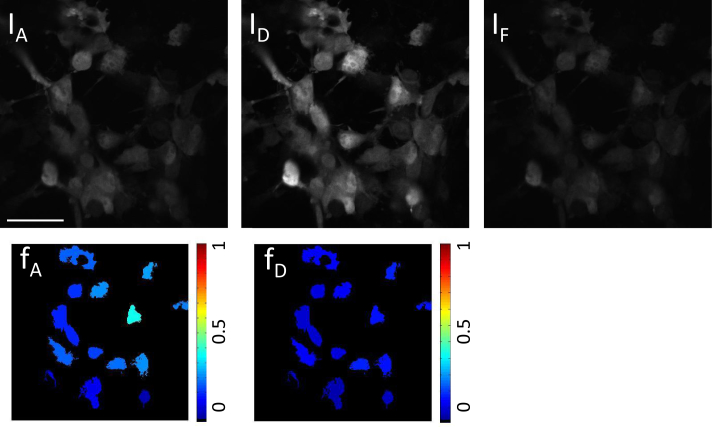
In Fig. 4, where cells are expressing the linked construct, our theory accurately predicts that the donor and acceptor fluorophores are completely linked, giving f_A = 1.0 ± 0.3 and f_D = 1.0 ± 0.2. The ratio image illustrates the variance from cell to cell. Cells co-transfected with donor and acceptor fluorophores (not in construct) are shown in Fig. 5. In this case, our theory accurately predicts the fluorophores to be completely non-interacting with f_A = 0.1 ± 0.1 and f_D = 0.0 ± 0.1. The concentration of donor and acceptor fluorophores expressed by each cell varies due to the intrinsic variability of co-transfection. In the absence of any FRET, the ratio of total acceptor to donor is a poorly defined quantity, so we do not show the ratio images. In the free donor and acceptor co-transfected cells the expression of the acceptor was much less than that of the donor fluorophore, resulting in the acceptor stoichiometry being more susceptible to noise.

Fig. 5.

Top: Raw microscope images from channels I_A, I_D, and I_F for cells expressing unlinked mAmetrine and tdTomato. Bottom: Color coded cells after analysis for cells expressing unlinked mAmetrine and tdTomato giving the ratio of acceptor in construct (f_A, expected value = 0), and ratio of donor in construct (f_D, expected value = 0). Scale bar insert: 55 μm

To further test the stoichiometry method, cells expressing the FRET construct plus excess donor (Fig. 6), and FRET construct plus excess acceptor (Fig. 7) were imaged with our technique. The ratio of the donor in construct f_D = [C]/[D_T] to the acceptor in construct f_A = [C]/[A_T] determines the absolute concentration ratio of acceptor to donor ie. [A_T]/[D_T], where [C] is the concentration of the donor-acceptor complex. Excess acceptor will result in R > 1, while excess donor will result in R < 1 and equal mole fractions of donor and acceptor in complex should yield R = 1. In the case where the FRET construct plus acceptor is expressed, the observed f_A was found to be 0.2 ± 0.1, while the recovered f_D was 0.8 ± 0.3. Although displaying a large variance, these values are consistent with the expected values. In the case where the FRET construct plus donor is expressed, the stoichiometric fractions were also consistent with expectations: the recovered f_D was found to be 0.2 ± 0.1, while f_A was 0.8 ± 0.3. In all cases, and in particular for the cells co-expressing the linked construct and donor, the generalized stoichiometry theory gave more accurate average values than the original theory, demonstrating the necessity of accounting for additional cross-talk terms with two-photon excitation.

Fig. 6.

Top: Raw microscope images from channels I_A, I_D, and I_F for cells expressing linked construct mAmetrine-tdTomato plus excess mAmetrine. Bottom: Color coded cells after analysis for cells expressing linked construct mAmetrine-tdTomato plus excess mAmetrine giving the ratio of acceptor in construct (f_A, expected value = 1), ratio of donor in construct (f_D, expected value < 1), and absolute concentration ratio (R, expected value < 1). Scale bar insert: 55 μm

The relatively large standard deviation in the stoichiometry numbers reported in Table 2 likely arises from a number of factors. Low expression of donor or acceptor could result in an increase in standard deviation as well as susceptibility to background noise. The computed stoichiometry from cells with low expression is likely to be more susceptible to small contributions from autofluorescence or photobleaching. The relatively small emission spectral overlap between the donor and acceptor also make crosstalk values more susceptible to noise. Fluorophore photobleaching over the duration of the experiment causes variations in absolute fluorophore concentrations, and also leads to a linked construct behaving like an individual fluorophore since the photobleached donor or acceptor no longer participate in FRET. An average power no greater than 2 mW was maintained throughout the experiments to minimize photobleaching. In addition, the large number of cross-talk correction factors applied in the generalized FRET stoichiometry calculations and their sequential evaluation allows the accumulation of small errors, leading to appreciable variability from cell to cell.

5. Conclusion

We have implemented pulse-shaping based two-photon FRET stoichiometry in live COS-7 cells and have demonstrated that we can accurately predict the donor/acceptor stoichiometry. Pulse-shaping-based two-photon excitation with a broadband laser allows for quick switching between excitation conditions (on the order of 35 ms), enabling quantitative intensity-based two-photon FRET measurements. This method offers improved time resolution compared to tuning a conventional (narrowband) titanium:sapphire laser to achieve the different excitation conditions necessary for intensity-based FRET stoichiometry. Our approach could be readily extended to multiplex FRET stoichiometry as has been done in one photon FRET studies [63,64] to enable greater insight into multiple protein-protein interactions. The use of pulse-shaping facilitates pulse-compression as well as tailoring of the spectral phase and amplitude for achieving desired multiphoton excitation conditions. While we have used pulse-shaping here to facilitate two-photon excitation of donor and acceptor fluorophores, the same approach of using pulse-shaping of broadband pulses could enable multimodal imaging with methods such as second harmonic generation [65, 66], third harmonic generation [67, 68] and coherent anti-Stokes Raman scattering (CARS) microscopy [69, 70]. Advances in unsupervised classification methods offer new and exciting routes towards extending stoichiometric analysis [71,72]. The combination of pulse-shaping-based multimodal imaging with these statistical tool sets promises new opportunities for robust and quantitative analysis of time-dependent molecular interactions in biological systems.

Appendix: Derivation of generalized FRET stoichiometry

The two-photon FRET stoichiometry theory developed here is a generalization of the one-photon FRET stoichiometry method published by Hoppe et al. [10]. The main distinction is that additional cross-talk terms are included that were found to be significant for the two-photon FRET pair used in this study. The same notation, $F_X\left({\lambda }_{\#}^{*}{\lambda }_{\#}^{*}\right)$, will be used for consistency. The subscript X represents the origin of the fluorescence signal, either D for donor, A for acceptor, or T for transferred fluorescence due to FRET. The # subscript identifies the wavelengths corresponding to the donor (D) or acceptor (A). Finally, the ^* superscript denotes the ex for excitation and em for emission condition respectively. As an example of this notation, the term $F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ refers to fluorescence signal from the donor molecules when excited at the acceptor’s excitation wavelengths and collected at the donor’s emission wavelengths.

A microscope image is made up of three signals: emission from free acceptors, F_A, emission from free donors, F_D, and emission from the donor-acceptor complexes, F_C. Signal from the donor-acceptor complex may be further broken down into emission from the donor, F_DC, emission from the acceptor not due to FRET, F_AC, and emission from the acceptor due to FRET, F_T. As FRET efficiency is not 100%, donor molecules in complex will have some emission resulting in F_DC ≠ 0. Similarly, the acceptor in complex may be directly excited by the same wavelengths used to excite the donor, resulting in direct acceptor emission, F_AC. It is not possible to distinguish fluorescence from the donor in complex from that of the free donor based purely on the signal intensity. Likewise, signal from the acceptor in complex cannot be distinguished from that of the free acceptor. As the terms F_D and F_A already contain the signal associated with F_DC and F_AC, the latter two terms will not be independently considered. The signal recorded at any given pixel in a microscope image can therefore be simplified into the three components: donor emission, F_D, acceptor emission (not due to FRET), F_A, and acceptor emission due to FRET, F_T.

The following derivation will relate microscope images to the previously mentioned terms. Three images are considered, a FRET image, I_F, an acceptor image, I_A, and a donor image, I_D, defined in terms of the contributing fluorophores signals:

$$\begin{array}{l}{I}_F=F\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\\ I_A=F\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\\ I_D=F\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)+F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)+F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)\end{array}$$ (11)

Depending on the experimental conditions used, namely, the choice of fluorophores, excitation wavelengths, and emission filters, some of the terms in these three equations may go to zero. For example, Hoppe et al. [10] assumed

$$\begin{array}{l}{F}_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=0\\ F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=0\end{array}$$ (12)

since they selected fluorophores with minimal cross-talk in the one-photon excitation regime. For the purposes of this derivation, the most general case is considered and all terms are kept. This is necessary in the case of two-photon excitation, where the donor and acceptor have significant two-photon cross-section overlap. For example, the donor’s excited state can be populated upon excitation with the acceptor excitation pulse. Similarly, the donor emission channel may be contaminated with signal originating from acceptor emission. Finally, when FRET does occur, the F_D terms must accommodate the associated decrease in signal contribution from donor fluorescence. For these reasons, the relations in Eq. (12) are no longer valid.

The first step in the two-photon FRET stoichiometry derivation requires us to find an expression for f_A, the fraction of acceptor molecules in complex, in terms of microscope observables. We start with a modified two-photon excitation FRET efficiency [62]

$$E=\frac{{\sigma }_A\left({\lambda }_D^{\mathit{ex}}\right)}{{\sigma }_D\left({\lambda }_D^{\mathit{ex}}\right)}\left[\frac{F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}-1\right]\left(\frac{1}{f_A}\right)$$ (13)

where F_AD is the fluorescence from the acceptor in the presence of the donor and F_A is the fluorescence from the acceptor in the absence of the donor. The ratio of the acceptor and donor two-photon cross-sections at the donor’s excitation wavelengths will be referred to as γ throughout the derivation, $\gamma ={\sigma }_A\left({\lambda }_D^{\mathit{ex}}\right)/{\sigma }_D\left({\lambda }_D^{\mathit{ex}}\right)$. The term $F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ can be written as

$$F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right),$$ (14)

where this signal originates only from the acceptor. In an actual experiment, the acceptor channel will contain some donor emission that overlaps with acceptor emission channel. This is accounted for by rewriting $F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ in terms of the microscope image, I_F, resulting in the relationship

$$F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_F-F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right).$$ (15)

Since $F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ must also be expressed in terms of the images I_A, I_D, and I_F, we introduce the cross-talk constant β given by

$$\beta =\frac{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{I_F}{I_D}$$ (16)

relating the donor fluorescence detected at the acceptor emission wavelength relative to that detected at the donor wavelength emission (due to the dichroic splitting ratio). We can write the expression for $F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ in terms of microscope images with the relationship

$$F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=I_D-F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)-F_F\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right).$$ (17)

We define the constant, η, corresponding to the ratio

$$\eta =\frac{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{I_A}{I_N},$$ (18)

which accounts for how the dichroic mirror splits the acceptor fluorescence between the detection channels. Substituting η into Eq. (17), we find

$$F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=I_D-\frac{1}{\eta }{F}_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)-F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right).$$ (19)

Since the acceptor will fluoresce at the same wavelengths whether it is excited directly or via FRET, η can also be used to quantify how the F_T signal splits between detection channels with the relationship

$$\eta =\frac{F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}.$$ (20)

Substituting Eq. (20) into Eq. (19) results in

$$F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=I_D-\frac{1}{\eta }\left(F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\right).$$ (21)

Using Eq. (16), we can substitute Eq. (21) into Eq. (15) to obtain

$$F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_F-\beta I_D+\frac{\beta }{\eta }\left(F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\right).$$ (22)

From Eq. (14) we recognize the third term on the R.H.S. of Eq. (22) as $F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ to obtain the relationship for $F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ as

$$F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=\frac{I_F-\beta I_D}{1-\frac{\beta }{\eta }}.$$ (23)

Now we may turn our attention to solving $F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ in terms of microscope observables. First, the constant α is defined as

$$\alpha =\frac{F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}=\frac{I_F}{I_A}$$ (24)

similar to that in Hoppe’s theory. Using Eq. (11) for image I_A, we can rearrange the terms to arrive at the relationship

$$F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_A-F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)-F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right).$$ (25)

An additional constant, θ, is defined as

$$\theta =\frac{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}{F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}=\frac{F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)}{F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)},$$ (26)

which is the ratio of donor excitation (and hence fluorescence) obtained when excited with donor vs. acceptor excitation wavelength. Implementing θ in Eq. (25) yields the relationship

$$F_A\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_A-\frac{1}{\theta }{F}_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)-F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right).$$ (27)

Since FRET efficiency is independent of donor excitation wavelength, the constant θ also equals the ratio $F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)/F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$. Using this definition of θ and rearranging Eq. (14), we get

$$F_T\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=\frac{1}{\theta }{F}_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=\frac{1}{\theta }\left[F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)-F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\right].$$ (28)

Substituting Eq. (28) into Eq. (27) and using Eq. (24), Eq. (27) can be rewritten as

$$\frac{1}{\alpha }{F}_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_A-\frac{1}{\theta }\left[F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)+F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\right]+\frac{1}{\theta }{F}_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right).$$ (29)

Collecting terms common in $F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ and substituting Eq. (15) in Eq. (29), we get

$$F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=\frac{\theta \alpha }{\theta -\alpha }{I}_A-\frac{\alpha }{\theta -\alpha }{I}_F.$$ (30)

Having solved for both $F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ and $F_{\mathit{AD}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ in terms of image parameters, the FRET efficiency (Eq. (13)) may be expressed as

$$E=\gamma \left[\frac{\frac{\eta }{\eta -\beta }{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D}{\frac{\theta \alpha }{\theta -\alpha }{I}_A-\frac{\alpha }{\theta -\alpha }{I}_F}-1\right]\frac{1}{f_A}.$$ (31)

In its current state, Eq. (31) has three unknowns: E, γ, and f_A. Our technique requires a priori knowledge of the FRET efficiency E, which may be determined experimentally via FLIM measurements (as discussed in the previous section). The variable γ may then be solved for by imaging a sample containing only the donor-acceptor construct, and assigning f_A = 1. Once γ has been determined, our last unknown, f_A, can be determined for samples containing an unknown quantity of acceptor molecules in complex.

The next step in our derivation is to determine the fraction of donor in complex, f_D. In this case, we use an alternate equation for FRET efficiency based on the characteristic decrease in donor fluorescence,

$$E=\left[1-\frac{F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}{F_{\mathit{DO}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)}\right]\left(\frac{1}{f_D}\right).$$ (32)

Here, $F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ represents the signal from the donor in the presence of the acceptor, and $F_{\mathit{DO}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ represents the signal from the donor in the absence of the acceptor. These two terms must be defined in terms of images taken in the microscope. First, $F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ is defined by rearranging Eq. (11) for I_D to obtain

$$F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=F\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=I_D-F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)-F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$$ (33)

Using Eq. (14), Eq. (18), Eq. (20) and Eq. (23) to rewrite the last two terms of Eq. (33), we find

$$F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=\frac{1}{\eta -\beta }\left(\eta I_D-I_F\right).$$ (34)

Solving for $F_{\mathit{DO}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ is performed following the same protocol as the original one-photon FRET stoichiometry theory [10] using

$$F_{\mathit{DO}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)=F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)\xi +F_{\mathit{DA}}\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right),$$ (35)

where the constant ξ accounts for the fact that excitation was transferred from donor to acceptor which would otherwise have been emitted in the donor channel. Thus, ξ is a function of quantum yields of donor and acceptor as well as detection efficiencies of donor and acceptor detection channels and must be determined experimentally. While the last term is defined in Eq. (34), the first term, $F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$, is found by rearranging Eq. (11) for I_F resulting in

$$F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_F-F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)-F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right),$$ (36)

where expressions for $F_D\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ and $F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ are found using Eq. (16), Eq. (34) and Eq. (30). The resulting expression for $F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ is

$$F_T\left({\lambda }_D^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)=I_F\frac{\eta \theta -\beta \alpha }{(\theta -\alpha )(\eta -\beta )}-I_D\frac{\beta \eta }{\eta -\beta }-I_A\frac{\alpha \theta }{\theta -\alpha }.$$ (37)

Combining Eq. (34), Eq. (35) and Eq. (37) into Eq. (32) results in the FRET efficiency relation

$$E=\left[1-\frac{\frac{1}{\eta -\beta }\left(\eta I_D-I_F\right)}{\xi \left(\frac{\eta \theta -\beta \alpha }{(\theta -\alpha )(\eta -\beta )}{I}_F-\frac{\beta \eta }{\eta -\beta }{I}_D-\frac{\alpha \theta }{\theta -\alpha }{I}_A\right)+\frac{1}{\eta -\beta }\left(\eta I_D-I_F\right)}\right]\frac{1}{f_D}.$$ (38)

Imaging a sample containing only the donor-acceptor construct ensures f_D = 1, and knowing the FRET efficiency, E, the variable ξ can be determined. The last unknown, f_D, can then be determined for samples containing an unknown quantity of donor molecules in complex. Taking the initial one-photon assumptions, where $F_A\left({\lambda }_D^{\mathit{ex}}{\lambda }_D^{\mathit{em}}\right)$ and $F_D\left({\lambda }_A^{\mathit{ex}}{\lambda }_A^{\mathit{em}}\right)$ go to zero (see Eq. (12)), η and θ go to infinity and our relations for γ, ξ, f_A, and f_D converge to the one-photon theory.

The final stoichiometric quantity desired is R, the molar ratio of acceptor molecules to donor molecules. The ratio of the expressions for f_D and f_A result in the expression

$$R=\frac{f_D}{f_A}=\frac{[A_T]}{[D_T]}.$$ (39)