Validation of a Method to Accurately Correct Anterior Superior Iliac Spine Marker Occlusion

Abstract

Anterior superior iliac spine (ASIS) marker occlusion commonly occurs during three-dimensional (3-D) motion capture of dynamic tasks with deep hip flexion. The purpose of this study was to validate a universal technique to correct ASIS occlusion. 420ms of bilateral ASIS marker occlusion was simulated in fourteen drop vertical jump (DVJ) trials (n=14). Kinematic and kinetic hip data calculated for pelvic segments based on iliac crest (IC) marker and virtual ASIS (produced by our algorithm and a commercial virtual join) trajectories was compared to true ASIS marker tracking data. Root mean squared errors (RMSEs; mean ± standard deviation) and intra-class correlations (ICCs) between pelvic tracking based on virtual ASIS trajectories filled by our algorithm and true ASIS position were 2.3±0.9° (ICC=0.982) flexion/extension, 0.8±0.2° (ICC=0.954) abduction/adduction for hip angles, and 0.40±0.17N-m (ICC=1.000) and 1.05±0.36N-m (ICC=0,998) for sagittal and frontal plane moments. RMSEs for IC pelvic tracking were 6.9±1.8° (ICC=0.888) flexion/extension, 0.8±0.3° (ICC=0.949) abduction/adduction for hip angles, and 0.31±0.13N-m (ICC=1.00) and 1.48±0.69N-m (ICC=0.996) for sagittal and frontal plane moments. Finally, the commercially-available virtual join demonstrated RMSEs of 4.4±1.5° (ICC=0.945) flexion/extension, 0.7±0.2° (ICC=0.972) abduction/adduction for hip angles, and 0.97±0.62N-m (ICC=1.000) and 1.49±0.67N-m (ICC=0.996) for sagittal and frontal plane moments. The presented algorithm exceeded the a priori ICC cutoff of 0.95 for excellent validity and is an acceptable tracking alternative. While ICCs for the commercially available virtual join did not exhibit excellent correlation, good validity was observed for all kinematics and kinetics. IC marker pelvic tracking is not a valid alternative.

Introduction

Retro-reflective markers placed at the anterior superior iliac spine (ASIS) to model and track the pelvis during human movement motion analysis are commonly obstructed by upper extremities or subcutaneous tissue (McClelland et al. 2010). While alternative solutions, such as tracking the pelvis with anatomic iliac crest (IC) markers or computer-generated virtual ASIS marker trajectories exist, these methods are not validated. The purpose of this study was to validate an algorithm that accurately reconstructs occluded ASIS marker trajectories. Hip kinematics and kinetics were compared for pelvic tracking with virtual ASIS markers created by our algorithm, a commercially available function, and using IC markers.

Methods

1. Study Design

1.1 Validation of ASIS Virtual Fill Algorithm

Fourteen (n=14) DVJ trials with complete left and right ASIS, left and right IC, and sacrum (SAC) marker trajectories were selected to validate the algorithm (Hewett et al. 2005). Motion data was collected at 240 samples/s using a 12 camera motion analysis system (Raptor-12 cameras, Motion Analysis Corp, Santa Rosa, CA), with a three-dimensional (3-D) residual error of <0.50mm. Retro-reflective markers were adhered to the skin with double-sided tape using a modified Cleveland Clinic marker set, which includes markers at both ASIS and IC, and a marker at the L5-S1 joint (Figure 1). Peak hip flexion was identified using true marker data. ASIS data fifty frames before and after peak hip flexion were erased to mimic 420ms of marker occlusion. The proposed algorithm (SHPI Virtual Fill) was used to reconstruct ASIS marker trajectories. Virtual and anatomic ASIS markers were used separately to model the pelvis in Visual3D. Hip joint angles and moments were calculated for left and right thigh segments using inverse dynamics (Winter 1983).

Figure 1. Retro-Reflective Marker Location.

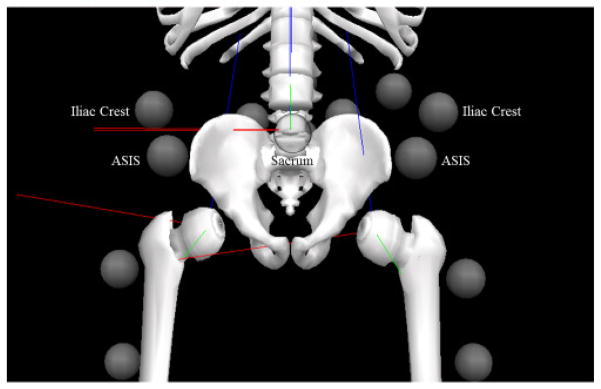
Location of all markers utilized by the proposed algorithm. The sacrum marker is located posteriorly on the skin at the L5-S1 junction.

1.2 Comparison to Standard ASIS Marker Obstruction Solutions

The same DVJ trials were utilized to study virtual ASIS and IC marker pelvic tracking reliability. In addition to SHPI ASIS Virtual Fill, a commercially available virtual fill algorithm was utilized to investigate virtual ASIS pelvic tracking (Cortex v4.1, Motion Analysis, Santa Rosa, CA). The same 420ms gaps were filled using the 3-Marker Virtual Join algorithm. Ipsi-lateral IC (IIC), contralateral IC (CIC), and SAC markers were designated as the origin, long-axis, and plane markers for this method, respectively. To study IC pelvic tracking, the pelvic segment was modified to track with IC markers instead of ASIS markers. Both alternative tracking methods were utilized to bilaterally calculate hip angles and moments, and these data were exported for statistical analysis.

2. ASIS Occlusion Correction Algorithm

The following algorithm utilizes 3-D rigid-body mechanics to virtually join ASIS trajectories (Marsh 2005). IIC, CIC, and SAC markers are used to estimate the location of the occluded ASIS marker for each frame, i. If one of these reference markers is also obstructed, the virtual ASIS trajectory is not created for that frame. The algorithm creates forward and backward solutions for a marker occlusion period starting at frame m and ending at frame n. Finally, a weighted average of the two solutions constructs the final projected virtual marker trajectory. The forward solution begins at m and utilizes ASIS trajectories in the previous frame, i−1, to create the new virtual ASIS marker at i. The reverse solution starts at n and utilizes ASIS location in the subsequent frame, i+1, to solve for the new virtual ASIS marker at i. The following derivation is for the forward solution but can be adapted to solve the backward system.

2.1 Definition of the Rigid-Body System

The rigid-body system is characterized by two reference vectors that originate at the IIC marker and terminate at the CIC ( $\overrightarrow{\text{IC}}$) and SAC ( $\overrightarrow{\text{IS}}$) markers (Figure 2. a). Vectors from IIC to the occluded ASIS ( $\overrightarrow{\text{IA}}$) are specified for the forward, m-1, and backward, n+1, solutions. The algorithm utilizes $\overrightarrow{\text{IA}}$ to estimate the change in distance between the IIC and ASIS markers throughout the period of ASIS marker occlusion.

Figure 2. Visualization of Rigid-Body System.

The algorithm employs rigid-body biomechanics to virtual join gaps in ASIS marker trajectories. a) The rigid-body system is defined. Two vectors that start at the centroid of the IIC marker and end at the centroids of the CIC and SAC markers are created ( $\overrightarrow{\mathit{IC}}$ and $\overrightarrow{\mathit{IS}}$, respectively). b) The translation of IIC, T_IIC, is tracked between each time point, i. c) The rotation of $\overrightarrow{\mathit{IC}}$ about the Z and Y is determined to find the pitch and yaw of the $\overrightarrow{\mathit{IC}}$ vector, ${\mathit{R}}_{{\overrightarrow{\mathit{IC}}}_{\mathit{Z},{\mathit{Y}}_{\mathit{i}}}}-{\mathit{R}}_{{\overrightarrow{\mathit{IC}}}_{\mathit{Z},{\mathit{Y}}_{\mathit{i}-\mathbf{1}}}}$. Next, the roll, R_SACi − R_SACi−1, of SAC about $\overrightarrow{\mathit{IC}}$ is calculated. d) Finally, the transformation matrix is generated, and the virtual ASIS marker is created at i.

2.2 Estimate Length of $\overrightarrow{\text{IA}}$ Throughout Period of Occlusion

The algorithm measures the difference in magnitude of $\overrightarrow{\text{IC}}$ and $\overrightarrow{\text{IS}}$ from their respective resting averages to their instantaneous length (length at i) to estimate the change in length of $\overrightarrow{\text{IA}}$ at each time step due to soft tissue artifact (STA). The resting average of each vector is calculated over the first 10 valid frames, where j is the first valid frame.

$$\overline{IA}=\frac{1}{10}\sum _j^{j+9}\Vert {\overrightarrow{IA}}_j\Vert ,\overline{IC}=\frac{1}{10}\sum _j^{j+9}\Vert {\overrightarrow{IC}}_j\Vert ,\overline{IS}=\frac{1}{10}\sum _j^{j+9}\Vert {\overrightarrow{IS}}_j\Vert$$ Eq. 1

Here, the first 10 frames were chosen to account for variations in distance between markers due to STA, but the number of frames utilized to calculate the resting average may be varied. Next, the difference, $\mathrm{\Delta }\Vert {\overrightarrow{IC}}_i\Vert$ and $\mathrm{\Delta }\Vert {\overrightarrow{IS}}_i\Vert$, between instantaneous magnitudes $\Vert \overrightarrow{\text{IC}}\Vert$ and $\Vert \overrightarrow{\text{IS}}\Vert$ and corresponding resting averages are determined for all occluded frames.

$$\mathrm{\Delta }\Vert {\overrightarrow{IC}}_i\Vert =\Vert {\overrightarrow{IC}}_i\Vert -\overline{IC},\mathrm{\Delta }\Vert {\overrightarrow{IS}}_i\Vert =\Vert {\overrightarrow{IS}}_i\Vert -\overline{IS}$$ Eq. 2

$\mathrm{\Delta }\Vert {\overrightarrow{IC}}_i\Vert$ and $\mathrm{\Delta }\Vert {\overrightarrow{IS}}_i\Vert$ are used to estimate the instantaneous magnitude of $\overrightarrow{\text{IA}},\Vert {\overrightarrow{\text{IA}}}_{{\text{EST}}_{\mathrm{i}}}\Vert$.

$$\Vert {\overrightarrow{IA}}_{{\mathit{EST}}_i}\Vert =\overline{IA}+\mathrm{\Delta }\Vert {\overrightarrow{IC}}_i\Vert -\mathrm{\Delta }\Vert {\overrightarrow{IS}}_i\Vert$$ Eq. 3

$\Vert {\overrightarrow{\text{IA}}}_{{\text{EST}}_{\mathrm{i}}}\Vert$ adjusted to maintain continuity of $\overrightarrow{\text{IA}}$ at the ends of the occlusion range. First, the difference between $\Vert {\overrightarrow{\text{IA}}}_{\text{EST}}\Vert$ and the anatomic lengths, ${\Vert \overrightarrow{IA}\Vert }_{m-1}$ and ${\Vert \overrightarrow{IA}\Vert }_{n+1}$, are determined at the marker occlusion period boundaries. Here, r refers to the length of the occlusion period, or n-m.

$$\mathrm{\Delta }\Vert {\overrightarrow{IA}}_m\Vert =\Vert {\overrightarrow{IA}}_{{\mathit{EST}}_1}\Vert -\Vert {\overrightarrow{IA}}_{m-1}\Vert ,\mathrm{\Delta }\Vert {\overrightarrow{IA}}_n\Vert =\Vert {\overrightarrow{IA}}_{{\mathit{EST}}_r}\Vert -\Vert {\overrightarrow{IA}}_{n+1}\Vert$$ Eq. 4

Finally, the length of $\overrightarrow{\text{IA}},\Vert {\overrightarrow{\text{IA}}}_{\mathrm{i}}\Vert$, is estimated for all frames that the anatomic ASIS marker is blocked. The algorithm subtracts a linear average of the difference between $\Vert {\overrightarrow{\text{IA}}}_{{\mathit{EST}}_i}\Vert$ and the occlusion period boundary magnitudes.

$$\Vert {\overrightarrow{IA}}_i\Vert =\Vert {\overrightarrow{IA}}_{{\mathit{TEMP}}_i}\Vert -\left[\frac{n-i}{r}\mathrm{\Delta }\Vert {\overrightarrow{IA}}_m\Vert +\frac{i-m}{r}\mathrm{\Delta }\Vert {\overrightarrow{IA}}_n\Vert \right]$$ Eq. 5

2.3 Creation of Transformation Matrix and Generate Forward and Backward Solutions

After $\Vert {\overrightarrow{IA}}_i\Vert$ is calculated for all obstructed frames, the algorithm creates transformation matrices comprised of:

1. IIC translation matrix, T_IICi, translates the system between time steps (Figure 2. b).

   $$T_{{\mathit{IIC}}_i}=\left[\begin{array}{c}{x}_{{\mathit{IIC}}_i}-x_{{\mathit{IIC}}_{i-1}}\\ y_{{\mathit{IIC}}_i}-y_{{\mathit{IIC}}_{i-1}}\\ z_{{\mathit{IIC}}_i}-Z_{{\mathit{IIC}}_{i-1}}\end{array}\right]$$ Eq. 6

2. $\overrightarrow{IC}$ rotation matrices, $R_{Z_{\overrightarrow{IC}}}$ and $R_{Y_{\overrightarrow{IC}}}$, align $\overrightarrow{IC}$ parallel with the X-axis (Figure 2. c).

3. $\overrightarrow{IS}$ rotation matrices, $R_{Z_{\overrightarrow{IS}}}$ and $R_{Y_{\overrightarrow{IS}}}$, are multiplied to create the SAC rotation matrix, R_SAC, that determines the roll of the SAC about $\overrightarrow{IC}$ between time steps (Figure 2. c).

A complete rotation matrix, R_i, estimates the rotation of the system between time steps.

$${\mathbf{R}}_{\mathit{i}}=R_{Z_{{\overrightarrow{IC}}_{i-1}}}^{-1}\ast R_{Y_{{\overrightarrow{IC}}_{i-1}}}^{-1}\ast R_{SA{C}_{i-1}}^{-1}\ast R_{SA{C}_i}\ast R_{Y_{{\overrightarrow{IC}}_i}}\ast R_{Z_{{\overrightarrow{IC}}_i}}$$ Eq. 7

Next, R_i and T_IICi are multiplied to construct the transformation matrix, T_i.

$${\mathbf{T}}_{\mathit{i}}={\mathbf{R}}_{\mathit{i}}\ast T_{{\mathit{IIC}}_i}$$ Eq. 8

Finally, the algorithm estimates the marker location at i for the forward solution (Figure 2. d). $\Vert {\overrightarrow{IA}}_i\Vert$ is normalized by $\Vert {\overrightarrow{IA}}_{i-1}\Vert$ to estimate the distance between IIC and ASIS at i.

$${\mathit{ASIS}}_i=\mathbf{T}\ast \frac{\Vert {\overrightarrow{IA}}_i\Vert }{\Vert {\overrightarrow{IA}}_{i-1}\Vert }\ast {\mathit{ASIS}}_{i-1}$$ Eq. 9

2.4 Weighted Average of Forward and Reverse Solutions

Once the algorithm creates the forward and backward solutions, a linear function assigns percentages to the forward (p_F) and backward (p_B) solutions.

$$p_{F_i}=1-\frac{i-1}{r},p_{B_i}=\frac{i-1}{r}$$ Eq. 10

The percentages from Eq. 10 are utilized to determine the virtual ASIS (ASIS_VF) trajectory from the forward (ASIS_F) and backward (ASIS_B) solutions.

$${\mathit{ASIS}}_{{VF}_i}=p_{F_i}\ast {\mathit{ASIS}}_{F_i}+p_{B_i}\ast {\mathit{ASIS}}_{B_i}$$ Eq. 11

3. Statistical Analysis

3.1 SHPI ASIS Virtual Fill Validation and Comparison to Alternate Solutions

Frontal and sagittal plane hip angle and moment root mean squared errors (RMSE) between pelvic segments based on the three alternative tracking methods and anatomic ASIS markers were calculated for each trial (Figures 3 and 4). Furthermore, one-way random single measures intra-class correlations (ICCs) between the alternative solutions and anatomic ASIS pelvic tracking were calculated for frontal and sagittal plane hip angles and moments. Given the sensitivity of biomechanical measures to marker location and the importance of precise biomechanical data, we considered an ICC greater than 0.95 to indicate excellent correlation (Ford K. R. 2007).

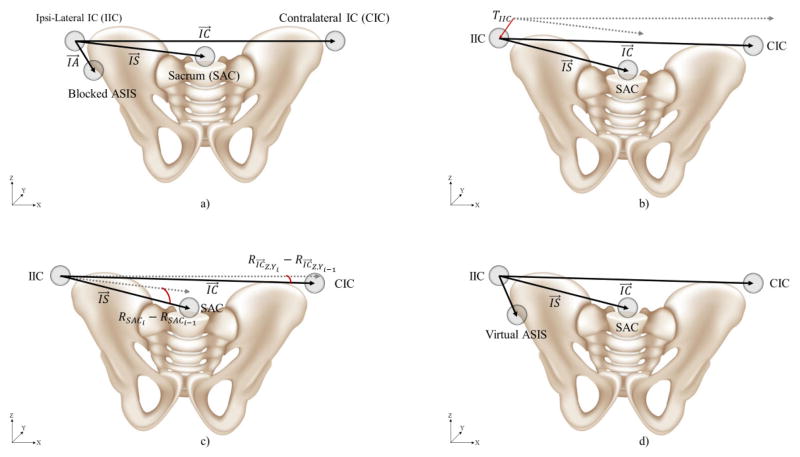
Figure 3. Frontal and Sagittal Plane Hip Angle RMSEs.

SHPI ASIS Virtual Fill, IC, and commercial software virtual fill pelvic tracking mean RMSEs with error bars representing the respective first standard deviation for frontal and sagittal plane hip angles. RMSEs for SHPI ASIS Virtual Fill, IC, and commercial software virtual fill pelvic tracking sagittal plane hip angles were 2.3±0.9°, 6.9±1.8°, and 4.4±1.5°, respectively. For frontal plane hip angles, RMSE values were 0.8±0.2°, 0.9±0.3°, and 0.7±0.2°.

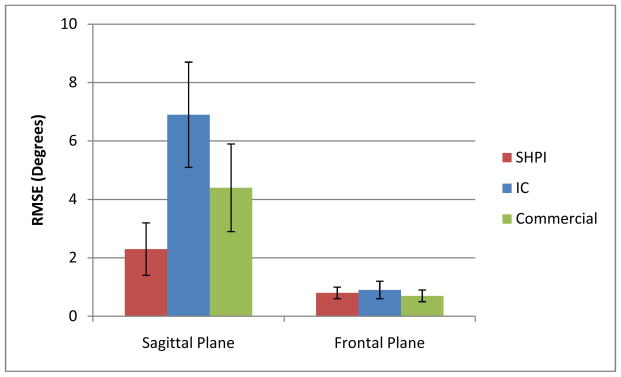
Figure 4. Frontal and Sagittal Plane Hip Moment RMSEs.

SHPI ASIS Virtual Fill, IC, and commercial software virtual fill pelvic tracking mean RMSEs with error bars representing the respective first standard deviation for frontal and sagittal plane hip moments. RMSEs for SHPI ASIS Virtual Fill, IC, and commercial software virtual fill pelvic tracking sagittal plane hip moments, RMSE values were 0.40±0.17 Nm, 0.31±0.13 Nm, and 0.97±0.62 Nm, respectively. For frontal plane hip moments, RMSE values were 1.06±0.36 Nm, 1.48±0.69 Nm, and 1.49±0.67 Nm.

3.2 Effects of Angle Magnitude and Frames from Closest Known ASIS Location

Linear regression between predicted and actual hip angle was used to study the effects of hip flexion angle on the accuracy of hip flexion calculated with SHPI ASIS Virtual Fill. The effect of the number of frames from closest known ASIS location was investigated. RMSEs and standard deviation of absolute error was calculated (Figure 5). The frame of maximum RMSE was noted, and the RMSEs and standard deviations were graphed by frame number.

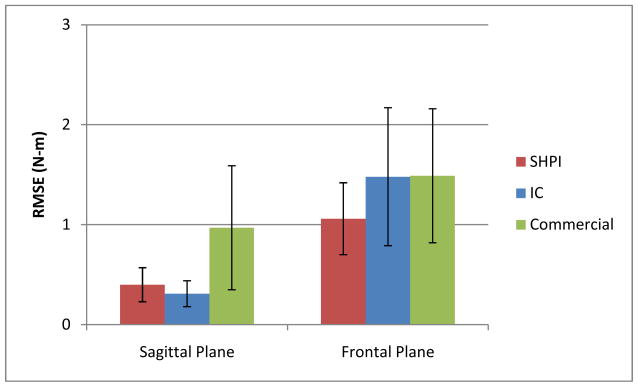
Figure 5. SHPI ASIS Virtual Fill Pelvic Tracking Hip Flexion Dependence on Frames from Closest Known ASIS Position.

Mean RMSE at each frame across all trials with error bars representing the first standard deviation for hip flexion angle. Two peaks are observed at 33 (3.0±2.2°) and 84 (3.0±2.0°) frames after the last known ASIS location.

Results

1. SHPI ASIS Virtual Fill Validation and Comparison to Standard ASIS Marker Obstruction Solutions

The SHPI virtual ASIS tracked hip angle RMSEs were 2.3±0.9° for sagittal plane and 0.8±0.2° for frontal plane (Table 1). RMSEs for SHPI virtual ASIS method sagittal and frontal plane hip moments were 0.40±0.17 Nm and 1.06±0.36 Nm, respectively (Table 2). ICCs for SHPI ASIS Virtual Fill pelvic tracking hip values were 0.982 for sagittal plane angles, 0.954 for frontal plane angles, 1.000 for sagittal plane moments, and 0.998 for sagittal plane moments.

Table 1. Statistical Analysis of Hip Angles Calculated for Various Pelvic Tracking Methods.

Mean RMSE plus or minus standard deviation and ICC values for angles in the frontal and sagittal plane for all three pelvic tracking methods.

	Angles
	SHPI Virtual Fill		IC Pelvic Tracking		Commercial Virtual Fill
	Sagittal	Frontal	Sagittal	Frontal	Sagittal	Frontal
RMSE	2.30±0.86°	0.85±0.19°	6.91±1.80°	0.85±0.33°	4.39±1.54°	0.65±0.23°
ICC	0.982	0.954	0.888	0.949	0.945	0.972

Table 2. Statistical Analysis of Hip Moments Calculated for Various Pelvic Tracking Methods.

Mean RMSE plus or minus standard deviation and ICC values for moments in the frontal and sagittal plane for all three pelvic tracking methods.

	Moments
	SHPI Virtual Fill		IC Pelvic Tracking		Commercial Virtual Fill
	Sagittal	Frontal	Sagittal	Frontal	Sagittal	Frontal
RMSE	0.40±0.17 Nm	1.06±0.36 Nm	0.31±0.13 Nm	1.48±0.69 Nm	0.97±0.62 Nm	1.49±0.67 Nm
ICC	1.000	0.998	1.000	0.996	1.000	0.996

Anatomic IC pelvic tracking hip angle RMSEs were 6.9±1.8° and 0.8±0.3° for sagittal and frontal plane, respectively (Table 1). Hip moment RMSEs were 0.31±0.13 Nm in the sagittal plane and 1.48±0.69 Nm in the frontal plane (Table 2). ICCs for IC pelvic tracking hip values were 0.888 for sagittal plane angles, 0.949 for frontal plane angles, 1.000 for sagittal plane moments, and 0.996 for sagittal plane moments. Hip angle RMSEs were 4.4±1.5° and 0.7±0.2° for sagittal and frontal plane, respectively, for pelvic tracking based on virtual ASIS markers created by a commercially available software algorithm (Table 1). Hip moment RMSEs were 0.97±0.62 Nm in the sagittal plane and 1.49±0.67 Nm in the frontal plane (Table 2). ICCs for the commercial software virtual ASIS pelvic tracking were 0.945 for sagittal plane angles, 0.972 for frontal plane angles, 1.000 for sagittal plane moments, and 0.996 for sagittal plane moments.

2. Effects of Angle Magnitude and Frames from Closest Known ASIS Location

The linear regression R²-value for predicted hip flexion angle and respective absolute error was 0.228. Peak values for RMSE by frame were 3.1±2.2° and 3.0±2.0° and occurred at frame 33 and 84 of ASIS marker occlusion, respectively (Figure 5).

Discussion

Hip angles and moments calculated for SHPI ASIS Virtual Fill pelvic tracking demonstrated excellent validity (r > 0.95) in the sagittal and frontal planes. The commercial software virtual fill demonstrated excellent correlation for frontal plane hip angles and frontal and sagittal plane hip moments. ICCs for frontal and sagittal plane moments indicated excellent correlation between anatomic ASIS and IC pelvic tracking. However, ICCs for IC pelvic tracking hip angles were less than 0.95. In addition, the RMSE of 6.91±1.80° for sagittal hip angles was the greatest for all calculated angles. Therefore, the use of an IC pelvic tracking is not suggested.

Two distinct RMSE peaks (3.1° at 33 frames and 3.0° at 84 frames) were observed over the period of simulated ASIS occlusion. We postulated that the greatest absolute error would be observed at 50% of the occlusion period, near peak hip flexion. However, the two distinct peaks indicate the greatest absolute errors closer to 25% and 75% of the obstructed period. Further investigation may improve averaging of the forward and backward solutions. Finally, the linear regression analysis of the effects of hip flexion angle on absolute error indicated a weak correlation between error and hip flexion angle (R² = 0.228).

While this study validates the proposed virtual join for ASIS marker trajectories, the effects of body mass index (BMI) and excess soft tissue on virtual marker reliability should be explicitly investigated. STA may produce over 40 mm difference between anatomic and skin marker location. Therefore, motion capture of individuals with more soft tissue mass likely produces less accurate hip angles and moments due to increased STA (Cappozzo et al. 1996; Akbarshahi et al. 2010). Another limitation is the SHPI ASIS Virtual Fill requires complete IIC, CIC, and SAC marker data to create the virtual ASIS. Without one of these markers, the proposed algorithm cannot estimate the location of an occluded ASIS. Finally, this study explored occlusions of 420ms, but soft tissue and upper extremities may block the ASIS markers for longer periods.

Future studies will explore the application of virtual join methods to subjects with greater soft tissue mass. BMI may affect the reliability of virtual fill algorithms, so the accuracy of virtual ASIS markers for various body types must be investigated. In addition, a valid virtual fill range should be determined that maintains excellent correlation between biomechanical values calculated for virtual and anatomic ASIS markers. This virtual join will also be tested on other commonly obstructed markers.