Automated Tumor Volumetry Using Computer-Aided Image Segmentation

Abstract

Rationale and Objectives

Accurate segmentation of brain tumors, and quantification of tumor volume, is important for diagnosis, monitoring, and planning therapeutic intervention. Manual segmentation is not widely used because of time constraints. Previous efforts have mainly produced methods that are tailored to a particular type of tumor or acquisition protocol and have mostly failed to produce a method that functions on different tumor types and is robust to changes in scanning parameters, resolution, and image quality, thereby limiting their clinical value. Herein, we present a semiautomatic method for tumor segmentation that is fast, accurate, and robust to a wide variation in image quality and resolution.

Materials and Methods

A semiautomatic segmentation method based on the geodesic distance transform was developed and validated by using it to segment 54 brain tumors. Glioblastomas, meningiomas, and brain metastases were segmented. Qualitative validation was based on physician ratings provided by three clinical experts. Quantitative validation was based on comparing semiautomatic and manual segmentations.

Results

Tumor segmentations obtained using manual and automatic methods were compared quantitatively using the Dice measure of overlap. Subjective evaluation was performed by having human experts rate the computerized segmentations on a 0–5 rating scale where 5 indicated perfect segmentation.

Conclusions

The proposed method addresses a significant, unmet need in the field of neuro-oncology. Specifically, this method enables clinicians to obtain accurate and reproducible tumor volumes without the need for manual segmentation.

Quantification of tumor volume has become increasingly important for diagnosis, staging, assessment of therapy response, and more recently determination of eligibility for clinical trial enrollment (1–3). Currently, assessment of tumor volume is based on two-dimensional (2D) measurements, using standards such as the MacDonald criteria (4) for gliomas, Herscovici criteria (5) for meningiomas, or the RECIST standards for general oncology (6).

These criteria allow clinicians to obtain a rough estimate of tumor volume by sacrificing accuracy for speed. An accurate measurement of tumor volume, however, requires a complete segmentation of the tumor. This type of segmentation, which can currently be performed manually, requires a tremendous amount of time and hence is not widely used. Thus, automation of tumor segmentation represents an important clinical need that would be invaluable for treating and monitoring patients with brain tumors. Furthermore, such automatic segmentations are likely to be more reproducible and therefore preferable over manual segmentations because of their consistency, which is especially important for longitudinal tumor monitoring.

The neuroimaging community has attempted to address the need for automatic tumor segmentation over the past two decades. The earliest methods included the use of fuzzy clustering-based approaches (7,8). Direct application of such methods leads to a large number of false-positive voxels labeled as tumors. Later methods based on level sets and active contours (9,10) often fail in the context of aggressive tumors harboring significant structural complexity. Machine-learning–based methods have been fairly successful at the task of tumor segmentation (11–21). However, these methods are often tumor type specific and very sensitive to changes in noise and acquisition protocol. Additionally, there is a constant need for retraining with most learning-based methods when there is a slight change in the imaging protocol or if the scanning site changes. Furthermore, many of these methods are based on complex algorithms that are expensive to reimplement and difficult to integrate into existing clinical workflows. Finally, most of these methods have been validated in a narrow and limited research setting and not necessarily in a clinical setting. In general, the narrow focus of previously described techniques has prevented their widespread utilization in the clinical arena.

In this work, we present a novel tumor segmentation technique that is semiautomatic, fast, and based on a relatively simple learning-free algorithm. We have validated our method on three different tumor types acquired under a diverse set of image acquisition protocols and resolutions and drawn from studies using different preprocessing steps. Qualitative and quantitative results present the efficacy of the proposed method in the presence of substantial noise, scanner variation, processing variation, and tissue (tumor) heterogeneity.

MATERIALS AND METHODS

Institutional review board approval was obtained for this study with waiver of informed consent for retrospective review of medical records. All imaging data came from patients treated at the Hospital of the University of Pennsylvania. In general, these imaging studies contained differences between cases in terms of resolution, noise level, and pixel spacing. Overall, our data set contained images of 24 glioblastomas, 15 meningiomas, and 15 metastatic brain tumors. T1 contrast-enhanced images were available for all tumors and were used for automatic and manual segmentations.

The data used in this project varied across cases in terms of acquisition protocol, resolution, and pixel spacing. It was sequentially chosen. Some of the data came from a 3.0-T magnetic resonance (MR) imaging scanner systems (Siemens and GE Healthcare) and some of it came from a 1.5-T systems. Similarly, the pixel spacing varied from 0.42 × 0.42 to 0.97 × 0.97, and image dimensions varied between 256 × 256 to 512 × 512. Slice thicknesses during acquisitions varied between 1 and 5 mm. The echo times and repetition times involved in computing the T1 images also varied. This was a retrospective study, and we used a random sample of cases available on the internal University of Pennsylvania Picture Archiving and Communication System.

Thus, there was tremendous variation between cases with respect to noise and inhomogeneity. The segmentation results presented here are testimony to that the proposed method is able to successfully segment these brain tumors in spite of the considerable variation in the underlying data.

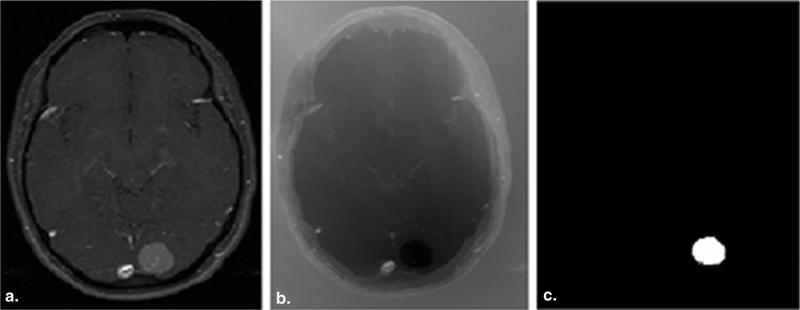
We use the adaptive geodesic algorithm described by Gaonkar and Shu (22) to segment brain tumors. This is a semiautomatic method that was originally devised to segment the vertebral column on computed tomographic images using the adaptive geodesic distance (23,24). The method is fast, easy to use, and robust to noise and bias. A seed region is placed by the clinician inside a tumor, and the segmentation algorithm is initiated. The “adaptive geodesic distance” is a mathematical measure that may be computed at any voxel within the image. At a given voxel, this measure provides a joint quantification of 1) the spatial distance of the voxel from the seed region and 2) the variation of the image intensity profile between the voxel and the seed, both of which are important clues for tumor segmentation The algorithm computes the adaptive geodesic distance at every voxel in the image to yield an “adaptive geodesic distance transform image.” This transformed image appears as a geodesic distance–weighted inverse of the original MR image (Fig 1b) and thresholding of this image generates the final segmentation mask. Because of the computational efficiency of this approach, the “adaptive geodesic transform image” can be performed in a matter of seconds. A detailed explanation of the algorithm and the associated intuition is provided in the following.

Figure 1.

(a) Original T1CE image with meningioma, (b) the geodesic transform generated using a seed placed inside the tumor, (c) and final segmentation generated by thresholding geodesic map.

Geodesics are the generalization of straight lines to curved spaces. The pedagogic example of a geodesic is given in relation to the earth's surface. If one were to travel along a straight line from the North Pole to the South Pole, one would have to burrow through the earth's core to travel. It is much easier to make this journey over the surface of the earth. In this case, the distance traveled along the earth's surface is the geodesic distance which is considerably larger than the straight line distance between the poles.

To apply the concept of geodesic distances to image segmentation, we can imagine the intensity profile of a 2D image to define a surface in 3D space. The geodesic distance between two points is the shortest path between the two points as measured while moving along the surface.

Given an initial voxel (or set of voxels) inside the tumor, we can compute the geodesic distance to this point (or set of points) from every other voxel in the image. This allows for the construction of a geodesically transformed image whose voxel intensities are the geodesic distances from the initially picked voxel. Geodesic segmentation then involves segmentation of the geodesically transformed image by thresholding.

For nonheterogeneous solid tumors such as meningiomas, direct application of the aforementioned geodesic segmentation technique is sufficient. The geodesic distance described by Criminisi (23) is still based on a metric that is locally dependent on image gradients alone. To adapt the technique to segment more complex and heterogeneous tumors such as glioblastomas, we need to locally vary the metric on the basis of prior knowledge. This leads to the adaptive geodesic distance which we used to segment all tumors in the paper.

The naive computation of the geodesic distance transform would entail visiting every voxel and computing the geodesic distance using a discretized form of the Euler–Lagrange equations. Mathematically, this involves solving the minimization:

$$d(x,x^{\prime })=\underset{P_{\{x,x^{\prime }\}}}{\min }{\int }_{u=x}^{u=x^{\prime }}\sqrt{1+\gamma \nabla I\left(u\right)}du$$

Where I denotes a gray-scale image defined over a 3D domain Ω and locations in the image domain are indicated by x∈Ω. M is the initial set of user provided voxels inside the tumor with x′∈M. Further, P(x; x′) denotes the set of all possible paths between x and x′, and u parameterizes a specific path in P. γ is a gradient weighting factor which may be used to incorporate prior information if needed. Solving the minimization at every voxel would be computationally intensive to the point of being impractical. Fortunately, there is a computational shortcut described in detail by Toivanen (1996) which makes the computation efficient by visiting each voxel twice.

Note that the aforementioned formulation includes the constant γ which enforces a distance metric locally dependent on image gradients alone. To incorporate prior information regarding a specific object into the segmentation, we can modify the definition of the distance to a spatially adaptive:

$$d(x,x^{\prime })=\underset{P\{x,x^{\prime }\}}{\min }{\int }_{u=x}^{u=x^{\prime }}\sqrt{1+\Gamma \left(x\right)\nabla I\left(u\right)}du$$

Thus, the metric is now dependent not only on image gradients but also on Γ(x) which we initialize to low values in the enhancing tumor and vasculature and high values elsewhere. This tells the method that the enhancing parts are more likely to be tumor than the nonenhancing regions around them. The adaptive geodesic transform may be computed in two raster passes over the image domain in a fashion similar to the geodesic distance itself.

In summary, segmentation of brain tumors from MR images performed in this study involves 1) manually initializing a small skeletal region inside the tumor on the contrast-enhanced T1-MR input image, 2) obtaining an adaptive geodesic transform of the input image with respect to the initialization using the procedure outlined by Gaonkar and Shu (22), and (3) thresholding the adaptive geodesic transform obtained in step 2 to get the final tumor segmentation mask.

Instructions for Initialization Initialization of Automatic Method by Operators

The main instructions that were given to operators initializing the automated segmentation algorithm were 1) if the tumor contained necrotic tissue, the initializations must lie completely inside the necrotic region of a tumor and 2) if there was no necrosis, the initialization should lie fully inside the enhancing tumor. We required that the initialization be either be a point or a small region containing neighboring points inside the tumor. We explicitly prohibited initializations provided in a manner such that they crossed the border between necrosis/enhancing tissue/edema. In the case of multifocal tumors, the method expects multifocal initializations as well.

Instructions Given to Manual Raters and Experts Delineating Tumors in Images

Objective evaluation of the segmentation involved comparison of the computer-generated segmentation map with manually delineated tumor volumes and diameters for all 54 tumors. Manual segmentation was performed by two experienced physicians (M.B. and M.S.S.).

We asked the physicians doing the manual segmentations to delineate the enhancing region of the tumor and the necrosis only. The edema was to be left out of the manual segmentation process. The tools used in the manual segmentation process allowed the physicians to draw a simple tumor mask by going through the T1CE and T1 images in a slice by slice fashion. Volume and diameter measurements based on manual and semiautomatic methods were compared for each tumor type separately.

Subjective Evaluation of the Automated Segmentation Method

Subjective evaluation by three physicians (M.A.A., Z.S.A., and L.M.) involved rating the computer-generated tumor segmentations on a scale from 1 (unacceptable) to 5 (perfect) segmentation. A rating of 5 was given by the physician when the semiautomatic method labeled all or almost the entire tumor correctly and did not produce any false-positive labeling. When the segmentation produced overshot the actual tumor significantly or when there was gross undersegmentation of the tumor, the ratings were subsequently reduced.

Objective Comparison of Automatic Segmentation to Manual Segmentation Using the Dice Ratio

The Dice measure of overlap (25) provides a formal way to evaluate overlap between two segmentations. Formally, if S_a and S_m are the automatic and manual segmentations for a given tumor and $S_a\cap S_m$ is the overlap between the two, then the dice ratio is defined as:

$$Dice=\frac{2V(S_a\cap S_m)}{V\left(S_a\right)+V\left(S_m\right)}$$

Where V (·) defines the volume of the relevant object. The closer a Dice ratio is to one, the more the overlap between the manual and automatic segmentation. A Dice ratio of zero implies no overlap between the automatic and manual segmentations. In practice, the Dice ratios usually lie somewhere in the middle of these two extremes.

RESULTS

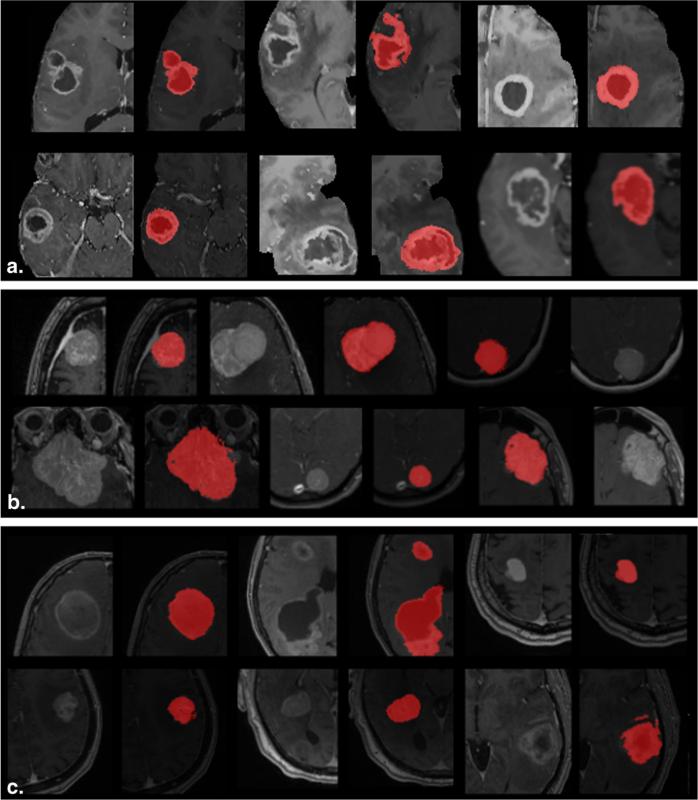
A visual representation of the segmentations generated by the proposed technique is shown in Figure 2. The figures show a representative section of an axial slice through each tumor on a T1 contrast-enhanced MR image. All three tumor types segmented as a part of this study are shown in the figure. Although the figure shows only one slice, the adaptive geodesic distance transform and the segmentation map were computed over the entire 3D tumor volume. As seen from Figure 2, all three types of tumors are adequately delineated by the proposed technique.

Figure 2.

Segmentations generated by our technique for (a) glioblastomas, (b) meningiomas, and (c) brain metastasis.

As outlined in the methods, qualitative validation was based on physician ratings (out of 5) provided by three experts. Table 1 summarizes the ratings provided by each of our three raters for all three tumor types included in this study. The overall mean across raters was 4.1 for glioblastomas, 4.6 for meningiomas, and 4.2 for brain metastasis segmentations. The slightly less values for glioblastomas are consistent with the fact that these tumors are heterogeneous and extremely challenging to segment, manually or semiautomatically. Meningiomas, on the other hand, are relatively homogeneous and therefore comparatively easier to segment.

TABLE 1.

Expert Rating of Tumor Segmentations

	Average Rating
Tumor	Rater 1	Rater 2	Rater 3
Glioblastoma	4.3 (±0.9)	4.2 (±1.0)	3.7 (±1.2)
Meningioma	4.6 (±0.6)	4.5 (±0.7)	4.7 (±0.5)
Metastasis	4.4 (±0.8)	4.0 (±1.0)	4.2 (±1.0)

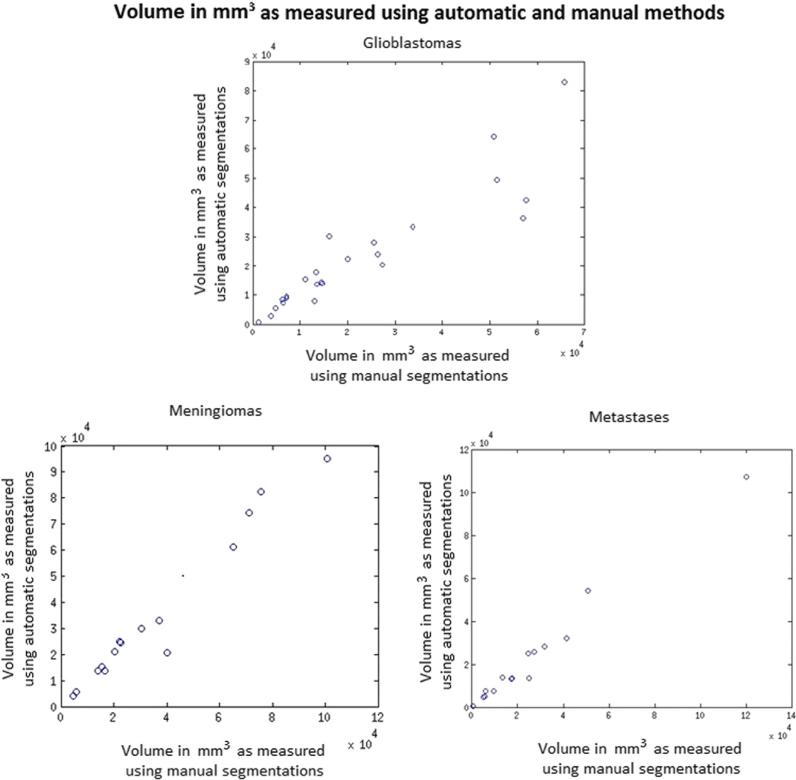
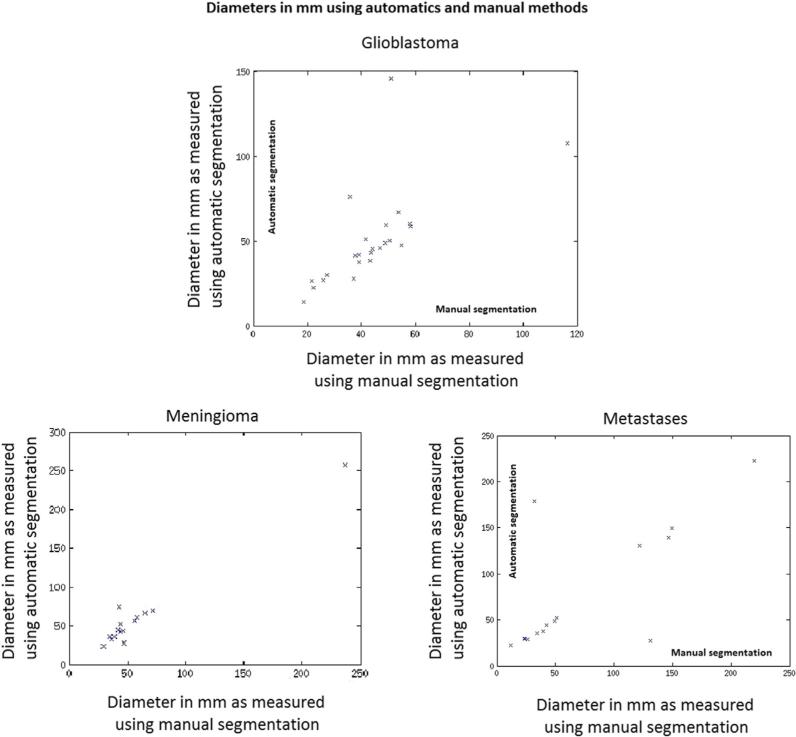
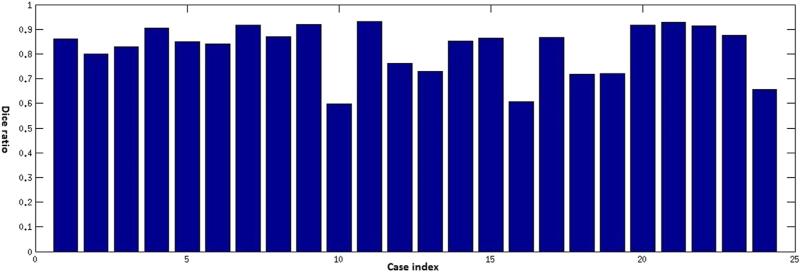
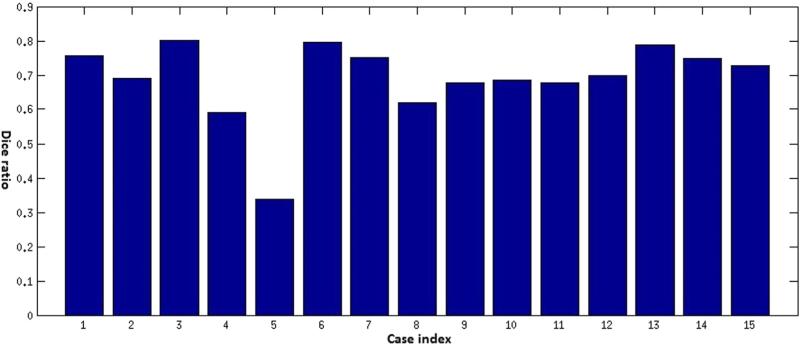
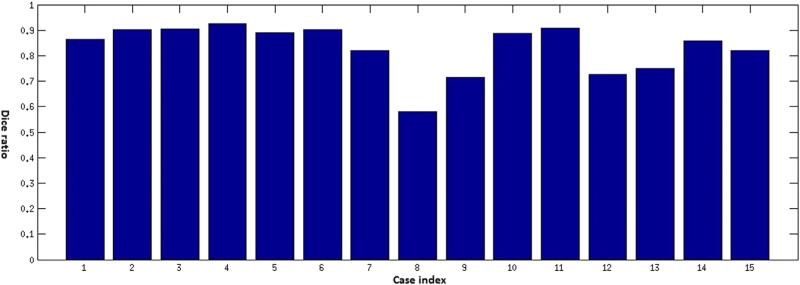
Traditionally, the most frequently used and important measures for characterizing human brain tumors included maximum diameter and volume, respectively. A quantitative evaluation comparing tumor diameters and volumes as measured by human experts versus computer-aided methods is critical for validation of the proposed methodology. A visual summary of these comparisons is presented in Figures 3 and 4. The Dice ratio, a quantitative measure of overlap between the manual and the automatic segmentations, is shown in Figures 5–7. The mean Dice ratios for the glioblastoma, meningioma, and metastases are 0.82, 0.83, and 0.69, respectively.

Figure 3.

Comparison of volumes of tumors computed using the automatic and manual methods. The size of the green circles represent volumes computed using manual segmentations and size of blue circles represent volumes computed using automatic segmentations.

Figure 4.

Comparison of diameters (in mm) of tumors computed using the automatic and manual methods. The height of the green bars represents diameters computed using manual segmentations and the height of the blue bars represents diameters computed using automatic segmentations.

Figure 5.

Dice ratios comparing automatic and manual segmentation of glioblastoma multiforme cases.

Figure 7.

Dice ratios comparing the automatic and manual segmentation of brain metastases cases.

DISCUSSION

Automated segmentation of brain tumors is a problem that has received substantial attention in the medical image analysis community over the last decade. Despite a substantial body of literature, a method that can segment different types of brain tumors in a clinical setting has remained elusive. A considerable proportion of proposed segmentation methods require specialized preprocessing. Additionally, computational time associated with some of these methods is significant enough that it prevents efficient clinical use. Furthermore, methods that are highly efficient and accurate are also tumor type specific and do not generalize well.

In this work, we present a semiautomated method for complete lesion segmentation for application in neuro-oncology. The outlined methodology represents a significant advancement over currently available segmentation tools available to clinicians. From a technical standpoint, the described methodology is computationally efficient and hence does not require any special computer hardware to run, it likewise does not require any image preprocessing, and remains insensitive to scanner parameters. Most importantly, this approach does not require any retraining or adjustment on the basis of tumor type and hence generalizes well to all the common pathology seen in neuro-oncology.

Our analysis demonstrates that this methodology produced segmentation results that are on par with a manual segmentation performed by a radiologist. We have validated the proposed method on data acquired under a diverse set of clinical imaging protocols. Although the inhomogeneity bias and noise level of our data varied significantly, we were able obtain segmentations results that were in line with physician expectations and equivalent to that of a manual segmentation. This suggests an inherent robustness of the algorithm to variation of these factors, rendering the methodology suitable for clinical application.

Furthermore, our implementation is also significantly simpler to use by a clinician. In contrast to current techniques for obtaining a complete segmentation map, the methodology described only requires the operator to select a couple of points located within the tumor boundary. The algorithm subsequently uses these initializing points to perform the analysis and produces a complete segmentation map, along with a computed tumor volume. This is obviously significantly faster and less labor intensive than performing a slice-by-slice manual segmentation and much more accurate than measuring the maximal diameter of a tumor. We feel these advantages are especially important for adoption of this methodology into a clinical workflow.

Volumetric analysis of tumors has been repeatedly shown to be much more accurate and reproducible than 1D or 2D methods (26–30). It has been shown that using a semiautomatic procedure increased consistency and sensitivity in detecting subtle tumor growth (27). Others have shown that accurate computer-aided volumetric analyses have a significant impact on assessment of tumor response to therapy, compared to 2D methods (27,29). Although the RECIST criteria advocate the use of 1D and 2D measurements for determining therapy response and quantifying disease progression, Warren et al. have shown that there is substantial discordance between these metrics when 1D or 2D methods are used, compared to a 3D volumetric assessment.

Hence, although more accurate, sensitive, and reproducible, the adoption of volumetric criteria in neuro-oncology has been limited by the availability of a methodology that was efficient and generalized well, independent of tumor type or scanner parameters. In this work, we present a computer-aided segmentation method that fulfills these criteria. Although the results presented here focus primarily on brain tumors, the method may be extended to and used for the segmentation of other large solid tumors as well. Likewise, because the algorithm is extremely fast, one could potentially use this methodology for real-time tumor tracking during invasive procedures such as thermal ablation or cryoablation (31).

The chief limitation of this method is the dependence of the segmentation on a manual initialization. The method depends on an experienced clinician to provide the small set of initial voxels that drive subsequent computation. If some of this initialization crosses the tumor boundary, the method will fail. Furthermore, in case of multifocal tumors, one needs to provide multiple initializations. Consequently, multifocal tumors require more clinician time as compared to unifocal ones. A secondary limitation associated with this method is that it will not operate in the presence of motion artifacts. Motion artifacts introduce undulatory imaging patterns that throw off the computation of the adaptive geodesic distance. Addressing each of these limitations is outside the scope of the present work.

Three-dimensional volumetric tumor analysis has always been clinically desirable, and image segmentation represents the closest assessment of the actual tumor size and volume. Being able to accurately assess tumor volume has important implications for both the diagnosis and management of patients with brain malignancies. The outlined methodology addresses this unmet clinical need for a segmentation technique that is robust to variation in image quality and tumor type. Going forward, we hope that the ease of use of described approach will lead to rapid clinical adoption. This change, from 1D to 3D calculation of tumor volume, growth, and response to treatment will have important implications in clinical and research applications.

MATLAB and C++ codes associated with this method are freely available at http://cbica.upenn.edu/Bilwaj.Gaonkar/tumor_segmentation.zip.

Figure 6.

Dice ratios comparing automatic and manual segmentation of meningioma tumor cases.