Abstract
Arteries can buckle axially under applied critical buckling pressure due to a mechanical instability. Buckling can cause arterial tortuosity leading to flow irregularities and stroke. Genetic mutations in elastic fiber proteins are associated with arterial tortuosity in humans and mice, and may be the result of alterations in critical buckling pressure. Hence, the objective of this study is to investigate how genetic defects in elastic fibers affect buckling pressure. We use mouse models of human disease with reduced amounts of elastin (Eln+/−) and with defects in elastic fiber assembly due to the absence of fibulin-5 (Fbln5−/−). We find that Eln+/− arteries have reduced buckling pressure compared to their wild-type controls. Fbln5−/− arteries have similar buckling pressure to wild-type at low axial stretch, but increased buckling pressure at high stretch. We fit material parameters to mechanical test data for Eln+/−, Fbln5−/− and wild-type arteries using Fung and four-fiber strain energy functions. Fitted parameters are used to predict theoretical buckling pressure based on equilibrium of an inflated, buckled, thick-walled cylinder. In general, the theoretical predictions underestimate the buckling pressure at low axial stretch and overestimate the buckling pressure at high stretch. The theoretical predictions with both models replicate the increased buckling pressure at high stretch for Fbln5−/− arteries, but the four-fiber model predictions best match the experimental trends in buckling pressure changes with axial stretch. This study provides experimental and theoretical methods for further investigating the influence of genetic mutations in elastic fibers on buckling behavior and the development of arterial tortuosity.
Keywords: elastin, fibulin-5, mechanics, tortuosity
1. Introduction
Recent studies have demonstrated that long cylindrical arteries may lose mechanical stability and buckle into curved or tortuous shapes (Han 2008; Rachev 2009). Arterial buckling depends on the applied pressure, axial stretch, residual stress, wall geometry, and wall mechanical properties. Arterial buckling can cause tortuosity, increased resistance to flow, kinking, and even occlusion. Severely kinked and tortuous arteries are associated with aging, atherosclerosis, diabetes, hypertension and genetic diseases (Han 2012). Genetic mutations in elastic fiber proteins are associated with tortuosity of the large conducting arteries in humans (Urban and Davis 2014) and mice (Yanagisawa et al. 2002; Wagenseil et al. 2009).
Genetically-modified mice with elastic fiber defects present an opportunity to determine how combined changes in wall mechanical properties, geometry, residual stress, and in vivo axial stretch affect critical buckling pressure and the development of tortuosity in models of human disease. Decreased amounts of elastic fibers in elastin haploinsufficient mice (Eln+/−) or disrupted elastic fibers in fibulin-5 null mice (Fbln5−/−) cause high blood pressure, increased arterial stiffness, and decreased in vivo arterial axial stretch ratios (Yanagisawa et al. 2002; Faury et al. 2003; Wagenseil et al. 2005; Wan et al. 2010), but it is not known how these factors affect critical buckling pressure.
Using Fung (Chuong and Fung 1986) or four-fiber (Holzapfel et al. 2000; Gleason et al. 2008) strain energy functions to describe arterial mechanical behavior, theoretical models have been developed to investigate buckling in porcine arteries after collagenase treatment (Martinez and Han 2012), after elastase treatment (Lee et al. 2012), and as a function of material parameters and residual strain (Liu et al. 2014). Theoretical models have not been used to predict results in mouse arteries with defects in elastic fiber proteins that model human disease. Hence, the objectives of this study are to 1) determine the effects of reduced amounts of functional elastic fibers on the experimental critical buckling pressure in genetically-modified mouse arteries and 2) compare the experimental values to theoretical buckling pressures calculated from Fung and four-fiber strain energy functions fitted to biaxial experimental data.
2. Materials and methods
2.1 Animals
Male mice haploinsufficient for the elastin gene (Eln+/−) and their wild-type littermates (Eln+/+) (Li et al. 1998), and mice lacking the fibulin-5 gene (Fbln5−/−) and their wild-type littermates (Fbln5+/+) (Budatha et al. 2011) were used between 2 – 3 months old. Littermates were used as controls because Eln and Fbln5 mice are in different genetic backgrounds (C57Bl6 and mixed, respectively). All protocols were approved by the Institutional Animal Care and Use Committee. Mice were sacrificed by CO2 inhalation, then the right and left carotid arteries were removed, placed in physiological saline solution (PSS), stored at 4° C, and used for mechanical tests within three days (Amin et al. 2011). Mechanical tests were performed with each carotid mounted in a pressure myograph system (Danish Myotechnology) in PSS at 37° C (Wagenseil et al. 2005). Separate arteries were used for experimental determination of critical buckling pressure and biaxial mechanical behavior. The in vivo stretch ratio () of each carotid artery used for biaxial mechanical behavior was measured by taking images of the artery before and after dissection with a digital camera connected to a dissection microscope.
2.2 Experimental measurement of critical buckling pressure
The carotid artery was set at axial stretch ratios (λz) from 1.0 – 1.4, then inflated under lumen pressure in increments of 5 mmHg until it buckled or until a maximum pressure of 200 mmHg was reached. Images were taken at each increment near buckling for offline determination of experimental critical buckling pressure (). The pressurized images were layered on top of the unloaded image and the outer edges and the midline of the artery were outlined using custom scripts in Matlab. was defined as the pressure at which the maximum lateral displacement of the midline of the pressurized artery was greater than the radius of the unloaded artery (Fig. 1).
Figure 1. Definition of experimental critical buckling pressure ().
Eln+/+ artery mounted in the myograph at an axial stretch (λz) of 1.0 at 0 mmHg and inflated to 35 and 60 mmHg. The outer edges (solid lines) and centerlines (dotted lines) of the unloaded (black lines) and inflated (grey lines) arteries were defined and overlaid using Matlab. was defined as the pressure at which the centerline of the loaded artery had a maximum displacement greater than the radius of the unloaded artery. This can be seen when the grey dotted line moves to the right of the right hand black solid line. Scale bar = 100 µm.
2.3 Experimental measurement of biaxial mechanical behavior
Biaxial mechanical tests were performed as previously described (Amin et al. 2012). The carotid artery was mounted in the myograph at the unloaded length and stretched axially to . The artery was preconditioned for three cycles in the circumferential (0 to 175 mmHg) and axial directions (, with a maximum force around 8 mN). The artery was then inflated three times from 0 – 175 mmHg at constant axial stretches and stretched axially three times at constant pressures (50, 100, and 150 mmHg). The axial stretch range with respect to the unloaded length varied for each artery, but was typically between λz = 1.2 – 1.7. The circumferential inflation cycles were performed automatically with the myograph software (steps of 25 mmHg, 12 sec/step), while the axial stretch cycles were performed by manual rotation of the micrometer attached to one end of the carotid artery (~10 µm/sec). Pressure, outer diameter, and axial force were recorded at 1 Hz for all cycles. The axial stretch ratio at each time point was calculated assuming a constant stretch rate. Custom scripts in Matlab software were used to isolate the third loading cycle of each protocol for further analyses. Unloaded dimensions were determined from images of cut arterial rings (200 – 300 µm thick) taken with a digital camera connected to a dissection microscope. The loaded inner diameter was calculated by incompressibility (Faury et al. 1999).
2.4 Fitting material parameters for the strain energy functions
Assuming an incompressible, axisymmetric, thick-walled cylinder with no shear, the inflation and extension of the carotid artery can be described by the stretch ratios in each direction [circumferential (θ), axial (z), and radial (r)],
| (1) |
where r = deformed radius, R = undeformed radius in the stress-free state, θo = 1/2 the central angle of the arc formed in the stress-free state (Chuong and Fung 1986), l = deformed length, and L = undeformed length. The stress-free state was not explicitly measured in this study. The unloaded state was measured and related to the stress-free state according to Matsumoto and Hayashi (1996) using published opening angles (Φ = π − θo) of 60° for Eln+/− and Eln+/+ (Wagenseil et al. 2005), 150° for Fbln5−/− and 90° for Fbln5+/+ (Wan et al. 2010) carotid arteries.
The strain energy functions (W) used to model the biaxial mechanical behavior of the carotid arteries are the Fung exponential model (WF) (Chuong and Fung 1986) and four-fiber model (W4) (Holzapfel et al. 2000; Gleason et al. 2008) given by,
| (2) |
| (3) |
| (4) |
where E is the Greens strain in each direction [Ei = ½(λi2 − 1)], Ik = 2Eθ sin2 αk +2Ez cos2 αk for each kth fiber family where the subscripts represent fiber families oriented in the θ (α1 = 90°), z (α2 = 0°), or two identical families in the d (diagonal) (α3 = −α4 = α0) direction and b0 − b32 are material parameters.
Accordingly, based on equilibrium, the lumen pressure (P) and axial force (N) of the artery are,
| (5) |
| (6) |
where ri and re are the deformed inner and outer radius, respectively. The integral term in Eqn. 6 is equal to the reduced axial force, , which is measured experimentally by the inline force transducer (Holzapfel et al. 2000).
Material parameters for the strain energy functions were estimated by minimizing the error between the experimental and theoretical pressures and reduced axial forces,
| (7) |
Fitting error was calculated by dividing the error function by the total number of data points (2n) (Wan et al. 2010). Six random starting values were used to ensure a global minimum was determined. The starting values were determined by a random number generator between 0 – 1 and then scaled for the expected order of magnitude of the parameter [× 1000 Pa for b0 (Fung), b11, b21, and b31 (four-fiber) and × 90° for α (four-fiber)].
2.5 Theoretical analysis of critical buckling pressures
The theoretical critical buckling pressure () can be determined by force and moment equilibrium of the buckled artery as derived previously using the Fung (Lee et al. 2012) and four-fiber strain energy functions (Liu et al. 2014),
| (8) |
where le is the equivalent length of the artery (equal to half the length for fixed ends), N is the axial force (Eqn. 6), and H is the “bending force” defined by
| (9) |
with Jz and Jθ depending on the strain energy function. For the Fung (F) strain energy function,
| (10) |
| (11) |
and for the four-fiber (4) strain energy function,
| (12) |
| (13) |
of each artery used in biaxial testing was determined using Eqn. 8 with the artery dimensions (diameter and wall thickness) and the fitted material constants as inputs. The average length from the arteries used in the experimental buckling group was used (le = 3.05/2 mm). The axial stretch range was prescribed from λz = 1.0 – 1.4, and λθ was determined iteratively as the value providing the minimum difference between (Eqn. 8) and the theoretical lumen pressure (Eqn. 5).
2.6 Statistics
One way ANOVA followed by a Tukey post hoc test was used to compare results between groups using SPSS software. Data are presented as mean ± sem.
3. Results
3.1 Unloaded dimensions and in vivo stretch ratios
The unloaded dimensions and are shown in Table 1. Similar to previous data (Wagenseil et al. 2005), Eln+/− carotid arteries have smaller unloaded outer diameters and reduced compared to Eln+/+. Also consistent with previous data (Wan et al. 2010), Fbln5−/− carotid arteries have similar unloaded outer diameters compared to Fbln5+/+, but have reduced . The absolute values of are consistent with previous values measured from images of mouse carotid arteries before and after dissection (Wagenseil et al. 2005), but are lower than values obtained by assuming that at , the axial force is constant with increasing pressure during in vitro tests (i.e. (Wan et al. 2010; Dye et al. 2007; Eberth et al. 2009)).
Table 1.
Unloaded outer diameters (OD) and inner diameters (ID) measured from cut rings of the carotid arteries after mechanical testing. In vivo axial stretch ratios () measured from images before and after dissection of the artery are also shown. Significant P values are shown in italics.
| Eln+/+ | Eln+/− | ||||||||
| Sample | OD (µm) | ID (µm) | Sample | OD (µm) | ID (µm) | ||||
| 1 | 376 | 259 | 1.44 | 1 | 341 | 229 | 1.04 | ||
| 2 | 353 | 252 | 1.20 | 2 | 347 | 236 | 1.19 | ||
| 3 | 440 | 316 | 1.38 | 3 | 370 | 246 | 1.13 | ||
| 4 | 427 | 316 | 1.23 | 4 | 368 | 264 | 1.11 | ||
| 5 | 402 | 282 | 1.13 | 5 | 352 | 241 | 1.31 | ||
| 6 | 409 | 284 | 1.49 | 6 | 347 | 246 | 1.10 | ||
| 7 | 407 | 289 | 1.50 | ||||||
| mean | 402 | 285 | 1.34 | mean | 354 | 244 | 1.15 | ||
| sem | 11 | 9 | 0.06 | sem | 5 | 5 | 0.04 | ||
| P (Eln+/+ to Eln+/−) | 0.013 | 0.009 | .012 | ||||||
| Fbln5+/+ | Fbln5−/− | ||||||||
| Sample | OD (µm) | ID (um) | Sample | OD (µm) | ID (µm) | ||||
| 1 | 373 | 241 | 1.53 | 1 | 401 | 290 | 1.20 | ||
| 2 | 383 | 266 | 1.31 | 2 | 384 | 277 | 1.18 | ||
| 3 | 407 | 298 | 1.36 | 3 | 359 | 253 | 1.19 | ||
| 4 | 339 | 230 | 1.35 | 4 | 444 | 306 | 1.22 | ||
| 5 | 365 | 257 | 1.33 | 5 | 389 | 274 | 1.12 | ||
| 6 | 351 | 232 | 1.45 | 6 | 370 | 258 | 1.14 | ||
| 7 | 414 | 287 | 1.33 | 7 | 383 | 273 | 1.26 | ||
| 8 | 403 | 278 | 1.25 | ||||||
| mean | 379 | 261 | 1.37 | mean | 390 | 276 | 1.19 | ||
| sem | 10 | 9 | 0.03 | sem | 10 | 7 | 0.02 | ||
| P (Eln+/+ to Fbln5+/+) | 0.339 | 0.153 | .963 | P (Fbln5+/+ to Fbln5−/−) | 0.852 | 0.552 | .013 |
3.2 Experimental buckling pressure
There are no significant differences in between the two wild-type groups. At all axial stretch ratios is 10 – 20% lower in Eln+/− arteries than Eln+/+ (Fig. 2a). Nine out of 10 Fbln5−/− arteries did not buckle at 200 mmHg at an axial stretch ratio of 1.4. To demonstrate the increased at high stretch in Fig. 2b, we assumed a linear increase in between axial stretches of 1.2 – 1.4 for each Fbln5−/− artery. The actual values may be higher. At lower axial stretch ratios is similar in Fbln5−/− and Fbln5+/+ arteries, but at higher axial stretch ratios is 15 – 25% higher in Fbln5−/− arteries than Fbln5+/+ (Fig. 2b). We fit a linear relationship between and axial stretch ratio (R2 = .98 – .99) to estimate in vivo using the average in vivo axial stretch ratios () in Table 1. The estimated in vivo (mmHg) is 157 for Eln+/+, 88 for Eln+/−, 165 for Fbln5+/+ and 121 for Fbln5−/− arteries. is above systolic blood pressure for Eln+/+ and Fbln5+/+ mice, but below systolic pressure for Eln+/− and Fbln5−/− mice (Yanagisawa et al. 2002; Faury et al. 2003; Wagenseil et al. 2005), so it is likely that Eln+/− and Fbln5−/− arteries buckle in vivo.
Figure 2. Experimental critical buckling pressure () in mouse arteries with altered elastic fibers.
Carotid arteries from mice with reduced elastin amounts (Eln+/−) have decreased buckling pressures compared to wild-type (Eln+/+) (a). Carotid arteries from mice was disrupted elastic fibers due to lack of fibulin-5 expression (Fbln5−/−) have similar buckling pressures at low axial stretch (λz), but increased buckling pressures at high λz compared to wild-type (Fbln5+/+) (b). * = 9/10 Fbln5−/− arteries did not buckle at λz = 1.4 at the maximum applied pressure of 200 mmHg. To show the high for Fbln5−/− arteries that did not buckle, we assumed increased linearly between axial stretches of 1.2 – 1.4. may be even higher. $ = p < .05 between genotypes, N = 10/group. Values are mean ± sem.
3.3 Experimental mechanical behavior and fitted material parameters
Average outer diameter-pressure relationships at and axial stretch-reduced force relationships at 100 mmHg are shown in Fig. 3. Similar to previous results (Faury et al. 2003; Wagenseil et al. 2005; Wan et al. 2010), Eln+/− and Fbln5−/− carotid arteries have smaller outer diameters at high pressures compared to their wild-type controls, indicating increased circumferential stiffness of the arterial wall. Fbln5−/− arteries have increased axial force at all overlapping axial stretch ratios compared to Fbln5+/+ arteries, consistent with previous results showing that axial force in Fbln5−/− carotid arteries becomes nonlinear at lower axial stretch ratios than Fbln5+/+ (Wan et al. 2010). In contrast, Eln+/− arteries have similar or slightly lower axial forces compared to Eln+/+ at most axial stretch ratios, consistent with previous data for axial stretch-stress relationships (Wagenseil et al. 2005).
Figure 3. Circumferential and axial mechanical behavior.
Average outer diameter-pressure relationships at (a) and average axial stretch-reduced force relationships at 100 mmHg (b) from the biaxial mechanical test protocols. Eln+/− and Fbln5−/− arteries show increased circumferential stiffness compared to their respective controls. Eln+/− arteries show similar or slightly reduced axial stiffness compared to Eln+/+, while Fbln5−/− arteries show increased axial stiffness compared to Fbln5+/+. N = 6 – 8/group for outer diameter-pressure curves. N = 3 – 7/group for axial stretch-reduced force curves. The numbers of axial samples are lower because axial stretch ratios were determined individually for each artery, so not all samples were stretched in the same range. Axial stretches of 1.35 and 1.40 are the only values that have enough samples in all groups for statistical comparison. * = P < .05 between Eln+/+ and Eln+/− and $ = P < .05 between Fbln5+/+ and Fbln5−/−.
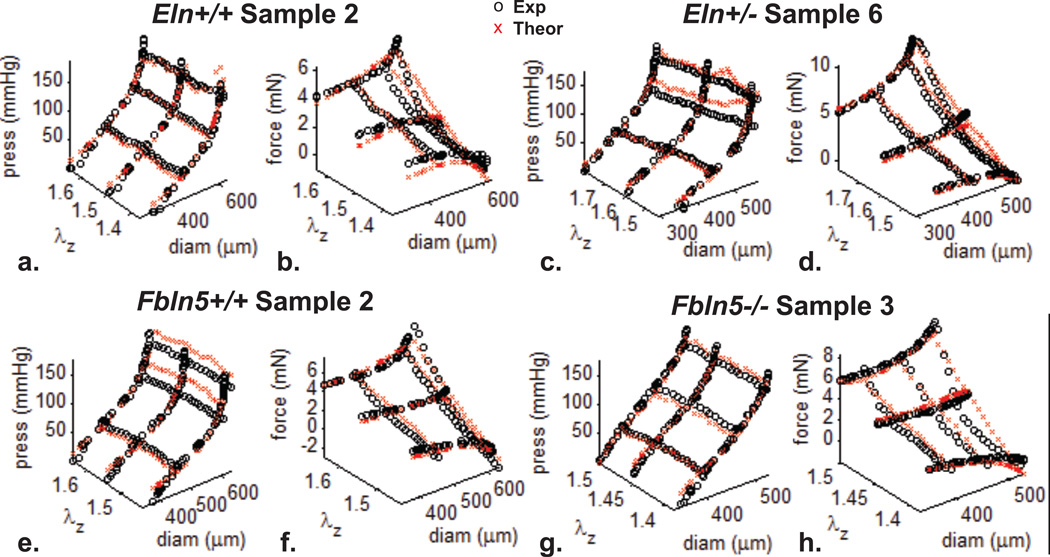
Material parameters in the Fung and four-fiber strain energy functions were fit for each artery using the unloaded dimensions (Table 1) and mechanical test data. Example fits for each group are shown in Fig. 4 (Fung) and Fig. 5 (four-fiber). For the Fung strain energy function (Table 2), there are no significant differences between parameters for the Eln+/− and Eln+/+ groups or the Eln+/+ and Fbln5+/+ groups. There are significant differences between 5/7 parameters for the Fbln5−/− and Fbln5+/+ groups. The bo constant is five times lower and the exponential constants (b1 – b3, b5, b6) are 4 – 90 times higher, showing more nonlinear stress-strain behavior in Fbln5−/− compared to Fbln5+/+ arteries. The constants for wild-type mouse carotid arteries are similar to those obtained previously with the Fung strain energy function (Gleason et al. 2008).
Figure 4. Example fits for the Fung strain energy function.
Mechanical test data from Eln+/+ (a,b), Eln+/− (c,d), Fbln5+/+ (e,f), and Fbln5−/− (g,h) carotid arteries were fit with a Fung strain energy function by minimizing the differences between the experimental and theoretical pressures and reduced axial forces (Eqn. 7) to determine the material constants shown in Table 2.
Figure 5. Example fits for the four-fiber strain energy function.
Mechanical test data from Eln+/+ (a,b), Eln+/− (c,d), Fbln5+/+ (e,f), and Fbln5−/− (g,h) carotid arteries were fit with a four-fiber strain energy function by minimizing the differences between the experimental and theoretical pressures and reduced axial forces (Eqn. 7) to determine the material constants shown in Table 3.
Table 2.
Material parameters and fit errors for the Fung strain energy function. Significant P values are shown in italics.
| Eln+/+ | ||||||||
| Sample | b0 (kPa) | b1 | b2 | b3 | b4 | b5 | b6 | fit error |
| 1 | 323 | 0.090 | 0.148 | 0.338 | 0.056 | 0.000 | 0.030 | 0.044 |
| 2 | 125 | 0.197 | 0.387 | 0.249 | 0.109 | 0.027 | 0.000 | 0.031 |
| 3 | 59 | 0.467 | 0.557 | 1.269 | 0.277 | 0.523 | 0.000 | 0.045 |
| 4 | 26 | 0.421 | 1.052 | 4.908 | 0.272 | 1.171 | 0.000 | 0.068 |
| 5 | 328 | 0.170 | 0.118 | 0.168 | 0.068 | 0.000 | 0.111 | 0.025 |
| 6 | 38 | 0.636 | 0.579 | 2.522 | 0.130 | 0.140 | 0.000 | 0.032 |
| 7 | 252 | 0.135 | 0.383 | 0.376 | 0.091 | 0.179 | 0.000 | 0.053 |
| mean | 165 | 0.302 | 0.461 | 1.404 | 0.143 | 0.291 | 0.020 | 0.043 |
| sem | 51 | 0.078 | 0.119 | 0.665 | 0.035 | 0.162 | 0.016 | 0.006 |
| Eln+/− | ||||||||
| Sample | b0 (kPa) | b1 | b2 | b3 | b4 | b5 | b6 | fit error |
| 1 | 180 | 0.107 | 0.306 | 0.515 | 0.074 | 0.213 | 0.000 | 0.047 |
| 2 | 31 | 0.330 | 0.990 | 3.490 | 0.126 | 0.793 | 0.000 | 0.020 |
| 3 | 125 | 0.156 | 0.190 | 0.439 | 0.085 | 0.000 | 0.041 | 0.048 |
| 4 | 32 | 0.380 | 1.142 | 4.436 | 0.231 | 1.299 | 0.000 | 0.045 |
| 5 | 48 | 0.353 | 1.117 | 3.359 | 0.083 | 0.990 | 0.000 | 0.063 |
| 6 | 41 | 0.442 | 0.862 | 1.937 | 0.177 | 0.620 | 0.000 | 0.034 |
| mean | 76 | 0.295 | 0.768 | 2.363 | 0.129 | 0.653 | 0.007 | 0.043 |
| sem | 25 | 0.054 | 0.170 | 0.680 | 0.026 | 0.198 | 0.007 | 0.006 |
| P (Eln+/+ to Eln+/−) | 0.753 | 1.000 | 0.642 | 0.976 | 0.757 | 0.998 | 0.980 | 0.999 |
| Fbln5+/+ | ||||||||
| Sample | b0 (kPa) | b1 | b2 | b3 | b4 | b5 | b6 | fit error |
| 1 | 88 | 0.213 | 0.559 | 1.076 | 0.132 | 0.396 | 0.000 | 0.038 |
| 2 | 39 | 0.360 | 1.367 | 4.455 | 0.160 | 1.488 | 0.000 | 0.038 |
| 3 | 490 | 0.093 | 0.164 | 0.148 | 0.061 | 0.055 | 0.000 | 0.019 |
| 4 | 737 | 0.031 | 0.137 | 0.045 | 0.035 | 0.052 | 0.000 | 0.027 |
| 5 | 27 | 0.218 | 1.186 | 4.639 | 0.000 | 0.203 | 0.023 | 0.025 |
| 6 | 171 | 0.086 | 0.632 | 1.061 | 0.136 | 0.719 | 0.000 | 0.054 |
| 7 | 117 | 0.181 | 0.819 | 2.547 | 0.196 | 1.036 | 0.000 | 0.009 |
| 8 | 50 | 0.185 | 1.955 | 5.052 | 0.402 | 2.624 | 0.000 | 0.039 |
| mean | 215 | 0.171 | 0.852 | 2.378 | 0.140 | 0.822 | 0.003 | 0.031 |
| sem | 92 | 0.036 | 0.220 | 0.737 | 0.044 | 0.313 | 0.003 | 0.005 |
| P (Eln+/+ to Fbln5+/+) | 0.928 | 0.871 | 0.912 | 0.970 | 1.000 | 0.927 | 0.996 | 0.351 |
| Fbln5−/− | ||||||||
| Sample | b0 (kPa) | b1 | b2 | b3 | b4 | b5 | b6 | fit error |
| 1 | 25 | 0.971 | 3.877 | 7.860 | 0.505 | 3.796 | 0.000 | 0.015 |
| 2 | 34 | 1.192 | 2.724 | 3.964 | 0.555 | 2.627 | 0.692 | 0.023 |
| 3 | 11 | 0.446 | 7.595 | 21.410 | 0.491 | 9.765 | 0.000 | 0.028 |
| 4 | 9 | 2.258 | 4.247 | 17.325 | 0.000 | 3.797 | 0.612 | 0.017 |
| 5 | 161 | 0.604 | 0.830 | 1.338 | 0.285 | 0.552 | 0.353 | 0.011 |
| 6 | 45 | 0.598 | 1.912 | 1.605 | 0.029 | 0.239 | 0.000 | 0.010 |
| 7 | 19 | 0.956 | 3.366 | 8.528 | 0.265 | 3.095 | 0.146 | 0.006 |
| mean | 43 | 1.003 | 3.507 | 8.861 | 0.304 | 3.410 | 0.258 | 0.016 |
| sem | 20 | 0.231 | 0.813 | 2.942 | 0.086 | 1.191 | 0.113 | 0.003 |
| P (Fbln5+/+ to Fbln5−/−) | 0.191 | <.001 | 0.001 | 0.031 | 0.147 | 0.031 | 0.016 | 0.134 |
For the four-fiber strain energy function (Table 3), there are no significant differences between parameters for the Eln+/− and Eln+/+ groups or the Eln+/+ and Fbln5+/+ groups. There are significant differences between 4/8 parameters for the Fbln5−/− and Fbln5+/+ groups. The b12, b22, and b32 constants are 2 – 22 times higher in Fbln5−/− arteries compared to Fbln5+/+, indicating increased nonlinearity of all four fiber families. The angle, α0, is about 10° larger in Fbln5−/− arteries than Fbln5+/+, predicting a more circumferential orientation of the diagonal fibers. Previous results showed increased nonlinearity for the axial and diagonal fiber families in Fbln5−/− carotid arteries, but not for the circumferential fibers and no difference in the angle of the diagonal fibers (Wan et al. 2010). For both genotypes, the fitted values for b0 are lower than Wan et al. (2010), but the values for b11, b21, and b31 are higher, demonstrating a trade-off between isotropic and anisotropic stress contributions in the model, which may be related to the loading protocols used for fitting.
Table 3.
Material parameters and fit errors for the four-fiber strain energy function. Significant P values are shown in italics.
| Eln+/+ | |||||||||
| Sample | b0 (kPa) | b11 (kPa) | b12 | b21 (kPa) | b22 | b31 (kPa) | b32 | α0 (deg) | fit error |
| 1 | 1.74 | 4.34 | 0.000 | 19.07 | 0.000 | 24.53 | 0.050 | 44.5 | 0.032 |
| 2 | 9.24 | 12.07 | 0.000 | 18.81 | 0.001 | 9.59 | 0.335 | 39.5 | 0.025 |
| 3 | 2.92 | 10.54 | 0.168 | 0.93 | 0.355 | 12.69 | 0.403 | 44.7 | 0.047 |
| 4 | 4.49 | 13.31 | 0.075 | 0.81 | 0.408 | 9.41 | 0.454 | 38.6 | 0.068 |
| 5 | 7.53 | 9.19 | 0.073 | 14.15 | 0.000 | 10.68 | 0.231 | 46.1 | 0.019 |
| 6 | 4.58 | 16.02 | 0.163 | 3.86 | 0.000 | 15.88 | 0.320 | 39.5 | 0.024 |
| 7 | 8.15 | 13.87 | 0.067 | 10.19 | 0.000 | 19.90 | 0.250 | 30.5 | 0.051 |
| mean | 5.52 | 11.33 | 0.078 | 9.69 | 0.109 | 14.67 | 0.292 | 40.5 | 0.038 |
| sem | 1.07 | 3.81 | 0.068 | 7.97 | 0.187 | 5.77 | 0.133 | 5.3 | 0.018 |
| Eln+/− | |||||||||
| Sample | b0 (kPa) | b11 (kPa) | b12 | b21 (kPa) | b22 | b31 (kPa) | b32 | α0 (deg) | fit error |
| 1 | 3.71 | 9.38 | 0.001 | 7.57 | 0.170 | 10.02 | 0.178 | 39.1 | 0.043 |
| 2 | 3.13 | 8.06 | 0.080 | 1.65 | 0.496 | 8.74 | 0.338 | 36.0 | 0.018 |
| 3 | 3.09 | 0.82 | 0.000 | 10.59 | 0.000 | 13.32 | 0.120 | 48.2 | 0.032 |
| 4 | 6.27 | 9.82 | 0.108 | 0.95 | 0.633 | 7.42 | 0.460 | 39.1 | 0.044 |
| 5 | 1.75 | 8.93 | 0.134 | 2.84 | 0.530 | 12.17 | 0.288 | 36.6 | 0.063 |
| 6 | 3.56 | 7.80 | 0.183 | 3.33 | 0.288 | 9.37 | 0.401 | 38.7 | 0.033 |
| mean | 3.59 | 7.47 | 0.084 | 4.49 | 0.353 | 10.17 | 0.298 | 39.6 | 0.039 |
| sem | 0.61 | 3.35 | 0.073 | 3.78 | 0.242 | 2.20 | 0.130 | 4.4 | 0.015 |
| P (Eln+/+ to Eln+/− | 0.314 | 0.199 | 1.000 | 0.442 | 0.799 | 0.749 | 1.000 | 0.990 | 0.999 |
| Fbln5+/+ | |||||||||
| Sample | b0 (kPa) | b11 (kPa) | b12 | b21 (kPa) | b22 | b31 (kPa) | b32 | α0 (deg) | fit error |
| 1 | 5.85 | 8.16 | 0.060 | 4.81 | 0.290 | 9.02 | 0.322 | 38.1 | 0.038 |
| 2 | 7.13 | 12.47 | 0.117 | 0.12 | 0.685 | 8.66 | 0.459 | 29.2 | 0.038 |
| 3 | 5.92 | 15.20 | 0.007 | 15.75 | 0.000 | 25.04 | 0.140 | 40.2 | 0.018 |
| 4 | 3.48 | 9.49 | 0.000 | 13.71 | 0.000 | 24.68 | 0.084 | 31.0 | 0.026 |
| 5 | 3.84 | 9.54 | 0.021 | 10.50 | 0.134 | 18.53 | 0.275 | 27.0 | 0.015 |
| 6 | 2.35 | 9.59 | 0.000 | 3.23 | 0.612 | 9.46 | 0.299 | 35.3 | 0.053 |
| 7 | 6.69 | 10.10 | 0.000 | 3.58 | 0.597 | 18.60 | 0.197 | 44.2 | 0.018 |
| 8 | 3.60 | 16.50 | 0.000 | 2.22 | 1.121 | 3.03 | 0.915 | 35.2 | 0.034 |
| mean | 4.86 | 11.38 | 0.026 | 6.74 | 0.430 | 14.63 | 0.336 | 35.1 | 0.030 |
| sem | 0.62 | 1.07 | 0.015 | 2.04 | 0.139 | 2.89 | 0.09 | 2.1 | 0.005 |
| P (Eln+/+ to Fbln5+/+) | 0.915 | 1.000 | 0.082 | 0.791 | 0.578 | 1.000 | 0.967 | 0.203 | 0.678 |
| Fbln5−/− | |||||||||
| Sample | b0 (kPa) | b11 (kPa) | b12 | b21 (kPa) | b22 | b31 (kPa) | b32 | α0 (deg) | fit error |
| 1 | 4.46 | 8.19 | 0.648 | 3.07 | 1.192 | 18.64 | 0.697 | 47.4 | 0.021 |
| 2 | 2.27 | 4.50 | 0.625 | 5.52 | 0.922 | 9.64 | 0.887 | 44.3 | 0.029 |
| 3 | 3.26 | 14.04 | 0.021 | 0.55 | 2.951 | 19.50 | 0.428 | 46.5 | 0.025 |
| 4 | 6.03 | 11.19 | 0.962 | 6.84 | 1.677 | 45.93 | 0.572 | 50.5 | 0.017 |
| 5 | 6.25 | 8.32 | 0.755 | 15.90 | 0.451 | 31.26 | 0.452 | 44.2 | 0.018 |
| 6 | 4.56 | 4.70 | 0.443 | 16.13 | 0.890 | 21.33 | 0.547 | 35.5 | 0.010 |
| 7 | 3.46 | 9.58 | 0.413 | 5.66 | 1.080 | 15.44 | 0.744 | 42.1 | 0.008 |
| mean | 4.33 | 8.65 | 0.552 | 7.67 | 1.309 | 23.11 | 0.678 | 44.4 | 0.018 |
| sem | 0.55 | 1.29 | 0.113 | 2.29 | 0.307 | 4.53 | 0.063 | 1.8 | 0.003 |
| P (Fbln5+/+ to Fbln5−/−) | 0.953 | 0.421 | <.001 | 0.991 | 0.009 | 0.203 | 0.035 | 0.010 | 0.389 |
There is no significant difference in the average fit error between strain energy functions (.033 ± .003 for Fung and .031 ± .003 for four-fiber). This is in contrast to previous data that showed the four-fiber family model to have about 20% less error in fitting than the Fung model for mouse carotid arteries (Gleason et al. 2008). The parameter values and fitting error are sensitive to the loading range for the experimental data. The applied pressure was higher and the axial stretch range was lower in this study than in Gleason et al. (2008), which may alter the fitting error for different strain energy functions. Additionally, the choice of error function can determine whether the strain energy function fits better at high or low stretch ratios (Ferruzzi et al. 2013) and different error functions were used in this study compared to Gleason et al. (2008).
3.4 Theoretical buckling pressure
The material parameters (Table 2 or 3) and unloaded dimensions (Table 1) for each artery were used to calculate the theoretical buckling pressure () (Fig. 6). For the wild-type groups, is within 8 – 43% of for both strain energy functions, with underpredictions at low axial stretch, overpredictions at high axial stretch, and the best match between predicted and experimental values at λz = 1.3 (8 – 12% difference). For Eln+/− arteries, is within 17 – 54% of for both strain energy functions across the axial stretch range, but is always lower than . For Fbln5−/− arteries, is within 0.1 – 603% of for the Fung strain energy function and 6 – 135% for the four-fiber strain energy function. The values from the Fung strain energy function have a more nonlinear dependence on axial stretch than those calculated with the four-fiber strain energy function, resulting in overprediction of the critical buckling pressure at high stretch for most groups.
Figure 6. Comparison of experimental () and theoretical () buckling pressures.
Material constants from the Fung or four-fiber strain energy function, along with the unloaded dimensions, were used to calculate according to Eqn. 8 for each artery. In general, is lower than at low axial stretch and higher than at high axial stretch. Similar to experimental results, both models predict increased buckling pressure in Fbln5−/− arteries at high axial stretch. Note the increased vertical scale for Fbln5−/− arteries. Values are mean ± sem.
The differences between groups for the predicted buckling pressure (Fig. 6) are consistent with the experimental data (Fig. 2). For Fbln5−/− arteries, both strain energy functions predict a large increase in with axial stretch and significantly higher values compared to Fbln5+/+ at λz = 1.3 and 1.4. This is supported by experimental observations that 9/10 Fbln5−/− arteries did not buckle at the maximum applied pressure of 200 mmHg for λz = 1.4. Additional buckling experiments at higher applied pressures are necessary to better compare and at high axial stretch for Fbln5−/− arteries.
4. Discussion
4.1 Effects of genetic defects in elastic fibers on biaxial mechanical behavior and experimental critical buckling pressure
Eln+/− mice have about 60% of the normal elastin amounts, smaller, thinner arteries, and increased blood pressure (Faury et al. 2003). Fbln5−/− mice have disordered elastic fibers, tortuous arteries, and high blood pressure (Nakamura et al. 2002; Yanagisawa et al. 2002). Previous studies show that Eln+/− and Fbln5−/− arteries have increased circumferential arterial stiffness and reduced in vivo axial stretch ratios compared to their wild-type controls (Wagenseil et al. 2005; Wan et al. 2010). The current study confirms past characterization of the circumferential mechanical behavior and shows that Fbln5−/− arteries have more significant stiffening than Eln+/− arteries, compared to their respective controls (Fig. 3a). The current study also adds new information about the axial mechanical behavior for arteries with altered elastic fibers, showing that Fbln5−/− arteries have significant stiffening in the axial direction compared to Fbln5+/+, while Eln+/− arteries are slightly less stiff than Eln+/+ in the axial direction (Fig. 3b). These data show that reductions in elastin amounts and defects in elastic fiber assembly may not necessarily cause similar changes in mechanical behavior, especially in the axial direction.
Eln+/− arteries display a consistent decrease in buckling pressure at all axial stretch values, while Fbln5−/− arteries display an increase in buckling pressure at high axial stretch values, compared to their respective controls. Although in different genetic backgrounds, the two wild-type control groups have similar buckling behavior (Fig. 2). These results show that while some simple measurements (i.e. circumferential stiffness and in vivo axial stretch ratio) may be comparable in Eln+/− and Fbln5−/− arteries, buckling behavior is very different. The increased axial stiffness of Fbln5−/− arteries is most likely responsible for their increased buckling pressure, while the decrease in axial stiffness of Eln+/− arteries accounts for their decreased buckling pressure. However, the critical buckling pressure depends on the three-dimensional mechanical properties, mechanical loading, and geometry of the arteries (Han 2008), and a complete characterization of these properties is necessary to better understand the contribution of genetic modifications in elastic fibers to arterial buckling.
Our data suggest that Eln+/− and Fbln5−/− arteries are buckled in vivo at systolic pressures. Note that our experiments were done under static pressure in a fluid bath, which is different from the in vivo state of the artery with pulsatile pressure and surrounding tissue support. Hence, our experimental results cannot be directly translated into quantitative in vivo buckling predictions. However, the qualitative trends remain true and if the arteries are buckled in vivo, this can lead to remodeling and arterial tortuosity. While arterial tortuosity has not been described in Eln+/− mice, Eln+/− carotid arteries form looped or curved shapes upon excision, suggesting residual torsion (Wagenseil et al. 2005). Carotid artery tortuosity has been observed in vivo for newborn mice with no elastin expression (Eln−/−) (Wagenseil et al. 2009). Arterial tortuosity in the descending thoracic aorta has been observed in vivo in Fbln5−/− mice (Nakamura et al. 2002). Additional in vitro experiments and modeling of different regions of the arterial tree may help predict which sections are prone to buckling and the development of tortuosity.
4.2 Comparison of theoretical and experimental critical buckling results
For most arteries and both strain energy functions, the theoretical buckling pressures are lower than the experimental values at low axial stretch and higher than the experimental values at high axial stretch (Fig. 6). One explanation for the difference at low axial stretch is that we chose a relatively stringent criterion for (Fig. 1) to ensure that the artery was buckled. Future experimental studies with less stringent buckling criteria may show better agreement between and at low axial stretch. At high axial stretch, showed the biggest differences from in groups with high axial stiffness (i.e. at λz = 1.4 for Fbln5−/− arteries was greater than both wild-types, which were greater than Eln+/−). This implies that the theoretical buckling pressures are overly influenced by the axial stiffness compared to the experimental buckling pressures. This could be due to differences between the experimental and theoretical mechanical behavior at high axial stretch or limiting assumptions in the theoretical analysis of buckling pressure.
We examined the material parameters of each group to better understand the buckling pressure predictions, especially the large for Fbln5−/− arteries at high axial stretch. For the Fung strain energy function, the constants b2, b4, and b5 indicate the contribution of the Greens strain in the axial direction. These parameters are 2 – 12 times higher in the Fbln5−/− group compared to the other groups. However, the axial parameters do not completely determine the buckling pressure, because b2, b4, and b5 for Eln+/− arteries in the Fung strain energy function are not reduced compared to Eln+/+, despite lower predicted buckling pressures. For the four-fiber strain energy function, the diagonal and axial fibers are important for determining the response to axial stretch. For the diagonal fibers, b31 and b32 are about two times greater in Fbln5−/− arteries than other groups. For the axial fibers, b21 is comparable to other groups, but b22 is 3 – 12 times greater in Fbln5−/− arteries than other groups. As for the Fung strain energy function, axial parameters do not completely determine the critical buckling pressure, because Eln+/− arteries show reductions in b31 and b21 compared to Eln+/+, but comparable b32 values and increases in b22, despite lower predicted buckling pressures. Our observations are consistent with previous analyses (Liu et al. 2014) and confirm that axial mechanical behavior of the artery is important, but not alone, in determining the critical buckling pressure.
We used two strain energy functions that have been shown to describe the mechanical behavior of mouse carotid arteries (Gleason et al. 2008). We found similar fitting errors for both strain energy functions and similar differences between and for most points. However, for the Fung strain energy function has a more nonlinear dependence on axial stretch than the four-fiber strain energy function, leading to significant overpredictions at λz = 1.4, especially in Fbln5−/− arteries with high axial stiffness. Overall, the predictions with the four-fiber strain energy function best match the experimental relationship between buckling pressure and axial stretch.
The theoretical buckling pressures in this study were calculated based on steady-state equilibrium of a buckled artery (Lee et al. 2012; Liu et al. 2014). Goriely and Vandiver (2010) develop a theoretical analysis of buckling instability in growing arteries. They find that the axial stretch-critical buckling pressure relationship depends on the values of differential axial growth and residual axial stretch. For similar residual stretch values, higher growth values are associated with increasing nonlinearity of the axial stretch-critical buckling pressure relationship The high critical buckling pressure in Fbln5−/− arteries at large axial stretch suggests that axial growth parameters may be higher in Fbln5−/− arteries than all other groups. Rachev (2009) develops a theoretical analysis of buckling stability in arteries subject to periodic pressure, which is a better representation of the in vivo state than a static pressure load. Buckling under periodic pressure occurs as a parametric resonance that depends on a combination of load parameters, including mean arterial pressure, pressure amplitude, pressure frequency, axial stretch, and axial length. However, experimental results have shown that the effect of periodic pressure is small at normal heart rates (Liu and Han 2012). Even though our theoretical calculations under static pressure cannot be directly translated into in vivo predictions of arterial buckling under more complicated loading conditions, the static theoretical model can be used for comparison to our static experimental results and the model helps us to better understand the contributions of elastic fibers to arterial buckling behavior, and provide guidance for further in vivo studies.
4.3 Clinical relevance
Arterial buckling is an instantaneous lateral deflection caused by increasing the internal pressure past the critical point for stable equilibrium (Han 2008) or by a parametric resonance that occurs during a critical combination of load parameters for unstable equilibrium (Rachev 2009). In both steady and pulsatile pressure analyses, high mean pressure is the major destabilizing factor and buckling is reversible if the mean pressure is subsequently decreased. However, sustained buckling and the loss of mechanical stability, could lead to the development of tortuous arteries in vivo. The mechanical factors that lead to buckling are risk factors for arterial tortuosity, including high blood pressure, weakened wall mechanical properties, and decreased axial stretch (Han 2012). Surgically reducing axial stretch in animal models causes arterial buckling (Zhang et al. 2014) and leads to arterial tortuosity (Jackson et al. 2005). Similar buckling occurs in veins, as well (Badel et al. 2013; Martinez et al. 2010). Alterations in elastic fibers are associated with genetic diseases characterized by tortuous arteries including arterial tortuosity syndrome (Wessels et al. 2004), cutis laxa (Urban and Davis 2014), Loeys-Dietz syndrome (Nakajima et al. 2014), and Williams syndrome (Winter et al. 1996). Cutis laxa is associated with mutations in fibulin-5 that lead to profound defects in elastic fiber formation (Urban and Davis 2014), similar to Fbln5−/− mice. Williams syndrome is caused by deletions within chromosome seven which includes the elastin gene and leads to elastin heterozygosity (Ewart et al. 1993), similar to Eln+/− mice. Mouse models of elastic fiber diseases allow us to further investigate the relationship between genetic defects in elastic fibers and arterial buckling and test theoretical models that may predict the development of tortuosity in vivo.
4.4 Limitations
We chose two commonly used strain energy functions to evaluate in this study, but other strain energy functions could be investigated, (i.e. (Zulliger et al. 2004)). Our best-fit parameter values may be influenced by the range of starting values, the loading protocols for the experimental data, and our choice of error function (Eqn. 7). Our average theoretical and experimental buckling pressures were compared from different sets of arteries. Our experimental applied pressures were limited to 200 mmHg and not all arteries buckled at this value. Our theoretical calculations assume a steady-state pressure load.
4.5 Conclusions
We measured arterial buckling pressure in arteries from genetically-modified mice with elastic fiber defects. Reduced elastin in Eln+/− arteries reduces buckling pressure, while disrupted elastic fibers in Fbln5−/− arteries increases buckling pressure at high axial stretches, compared to their respective controls. Theoretical buckling pressure calculated with a four-fiber strain energy function fit to biaxial mechanical test data better matched the dependence of experimental buckling pressure on axial stretch than values calculated with a Fung strain energy function. The experimental and theoretical results can help us better understand the contribution of genetic defects in elastic fibers to arterial mechanics, arterial buckling and the development of arterial tortuosity.
Highlights.
Buckling pressure may be related to the development of arterial tortuosity
Mouse arteries with reduced elastin amounts have decreased buckling pressure
Arteries without fibulin-5 have increased buckling pressure at high axial stretch
Theoretical models can predict experimental buckling pressure
A four-fiber strain energy function best predicts buckling behavior
Acknowledgements
This work was supported by NIH R01HL115560 (JEW), R01HL105314 (JEW), and R01HL095852 (HCH). We thank Dr. Dean Li at the University of Utah for the Eln+/− mice and Dr. Hiromi Yanagisawa at UT Southwestern Medical Center for the Fbln5+/− mice.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
There are no conflicts of interest.
References
- Amin M, Kunkel AG, Le VP, Wagenseil JE. Effect of storage duration on the mechanical behavior of mouse carotid artery. J Biomech Eng. 2011;133(7):071007. doi: 10.1115/1.4004415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amin M, Le VP, Wagenseil JE. Mechanical testing of mouse carotid arteries: from newborn to adult. Journal of visualized experiments : JoVE. 2012;(60) doi: 10.3791/3733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badel P, Rohan CP, Avril S. Finite Element simulation of buckling-induced vein tortuosity and influence of the wall constitutive properties. J Mech Behav Biomed Mater. 2013;26:119–126. doi: 10.1016/j.jmbbm.2013.05.006. [DOI] [PubMed] [Google Scholar]
- Budatha M, Roshanravan S, Zheng Q, Weislander C, Chapman SL, Davis EC, Starcher B, Word RA, Yanagisawa H. Extracellular matrix proteases contribute to progression of pelvic organ prolapse in mice and humans. J Clin Invest. 2011;121(5):2048–2059. doi: 10.1172/JCI45636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. On residual stresses in arteries. J Biomech Eng. 1986;108(2):189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- Dye WW, Gleason RL, Wilson E, Humphrey JD. Altered biomechanical properties of carotid arteries in two mouse models of muscular dystrophy. J Appl Physiol. 2007;103(2):664–672. doi: 10.1152/japplphysiol.00118.2007. [DOI] [PubMed] [Google Scholar]
- Eberth JF, Taucer AI, Wilson E, Humphrey JD. Mechanics of carotid arteries in a mouse model of Marfan Syndrome. Ann Biomed Eng. 2009;37(6):1093–1104. doi: 10.1007/s10439-009-9686-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewart AK, Morris CA, Atkinson D, Jin W, Sternes K, Spallone P, Stock AD, Leppert M, Keating MT. Hemizygosity at the elastin locus in a developmental disorder, Williams syndrome. Nature genetics. 1993;5(1):11–16. doi: 10.1038/ng0993-11. [DOI] [PubMed] [Google Scholar]
- Faury G, Maher GM, Li DY, Keating MT, Mecham RP, Boyle WA. Relation between outer and luminal diameter in cannulated arteries. Am J Physiol. 1999;277(5 Pt 2):H1745–H1753. doi: 10.1152/ajpheart.1999.277.5.H1745. [DOI] [PubMed] [Google Scholar]
- Faury G, Pezet M, Knutsen RH, Boyle WA, Heximer SP, McLean SE, Minkes RK, Blumer KJ, Kovacs A, Kelly DP, Li DY, Starcher B, Mecham RP. Developmental adaptation of the mouse cardiovascular system to elastin haploinsufficiency. J Clin Invest. 2003;112(9):1419–1428. doi: 10.1172/JCI19028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferruzzi J, Bersi MR, Humphrey JD. Biomechanical phenotyping of central arteries in health and disease: advantages of and methods for murine models. Ann Biomed Eng. 2013;41(7):1311–1330. doi: 10.1007/s10439-013-0799-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gleason RL, Dye WW, Wilson E. Quantification of the mechanical behavior of carotid arteries from wild-type, dystrophin-deficient, and sarcoglycan-δ knockout mice. Journal of Biomechanics. 2008;41(15):3213–3218. doi: 10.1016/j.jbiomech.2008.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goriely A, Vandiver R. On the mechanical stability of growing arteries. Ima J Appl Math. 2010;75(4):549–570. [Google Scholar]
- Han HC. Nonlinear buckling of blood vessels: a theoretical study. J Biomech. 2008;41(12):2708–2713. doi: 10.1016/j.jbiomech.2008.06.012. [DOI] [PubMed] [Google Scholar]
- Han HC. Twisted blood vessels: symptoms, etiology and biomechanical mechanisms. J Vasc Res. 2012;49(3):185–197. doi: 10.1159/000335123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61(1–3):1–48. [Google Scholar]
- Jackson ZS, Dajnowiec D, Gotlieb AI, Langille BL. Partial off-loading of longitudinal tension induces arterial tortuosity. Arterioscler Thromb Vasc Biol. 2005;25(5):957–962. doi: 10.1161/01.ATV.0000161277.46464.11. [DOI] [PubMed] [Google Scholar]
- Lee AY, Han B, Lamm SD, Fierro CA, Han HC. Effects of elastin degradation and surrounding matrix support on artery stability. Am J Physiol Heart Circ Physiol. 2012;302(4):H873–H884. doi: 10.1152/ajpheart.00463.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li DY, Faury G, Taylor DG, Davis EC, Boyle WA, Mecham RP, Stenzel P, Boak B, Keating MT. Novel arterial pathology in mice and humans hemizygous for elastin. J Clin Invest. 1998;102(10):1783–1787. doi: 10.1172/JCI4487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q, Han HC. Mechanical buckling of artery under pulsatile pressure. Journal of biomechanics. 2012;45(7):1192–1198. doi: 10.1016/j.jbiomech.2012.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q, Wen Q, Mottahedi M, Han HC. Artery buckling analysis using a four-fiber wall model. J Biomech. 2014 doi: 10.1016/j.jbiomech.2014.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez R, Fierro CA, Shireman PK, Han HC. Mechanical buckling of veins under internal pressure. Ann Biomed Eng. 2010;38(4):1345–1353. doi: 10.1007/s10439-010-9929-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez R, Han HC. The effect of collagenase on the critical buckling pressure of arteries. Molecular & cellular biomechanics : MCB. 2012;9(1):55–75. [PMC free article] [PubMed] [Google Scholar]
- Matsumoto T, Hayashi K. Stress and strain distribution in hypertensive and normotensive rat aorta considering residual strain. J Biomech Eng. 1996;118(1):62–73. doi: 10.1115/1.2795947. [DOI] [PubMed] [Google Scholar]
- Nakajima T, Tachibana K, Miyaki Y, Takagi N, Morisaki T, Higami T. Acute dilatation of the ascending aorta and aortic valve regurgitation in loeys-dietz syndrome. Ann Thorac Surg. 2014;97(6):2188–2190. doi: 10.1016/j.athoracsur.2013.08.021. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Lozano PR, Ikeda Y, Iwanaga Y, Hinek A, Minamisawa S, Cheng CF, Kobuke K, Dalton N, Takada Y, Tashiro K, Ross J, Jr, Honjo T, Chien KR. Fibulin-5/DANCE is essential for elastogenesis in vivo. Nature. 2002;415(6868):171–175. doi: 10.1038/415171a. [DOI] [PubMed] [Google Scholar]
- Rachev A. A theoretical study of mechanical stability of arteries. J Biomech Eng. 2009;131(5):051006. doi: 10.1115/1.3078188. [DOI] [PubMed] [Google Scholar]
- Urban Z, Davis EC. Cutis laxa: Intersection of elastic fiber biogenesis, TGFbeta signaling, the secretory pathway and metabolism. Matrix Biol. 2014;33C:16–22. doi: 10.1016/j.matbio.2013.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenseil JE, Ciliberto CH, Knutsen RH, Levy MA, Kovacs A, Mecham RP. Reduced vessel elasticity alters cardiovascular structure and function in newborn mice. Circ Res. 2009;104(10):1217–1224. doi: 10.1161/CIRCRESAHA.108.192054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenseil JE, Nerurkar NL, Knutsen RH, Okamoto RJ, Li DY, Mecham RP. Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am J Physiol Heart Circ Physiol. 2005;289(3):H1209–H1217. doi: 10.1152/ajpheart.00046.2005. [DOI] [PubMed] [Google Scholar]
- Wan W, Yanagisawa H, Gleason RL., Jr Biomechanical and microstructural properties of common carotid arteries from fibulin-5 null mice. Ann Biomed Eng. 2010;38(12):3605–3617. doi: 10.1007/s10439-010-0114-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessels MW, Catsman-Berrevoets CE, Mancini GM, Breuning MH, Hoogeboom JJ, Stroink H, Frohn-Mulder I, Coucke PJ, Paepe AD, Niermeijer MF, Willems PJ. Three new families with arterial tortuosity syndrome. American journal of medical genetics Part A. 2004;131(2):134–143. doi: 10.1002/ajmg.a.30272. [DOI] [PubMed] [Google Scholar]
- Winter M, Pankau R, Amm M, Gosch A, Wessel A. The spectrum of ocular features in the Williams-Beuren syndrome. Clin Genet. 1996;49(1):28–31. doi: 10.1111/j.1399-0004.1996.tb04320.x. [DOI] [PubMed] [Google Scholar]
- Yanagisawa H, Davis EC, Starcher BC, Ouchi T, Yanagisawa M, Richardson JA, Olson EN. Fibulin-5 is an elastin-binding protein essential for elastic fibre development in vivo. Nature. 2002;415(6868):168–171. doi: 10.1038/415168a. [DOI] [PubMed] [Google Scholar]
- Zhang J, Liu Q, Han HC. An in vivo rat model of artery buckling for studying wall remodeling. Ann Biomed Eng. 2014;42(8):1658–1667. doi: 10.1007/s10439-014-1017-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zulliger MA, Fridez P, Hayashi K, Stergiopulos N. A strain energy function for arteries accounting for wall composition and structure. J Biomech. 2004;37(7):989–1000. doi: 10.1016/j.jbiomech.2003.11.026. [DOI] [PubMed] [Google Scholar]