Abstract
Introduction
The prediction of late effects after radiotherapy in organs outside a treatment field requires accurate estimations of out-of-field dose. However, out-of-field dose is not calculated accurately by commercial treatment planning systems (TPSs). The purpose of this study was to develop and test an analytical model for out-of-field dose during craniospinal irradiation (CSI) from photon beams produced by a linear accelerator.
Materials & Methods
In two separate evaluations of the model, we measured absorbed dose for a 6-MV CSI using thermoluminescent dosimeters placed throughout an anthropomorphic phantom and fit the measured data to an analytical model of absorbed dose versus distance outside of the composite field edge. These measurements were performed in two separate clinics—The University of Texas MD Anderson Cancer Center (MD Anderson) and the American University of Beirut Medical Center (AUBMC)—using the same phantom but different linear accelerators and TPSs commissioned for patient treatments. The measurement at AUBMC also included in-field locations. Measured dose values were compared to those predicted by TPSs and parameters were fit to the model in each setting.
Results
In each clinic, 95% of the measured data were contained within a factor of 0.2 and one root mean square deviation of the model-based values. The root mean square deviations of the mathematical model were 0.91 cGy/Gy and 1.67 cGy/Gy in the MD Anderson and AUBMC clinics, respectively. The TPS predictions agreed poorly with measurements in regions of sharp dose gradient, e.g., near the field edge. At distances greater than 1 cm from the field edge, the TPS underestimated the dose by an average of 14% ± 24% and 44% ± 19% in the MD Anderson and AUBMC clinics, respectively. The in-field measured dose values of the measurement at AUBMC matched the dose values calculated by the TPS to within 2%.
Conclusions
Dose algorithms in TPSs systematically underestimated the actual out-of-field dose. Therefore, it is important to use an improved model based on measurements when estimating out-of-field dose. The model proposed in this study performed well for this purpose in two clinics and may be applicable in other clinics with similar treatment field configurations.
Keywords: craniospinal irradiation, out-of-field dose, anthropomorphic phantom, thermoluminescent dosimeter, modeling absorbed dose
1. Introduction
Modern radiotherapy techniques seek to cure or control local disease while minimizing acute and late-occurring side effects from radiation. These radiogenic side effects most frequently occur in or near the treatment site but may occur throughout the body because of both in-field and out-of-field radiation exposures (Diallo et al 2009, Armstrong et al 2010). Radiation that contributes to out-of-field, or stray, dose originates in the treatment unit (i.e., leakage radiation and scatter radiation emanating from the treatment head) and in the patient (i.e., patient scatter radiation). Although the amount of stray radiation is small compared to therapeutic doses, they are unavoidable and, in some cases, non-negligible. Exposure to stray radiation increases the risk of biologic detriment, that is, the risk of stochastic effects, including radiogenic cancer, and the severity of deterministic effects, including cataractogenesis. Therefore, it is important to have models that can predict the out-of-field dose from radiation therapy in order to minimize the out-of-field dose to normal tissues while still achieving the desired dose to targeted tissues.
Treatment planning systems (TPSs) are used to model treatment fields that deliver absorbed dose to a clinical target volume while minimizing the dose in normal tissues, ensuring dose is below population-based tolerance levels and avoiding non-target critical structures (Bentzen et al 2010). A great deal of attention has been paid in the literature to the development of a variety of algorithmic models to accurately predict the in-field dose (Mackie et al 1985, Mohan et al 1986, Ahnesjo 1989, Papanikolaou et al 1993, Papanikolaou et al 2004, Sievinen et al 2005, Vassiliev et al 2010, Han et al 2011). However, despite the many decades of research on TPS dose modeling, the accuracy of some commercial TPSs beyond a few centimeters outside the treatment field is poor (Taylor and Kron 2011). For example, a recent study by Howell et al (2010) reported that a widely-used commercial TPS systematically underestimated the out-of-field dose by an average of 40% for a mantle-field irradiation. Huang et al (2013) found a similar result using a different commercial TPS to calculate dose for three modern radiotherapy treatments.
Compared to in-field dose, relatively less attention has been paid to algorithms to model out-of-field doses. Through water-phantom measurements, Stovall et al (1995) showed that a key parameter for modeling out of field dose is the distance from the field edge. In addition, it may be necessary to take into account dependencies on the treatment apparatus (e.g., radiotherapy equipment and its shielding) and the treatment technique (e.g., energy, field size, source-to-skin distance, and treatment site) (Taylor and Kron 2011). A number of other out-of-field dose studies involving measurements of photons produced from electron linear accelerators have been performed (Kase et al 1983, Stovall et al 1995, Howell et al 2006, Kry et al 2007, Wang and Xu 2008, Fontenot et al 2009, Georgiev 2009, Scarboro et al 2010, Ruben et al 2011, Kaderka et al 2012), as have Monte Carlo simulations (Kry et al 2006, Bednarz and Xu 2008, 2009, Athar et al 2010, Kry et al 2010). Most out-of-field dose modeling studies have applied simple empirical analytical methods or Monte Carlo techniques. The empirical models neglect most dependencies and are simple and computationally fast while Monte Carlo simulations typically model more dependencies and result in a high level of accuracy but are consequently more complex geometrically and slower computationally.
Modeling out-of-field dose is particularly important for risk estimation, especially for the treatment of children (Stovall et al 2006, Newhauser and Durante 2011). One of the most common radiotherapies for children with cancer is craniospinal irradiation (CSI). Several dosimetric studies on patients receiving CSI neglected out-of-field doses (St Clair et al 2004, Mu et al 2005, Cochran et al 2008, Merchant et al 2008, South et al 2008, Fogliata et al 2011, Yoon et al 2011, Howell et al 2012). Recently, studies on CSI with proton beams have included stray dose modeling using Monte Carlo methods (Newhauser et al 2009, Taddei et al 2009a, Taddei et al 2009b, Athar et al 2010, Taddei et al 2010a, Taddei et al 2010b, Athar and Paganetti 2011, Perez-Andujar et al 2013, Zhang et al in review). Also recently, analytical models for modeling out-of-field dose from proton therapy have been developed (Zheng et al 2007a, Zheng et al 2007b, Zhang et al 2010); similar analytical models for photon CSI are lacking despite the globally broader use compared to proton CSI. A few very recent studies have estimated out-of-field dose photon CSI (Athar et al 2010, Perez-Andujar et al 2013). However, none of these studies has proposed or tested an analytical model to predict out-of-field dose from photon CSI.
The objective of this study was to develop an analytical model that estimates out-of-field dose from photon CSI. To accomplish this objective, we measured the out-of-field dose by delivering CSI to an anthropomorphic phantom loaded with thermoluminescent dosimeters (TLDs) and developed an analytical model using the measured data. To test whether the model described the system accurately, the model was applied in two independent clinics employing different electron linear accelerators. The resulting, tested model estimates out-of-field dose as a function of distance from the field edge (i.e., from the 50% isodose surface).
2. Methods and Materials
2.1. Treatment apparatus in each clinic
Measurements of absorbed dose for CSI were made in two independent clinics: The University of Texas MD Anderson Cancer Center (MD Anderson) and the American University of Beirut Medical Center (AUBMC). At MD Anderson, the photon CSI was delivered with a clinical linear accelerator (Varian Clinac 2100, Varian Medical Systems, Inc., Palo Alto, California), equipped with a multileaf collimator (Millennium MLC 120-Leaf, Varian Medical Systems, Inc., Palo Alto, California). At AUBMC, the photon CSI was delivered with a different clinical linear accelerator (Artiste, Siemens Medical Solutions USA, Inc., Malvern, Pennsylvania) (Tacke et al 2008, Kluter et al 2011) in clinical operation at the American University of Beirut Medical Center (AUBMC), which is equipped with a multileaf collimator (160 MLC, Siemens Healthcare, Erlangen, Germany). The multileaf collimator was the only accessory used to shape the beam. We attempted to control for confounding factors that might influence comparisons of the results between the two settings by using consistent methods in both clinics. For example, the same phantom and the same type of TLDs were used in each measurement, and the same data analysis methods were applied in each case. However, to ensure clinical realism, slightly different field setups were designed according to the standards of care for photon CSI in the respective clinics, as described in the next section. In each clinic, the TPS, CT scanner, and linear accelerator were commissioned previously for clinical use following widely-accepted procedures (Mutic et al 2003, Das et al 2008, Klein et al 2009).
2.2. Treatment planning, phantom, and imaging
Treatment plans were created following the clinical standards of care for CSI of the central nervous system at each institution. In both settings, the field orientations included lateral opposed cranial fields (right and left) and two posterior-anterior spinal fields (upper and lower). At MD Anderson, the clinical standard of care for photon CSI was followed to design a treatment plan using 6-MV photon fields delivered with the field-in-field technique, with an additional lower-spine field. At AUBMC, the clinical standard of care for photon CSI was followed to design a treatment plan using 6-MV photon fields delivered with three-dimensional conformal radiotherapy. For the purposes of this study, which investigated out-of-field dose, the small difference in the irradiation techniques (i.e., additional fields) had little impact on the results of this study because the contribution to out-of-field dose from leakage radiation for each field was proportional to the monitor units of the field, and the additional lower spine field for the field-in-field technique amounted to less than 2.5% of the monitor units for the CSI treatment. Therefore, for the purpose of developing and testing a model for estimating out-of-field dose in CSI, the two CSI techniques were very similar. Because this study was concerned with out-of-field dose and the dose was delivered in a single fraction, the junctions of the fields were not feathered.
In each clinic, an anthropomorphic phantom (ATOM® Adult Male 701, Computerized Imaging Reference Systems, Inc., Norfolk, Virginia) was imaged, and treatment plans were created as if it were a patient diagnosed with medulloblastoma. The phantom was constructed to represent a reference man 173 cm tall and weighing 73 kg. The phantom was sectioned transaxially into 2.5-cm-thick slices, and the slices used in this study extended from the head to the pelvis, yielding 40 slices in total. Each slice contained a matrix of 0.5-cm-diameter detector plugs with grid spacing of 1.5 cm × 1.5 cm. Additional detector plugs were placed in locations for optimization of organ doses. Materials in the phantom are composed of epoxy resins and polymers that are radiologically tissue equivalent—specifically, to soft tissue, inflated lung, brain, and bone (CIRS 2010). The assembled phantom in the treatment position for the lower spinal field at AUBMC is shown in figure 1.
Figure 1.
Photograph of the anthropomorphic phantom placed in the treatment position at AUBMC for the lower spinal field with indicators verifying the source-to-skin distance and the multileaf collimator leaves. TLDs were placed in plug holes throughout the phantom, and they were also taped to the surface of the phantom to measure skin dose in these locations. The axes show the directions of each coordinate in the DICOM patient coordinate system.
Kilovoltage computed tomography (CT) images were acquired for treatment planning using methods similar to those used for photon CSI at each institution. At MD Anderson, the phantom was placed in the head-first, supine position, the images were reconstructed with a slice thickness of 0.25 cm, and the image set covered the full length of the phantom. At AUBMC, the phantom was placed in the head-first, prone position, the images were reconstructed with a slice thickness of 1 cm, and the image set covered the full length of the phantom.
Using commercial TPSs and the CT image sets, we created two CSI treatment plans. The TPS at MD Anderson was Eclipse (version 8.9, Varian Medical Systems, Inc., Palo Alto, California) with the analytical anisotropic algorithm (AAA) dose algorithm (Sievinen et al 2005), heterogeneity correction, and a 2-mm calculation grid, and the TPS at AUBMC was Panther (version 5.01, Prowess Inc., Concord, California) with the collapsed cone convolution superposition algorithm (Ahnesjo 1989), heterogeneity correction, and a 3-mm calculation grid. The treatment plans in both clinics comprised the following primary treatment fields: two lateral opposed cranial fields and two posterior-anterior spinal fields. Boost fields were not used. The spinal fields were matched so that the proximal field edges met just posterior of the spinal cord. Cranial and upper spinal fields were matched by using a collimator rotation for the cranial fields so that the inferior edge of the cranial fields matched with the superior edge of the upper spinal field. No couch rotation was applied. The plans were designed to deliver the prescription to the brain and cord while keeping the dose at any point in the cord or brain below 115% of the prescribed dose and blocking the face below the anterior and middle cranial fossae. A prescribed dose, DRx, of 30.6 Gy was used for the treatment plans and was delivered in a single fraction during the phantom irradiations. Additional details about the treatment fields are listed in table 1.
Table 1.
Characteristics of each field for the 30.6-Gy, 6-MV CSI treatment. For easier readability, the characteristics of the fields of feathered junctions and field-in-field fields were averaged (Y-jaw settings) or summed (monitor units) in this table.
| AUBMC Fields |
||||
|---|---|---|---|---|
| Description | Right Cranial | Left Cranial | Upper Spinal | Lower Spinal |
| Monitor units | 1701 | 1665 | 3374 | 3656 |
| Gantry angle (°) | 90 | 270 | 0 | 0 |
| Collimator angle (°) | 5.0 | 355.0 | 0 | 0 |
| Dose to calculation point (Gy) | 15.3 | 15.3 | 30.6 | 30.6 |
| X1 jaw (cm) | −11.4 | −9.0 | −3.6 | −4.0 |
| X2 jaw (cm) | 9.0 | 11.4 | 3.1 | 5.0 |
| Y1 jaw (cm) | −9.3 | −9.3 | −12.4 | −17.7 |
| Y2 jaw (cm) | 15.1 | 15.1 | 9.6 | 15.0 |
| Water equivalent depth of calculation point (cm) | 7.64 | 7.86 | 3.74 | 5.66 |
| Effective square (cm) | 15.3 | 15.3 | 9.0 | 10.5 |
| Source-to-skin distance (cm) | 93.4 | 92.0 | 100.0 | 100.0 |
| MD Anderson Fields |
||||
|---|---|---|---|---|
| Description | Right Cranial | Left Cranial | Upper Spinal | Lower Spinal |
| Monitor units | 1700 | 1700 | 3009 | 3213 |
| Gantry angle (°) | 270 | 90 | 0 | 0 |
| Collimator angle (°) | 8.0 | 352.0 | 0 | 0 |
| Dose to calculation point (Gy) | 15.4 | 15.4 | 32.6* | 32.4* |
| X1 jaw (cm) | −12.0 | −12 | −4.2 | −5.3 |
| X2 jaw (cm) | 12.0 | 12 | 4.3 | 4.8 |
| Y1 jaw (cm) | −13.0 | −13.0 | −13.5 | −14.0 |
| Y2 jaw (cm) | 11.0 | 11.0 | 14.6 | 14.6 |
| Water equivalent depth of calculation point (cm) | 10.3 | 10.3 | 4.2 | 6.7 |
| Effective square (cm) | 15.0 | 15.0 | 13.0 | 14.9 |
| Source-to-skin distance (cm) | 92.1 | 92.1 | 100 | 100 |
The spinal fields were normalized to deliver a DRx of 30.6 Gy before the field-in-field fields were added to the plan. The addition of these fields resulted in a 6% increase in the absorbed dose at the calculation points of the spinal fields for the MD Anderson plan. This did not affect the model results because the model was reported in absorbed dose per prescribed dose.
2.3. Measuring absorbed dose
TLD measurements of absorbed dose were made in the anthropomorphic phantom to determine the out-of-field stray radiation dose relative to the in-field therapeutic radiation dose. The linear accelerators used in this study were calibrated according to the American Association of Physicists in Medicine Task Group 51 calibration protocol (Almond et al 1999) by a medical physicist certified by the American Board of Radiology. Additionally, the outputs of the linear accelerators were verified to within 2% on the days of phantom irradiation. In the measurement at MD Anderson, there were 72 TLD locations in organs and tissues throughout the phantom outside of the field or near the field edge. In the measurement at AUBMC, there were 209 TLD locations: 184 were in organs and tissues throughout the phantom outside of the field or near the field edge, 20 were attached to the surface of the phantom to measure skin dose, 3 were at in-field calculation points to verify delivery of the prescribed dose, and 2 were kept outside of the treatment room to quantify background radiation at the facility. A list that maps the TLD locations to organs at risk for radiation-induced cancer was provided by the phantom manufacturer, which included brain, eyes, thyroid, bone marrow, esophagus, thymus, breasts, lungs, liver, pancreas, gall bladder, spleen, stomach, kidneys, adrenals, intestine, prostate, bladder, and testicles.
The dosimeters were composed of lithium fluoride TLD-100 powder capsules (Quantaflux Radiological Services, San Jose, California). This TLD is suitable for measuring out-of-field photon dose in 6-MV radiotherapy (Kry et al 2007, Scarboro et al 2010). The TLDs were calibrated and read by certified technicians at the Radiological Physics Center (MD Anderson, Houston, Texas), which includes an accredited dosimetry calibration laboratory.
The absorbed doses at all TLD locations were collected from the TLD measurements and from the TPS calculations at points corresponding to the TLD locations and compared. The values of D were reported relative to the prescribed therapeutic dose of 30.6 Gy, or D/DRx (in cGy/Gy), for the treatment plan.
The overall uncertainty of the absorbed dose measured by each in-field TLD was 2.5% (Kirby et al 1992). We assumed the uncertainty in the in-field dose calculation would be approximately 2% on the basis of validation measurements obtained at the time of commissioning of each linear accelerator. We did not account for the possibility of systematic uncertainty in the absorbed dose measured by each outof-field TLD because of the non-uniformity of photon spectral fluence in that region (see section 4), however, we would estimate this uncertainty to be less than 12% (Kry et al 2006, Olko et al 2006, Scarboro et al 2011). No information about the uncertainty in the out-of-field dose calculations by the TPSs was available from the manufacturers.
2.4. Distance from the field edge
Absorbed dose in each TLD was plotted as a function of distance from the field edge, r. Distance from the field edge was chosen as the model’s main parameter because, within about 30 cm of the field edge, patient scatter and head scatter are the primary components of out-of-field dose (Kase et al 1983, Stovall et al 1995, Ruben et al 2011) and because in CSI, most points in organs and tissues that are sensitive to radiation damage are within 30 cm of the field edge.
Values of r were determined using the following method. The Cartesian coordinates of each TLD location in the Digital Imaging and Communications in Medicine (DICOM) patient coordinate system (IEC 2000) (figure 1) were identified to within ±0.5 cm for each TLD location using the TPS. The field edge was defined by the boundary of the 50% isodose surface in the TPS, including points lateral to each field and within the geometric path of the field but beyond 50% isodose surface. The 50% isodose surface was converted automatically to a contoured structure using the TPS and exported to an RTSTRUCT DICOM file. Using in-house computational codes on that DICOM file, we extracted the coordinates of each node of the polygon defining the field edge. Then, for each TLD location, we found the coordinates of the node having the shortest distance to that TLD location. This point was determined to within ±0.5 cm. The distance, r, between the two points was calculated using the Euclidean norm, and r was applied to each of the TLD locations. A minor limitation of this process was that the physical distance was used for each point rather than the water-equivalent distance. However, because a large number of TLD locations were used to optimize the parameters of the model, with various materials across the distances, it is reasonable to assume that this did not appreciably influence the applicability of our model. The error in r was taken as the root sum of squares of each independent error in position, or ±0.7 cm.
2.5. Analytical model of dose as a function of distance from the field edge
Following the methods of Zhang et al (2010), we constructed a model having two Gaussian components, with a term for locations near to the composite field edge and a term for locations farther from the composite field edge. Previous experimental studies have suggested exponential (Stovall et al 1995) and power-law (Georgiev 2009) relationships between absorbed dose and distance from the field edge. In each measurement, parameters were fit to a double-Gaussian model for absorbed dose, D (in cGy/Gy), versus r (in cm) as follows:
| (1) |
where σ1 and σ2 were the standard deviations of each Gaussian component, μ1 and μ2 were the means of each Gaussian component, and α1 and α2 were applied to scale the magnitude of each Gaussian component. The parameters σ1, σ2, μ1, μ2, α1, and α2 were allowed to vary. The two Gaussian components were analyzed together and their parameters were fit to the model by minimizing the root mean square deviation, RMSD. The RMSD (in cGy/Gy) was defined as
| (2) |
for each TLD location, i, evaluated for n TLD locations. Because the slope of dose versus distance from the field edge was sharp near the field, the uncertainty in position resulted in a large uncertainty in dose. The penumbra from the beam data for the clinical commissioning of the linear accelerators was approximately 0.8 cm for fields similar to those in this study. Therefore, we limited the fitting of the model to TLD locations that were at least 0.3 cm from the field edge (n = 71 for the MD Anderson measurement and n = 169 for the AUBMC measurement). Because of the known inaccuracies of the TPS in calculating dose in the in-field build-up region, to avoid incorrectly influencing the out-of-field results and model, we excluded those points in the model fitting.
Upper and lower confidence limits were defined to contain 95% of the data points. For the model applied to each data set, a confidence limit, CL, was defined as a multiplicative-factor increase in D plus or minus the RMSD between the model-predicted dose and the measured or calculated dose, or
| (3) |
where A was the multiplicative-factor. The empirical multiplicative factors were determined separately for the confidence limits of each data set so that 95% of the data points were within the confidence limits.
3. Results
3.1. Measured and calculated absorbed dose
The field edge calculated by the TPS in the MD Anderson clinic is shown in figure 2, and the field edge and the location of the calculation points from each field calculated by the TPS in the AUBMC clinic are shown in figure 3. With the exceptions noted in section 2.5, points inside the field edge were considered locations of in-field dose, and points outside the field edge were considered out-of-field dose. In the AUBMC measurement, more TLD locations were in-field, and the in-field doses are listed in table 2 by organ. Of the 36 in-field locations, 10 had differences between the measured and calculated D values of more than 6%. These locations were in sharp gradients in the dose distribution, e.g., near the field edge and build-up regions. At the calculation points for each field, where the dose gradient was not sharp, the measured D values were within 2% of the calculated D values. This result supports the use of these dosimeters to measure absorbed dose up to at least 30 Gy in radiotherapy beams. The broad range of dose values within some organs (skin, liver, bone marrow of the ribs, and rectum) reflects the fact that these organs contain sharp dose gradients.
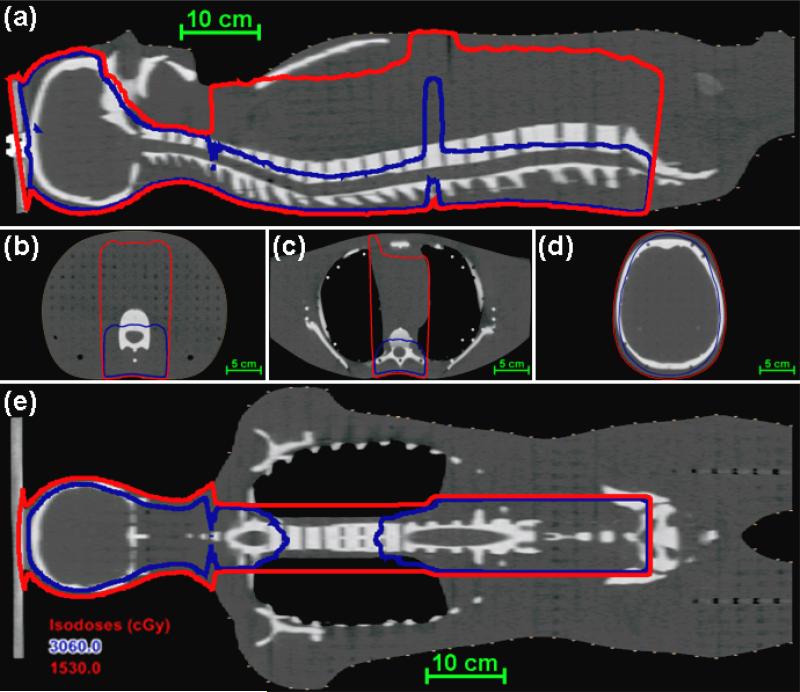
Figure 2.
Dose distribution from the MD Anderson TPS for the CSI of an anthropomorphic phantom in the mid-sagittal plane (a), axial planes (b-d), and a coronal plane (e). The 50% isodose line (D = 0.5DRx) is shown in red, and the 100% isodose (D = DRx) line is shown in blue.
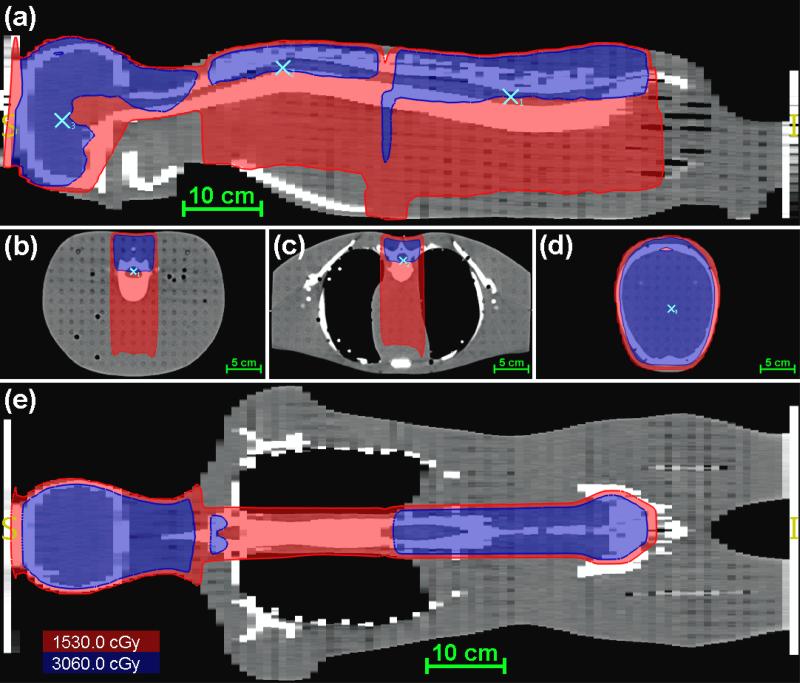
Figure 3.
Dose distribution from the AUBMC TPS for the CSI of an anthropomorphic phantom in the mid-sagittal plane (a), axial planes of the calculation points (b-d), and a coronal plane (e). The red isofill represents the region within the field edge (D ≥ 0.5DRx), the blue isofill represents the region receiving the prescribed dose (D ≥ DRx), and the light blue markers indicate the locations of the calculation points.
Table 2.
Values of absorbed dose for each in-field TLD location for AUBMC, measured by a TLD, DTLD, and calculated by the TPS, DTPS. The organ location of each TLD is listed, but these values were not sampled representatively throughout the organ.
| Organ or location | Slice | DTLD (cGy/Gy) | DTPS (cGy/Gy) |
|---|---|---|---|
| Calculation point, cranial field | 3 | 102.6 | 100.8 |
| Near calculation point, upper spinal field | 15 | 103.1 | 102.7 |
| Calculation point, lower spinal field | 26 | 98.0 | 99.8 |
| Bladder | 32 | 61.2 | 54.7 |
| Bladder | 32 | 56.1 | 59.2 |
| Bladder | 32 | 66.7 | 64.3 |
| Bladder | 32 | 58.9 | 58.5 |
| Bladder | 33 | 53.4 | 52.4 |
| Bladder | 33 | 60.3 | 57.1 |
| Bladder | 33 | 76.6 | 71.7 |
| Bone marrow – ribs | 14 | 23.9 | 53.8 |
| Bone marrow – ribs | 17 | 103.6 | 101.7 |
| Intestine | 27 | 54.4 | 55.7 |
| Intestine | 29 | 57.0 | 57.8 |
| Intestine | 31 | 50.5 | 50.9 |
| Intestine | 31 | 65.9 | 64.2 |
| Liver | 20 | 63.0 | 86.0 |
| Liver | 20 | 55.8 | 71.3 |
| Liver | 20 | 65.9 | 99.5 |
| Liver | 21 | 44.9 | 51.3 |
| Liver | 21 | 60.6 | 61.4 |
| Liver | 21 | 66.8 | 66.3 |
| Liver | 22 | 53.7 | 54.6 |
| Liver | 22 | 56.4 | 56.0 |
| Liver | 22 | 73.1 | 72.7 |
| Approximate position of ovaries | 31 | 72.2 | 68.3 |
| Pancreas | 23 | 64.9 | 64.4 |
| Pancreas | 24 | 75.9 | 75.5 |
| Rectum | 33 | 11.3 | 82.4 |
| Skin, mid-posterior | 4 | 92.8 | 64.5 |
| Skin, mid-posterior | 16 | 63.6 | 32.8 |
| Skin, mid-posterior | 27 | 67.7 | 2.8 |
| Stomach | 21 | 70.8 | 71.6 |
| Stomach | 22 | 56.9 | 58.2 |
| Stomach | 24 | 55.7 | 56.9 |
| Stomach | 26 | 53.6 | 55.0 |
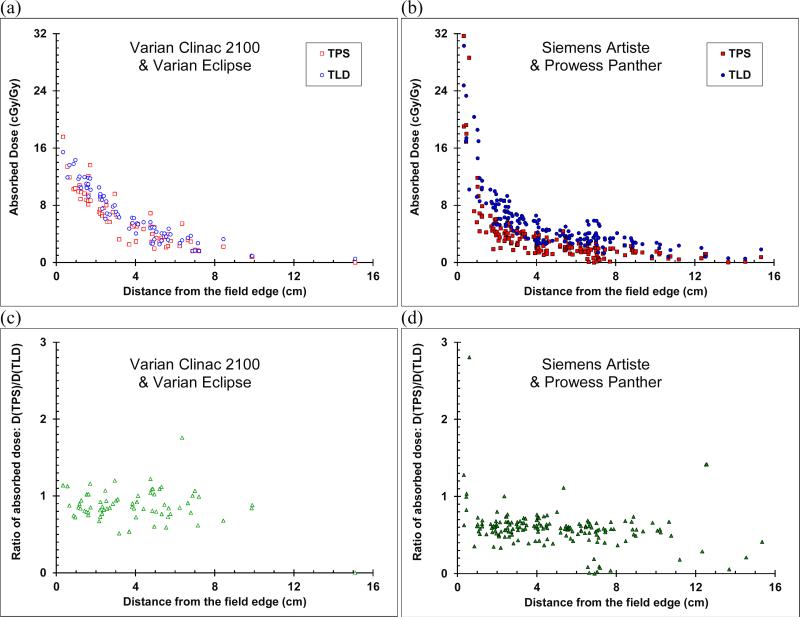
The out-of-field absorbed dose values versus distance from field edge for both the TLD measurements and the TPS calculations are plotted in figure 4a in the MD Anderson setting (Varian Clinac 2100) and figure 4b for the AUBMC setting (Siemens Artiste). In the latter setting, with increasing distance, the dose decreased more rapidly very near the field edge (r < 1.0 cm), less rapidly near the field edge (1.0 cm ≤ r < 2.5 cm) and gradually away from the field edge (r ≥ 2.5 cm). However, in the former setting, the dose decreased less rapidly very near and near the field edge (r < 2.5 cm) and gradually away from the field edge (r ≥ 2.5 cm).
Figure 4.
Out-of-field absorbed dose versus distance from the field edge for the CSI of an anthropomorphic phantom, calculated by the TPS (red squares) and measured with TLDs (blue circles) for (a) the clinic at MD Anderson and (b) the clinic at AUBMC. The ratio of dose calculated by the TPS to dose measured by the TLD (green triangles) (c) at MD Anderson and (d) at AUBMC. For clarity, error bars were not plotted. Uncertainties in values are given in the text in section 2.3.
In both cases, away from the field edge, the TPS generally underestimated the absorbed dose, and more so at AUBMC with the Siemens Artiste and the Prowess Panther TPS. This result is illustrated in figures 4c and 4d, which plots the ratio of absorbed dose calculated by the TPS to the corresponding measured absorbed dose. For all points outside the field edge, the average ratio of TPS dose to TLD dose was 0.87 (standard deviation 0.24) and 0.59 (standard deviation 0.27) for the MD Anderson and AUBMC clinics, respectively. For r > 1.0 cm, the average ratio of TPS dose to TLD dose was 0.86 (standard deviation 0.24) and 0.56 (standard deviation 0.19) for the MD Anderson and AUBMC clinics, respectively. In the AUBMC measurement, very near (r < 1.0 cm), near (1.0 cm ≤ r < 2.5 cm), and away (r ≥ 2.5 cm) from the field edge, the average ratios were 0.92, 0.88, and 0.86 (standard deviations 0.20, 0.12, and 0.28), respectively. In the AUBMC measurement, these average ratios were 1.07, 0.60, and 0.55 (standard deviations 0.76, 0.13, and 0.21), respectively.
3.2. Model of dose as a function of distance from the field edge
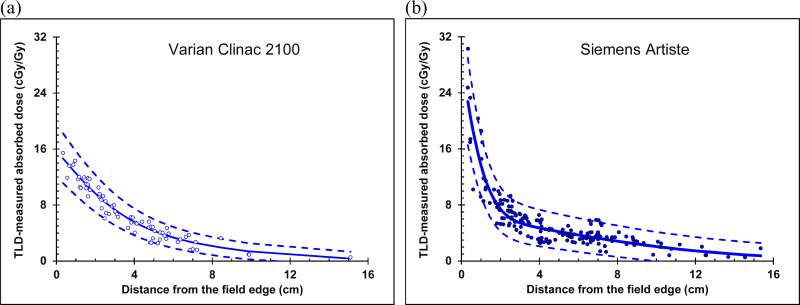
The double-Gaussian model parameters were fit to the measured data separately for the measurement in each clinic. Parameter values are listed in table 3. The model-predicted curves of absorbed dose as a function of distance from the field edge are plotted in figure 5 along with the measured data. In the near-field region (r < 2.5 cm), the data for the MD Anderson measurement had a steeper slope than data for the AUBMC measurement. Because of this, the coefficient of the first term (α1) was much larger for the AUBMC clinic than the MD Anderson clinic. Away from the field (r ≥ 2.5 cm), the out of field dose curves versus distance were very similar in shape, giving them comparable values of sigma for the second term of the double-Gaussian model (σ2).
Table 3.
Fitting parameters for the double-Gaussian model for the TLD measurements in this study for r > 0.3 cm in the two clinical settings.
| Parameter | MD Anderson model fit | AUBMC model fit |
|---|---|---|
| α1 (cm-cGy/Gy) | 148.3 | 224.8 |
| μ1 (cm) | −3.89 | −2.16 |
| α1 (cm) | 3.57 | 1.57 |
| α2 (cm-cGy/Gy) | 196.7 | 224.3 |
| μ2 (cm) | −6.80 | −7.43 |
| σ2 (cm) | 8.58 | 10.28 |
Figure 5.
Out-of-field absorbed dose (blue circles) versus distance from the field edge for the CSI of an anthropomorphic phantom measured with TLDs overlaid by the double-Gaussian model fit (blue line) to the data, with upper and lower confidence limits (blue dashed lines) for (a) the measurement at MD Anderson and (b) the measurement at AUBMC.
The confidence limits were slightly narrower for the MD Anderson data than for the AUBMC data. For the confidence limits in the MD Anderson measured data, the multiplicative factor was 0.18, and the RMSD of the deviation between the fit and the data was 0.91 cGy/Gy. Both values were larger for the confidence limits in the AUBMC measured data, with a multiplicative factor of 0.20, and the RMSD between the fit and the data was 1.67 cGy/Gy.
4. Discussion
In two different clinical settings, we measured out-of-field dose for a photon CSI and fit an analytical model to the data. The model was tested separately with measured data from MD Anderson, using a Varian Clinac 2100 linear accelerator, and with measured data from AUBMC, using a Siemens Artiste linear accelerator. Our results show that out-of-field absorbed dose in CSI decreases with increasing distance from the field edge, approximately following a double-Gaussian model. This model estimated out-of-field dose particularly well for distances greater than 1 cm from the field edge whereas the TPS calculations systematically underestimated the dose in this region. Between the two clinics, the fitted parameters of the model were different near the field and similar away from the field edge. Based on these findings, it appears that a hybrid approach is most appropriate in estimating out-of-field dose in photon CSI, in which the TPS is used in regions of high dose or sharp dose gradients, i.e., in the in-field and very-near-field (r < 1 cm) regions, and the analytical model is used elsewhere.
Our dose measurements and fitted model parameters were specific to the treatment site, treatment apparatus, and treatment technique used. The model parameters found in this study may be applied directly for 6-MV photon CSI with linear accelerators and multileaf collimators similar to the two settings in this study (i.e., delivered with three-dimensional conformal or very similar radiotherapy) but should be reassessed for clinics with different linear accelerators or very different treatment techniques (e.g., intensity-modulated radiation therapy). The findings of other previous studies support this view. For example, Stovall et al (1995) reported out-of-field doses for 6-MV 10 cm × 10 cm reference fields delivered by another commercial linear accelerator (Clinac 2100C, Varian Medical Systems, Inc., Palo Alto, California) without a multileaf collimator that were about a factor of 2 lower than our absorbed dose values. In another study, for pelvic fields to treat prostate cancer delivered with 18-MV intensity-modulated radiation therapy (21EX, Varian Medical Systems, Inc., Palo Alto, California), Kry et al (2009) reported out-of-field photon absorbed doses that were about a factor of 10 less than our values.
Our findings are in good agreement with previous out-of-field dose studies in the literature. In the most closely-matched study, Georgiev (2009) measured the absorbed dose in organs in a pediatric anthropomorphic phantom for a 6-MV CSI delivered with three-dimensional conformal radiotherapy by a with a Varian 21EX linear accelerator. He reported dose values at 2.26 cGy/Gy and 1.18 cGy/Gy in the breast bud and pelvic bone marrow, respectively, while our dose values in the AUBMC measurement setting were 3.80 cGy/Gy and 4.62 cGy/Gy in the breast and pelvic bone marrow regions, respectively. Considering that he used a different linear accelerator and phantom, his results were in reasonably good agreement with ours. The variation in out-of-field dose between studies underscores the importance of re-fitting the measurement-based parameters in the model to be specific to the treatment apparatus, site, and technique by minimizing the RMSD. The model may also be applicable to other treatment sites. However, this possibility should first be confirmed by performing experiments with conditions similar to those in our study.
At high dose points in a region with a sharp gradient, e.g., near the field edge, the dose measured by the TLDs generally did not match the dose predicted by the TPS. In this region, even a small uncertainty in the location of the TLD (estimated at ±0.7 cm), together with the possibility of a sharp dose gradient, may have caused a large discrepancy between the TPS prediction and the TLD measurement. Additionally, other factors may have contributed to this discrepancy, for example, the difference in the beam quality in our clinical scenario versus reference conditions. For these reasons, we recommend using TPS calculations for dosimetric analysis of in-field or very-near-field (r < 1 cm) dose and not doses from TLDs or from the model developed in this study.
Except in the region very near the field edge (r < 1.0 cm), the TPS underestimated the out-of-field dose, and this underestimation generally increased with distance from the field edge. These findings agree with those of Howell et al (2010) for a different treatment site. They found that, for a 6-MV mantle field irradiation, their TPS underestimated the out-of-field dose by an average of 40% for 3.75 < r < 11.25 cm and that the underestimation increased with increasing distance from the field edge. This confirms the importance of using a hybrid approach such as the one developed in this study instead of relying solely on a TPS to calculate dose throughout a patient's body.
This study had three notable strengths. First, the out-of-field dose measurements were performed in clinically-realistic fields and in a phantom designed to simulate an actual patient. Previous out-of-field dose studies were based on non-clinical or reference fields. Second, it provided an analytical model for potential applications in other clinics or laboratories making similar out-of-field measurements. This model is useful for CSI studies that require estimates of out-of-field dose, for example studies that assess the incidence of biological effects in healthy tissue. Third, the model was tested and shown to be applicable in two different clinical scenarios, with linear accelerators and multileaf collimators from different manufacturers.
One limitation of our approach to determining out-of-field dose is that this model does not take into account the depth dependence of out-of-field dose. For example, although some TLD locations were included in the parameter fitting that were in the geometric path of the field but beyond the distal 50% isodose surface, the model should not be applied in this region. This limitation of the model may be important in complex field setups, e.g., arc therapy. However, in the case of photon CSI, this is a minor limitation because the 50% isodose surface extends to or near the distal surface of the patient along the beam path. Another minor limitation of our study was the imprecise determination of distance from the field edge, but this limitation only weakly affects the estimation of dose for r > 1 cm, which is our recommended minimum distance at which to apply this model. Finally, the variations in photon spectral fluence for locations out of field can affect the accuracy of TLD measurements. Scarboro et al (2011) observed a systematic overestimation by TLDs used in non-calibration conditions, e.g., out-of-field dose measurements, and proposed correction factors between 0.88 to 0.99. However, it was infeasible to apply these factors in our study having composite plans, elongated fields, and unknown photon spectral fluence and mean energy at each TLD location. Therefore, based on their findings, the absorbed dose values in our TLD measurements may have been slightly overestimated yet were still a vast improvement in accuracy compared to the TPS-calculated values.
In conclusion, we have measured out-of-field dose for two 6-MV CSIs in two clinical settings, and we developed and tested an analytical model that estimates the out-of-field dose versus distance from the field edge. This model is useful for studies that require an estimate of out-of-field dose for patients who receive 6-MV CSI, for example those that estimate the risk of radiogenic acute and late effects in healthy tissue.
Acknowledgments
We are indebted to Kathryn Carnes for her assistance in the preparation of this manuscript. The authors are grateful to Drs. Bassem Youssef and Toufic Eid for treatment planning and Mr. Wissam Kiwan for his assistance with the CT data set. We thank the Radiological Physics Center for dosimetric analysis of the TLDs and assistance with the selection of an appropriate phantom. This work was supported in part by Fogarty International Center award K01TW008409 (PI Taddei), by National Cancer Institute award R01CA131463-01A1 (PI Newhauser) and a subcontract of that award (PI Howell), and by Northern Illinois University through a subcontract of Department of Defense (award W81XWH-08-1-0205). The content is solely the responsibility of the authors and does not necessarily represent the official views of the sponsors.
Footnotes
Each author does not have a conflict of interest.
References
- Ahnesjo A. Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media. Med Phys. 1989;16:577–92. doi: 10.1118/1.596360. [DOI] [PubMed] [Google Scholar]
- Almond PR, Biggs PJ, Coursey BM, Hanson WF, Huq MS, Nath R, Rogers DW. AAPM's TG-51 protocol for clinical reference dosimetry of high-energy photon and electron beams. Med Phys. 1999;26:1847–70. doi: 10.1118/1.598691. [DOI] [PubMed] [Google Scholar]
- Armstrong GT, Stovall M, Robison LL. Long-Term Effects of Radiation Exposure among Adult Survivors of Childhood Cancer: Results from the Childhood Cancer Survivor Study. Radiat Res. 2010;174:840–50. doi: 10.1667/RR1903.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athar BS, Bednarz B, Seco J, Hancox C, Paganetti H. Comparison of out-of-field photon doses in 6 MV IMRT and neutron doses in proton therapy for adult and pediatric patients. Phys Med Biol. 2010;55:2879–91. doi: 10.1088/0031-9155/55/10/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athar BS, Paganetti H. Comparison of second cancer risk due to out-of-field doses from 6-MV IMRT and proton therapy based on 6 pediatric patient treatment plans. Radiother Oncol. 2011;98:87–92. doi: 10.1016/j.radonc.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednarz B, Xu XG. A feasibility study to calculate unshielded fetal doses to pregnant patients in 6-MV photon treatments using Monte Carlo methods and anatomically realistic phantoms. Med Phys. 2008;35:3054–61. doi: 10.1118/1.2938519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednarz B, Xu XG. Monte Carlo modeling of a 6 and 18 MV Varian Clinac medical accelerator for in-field and out-of-field dose calculations: development and validation. Phys Med Biol. 2009;54:N43–57. doi: 10.1088/0031-9155/54/4/N01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentzen SM, Constine LS, Deasy JO, Eisbruch A, Jackson A, Marks LB, Haken RK, Yorke ED. Quantitative Analyses of Normal Tissue Effects in the Clinic (QUANTEC): an introduction to the scientific issues. Int J Radiat Oncol Biol Phys. 2010;76:S3–9. doi: 10.1016/j.ijrobp.2009.09.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CIRS . ATOM® Dosimetry Phantoms: Models 700 – 705, Reference PB ATOM 082310. Computerized Imaging Reference Systems, Inc.; Norfolk, Virginia: 2010. [Google Scholar]
- Cochran DM, Yock TI, Adams JA, Tarbell NJ. Radiation dose to the lens during craniospinal irradiation-an improvement in proton radiotherapy technique. Int J Radiat Oncol Biol Phys. 2008;70:1336–42. doi: 10.1016/j.ijrobp.2007.08.027. [DOI] [PubMed] [Google Scholar]
- Das IJ, Cheng CW, Watts RJ, Ahnesjo A, Gibbons J, Li XA, Lowenstein J, Mitra RK, Simon WE, Zhu TC. Accelerator beam data commissioning equipment and procedures: report of the TG-106 of the Therapy Physics Committee of the AAPM. Med Phys. 2008;35:4186–215. doi: 10.1118/1.2969070. [DOI] [PubMed] [Google Scholar]
- Diallo I, et al. Frequency distribution of second solid cancer locations in relation to the irradiated volume among 115 patients treated for childhood cancer. Int J Radiat Oncol Biol Phys. 2009;74:876–83. doi: 10.1016/j.ijrobp.2009.01.040. [DOI] [PubMed] [Google Scholar]
- Fogliata A, et al. Cranio-spinal irradiation with volumetric modulated arc therapy: a multi-institutional treatment experience. Radiother Oncol. 2011;99:79–85. doi: 10.1016/j.radonc.2011.01.023. [DOI] [PubMed] [Google Scholar]
- Fontenot JD, Lee AK, Newhauser WD. Risk of secondary malignant neoplasms from proton therapy and intensity-modulated x-ray therapy for early-stage prostate cancer. Int J Radiat Oncol Biol Phys. 2009;74:616–22. doi: 10.1016/j.ijrobp.2009.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgiev GN. Comparison of secondary doses in pediatric patients from craniospinal irradiations using photon, proton and electron spinal fields (Master's Thesis) The University of Texas Graduate School of Biomedical Sciences at Houston; Houston, TX: 2009. [Google Scholar]
- Han T, Mikell JK, Salehpour M, Mourtada F. Dosimetric comparison of Acuros XB deterministic radiation transport method with Monte Carlo and model-based convolution methods in heterogeneous media. Med Phys. 2011;38:2651–64. doi: 10.1118/1.3582690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell RM, Giebeler A, Koontz-Raisig W, Mahajan A, Etzel CJ, D'Amelio AM, Jr., Homann KL, Newhauser WD. Comparison of therapeutic dosimetric data from passively scattered proton and photon craniospinal irradiations for medulloblastoma. Radiat Oncol. 2012;7:116. doi: 10.1186/1748-717X-7-116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell RM, Hertel NE, Wang Z, Hutchinson J, Fullerton GD. Calculation of effective dose from measurements of secondary neutron spectra and scattered photon dose from dynamic MLC IMRT for 6 MV, 15 MV, and 18 MV beam energies. Med Phys. 2006;33:360–8. doi: 10.1118/1.2140119. [DOI] [PubMed] [Google Scholar]
- Howell RM, Scarboro SB, Kry SF, Yaldo DZ. Accuracy of out-of-field dose calculations by a commercial treatment planning system. Phys Med Biol. 2010;55:6999–7008. doi: 10.1088/0031-9155/55/23/S03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang JY, Followill DS, Wang XA, Kry SF. Accuracy and sources of error of out-of field dose calculations by a commercial treatment planning system for intensity-modulated radiation therapy treatments. J Appl Clin Med Phys. 2013;14:186. doi: 10.1120/jacmp.v14i2.4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IEC . International Standard, Amendment 1: Radiotherapy equipment – Coordinates, movements and scales. Report 61217 of the International Electrotechnical Commission. International Electrotechnical Commission; Geneva, Switzerland: 2000. [Google Scholar]
- Kaderka R, Schardt D, Durante M, Berger T, Ramm U, Licher J, La Tessa C. Out-of-field dose measurements in a water phantom using different radiotherapy modalities. Phys Med Biol. 2012;57:5059–74. doi: 10.1088/0031-9155/57/16/5059. [DOI] [PubMed] [Google Scholar]
- Kase KR, Svensson GK, Wolbarst AB, Marks MA. Measurements of dose from secondary radiation outside a treatment field. Int J Radiat Oncol Biol Phys. 1983;9:1177–83. doi: 10.1016/0360-3016(83)90177-3. [DOI] [PubMed] [Google Scholar]
- Kirby TH, Hanson WF, Johnston DA. Uncertainty analysis of absorbed dose calculations from thermoluminescence dosimeters. Med Phys. 1992;19:1427–33. doi: 10.1118/1.596797. [DOI] [PubMed] [Google Scholar]
- Klein EE, et al. Task Group 142 report: quality assurance of medical accelerators. Med Phys. 2009;36:4197–212. doi: 10.1118/1.3190392. [DOI] [PubMed] [Google Scholar]
- Kluter S, Sroka-Perez G, Schubert K, Debus J. Leakage of the Siemens 160 MLC multileaf collimator on a dual energy linear accelerator. Phys Med Biol. 2011;56:N29–37. doi: 10.1088/0031-9155/56/2/N02. [DOI] [PubMed] [Google Scholar]
- Kry SF, Price M, Followill D, Mourtada F, Salehpour M. The use of LiF (TLD-100) as an out of-field dosimeter. J Appl Clin Med Phys. 2007;8:2679. doi: 10.1120/jacmp.v8i4.2679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kry SF, Salehpour M, Titt U, White RA, Stovall M, Followill D. Monte Carlo study shows no significant difference in second cancer risk between 6-and 18-MV intensity-modulated radiation therapy. Radiother Oncol. 2009;91:132–7. doi: 10.1016/j.radonc.2008.11.020. [DOI] [PubMed] [Google Scholar]
- Kry SF, Titt U, Ponisch F, Followill D, Vassiliev ON, White RA, Mohan R, Salehpour M. A Monte Carlo model for calculating out-of-field dose from a Varian 6 MV beam. Med Phys. 2006;33:4405–13. doi: 10.1118/1.2360013. [DOI] [PubMed] [Google Scholar]
- Kry SF, Vassiliev ON, Mohan R. Out-of-field photon dose following removal of the flattening filter from a medical accelerator. Phys Med Biol. 2010;55:2155–66. doi: 10.1088/0031-9155/55/8/003. [DOI] [PubMed] [Google Scholar]
- Mackie TR, Scrimger JW, Battista JJ. A convolution method of calculating dose for 15-MV x rays. Med Phys. 1985;12:188–96. doi: 10.1118/1.595774. [DOI] [PubMed] [Google Scholar]
- Merchant TE, Hua CH, Shukla H, Ying X, Nill S, Oelfke U. Proton versus photon radiotherapy for common pediatric brain tumors: comparison of models of dose characteristics and their relationship to cognitive function. Pediatr Blood Cancer. 2008;51:110–7. doi: 10.1002/pbc.21530. [DOI] [PubMed] [Google Scholar]
- Mohan R, Chui C, Lidofsky L. Differential pencil beam dose computation model for photons. Med Phys. 1986;13:64–73. doi: 10.1118/1.595924. [DOI] [PubMed] [Google Scholar]
- Mu X, Bjork-Eriksson T, Nill S, Oelfke U, Johansson KA, Gagliardi G, Johansson L, Karlsson M, Zackrisson DB. Does electron and proton therapy reduce the risk of radiation induced cancer after spinal irradiation for childhood medulloblastoma? A comparative treatment planning study. Acta Oncol. 2005;44:554–62. doi: 10.1080/02841860500218819. [DOI] [PubMed] [Google Scholar]
- Mutic S, Palta JR, Butker EK, Das IJ, Huq MS, Loo LN, Salter BJ, McCollough CH, Van Dyk J. Quality assurance for computed-tomography simulators and the computed-tomography-simulation process: report of the AAPM Radiation Therapy Committee Task Group No. 66. Med Phys. 2003;30:2762–92. doi: 10.1118/1.1609271. [DOI] [PubMed] [Google Scholar]
- Newhauser WD, Durante M. Assessing the risk of second malignancies after modern radiotherapy. Nat Rev Cancer. 2011;11:438–48. doi: 10.1038/nrc3069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhauser WD, et al. The risk of developing a second cancer after receiving craniospinal proton irradiation. Phys Med Biol. 2009;54:2277–91. doi: 10.1088/0031-9155/54/8/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olko P, Bilski P, El-Faramawy NA, Goksu HY, Kim JL, Kopec R, Waligorski MP. On the relationship between dose-, energy-and LET-response of thermoluminescent detectors. Radiat Prot Dosimetry. 2006;119:15–22. doi: 10.1093/rpd/nci611. [DOI] [PubMed] [Google Scholar]
- Papanikolaou N, Battista JJ, Boyer AL, Kappas C, Klein E, Mackie TR, Sharpe M, Van Dyke J. AAPM Report 85: Tissue inhomogeneity corrections for MV photon beams. Report of Task Group No. 65 of the Radiation Therapy Committee of the American Association of Physicists in Medicine. Medical Physics Publishing; Madison, Wisconsin: 2004. [Google Scholar]
- Papanikolaou N, Mackie TR, Meger-Wells C, Gehring M, Reckwerdt P. Investigation of the convolution method for polyenergetic spectra. Med Phys. 1993;20:1327–36. doi: 10.1118/1.597154. [DOI] [PubMed] [Google Scholar]
- Perez-Andujar A, Newhauser WD, Taddei PJ, Mahajan A, Howell RM. The predicted relative risk of premature ovarian failure for three radiotherapy modalities in a girl receiving craniospinal irradiation. Phys Med Biol. 2013;58:3107–23. doi: 10.1088/0031-9155/58/10/3107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruben JD, Lancaster CM, Jones P, Smith RL. A comparison of out-of-field dose and its constituent components for intensity-modulated radiation therapy versus conformal radiation therapy: implications for carcinogenesis. Int J Radiat Oncol Biol Phys. 2011;81:1458–64. doi: 10.1016/j.ijrobp.2010.08.008. [DOI] [PubMed] [Google Scholar]
- Scarboro SB, Followill DS, Howell RM, Kry SF. Variations in photon energy spectra of a 6 MV beam and their impact on TLD response. Med Phys. 2011;38:2619–28. doi: 10.1118/1.3575419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarboro SB, Stovall M, White A, Smith SA, Yaldo D, Kry SF, Howell RM. Effect of organ size and position on out-of-field dose distributions during radiation therapy. Phys Med Biol. 2010;55:7025–36. doi: 10.1088/0031-9155/55/23/S05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sievinen J, Ulmer W, Kaissl W. AAA Photon Dose Calculation Model in Eclipse™ RAD #7170A. Varian Medical Systems, Inc.; Palo Alto, California: 2005. [Google Scholar]
- South M, Chiu JK, Teh BS, Bloch C, Schroeder TM, Paulino AC. Supine craniospinal irradiation using intrafractional junction shifts and field-in-field dose shaping: early experience at Methodist Hospital. Int J Radiat Oncol Biol Phys. 2008;71:477–83. doi: 10.1016/j.ijrobp.2007.10.029. [DOI] [PubMed] [Google Scholar]
- St Clair WH, Adams JA, Bues M, Fullerton BC, La Shell S, Kooy HM, Loeffler JS, Tarbell NJ. Advantage of protons compared to conventional X-ray or IMRT in the treatment of a pediatric patient with medulloblastoma. Int J Radiat Oncol Biol Phys. 2004;58:727–34. doi: 10.1016/S0360-3016(03)01574-8. [DOI] [PubMed] [Google Scholar]
- Stovall M, Blackwell CR, Cundiff J, Novack DH, Palta JR, Wagner LK, Webster EW, Shalek RJ. Fetal dose from radiotherapy with photon beams: report of AAPM Radiation Therapy Committee Task Group No. 36. Med Phys. 1995;22:63–82. doi: 10.1118/1.597525. [DOI] [PubMed] [Google Scholar]
- Stovall M, Weathers R, Kasper C, Smith SA, Travis L, Ron E, Kleinerman R. Dose reconstruction for therapeutic and diagnostic radiation exposures: use in epidemiological studies. Radiat Res. 2006;166:141–57. doi: 10.1667/RR3525.1. [DOI] [PubMed] [Google Scholar]
- Tacke MB, Nill S, Haring P, Oelfke U. 6 MV dosimetric characterization of the 160 MLC, the new Siemens multileaf collimator. Med Phys. 2008;35:1634–42. doi: 10.1118/1.2889782. [DOI] [PubMed] [Google Scholar]
- Taddei PJ, Howell RM, Krishnan S, Scarboro SB, Mirkovic D, Newhauser WD. Risk of second malignant neoplasm following proton versus intensity-modulated photon radiotherapies for hepatocellular carcinoma. Phys Med Biol. 2010a;55:7055–65. doi: 10.1088/0031-9155/55/23/S07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei PJ, Mahajan A, Mirkovic D, Zhang R, Giebeler A, Kornguth D, Harvey M, Woo S, Newhauser WD. Predicted risks of second malignant neoplasm incidence and mortality due to secondary neutrons in a girl and boy receiving proton craniospinal irradiation. Phys Med Biol. 2010b;55:7067–80. doi: 10.1088/0031-9155/55/23/S08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei PJ, Mirkovic D, Fontenot JD, Giebeler A, Zheng Y, Kornguth D, Mohan R, Newhauser WD. Stray radiation dose and second cancer risk for a pediatric patient receiving craniospinal irradiation with proton beams. Phys Med Biol. 2009a;54:2259–75. doi: 10.1088/0031-9155/54/8/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddei PJ, Mirkovic D, Fontenot JD, Giebeler A, Zheng Y, Titt U, Woo S, Newhauser WD. Reducing stray radiation dose for a pediatric patient receiving proton craniospinal irradiation. Nucl Technol. 2009b;168:108–12. doi: 10.13182/nt09-a9108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor ML, Kron T. Consideration of the radiation dose delivered away from the treatment field to patients in radiotherapy. J Med Phys. 2011;36:59–71. doi: 10.4103/0971-6203.79686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vassiliev ON, Wareing TA, McGhee J, Failla G, Salehpour MR, Mourtada F. Validation of a new grid-based Boltzmann equation solver for dose calculation in radiotherapy with photon beams. Phys Med Biol. 2010;55:581–98. doi: 10.1088/0031-9155/55/3/002. [DOI] [PubMed] [Google Scholar]
- Wang B, Xu XG. Measurements of non-target organ doses using MOSFET dosemeters for selected IMRT and 3D CRT radiation treatment procedures. Radiat Prot Dosim. 2008;128:336–42. doi: 10.1093/rpd/ncm363. [DOI] [PubMed] [Google Scholar]
- Yoon M, et al. Craniospinal irradiation techniques: a dosimetric comparison of proton beams with standard and advanced photon radiotherapy. Int J Radiat Oncol Biol Phys. 2011;81:637–46. doi: 10.1016/j.ijrobp.2010.06.039. [DOI] [PubMed] [Google Scholar]
- Zhang R, Howell RH, Homann K, Giebeler A, Taddei PJ, Mahajan A, Newhauser WD. Predicted risks of radiogenic cardiac toxicity in pediatric patients undergoing photon or proton radiotherapy. doi: 10.1186/1748-717X-8-184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Perez-Andujar A, Fontenot JD, Taddei PJ, Newhauser WD. An analytic model of neutron ambient dose equivalent and equivalent dose for proton radiotherapy. Phys Med Biol. 2010;55:6975–85. doi: 10.1088/0031-9155/55/23/S01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Newhauser W, Fontenot J, Koch N, Mohan R. Monte Carlo simulations of stray neutron radiation exposures in proton therapy. J Nucl Matl. 2007a;361:289–97. [Google Scholar]
- Zheng Y, Newhauser W, Fontenot J, Taddei P, Mohan R. Monte Carlo study of neutron dose equivalent during passive scattering proton therapy. Phys Med Biol. 2007b;52:4481–96. doi: 10.1088/0031-9155/52/15/008. [DOI] [PubMed] [Google Scholar]