Estimation of a Semiparametric Natural Direct Effect Model Incorporating Baseline Covariates

SUMMARY

Establishing cause-effect relationships is a standard goal of empirical science. Once the presence of a causal relationship is established, the precise causal mechanism involved becomes a topic of interest. A particularly popular type of mechanism analysis concerns questions of mediation, that is to what extent an effect is direct, and to what extent it is mediated by a third variable. A semiparametric theory has recently been proposed which allows multiply robust estimation of direct and mediated marginal effect functionals in observational studies (Tchetgen Tchetgen & Shpitser, 2012). In this paper we extend the new theory to handle parametric models of natural direct and indirect effects within levels of pre-exposure variables with an identity or log link function, where the model for the observed data likelihood is otherwise unrestricted. We show that estimation is generally not feasible in this model because of the curse of dimensionality associated with the required estimation of auxiliary conditional densities or expectations, given high-dimensional covariates. Thus, we consider multiply robust estimation and propose a more general model which assumes that a subset but not all of several working models holds.

1. INTRODUCTION

Researchers in the health and social sciences are becoming increasingly interested in mediation analysis. After establishing the total effect of an exposure, investigators routinely wish to make inferences about the direct or indirect pathway of the effect of the exposure mediated by a third variable. The natural, also known as the pure, direct effect captures the effect of the exposure when one intervenes to set the mediator to the level it would have taken in the absence of exposure (Robins & Greenland, 1992; Pearl, 2001). Such an effect generally differs from the controlled direct effect, which refers to the exposure effect that arises after intervening to set the mediator to a fixed level that may differ from its actual observed value (Robins & Greenland, 1992; Pearl, 2001; Robins, 2003). As noted by Pearl (2001), controlled direct effects are particularly relevant for policy making, whereas natural direct and indirect effects are more useful for understanding the underlying mechanism by which the exposure operates.

A semiparametric theory has recently been proposed to make inferences about marginal average natural direct and indirect effects in observational studies (Tchetgen Tchetgen & Shpitser, 2012). The approach is appealing because it delivers multiply robust locally efficient estimators of the marginal direct and indirect effects, and thus generalizes previous results for total effects to the context of mediation. In this paper we extend the new theory to handle parametric models of natural direct and indirect effects within levels of pre-exposure variables with an identity or log link function, where the model for the observed data likelihood is otherwise unrestricted. Conditional models for direct and indirect effects are of interest in making inferences about so-called moderated mediation effects, a topic of interest particularly in psychology (Muller et al., 2005; Preacher et al., 2007; Mackinnon, 2008). These models are useful for assessing the extent to which a pre-exposure variable modifies either the natural direct, or indirect effect of exposure.

We show that estimation of the parameter indexing a model for the direct or indirect effect is infeasible in this model because of the curse of dimensionality associated with the required estimation of auxiliary conditional densities or expectations, given high-dimensional covariates. To address this, we consider a multiply robust approach and propose a more general model under which a subset of several working models holds. We recover the results of Tchetgen Tchetgen & Shpitser (2012) as a special case. We characterize the efficiency bound for the finite dimensional parameter of a model for a conditional natural direct or indirect effect, and we develop a corresponding multiply robust locally efficient estimator, which is consistent and asymptotically normal in the more general semiparametric model and achieves the efficiency bound when all models are correct. We adopt the sequential ignorability assumption of Imai et al. (2010b), together with standard consistency and positivity assumptions. Under these assumptions, we derive the set of all influence functions including the semiparametric efficient influence function for the parameter of a model for the natural direct and indirect effects given a subset of baseline covariates, in the semiparametric model ${\mathcal{M}}_{\mathrm{np}}$ in which the likelihood is otherwise unrestricted. We further show that in order to make inferences about conditional mediation effects in ${\mathcal{M}}_{\mathrm{np}}$ one must estimate an appropriate subset of (i) the expectation of the outcome conditional on the mediator, exposure and confounding factors; (ii) the density of the mediator given the exposure and the confounders; (iii) the density of the exposure given the confounders.

To minimize the possibility of modeling bias, one may wish to estimate each of these quantities nonparametrically but such estimators perform poorly in settings with high dimensional vectors of confounders. In this paper, we develop an alternative strategy. We consider three submodels of ${\mathcal{M}}_{\mathrm{np}}:{\mathcal{M}}_1$, where (i) and (ii) are correctly specified; ${\mathcal{M}}_2$, where (i) and (iii) are correctly specified; and ${\mathcal{M}}_3$, where (ii) and (iii) are correctly specified. We propose to combine all three parametric models of (i), (ii), and (iii) into a single estimator of the conditional mean effect that remains consistent and asymptotically normal in a union model ${\mathcal{M}}_{\text{union}}^{123}={\mathcal{M}}_1\cup {\mathcal{M}}_2\cup {\mathcal{M}}_3$, that is, in a model where any two of (i), (ii), (iii) are correctly specified. We show that when we are interested in natural direct and indirect effects conditional on a strict subset of the confounders, our proposed estimator is triply robust. When we are interested in natural direct and indirect effect conditional on all confounders, our proposed estimator is doubly robust, and delivers valid inferences in the larger union model ${\mathcal{M}}_{\text{union}}^{y3}={\mathcal{M}}_{\mathrm{y}}\cup {\mathcal{M}}_3\supset {\mathcal{M}}_{\text{union}}^{123}$, where ${\mathcal{M}}_{\mathrm{y}}$ is a model where only (i) is correctly specified. Furthermore, we construct locally semiparametric efficient estimators, that achieve the efficiency bound in ${\mathcal{M}}_{\text{union}}^{123}$ and ${\mathcal{M}}_{\text{union}}^{\mathrm{y}3}$ respectively, at the intersection submodel where all three models are correct.

When the density of the exposure is known, as is the case in randomized experiments, our estimators continue to apply, but only require for consistency that either (i) or (ii) is correct. As the exposure density is ancillary when estimating natural direct and indirect effects, the efficient score remains the same whether or not the exposure density is known, so the proposed locally efficient estimators remain locally efficient even in the context of randomized experiments with known randomization probability.

We illustrate the proposed methodology in a simulation study and in a data application, and conclude that its main advantage is that it produces valid inferences under many more data generating laws than other approaches.

By contrast with our approach, the classical approach of Baron and Kenny assumes the model ${\mathcal{M}}_1$, as do the parametric approaches considered in Imai et al. (2010b,a) and VanderWeele & Vansteelandt (2010), whereas Petersen & van der Laan (2008) consider the union model ${\mathcal{M}}_1\cup {\mathcal{M}}_3$. We argue that the approach of Petersen & van der Laan (2008), developed for the case where V ⊂ X, is not entirely satisfactory for estimating conditional direct effects, since their estimator requires a correct model for the density of the mediator. In other words, their estimator is only consistent under the union model ${\mathcal{M}}_1\cup {\mathcal{M}}_3$, rather than the union model ${\mathcal{M}}_1\cup {\mathcal{M}}_2\cup {\mathcal{M}}_3$.

Finally, we develop a novel double robust sensitivity analysis framework to assess the impact on inferences about direct and indirect effects of a departure from the ignorability assumption of the mediator variable. Unless otherwise stated, we shall assume that exposure is binary. Formal proofs of theorems, and extensions to polytomous exposures are available in the Supplementary Material.

2. SEMIPARAMETRIC THEORY FOR DIRECT EFFECT MODELS

2.1. Identification and influence functions

Suppose that independent and identically distributed data on O = (Y, A, M, X) are collected for n subjects. Here, Y is an outcome of interest, A is the binary exposure, M is a mediator with support S, known to occur after A and prior to Y, and X = (V, L) is a vector of pre-exposure variables with support $\mathcal{X}=\mathcal{V}\times \mathcal{L}$ that account for confounding of the mutual associations between A, M and Y. The vector V includes variables hypothesized to modify the natural direct or indirect effect of the exposure. For each level (a, m) we assume that there exists a counterfactual variable Y_a,m corresponding to the outcome had, possibly contrary to fact, the exposure and mediator taken the value (a, m) and, likewise, there exists a counterfactual variable M_a corresponding to the mediator had, possibly contrary to fact, the exposure taken the value a. We aim to make inference about the unknown p-dimensional parameter ψ indexing a model γ_DIR(A, V; ψ) for the conditional mean natural direct effect

$${\mathrm{\gamma }}_{\text{DIR}}(a,V)=g\{E(Y_{a,M_0}|V)\}-g\{E(Y_{0,M_0}|V)\},$$ (1)

where E stands for expectation and g is the identity or log link function. The function γ_DIR(A, V; ·) is assumed to be a smooth function that satisfies γ_DIR(A, V ; 0) = γ_DIR(0, V; ·) = 0, so ψ = 0 encodes the null hypothesis of no natural direct effect. A simple example of the contrast γ_DIR(A, V ; ψ) takes the familiar linear form ψ A, which assumes the natural direct effect of A is constant across levels of V. An alternative model might posit that log γ_DIR(A, V ; ψ) takes the linear form (A, A × V₁)ψ, which encodes effect modification on the log scale of the natural direct effect of the exposure by V₁ a component of V.

The model γ_DIR(a, V; ψ) is generally not identified without additional assumptions. To proceed, we make the consistency assumption:

$$\begin{array}{l}\text{if}A=a,\text{then}{M}_a=M\text{almost surely},\\ \text{and if}A=a\text{and}M=m,\text{then}{Y}_{a,m}=Y\text{almost surely}.\end{array}$$ (2)

In addition, we adopt the sequential ignorability assumption of Imai et al. (2010b), which states that for a, a′ ∈ {0, 1},

$$\begin{array}{l}\{Y_{a\prime ,m},M_a\}\perp \perp A|X\\ Y_{a\prime m}\perp \perp M|A=a,X,\end{array}$$ (3)

paired with the positivity assumption

$$\begin{array}{l}{f}_{M|A,X}(m|A,X)>0\text{almost surely for each}m\in \mathcal{S},\\ \text{and}{f}_{A|X}(a|X)>0\text{almost surely for each}a\in \{0,1\}.\end{array}$$ (4)

Then, under the assumptions (2), (3), and (4), one can show that (Imai et al., 2010b)

$$E(Y_{a,M_0}|v)=\underset{\mathcal{S}\times \mathcal{L}}{{\displaystyle \iint }}E(Y|a,m,l,v)f_{M|A,X}(m|A=0,l,v)f_{L|V}(l|v)\mathit{d\mu }(m,l),$$ (5)

where f_M|A,X and f_L|V are respectively the conditional densities of the mediator M given (A, X) and of L given V, and μ is a dominating measure for the distribution of (M, L). Thus γ_DIR(a, v) is identified from the observed data; see Pearl (2011) and Petersen & van der Laan (2008) for related identification results. Tchetgen Tchetgen & Shpitser (2012) considered the special case where V = ∅, in which case γ_DIR(a, V) = γ_DIR(a) is a nonparametric functional.

To motivate the sequential ignorability assumption, it is helpful to consider a particular approach to generating potential outcomes such that the assumption is satisfied. We briefly consider the nonparametric structural equations model of Judea Pearl. Structural equations provide an algebraic interpretation of the causal graph of Figure 1 corresponding to four functions, one for each vertex on the graph:

$$\begin{array}{l}X=g_X({\epsilon }_X),\\ A=g_A(X,{\epsilon }_A),\\ M=g_M(X,A,{\epsilon }_M),\\ Y=g_Y(X,A,M,{\epsilon }_Y).\end{array}$$ (6)

Each of these functions represents a causal mechanism that determines the value of the left-hand-side variable, known as the output, from variables on the right, known as the inputs. The errors ε_X, ε_A, ε_M, ε_Y stand for all factors not included on the graph that could possibly affect their outputs when all other inputs are held constant. To be consistent with Figure 1, we require that these errors be mutually independent, but we allow their distribution to remain arbitrary. Although we do not do so here, it is also possible to represent dependent errors graphically by means of additional vertices on the graph. The lack of a causal effect of a given variable on an output is encoded by an absence of the variable from the right-hand side. For example, consider a modification of Figure 1 obtained after deleting the arrow A → Y. This indicates the absence of a direct effect of A on Y. This is encoded by replacing the last equation in (6) with Y = g_Y(X, M, ε_Y). The absence of A from the arguments of g_Y encodes the assumption that variation in A leaves Y unchanged, as long as variables X, M and ε_Y remain constant.

Fig. 1.

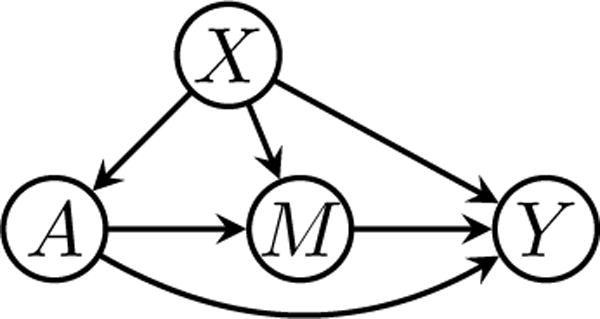
Example of mediation with exposure A, mediator M, outcome Y, and confounders X.

As stated by Pearl (2009), the invariance of structural equations permits their use for modeling causal effects and potential outcomes. In fact, to emulate the intervention in which one sets A to a almost surely, we replace the equation for A with A = a, producing the equations

$$\begin{array}{l}X=g_X({\epsilon }_X),\\ A=a,\\ M_a=g_M(X,a,{\epsilon }_M),\\ Y_a=g_Y(X,a,M_a,{\epsilon }_Y).\end{array}$$

The independence of errors, ε_M ⊥⊥ ε_Y, implies independence of potential outcomes for any set of exposure values a, a^*,

$$Y_{a,m,x}\perp \perp M_{a^{\ast },x},$$ (7)

where M_a*,x = g_M(x, a^*, ε_M) and Y_a,m,x = g_Y(x, a, m, ε_Y) are obtained after intervening on (A, X) and (A, M, X) respectively, and a, a^* ∈ {0,1}. It is straightforward to verify that independence of ε_X, ε_A, ε_M, ε_Y implies sequential ignorability.

As emphasized by Imai et al. (2010b), the second part of (3) is a strong assumption and must be made with care, because it posits the absence of unobserved confounders for conflicting values of the exposure, as in (7). Avin et al. (2005) proved that without additional assumptions, one cannot identify natural direct and indirect effects if there are confounding variables between mediator and outcome that are affected by the exposure, even if such variables are observed. Also see Tchetgen Tchetgen & VanderWeele (2013) for additional sufficient conditions for identification, and Tchetgen Tchetgen & Phiri (2014) for partial identification results in this context. Ignorability of the mediator cannot be established with certainty even after collecting as many pre-exposure confounders as possible. This assumption cannot be tested by observational or interventional means, so later in the paper we adapt and extend the sensitivity analysis technique of Tchetgen Tchetgen & Shpitser (2012), which allows the analyst to quantify the degree to which mediation analysis is robust to a potential violation of the second part of (3). A general theory of identification of mediated effects now available incorporates both longitudinal settings and unobserved confounders (Shpitser, 2013); it expresses identification criteria directly on the graph representing a set of non-parametric structural equations, rather than in terms of independence assumptions among potential outcomes, as in (Imai et al., 2010b) and elsewhere.

We give our first result, which serves as motivation for our multiply robust approach. First, for a, a^* ∈ {0, 1}, we define

$$\eta (a,a^{\ast },x)={{\displaystyle \int }}_{\mathcal{S}}B(a,m,x)f_{M|A,X}(m|a^{\ast },x)\mathit{d\mu }(m),$$

where B(a, m, x) = E(Y | a, m, x) and note that η(a, a, x) = E(Y | x, a), for a = 0, 1.

Let

$$\begin{array}{l}K=\frac{f_{M|A,X}(M|A=0,X)}{f_{M|A,X}(M|A=1,X)},\\ N_1=\frac{1}{f_{A|X}(1|X)},\\ N_0=\frac{1}{f_{A|X}(0|X)},\\ ∊=Y-B(1,M,X),\text{and}\\ \overline{\eta }=\eta (1,0,X)-\eta (0,0,X).\end{array}$$

THEOREM 1

Under the consistency, sequential ignorability and positivity assumptions, if $\widehat{\psi }$ is a regular asymptotically linear estimator of ψ in model ${\mathcal{M}}_{\mathrm{np}}$ then there exists a p × 1 function h(V) of V such that $\widehat{\psi }$ has the influence function $E{\{\partial S_{\psi }^{\mathrm{np}}(h;\psi )/\partial {\psi }^T\}}^{-1}\times S_{\psi }^{\mathrm{np}}(h;\psi )$, where for the identity link g, $S_{\psi }^{\mathrm{np}}(h;\psi )=h(V)U_1(\psi )$, with

$$U_1(\psi )=I(A=1){\mathit{KN}}_1∊-I(A=0)N_0\{∊+\overline{\eta }\}+\{\overline{\eta }-{\mathrm{\gamma }}_{\text{DIR}}(1,V;\psi )\},$$

and for the log-link g, $S_{\psi }^{\mathrm{np}}(h;\psi )=h(V)U_2(\psi )$, with

$$\begin{array}{l}{U}_2(\psi )=[I(A=1){\mathit{KN}}_1∊+I(A=0)N_0\{B(1,M,X)-\eta (1,0,X)\}+\eta (1,0,X)]\times \\ \exp \{-{\mathrm{\gamma }}_{\text{DIR}}(1,V;\psi )\}-I(A=0)N_0\{Y-\eta (0,0,X)\}-\eta (0,0,X).\end{array}$$

That is, $n^{1/2}(\widehat{\psi }-\psi )=E{\{\partial S_{\psi }^{\mathrm{np}}(h;\psi )/\partial {\psi }^T\}}^{-1}\{n^{-1/2}{{\displaystyle \sum }}_{i=1}^n{S}_{\psi ,i}^{\mathrm{np}}(h;\psi )\}+o_p(1)$. In the special case where V = X,

$$U_1(\psi )=I(A=1){\mathit{KN}}_1∊-I(A=0)N_0\{∊+{\mathrm{\gamma }}_{\text{DIR}}(1,X;\psi )\},$$

and

$$U_2(\psi )=\{I(A=1){\mathit{KN}}_1∊+I(A=0)N_{0}B(1,M,X)\}\exp \{-{\mathrm{\gamma }}_{\text{DIR}}(1,V;\psi )\}-I(A=0)N_{0}Y$$

The efficient score of ψ in model ${\mathcal{M}}_{\mathrm{np}}$ is $S_{\psi }^{\mathrm{eff},\mathrm{np}}(\psi )=S_{\psi }^{\mathrm{np}}(h_{\mathrm{opt}};\psi )$ where

$$h_{\mathrm{opt}}(V)=E\{\partial U(\psi )/(\partial \psi )|V\}E{\{U{(\psi )}^2|V\}}^{-1}$$

with U(ψ) = U₁(ψ) for the identity link and U(ψ) = U₂(ψ) for the log-link.

Based on Theorem 1, standard semiparametric theory allows us to conclude that all regular and asymptotically linear estimators of ψ in model ${\mathcal{M}}_{\mathrm{np}}$ can be obtained, up to asymptotic equivalence, as the solution $\tilde{\psi }(h)$ to the equation

$${\mathbb{P}}_n{S}_{\psi }^{\mathrm{np}}(h;\psi )=0,$$ (8)

for some p-dimensional function h, where ${\mathbb{P}}_n(·)=n^{-1}{{\displaystyle \sum }}_i{(·)}_i$. This follows primarily from the unbiasedness of the estimating function $S_{\psi }^{\mathrm{np}}(h;\psi )$, which is a consequence of the unbiasedness of U(ψ). For instance, when V = X, U₁(ψ) has mean zero at ψ since the residual I(A = 1)∊ has mean zero for all ψ and therefore the first term of U₁(ψ) has mean zero, and likewise, the second term $I(A=0)N_0\{∊+\overline{\eta }\}$ can be shown to have mean zero. Although the first term of U₁(ψ) does not depend on ψ, we will see below that this term is important not only for robustness but also for efficiency. Unfortunately, the solution $\tilde{\psi }(h)$ to equation (8) is not a feasible estimator since functions in $\{S_{\psi }^{\mathrm{np}}(h;\psi ):h\}$ all depend on B(A, M, X), f_A|X and f_M|A,X. A feasible estimator requires consistent estimators of these unknown functions.

If the vector of covariates X is high-dimensional or contains more than two continuous components, nonparametric methods become infeasible for estimating ψ in ${\mathcal{M}}_{\mathrm{np}}$, due to the curse of dimensionality. In such settings, dimension-reducing, e.g., semiparametric working models must be used to estimate B(A, M, X), f_M|A,X and f_A|X. We consider inferences that employ parametric working models for these functions. Consider the working model $B(A,M,X;{\beta }_y)=g^{-1}\{{\beta }_y^{T}r(X,M,A)\}$ for B(A, M, X), where r is a user-specified function of (X, M, A), g is a link function, and β_y is estimated by ${\widehat{\beta }}_y$, which solves the estimating equation

$$0={\mathbb{P}}_n\left\{S_y\right({\widehat{\beta }}_y\left)\right\}={\mathbb{P}}_n[r(X,M,A)\{Y-B(A,M,X;{\widehat{\beta }}_y)\left\}\right].$$

Similarly, let ${\widehat{f}}_{M|A,X}(m|A,X)=f_{M|A,X}(m|A,X;{\widehat{\beta }}_m)$ denote the maximum likelihood estimator of f_M|A,X(m | A, X; β_m), a model for the density of M given (A, X). The estimator ${\widehat{\beta }}_M$ solves the score equation

$$0={\mathbb{P}}_n\left\{S_m\right({\widehat{\beta }}_m\left)\right\}={\mathbb{P}}_n\left\{\frac{\partial }{\partial {\beta }_m}\log f_{M|A,X}\right(M|A,X;{\widehat{\beta }}_m)\}.$$

Likewise, let ${\widehat{f}}_{A|X}(a|X)=f_{A|X}(a|X;{\widehat{\beta }}_a)$ denote the maximum likelihood estimator of f_A|X(a | X; β_a), with ${\widehat{\beta }}_a$ solving

$$0={\mathbb{P}}_n\left\{S_a\right({\widehat{\beta }}_a\left)\right\}={\mathbb{P}}_n\left\{\frac{\partial }{\partial {\beta }_a}\log f_{E|X}\right(A|X;{\widehat{\beta }}_a)\}.$$

In principle, we could obtain inferences about ψ using only two of the three working models B(A, M, X; β_y), f_M|A,X(m | A, X; β_m) and f_A|X(a | X; β_a), say for instance under ${\mathcal{M}}_1$, by obtaining by obtaining ${\widehat{\psi }}_{{\mathcal{M}}_1}$ as a solution to

$${\mathbb{P}}_n[h(V)\{\widehat{\eta }(1,0,X)-\widehat{\eta }(0,0,X)-{\mathrm{\gamma }}_{\text{DIR}}(1,V;{\widehat{\psi }}_{{\mathcal{M}}_1})\left\}\right]=0,$$

for g the identity link, and a user-specified function h of dimension p, where

$$\widehat{\eta }(a,a^{\ast },X)={{\displaystyle \int }}_{\mathcal{S}}B(a,m,X;{\widehat{\beta }}_y){\widehat{f}}_{M|A,X}(m|A=a^{\ast },X)\mathit{d\mu }(m).$$

But ${\widehat{\psi }}_{{\mathcal{M}}_1}$ would generally be inconsistent if either B(A, M, X; β_y) or f_M|A,X(m | A, X; β_m) were incorrect, even if one of the two models were correct and f_A|X(a | X; β_a) was also correct. One of two alternative strategies might be considered. In the first, one could obtain an estimator based on B(A, M, X; β_y) and f_A|X(A | X; β_a) under model ${\mathcal{M}}_2$. In the second, one could obtain an estimator based on f_M|A,X(M | A, X; β_m) and f_A|X(A | X; β_a) under model ${\mathcal{M}}_3$. Both of these approaches may give biased results under mis-specification of any required working model and will not be pursued further.

To handle the setting of V ⊂ X, in Section 2.2 we develop a multiply robust approach that uses all three working models, and gives the correct answer under the union model ${\mathcal{M}}_{\text{union}}^{123}={\mathcal{M}}_1\cup {\mathcal{M}}_2\cup {\mathcal{M}}_3$ in which any of the three working models (i), (ii) and (iii), may be incorrect if the other two are correct. Remarkably, the analyst does not need to know which two models are correct for valid inference. Doubly robust estimators for direct effect models, that are consistent and asymptotically normal in ${\mathcal{M}}_{\text{union}}^{y3}$ union are obtained when V = X.

2.2. Multiply robust estimation

The proposed estimator $\widehat{\psi }=\widehat{\psi }(h)$ solves

$${\mathbb{P}}_n{\widehat{S}}_{\psi }^{\mathrm{np}}(h;\widehat{\psi })=0,$$

where h is a user-specified function of V, and ${\widehat{S}}_{\psi }^{\mathrm{np}}(h;\widehat{\psi })=S_{\psi }^{\mathrm{np}}(h;{\widehat{\beta }}_m,{\widehat{\beta }}_a,{\widehat{\beta }}_y,\widehat{\psi })$ is equal to $S_{\psi }^{\mathrm{np}}(h;\widehat{\psi })$ evaluated at $\{B(A,M,X;{\widehat{\beta }}_y)$, ${\widehat{f}}_{M|A,X}(m|A,X)$, ${\widehat{f}}_{A|X}(A|X)\}$ instead of {B(A, M, X), f_M|A,X(m | A, X), f_A|X(a | X)}. Thus $\widehat{\psi }$ is consistent and asymptotically normal in model ${\mathcal{M}}_{\text{union}}^{123}$ when V ⊂ X and in model ${\mathcal{M}}_{\text{union}}^{y3}$ when V = X. The following theorem gives the formal result.

THEOREM 2

Suppose that the assumptions of Theorem 1 hold, that the regularity conditions stated in the Appendix hold and that β_m, β_e and β_y are variation independent. Then $n^{1/2}(\widehat{\psi }-\psi )$ is regular and asymptotically linear respectively under model ${\mathcal{M}}_{\text{union}}^{y3}$ when V = X, with influence function $E{\{\partial S_{\psi }^{\mathrm{np}}(h;\beta ,\overline{\psi })/(\partial {\overline{\psi }}^T){|}_{\psi }\}}^{-1}{S}_{\psi }^{\text{union}}(h;{\beta }^{\ast },\psi )$, where

$$S_{\psi }^{\text{union}}(h;{\beta }^{\ast },\psi )=S_{\psi }^{\mathrm{np}}(h;{\beta }^{\ast },\psi )-{\frac{\partial E\{S_{\psi }^{\mathrm{np}}(h;\beta ,\psi )\}}{\partial {\beta }^T}|}_{{\beta }^{\ast }}E{\left\{{\frac{\partial S_{\beta }(\beta )}{(\partial {\beta }^T)}|}_{{\beta }^{\ast }}\right\}}^{-1}{S}_{\beta }({\beta }^{\ast }),$$

and thus as n → ∞ it converges in distribution to a N(0, Σ_ψ) variate, where

$${\sum }_{\psi }(h;\psi ,{\beta }^{\ast })=E\left\{S_{\psi }^{\text{union}}{(h;{\beta }^{\ast },\psi )}^{\otimes 2}\right\},$$

with ${\beta }^T=({\beta }_m^T,{\beta }_a^T,{\beta }_y^T)$ and $S_{\beta }(\beta )={\{S_m^T({\beta }_m),S_a^T({\beta }_a),S_y^T({\beta }_y)\}}^T$, and with β* denoting the probability limit of the estimator $\widehat{\beta }={({\widehat{\beta }}_m^T,{\widehat{\beta }}_a^T,{\widehat{\beta }}_y^T)}^T$. If ${\widehat{h}}_{\mathrm{opt}}$ denotes a consistent estimator of h_opt, then ${\widehat{\psi }}_{\mathrm{eff}}=\widehat{\psi }({\widehat{h}}_{\mathrm{opt}})$ is semiparametric locally efficient in the sense that it is regular and asymptotically linear in model ${\mathcal{M}}_{\text{union}}^{123}$ and $M_{\text{union}}^{y3}$ respectively. Furthermore, ${\widehat{\psi }}_{\mathrm{eff}}$ achieves the semiparametric efficiency bound for model ${\mathcal{M}}_{\text{union}}^{123}$ and ${\mathcal{M}}_{\text{union}}^{y3}$ respectively, at the intersection submodel ${\mathcal{M}}_1\cap {\mathcal{M}}_2\cap {\mathcal{M}}_3$ with efficient influence function

$$E{\left\{{\partial S_{\psi }^{\mathrm{np}}(h_{\mathrm{opt}};\beta ,\overline{\psi })/(\partial {\overline{\psi }}^T)|}_{\psi }\right\}}^{-1}{S}_{\psi }^{\mathrm{np}}(h_{\mathrm{opt}};{\beta }^{\ast },\psi ).$$

An empirical version of Σ_ψ(h; ψ, β*) is easily obtained and can be used to construct Wald-type confidence intervals: Theorem 2 implies that when all models are correct ${\widehat{\psi }}_{\mathrm{eff}}$ is semiparametric efficient in ${\mathcal{M}}_{\mathrm{np}}$ at the intersection submodel ${\mathcal{M}}_1\cap {\mathcal{M}}_2\cap {\mathcal{M}}_3$, provided that ${\widehat{h}}_{\mathrm{opt}}$ converges to h_opt in probability.

When V = X, only a working model for the outcome regression B(1, M, X) is needed, and therefore, B(A, M, X; β_y) can be replaced by the more parsimonious model $B_1(M,X;{\omega }_y)=g^{-1}\{{\omega }_y^{T}r(X,M)\}$, with g a link function, and r a user specified function of (X, M) and β_y estimated by the solution ${\widehat{\beta }}_y$ to

$$0={\mathbb{P}}_n\left\{S_y\right({\widehat{\beta }}_y\left)\right\}={\mathbb{P}}_n[I(A=1)r(X,M)\{Y-B_1(M,X;{\omega }_y)\}]$$

Obtaining a locally efficient estimator of ψ will generally involve additional modeling to obtain ${\widehat{h}}_{\mathrm{opt}}$ than strictly required for multiple robustness. To clarify this, consider the log-link. Then, one can verify that

$$h_{\mathrm{opt}}(V)=\frac{\partial {\gamma }_{\text{DIR}}(1,V;\psi )}{\partial \psi }E\{\eta (0,0,X)|V\}E{\left\{U_2{(\psi )}^2\right|V\}}^{-1},$$

and, therefore,

$${\widehat{h}}_{\mathrm{opt}}=\frac{\partial {\mathrm{\gamma }}_{\text{DIR}}(1,V;{\widehat{\psi }}_{\text{prelim}})}{\partial \psi }\widehat{E}\{\widehat{\eta }(0,0,X)|V\}\widehat{E}{\left\{U_2{\left({\widehat{\psi }}_{\text{prelim}}\right)}^2\right|V\}}^{-1},$$

where ${\widehat{\psi }}_{\text{prelim}}$ is a preliminary, possibly multiply robust, estimator of ψ, $\widehat{E}\{\widehat{\eta }(0,0,X)|V\}$ is an estimate of a parametric regression of η(0, 0, X) on V, and $\widehat{E}\{U_2{({\widehat{\psi }}_{\text{prelim}})}^2|V\}$ is an estimate of a parametric model for the variance of U₂(ψ) given V. Thus, local efficiency is contingent on consistency of $\widehat{E}\{\widehat{\eta }(0,0,X)|V\}$ and $\widehat{E}\{U_2{({\widehat{\psi }}_{\text{prelim}})}^2|V\}$. Likewise, additional modeling may be required for local efficiency in the case of the identity link.

3. SIMULATION AND APPLICATION

3.1. A simulation study of estimators of direct effect

In this section, we report a simulation study which illustrates the finite sample performance of estimators introduced in previous sections. We generated 1000 samples of size n = 200, 1000 from a model in which X₁ ~ Bernoulli(0.4), X₂ | X₁ ~ Bernoulli(0.3 + 0.4X₁), X₃ | X₁, X₂ ~ −0.024 − 0.4X₁ + 0.4X₂ + N(0, 1), and

$$\begin{array}{l}A|X_1,X_2,X_3~\mathit{\text{Bernoulli}}({[1+\exp \{-(0.4+X_1-X_2+0.1X_3-1.5X_1{X}_3)\left\}\right]}^{-1}),\\ M|A,X_1,X_2,X_3~0.5-X_1+0.5X_2-0.9X_3+A-1.5X_1{X}_3+N(0,1),\\ Y|M,A,X_1,X_2,X_3~1+0.2X_1+0.3X_2+1.4X_3-2.5A-3.5M+5\mathit{AM}+N(0,1).\end{array}$$

By evaluating equation (5) under these models, we obtain γ_DIR(1, X, ψ) = ψ₀ + ψ₁X₁ + ψ₂X₂ + ψ₃X₃ + ψ₄X₁X₃, where ψ = (0, −5, 2.5, −4.5, −7.5)^T, which implies that γ_DIR(1, x^*; ψ) = 0, for x^* = (0, 0, 0). The simulation study compares the simple plug-in estimator of Imai et al. (2010b,a), which essentially evaluates (5) using parametric models, with our estimator. To assess the impact of modeling error, we evaluated them in eight scenarios shown in Table 1. In the first scenario, all models were correctly specified, the next three scenarios mis-specified exactly one of f_A|X, f_M|A,X and f_Y|A,M,X, the next three mis-specified exactly two of the same models, and the last scenario mis-specified all three models. In order to mis-specify f_A|X and f_M|A,X, we respectively left out the X₁ X₃ interaction when fitting each model, and incorrectly assumed a log-log link for the propensity score model. The incorrect model for Y simply assumed no AM interaction.

Table 1.

Absolute mean bias and Monte Carlo standard error (×10⁻²) for γ_DIR(1, x*; ψ) = 0 where x* = (0, 0, 0), and 1000 replicates.

		n=200 Plug-in	Multiply-robust	n=1000 Plug-in	Multiply-robust
All correct	|bias|	0.37	3.05	1.27	1.74
	MC s.e.	2.60	2.85	0.96	1.29
Y wrong	|bias|	64	1.66	66.5	3.49
	MC s.e.	2.80	4.34	1.26	1.87
M wrong	|bias|	89.3	2.62	89.4	1.56
	MC s.e.	2.64	3.24	1.53	1.28
A wrong	|bias|	0.37	3.24	1.27	1.93
	MC s.e.	2.60	2.83	0.96	1.22
Y, A wrong	|bias|	63.9	91.6	66.5	92.5
	MC s.e.	2.80	2.80	1.26	2.03
Y, M wrong	|bias|	63.9	155	66.5	153.2
	MC s.e.	2.85	4.79	1.26	2.45
A, M wrong	|bias|	89.3	3.04	89.4	1.82
	MC s.e.	2.64	2.78	1.53	1.20
Y, A, M wrong	|bias|	63.9	70.3	66.5	71.4
	MC s.e.	2.85	2.93	1.26	1.20

Table 1 summarizes the simulation results for inferences about γ_DIR(1, x^*; ψ). The results agree with our theory. Both estimators performed well at both moderate and large sample sizes in the absence of modeling error. In this case, the multiply robust estimator was less efficient than the plug-in estimator, which is also the maximum likelihood estimator in model ${\mathcal{M}}_1$. Under the partially mis-specified model in which only the model for Y was incorrect, the plug-in estimator showed significant bias, and the multiply robust estimator performed well. When only the mediator model was incorrect, the plug-in estimator had a much larger bias than the proposed estimator. Finally, only mis-specifying the exposure model did not produce bias for either estimator. As theory predicts, the new estimator remained consistent when both the mediator and exposure models were incorrect provided the outcome regression was correct, but was biased when the mediator and outcome were both incorrectly modeled, or the exposure and outcome models were both incorrect.

3.2. Application

We re-analyze data from the Job Search Intervention Study also analyzed by Imai et al. (2010a). This was a randomized field experiment that investigated the efficacy of a job training intervention on unemployed workers. The program was designed not only to increase reemployment among the unemployed but also to enhance their mental health. In the study, 1,801 unemployed workers received a pre-screening questionnaire and were then randomly assigned to treatment and control groups. The treatment group with A = 1 participated in workshops in which participants learned job search skills and coping strategies for dealing with setbacks in the search process. The control group with A = 0 received a booklet describing job search tips. Our analysis considered a continuous outcome measure Y of depressive symptoms based on the Hopkins Symptom Checklist (Vinokur et al., 1995; Vinokur & Schul, 1997; Imai et al., 2010a). A continuous measure of job search self-efficacy represented the hypothesized mediating variable M. The data also included baseline covariates X measured before administering the treatment, including level of depression, education, income, race, marital status, age, sex, previous occupation, and level of economic hardship. The density of A given X was randomized and so did not depend on covariates, and so its estimation is not prone to model mis-specification. The continuous outcome and mediator variables were modeled using linear regression with Gaussian error, with main effects for (A, M, X) and an interaction between A and M included in the outcome regression, and main effects for (A, X) included in the mediator regression. The conditional total effect was estimated using a standard main-effects only linear regression of Y on (A, X), which gave a total effect of −0.048, with standard error 0.035, suggesting that individuals in the active arm experienced fewer depressive symptoms on average than those in the control arm. The natural direct effect was estimated using two different strategies. The first consisted of the plug-in estimator which evaluates equation (5) with V = X, so no integration over L was necessary. Since a main-effects-only linear model was used for Y, the plug-in estimator only required a model for the mean of M given (A, X) and not for the entire density. A standard main-effects only linear regression was also used to model M. The second strategy used the multiply robust estimator, which also required a regression of A on X. A standard main-effects only logistic regression was used to model A. Both approaches estimated a linear natural direct effect model γ_DIR(a, X, ψ) = (1, X^T)ψa, which accommodates possible heterogeneity in the natural direct effect by pre-treatment variables. See Table 2.

Table 2.

Estimated Natural Direct Effects of Interest Using the Job Search Intervention Study

	ψ0	ψ1	ψ2	ψ3	ψ4	ψ5	ψ6	ψ7	ψ8	ψ9
Plug-in	−2.83	0.63	−1.79	−3.6×10−3	0.36	0.33	−4.8×10−2	0.66	0.24	−0.32
s.e.	3.63	0.54	1.37	0.01	0.32	0.45	0.37	0.51	0.20	0.25
3-Robust	−14.9	−8.93	−0.16	6.11	1.47	5.54	0.03	1.67	0.76	−0.45
s.e.	28.1	6.98	0.31	3.92	8.40	9.89	4.62	3.87	2.20	3.59

Neither estimation strategy detected direct effect modification, and both estimators agreed within sampling variability and indicated no statistically significant direct effect. However, the multiply robust estimator is notably less efficient for several of the parameters, which may be a result of highly variable weights or partial model mis-specification. One could adapt the approach of Tchetgen Tchetgen & Shpitser (2012) to minimize the impact of highly variable weights.

3.3. A further comparison to existing methods

We briefly compare the proposed approach to existing estimators. Perhaps the most common approach for estimating direct and indirect effects when Y is continuous uses a system of linear structural equations, whereby, a linear structural equation for the outcome given the exposure, the mediator and the confounders is combined with a linear structural equation for the mediator given the exposure and confounders to produce an estimator of natural direct and indirect effects. The classical work of Baron & Kenny (1986) is a particular instance of this. In recent work mainly motivated by Pearl’s mediation functional (Pearl, 2001), Imai et al. (2010b), Pearl (2011) and VanderWeele (2009) have demonstrated how the simple linear structural equation approach generalizes to accommodate an interaction between exposure and mediator variables, or a nonlinear link either for the outcome or for the mediator. When the effect of confounders must be modeled, inferences based on parametric structural equations (Pearl, 2011; Imai et al., 2010b; VanderWeele, 2009; VanderWeele & Vansteelandt, 2010) correspond for a particular specification of model ${\mathcal{M}}_1$ for the outcome and the mediator densities, similar to the plug-in estimator used in the simulation study and in the application. As confirmed in our simulation study, an estimator obtained under such a system of structural equations, whether linear or nonlinear, will generally be inconsistent if ${\mathcal{M}}_1$ is even partially incorrect, whereas the proposed multiply robust estimator gives valid inferences under the union model ${\mathcal{M}}_2\cup {\mathcal{M}}_3$, even if ${\mathcal{M}}_1$ is incorrect.

A notable improvement on the system of structural equations approach is the estimator of a natural direct effect due to Petersen & van der Laan (2008) in the case where V ⊂ X. Their estimator remains consistent and asymptotically normal in the larger submodel ${\mathcal{M}}_1\cup {\mathcal{M}}_3$, so they can recover valid inferences even when the outcome model is incorrect, provided both exposure and mediator models are correct. Their estimator is not entirely satisfactory because it requires the model for the mediator density to be correct. Petersen & van der Laan (2008) did not consider the estimation of natural indirect effect models. Tchetgen Tchetgen & Shpitser (2012) give more discussion of this approach and of implications for efficiency associated with specification of a model for the mediator density. In the next section, we develop a multiply robust strategy to estimate the parameter indexing a model for a conditional natural indirect effect.

It may be difficult to posit congenial models for f_Y|A,M,X, f_M|A,X, f_A|X and γ_DIR to ensure that there exists a data generating mechanism for which they hold simultaneously. This issue arises for instance when M takes a finite number of values and a nonlinear link function is used to estimate its density. Our approach then gives a generalized multiply robust estimator (Robins & Rotnitzky, 2001). However, the issue of model incompatibility is alleviated when M is continuous and modeled using standard linear regression or when γ_DIR is either modeled nonparametrically, or is richly parameterized with sufficient nonlinear terms and high-order interactions involving components of X. Mediation analysis has been extended to survival data (Tchetgen Tchetgen, 2011; Lange & Hansen, 2012), and alternative doubly robust methods have been proposed recently (Tchetgen Tchetgen, 2013; Vansteelandt et al., 2012; Zheng & van der Laan, 2012; Lange et al., 2012). While we have considered methods that target a direct effect contrast conditional on V ⊆ X, these other estimators target either marginal direct effects, similar to Tchetgen Tchetgen & Shpitser (2012), or posit a parametric model for the mediation mean functional conditional on X, not only the direct effect contrast.

4. ESTIMATION OF CONDITIONAL NATURAL INDIRECT EFFECTS

In this section we develop a theory of estimation of the unknown q-dimensional parameter θ indexing a parametric model γ_IND(A, V; θ) for the conditional mean natural indirect effect

$${\mathrm{\gamma }}_{\text{IND}}(a,V)=g\{E(Y_{1,M_a}|V)\}-g\{E(Y_{1,M_0}|V)\},$$

where g is either the identity or log link function. The function γ_IND(A, V; ·) is assumed to be smooth and to satisfy γ_IND(A, V; 0)= γ_IND(0, V; ·) = 0, so θ = 0 encodes the null hypothesis of no natural indirect effect. A simple example of γ_IND(A, V; θ) takes the familiar form A θ, then the natural indirect effect of A does not depend on V. An alternative model might posit that log γ_IND(A, V; θ) equals (A, A × V₁)θ which encodes effect modification on the log scale of the indirect effect of the exposure by V₁, which is a component of V.

The contrast γ_IND(a, V) is identified under the consistency, positivity and sequential ignorability assumptions (2), (3) and (4), since $E(Y_{1,M_1}|V)=E(Y_1|V)$ and $E(Y_{1,M_0}|V)$ are then both identified.

Let $\tilde{\eta }=\eta (1,1,X)-\eta (1,0,X)$. We have the following result.

THEOREM 3

Under (2), (3) and (4), if $\widehat{\theta }$ is a regular asymptotically linear estimator of θ in model ${\mathcal{M}}_{\mathrm{np}}$, then there exists a q × 1 function h(V) of V such that $\widehat{\theta }$ has the influence function $E{\{\partial S_{\theta }^{\mathrm{np}}(h;\theta )/\partial {\psi }^T\}}^{-1}\times S_{\theta }^{\mathrm{np}}(h;\theta )$, where for the identity link g, $S_{\theta }^{\mathrm{np}}(h;\theta )=h(V)W_1(\theta )$, with

$$\begin{array}{l}{W}_1(\theta )=I(A=1)N_1[Y-\eta (1,1,X)-K\{Y-B(1,M,X)\}]-\\ I(A=0)N_0\{B(1,M,X)-\eta (1,0,X)\}+\tilde{\eta }-{\mathrm{\gamma }}_{\text{IND}}(1,V;\theta ),\end{array}$$

and for the log-link g, $S_{\theta }^{\mathrm{np}}(h;\theta )=h(V)W_2(\theta )$, where

$$\begin{array}{l}{W}_2(\theta )=I(A=1)N_1[\{Y-\eta (1,1,X)\}\exp \{-{\mathrm{\gamma }}_{\text{IND}}(1,V;\theta )\}\\ -K\{Y-B(1,M,X)\}]-I(A=0)N_0\{B(1,M,X)-\eta (1,0,X)\}\\ +\eta (1,1,X)\exp \{-{\mathrm{\gamma }}_{\text{IND}}(1,V;\theta )\}-\eta (1,0,X).\end{array}$$

That is, $n^{1/2}(\widehat{\theta }-\theta )=E{\{\partial S_{\theta }^{\mathrm{np}}(h;\theta )/\partial {\psi }^T\}}^{-1}\{n^{-1/2}{{\displaystyle \sum }}_{i=1}^n{S}_{\theta ,i}^{\mathrm{np}}(h;\theta )\}+o_p(1)$. In the special case where V = X,

$$\begin{array}{l}{W}_1(\theta )=I(A=1)N_1[Y-\eta (1,1,X)-K\{Y-B(1,M,X)\}]\\ -I(A=0)N_0\{B(1,M,X)-\eta (1,1,X)+{\mathrm{\gamma }}_{\text{IND}}(1,X;\theta )\}\end{array}$$

and for g the log-link

$$\begin{array}{l}{W}_2(\theta )=I(A=1)N_1[\{Y-\eta (1,1,X)\}\exp \{-{\mathrm{\gamma }}_{\text{IND}}(1,X;\theta )\}-K\{Y-B(1,M,X)\}]\\ -I(A=0)N_0[B(1,M,X)-\eta (1,1,X)\exp \{-{\mathrm{\gamma }}_{\text{IND}}(1,X;\theta )\}]\end{array}$$

The efficient score of θ in model ${\mathcal{M}}_{\mathrm{np}}$ is given by $S_{\theta }^{\mathrm{eff},\mathrm{np}}(\theta )=S_{\theta }^{\mathrm{np}}(h_{\mathrm{opt}};\theta )$ where h_opt(V) = E{∂W(θ)/∂θ | V}E{W(θ)² | V}⁻¹ and W(θ) = W₁(θ) in the case of the identity link and W(θ) = W₂(θ) for the log-link.

As in the previous section, we base inferences about θ on the triply robust estimator $\widehat{\theta }=\widehat{\theta }(h)$ which solves

$${\mathbb{P}}_n{\widehat{S}}_{\theta }^{\mathrm{np}}(h;\widehat{\theta })=0,$$

where h is a user-specified function of V of dimension q, and ${\widehat{S}}_{\theta }^{\mathrm{np}}(h;\widehat{\theta })=S_{\psi }^{\mathrm{np}}(h;{\widehat{\beta }}_m,{\widehat{\beta }}_a,{\widehat{\beta }}_y,\widehat{\theta })$ equals $S_{\theta }^{\mathrm{np}}(h;\widehat{\theta })$ evaluated at $\{B(A,M,X|{\widehat{\beta }}_y);{\widehat{f}}_{M|A,X}(m|A,X);{\widehat{f}}_{A|X}(a|X)\}$. An analogue to Theorem 2 stating that $\widehat{\theta }$ is consistent and asymptotically normal in model ${\mathcal{M}}_{\text{union}}^{123}$ can also be established, and locally efficient estimation is similarly obtained. Similar to direct effect models, an essential condition for multiple robustness is that the estimating function $S_{\psi }^{\mathrm{np}}(h;{\beta }_m,{\beta }_a,{\beta }_y,\theta )$ for V ⊂ X is triply robust with mean zero in model ${\mathcal{M}}_{\text{union}}^{123}$, which can be verified using similar arguments as in the proof of Theorem 2. When V = X, the remark made in Section 2.2 is again true: one only needs to model B₁(M, X) and not B(A, M, X). However, unlike $\widehat{\psi }$, the triply robust estimator $\widehat{\theta }$ is not doubly robust in this case.

We finally note that by definition

$$\begin{array}{l}g\{E(Y_1|V)\}-g\{E(Y_0|V)\}=g\{E(Y_{1,M_1}|V)\}-g\{E(Y_{1,M_0}|V)\}+\\ g\{E(Y_{1,M_0}|V)\}-g\{E(Y_{0,M_0}|V)\},\end{array}$$

so γ_DIR(A, V; ψ) and γ_IND(A, V; θ) combine to produce a model of the total exposure effect in terms of its direct and indirect components on the g scale.

5. A SEMIPARAMETRIC SENSITIVITY ANALYSIS

We extend the semiparametric sensitivity analysis technique of Tchetgen Tchetgen & Shpitser (2012), to assess whether a violation of the ignorability assumption for the mediator might alter inferences about a conditional natural direct effect. The extension for indirect effects is given in the Supplementary Material. Let

$$t(a,m,x)=E(Y_{1,m}|a,m,x)-E(Y_{1,m}|a,M\ne m,x).$$

Then

i.e., a violation of the ignorability assumption for the mediator variable generally implies that t(a, m, x) ≠ 0 for some (a, m, x). Suppose that M is binary and higher values of Y are beneficial for health, and that if t(a, 1, x) > 0 but t(a, 0, x) < 0, then on average, individuals with A = a, X = x and mediator value M = 1 have higher potential outcomes {Y₁₁, Y₁₀} than do individuals with A = a, X = x but M = 0; i.e., healthier individuals are more likely to receive the mediator. On the other hand, if t(a, 1, x) < 0 but t(a, 0, x) > 0 suggests confounding by indication for the mediator variable; i.e., unhealthier individuals are more likely to have M = 1. We proceed as in Robins et al. (1999), who proposed using a selection bias function to conduct a sensitivity analysis for total effects, and Tchetgen Tchetgen & Shpitser (2012), who adapted the approach to assess the impact of unmeasured confounding on the estimation of a marginal natural direct effect. Here we propose to recover inferences about the direct effect by assuming that the selection bias function t(a, m, x), which encodes the magnitude and direction of the unmeasured confounding for the mediator, is known. In the following, S is assumed to be finite. Let

$$\delta (m,x)=t(1,m,x)\{1-f_{M|A,X}(m|A=1,x)\}-t(0,m,x)\{1-f_{M|A,X}(m|A=0,x)\}.$$

If f_M|A,X were known, then under the assumption that the exposure is ignorable given X, Tchetgen Tchetgen & Shpitser (2012) established that

$$E(Y_{1,m}|M_0=m,x)=E(Y_{1,m}|A=0,m,x)=B(1,m,x)-\delta (m,x),$$

and therefore

$$E(Y_{1,M_0}|V)=E[{\displaystyle \sum }_{m\in \mathcal{S}}\{B(1,m,X)-\delta (m,X)\}\times f_{M|A,X}(m|A=0,X)|V],$$ (9)

which is equivalently written

$$E[I(A=1)N_{1}K\{Y-\delta (M,X)\}|V].$$ (10)

Below, representations (9) and (10) are combined to obtain a doubly robust estimator of ψ assuming t(·,·,·) is known. A sensitivity analysis is then obtained by repeating this process and by reporting inferences for each choice of t(·,·,·) in a finite set of user–specified functions $\mathcal{T}=\{t_{\mathrm{\lambda }}(·,·,·,):\mathrm{\lambda }\}$ indexed by a finite-dimensional parameter λ, with $t_0(·,·,·)\in \mathcal{T}$ corresponding to the ignorability of M in the sense of (3), i.e., t₀(·,·,·) ≡ 0. Throughout, the model f_M|A,X(·|A, X; β_m) for the probability mass function of M is assumed to be correct. Thus, to implement the sensitivity analysis, we develop a semiparametric estimator of ψ in the union model ${\mathcal{M}}_1\cup {\mathcal{M}}_3$, assuming t(·,·,·) = t_λ*(·,·,·) for a fixed λ*. If V is a proper subset of X, then the proposed doubly robust estimator of the natural direct effect is given by ${\widehat{\psi }}^{\text{doubly}}({\mathrm{\lambda }}^{\ast })={\widehat{\psi }}^{\text{doubly}}(h;{\mathrm{\lambda }}^{\ast })$, which solves, for g the identity link,

$${\mathbb{P}}_n\{{\widehat{S}}_{\psi }^{\text{doubly}}(h;\psi ,{\mathrm{\lambda }}^{\ast })\}={\mathbb{P}}_n\{h(V){\widehat{U}}_1(\psi ;{\mathrm{\lambda }}^{\ast })\}=0,$$

where

$$\begin{array}{l}{\widehat{U}}_1(\psi ;{\mathrm{\lambda }}^{\ast })=I(A=1){\widehat{N}}_1\widehat{K}\{Y-B(1,M,X;{\widehat{\beta }}_y\left)\right\}\\ -I(A=0){\widehat{N}}_0\{Y-B(0,M,X;{\widehat{\beta }}_y\left)\right\}\\ +{\eta }_{{\mathrm{\lambda }}^{\ast }}(1,0,X)-\widehat{\eta }(0,0,X)-{\mathrm{\gamma }}_{\text{DIR}}(1,V;\psi ),\end{array}$$

$${\eta }_{{\mathrm{\lambda }}^{\ast }}(1,0,X)={\displaystyle \sum }_{m\in \mathcal{S}}\left\{B\right(1,m,X;{\widehat{\beta }}_y)-\widehat{\delta }(m,X)\}{\widehat{f}}_{M|A,X}(m|A=0,X),$$

and $\widehat{N_1}$, $\widehat{N_0}$, $\widehat{K}$, and $\widehat{\delta }(m,X)$ are estimates of N₁, N₀, K, and δ(m, X) respectively.

A sensitivity analysis then entails reporting the set $\{{\widehat{\psi }}^{\text{doubly}}(\mathrm{\lambda }):\mathrm{\lambda }\}$, and the associated confidence intervals, which summarize how sensitive inferences may be to deviations from ignorability. The formal justification for the approach is given by the following result, which generalizes Theorem 4 of Tchetgen Tchetgen & Shpitser (2012). Its proof is given in the Supplementary Material.

THEOREM 4

If t(·,·,·) = t_λ*(·,·,·), then under the consistency and positivity assumptions, and the ignorability assumption for the exposure, ${\widehat{\psi }}^{\text{doubly}}({\mathrm{\lambda }}^{\ast })$ is a consistent and asymptotically normal estimator of ψ in ${\mathcal{M}}_1\cup {\mathcal{M}}_3$.

The influence function of ${\widehat{\psi }}^{\text{doubly}}({\lambda }^{\ast })$ is given in the Supplementary Material, and can be used to construct confidence intervals. The Supplementary Material also gives an analogous double robust sensitivity analysis technique for direct effects when V = X or g is the log-link, as well as corresponding methodology for indirect effects. If we have correctly specified a model for the mediator density f_M|A,X, the proposed sensitivity analysis technique for indirect effects does not require additional working models for f_{Y|M, A, X} and f_A|X when V = X. In this setting, the approach is completely robust to model mis-specification. We discuss a number of simple functional forms for t_λ(·,·,·) in the Supplementary Material.

The sensitivity analysis technique presented here differs from those developed by Vander-Weele (2010) and Imai et al. (2010b). VanderWeele (2010) postulates the existence of an unmeasured confounder U, possibly vector valued, which when included in X recovers the sequential ignorability assumption. His proposed sensitivity analysis requires specification of a parameter encoding the effect of the unmeasured confounder on the outcome within levels of (A, X, M), and another parameter for the effect of the exposure on the density of the unmeasured confounder given (X, M). This can be a daunting task, which renders the approach generally impractical, except when it is reasonable to postulate a single unobserved binary confounder, and one is willing to make further simplifying assumptions about the required sensitivity parameters. Our approach partially circumvents this difficulty by encoding a violation of the ignorability assumption for the mediator through the selection bias function t_λ(a, m, x). In practice a finite dimensional model must still be used for this quantity. The advantage of our approach is that it is agnostic about the existence, dimension, and nature of unmeasured confounders U. Furthermore, a violation of ignorability of the mediator can arise due to an exposure-induced confounder of the mediator-outcome relationship that is also an effect of the exposure variable, a setting which cannot be handled by the technique of VanderWeele (2010). In addition, in contrast with the proposed double robust approach, coherent implementation of the sensitivity analysis techniques of Imai et al. (2010b), Imai et al. (2010a), and VanderWeele (2010) requires correct specification of all models. Finally, unlike ours, their approach has not been developed for conditional direct effects given a subset of baseline variables. While we assume for the sensitivity analysis that the support of M is finite, the approach can be extended to handle a continuous mediator by further adapting the approach of Robins et al. (1999).