Psychometric Analysis of the Diagnostic Evaluation of Language Variation Assessment

Over- and under-identification of specific language impairments for minority students is an important problem with ramifications for students and for school resources (Oller, Kim, & Choe, 2000; Seymour, Roeper, & deVilliers, 2003). Hence, culturally fair assessments that would be sensitive enough to identify children with significant language delays without mis-identifying children who speak dialects that differ from mainstream American English (MAE) are needed (Stockman, 2008; Willis, 2008). The difficulty has been that many of the markers for language impairments, such as dropping the copula (he is go-ing to school) (Rice & Wexler, 1996) are acceptable variations in several American English dialects, such as African American English and Southern American English (Wolfram & Schilling-Estes, 2006). The Diagnostic Evaluation of English Variation-Screening Test (DELV-S, Seymour et al., 2003) was developed to address these issues. Although it represents a potential milestone for improving the cultural sensitivity of language assessment, the psychometric properties of the DELV-S have been largely unexplored and newer analyses, such as item response theory (Embretson & Reise, 2000), have not been applied. As a result, the DELV-S offers limited utility for many research and clinical purposes, especially for documenting gains in language skills as children mature or respond to therapy. The purpose of this paper is to present new psychometric data for the DELVS based on a sample of 1,764 children from kindergarten through second grade who use a variety of non-mainstream dialects and MAE, are ethnically diverse, and who attend schools in a Southeastern US school district.

Developing a Culture-fair Assessment of Language

Concerns about the well documented achievement gap and test bias with regard to underrepresented minorities provide the over-arching rationale for the development of unbiased language assessments (Jencks, 1998). Craig and Washington (2000) developed informal instruments that reliably captured the unique phonological and morphosyntactic features found in African American English (AAE). These criterion-referenced measures identified dialect features as the appropriate reflections of the language variant they represented, rather as than a disorder of language or speech. Similarly, other researchers developed expressive assessments of word learning, which also relied on assessment in naturalistic environments (Brackenbury & Pye, 2005; Burton & Watkins, 2007). In 1998, The Diagnostic Evaluation of Language Variation-Screening Test (DELV-S) was developed with funding from the National Institute of Deafness and Communication Disorders. Seymour and colleagues (Seymour et al., 2003) developed the DELV-S for use with culturally and linguistically diverse populations.

The DELV-S

The DELV-S is a screening assessment designed to be used with children who speak MAE and variations of MAE such as AAE, Southern American English (SoAE), Cajun, and Creole. The main purpose of the DELV-S is to begin to distinguish between language variations attributable to true linguistic dialect use from language delays or variations exhibited in children with language disorders, regardless of dialect. The measure was constructed to avoid linguistic bias by identifying linguistic differences that were specific to Non-mainstream American English (NMAE) and yet distinct from clinical language disorders. Item selection was guided by language sample research from children who speak predominantly AAE, but also other varieties of NMAE including Appalachian English, Cajun, Hispanic English and Southern English. Pilot research then indicated which phonological and morphosyntactic features were contrastive, or best discriminated NMAE speaking children from MAE speaking children, as well as those features that were shared, or non-contrastive and thus would be expected to be found in the language samples of typically developing children regardless of dialect use.

The DELV-S has two parts, the Language Variation Status -- Part I, which identifies whether the child uses MAE or NMAE; and the Diagnostic Risk Status -- Part II, which is designed to assess the child's level of risk for language disorder. In this study, we focused only on Part II, which is designed to assess children's language skills.

Part II of the DELV-S, and the focus of this study, assesses children's risk for language disorder by testing their syntactic knowledge via wh-questions and use of verbs, as well as their linguistic processing ability using a nonword repetition task. We describe Part II in more depth below. Because this portion of the assessment was designed to be used as a screening tool, according to the test developers, actual diagnosis of language status would be accomplished through the use of the Norm Referenced or Criterion Referenced tests by the same authors (Retrieved May 28, 2009, from http://pearsonassess.com/HAIWEB/Cultures/enus/Productdetail.htm?Pid=015-8092-112&Mode=resourceSeymourtest).

Development of the DELV-S and Psychometric Studies to Date

Part II of the DELV-S is comprised of 17 items of three types: morphosyntactic, wh-question movement, and non-word repetition. Items were selected based on their ability to discriminate between children with typical language development and those with language impairments, without regard for whether children used MAE or NMAE (Seymour et al., 2003). Please refer to the examiner's manual for a more complete description of item selection.

There are two types of morphosyntactic items. The first includes a singular subject with “was” copula or auxiliary, for example, “I see a sunny day.” [examiner points to picture]. “Today it is sunny and the children have their homework.” [examiner points to picture] “But yesterday their homework blew away. Why?” the correct response would be similar to, “It was windy.” or “The wind was blowing;” An incorrect answer might be “The wind be blowing.” The second involves possessive pronouns “hers” and “theirs.” For example, [examiner points to picture of boy] “He has a kite.” [examiner points to picture of girl] “She has a ball.” “The kite is his.” [point to ball] “The ball is _” with a correct response of “hers.” An incorrect answer would be

Based on the work of Campbell and colleagues (Campbell, Dollaghan, Needleman, & Janosky, 1997), the non-word items ask children to repeat increasingly difficult non-words where the number of syllables increases from two to four. For example, “goyfown” and foybaygowchipe.” The number of phonemes missed are recorded dichotomously: 0-1 errors; or 2 or more errors. Again, how is this different than typical nonword in a way that makes in less culturally biased?

The current norms are based on a sample of 1218 typically developing and language impaired children, both MAE and NMAE speakers. Most spoke AAE but 80 children were intentionally selected from other dialect groups, including Spanish Influenced English. Children's ages ranged from ages 4 years through 12 years although more than half of the children were under 7 years of age (n=783). The sample was fairly evenly distributed across the US (Seymour et al., 2003).

The test authors developed Part II Diagnostic Risk Status Cut Scores to discriminate between children with typical language skills and those with language impairments (LI) in two ways. First, cut scores were set to maximize identification of children who had been clinically identified with LI as compared to their typically developing peers. Second, they were set based on the score's association with the child's score on the DELV-Norm Referenced test. Thus, children who fell below the cut score on the DELV-S tended to be already identified as LI and did not perform well on the DELV-Norm Referenced test.

Using classical test theory, the test authors reported that the DELV-S appears to perform well with regard to test-retest and inter-examiner reliability, including when administered by examiners who are of different ethnic backgrounds. However, the latter was conducted with a small sample of children (n=25). Whereas Part II, showed that none of the children were incorrectly classified by either examiner, only 36% of the children were classified exactly the same. The correlation among examiners was .80 (Seymour et al., 2003). The manual does not report internal consistency among items. Assessment of sensitivity (does the test correctly identify children with LI) and specificity (does the test not identify children with typical language skills) comparing the typical with the LI identified sample revealed fairly high sensitivity (e.g., among 4 year olds, 71% of children with LI were placed in the Highest Risk for Disorder category) but low specificity (e.g. among 4 year olds, 24% of children who were not LI were placed in the Highest Risk for Disorder category). Specificity improved but sensitivity became worse for older children. There was no significant difference in sensitivity or specificity based on children's dialect use.

Because of the lack of internal consistency analyses for the DELV and tests for the discriminate validity of factors, serious limitations exist with regard to the utility of the DELV-S as a screening assessment of language variation. Without such basic psychometric analyses, differential bias in the identification of students with language variation problems could exist in the scores. Moreover, the authors of the DELV-S systematically test different aspects of language variation (i.e., morphosyntactic, wh-questions movement, and non-word repetition).

Thus, it is a reasonable question to ask whether or not the items cluster together in a multidimensional, rather than a unidimensional framework. The purpose of the present study was to examine the factor structure of DELV-Part II and examine how well items discriminate among examinees in a sample that may be generalized to the population. Furthermore, prior research by Patton-Terry, Connor, Petscher, and Conlin (2010) highlighted that differential change in NMAE dialect occurred in first and second grades. As such, we were interested in vertically scaling scores from the DELV-Part II in order to produce developmental scale scores on language variation across multiple grades.

Method

Participants

A total of 1,764 students were administered the DELV across the five time points: 250 kindergarten students were assessed in the fall, 867 grade 1 students were assessed in both the fall and spring, and 647 grade 2 students were assessed in the both the fall and spring. As such, 3,277 unique data points existed across all time points. Student characteristics in the sample were as follows: 51% Male, 46% White, 38% Black, 4% Asian, 5% Multiracial, 3% Latino, 3% were Unidentified, and <1% Native American, Pacific Islander, or Other. Based on DELV-S Part II results, overall 47.1% of the children were at lowest risk for a language disorder, 15.6% at low to medium risk, 20.4% at medium to high risk, and 16.9% at highest risk for language disorders.

Statistical Procedures

Several analytic strategies were used to evaluate the factor structure of the DELV, estimate parameters in an item response theory (IRT) model, and scale the ability scores over the five time points. First, an exploratory factor analysis was used to test the number of factors that could be reasonably retained from the data, and to determine if the pattern loadings on the factors compromised theoretically meaningful constructs. Eigenvalues in the sample correlation matrix above 1.0 were used as an initial criterion for inclusion in testing in subsequent models. Moreover, the comparative fit index (CFI, Bentler, 1990), Tucker-Lewis index (TLI, Bentler & Bonnett, 1980), root mean square error of approximation (RMSEA, Browne & Cudeck, 1992), and standardized root mean residual (SRMR) were used to evaluate model fit. CFI and TLI values greater than or equal to 0.95 are considered to be minimally sufficient criteria for acceptable model fit, and RMSEA and SRMR estimates <0.05 are desirable as well.

Secondly, a series of confirmatory factor analytic (CFA) models were used to explore parsimony and model fit. In addition to the previously described indices, the ratio between the model chi-square and degrees of freedom was calculated to assist in evaluating model fit; values <3.0 were deemed as acceptable (cite?). Then, following the CFA models,IRT analyses were conducted for each of the factors to produce vertical equated difficulty parameters, and vertically scaled ability scores. Because the items on the DELV-S are dichotomously scored (i.e., correct/incorrect), we used Mplus software (Muthen & Muthen, 2007) for the exploratory and confirmatory factor analyses in order to appropriately estimate the tetrachoric correlation matrix, while IRT analyses were conducted using BILOG-MG (Zimowski, Muraki, Mislevy, & Bock, 2007).

Results

Estimates from the EFA for factors with eigenvalues greater than 1.0 are reported in Table 1. The findings suggested that up to four factors could be retained; as expected, the eigenvalues decreased, with the greatest drop between factors 1 and 2, and the smallest between factors 3 and 4. The fit indices across the four factors suggested that a three or four factor solution might fit the data best, as the CFI and TLI indices were both greater than 0.95 and the RMSEA was <0.05. Additionally, the χ²/df was <2.0 for the three and four factor solutions. Using this preliminary evidence, the geomin rotated loadings were examined for magnitude (i.e., >0.30; Tabachnick & Fidell, 2001) and for parsimony as well. Thus, it was important to determine the number of items loadings on the multifactor solutions to see if multiple factors were described by more than a few items. In the one-factor solution, 16 of the 17 items had loading values >0.30, with one item at 0.23. The two-factor solution demonstrated fair orthogonality between the factors (i.e., 0.27), with six items loading on one factor and eleven on the other, and all item loadings had values >0.30 on its highest loading factor. The three- and four-factor solutions both retained high loading values for the items; however, relatively few items were observed on at least one of the factors, which suggested that the solution may fit well, albeit, not parsimoniously.

Table 1.

Exploratory Factor Analysis Results for the DELV

	Number of Factors in Solution
Statistic	1	2	3	4
Eigenvalue	4.99	2.40	1.50	1.24
RMSEA	0.07	0.04	0.03	0.02
SRMR	0.13	0.08	0.06	0.05
CFI	0.80	0.93	0.98	0.99
TLI	0.77	0.91	0.96	0.98
χ2/df	4.02	2.27	1.49	1.24

Note. RMSEA = root mean square error of approximation; SRMR = standardized root mean residual; CFI = comparative fit index; TLI = Tucker-Lewis index.

Using the factor loading matrix, three separate CFAs were tested using a one-, two-, or three-factor solution. The model fit for the unidimensional model was poor (χ² (84) = 697.49, p < 0.001; χ²/df = 8.30; CFI = 0.75; TLI = 0.84; RMSEA = 0.07), but improved greatly in the two-factor (χ² (84) =359.16, p < 0.001; χ²/df = 4.28; CFA = 0.89; TLI = 0.93; RMSEA = 0.05), and three-factor models (χ² (84) =192.43, p < 0.001; χ²/df = 2.29; CFI = 0.96; TLI = 0.97; RMSEA = 0.03). Generally speaking, the three-factor provided the most appropriate fit to the data; however, when reviewing the factor loading matrix for each solution (Table 2) it appeared that a two-factor model could be a more parsimonious solution. Items 10 and 11 described its own factor in the three-factor solution with relationships to that factor that were stronger than individual loadings in the other model.

Table 2.

Standardized CFA loadings

	One-Factor	Two-Factor		Three-Factor
Items	F1	F1	F2	F1	F2	F3
Item 1	0.58	0.60	-	0.78	-	-
Item 2	0.73	0.76	-	0.73	-	-
Item 3	0.40	0.42	-	0.62	-	-
Item 4	0.70	0.73	-	0.54	-	-
Item 5	0.66	0.69	-	0.46	-	-
Item 6	0.57	0.59	-	0.65	-	-
Item 7	0.49	0.51	-	0.68	-	-
Item 8	0.77	0.79	-	0.84	-	-
Item 9	0.64	0.67	-	0.49	-	-
Item 10	0.42	0.44	-	-	0.87	-
Item 11	0.59	0.61	-	-	0.74	-
Item 12	0.49	-	0.63	-	-	0.63
Item 13	0.50	-	0.67	-	-	0.67
Item 14	0.42	-	0.57	-	-	0.57
Item 15	0.46	-	0.61	-	-	0.60
Item 16	0.52	-	0.70	-	-	0.70
Item 17	0.48	-	0.61	-	-	0.61

Further, upon further review of the items in the DELV, the two-factor model is more consistent with how the study authors addressed diagnostic risk status – namely items are collapsed into two sections: syntactic skills and non-word repetition ability. The syntactic skills section is comprised of the first eleven items while non-word repetition is made up of the remaining six items. In light of this conceptual separation, we opted to retain the two-factor solution for estimating the item parameters and scaling ability scores.

Of the three available IRT models (i.e., 1PL, 2PL, and 3PL), we opted to use the more conservative??? 1PL for several reasons. First, a 1PL model requires fewer examinees to produce stable estimates of item difficulty. Although the full sample size was small, the number of students in kindergarten was relatively small (n = 250) compared to the other groups. Although no consensus yet exists on minimal sample sizes needed for IRT models, due to the number of considerations in a model, Petscher and Schatschneider (2010) noted that a number of sources have indicated that at least 200 participants should be used. Secondly, the scoring model for a 1PL model has the benefit of mapping the estimated ability scores directly on to the raw scores, and considers both the discrimination and pseudo-guessing estimates of an item to be a symptom of item bias and/or multidimensionality (Wright, 1992).

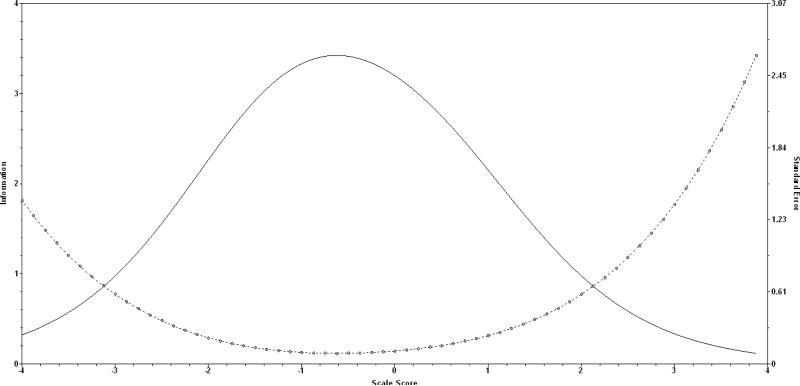
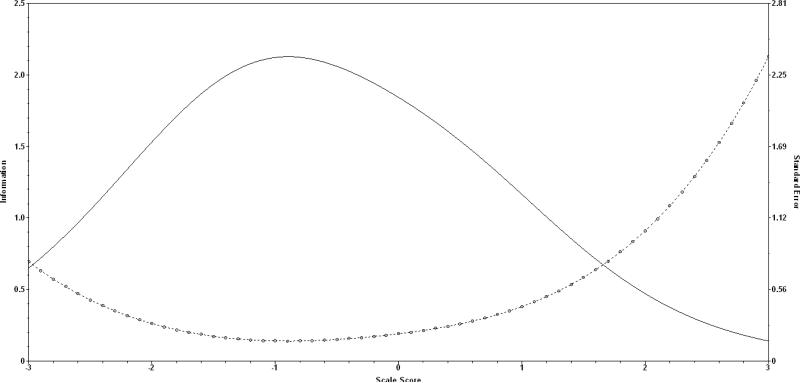
In order to appropriately estimate the item parameters and vertically scaled ability scores, a multiple-group 1PL model was used, using the kindergarten fall scores as the referent group. The item estimated item difficulties for the two separate factors are reported in Table 3. For the syntactic skills, the items ranged in difficulty from -1.44 (Item 11) to 0.68 (Item 7) with a mean of -0.46, and for non-word repetition the easiest item difficulty was observed for Item 1 (-1.53), with Item 6 being the most difficult (0.56) and a mean of -0.55. In both factors, the items tended to be negative, an indication of the relative easiness of the items when vertically equated across the five groups. An important feature of a set of items within a dimension is the amount of information (i.e., precision) that exists for the range of ability. The test information function for syntactic skills and non-word repetition are presented in Figures 1 and 2, respectively. Both figures highlight two common features for the tests of syntactic skills and non-word repetition: (1) more information is provided for students who are low in the skill, and the (2) information covers a relatively wide range of ability. Within Figure 1, the maximum level of information is at a scale score of approximately -0.50, suggesting that this test can most reliably describe students’ language skills when they exhibit weak language skills. The range of maximum precision of syntactic skills appeared to be from -1.50 to 0.25. Pertaining to non-word repetition ability, the subtest was most informative for students where their ability was closer to -1.00, with higher levels of precision in the ability range of -1.75 to 0.00.

Table 3.

1PL Equated Item Parameters

Items	Syntactic Skills		Non-Word Repetition
	a	b	a	b
Item 1	1.55	-0.391	1.688	-1.53
Item 2	1.55	-1.048	1.688	-1.003
Item 3	1.55	-0.261	1.688	0.215
Item 4	1.55	-0.169	1.688	-0.675
Item 5	1.55	0.399	1.688	-0.852
Item 6	1.55	0.431	1.688	0.563
Item 7	1.55	0.682	-	-
Item 8	1.55	-1.182	-	-
Item 9	1.55	-0.83	-	-
Item 10	1.55	-1.268	-	-
Item 11	1.55	-1.442	-	-

Figure 1.

Test Information Function and Standard Error for Syntactic Skills

Figure 2.

Test Information Function and Standard Error for Non-Word Repetition

Using the theta scores generated from BILOG for each dimension, a series of look-up tables were created to provide information about the relationship between the raw score and a series of assessment scores. Three different scores were created in order to contextualize the results for both growth and standard score purposes. Within each of the administrative periods (i.e., fall-kindergarten, fall-grade 1, spring-grade1, fall-grade 2, spring-grade 2), a standard score with a mean of 100 and standard deviation of 15 was developed, as was a percentile rank, and a developmental scale score (i.e., D-Score). The standard score and percentile ranks were provided so that clinicians and practitioners may contextualize students’ ability within a given point in time. Because children's language skills change over time (Gleason, 1997) it was important to provide a type of standard score that is appropriate for modeling growth. Subsequently, a D-Score was created that describes the range of ability from kindergarten through second grade. This score has a mean of 500 and a standard deviation of 100 and operates in a similar fashion to a W-score in the Woodcock-Johnson battery of assessments.

Tables 4 and 5 provide the look-up table relationships between the raw scores on the two separate dimensions and the D-Score, Standard Score, and percentile rank. Notice that in Table 4, when examining the values close to the mean at each time point, the D-Score changes. For example, in the fall of kindergarten, a mean score of 100 corresponds to a raw score of 7 and a D-Score of 501, which is expected due to using this group as the referent in the scaling analysis. At the fall-grade 1 time point, the mean of 100 now approximately corresponds to a raw score of 9 and a D-Score of 575. Thus, while a student may have the same standard score at each time point, the D-Score will reflect the actual growth in the latent ability. This observation is replicated for non-word repetition skills in Table 5 where the mean score of 100 at the fall of kindergarten corresponds to a raw score of 4 and D-Score of 498, and increases to a D-Score of 568 in the fall of grade 2.

Table 4.

Developmental and Administrative Scale Scores – Syntactic Skills

Time Point	Raw Score	D-Score	Standard	Percentile Rank
Fall - Kindergarten	0	220	58	1
	1	283	67	2
	2	339	76	5
	3	377	82	11
	4	410	87	18
	5	440	91	27
	6	470	95	38
	7	501	100	50
	8	535	105	64
	9	575	111	77
	10	633	120	91
	11	702	130	98
Fall - Grade 1	0	220	54	1
	1	283	54	1
	2	339	54	1
	3	377	61	1
	4	410	68	2
	5	440	73	4
	6	470	79	8
	7	501	85	15
	8	535	91	28
	9	575	99	47
	10	633	110	74
	11	702	123	94
Spring - Grade 1	0	220	53	1
	1	283	53	1
	2	339	53	1
	3	377	53	1
	4	410	60	1
	5	440	66	1
	6	470	71	3
	7	501	78	7
	8	535	84	15
	9	575	93	31
	10	633	104	61
	11	702	118	88
Fall - Grade 2	0	220	50	1
	1	283	50	1
	2	339	50	1
	3	377	50	1
	4	410	57	1
	5	440	63	1
	6	470	69	2
	7	501	76	5
	8	535	82	12
	9	575	91	27
	10	633	103	57
	11	702	117	87
Spring - Grade 2	0	220	47	1
	1	283	47	1
	2	339	47	1
	3	377	47	1
	4	410	47	1
	5	440	54	1
	6	470	61	1
	7	501	68	2
	8	535	76	5
	9	575	85	16
	10	633	98	46
	11	702	114	83

Table 5.

Developmental and Administrative Scale Scores – Non-word Repetition

Time Point	Raw Score	D-Score	Standard	Percentile Rank
Fall - Kindergarten	0	248	62	1
	1	325	74	4
	2	389	83	13
	3	442	91	28
	4	498	100	49
	5	568	110	75
	6	651	123	93
Fall - Grade 1	0	248	49	1
	1	325	62	1
	2	389	73	4
	3	442	83	12
	4	498	92	30
	5	568	104	61
	6	651	119	89
Spring - Grade 1	0	248	47	1
	1	325	60	1
	2	389	71	3
	3	442	80	9
	4	498	90	25
	5	568	102	55
	6	651	116	86
Fall - Grade 2	0	248	39	1
	1	325	53	1
	2	389	65	1
	3	442	75	5
	4	498	86	17
	5	568	99	48
	6	651	115	84
Spring - Grade 2	0	248	43	1
	1	325	56	1
	2	389	68	2
	3	442	77	6
	4	498	87	19
	5	568	99	48
	6	651	114	82

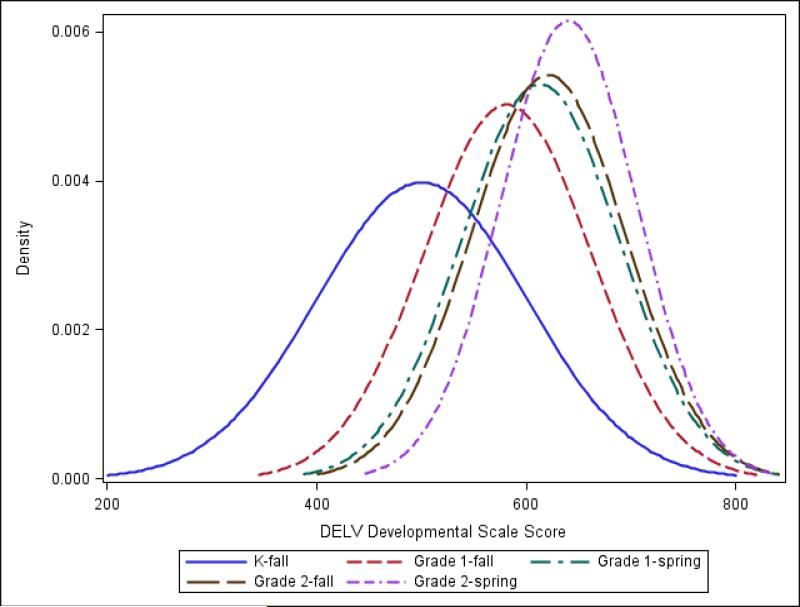
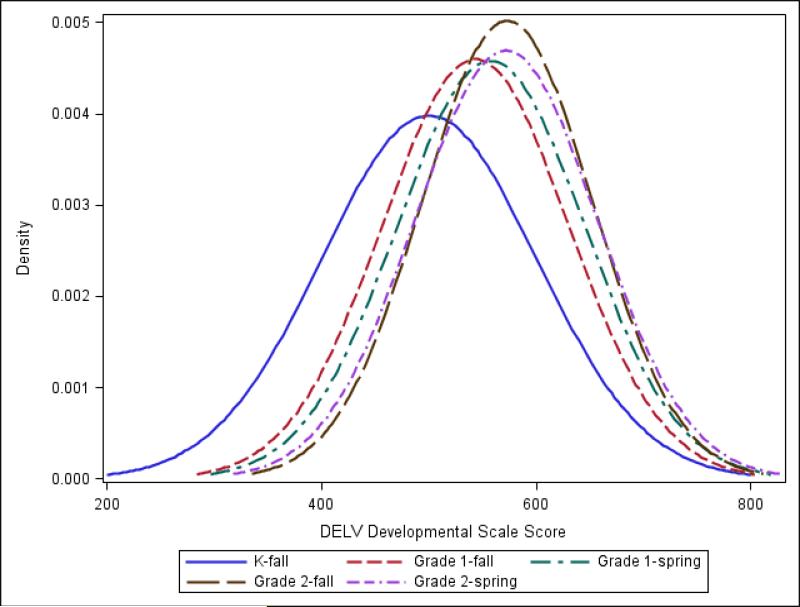
The values in both look-up tables suggest that it takes longer for students’ ability scores in non-word repetition to grow relative to their syntactic skills. In fact, this is the case when modeling the distribution of ability scores for each time point by factor. Figure 3 models the ability scores for syntactic skills, and the distributions indicate that a large shift in the distribution occurs between the fall of kindergarten and the fall of grade 1. Although small changes occurred within first grade, another larger shift occurred between the fall of grade 1 and the spring of grade 2. When considering non-word repetition skills (Figure 5), the largest ability shift occurs between fall of kindergarten and the fall of grade 1, with minimal observed changes from grade 1 to grade 2.

Figure 3.

Ability distribution of Syntactic Skills over time

Discussion

The aim of this study was to explore the psychometric properties of the DELV-S Part II in order to provide better recommendations to clinicians and practioners presently using this culturally-fair assessment for screening students who may have oral language impairments. The study was conducted with a larger number of students than were in the original normative sample and focused on children in grades K through G2, which is the time many children are referred for language delays within school systems. Using a vertically scaled item response theory model, item parameters were provided to describe the relative difficulty of items, and ability scores were generated in order to contextualize students’ ability both within a current assessment as well as over time. The results from the present study underscore the importance of reporting the psychometrics of scores for new assessments. Although the authors of the DELV reported basic information pertaining to inter-rater reliability and concurrent validity, our findings extend their reporting by suggesting that a multidimensional model provides the best description of the data. Additionally, by using an IRT framework, it was possible to highlight for whom the diagnostic assessment is most informative. The implicit assumption of this type of assessment is that it should provide the most information about students who demonstrate weaker language skills. This idea was, in fact, confirmed, for both syntactic and non-word repetition ability as the test had the highest level of information for students whose language ability was less than average. For students whose ability was less than -3.0, the assessment provides little information; however, when appropriately contextualized, this should only be <1% of students in the population who have high error in their scores.

Future work should include a larger sample of kindergarten students and extend the findings to oral language skill variation in the spring of kindergarten. Additionally, with larger samples, multiple group and MIMIC models could be applied to examine the configural and metric invariance of the factors across different ethnic and demographic groups.In addition it will be important to replicate this work in other locations, other than the Southeast, where NMAE is widely spoken regardless of ethnicity.???

The need for additional research, notwithstanding, findings from the present study provide increased resources to assessors presently using the DELV-S in the way of look-up tables to compare student performance at specific points in time. Inclusion of the created D-scores also facilitates a more comprehensive metric for describing students’ change in language skills over time compared to raw scores. As such, using the DELV-S may have greater appeal to both clinicians and researchers in this field of study and help to prevent misdiagnosis of children who use dialects that vary from mainstream English.

Figure 4.

Ability score distribution of Non-Word Skills over time.