Alcohol Binding to the Odorant Binding Protein LUSH: Multiple Factors Affecting Binding Affinities

Abstract

Density function theory (DFT) calculations have been carried out to investigate the binding of alcohols to the odorant binding protein LUSH from Drosophila melanogaster. LUSH is one of the few proteins known to bind to ethanol at physiologically relevant concentrations and where high-resolution structural information is available for the protein bound to alcohol at these concentrations. The structures of the LUSH–alcohol complexes identify a set of specific hydrogen-bonding interactions as critical for optimal binding of ethanol. A set of truncated models based on the structure of the LUSH–butanol complex were constructed for the wild-type and mutant (T57S, S52A, and T57A) proteins in complexes with a series of n-alcohols and for the apoprotein bound to water and for the ligand-free protein. Using both gas-phase calculations and continuum solvation model calculations, we found that the widely used DFT model, B3LYP, failed to reproduce the experimentally observed trend of increasing binding affinity with the increasing length of the alkyl chain in the alcohol. In contrast, the recently developed M05-2X DFT model successfully reproduced this subtle trend. Analysis of the results indicated that multiple factors contribute to the differences in alcohol binding affinity: the H-bonding with Thr57 and Ser52 (4–5 kcal/mol per H-bond), the desolvation contribution (4–6 kcal/mol for alcohols and 8–10 kcal/mol for water), and the other noncovalent interaction (1.2 kcal/mol per CH₂ group of the alcohol alkyl chain). These results reveal the outstanding potential for using the M05-2X model in calculations of protein–substrate complexes where noncovalent interactions are important.

Background

Historically, ethanol has been considered to act as a nonspecific drug at physiologically relevant concentrations of 5–50 mM. (For reference, a blood alcohol concentration of 0.08 mg %, which is the legal limit for driving in most US states, corresponds to ~17 mM.) However, despite the limited chemical functionality that limits the type and number of interactions that ethanol can form with a protein, it is now clear that ethanol shows a significant degree of selectivity for a number of cellular targets that include receptors, ion channels, and signaling kinases (1, 2). Indeed, studies have identified both regiospecific effects of ethanol (3–5) and in some cases single amino acids that are required for conferring alcohol sensitivity to these proteins (6–9). Therefore, it is now widely accepted that many of the physiological effects associated with alcohol consumption are a result of ethanol binding to specific sites in these targets, and these sites have unique features that confer alcohol sensitivity. Presently, relatively little is known about the nature of these proposed alcohol binding sites. This is primarily because many of the targets of ethanol's actions are integral membrane proteins that are difficult to study using high-resolution structural methods such as NMR spectroscopy or X-ray crystallography. Molecular modeling studies have gone a long way to explaining how alcohol may alter channel gating properties (1, 8, 10). However, until a structure of these channels is available, the exact location and nature of the interactions with ethanol will remain elusive.

At present the only available high-resolution structures of proteins bound to alcohol at physiologically relevant concentrations are those of alcohol dehydrogenase (ADH)¹ (11) and of the odorant binding protein LUSH from Drosophila melanogaster (12, 13). These two proteins bind alcohol in fundamentally different ways. In the case of ADH the alcohol is bound to a zinc atom, while LUSH binds alcohol through a set of concerted hydrogen bonds. The alcohol binding site in LUSH is located in a hydrophobic, water-filled cavity formed by the convergence of a set of α-helices, and so it is more likely to represent the types of binding sites present in the transmembrane domains of alcohol-sensitive ligand-gated ion channels.

Structural studies of LUSH–alcohol complexes revealed the presence of a single ethanol binding site located at one end of the central hydrophobic cavity (12). As illustrated in Figure 1, the alcohol molecule forms hydrogen-bonding interactions with two polar residues, Ser52 and Thr57. Mutational analyses revealed that the identity of the residues forming these hydrogen bonds is critical in defining a high-affinity ethanol binding site (13). Substitution of Thr57 with a serine, which maintained the hydrogen-bonding interactions, significantly reduced the binding affinity for ethanol in solution but had little or no effect on the binding of longer chain alcohols such as butanol or pentanol. In contrast, removal of the hydrogen-bonding interactions by substitution of Thr57 or Ser52 with alanine dramatically reduces the binding affinity for all short-chain alcohols. Binding of ethanol to LUSH therefore appears to be dominated by hydrogen-bonding interactions and surprisingly suggests that the identity of the residues involved in these hydrogen bonds is critical for forming optimal interactions with ethanol. For longer chain alcohols, the identity of these residues is less critical, presumably because the additional noncovalent interactions that can be formed with the longer alkyl chains can compensate for the loss of high energy hydrogen-bonding interactions. Other factors that could significantly affect alcohol binding include both the presence of ordered waters within the binding site (14–16) and changes in the electronic structure of both proteins and alcohols. Differences in molecular polarizability have been suggested to play an important part in contributing to increased binding affinities of anesthetics and alcohols to proteins (17–20).

Figure 1.

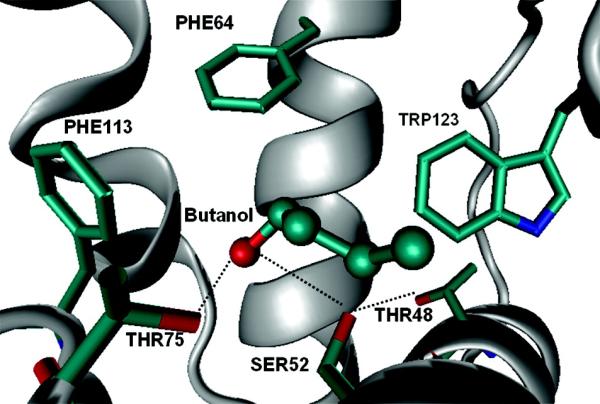
The H-bonding network stabilizes the butanol in the binding site of LUSH.

In order to develop a more complete understanding of the specific determinants of a high-affinity ethanol binding site, we have initiated a series of theoretical calculations to examine if changes in the electronic properties of the atoms involved in binding could contribute to increased binding affinities for ethanol at this site. As a first step in developing the approach for these calculations, we have investigated the application of density functional theory (DFT) calculations with both the widely used B3LYP (21–23) model and the more recently developed M05-2X (24, 25) model. Comparing these two DFT models, we find that the M05-2X model more accurately reproduces the experimentally observed trends in the binding energies of both the wild-type and mutant LUSH proteins with a series of n-alcohols that includes ethanol, propanol, and butanol. The M05-2X calculations confirm that binding of alcohol to LUSH requires contributions from hydrogen bonding, solvation, and other noncovalent interactions. In contrast, the B3LYP model fails to reproduce the experimentally observed trends in the binding energies. These calculations provide a foundation on which one can develop more comprehensive QM/MM (26–30) calculations to fully define the nature of the alcohol binding site in LUSH.

Computational Details

Models of LUSH–Alcohol Complexes

As all of the structures of the LUSH–alcohol complexes solved to date essentially have the same overall structure, a model of the alcohol binding site in LUSH was constructed containing a minimal set of atoms based on the crystal structure of the LUSH–butanol complex (PDB code: 1OOH) (12). This is the highest resolution structure of these complexes available and so is likely to have the highest accuracy. The model of the binding site consisted of atoms from the butanol molecule and from the nearby amino acid side chains of Ser52, Val51, Val58, Thr57, Phe64, Leu76, Val106, Thr109, Phe113, and Trp123; those residues were truncated at the C_β position, and a hydrogen atom was used in place of the C_α carbon. The backbone carbonyl group of Thr48 was modeled as formaldehyde. Residues Ala55 and Ala110 were modeled as ethane. No crystallographic water molecules were included in this model, because all of the experimentally observed waters are located outside the binding site and do not make contacts with the alcohol in these structures. Figure 2 displays the resulting model of the butanol binding site after the hydrogen atoms were added, with the H-bonding network indicated by dotted lines. The model consists of 155 atoms. We point out that basing our model on crystal structures has imposed certain limits in our analysis (as will be further discussed in the Results Section). However, making the truncated models resemble the crystal structures is arguably the best approach when no other experimental structural information is available.

Figure 2.

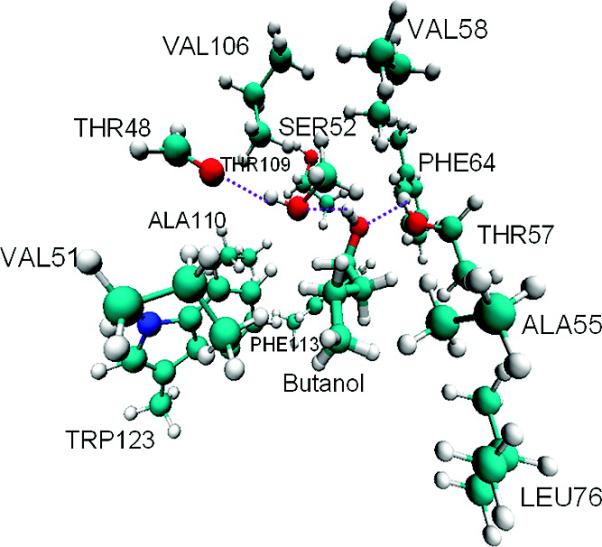
The butanol–protein complex model.

Initial Minimization

The initial model of the butanol binding pocket was relaxed at the AM1 (31) level of theory in two steps. First, the hydrogen atoms were relaxed while keeping all heavy atoms fixed at their original positions. Next, the geometry was optimized with a set of selected atoms fixed at their positions in the crystal structure. These atoms included Thr48, where both of the heavy atoms in the formaldehyde model were fixed. The C_β atom and O_γ atoms in Ser52 were fixed, because O_γ is critical in defining the hydrogen-bonding network. For alanine residues, the C_α and C_β atoms were fixed. For each of Val51, Thr57, Leu76, and Phe113, the C_β atom and the hydrogen atom that substitutes the C_α atom were fixed. For the other residues, the C_β and C_γ atoms were fixed. The set of fixed atoms prevented significant deviations away from the coordinate positions observed in the crystal structure. The crystallographic temperature factors for the set of fixed atoms are those smallest among all of the atoms in the models, indicating that they are least mobile in general. In contrast, the ligand was allowed to move freely.

Construction of Other Protein–Alcohol Complexes

Models for the binding sites of other LUSH–alcohol complexes were constructed using the coordinates of the relaxed butanol–protein model as a starting point. Sequentially replacing the terminal methyl group of butanol with a proton generated the model for propanol and subsequently the ethanol complexes. The replacement of the alcohol by a water molecule generated the apoprotein complex model. Previous structural studies using X-ray crystallography have shown that the alcohols bind in the same site (12) and that in the absence of alcohol a water molecule occupies the site of the alcohol hydroxyl group (13). The model of the empty binding site was constructed by deleting the butanol ligand. Additional models of the binding site in the three LUSH mutants, namely, T57S, S52A, and T57A, were generated by substituting the appropriate functional groups in the mutated residue (Thr57 or Ser52). After these models were built, they were relaxed following the same two-step procedure outlined above. This treatment aimed to ensure that protein adopts similar conformations for different ligands and to control for the effects of having the protein conformations in different local minima that would make it difficult to make a direct comparison between the effects of the ligand. Again, previous X-ray crystallography studies establish that the protein adopts almost identical structures in each of the complexes formed with ethanol, propanol, and butanol (12, 13).

Electronic Structure Calculations

After the ligand–protein complex models were generated, partial geometry optimizations were carried out by again fixing the set of atoms listed above in their original positions. Electronic structure calculations were performed using both the B3LYP model and the M05-2X model. Geometry optimization utilized the 6-31G(d) basis set (32–34) (called B1 in this work). For the butanol–protein complex model, this treatment yielded 1038 basis functions. Single-point energy calculations on the optimized geometry were then performed employing a larger size basis set 6-31+G(d,p) (32–36), which is referred to as B2. The corresponding calculations will be denoted in this paper as DFT/B2//DFT/B1 (or DFT/B2 for short when no confusion will be incurred), where DFT = B3LYP and M05-2X. The use of the B2 basis set resulted in 1559 basis functions for the butanol–protein complex. As a result of their small sizes, the isolated ligands were fully optimized at the DFT/B1 and DFT/B2 levels.

For continuum solvation calculations, the charge density-based solvation (SMD) (37) model was selected, where the solvent for the ligands was set to water with a dielectric constant of 78.4 and the solvent for the protein was chosen to be olive oil with a dielectric constant of 3.1 (38). The olive oil has been demonstrated to be a faithful mimic of a lipophilic environment of protein (38). The continuum solvation model calculations were performed using the gas-phase optimized geometries for all ligands and model systems.

The gas-phase calculations were carried out employing the Gaussian03(39) program. The continuum solvation calculations were done employing the GESOL (40) program, which invokes Gaussian03 for doing the integral–equation–formalism polarizable continuum model (IEFPCM) (41–44) computation. The calculations were performed on the IBM Blade Center Linux Cluster and the SGI Calhoun Altix 1300 Linux Cluster at the Minnesota Supercomputing Institute. The computational costs with B3LYP and M05-2X are similar. For example, a single-point energy calculation in the gas phase with the B2 basis set took about 10 h to finish using eight processors (two quad-core 2.66 GHz Intel Xeon 5355 CPUs). A single-point solvation calculation was typically done within 20 h.

Analysis of Results

The binding affinity for a given ligand was computed according to eq 1

$$E_{\text{bind}}=E_{\text{ligand}}+E_{\text{site}}-E_{\text{complex}}$$ (1)

where E_ligand and E_site are the energies of the well-separated ligand and the protein with an empty binding site, respectively, and E_complex is the energy of the ligand–protein complex. A negative E_bind indicates unfavorable binding.

Results and Discussion

Choice of DFT Model

We are interested in determining if theoretical treatments can accurately account for the different contributions to the binding of alcohols to proteins. Therefore, we started by testing the effect of different models. We first performed calculations on the wild-type LUSH protein. As will be shown below, while the M05-2X model reproduced the correct trend for the binding affinities for the alcohols, the B3LYP model did not. This reflects the failure of the B3LYP model in accurately treating the noncovalent interactions, which remain a challenge for most DFT models available today. As a result, we only applied the M05-2X model to the studies of the LUSH mutants.

Table 1 displays the binding affinities calculated for alcohols binding to the wild-type LUSH protein relative to water. The B3LYP gas-phase calculations predict that water has larger binding affinities than alcohols by 2–4 kcal/mol, which contrasts with the experimental observations (13). The results were improved after taking into consideration the solvation effects, and the B3LYP calculations indicated that alcohols are slightly (less than 1.6 kcal/mol) preferred compared to water. However, the B3LYP models failed to reproduce the experimentally observed trend of increasing binding affinity of an alcohol molecule as a function of its increasing alkyl chain length (13). The use of larger (B2) basis set yielded results qualitatively similar to those obtained employing the smaller (B1) basis set. This clearly indicates that B3LYP, despite its widespread application, is not an appropriate choice of theoretical model in the present study.

Table 1.

Relative Affinities (kcal/mol) of Alcohols with Respect to Water Binding to Wild-Type LUSH Protein^a

	butanol	propanol	ethanol	water
B3LYP/B1
gas	−2.54	−2.90	−1.76	0
solb	1.57	1.06	1.44	0
B3LYP/B2//B3LYP/B1
gas	−3.65	−3.48	−2.10	0
solb	0.18	0.39	0.73	0
M05-2X/B1
gas	3.83	1.56	1.42	0
solb	8.30	6.43	5.35	0
M05-2X/B2//M05-2X/B1
gas	4.20	2.15	1.79	0
solb	8.43	6.91	5.43	0

^aThe model is shown in Figure 2. The energy zero is set to the binding energy of a water molecule to LUSH in a given level of theory. B1 = 6-31G(d), and B2 = 6-31+G(d,p).

^bSMD solvation model calculations on the gas-phase optimized geometries

Test calculations (24, 25) of M05-2X on small model systems have shown that this DFT model yields remarkably good accuracy in a broad range of applications, and the current study is a critical test of the M05-2X model on larger biological systems. The M05-2X gas-phase calculations showed that binding of alcohol to LUSH is more favorable than water; e.g., the ethanol is favored by 1.4–1.8 kcal mol⁻¹ over water. Moreover, the binding affinity increases in the order of ethanol → propanol → butanol, in good agreement with experimental findings (13). The increase in binding affinity can be attributed to the increase in the noncovalent interactions that can be formed with the longer alkyl chain. For example, the M05-2X/B2 calculations showed that the binding energy increases by 0.4 kcal/mol when going from ethanol to propanol and by about 2 kcal/mol when moving from propanol to butanol. The larger increase in the propanol → butanol case is probably due to the newly available interaction between butanol and Trp123. This result correlates well with experimental observations of the protein stability as a function of increasing alcohol chain length (45). In these latter experiments, which monitor protein unfolding as a function of alcohol chain length, there is a shift to a significantly more cooperative unfolding transition when using butanol compared to shorter chain alcohols. This may be explained by the formation of more extensive noncovalent interactions between the protein and the longer chain alcohols.

The observed trend in binding energies with the M05-2X model is further enhanced by the solvation effects; the M05-2X/B2 solvation calculations suggested that binding of ethanol is preferred to water by a significant amount (5.4 kcal/mol), and the binding affinity increases by approximately 1.5 kcal/mol per CH₂ group. Although the 1.5 kcal/mol result overestimates the experimental value (0.8 kcal/mol per CH₂ group (13)), it is still a remarkable success for DFT, where accuracy better than 1 kcal/mol is difficult to achieve. The close agreement with experimental observations clearly indicates that M05-2X model is well suited for calculations with the LUSH protein.

Effects of Solvation

In order to gain insight into the effects of solvation, we compared the solvation free energy contributions of the ligands, protein, and ligand–protein complexes (Table 2). This provides an opportunity to compare the performances by B3LYP and M05-2X in the solvation calculations. Overall, one finds that solvation stabilizes all components (ligands, protein, and ligand–protein complexes). Although the calculated absolute energy of stabilization for a given component differs in the four DFT-model/basis-set combinations, the relative energy of stabilization for the same component is very similar in the four levels of theory. This implies that the failure of B3LYP is not due to the inaccurate calculations of the solvation free energy at this level of theory; rather, it is because of the inability to accurately account for the effects of the noncovalent interactions.

Table 2.

Solvation Free Energy Contribution (kcal/mol) of Alcohols and Water Binding to Wild-Type LUSH Protein^a

	butanol	propanol	ethanol	water
B3LYP/B1
protein	−27.93	−27.93	−27.93	−27.93
ligand	−3.72	−3.88	−4.30	−8.27
complex	−27.83	−27.85	−27.51	−28.27
C – (P + L)b	3.82	3.96	4.73	7.93
B3LYP/B2//B3LYP/B1
protein	−29.25	−29.25	−29.25	−29.25
ligand	−4.43	−4.65	−5.18	−8.82
complex	−29.06	−29.32	−28.82	−29.62
C – (P + L)b	4.62	4.58	5.62	8.45
M05-2X/B1
protein	−30.00	−30.00	−30.00	−30.00
ligand	−4.26	−4.46	−4.91	−8.90
complex	−29.17	−29.77	−29.29	−29.34
C – (P + L)b	5.09	4.69	5.62	9.55
M05-2X/B2//M05-2X/B1
protein	−31.44	−31.44	−31.44	−31.44
ligand	−4.86	−5.09	−5.67	−9.23
complex	−30.49	−31.24	−30.71	−30.63
C – (P + L)b	5.82	5.29	6.41	10.05

^aSMD solvation model calculations on the gas-phase optimized geometries. B1 = 6-31G(d), and B2 = 6-31+G(d,p). A negative value indicates stabilization due to solvation.

^bComputed as complex – (protein + ligand).

Furthermore, Table 2 reveals that the stabilization due to solvation is approximately the same for the protein and for all alcohol–protein complexes in the calculations at a given level of theory. This is not surprising because the ligand is buried in the active site, which is embraced by hydrophobic residues. Therefore, the corresponding solvation free energy does not show a significant dependency (<3%) on whether there is a ligand in the active site or which ligand (water or alcohol) is in the active site. On the other hand, the solvation free energy for an isolated ligand varies noticeably from one ligand to another; this is especially true when going from water to butanol, which shows about 50% change in the solvation free energy (from 8–9 to 4–5 kcal/mol, depending on the level of theory employed). Consequently, the net effects of solvation are dominated by the ligands. Again, taking the M05-2X/B2 calculations as an example, solvation stabilizes binding of butanol, propanol, and ethanol with respect to water in the active site by 4.2, 4.7, and 3.6 kcal/mol, respectively (last line in Table 2). The solvation effects, together with the noncovalent interactions with the alkyl chain of alcohols, make the longer chain butanol the more favored ligand in the binding site of the LUSH protein.

We note that treating the protein environment by a uniform continuous medium with specific dielectric properties is certainly a significant simplification. Such an approach does not consider the short-range effects or the nonuniformity of the environment, which may influence some of the electronic properties of the interacting partners. However, such a treatment does account for the long-range polarization effects, which are of primary importance in the present study, namely, the transfer of the alcohol from a highly polar bulk solvent (water) into a hydrophobic binding site buried in the protein. Although the binding site may be partially hydrated, the bound state of the alcohol is such that the alkyl chain is oriented pointing out into the pocket and that the hydroxyl group of the alcohol does not form any H-bonding interactions with water molecules in the pocket. Therefore, although the nonuniformity of the protein environment may not be completely modeled in these calculations, these effects are likely to be subtle, and the use of the uniform continuous medium is expected to be a good initial approximation. Fully accounting for the effects of a nonuniform environment requires an explicit solvation (combined QM/MM) model, which will be carried out in the future.

Contributions from H-Bonding Networks

High-resolution crystal structures of LUSH–alcohol complexes indicate that the H-bonding network formed by Thr57, Ser52, and Thr48 is essential in anchoring the alcohol in the binding site through interactions with the alcohol hydroxyl group. The significance of these interactions has been investigated experimentally (13) and in the present studies by making specific substitutions to Thr57 and Ser52. The interactions with Thr48 occur through the backbone carbonyl which also plays a role in stabilizing the helical conformation of this region of the protein. Consequently, it is not possible to make experimental substitutions at this position, and there is no experimental data available that could be used to validate computational results. Therefore, calculations with changes in Thr48 have not been considered at this time (12). Table 3 summarizes the results for calculations performed for the mutated proteins, in particular, the relative affinities of alcohols and water binding to the mutants with respect to water binding to the wild-type protein. Our discussion will focus on the solvation calculation results (although for completeness, we have also listed the gas-phase results in Table 3). First, we note that there is no significant difference in the calculated binding affinities between the wild-type protein and the T57S mutant, indicating the T57S mutation has little or minor effects on alcohol binding. The binding of ethanol in the T57S mutant is less favorable than in the wild-type protein (5.0 vs 5.4 kcal/mol), but the difference seems less significant than experimental observations have suggested (13). Solution-based studies indicated a significant disruption in binding of ethanol in the T57S mutant. However, these differences were less apparent in the crystal structures of these mutants, and, indeed, ethanol was still observed in the binding pocket of the T57S crystal structure albeit with lower occupancy (13). This may reflect differences in the structure of the solution state vs crystal structure, as it has been shown that alcohols stabilize the structure of LUSH in a chain length dependent manner (45).

Table 3.

Relative Affinities (kcal/mol) of Alcohols and Water Binding to LUSH Wild-Type Protein and Mutants with Respect to Water Binding to Wild-Type LUSH Protein^a

	gas				solb
	butanol	propanol	ethanol	water	butanol	propanol	ethanol	water
WT
Blc	3.83	1.56	1.42	0.00	8.30	6.43	5.35	0.00
B2d	4.20	2.15	1.79	0.00	8.43	6.91	5.43	0.00
T57S
Blc	4.11	1.48	1.10	0.29	9.09	6.49	5.09	0.20
B2d	4.31	2.16	1.36	0.47	9.04	7.04	5.03	0.30
S52A
Blc	−2.55	−4.89	−5.74	−7.33	3.03	1.32	−0.46	−5.80
B2d	−1.50	−3.26	−4.22	−6.87	4.00	2.98	0.89	−5.27
T57A
Blc	−1.64	−4.96	−4.54	−6.25	4.48	0.76	0.20	−4.64
B2d	−0.38	−3.43	−3.47	−5.28	5.53	2.14	0.93	−3.48

^aThe energy zero is set to the binding energy of a water molecule to wild-type LUSH in a given level of theory.

^bIEFPCM solvation model calculations on the gas-phase optimized geometries.

^cM05-2X/6-31G(d) calculations.

^dM05-2X/6-31+G(d,p)//M05-2X/6-31G(d) calculations.

Second, for the S52A and T57A mutants the binding affinities for all ligands are dramatically reduced by 4–5 kcal/mol, supporting the critical involvement of the H-bonding network in stabilizing binding of alcohols as may be expected. In particular, the binding affinity of ethanol is reduced to less than 1 kcal/mol or even a negative value (in the M05/B1 calculations of S52A), strongly suggesting that ethanol binding is likely disrupted in the S52A and T57A mutants. The binding of propanol is also significantly disfavored, with the binding affinity of 1–3 kcal/mol. The butanol binding affinity in S52A is between 3 and 4 kcal/mol, implying that butanol binding in S52A is still possible. All of these results agree well with experiments. Indeed, crystal structures and solutions studies observe binding of butanol to the S52A mutant, albeit with significantly reduced affinity. For the T57A mutant, our calculations report affinities of 4–5 kcal/mol for the binding of butanol. This would suggest that butanol should still bind in the T57A mutant. However, this does conflict with experimental observations, and this is likely because the M05-2X model employed in these DFT calculations overestimates the binding affinities of alcohols (see earlier discussion in this section). It may also be due to effects of the complex protein–solvent environment which are not accounted for in our calculations due to the simplified treatment of these effects by using a continuum solvation model in the calculations. Further, our calculations use models that are based on the high-resolution crystal structures where few, if any, differences are observed between the apo, ethanol, and butanol bound states, whereas there are likely to be important differences in the structures in the solution states of different LUSH–alcohol complexes, as it has been shown that alcohols stabilize the solution state of the protein in a chain length dependent manner. However, we have no information about specific differences that may exist in solution, except that the conformational changes that do occur are taking place in the micro- to millisecond time scale and, therefore, are difficult to accurately model even with simplified molecular dynamics calculations (45).

Conclusions

In summary, our calculations on the alcohol binding to wild-type and mutated LUSH proteins have obtained reasonable agreement with experimental findings. In particular, we show that the alcohol binding in the LUSH protein is the consequence of three important factors: H-bonding, solvation, and the other noncovalent interaction. The H-bonding contribution (with T57 and S52) is about 4–5 kcal/mol per H-bond. The solvation contribution, which is mainly determined by the desolvation of the ligands, is 4–6 kcal/mol for alcohols and 8–10 kcal/mol for water. The other noncovalent interaction, which is measured in the increasing binding affinity with respect to the increasing alkyl chain length of the alcohol, is computed to be 1.2 kcal/mol per CH₂ group. Although such partitioning of the binding energy into the H-bonding, desolvation, and dispersion contributions is only approximate, the results seem to be reasonable and do provide insights in the alcohol binding affinities. Altogether, these three kinds of interaction make the accommodation of alcohols in the binding site possible, leading to a 1.5 kcal/mol increase in the binding affinity with respect to adding one CH₂ group in the alcohol alkyl chain. Inclusion of basis set superimposition error corrections and/or having the results extrapolated to the complete basis set will probably improve the accuracy of the energies, leading to possibly better agreement with experimental data (0.8 kcal/mol per CH₂ group), but those calculations are too expensive to be practical for the current study. An important finding from these studies is that the widely used B3LYP DFT model fails to give accurate results for systems where noncovalent interactions play an important role. For those systems, if they are too large for post-Hartree–Fock wave function theory such as MP2 (46) or CCSD(T) (47, 48) to be feasible, the DFT model M05-2X is recommended for its good balance in accuracy and affordability.

Abbreviations

DFT

density functional theory

B3LYP

Becke three-parameter Lee–Yang–Parr density functional model

M05-2X

Minnesota density functional 05-2X model

AM1

Austin model 1

ADH

alcohol dehydrogenase

SMD

charge density-based Minnesota solvation model

QM/MM

quantum mechanics/molecular mechanics

IEFPCM

integral–equation–formalism polarizable continuum model

MP2

Møller–Plesset perturbation theory truncated at the second order

CCSD(T)

coupled cluster theory with single and double excitations included fully and triple excitation calculated with perturbation theory.