A Comparison of Prediction Equations for the Estimation of Body Fat Percentage in Non-obese and Obese Older Caucasian Adults in the United States

Abstract

Objectives

The predictive capabilities of skinfold regression equations are limited across populations and current equations may not be well suited for the prediction of body fat in older adults or obese Americans. The goal of this study was to compare percent body fat (%BF) predicted by several skinfold regression equations to %BF determined by Dual-Energy X-ray Absorptiometry (DXA) in obese and non-obese Caucasian men and women in the United states over the age of 65 years.

Design

A block design was used with two blocks: obesity (non-obese/obese) and gender (male/female). All subjects underwent the same testing procedures in one visit.

Setting

University of Pittsburgh Clinical and Translation Research Center.

Participants

Seventy-eight older healthy adults were recruited for participation.

Measurements

Actual percent body fat was determined from a whole body DXA scan. Estimated percent body fat (%BF) was calculated using skinfold measurements and established regression equations. The predictive accuracy of the regression equations was evaluated by comparing the estimated %BF to the actual %BF measured with DXA using a within subject ANOVA (α=0.05). This was done within subgroups: obese males, obese females, non-obese males and non-obese females.

Results

Durnin and Womersly and Jackson and Pollock had reasonably good agreement with DXA in older Caucasian American females and males, respectively. The remaining equations significantly overestimated %BF in older Caucasian American males. Mixed results were found in females with Gause-Nilsson and Jackson and Pollock significantly underestimating %BF, while Visser and Kwok overestimated %BF.

Conclusion

Numerous factors of a population including age, race, ethnicity, gender and obesity should be considered when selecting a skinfold regression equation to estimate %BF. While Durnin and Womersly and Jackson and Pollock are recommended for predicting %BF in older Caucasian American females and males, respectively, there exists a need to develop accurate regression models that consider obesity, gender, race or ethnicity when predicting %BF in a diverse geriatric American population.

Introduction

Obesity is a growing concern among older adults in the United states. In 2009-2010 nearly three quarters of American adults aged 60 and older were either overweight (25.0 ≤ BMI ≤ 29.9) or obese (BMI ≥ 30.0) (1, 2). Additionally, older adults are more likely to be obese than young adults (2). Obesity has been linked to serious health risks with overweight older adults having a greater risk of impaired physical function and higher risk of injury (3, 4). In 2008, an estimated $147 billion in medical costs were associated with obesity (5). Current trends, specifically an aging population in combination with older adults having the highest rate of obesity increase, suggest that the scope of this problem will likely be steadily increasing as well (1, 2, 6). estimating body fat percentage (%BF) is important in health care and obesity management. With growing obesity rates, accurate and affordable techniques for the estimation %BF in older or obese Americans are necessary.

Dual-Energy X-ray Absorptiometry (DXA) is a well-established method to provide an accurate measure of %BF (7). However, due to cost and other limitations, DXA is not always practical for determining %BF (7-10). Alternative techniques, such anthropometric prediction equations using skinfold thickness, are commonly used to estimate %BF (11-13). The American College of Sports Medicine currently recommends the use of Jackson and Pollock (JP) body density equations combined with an equation to convert to %BF (14-17). These equations were developed from non-obese middle-aged Americans and are based on the assumption that fat is distributed subcutaneously and internally in a similar manner for all individuals (18). It has been shown that fat distribution varies across gender, ethnicity, body type, and age (19, 20). Thus, the predictive capabilities of these skinfold regression equations are limited across populations. As such, these equations, and others, may not be well suited for the prediction of %BF in older or obese Caucasian Americans.

Skinfold-based regression equations used to predict %BF specifically in older adults have been published, including Visser (V), Durnin and Womersly (DW), Gause-Nilsson (GN) and Kwok (K) (21-24). Due to their inherent bias towards the populations used for development, attempts at validation of these equations have yielded mixed results in various populations of older adults. Two studies found DW to accurately predict %BF in non-obese (25, 26), while other studies found that DW overestimated %BF in males and underestimated %BF in females (23, 27) or underestimated %BF in middle-aged obese Americans (28, 29). Previous research has found that JP significantly underestimate %BF in older non-obese and middle-aged obese Americans (18, 28, 30). Additionally, previous studies have suggested that V overestimates %BF in non-obese older Portuguese and Swedish populations (23, 31). To our knowledge, no studies have examined DW, JP, V or K in an obese older Caucasian American population. As previously mentioned, %BF and fat distribution vary across age, ethnicity, race and obesity, as such, the aforementioned regression equations may not be well suited for an older obese Caucasian population in the United States.

It has yet to be established which %BF prediction equations, if any, are best suited for an older obese Caucasian population in the United States. In order to understand the effects of age and obesity on the accuracy of %BF predictive equations, the aim of this study was to compare %BF predicted by several skinfold regression equations to %BF determined by DXA in obese and non-obese men and women in the United States over the age of 65 years.

Methods

Seventy-eight healthy Caucasian American adults aged 65 and older, screened for metal implants, were recruited from the community. Participants were divided into four subgroups based on gender (female; male) and obesity determined from body mass index (BMI≤30, non-obese; BMI>30, obese) (Table 1). Written informed consent, previously approved by the University of Pittsburgh Institutional Review Board, was obtained from each participant. Participants underwent a whole body DXA scan (Hologic QDR 1000/W, Bedford, MA, USA) lying supine and %BF was determined as total body fat mass/total body mass.

Table 1. Subject Population Characteristics.

Mean (SD) [Range]	Females		Males
	Non-obese (n=20)	Obese (n=19)	Non-obese (n=20)	Obese (n=19)
Age (yrs)	75.97 (5.27) [66.95-85.66]	75.91 (4.99) [66.69-83.68]	76.02 (5.58) [65.68- 85.02]	74.17 (4.47) [66.46-82.24]
BMI (kg/m2)	25.08 (3.07) [19.86-29.76]	34.27 (3.94) [30.18-47.03]	26.31 (2.70) [19.75-29.71]	33.70 (3.24) [30.14-41.26]
Mass (kg)	62.95 (7.15) [52.2-76.50]	85.08 (13.33) [65.3-124.2]	79.40 (10.78) [56.00-97.10]	101.61 (15.05) [83.30-133.81]
Height (m)	1.59 (0.06) [1.46-1.66]	1.57 (0.07) [1.46-1.71]	1.73 (0.06) [1.62-1.82]	1.73 (0.06) [1.62-1.85]

Skinfold thickness measurements (ST) were performed by a trained technician with a Lange skinfold caliper (Beta Technology Inc, Cambridge, MD, USA) at chest, midaxillary, tricep, bicep, subscapular, abdomen, suprailiac, and thigh sites on the right side of the body while standing in a relaxed position. Measurements were taken three times at each site and averaged. Body fat percentage was calculated for each regression equation using the appropriate skinfold measurements (Table 2). V, DW and JP were converted to %BF using Siri's 2-compartment equation (32). Siri's equation was selected to allow for comparisons to previous research (18, 22, 25-27, 29, 30, 33). It should also be noted that Heyward et al. has previously reported nearly identical %BF estimates using either Siri's equation or Brozek's equation (18).

Table 2. Skinfold thickness equations to estimate %BF.

Model	Ref. No.	Equation
Visser 4 skinfold (V)	[21]	BD = 1.0688 + 0.0212(SexA) − 0.0356log10 (Sum 4)
Durnin and Womersley (DW)	[22]
Men		BD = 1.1715 - 0.0779log10(Sum 4)
Women		BD = 1.1339 − 0.0645log10(Sum 4)
Gause-Nilsson (GN)	[23]	%BF = 36.078 + 3.917log10(Sum 4) - 5.114(SexA) + 0.384(Weight) - 0.289(Height)
Jackson and Pollock (JP)	[8,9]
Men		BD = 1.112 - 0.00043499(Sum 7) + 0.00000055(Sum 7)2 - 0.00028826(Age)
Women		BD = 1.097 - 0.00046971(Sum 7) + 0.00000056(Sum 7)2 - 0.00012828(Age)
Kwok	[24]	%BF = -27.149 + 6.137(SexB) + 1.120(BMI) + 17.308 log10(Sum 2)

%BF, body fat percentage; BD, body density (kg/m3); SexA, female=0, male=1; Sum 4, triceps + biceps + subscapular + suprailliac; Sum 2, triceps + biceps; Sum 7, chest + midaxillary + triceps + subscapular + abdomen + suprailiac + thigh; age, age in years; SexB, female=2, male=1; Weight (kg); Height (cm)

Statistical analysis consisted of comparing %BF determined from DXA to %BF determined from each skinfold equation (Table 2). ANOVAs were performed within each subgroup of participants (obese males, obese females, non-obese males, non-obese females). Method type (DXA/JP/V/DW/GN/K) was included as an independent fixed effects and subject as a random effect. The dependent variable was %BF. Statistical significance was set at 0.05 and post hoc analysis was performed using Tukey tests to compare %BF determined from DXA to %BF determined from each skinfold equation (Table 2).

Results

Mean %BF by method type (DXA/JP/V/DW/GN/K) for each subgroup is presented in Table 3. The main effect of method type was statistically significant for all subgroups (p<0.0001).

Table 3. Mean %BF Across Method Types By Gender and Obesity.

Mean (SD) [Range] Method	Females		Males
	Non-obese (n=20) %BF	Obese (n=19) %BF	Non-obese (n=20) %BF	Obese (n=19) %BF
DXA	34.18 (6.23)	44.64 (3.06)	25.47 (5.54)	32.96 (4.21)
	[21.00-41.80]	[40.40-52.10]	[15.60-36.60]	[25.20-41.90]
V	42.45 (2.55)*	46.28 (1.08)	32.07 (1.75)*	35.36 (1.61)*
	[36.59-45.63]	[43.41-47.76]	[29.02-35.98]	[31.16-38.41]
DW	35.96 (4.50)	42.76 (1.92)	29.07 (3.78)*	36.28 (3.52)*
	[25.71-41.59]	[37.64-45.39]	[22.53-37.59]	[27.11-42.99]
GN	30.71 (3.31)*	40.07 (5.23)*	31.82 (4.29)*	41.12 (5.99)*
	[26.08-36.37]	[32.42-55.18]	[22.42-38.56]	[34.18-54.16]
JP	27.06 (5.01)*	37.02 (3.57)*	23.08 (3.96)	31.35 (3.90)
	[16.17-33.02]	[27.68-42.91]	[17.69-33.73]	[21.77-39.07]
K	39.15 (5.28)*	52.52 (4.66)*	33.21 (4.11)*	44.52 (4.97)*
	[28.88-46.99]	[46.07-65.99]	[24.67-41.28]	[37.42-55.43]

^*Denotes significantly different than DXA (p<0.05). Body Fat Percentage (%BF).

In females, post hoc-analysis revealed that GN and JP significantly underestimated %BF compared to DXA by 3.47%BF and 7.12%BF (mean of within subject differences from DXA) in non-obese females and by 4.57%BF and 7.62%BF in obese females, respectively. V was found to significantly overestimate %BF by 8.26%BF in non-obese females, while in obese subjects there was no significant difference. No significant difference was found between DW %BF and DXA %BF in females regardless of obesity (Figure 1). K significantly overestimated %BF in both non-obese and obese females by 4.97%BF and 7.88%BF, respectively.

Figure 1.

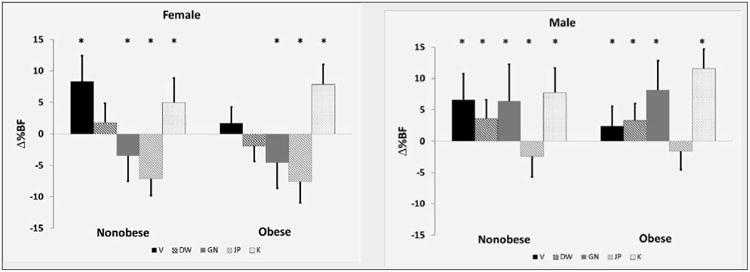
Mean Δ%BF (mean of within subject differences from DXA) for females (left) and males (right). Visser (V) shown by solid black bars, Durnin and Womersley (DW) shown by hashed black bars, Gause_Nilsson (GN) shown by solid gray bars, Jackson and Pollock (JP) shown by hashed gray bars and Kwok (K) shown by dotted bars. Standard deviations are provided. * Denotes significantly different from DXA for each group (p<0.05)

GN and DW significantly overestimated %BF by 6.35%BF and 3.61%BF in non-obese males and by 8.16%BF and 3.32%BF in obese males, respectively. Additionally, V and K significantly overestimated %BF in non-obese males by 6.60%BF and 7.74%BF and in obese males by 2.41%BF and 11.56%BF, respectively. JP %BF was not significantly different than DXA regardless of obesity in males (Figure 1).

Discussion

The goal of this study was to compare %BF determined by DXA to estimated %BF determined by several regression equations using skinfold measurements in non-obese and obese older adults in the United States. Not all regression equations in this study accurately predicted %BF in older Americans. Obesity and gender significantly impacted the accuracy of the skinfold regression equations in varying ways when applied to an older Caucasian American population.

In older Caucasian Americans, DW accurately predicted %BF in females but significantly overestimated %BF in males, regardless of obesity. Previous studies have found mixed results when analyzing the accuracy of DW. Reilly et al. reported no significant differences between DW %BF and %BF in the older adults of the United Kingdom (26). Others found that it underestimated %BF in obese middle-aged females (28, 29). Additionally, studies outside of the United States found conflicting results regarding the accuracy of DW in non-obese males (23, 25-27). DW was found to underestimate %BF in middle-aged obese American males (28, 29). DW was developed using a British population with a larger range of body types and ages. It is also likely more similar in race or ethnicity to American population presented here which could explain its ability to predict %BF in females (22).

JP was found to accurately predict %BF in older Caucasian American males but underestimated %BF in females, regardless of obesity. This is consistent with previous literature which found JP to underestimate %BF in non-obese older females and obese middle-aged females (18, 28, 30). JP was developed in a middle-aged American population with a mean %BF of 24.09% (15), which could account for the underestimation of %BF. Body composition changes with aging as more fat is located internally (18, 20). As such, it is likely that typical skinfold regression equations would underestimate %BF in older adults, especially females.

In general, the remaining regression equations, GN, V and K, did not accurately predict %BF in older Caucasian Americans. GN significantly underestimated %BF in females while overestimating %BF in males. GN used a non-obese Swedish population for the development of their regression equations (23). Although the %BF of GN's population (23) is similar to our non-obese females, GN did not accurately predict %BF in either non-obese or obese females examined. V significantly overestimated %BF in non-obese females and all males, but accurately estimated %BF in obese females. These results, as do previous (31), suggest that V systematically overestimates %BF in non-obese populations due to the body composition of the population used. Visser's female population in the Netherlands, mean %BF of 43.3% and mean BMI of 26.1 kg/m² (21), had a drastically higher fat content to BMI ratio than the American female population represented in this analysis, mean %BF of 33.4% and mean BMI of 24.9 kg/m² (non-obese). Thus, V would tend to overestimate %BF in non-obese due to the relatively higher fat content in their population's body composition. Finally, K significantly overestimated %BF in females and males, regardless of obesity. K was developed in a non-obese older Chinese population (24). Differences in obesity, race or ethnicity likely account for the poor prediction accuracy of GN, V and K in our population of older Caucasian Americans.

The population used for this study was an older Caucasian American population and should be considered when applying the findings to other populations. Although a range of body types was used in this analysis, the average BMI of the non-obese groups was close to overweight. While it is possible that different regressions could be more accurate in a normal weight population, the regressions found to be accurate in older Caucasian Americans were accurate regardless of obesity. The equations used for comparison were developed in populations with varying ages, races, ethnicities and incorporated different measurement sites. No clear association between one of these factors and predictive accuracy was obvious. Numerous factors including age, race, ethnicity, gender and obesity should be considered when selecting a predictive regression equation. Finally, DXA was utilized as the reference standard and is a well-established method to provide an accurate measure of %BF (7). Additional accepted methods exist, such as the compartment model, to estimate body composition. While the current findings are limited to DXA as a reference standard, future work should include comparing other accepted reference standards to currently available regression equations.

In conclusion, DW and JP had reasonably good agreement with DXA in older Caucasian American females and males, respectively. The remaining equations significantly overestimated %BF in older Caucasian American males. In general, mixed results were found in females with GN and JP significantly underestimating %BF, while V and K overestimated %BF. These differences translate into potential errors associated with using certain skinfold regression equations to predict %BF in older Caucasian Americans. Numerous factors of a population including age, race, ethnicity, gender and obesity should be considered when selecting a skinfold regression equation to estimate %BF. Additionally, there exists a need to develop accurate regression models that consider obesity, gender, race or ethnicity when predicting %BF in a geriatric American population.