Comparing methods of measuring geographic patterns in temporal trends: An application to county-level heart disease mortality in the United States, 1973–2010

Abstract

Purpose

To demonstrate the implications of choosing analytic methods for quantifying spatio-temporal trends, we compare the assumptions, implementation, and outcomes of popular methods using county-level heart disease mortality in the United States between 1973 and 2010.

Methods

We applied four regression-based approaches (joinpoint regression, both aspatial and spatial generalized linear mixed models, and Bayesian space-time model) and compared resulting inferences for geographic patterns of local estimates of annual percent change and associated uncertainty.

Results

The average local percent change in heart disease mortality from each method was −4.5%, with the Bayesian model having the smallest range of values. The associated uncertainty in percent change differed markedly across the methods, with the Bayesian space-time model producing the narrowest range of variance (0.0–0.8). The geographic pattern of percent change was consistent across methods with smaller declines in the south-central US and larger declines in the Northeast and Midwest. However, the geographic patterns of uncertainty differed markedly between methods.

Conclusions

The similarity of results, including geographic patterns, for magnitude of percent change across these methods validates the underlying spatial pattern of declines in heart disease mortality. However, marked differences in degree of uncertainty indicate that Bayesian modelling offers substantially more precise estimates.

INTRODUCTION

Analytic and computing advances have greatly increased the numbers of methods and tools available to quantify spatio-temporal trends of disease. Although these methods vary in their underlying assumptions, methodological and computational complexity, data requirements, and interpretability, a paucity of literature compares these methods to provide practical guidance to epidemiologists and public health practitioners.

Regression-based approaches commonly used to quantify spatio-temporal trends in local rates of chronic disease include joinpoint regression, generalized linear mixed models (GLMM), and Bayesian space-time models. Each approach quantifies temporal trends by estimating valid, succinct, and interpretable summaries of changing rates using software and methods that are accessible to many in public health. Comparing these methods’ results within the context of their respective underlying assumptions provides important information for appropriate method selection in spatio-temporal studies of health outcomes.

We illustrate these methods using county-level heart disease death rates in the United States. Between 1950 and the turn of the 21^st century, US heart disease mortality decreased by roughly 60%[1, 2]. Although studies have reported differential trends in heart disease mortality by larger geographic areas and urbanicity [3–10], few have utilized rigorous methods currently available for small-area trend estimation. In this study, we describe the key features of four regression-based spatio-temporal methods (joinpoint regression, aspatial GLMM, spatial GLMM, and Bayesian space-time models) and compare the resulting estimates of county-level percent change in heart disease death rates from 1973–2010.

METHODS

Data Sources

Annual age-specific counts of heart disease deaths in each US county from 1973–2010 for people aged ≥35 years were obtained from the National Vital Statistics System. Over this continuous time period, a census, rather than a sample, of deaths in the United States was recorded. Heart disease deaths were defined based on underlying cause of death according to the following International Classification of Diseases (ICD) codes: ICD-8: 390–398, 402, 404, 410–429; ICD-9: 390–398, 402, 404–429; ICD-10: I00–I09, I11, I13, I20–I51. Comparability ratios between each ICD revision are approximately unity, indicating that temporal changes in ICD codes introduced little to no bias into the study and no adjustments were necessary [11, 12]. County-level annual estimates of the population aged ≥35 years, produced by the US Census Bureau in collaboration with the National Center for Health Statistics (NCHS), were compiled [13]. To enhance rate stability, all data were aggregated into two-year intervals starting in 1973, resulting in 19 biennial intervals. Aggregated to a common set of 3,099 counties in the contiguous US, rates were age-standardized using the 2000 US standard population. The biennial age-standardized rate was multiplied by the biennial county population aged ≥35 years to produce a biennial age-standardized death count [14, 15].

Estimation of Temporal Trends

County-level average biennial percent change in heart disease mortality (hereafter referred to as “percent change”) was estimated using four model-based methods: joinpoint regression, aspatial GLMM, spatial GLMM, and Bayesian space-time models. For each, we estimate percent change in heart disease death rates and its associated variance, where the variance represents uncertainty/precision in the estimated percent change. Appendix A contains additional details.

Joinpoint Regression

Joinpoint regression, popularly used in examining temporal changes in cancer incidence, models rates of disease as piece-wise log-linear functions of time [16–19]. For each areal unit (e.g. county), this method finds inflection points (or joinpoints) representing the time at which the slope changes. As temporal trends may be represented by a single line or a series of linked segments, the trend across the entire study period is not required to be log-linear.

The slopes of the segments adjacent to the joinpoint quantify change in the rate over time and define an annual percent change (APC). APC of multiple segments can be summarized as average annual percent change (AAPC), or for our two-year pooled data, as average biennial percent change [20].

Using joinpoint regression, county-level age-standardized case counts were independently modeled as log-linear piece-wise functions of time with Poisson variance, log-population offset, uncorrelated errors, and a maximum of five joinpoints (Equation A.1) in Joinpoint Regression Program v4.0.4 (National Cancer Institute, Calverton, MD). Model fit and the numbers of joinpoints were assessed with the modified Bayesian information criterion.

Aspatial and Spatial Generalized Linear Mixed Models (GLMMs)

GLMMs quantify global and local temporal trends in disease by modeling counts and population-at-risk in a Poisson model or rates in a linear or log-linear model [21]. These models can be readily fit using standard statistical software packages (e.g. SAS, Stata). The assumption of log-linearity in this method should be evaluated, with alternative specifications considered as needed.

For the GLMM analysis, Poisson regression modeled age-standardized county-level heart disease death rates as log-linear functions of a global intercept and temporal slope, and county-level random intercept and slope (Equation A.2) using PROC GLIMMIX in SAS v9.3 (SAS Institute, Cary, NC). Both aspatial GLMM (assuming spatial independence) and spatial GLMM (assuming distance-based spatially correlated rates within each two-year interval) were completed.

Bayesian Space-time Models

Bayesian space-time models are hierarchical mixed models where area-level rates are spatially correlated within and across time. Widely applied in small area analysis and disease mapping applications, Bayesian models produce locally interpretable, statistically stable estimates while minimizing concerns for multiple testing [14, 22–24].

The Bayesian space-time approach modeled age-standardized rates of heart disease mortality using Poisson regression (Equation A.5). Given our large number of counties and to ensure model convergence, spatially independent random effects were not used [25]. County-specific random intercepts and slopes were assigned a conditionally autoregressive (CAR) normal prior which borrows information and statistical strength from adjacent counties using queen contiguity. Variance hyperpriors were assigned a uniform distribution between 0 and 1 [26]. Models were implemented in WinBUGS v1.4.3 (Imperial College and Medical Research Council, Cambridge, UK) using R package R2WinBUGS [27]. Each model was run with two chains for 30,000 iterations with thinning and the first half discarded. Chain convergence was evaluated through examination of trace plots of posterior parameter estimates and the Brooks-Gelman-Rubin statistic [28].

Calculating County-level Percent Change and Its Variance

The joinpoint software directly estimates biennial percent change (as AAPC) and its variance. For GLMM, the percent change and variance are calculated as a function of parameter estimates. For the Bayesian model, percent change is calculated as a function of parameter estimates, and its variance is estimated using the distribution of the posterior. See Appendix A for details.

Comparison of model results

To compare methods, descriptive statistics for estimated county-level percent changes and their variances were calculated nationally and by region. The mean percent change in heart disease death rates represents the central tendency of percent change across all counties, and the variance of the mean percent change represents the dispersion of percent change across counties. Similarly, the median variance of estimated percent change represents the central tendency of uncertainty in county-level estimated percent change, and the inter-quartile range (IQR) of the variance represents the dispersion of uncertainty in estimated percent change across counties.

To compare county-level geographic patterns, we mapped estimated percent change and its variance for each method using ArcMap v10.1 (ESRI, Mountain View, CA).

RESULTS

For each two-year interval, age-standardized county-level heart disease death rates were approximately normally distributed (Figure 1). The mean, variance, and median death rate consistently decreased over the study period. Of 3,099 counties, joinpoint regression modeled 2,597 (84%) counties with a single declining segment and an additional 366 (12%) counties with multiple declining segments.

Figure 1. Distributions of county-level age-adjusted heart disease death rates, per 100,000, ages 35 and older, 1973–2010.

Plot shows median, 25^th and 75^th percentile rates as a box. Whiskers represent 1.5 IQRs above and below the 25^th and 75^th percentile, respectively. The y-axis has been truncated to remove extreme outliers. (n=3,099). Rates are age adjusted to the US standard 2000 population.

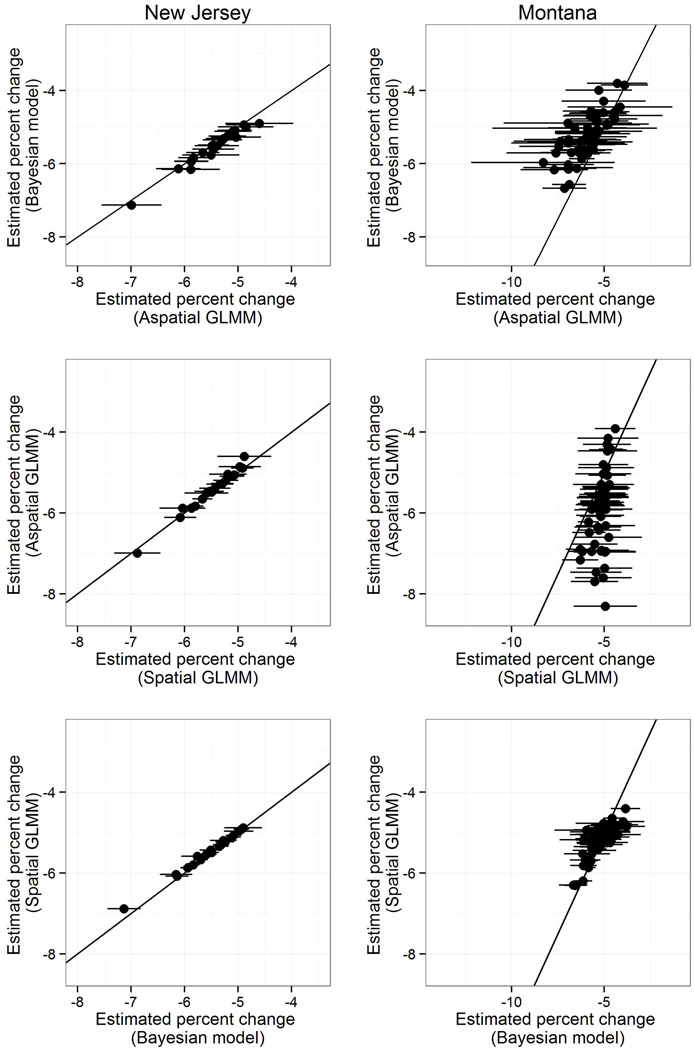
The methods produced similar estimates of percent change, with greater similarity for counties with large populations (e.g. New Jersey counties) than with small populations (e.g. Montana counties) (Figure 2). Generally, estimates were more precise for spatial GLMM than aspatial GLMM, with the greatest precision for the Bayesian model. Joinpoint regression resulted in the least precise estimates (Supplemental Figure B).

Figure 2. Estimated percent change for heart disease death rates by method, New Jersey and Montana, 1973–2010.

Graphs compare estimates of biennial percent change in heart disease death rates for a single county across selected pairs of analytic methods. Horizontal lines represent the 95% confidence interval for the method listed on the x-axis. The black line represents the identity line (i.e. where the two methods estimate the same value). This figure is provided for these two states as an illustration of the results of these methods using states that generally contain counties with large and small populations (New Jersey and Montana, respectively). Graphs of comparisons between joinpoint regression and each method for these two states are provided in Supplemental Figure B. Note that the range of the x-axis is consistent for all graphs within a state, but not across states, and the y-axis is consistent across all graphs.

Distributions of the estimated county-level percent change were similar across methods (Table 1, Supplemental Figure A). For joinpoint regression, aspatial GLMM, spatial GLMM, and the Bayesian model, the mean estimated percent change across all counties and dispersion of the mean (as given by the standard deviation) were −4.5% (SD: 1.5%), −4.6% (SD: 1.3%), −4.5% (SD: 0.9%), and −4.5% (SD: 1.2%), respectively. Compared to the results from joinpoint regression, the GLMM and Bayesian models produced tighter ranges of percent change, due to the statistical pooling of information induced by the random intercepts. The spatial GLMM produced estimates with a markedly smaller range due to greater smoothing when using distance-based spatial correlation, as opposed to the Bayesian model’s queen contiguity.

TABLE 1.

Summary statistics for estimated county-level biennial percent changes in heart disease mortality, United States, 1973–2010.

	Joinpoint Regression	Aspatial GLMM	Spatial GLMM	Bayesian Space- Time Model
Median percent change (IQR)	−4.6 (−5.5, −3.6)	−4.7 (−5.5, 3.7)	−4.6 (−5.2, −3.9)	−4.6 (−5.4, −3.7)
Northeast	−5.5 (−5.9, −5.0)	−5.2 (−5.7, −4.8)	−5.2 (−5.6, −4.9)	−5.4 (−5.8, −4.9)
Midwest	−4.9 (−5.7, −4.2)	−5.0 (−5.8, −4.4)	−4.9 (−5.2, −4.5)	−4.9 (−5.6, −4.3)
South	−3.9 (−4.8, −3.0)	−3.9 (−4.7, −3.1)	−4.0 (−4.6, −3.4)	−3.8 (−4.7, −3.0)
West	−5.2 (−5.9, −4.4)	−5.6 (−6.3, −4.9)	−5.2 (−5.5, −4.8)	−5.2 (−5.7, −4.6)
Range of percent change	−14.2, 14.1	−12.2, 0.1	−7.7, −0.7	−8.7, 0.6
Northeast	−7.2, −2.4	−7.0, −2.5	−6.9, −3.0	−7.1, −2.7
Midwest	−11.0, 3.2	−8.7, −0.8	−7.6, −1.6	−7.9, −1.0
South	−14.2, 14.1	−8.8, 0.1	−7.4, −0.7	−7.9, 0.6
West	−12.6, −1.8	−12.2, −2.4	−7.7. −2.8	−8.7, −2.2
Median variance of percent change (IQR)	0.2 (0.1, 0.5)	0.2 (0.1, 0.4)	0.2 (0.1, 0.3)	0.1 (0.0, 0.2)
Northeast	0.1 (0.1, 0.2)	0.1 (0.0, 0.1)	0.1 (0.0, 0.1)	0.0 (0.0, 0.0)
Midwest	0.2 (0.1, 0.5)	0.3 (0.2, 0.5)	0.2 (0.1, 0.3)	0.1 (0.1, 0.2)
South	0.3 (0.2, 0.5)	0.2 (0.1, 0.3)	0.2 (0.1, 0.2)	0.1 (0.0, 0.1)
West	0.3 (0.1, 0.9)	0.3 (0.1, 0.6)	0.2 (0.1, 0.4)	0.1 (0.0, 0.2)
Range of variance of percent change	0.0, 225.0	0.0, 15.3	0.0, 1.0	0.0, 0.8
Northeast	0.0, 2.3	0.0, 0.6	0.0, 0.4	0.0, 0.4
Midwest	0.0, 23.8	0.0, 6.0	0.0, 0.9	0.0, 0.7
South	0.0, 225.0	0.0, 15.3	0.0, 1.0	0.0, 0.7
West	0.0, 34.5	0.0, 6.2	0.0, 0.8	0.0, 0.8

Uncertainty in the estimated county-level percent change (i.e., the variance) varied across methods (Table 1, Supplemental Figure A). Although the medians of the variance of percent change were similar for spatial GLMM (0.2, IQR: 0.1, 0.3), aspatial GLMM (0.2, IQR: 0.1–0.4) and joinpoint regression (0.2, IQR: 0.1–0.5), the Bayesian model’s variance was markedly smaller (0.1, IQR: 0.0–0.2). These inter-method differences were reflected in statistical significance of the estimates. The numbers of counties with statistically non-significant estimated percent change for joinpoint regression, aspatial GLMM, spatial GLMM, and the Bayesian model were 102, 14, 0, and 7, respectively.

The distributions of estimated county-level percent change within each US Census region remained similar across methods, although those of the spatial GLMM were consistently narrower. There were important inter-regional differences (Table 1). Biennial declines in heart disease death rates were slowest in the South and fastest in the Northeast. Uncertainty of the estimated percent change also varied across regions, with the West and Northeast having the largest and smallest uncertainty, respectively, for all models.

County-level geographic patterns of percent change were similar across models, although some differences exist in sparsely populated counties in the Great Plains and Rocky Mountains and the narrower range of spatial GLMM estimated percent change is evident (Figure 3). The slowest declines in heart disease mortality were concentrated primarily in counties in Alabama, Mississippi, Arkansas, Oklahoma and parts of Texas. However, geographic patterns in the uncertainty of the percent change varied markedly across methods (Figure 4). The geographic pattern of variance of the aspatial GLMM estimates was similar to that of joinpoint regression. In contrast, the Bayesian model improved county-level precision for all counties, with only a small band of counties with relatively higher variance remaining across the Great Plains and Rocky Mountains. The spatial GLMM represents an intermediate level of precision between the Bayesian model and the aspatial GLMM.

Figure 3. County-level estimated biennial percent change in heart disease death rates, United States, 1973–2010, by method.

Estimates calculated using (A) joinpoint regression, (B) aspatial GLMM, (C) spatial GLMM, and (D) Bayesian space-time model. (Note that this figure is for color reproduction.)

Figure 4. Variance of county-level estimated biennial percent change in heart disease death rates, United States, 1973–2010, by method.

Variance estimated by (A) joinpoint regression, (B) aspatial GLMM, (C) spatial GLMM, (D) Bayesian space-time model. (Note that this figure is for color reproduction.)

DISCUSSION

Using county-level heart disease death rates, we compared four commonly used regression-based methods for estimating temporal disease trends: joinpoint regression, aspatial GLMM, spatial GLMM, and Bayesian space-time models. Joinpoint regression estimates trends using only a particular county’s data. GLMM provides statistical stability by generating county-level estimates that represent statistical compromises between the county’s data and an overall estimate, with the option of incorporating distance-based spatial autocorrelation. The Bayesian spatio-temporal model borrows information from adjacent counties depending on the amount of data in each county.

Informed by these underlying properties, our results conformed to our expectations. Relative to the joinpoint results, the large reductions in range and the decrease in variance observed in the GLMM and Bayesian models reflect the attenuation of outlying estimates as these models generated more precise estimates in sparsely populated counties by shrinking estimates towards either global (GLMM) or local (Bayesian model) means. Since all methods used an underlying Poisson regression model, greater uncertainty of estimates was expected in counties with smaller population sizes. This expectation was evident in the relative imprecision of the joinpoint regression and aspatial GLMM estimates, where low-population counties yielded less precise estimates when based on local data only (joinpoint) or adjusted to the overall mean (GLMM). With very precise estimates, both the spatial GLMM and Bayesian models benefit from positive spatial correlation in county-specific rates, suggesting that, for our data, neighboring information provides greater benefit than overall global information.

Our study extends the understanding of these models beyond what was possible by only considering their fundamental properties. By applying these models to a single dataset, we were able to make inter-method comparisons of estimated percent change and the geographic distributions of both the estimated percent change and its variance. On average, the methods produced similar estimates and geographic patterns of county-level percent change. However, the spatial GLMM may have oversmoothed the data, as reflected in the relatively narrow range of estimates.

In addition to the expected inter-method differences in variance, our analysis revealed nuance in spatial patterns of the county-level variances. The degrees of decrease in variance resulting from the Bayesian model and spatial GLMM were striking and unexpected, illustrating the importance of incorporating spatial autocorrelation in spatial analyses. In the Bayesian model, uncertainty in counties across the United States was reduced to levels seen only in counties with large populations for the other two methods. For example, the variance in percent change in Ohio County, West Virginia (2010 population of 44,443 persons) as estimated by the Bayesian model was 0.039, comparable to the variance in Washington, DC (2010 population of 601,723 persons) of 0.037 and 0.026 as estimated by joinpoint regression and aspatial GLMM, respectively. While the spatial GLMM also reduced variance relative to joinpoint regression and aspatial GLMM, this improvement came at the possible expense of oversmoothed estimates.

The exception to this finding notably occurred in the Great Plains, where geographically small counties with small populations are adjacent to similarly populated counties, thereby limiting information that could be borrowed from adjacent counties (i.e., neighboring rates are also imprecise) (Figure 2) [29].

These methods confirmed, at the county level, the national accomplishment of declining heart disease mortality and demonstrated geographic variation in declining heart disease death rates. Counties in the South declined less than in any other region, with the smallest declines occurring primarily in a band of counties stretching from Texas through Alabama. The primary strength of joinpoint regression is assessment of the shape of the temporal trend and our analysis found temporal trends in county-level heart disease mortality between 1973 and 2010 to be overwhelmingly log-linear. Testing assumptions is critical for carrying out subsequent regression which assumes log-linear patterns. In the absence of log-linearity, alternative model specifications would have been possible.

Given substantial geographic disparities in the rates of declining heart disease mortality for the total US population, additional studies are needed to understand factors associated with the differential declines [3, 5]. Previous studies have hypothesized contributions of differential access to health care and socioeconomic resources [5]. Recent evidence suggests that rates of declining heart disease mortality may vary by urban/rural status, with rural counties declining more slowly [3, 30]. Better understanding the correlates of decline will aid public health practitioners in understanding contributions of socioeconomic conditions to geographic differences in rates of decline [4, 6, 9, 31].

A limitation of this study is that not all possible methods and model specifications have been included. We only included methods that have been used recently to evaluate spatio-temporal trends of health outcomes and are accessible to a broad public health audience [16, 22, 32]. The spatial GLMM and Bayesian model’s borrowing of statistical strength from adjacent counties may also represent a possible limitation. Although the first law of geography [33] supports this underlying process, the borrowing of adjacent information may be erroneous if adjacent counties have very different distributions of factors associated with the temporal trend (e.g. a very urban county adjacent to a very rural county). We believe that the increased precision of these models minimizes this limitation.

Generalizations of this method comparison are limited to health outcomes that exhibit primarily linear or log-linear temporal trends, as does heart disease mortality. For health outcomes with greater heterogeneity in local trends, alternate specifications would be necessary. However these parameterizations limit summarization of the data and require a priori knowledge of global and local temporal trends [34–36]. Additionally, heart disease mortality is a common outcome in the United States; the generalizability of these results to a less common outcome is unclear.

Despite these limitations, our results have important implications for selection of methods to study small-area geographic patterns of changing chronic disease death rates. Investigators should consider whether the study requires precise estimates. Given inter-method similarity in results, applications requiring only a county-level point estimate of temporal trend of heart disease mortality may use more common methods (i.e. joinpoint regression or GLMM) with little penalty. For example, disease mapping, which makes inference only about the spatial variation in temporal trend, rather than precisely estimating county-level disease trends, may reasonably proceed using joinpoint regression or GLMM. These methods are less resource intensive and more accessible to a broader public health audience than Bayesian methods.

However, analyses requiring a highly precise estimate of temporal trend (e.g. examining correlates of trends) may better employ the Bayesian model. Despite the relative complexity of applying the Bayesian model, it is also preferable in situations with low case counts or low populations, particularly in the presence of positive spatial autocorrelation, as it provides precise estimates in these situations while avoiding possible oversmoothing resulting from spatial GLMM with distance-based spatial autocorrelation. Additionally, even if precise estimates are required, joinpoint regression can diagnose a linear or log-linear trend, supporting underlying assumptions of log-linearity. As such, these methods may be complementary.

Although outside of the scope of this paper, model selection in future studies may require covariate adjustment or additional correlation (e.g. temporal or between sub-populations within a county). All methods employed in this paper can adjust for covariates (although joinpoint regression is currently limited to adjustment by a single covariate). Additional correlation structures within the data may be modeled using either GLMM or Bayesian models.

By comparing methods of estimating county-level temporal trends in heart disease mortality, our study demonstrates model properties and provides insight into the implications of method selection for studies of geographic inequities in heart disease mortality and other common chronic diseases. While the estimated county-level percent change and the resulting geographic patterns were similar across methods, uncertainty varied markedly by method, with the Bayesian model producing estimates with the smallest variances and the spatial GLMM producing the smallest range of estimated percent change. These results provide important information for researchers to choose the appropriate spatiotemporal model for their research needs.

List of Abbreviations

AAPC

Average annual percent change

GLMM

Generalized linear mixed model