Reward and punishment act as distinct factors in guiding behavior

Abstract

Behavior rests on the experience of reinforcement and punishment. It has been unclear whether reinforcement and punishment act as oppositely valenced components of a single behavioral factor, or whether these two kinds of outcomes play fundamentally distinct behavioral roles. To this end, we varied the magnitude of a reward or a penalty experienced following a choice using monetary tokens. The outcome of each trial was independent of the outcome of the previous trial, which enabled us to isolate and study the effect on behavior of each outcome magnitude in single trials. As expected, we found that a reward led to a repetition of the previous choice, whereas a penalty led to an avoidance of the previous choice. However, the effects of the reward magnitude and the penalty magnitude revealed a striking asymmetry. The choice repetition effect of a reward strongly scaled with the magnitude of the reward. In a marked contrast, the avoidance effect of a penalty was flat, not influenced by the magnitude of the penalty. These effects were mechanistically described using the Reinforcement Learning model after the model was updated to account for the penalty-based asymmetry. The asymmetry in the effects of the reward magnitude and the punishment magnitude was so striking that it is diffcult to conceive that one factor is just a weighted or transformed form of the other factor. Instead, the data suggest that rewards and penalties are fundamentally distinct factors in governing behavior.

1. Introduction

Reinforcement and punishment constitute Nature's arsenal in guiding behavior (Thorndike 1898, 1911; Skinner 1963; Tversky and Kahneman 1986; Davison 1991; Gray et al. 1991; Ehrlich 1996; Hackenberg 2009). It is well established that reinforcers and punishers both critically influence behavior, but it has been unclear whether these factors exert symmetric or qualitatively distinct behavioral effects (Skinner 1953; Farley and Fantino 1978; Gray et al. 1991; Dinsmoor 1998; Lerman and Vorndran 2002; Critchfield et al. 2003; Lie and Alsop 2007). One-factor theories have proposed a symmetric law of effect (Thorndike 1927). In this view, reinforcement increases behavior frequency, punishment decreases behavioral frequency, and the magnitudes of these effects are equal, just of opposite signs (Thorndike 1911; Sidman 1962; Herrnstein and Hineline 1966; Schuster and Rachlin 1968; Rachlin and Herrnstein 1969; Villiers 1980). In contrast, two-factor theories view reinforcement and punishment as qualitatively distinct influences on operant behavior (Mowrer 1947; Dinsmoor 1954; Epstein 1985; Yechiam and Hochman 2013).

This debate remains, for the most part, unresolved (Hineline 1984; Gray et al. 1991; Dinsmoor 1998, 2001; Critchfield et al. 2003; Lie and Alsop 2007). This is mainly due to two reasons. First, it is diffcult to compare qualitatively different factors (e.g., food versus electric shock) on a common scale (Schuster and Rachlin 1968; Farley and Fantino 1978; Villiers 1980; Fiorillo 2013). A solution to this problem is to work with reinforcers and punishers that are of the same kind—using tokens that represent gains and losses (Hackenberg 2009). Second, previous studies targeting this question have employed relatively complex paradigms (Bradshaw et al. 1979; Gray et al. 1991; Critchfield et al. 2003; Rasmussen and Newland 2008). The complex paradigms make it diffcult to readily investigate the effect of a reward or a punishment on a behavioral response.

We addressed this question in a simple choice paradigm in which we varied the magnitude of a reward or a penalty experienced following each choice. This allowed us to measure subjects’ tendency to repeat their previous choice as a function of the magnitude of the experienced reward or penalty. In this simple paradigm, one-factor theories predict that the reward and penalty magnitudes will lead to qualitatively similar, just oppositely signed tendencies to repeat the previous choice. In contrast, two-factor theories predict that the choice repetition tendencies will be qualitatively distinct for the two factors. The data indeed revealed a striking asymmetry in the effects of the reward and penalty magnitudes on the choice behavior. The asymmetry was so profound that it suggests that the two behavioral factors are of distinct natures.

2. Materials and Methods

2.1. Subjects

Eighty-eight Washington University undergraduate students participated in this study. The subjects performed an Auditory Task or a Visual Task. The Auditory Task was performed by 54 students (37 females, 17 males), aged 18 to 21 (mean 19.2). The Visual Task was performed by a distinct set of 34 students (24 females, 10 males), aged 18 to 23 (mean 19.4). All subjects were healthy, had normal hearing capacity, and gave an informed consent. Subjects participated for class credit.

2.2. Auditory Task

Subjects sat in a comfortable chair 70 cm in front of a flat-screen monitor. Subjects wore headphones (MDR-V600, Sony), which presented a stereo auditory stimulus (see Auditory stimulus). The subjects’ hands were comfortably positioned at a computer keyboard, with the left index finger placed over the left Command key and with their right index finger placed over the right Command key. The control of the experimental design was accomplished using a custom program written in Matlab (The Mathworks, Inc., Natick, MA, RRID:nlx_153890).

Each trial started with the presentation of a red fixation cross, 2 degrees in size. Subjects were instructed to fixate at the center of the cross. At the same time, subjects were presented with a stereo auditory stimulus (click sounds, see Auditory stimulus), 1.0 s in duration (Fig. 1A). After the stimulus has been presented, the fixation cross shrank to 1 degree and changed its color to green. This event cued the subjects to make a movement (choice). Subjects performed 2 blocks of 300 trials each, with a brief period in between. In the first block of 300 trials, subjects were instructed to press the left Command key with their left index finger if they heard more clicks in the left ear and to press the right Command key with their right index finger if they heard more clicks in the right ear. In the second block of 300 trials, this instructed contingency was reversed. We found similar results in both blocks and therefore pooled the data over the two blocks. In 20% of trials, we randomly interleaved cases in which no auditory stimulus was present. When no sound was heard, subjects were instructed to choose either key (i.e., to either press the left key with the left index finger or the right key with the right index finger). The purpose of these trials was to investigate the effect of outcome on choice when no perceptual stimulus is present (Fig. 3B).

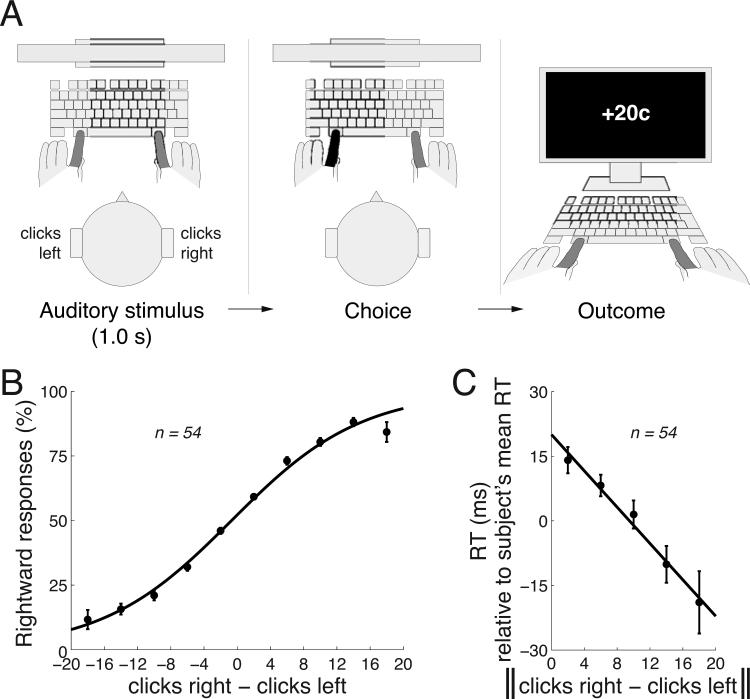
Fig. 1. Task and stimulus-based behavior.

A) Subjects listened to a binaurally presented auditory stimulus that comprised a 1.0 s train of Poisson-distributed click sounds (Methods). Following the stimulus presentation, subjects pressed either the left Command key with their left index finger or the right Command key with their right index finger, if they heard more clicks in the right ear or more clicks in the left ear. A response was followed by an outcome (see text for details).

B) Mean±s.e.m. proportion of rightward choices as a function of the difference in the number of clicks in the right and the left ear. The curve represents logistic fit to the 10 data points. The s.e.m. are larger for larger click differences because there were relatively few cases in which subjects were presented with large click differences (i.e., easy stimuli).

C) Mean±s.e.m. RT as a function of the absolute value of the difference in the number of clicks in the right and the left ear. To control for differences in mean RT over the subjects (445±123 ms, mean±s.d.), the mean RT was subtracted from each RT value in each subject.

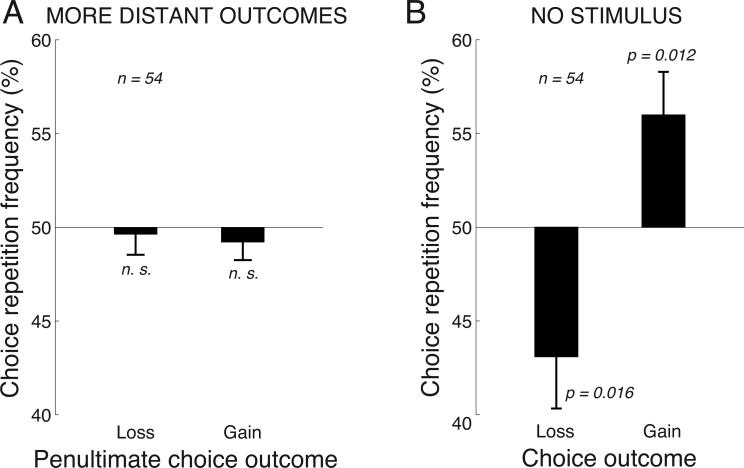
Fig. 3. Properties of the effect.

A) Outcomes in more distant past relative to the current choice have no effect on the choice. Same format as in Fig. 2, for outcomes that precede a current choice by 2 trials.

B) The effect of the outcome is observed also in the absence of the auditory stimulus. Same format as in Fig. 2, for the 20% of trials in which the auditory stimulus was absent and subjects could choose freely either response alternative.

If subjects responded prior to the green cue or if they failed to indicate a response within 1200 ms after the cue, the trial was considered invalid, and was aborted and excluded from the analyses. The type of error was indicated to the subjects in red, large-font text (‘TOO EARLY’, ‘TOO LATE’). The proportion of valid choices over the subjects was 96.0%±1.0 (mean±s.d.). A response was immediately followed by a display of the outcome. Specifically, a correct response was followed by the display of a green string that was randomly drawn from the set {+5c, +10c, +15c, +20c, +25c}. An incorrect response was followed by the display of a red string randomly drawn from the set {−5c, −10c, −15c, −20c, −25c}. These strings were chosen to represent “cents”; the subjects received no instruction in this regard. The outcome was displayed for 0.5 s. The next trial started immediately following the offset of the outcome.

2.3. Auditory stimulus

The auditory stimulus was equivalent to that used previously (Kubanek et al. 2013). Briefly, each ear was presented with a train of brief (0.2 ms) clicks sounds drawn from a homogeneous Poisson process. Each train lasted 1.0 s. The stereo stimulus was composed such that the sum of clicks presented to the left ear (C_l) plus the sum of clicks presented to the right ear (C_r) summed to a fixed number C_l + C_r = Ω, Ω ∈ {25, 32, 39, 46}. Since C_r and C_l were drawn randomly in each trial (and randomly in each subject), the polarity (leftward, rightward evidence) of the stimulus was random in each trial. The value of Ω was drawn randomly on each trial. The Ω randomization was imposed to ensure that subject had to pay attention to the click sounds in both ears.

2.4. Visual Task

The Visual Task was analogous to the Auditory Task. We therefore only specify the differences. In the Visual Task, instead of auditory clicks presented to the right and the left ears, subjects were presented with two blue targets (2 visual degrees in size) in the left part and the right part of the screen. The left (right) target were flickering at a rate corresponding to C_l (C_r). These stimuli were constructed in the same way as the auditory clicks, with the exception that they were constraint by the screen refresh rate (80 Hz). In particular, no target could flicker more than 40 times per second. If such stimulus was generated, it was replaced by a newly generated stimulus. The stimuli were synchronized with the screen refresh rate; each target flicker lasted one frame (12.5 ms; 1/80 s), and was followed by at least one frame in which the target was black (invisible). The proportion of valid choices over the subjects was 98.1%±1.4 (mean±s.d.).

2.5. Online adaptive procedure

We set the diffculty of the perceptual tasks such that subjects were correct in 60% of cases. We achieved this using an adaptive staircase procedure (Kubanek et al. 2013). In particular, prior to the start of each trial, we randomly drew a number E from a uniform distribution over the interval (−1, +1). The program then randomly selected one of the 10 pre-generated auditory stimuli with such C_r and C_l that—according to the current model—most closely corresponded to the generated E. Using the same behavioral model as previously (Kubanek et al. 2013):

$$E=\frac{2}{1+\exp \left(-\beta \left(\frac{C_r-C_l}{C_r+C_l}\right)\right)}-1,$$ (1)

it follows that

$$C_r=\frac{1}{\beta }\ln \left(\frac{E}{1-E}\right)\Omega$$

where Ω = C_r + C_l and thus C_l = Ω − C_r.

To keep each subject at 60% of correct responses, the program adapted the value of β in eq. 1, (initial value β = 8) to each subject's performance over the last 20 trials according to the following update rule:

$${\beta }_{new}={\beta }_{old}{1.2}^{(A-60)∕10}$$

where A is the accuracy, in %, over the past 20 trials.

3. Results

3.1. Task

Fifty-four human subjects performed a choice task in which they were instructed to make a response based on the polarity of brief trains of click sounds simultaneously presented to both ears. The polarity was drawn randomly on each trial. If subjects heard more click sounds in the right ear, they pressed the right Command key with the right index finger. If they heard more click sounds in the left ear, they pressed the left Command key with the left index finger (Fig. 1A). Critically, a response was followed by an outcome displayed on the screen. If the response was correct, the screen displayed a string randomly drawn from the set {+5c, +10c, +15c, +20c, +25c}. If the response was incorrect, a string randomly drawn from the set {−5c, −10c, −15c, −20c, −25c} was displayed. The presence of outcomes was mentioned neither during the recruitment nor when instructing the subjects. Subjects participated for fixed class credit.

While subjects performed the task, an algorithm monitored each subject's performance and adaptively adjusted task diffculty so that subjects were correct in 60% of cases. Indeed, subjects made a correct choice at the desired ratio, in 61.1 ± 4.8% (mean±s.d., n = 54) of cases. We set the ratio to this value for two reasons. First, a task with a 60% correct ratio generates a balanced proportion of rewards (60%) and penalties (40%). Second, a challenging task (60% correct) may encourage subjects’ attention to the auditory stimulus.

3.2. Stimulus-based behavior

Subjects’ responses followed the given instruction (Fig. 1B). When subjects heard substantially more (e.g., 10 more) clicks in one ear than the other, they predominantly pressed the appropriate button. When the click magnitudes were similar, subjects produced both responses with similar frequency (Fig. 1B). To quantify the subjects’ sensitivity to the click magnitude difference, we fitted the data using logistic regression, in the same way as shown in Fig. 1B, to choices of each subject. We then measured the weight assigned to the click difference in this regression. The weight indeed significantly differed from zero over the subjects (p < 0.0001, t₅₃ = 16.41, two-sided t-test). Thus, the click difference was a significant factor in guiding the subjects’ responses.

The amount of information in the stimulus may influence the time it takes to produce a response, the reaction time (RT). We indeed found that the more information in the stimulus (the higher the difference in the number of the clicks), the faster the subjects responded (Fig. 1C). We quantified this relationship by fitting a line to this relationship in each subject, and measured the slope of the line. The mean modulation of RT was −34.6 ms per the click range shown in Fig. 1C, and this slope significantly differed from zero (p = 0.00012, t₅₃ = −4.14, two-sided t-test).

3.3. Effects of reinforcement and punishment

Crucially, we investigated how the outcome of a choice, a reward (also referred to as “gain”) or a penalty (also referred to as “loss”), influenced the subjects’ choice in the subsequent trial. Notably, in this task, the polarity of a stimulus (rightward, leftward) on a given trial was independent of the stimulus polarity on the previous trial. Therefore, the outcome of the previous trial should have no bearing on the choice on the current trial.

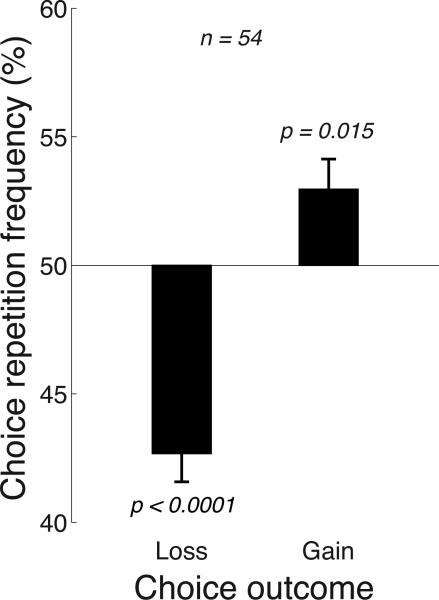
We nevertheless found that a reward or a penalty affected choice (Fig. 2). When a choice was followed by a reward, subjects were biased to repeat that choice (right bar in Fig. 2). This repetition frequency was higher than the 50% expected if there was no influence of the outcome on subsequent choice. In particular, subjects repeated their previous behavior, following a reward, in 53.0% of cases, and this proportion significantly differed from the 50% over the subjects (p = 0.015, t₅₃ = 2.53, two-sided t-test). In contrast to rewards, penalties exerted an opposite effect on the choice behavior (left bar in Fig. 2). Specifically, penalties led to an avoidance of the previous choice. Following a penalty, subjects repeated their past choice only in 42.7% of trials (i.e., avoided that choice in 57.3% of trials), and this frequency was significantly different from the 50% expected if there was no influence of the outcome on choice (p < 0.0001, t₅₃ = −6.63, two-sided t-test).

Fig. 2. The effect of an outcome on subsequent choice.

Mean±s.e.m. proportion of trials in which subjects repeated their previous choice given the outcome of that previous choice (a gain or a loss). If there was no effect of the outcome, subjects would be expected to repeat each choice in 50% of cases because the polarity of the stimulus was random in each trial (horizontal line). Instead, following a gain, subjects showed a significant tendency to repeat their previous choice; following a loss, subjects tended to avoid the same choice. The p values give the significance of the test that a mean significantly differs from 50% (two-sided t-test, n = 54).

These findings reproduce the findings of previous studies that rewards generally increase behavioral frequency and penalties generally decrease behavioral frequency (Skinner 1953; Lerman and Vorndran 2002). Interestingly, however, in those studies, there were statistical relationships between outcomes and behaviors, i.e., an outcome of a behavior was in some way related to and so predictable from the outcomes of previous behaviors. In our task, in which a behavior was based on a perceptual stimulus, an outcome was independent of previous outcomes, and so previous outcomes should not influence current behavior. Yet, a law of effect based on previous experience (Thorndike 1927) was still at work (Fig. 2).

The absolute mean deviation from 50% for losses (7.3%) was 2.43 times larger than the absolute mean deviation from 50% for gains (3.0%), and the difference was significant across the subjects (p = 0.024, t₅₃ = 2.32, paired two-sided t-test). This effect aligns with the findings that a punisher subtracts more value than a reinforcer adds (Epstein 1985; Rasmussen and Newland 2008). However, this finding should be considered with care. The polarity of a stimulus was random on each trial and so there was a 50% chance that a subject would repeat a previous choice. Nonetheless, there may be cognitive factors that may influence the rate of the behavioral inertia (i.e., the repetition rate). To investigate whether the default repetition rate is close to 50%, we tested how choices are influenced by outcomes that occur in the more distant past—two trials prior to the current choice. We found that choices were not significantly influenced by outcomes occurring in this more distant past and that the choice repetition frequencies were indistinguishable from 50% (Fig. 3A; gains: mean 49.2%, p = 0.42, t₅₃ = −0.82; losses: mean 49.6%, p = 0.73, t₅₃ = −0.34). Thus, the default repetition rate in this task was indeed very close to 50%.

The analysis of Fig. 3A provides an important further insight into the temporal dynamics of the effects. The effect of the outcome on choice is rapid—it demonstrates itself immediately during the choice following an outcome (Fig. 2), and transient—it vanishes after that choice is made (Fig. 3A). Transient effects of this sort have been observed for reinforcers previously (Davison and Baum 2000). In this regard, our data suggest that punishers may follow similarly local effects.

An outstanding question is whether the effect of the outcome O (a reward or a penalty) is due to an association with the stimulus S (an O–S relationship), or due to an association with the response R (an O–R relationship). For instance, if the left response is followed by a reward, subjects may allocate their attention to the left on the next trial and so amplify the representation of the leftward stimulus. This may lead to an increased rate of repetition of the left response. Alternatively, an outcome may be directly tied to the response that has led to the outcome, a relationship that bypasses the sensory processing. To distinguish between these possibilities, we incorporated into the experiment 20% of trials during which the auditory stimulus was absent. In these trials, subjects were instructed to choose freely either alternative. We found that a gain or a loss impacted subsequent choice even when prior to that choice there was no stimulus (Fig. 3B). The effects were similar to those observed when the stimulus was present—subjects tended to repeat the same choice following a gain (mean repetition frequency 56.0%, p = 0.012, t₅₃ = 2.61, two-sided t-test), and tended to avoid the same choice following a loss (mean repetition frequency 43.1%, p = 0.016, t₅₃ = −2.50). Notably, the significance of the effect of losses is lower than the significance of the same effect when the stimulus is present (Fig. 2). This is likely because the current analysis is based only on 1/5th of the data, and so the corresponding results are statistically less firm, which is apparent in the relatively large error bars in Fig. 3B. Nonetheless, since the effects are preserved in the trials in which there is no stimulus, the effect of the outcome is diffcult to be explained though an O–S association. Thus, this analysis suggests that the response is directly paired (in either the positive or the negative sense) with an outcome, i.e., the effect involves an O–R link.

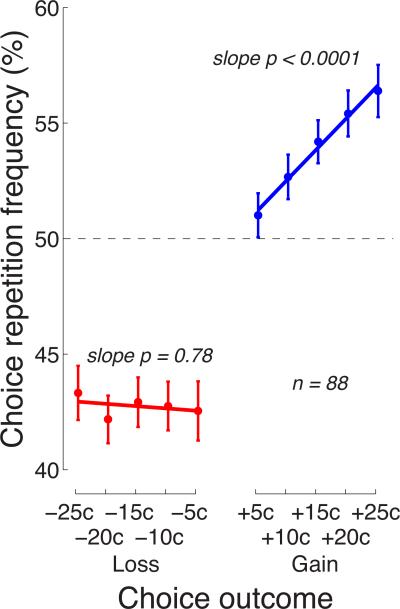
3.4. Effects of the reward and penalty magnitudes

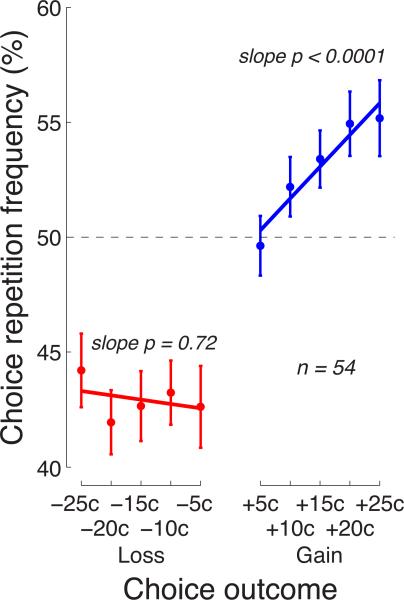
The main goal of this study was to investigate how the subjects’ choices were affected by the magnitude of a reward or a penalty. The behavioral effects of a particular magnitude of a reward or a penalty are shown in Fig. 4. The figure reveals that for gains (blue), the effect scales as a strictly monotonic function of the gain magnitude: the higher the gain, the stronger the tendency to repeat the previous choice. We fitted this relationship, for each subject, with a quadratic curve, to account for the apparent saturation of the effect with larger gains (Kahneman and Tversky 1979). However, the quadratic term did not reach significance over the subjects (p = 0.15, t₅₃ = −1.45, two-sided t-test). We therefore fitted the relationship with a line. The mean linear modulation of the choice repetition percentage by the gain magnitude over the subjects was 0.27% per outcome cent, and this modulation was highly significant (p < 0.0001, t₅₃ = 4.33, two-sided t-test).

Fig. 4. Effects of the reward magnitude and the penalty magnitude on subsequent choice.

Mean±s.e.m. proportion of trials in which subjects repeated their previous choice given a particular value of the outcome of that choice. The p values give the significance of the test that the lines fitted to the data of the individual subjects have slopes different from zero (two-sided t-test, n = 54).

In a striking contrast, the choice behavior was not modulated by the magnitude of a penalty (red). Losses elicited a universal avoidance of the choice that was followed by a loss, regardless of how small a loss was. Fitting a line to these data in the same way as for gains, we found that the slope of the line was small (mean modulation −0.038% per outcome cent) and statistically indistinguishable from zero (p = 0.72, t₅₃ = −0.36). Furthermore, the variance in the slopes over the individual subjects was larger for losses (variance in slope 0.58) compared to gains (variance in slope 0.22), and the difference was significant (p = 0.00055, F_53,53 = 0.38, F-test for equal variance). Thus, the magnitude of a gain had a consistently strong effect on the choice behavior, whereas the magnitude of a loss had no effect. These data demonstrate a prominent asymmetry in the law of effect, and suggest that rewards and punishments act as distinct factors in directing behavior.

3.5. Mechanistic models

We investigated how the effects of rewards and penalties on choice could be described at the molecular level. To this end, we tested several mechanistic models. The models were fitted to the same outcomes as those experienced by each subject. Given these outcomes, the models made choices, on each trial, with choice repetition frequency P_repeat as indicated by the specific equations below. The results, by definition, do not depend on whether we directly use a model's output P_repeat as the estimate of the choice repetition frequency, or whether we first draw the individual binary (left, right) choices with the probability P_repeat and from these choices retrospectively estimate the choice repetition frequency. The models’ parameters were fitted such as to minimize the mean squared error, between the model and the behavior of each subject, in the mean choice repetition frequency over each value of the outcome (n = 10 data points for each subject). The search for the minimum was performed by the Matlab function fminsearch.

3.5.1. Reinforcement Learning model

We first tested whether the subject's behavior could be reproduced using a Reinforcement Learning model. The Reinforcement Learning model is a mechanistic model that has been successfully applied to explain choice behavior in a variety of reward-based tasks (Sutton and Barto 1998; Dorris and Glimcher 2004; Seo et al. 2009; Niv 2009). In this model, each choice is associated with a value Q. When a choice is made and an according outcome O is registered, a new value of the choice Q_new is computed according to the rule:

$$Q_{new}=Q_{old}+\alpha (O-Q_{old})$$ (2)

Here the term α(O − Q_old) embodies an instrumental version of the Rescorla-Wagner learning rule initially used to describe the dynamics of the strength of associations during classical conditioning (Rescorla et al. 1972). This learning rule states that the value is updated when the predicted, old value Q_old differs from the actual, new outcome O. The learning rate α dictates how much weight the outcome O has on this updating. This constant also governs the memory of the model—with smaller values of α (say α = 0.1), the value of choice is updated only minimally and thus its old value is largely retained. On the other hand, when α = 1.0, the old value is entirely replaced by the current outcome O.

Given the values associated with each choice at each time, an action in this model is on each trial selected with a probability that is a function of these values. In a two-choice (left, right) setting, an action is often (Seo et al. 2009) selected with the probability given by the Boltzmann distribution over the difference in the two action values:

$$P_{left}=f(Q_{left}-Q_{right})=\frac{1}{1+{\mathrm{e}}^{-\beta (Q_{left}-Q_{right})}},$$ (3)

where β is the inverse temperature parameter. This parameter controls how sensitive a subject's choice-making is to the values Q (and thereby (eq. 2) to the outcomes O).

The model then computes the choice repetition frequency P_repeat for each trial as

$$P_{repeat}=\{\begin{array}{cc}{P}_{left}\hfill & \text{for a left choice on the previous trial}\hfill \\ 1-P_{left}\hfill & \text{for a right choice on the previous trial}.\hfill \end{array}\phantom{\}}$$ (4)

We first simplified this model by incorporating the finding that choices are influenced by the most recent outcomes, not by outcomes occurring in the more distant past (Fig. 3A). We therefore set α = 1 to model this rapid form of conditioning. The resulting Reinforcement Learning model has just one free parameter, β.

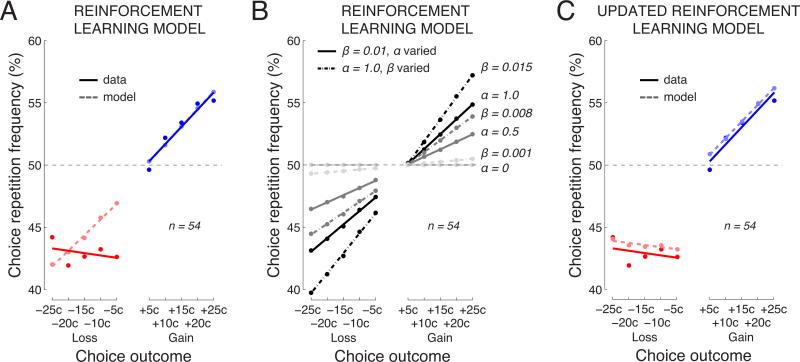
We presented this Reinforcement Learning model with the same outcomes as those experienced by each subject. We then asked whether the model can reproduce the behavior of each subject, after fitting its parameter β. The fit resulted in β = 0.013±0.0016 (mean±s.e.m.). The data and the model's predictions, averaged over the individual subjects, are shown in Fig. 5A. The overlap of the dark and light blue lines indicates that this model provides a good account of the subjects’ behavior following gains (model versus data, difference in means: p = 0.99, t₅₃ = −0.012; difference in slopes: p = 0.94, t₅₃ = −0.082; paired two-sided t-tests). However, the discrepancy between the dark and light red lines indicates that the model fails to capture the effects of losses. For losses (red), there is a significant difference in means (p = 0.030, t₅₃ = −2.23). This finding of a significant difference in the mean levels for losses, between the model and the subjects’ behavior, is important because it confirms that the asymmetry in gains and losses (Fig. 2) cannot be explained due to task-related factors such as the somewhat imbalanced proportion of gains and losses (60% versus 40%; see next paragraph for details). The model would capture this imbalance because it experienced the same outcomes as the subjects. Furthermore, the figure reveals that the model has a particular diffculty with capturing the lack of modulation due to the loss magnitude, which is reflected in a particularly significant difference in the slopes (p = 0.0066, t₅₃ = −2.83).

Fig. 5. A mechanistic account of the choice behavior using a Reinforcement Learning model.

A) Behavior of the subjects and of a Reinforcement Learning model. The figure shows the mean choice repetition frequency as a function of the outcome magnitude, for the subjects (dark solid) and the model (light dashed). The model was fitted separately to the data of individual subjects, and the average is shown.

B) Effects of varying parameters in the Reinforcement Learning model. The individual data points and lines represent the individual combinations of parameter values. The parameter values are given next to each line on the right.

C) Same as in A but for a Reinforcement Learning model in which the outcome is modeled as a constant for all trials that follow a loss (see text for details).

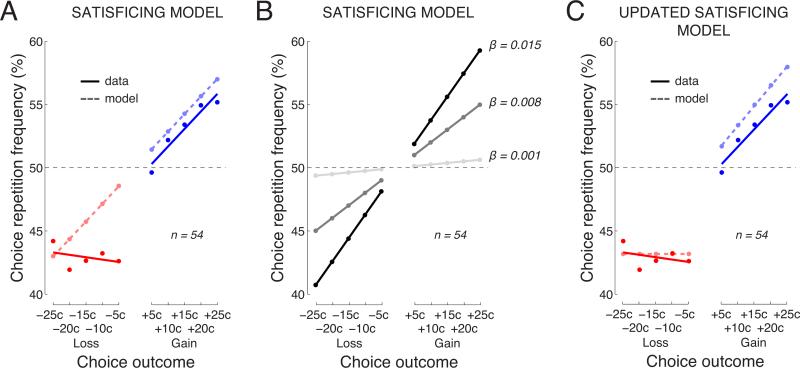
Notably, the predictions of this model (Fig. 5A) are not symmetric about the 50% axis. This is because subjects gain more often than they lose (proportion of gains, 61.1%), and because the Reinforcement Learning model keeps track of the Q values of both choices (eq. 3). Due to the gain–loss asymmetry, receiving a gain (loss) in the relatively likely situation in which both Q values in eq. 3 already reflect a gain entails a relatively small (large) effect on behavior. Indeed, when the proportions of gains and losses are made equal (simulation, data not shown), or when the same data are submitted to a simpler model that does not keep track of the Q values of both options (Fig. 6A), this effect vanishes.

Fig. 6. A mechanistic account of the choice behavior using a satisficing model.

The behavior of a simple satisficing model in this task (see text for details). Same format as in Fig. 5.

We tested whether the uniform effect of the loss magnitude could be accounted for by a combination of the two parameters of the Reinforcement Learning model β and α (Fig. 5B). The figure shows that both parameters modulate the slope of the relationship between the choice repetition frequency and the outcome magnitude (Fig. 5B). Thus, the parameters dictate the sensitivity of the choice behavior to the outcome magnitude. The figure demonstrates that neither parameter nor their combination can account for the effect of losses.

3.5.2. Updated Reinforcement Learning model

To capture this effect, the Reinforcement Learning model must be modified. In particular, we substituted the outcome O in eq. 2 by λ,

$$Q_{new}=Q_{old}+\alpha (\lambda -Q_{old}),$$

such that

$$\lambda =\{\begin{array}{cc}O\hfill & \text{for a reward}\hfill \\ {\lambda }_{penalty}\hfill & \text{for a penalty}.\hfill \end{array}\phantom{\}}$$ (5)

The new parameter _λpenalty represents the outcome that, according to the model, a subject experiences when facing a penalty. The fit resulted in β = 0.012 ± 0.0018 and _λpenalty = −28.9 ± 4.6. With this modification, the Reinforcement Learning model faithfully reproduced the subjects’ behavior (Fig. 5C). There are now no significant differences, between the data and the model, in either the mean levels or the slopes, for either gains or losses (all p > 0.28).

3.5.3. Satisficing model

The Reinforcement Learning model keeps track of the values of both choices. In particular, for α = 1, choices are made with a probability that is a function of the difference of the last outcome experienced following a left and a right choice:

$$P_{left}=f(O_{left}-O_{right})=\frac{1}{1+{\mathrm{e}}^{-\beta (O_{left}-O_{right})}}.$$ (6)

However, subjects may not keep track of the outcomes for both choices. Instead, they may follow a satisficing or a melioration-related strategy (Simon 1959; Wierzbicki 1982; Herrnstein et al. 1997). In particular, subjects may tend to repeat a choice following a gain, tend to avoid a choice following a loss, and entirely disregard the value of the unchosen alternative. This way, the outcome assigned to the unchosen alternative is equal to 0, and eq. 9 thereby simplifies to

$$P_{repeat}=f\left(O\right)=\frac{1}{1+{\mathrm{e}}^{-\beta O}}.$$ (7)

The behavior of this simple model (β = 0.012 ± 0.0015) is shown in Fig. 6A. The figure reveals that also this model has diffculties to account for the effects of losses (red). For losses, there is a significant difference, between the model and the data, in the mean values (p = 0.0038, t₅₃ = −3.03; paired two-sided t-test). Again, this finding is important because it further confirms that the finding of a stronger effect of losses than gains (Fig. 2) is not due to an asymmetry in the frequency of obtaining a loss or a gain (see the note on this above). Furthermore, for losses, there is a significant difference in the slopes (p = 0.0025, t₅₃ = −3.17; paired two-sided t-test). Variability in the parameter β leads to variability in the slope of the effect (Fig. 6B), but this variability does not provide the means to account for the effect of losses.

3.5.4. Updated Satisficing model

Similarly as with the Reinforcement Learning model, to capture the effect of losses, we extended the model (eq. 7) by substituting the outcome O with λ:

$$P_{repeat}=f\left(\lambda \right)=\frac{1}{1+{\mathrm{e}}^{-\beta \lambda }},$$

where

$$\lambda =\{\begin{array}{cc}O\hfill & \text{for a reward}\hfill \\ {\lambda }_{penalty}\hfill & \text{for a penalty}.\hfill \end{array}\phantom{\}}$$ (8)

This updated model (β = 0.014±0.0022 λ_penalty = −64.0±9.0) now accounts for the general trends in the data (Fig. 6C). However, the updated satisficing model does not provide as accurate a fit to the data of the individual subjects as does the updated Reinforcement Learning model. In particular, the updated satisficing model shows significant differences, between the data and the model, in the mean effects (gains: p = 0.0021, t₅₃ = −3.23; losses: p = 0.00074, t₅₃ = −3.58; paired two-sided t-tests). This structurally simple model therefore does not capture the subjects’ behavior in this task as faithfully as the structurally richer Reinforcement Learning model, despite the fact that both models have 2 free parameters.

3.5.5. Win-Stay Lose-Shift model

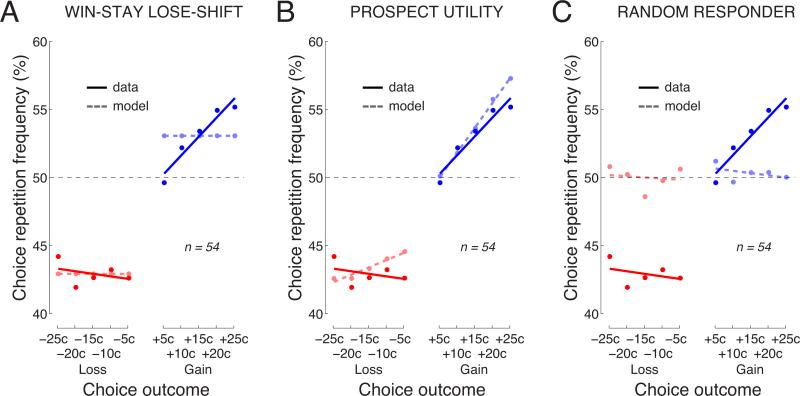
In a Win-Stay Lose-Shift model (Worthy et al. 2013), a subject repeats a choice following a reward, and shifts (switches) a choice following a penalty. The probability with which the repetition and the shift occur are determined by two free parameters, P_reward and P_penalty. The fit resulted in P_reward = 0.53 ± 0.012 and P_penalty = 0.43 ± 0.010. The behavior of this model is shown in Fig. 7A. As apparent from the figure, the two free parameters allow the model to faithfully capture the mean levels; there were no significant differences between the model and the data in the mean levels for either gains or losses (p > 0.27). However, because this model is insensitive to the magnitude of an outcome, it fails to account for the positive slope for gains, exhibiting a significant difference between the model and the data in this respect (p < 0.001, t₅₃ = −4.33).

Fig. 7. The behavior of Win-Stay Lose-Shift, Prospect Utility, and Random Responder models.

Model fits for the A) Win-Stay Lose-Shift B) Prospect Utility and C) Random Responder models. See text for description of the individual models. Same format as in Fig. 5.

3.5.6. Prospect Utility model

The Prospect Utility model (Ahn et al. 2008) is similar to the Updated Reinforcement Learning model. The difference is that in the Prospect Utility model the outcomes O are replaced by “prospects” Π:

$$P_{left}=f({\Pi }_{left}-{\Pi }_{right})=\frac{1}{1+{\mathrm{e}}^{-\beta ({\Pi }_{left}-{\Pi }_{right})}},$$ (9)

where the prospects are computed as

$$\Pi =\{\begin{array}{cc}O\hfill & \text{for a reward}\hfill \\ -\lambda {\mid O\mid }^{\alpha }\hfill & \text{for a penalty}.\hfill \end{array}\phantom{\}}$$ (10)

The parameter α controls the sensitivity to an outcome O. The parameter λ allows for specific weighting of losses. This three-parameter model (α = 0.97 ± 0.007, β = 0.032 ± 0.0039, λ = 0.75 ± 0.126) accounted for the data reasonably well (Fig. 7B), but showed a significant difference between the actual and modeled slopes for losses (p = 0.032, t₅₃ = 2.20).

3.5.7. Random Responder model

We also considered a model which makes choices randomly regardless of the outcome of the previous trial. This model, Random Responder, has no free parameters. Considering this model was important in assessing the floor performance. The behavior of this model is shown in Fig. 7C. As expected, this model does not account for the data, which is demonstrated in significant deviations between the model and the data in the mean levels (gains: p = 0.0077, t₅₃ = −2.77; losses: p < 0.0001, t₅₃ = 6.36) and in the slope for gains (p < 0.001, t₅₃ = −3.81).

3.5.8. Summary of the models’ performance

We compared the performance of the models considered in this study in Tab. 1. The performance is assessed using two metrics. The first metric is the proportion of variance explained (R²). Albeit easy to interpret, this metric does not take into account model complexity. To take the model complexity into account, we used the Bayesian information criterion (BIC; Schwarz et al. (1978)). The BIC evaluates the likelihood of a model candidate to be suitable to account for data while penalizing the number of free parameters to be estimated. The penalty for the number of parameters bypasses the necessity to match the number of parameters in each model in order for a comparison to be fair. A lower BIC value indicates a better model.

Tab. 1.

Comparison of model fits. The table lists the proportion of variance explained (R²) and the Bayesian information criterion (BIC) for the tested models. The models were fitted to the individual data points in Fig. 4 by minimizing the least square error. In addition to the absolute BIC value, the BIC is also provided relative to the BIC for the Random model in which choices are drawn randomly. A lower BIC value indicates a more suitable model. RL: Reinforcement Learning. WSLS: Win-Stay Lose-Shift. The Updated Reinforcement Learning model (Fig. 5) is found to be the most suitable model by the BIC and accounts for most of the variance in the data.

	Random	WSLS	RL	Updated RL	Prospect Utility	Satisficing	Updated Satisficing
R 2	0.03	0.92	0.89	0.99	0.96	0. 88	0. 96
BIC	–57.4	–78.9	–73.7	–92.3	–82.2	–69.7	–79.8
BIC (re Random)	0	–21.5	–16.3	–34.9	–24.8	–12.3	–22.4

The table confirms the impression of Fig. 5C that the Updated Reinforcement Learning (RL) model fits the data best, exhibiting the lowest BIC value and explaining 98.7% of the variance in the 10 data points. According to the BIC, the second best fitting model was the Prospect Utility model, which explained 96.3% of the variance. The difference in the BIC values between the Updated Reinforcement Learning model and the Prospect Utility model amounts to −10.1. This BIC difference is substantial and corresponds to the probability ratio of 156.0 : 1 (Eq. (22) in Raftery (1995)) that the Updated Reinforcement Learning model model is the better fitting model.

3.6. Robustness of the effects across tasks

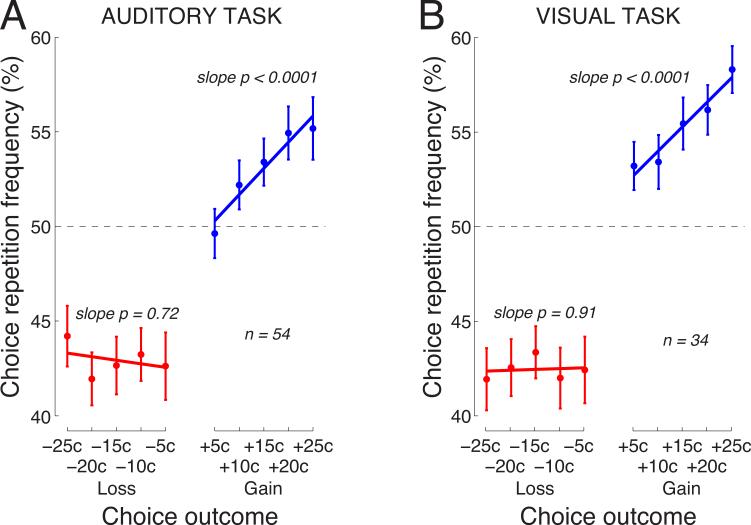
Finally, we tested the robustness of the reported distinction between the effects of reinforcement and punishment. To do so, we collected data in additional 34 subjects in a visual-flash task. The task was analogous to the auditory-click task, with the exception that instead of auditory clicks in the left and right ears, subjects were presented with visual targets flashing in the left and right part of the screen. As in the auditory task, task diffculty was adaptively adjusted so that subjects were correct in 60% of cases. Indeed, subjects made a correct choice at the desired ratio, in 60.5 ± 2.3% (mean±s.d., n = 34) of cases.

This task confirmed the marked distinction in the effects of rewards and penalties (Fig. 8B). As in the auditory task (Fig. 8A), the tendency to repeat previous choice following a gain was strongly governed by the gain magnitude. The mean linear modulation of the choice repetition percentage by the gain magnitude over the subjects was 0.26% per outcome cent, and this modulation is highly significant (p < 0.0001, t₃₃ = 4.45, two-sided t-test). In contrast, the tendency to avoid previous choice following a loss was flat (0.01% per outcome cent, p = 0.91). The mean repetition frequency for gains was 55.3%, for losses 42.5%. These numbers deviated from 50% by 5.3% and 7.5% for gains and losses, respectively. This difference in the means showed a trend to significance (p = 0.087, t₃₃ = −1.76).

Fig. 8. The distinction in the effects of reinforcers and punishers holds across different tasks.

A) Replotted Fig. 4.

B) The effects of the reward and penalty magnitude on the choice repetition frequency in a task in which subjects’ choice was based on two flashing targets instead of on auditory clicks. Same format as in A.

Since the two tasks exhibit very similar effects, we concatenated the data over both tasks and present the result in Fig. 9. The mean linear modulation of the choice repetition frequency by the gain magnitude over the subjects was 0.27% per outcome cent, and this modulation is highly significant (p < 0.0001, t₈₇ = 6.00). No such modulation is observed for losses (−0.02%; n.s.). The mean choice repetition frequency for gains (losses) was 53.9% (42.7%), and the residuals from 50%, i.e., 3.9% and 7.3% were significantly different (p < 0.0001, t₈₇ = −4.29).

Fig. 9. The distinct natures of the effects of reinforcement and punishment on behavior.

Same format as in Fig. 4 and Fig. 8, for data pooled over the two tasks.

4. Discussion

Whether Thorndike's law of effect is symmetric or asymmetric in regard to reinforcement and punishment remains an unresolved question (Skinner 1953; Farley and Fantino 1978; Gray et al. 1991; Dinsmoor 1998; Lerman and Vorndran 2002; Critchfield et al. 2003; Lie and Alsop 2007). We addressed this question in simple choice tasks that allowed us to study the behavioral effects of the magnitudes of reinforcement and punishment in single trials. We found overwhelmingly asymmetric effects of reinforcement and punishment on the choice behavior (Fig. 9).

Given the well established behavioral effects of rewards and penalties (Fig. 2), one would expect that the larger a reward, the higher the tendency to repeat a choice, and the larger a loss, the higher the avoidance rate. We found that this indeed is the case for rewards (Fig. 9, blue), but strikingly, there is no modulation of the effect by the magnitude of a penalty (red). A loss drove a uniform avoidance of the choice that led to the loss.

Asymmetries in the effects of rewards and penalties have been observed across multiple fields, including the cognitive-decision literature (Rachlin et al. 1986; Rachlin 1989) and behavioral economics (Kahneman and Tversky 1979). In these literatures, the subjective value, or a prospect of a loss weighs more heavily upon a choice than the prospect of a gain. Specifically, the subjective value function is often found to be concave for gains and convex and relatively steeper for losses (Kahneman and Tversky 1979). In these literatures, the estimated subjective values of rewards and penalties exhibit different relationships to their respective objective values. However, these relationships do not differ radically between rewards and penalties; the differences are a matter of relatively simple weighting or strictly monotonic transformations (Kahneman and Tversky 1979). Our study, in contrast, revealed a profoundly distinct effect of rewards and penalties (Fig. 9). The plot cannot be accurately fitted with a strictly monotonic function; the data appear to involve two distinct functions—a constant function (red) and a linear function with positive slope (blue). The data therefore suggest that the two factors—rewards and penalties—involve two distinct cognitive processes.

Notably, any attempt to relate our findings to the findings of the above literatures must be taken with care. In particular, it is unclear whether the value functions in these literatures capture similar effects as the choice repetition frequency used in the present study. Furthermore, it is unclear whether the estimates of the value functions, achieved by comparing subjects’ choice preferences, reflect the same valuation processes as an outcome that follows a choice—the approach used in our study.

To mechanistically explain the peculiarly asymmetric effect, we passed the outcomes experienced by each subject to a Reinforcement Learning model, and investigated the model's behavior. The model replicated the behavior of each subject following a reward, but due to its symmetry had diffculties to account for the lack of modulation due to the penalty magnitude (Fig. 5A). To account for this effect, the model had to be modified by substituting the outcome term O with a constant λ_penalty that embodies a flat loss (eq. 5). Following this update, the Reinforcement Learning model accurately accounted for the subjects’ behavior (Fig. 5C). A similar conclusion was drawn using a simpler, satisficing model in which a loss also had to be substituted with λ_penalty to approximate the subjects’ behavior (Fig. 6A and Fig. 6C). This finding suggests that the reward-prediction error (eq. 2), the temporal difference, or other terms based on the Rescorla-Wagner learning rule (Rescorla et al. 1972; Sutton and Barto 1998; Niv 2009) that drive learning in computational models of choice behavior, like in the Reinforcement Learning model here, may not be symmetric to corresponding punishment-prediction error terms. In this regard, interestingly, it has recently been found that dopaminergic neurons in monkey ventral midbrain, which have been long known to encode the reward-prediction error (Schultz 1998; Bayer and Glimcher 2005; Schultz 2007), do not encode the corresponding term for punishments (Fiorillo 2013). That is even though the magnitudes of rewards and punishments were set to a subjectively corresponding level (Fiorillo 2013).

The result of Fiorillo (2013) is a demonstration of a neural representation of an asymmetry in the effects of rewards and punishments in a brain region that encodes the learning terms in computational models of operant behavior. This finding together with our finding encourages the investigation of how reward- and punishment-related asymmetries are encoded in the brain following directly comparable reinforcers and punishers, such as monetary outcomes. A candidate for such a neural effect is the error-related negativity in cortical potentials that is specifically observed following a subject's error (Holroyd and Coles 2002; Frank et al. 2005). However, errors do not necessarily lead to losses. Furthermore, it has been found that cortical potentials encode the difference between a gain and a loss regardless of whether a subject made an error or not (Gehring and Willoughby 2002). The error-related negativity may therefore not be a reflection of an asymmetric encoding of gains and losses. In regard to the cortical encoding of the magnitude of a gain or a loss, it was found that the event-related P300 potential encodes the general effect of an outcome magnitude (Yeung and Sanfey 2004). In particular, for losses (but not for gains), the neural effect of this potential pointed in the direction opposite to that expected according to the ordering [large loss < small loss]. However, it is diffcult to interpret the results of tasks that used relatively complex gambles (Yeung and Sanfey 2004; Gehring and Willoughby 2002). It would be interesting to record cortical potentials in a task similar to ours in which subjects’ choices are not a complex function of subjects’ expectations about the outcome, and in which the magnitude of an outcome is not confounded with subjects’ choice.

Various disciplines have converged on the view that unpleasant, negative events or outcomes have subjectively larger value than pleasant, positive events or outcomes (Kahneman and Tversky 1979; Baumeister et al. 2001). Bad outcomes invoke relatively more attention than good outcomes, produce stronger changes in mood or emotion, or demonstrate themselves in relatively increased electrophysiological responses, among other effects (Taylor 1991; Rozin and Royzman 2001; Baumeister et al. 2001). Of special importance—and in line with our findings—a punishment of errors appears to have stronger effects on learning than a reinforcement of correct responses (Penney and Lupton 1961; Meyer and Offenbach 1962; Spence 1966; Penney 1967; Tindall and Ratliff 1974; Costantini and Hoving 1973). Having investigated the effects of the reward and punishment magnitudes using a simple paradigm, we now show that penalties have a profoundly distinct influence on choice behavior compared to rewards (Fig. 9).

It has been proposed that the unique effects of losses may be due to a momentary increase in arousal and attention following a loss (Yechiam and Hochman 2013). According to that hypothesis, the increase in arousal and attention generally heightens the sensitivity to subsequent outcomes. This hypothesis cannot directly account for our data because in our task gains and losses are randomly interleaved (and occur in the probability ratio of 60:40). Therefore, in this task, a momentary increase in arousal following a loss would affect a subsequent gain or a loss in a similar manner. Yet, we observe a profound difference in the effects of gains and losses. However, the arousal hypothesis may be reformulated to potentially account for the effects in our study. It is possible that an increase in arousal is transient, and that following a loss such arousal increase may drive switching behavior. Because a loss can be harmful to an organism, there should be a mechanism that reliably triggers an alternative action following a loss. In a two-alternative choice task, the alternative action is a choice switch. The validity of such hypothetical mechanism should be investigated in the future.

We found that losses had 2–3 times stronger effects on choice behavior than gains (Fig. 2). This result corroborates the finding of a previous study that compared the effects of gain and loss frequencies on choice behavior by modeling molar behavior under concurrent superimposed schedules of a gain or a loss (Rasmussen and Newland 2008). The modeling suggested that the effects of losses on choice behavior were about 3 times more potent than the effects of gains. It is to note that this particular finding operates under the assumption that the default rate to repeat previous choice is 50%, which seems valid (Fig. 3A).

In the future, it will important to investigate also the effects of no reward (reward = 0) and the effects of rewards and penalties in the vicinity of that point, with high granularity (less than the minimum of ||5c|| used here). This would allow to asses the steepness of the apparent disconnect between the effects of rewards and penalties that figures so strikingly in our data (Fig. 9). Furthermore, it will be important to investigate the effects of rewards and penalties in a task in which subjects know that they will be paid the earned sum.

In summary, we investigated the effects of the magnitudes of reward and punishment on behavior in simple choice tasks in single trials. We found a marked asymmetry in the effects of rewards and penalties on the choice behavior. In contrast to reinforcement whose effect linearly scaled with the reward magnitude, the effect of punishment was flat, independent of the magnitude of a penalty. This profound disconnect suggests that reinforcement and punishment represent distinct, not just oppositely signed factors in guiding behavior.