Abstract
The aim of the present study was to investigate the influence of emulsifying conditions on some physical and rheological properties of orange peel essential oil (OPEO) in water nanoemulsions. In this regard, using the response surface methodology, the influence of ultrasonication conditions including sonication amplitude (70–100 %), sonication time (90–150 s) and process temperature (5–45 °C) on the mean droplets diameter (Z-average value), polydispersity index (PDI), and viscosity of the OPEO nanoemulsions was evaluated. In addition, the flow behavior and stability of selected nanoemulsions was evaluated during storage (up to 3 months) at different temperatures (5, 25 and 45 °C). Based on the results of the optimization, the optimum conditions for producing OPEO nanoemulsions (Z-average value 18.16 nm) were determined as 94 % (sonication amplitude), 138 s (sonication time) and 37 °C (process temperature). Moreover, analysis of variance (ANOVA) showed high coefficients of determination values (R2 > 0.95) for the response surface models of the energy input and Z-average. In addition, the flow behavior of produced nanoemulsions was Newtonian, and the effect of time and storage temperature as well as their interactions on the Z-average value was highly significant (P < 0.0001).
Keywords: Polydispersity index, Response surface methodology, Rheology, Ultrasound, Z-average value
Introduction
Nowadays, natural aromatic compounds and flavors such as vegetable essential oils are extensively used in food products (Teixeira et al. 2004). In this regard, orange peel essential oil (OPEO) is one of the most common essential oils used in food and pharmaceutical industries. For example, in the manufacture of beverages, confectioneries, pharmaceuticals, cosmetics and detergent products (Duke et al. 2002; Madene et al. 2006). The popularity of OPEO is due to its pleasant aromatic scent as well as facilitating its acceptance by the individuals to benefit from its therapeutic properties (Duke et al. 2002).
Because of their particular aromas and low costs, the use of such compounds has always been considered by food industries, but their applications have been associated with problems such as lack of compatibility and solubility in most food environments, volatility and instability during processing and storage. Therefore, finding some methods to increase the stability of these essential oils in food environments and its controlled release when needed is very important, being a turning point in the production, trade and use of aromatic compounds and flavors in foodstuffs and other non-food products (Solans et al. 2005; Sanguansri and Augustin 2006; Gutierrez et al. 2008; Li and Chiang 2012). In this regard, the emulsion technology, especially the nanoemulsion technique, seems to be one of the most essential processes to enhance their solubility, nanocapsulation, and protection of these compounds (Peter and Given 2009; Silva et al. 2012).
Emulsions with droplet size in the nano scale (typically 20–200 nm) with kinetic stability are often called miniemulsions, nanoemulsions, ultrafine emulsions, or submicron emulsions. As a consequence of their size, nanoemulsions are transparent and translucent droplets with the naked eye, and have been used for many industrial applications due to high kinetic stability, low viscosity, high transparency, and high stability against sedimentation, creaming, coalescence, and flocculation (McClements and Decker 2000; McClements 2005; Solans et al. 2005; Jafari et al. 2007a). Meanwhile, nanoemulsions are unbalanced systems with a spontaneous tendency to dissociate into constituent phases. However, nanoemulsions may maintain high kinetic equilibrium even for several years, and such a long period of physical stability has distinguished them (Solans et al. 2005; Gutierrez et al. 2008; Cheong et al. 2008).
In emulsion systems, properties such as stability, rheology, appearance, color, and texture depend on the size of emulsion droplets and particle size distribution (Tadros et al. 2004; Gutierrez et al. 2008). The characteristics of emulsions are also dependent upon the techniques used to prepare the emulsion and emulsification process. There are also many techniques for producing nanoemulsions, each of which with its own advantages and disadvantages generating emulsions with different properties (Tadros et al. 2004; Gutierrez et al. 2008; Silva et al. 2012).
As mentioned earlier, nanoemulsions are unbalanced systems which are not formed spontaneously. Therefore, some kinds of energy (mechanical or chemical) are required for their formation (Tadros et al. 2004; Solans et al. 2005; Jafari et al. 2007a; Gutierrez et al. 2008; Silva et al. 2012). Therefore, their optimization would be achievable through optimizing the composition and variables related to the preparation methods and conditions. In addition, the ultimate objective in optimizing is often to reach the minimum droplet size, minimum polydispersity, and maximum stability (Tadros et al. 2004; Gutierrez et al. 2008).
In general, there are two methods to produce nanoemulsions: low- and high-energy emulsifications (Tadros et al. 2004; Solans et al. 2005; Acosta 2009). In the former one, nanoemulsions are obtained as a result of phase inversion and spontaneous emulsification methods (Izquierdo et al. 2001; Bouchemal et al. 2004; Uson et al. 2004; Sanguansri and Augustin 2006; Anton et al. 2008; Rao and McClements 2011a). Despite a number of benefits, this method has some limitations including the need for large amounts of surface active agents (surfactants) along with careful selection of surfactants and co-surfactants (Tadros et al. 2004; Jafari et al. 2007a; Kentish et al. 2008; Silva et al. 2012). While, in high-energy method, the emulsification is done using mechanical equipments including colloid mills, high speed or high pressure homogenizers and ultrasonic homogenizers (Abismail et al. 1999; Tadros et al. 2004; Jafari et al. 2007b). In an ultrasonic emulsification technique, high-intensity ultrasound waves can change the characteristics of treated matter through intensive shear forces, pressure, and temperature due to cavitation (Kentish et al. 2008; Rao and McClements 2011a; Li and Chiang 2012). Lower energy and emulsifier consumption, smaller droplet size, lower polydispersity, and higher stability of nanoemulsions are among the major benefits of this method (Tadros et al. 2004; Jafari et al. 2007a; Kentish et al. 2008; Li and Chiang 2012).
As previously noted, optimization of nanoemulsion features is made possible through optimizing the variables related to emulsification methods and conditions. As a result, we believe in the production of OPEO nanoemulsions using ultrasonication, some variables such as amplitude and duration of sonication, as well as temperature can be effective upon the physical and rheological properties as well as stability of nanoemulsions. On the other hand, the sonication as a novel emulsification method has a number of advantages over the other methods. Therefore, the aims of this study were to investigate the effect of ultrasonic emulsification conditions on some physical and rheological properties of nanoemulsions of OPEO using response surface methodology (RSM) and determining the optimal combination of these variables to produce OPEO nanoemulsions with minimum droplet size and highest stability.
Materials and methods
Materials
Natural orange peel essential oil (OPEO), without any purification, was supplied by a local manufacturer (Giah Essance, Gorgan, Iran). Tween 80 was purchased from Merck Chemicals Company (Darmstadt, Germany). Deionized water (Electrical resistivity = 18 MΩ.cm) was used for the production of nanoemulsions.
Designing of ultrasonic chamber to control the process temperature
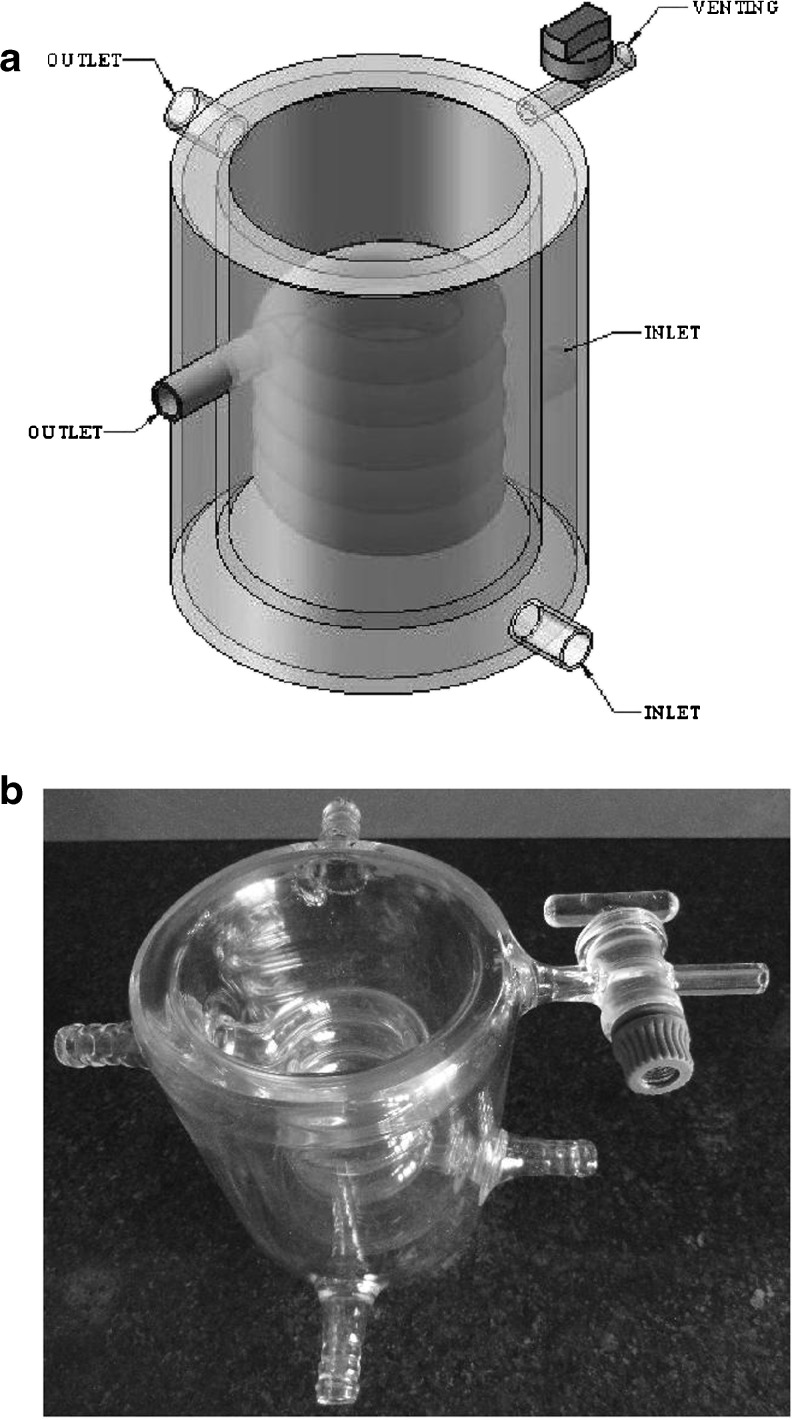
In order to control the temperature during the sonication process, a double-walled cylindrical glass container (inner diameter 65, depth 90 mm) was designed (Fig. 1). Due to the continuous circulation of the antifreeze (propylene glycol) liquid through the jacket and the embedded spiral coil, the temperature of premix was kept constant at intended temperature throughout sonication.
Fig. 1.
Illustration of a schematic and b real design of ultrasonic cooling chamber
Preparation of nanoemulsions
The oil-in-water (O/W) emulsions were prepared using OPEO (1 % w/w), as the oil phase, and mixture of Tween 80 (2 % w/w) and deionized water (97 % w/w), as the aqueous phase. All emulsions were prepared through a two-stage process. At first, the oil and aqueous phases (total of 100 g) were placed in a glass beaker and mixed at room temperature (≈ 25 °C) using a magnetic stirrer (700 rpm for 15 min). Afterwards, they were sonicated (Sonicator 4000, 20 kHz, high gain sonotrode dia = 19.1 mm, Misonix, Inc, New York) in a double-walled cylindrical glass cell (Fig. 1) where the sonotrode was immersed 1 cm below the surface of the emulsion. The sonication was carried out at various amplitudes (70–100 %) for different times (90–150 s) controlled by the software of the device. The total input energy (J) was recorded for every treatment. The sonication was carried out at various temperatures that were kept constant at intended temperature (5–45 °C) throughout sonication by circulating coolant fluid through the jacket of chamber.
Droplet size and size distribution measurements
The mean droplet diameter (Z-average) and polydispersity index (PDI) of OPEO nanoemulsions were determined by dynamic light scattering (Nano-ZS90, Malvern Instruments, Worcestershire, UK) using a Zetasizer (Tang et al. 2012).
Rheological measurements
The rheological properties of nanoemulsions were determined at 25 °C, a day after preparation, with a Brookfield rheometer (LV DV-ΙΙΙ Ultra, Brookfield Engineering Laboratories Inc., MA, USA), equipped with an enhanced UL Adapter. In order to determine the shear stress and viscosity as functions of shear rate, as well as the flow behavior of nanoemulsions, the shear rate (0.01–171.2 s–1 in 5 min and 171.2–0.01 s–1 within next 5 min) was changed. The data were fitted with the Newtonian model using linear regressions. Meanwhile, their time-dependency (constant shear rate of 91.73 s−1, temperature of 25 °C, 2 min) were assessed (Barnes 2000; Bourne 2002).
Stability at different storage temperature
For this purpose, about 20 g of nanoemulsions were transferred into a 25 ml glass bottles, tightly sealed with plastic caps, wrapped with aluminum foil, and stored at 5, 25 and 45 °C for 12 weeks. Then, their stability was assessed by measuring the mean droplet diameter and size distribution at 4 week intervals.
Experimental design
Response surface methodology (RSM) was used to evaluate the effects of independent variables [sonication amplitude 76–94 % (X1), sonication time 102–138 s (X2), and process temperature 13–37 °C (X3)] as well as their interactions on responses [energy input during ultrasonication (Y1), viscosity (Y2), Z-average (Y3) and PDI (Y4)] of OPEO nanoemulsions. The coded and uncoded independent variables used in the RSM design are shown in Table 1. The experiments were designed according to the central composite design (CCD) using a 23 factorial and star design with six central points as shown in Table 2. A second-order polynomial equation was used to express the responses as a function of the independent variables as follows:
| 1 |
Table 1.
Uncoded and coded independent variables used in RSM design
| Symbol | Independent variable | Coded levels | ||||
|---|---|---|---|---|---|---|
| −1.68 | −1 | 0 | 1 | 1.68 | ||
| X 1 | Amplitude (%) | 69.86 | 76 | 85 | 94 | 100.14 |
| X 2 | Time (s) | 89.73 | 102 | 120 | 138 | 150.27 |
| X 3 | Temperature (°C) | 4.82 | 13 | 25 | 37 | 45.18 |
Table 2.
Effect of different ultrasonication conditions (time, amplitude, temperature) on energy input, viscosity, Z-average, and PDI of nanoemulsion (1 wt% OPEO, 2 wt% Tween 80)
| Run | Independent variablea | Responseb | |||||
|---|---|---|---|---|---|---|---|
| X 1 | X 2 | X 3 | Y 1 | Y 2 | Y 3 | Y 4 | |
| 1 | 85 | 89.73 | 25 | 9,354 | 1.05 | 64.17 | 0.540 |
| 2 | 85 | 150.27 | 25 | 16,135 | 1.05 | 27.22 | 0.587 |
| 3 | 94 | 138 | 37 | 16,381 | 1.19 | 18.16 | 0.810 |
| 4 | 69.86 | 120 | 25 | 10,023 | 1.04 | 66.83 | 0.552 |
| 5 | 76 | 102 | 37 | 9,306 | 1.20 | 56.71 | 0.567 |
| 6 | 85 | 120 | 45.18 | 12,304 | 1.19 | 33.47 | 0.645 |
| 7 | 85 | 120 | 25 | 12,712 | 1.04 | 44.22 | 0.677 |
| 8 | 76 | 138 | 37 | 13,011 | 1.19 | 37.23 | 0.707 |
| 9 | 85 | 120 | 25 | 12,426 | 1.05 | 39.53 | 0.647 |
| 10 | 85 | 120 | 4.82 | 13,181 | 1.21 | 30.10 | 0.656 |
| 11 | 94 | 102 | 37 | 12,203 | 1.19 | 36.82 | 0.688 |
| 12 | 85 | 120 | 25 | 12,620 | 1.05 | 46.76 | 0.709 |
| 13 | 85 | 120 | 25 | 12,531 | 1.05 | 51.17 | 0.621 |
| 14 | 85 | 120 | 25 | 12,703 | 1.06 | 49.60 | 0.608 |
| 15 | 76 | 102 | 13 | 9,776 | 1.20 | 62.69 | 0.550 |
| 16 | 94 | 102 | 13 | 12,725 | 1.20 | 37.18 | 0.655 |
| 17 | 100.14 | 120 | 25 | 15,099 | 1.05 | 32.09 | 0.676 |
| 18 | 76 | 138 | 13 | 12,952 | 1.19 | 39.48 | 0.675 |
| 19 | 94 | 138 | 13 | 16,629 | 1.19 | 21.38 | 0.868 |
| 20 | 85 | 120 | 25 | 12,454 | 1.06 | 49.43 | 0.603 |
a X 1, sonication amplitude (%); X 2, sonication time (s); X 3, process temperature (°C)
b Y 1, energy input (J); Y 2, viscosity (mPa.s); Y 3, Z-average (nm); Y 4, PDI
Where a0 is a constant, ai, aii and aij are the linear, quadratic and interactive coefficients, respectively. The coefficients of the response surface equation were determined using Design-Expert 7.1.1 software.
Statistical analysis
The analysis of variance (ANOVA), regression coefficient calculation, performance stepwise procedure to simplify the models and generating of three-dimensional surface plots were carried out using Design-Expert 7.1.1 software. The significance of the equation parameters for each response was assessed by F-value at a probability (P) of 0.05. In addition, the adequacy of the models was determined using model analysis, lack-of-fit test and coefficient of determination (R2) analysis. It needs to be mentioned that all results were expressed as the mean values of two independent experiments.
Results and discussion
Design of ultrasonic chamber
Due to the exothermic nature of sonication process, the temperature of system may rise up to tens of degrees Celsius depending on the period and intensity of sonication. On the other hand, temperature has a complex effect where in some cases it can unfavorably affect the emulsifying properties of surfactants or to decrease the emulsion viscosity, interfacial tension, and Laplace pressure which all these can facilitate droplet disruption, enhancement of the coalescence rate as well as droplet size increase (Jafari et al. 2007a). Owing to these reasons, temperature control is considered as one of the most important parameters in high-energy emulsification processes including sonication (Jafari et al. 2007a). Therefore, in the present study we focused on designing an ultrasonic chamber (double-walled cylindrical glass container as shown in Fig. 1) to control the process temperature at the desired levels with high precision (±1 °C). The special features of the vessel were that of being double-walled as well as fitted with a coil within it, which could provide the possibility of multilateral heat exchanging between sample and coolant. In order to obtain a constant temperature during sonication process, the circulating coolant temperature was maintained about 20 °C lower than experimental temperatures. This setting was found to be very efficient and useful to control the temperature without making any disturbance for the turbulence and circulation of emulsion during sonication. In addition, with the best of our knowledge there is not any other report on the chamber design and most researchers only used double-walled cylindrical containers which are not capable to cool the emulsion during sonication due to the high rate of temperature increase.
Fitting the models
The total energy input during ultrasonication, viscosity, Z-average and polydispersity index values of the OPEO nanoemulsions obtained from all the experiments are shown in Table 2. The experimental data was used to compute the coefficients of the quadratic polynomial equations, and the derived equations (Eqs. 2, 3, 4, 5) were used to predict the values of dependent variables of the nanoemulsions. According to Tables 3 and 4, analysis of variance (ANOVA) showed that the coefficient of multiple determinations (R2) of the models for the dependent variables was 0.996, 0.737, 0.955 and 0.549, respectively. This indicates that the quadratic polynomial models were only adequate to describe and predict the influence of the independent variables on the energy input and Z-average. The estimated regression coefficients of the polynomial response surface models along with the corresponding R2 values and lack of fit tests are also shown in Tables 3 and 4. The significance of each term was evaluated using the F-value and P-value where a small P-value and a large F-value would indicate a more significant effect on the respective independent variables. Thus, during ultrasonication the variables with the largest effect on the energy input were the linear terms of sonication time and sonication amplitude (P < 0.0001), followed by the linear term of process temperature (P < 0.01). The interaction between amplitude and sonication time also had a significant effect (P< 0.05) on the energy input. Furthermore, none of the quadratic terms had a significant effect (P > 0.05) on the energy input (Table 3). In addition, the lack of fit test was not significant for this response.
Table 3.
ANOVA of the regression coefficients of the fitted quadratic equations for the energy input (Y 1) and viscosity (Y 2) of the nanoemulsions (1 wt% OPEO, 2 wt% Tween 80)
| Variable | Energy input (Y 1) | Viscosity (Y 2) | ||||
|---|---|---|---|---|---|---|
| Regression coefficient | F-value | P-value | Regression coefficient | F-value | P-value | |
| a 0 | 12,568.40 | 1.05 | ||||
| Linear | ||||||
| a 1 | 1,569.16 | 991.12 | < 0.0001 | 0.000499 | 0.001222 | 0.9728 |
| a 2 | 1,930.70 | 1,500.44 | < 0.0001 | −0.002197 | 0.024 | 0.8808 |
| a 3 | −194.48 | 15.22 | 0.0030 | −0.003195 | 0.050 | 0.8275 |
| Interaction | ||||||
| a 12 | 150.13 | 5.31 | 0.0439 | 0.001250 | 0.004488 | 0.9479 |
| a 13 | −44.87 | 0.47 | 0.5064 | −0.001250 | 0.004488 | 0.9479 |
| a 23 | 100.38 | 2.38 | 0.1543 | 0.001250 | 0.004488 | 0.9479 |
| Quadratic | ||||||
| a 11 | 34.04 | 0.49 | 0.4990 | 0.017 | 1.53 | 0.2448 |
| a 22 | 98.91 | 4.16 | 0.0688 | 0.019 | 1.86 | 0.2028 |
| a 33 | 98.21 | 4.10 | 0.0705 | 0.072 | 26.81 | 0.0004 |
| Model | 280.29 | < 0.0001 | 3.12 | 0.0456 | ||
| Lack of fit | 3.47 | 0.0993 | 97.30 | < 0.0001 | ||
| R 2 | 0.9961 | 0.7372 | ||||
Table 4.
ANOVA of the regression coefficients of the fitted quadratic equations for the Z-average (Y 3) and polydispersity index (Y 4) of the nanoemulsions (1 wt% OPEO, 2 wt% Tween 80)
| Variable | Z-average (Y 3) | Polydispersity index (Y 4) | ||||
|---|---|---|---|---|---|---|
| Regression coefficient | F-value | P-value | Regression coefficient | F-value | P-value | |
| a 0 | 46.89 | 0.65 | ||||
| Linear | ||||||
| a 1 | −10.32 | 90.61 | <0.0001 | 0.053 | 10.47 | 0.0052 |
| a 2 | −10.20 | 88.44 | <0.0001 | 0.049 | 9.03 | 0.0084 |
| a 3 | −0.45 | 0.17 | 0.6871 | 0.001062 | 0.004229 | 0.9490 |
| Interaction | ||||||
| a 12 | 1.03 | 0.53 | 0.4845 | – | – | – |
| a 13 | 0.58 | 0.17 | 0.6903 | – | – | – |
| a 23 | 0.11 | 0.005890 | 0.9403 | – | – | – |
| Quadratic | ||||||
| a 11 | 0.24 | 0.052 | 0.8235 | – | – | – |
| a 22 | −1.09 | 1.06 | 0.3265 | – | – | – |
| a 33 | −6.01 | 32.37 | 0.0002 | – | – | – |
| Model | 23.69 | < 0.0001 | 6.50 | 0.0044 | ||
| Lack of fit | 0.72 | 0.6360 | 2.54 | 0.1564 | ||
| R 2 | 0.9552 | 0.5494 | ||||
In terms of the viscosity, analysis of variance showed a low coefficient of determination value (R2 = 0.737) and also, the lack of fit test was significant (Table 3.). For this response, only the quadratic term of process temperature had a significant effect (P < 0.001).
For the Z-average of the nanoemulsions (Table 4), the variables having the largest effect on this response were the linear terms of amplitude and sonication time (P < 0.0001), followed by the quadratic term of process temperature (P < 0.001), while the effect of the other terms was insignificant (P > 0.05). Meanwhile, the lack of fit test was not significant for this response.
Regarding the polydispersity index (Table 4), the fitted model of this variable showed a very low coefficient of determination (R2 = 0.549) and also, the lack of fit test was not significant for this response. Moreover, only the linear terms of amplitude and sonication time had a significant effect (P < 0.01). As the equation (Eq. 5) showed, rising the amplitude and sonication time led to higher polydispersity indices.
| 2 |
| 3 |
| 4 |
| 5 |
Analysis of response surfaces
In order to recognize the effect of the independent variables on the dependent ones, surface response plots of the quadratic polynomial models were generated by varying two of the independent variables, within the experimental range, while holding another one constant at the central point.
Energy input
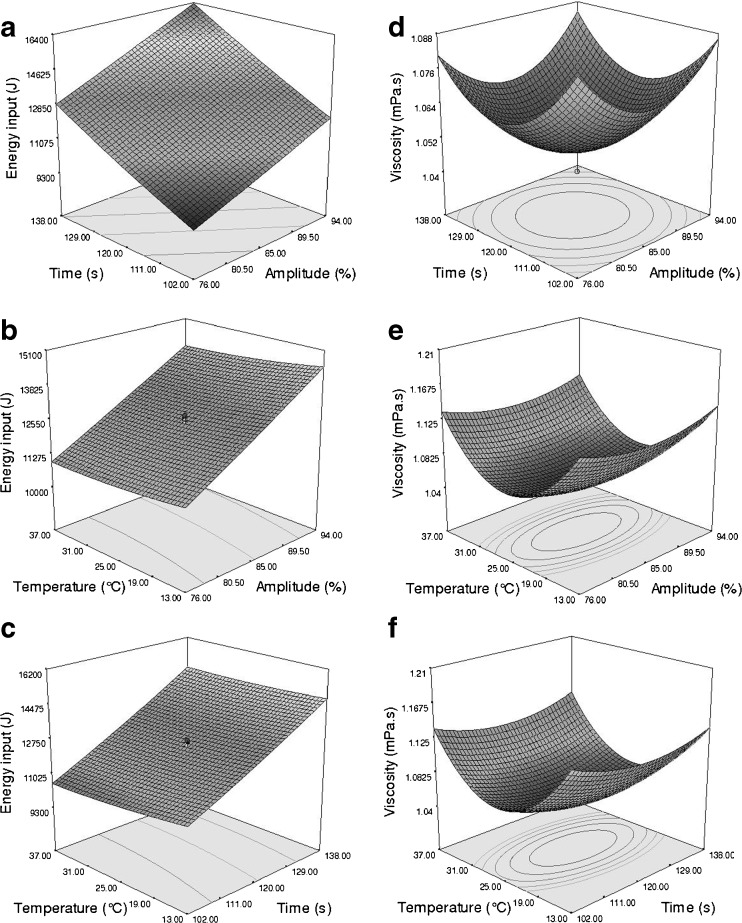
The effect of changes in sonication time and amplitude at constant temperature (25 °C) on the amount of consumed energy is shown in Fig. 2a. As can be seen, with increasing sonication time and amplitude, the consumed energy was increased and its maximum value was achieved at 94 % (amplitude) and 138 s (sonication period).
Fig. 2.
Response surface plots of the energy input during ultrasonication (a, b, and c) and the viscosity of the nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) (d, e, and f) as a function of time and amplitude, temperature and amplitude, temperature and time
The effect of amplitude and temperature at a constant time (120 s) on the energy consumption is shown in Fig. 2b. As can be seen, the impact of amplitude was much higher than temperature. Accordingly, increasing the temperature up to 25 °C decreased the amount of consumed energy and at higher temperatures, energy consumption was relatively constant. This trend seems to be due to the high viscosity and cavitation threshold in low temperatures, because at high temperatures, the viscosity reduction leads to low cavitation threshold and consequently diminished energy consumption (Mason 1999). Moreover, at constant amplitude (85 %), the effect of process time on energy consumption was much higher than temperature (Fig. 2c). In this regard, regression coefficients of the linear terms also showed that the effect of sonication time and sonication amplitude (P < 0.001) on the quantity of consumed energy were higher than process temperature (P = 0.003). On the other hand, it is evident that with increasing intensity and duration of sonication, more energy will be consumed (Mason 1999; Delmas et al. 2011; Li and Chiang 2012).
Viscosity
Three-dimensional response surface plots of viscosity are shown in Fig. 2d–f. As can be seen, the effect of independent variables on viscosity has a downward trend up to the central point, after which the trend is changed. In other words, around the central point, minimum viscosity is reached. Meanwhile, in comparison to other variables, the effect of process temperature has been significantly higher (P < 0.001).
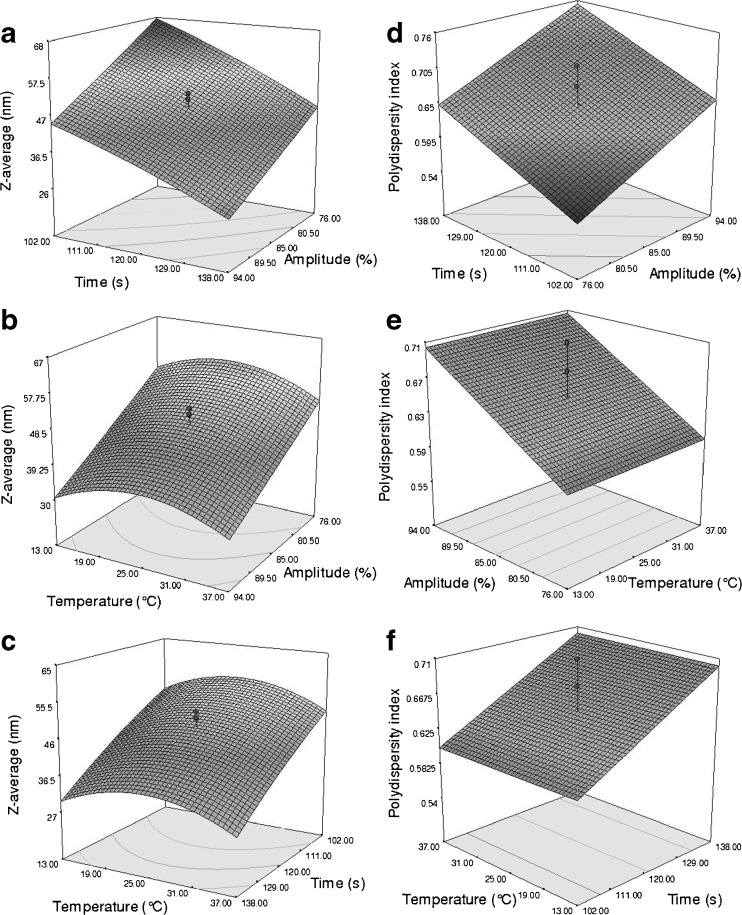
Z-average
The effect of sonication time and amplitude in constant temperature (25 °C) on Z-average value of nanoemulsions is shown in Fig. 3a. As can be seen, with increasing intensity and duration of sonication, Z-average value is decreased, and its minimum was reached at 94 % (sonication amplitude) and 138 s (sonication time). The droplet disruption, as the major mechanism of emulsion formation, is depended on the type and quantity of applied shear force (Tadros et al. 2004; Kentish et al. 2008; Li and Chiang 2012). As a consequence, in this study with increasing the intensity or amplitude of sonication (up to 94 %), the size of emulsion droplets significantly decreased (P < 0.0001). However, higher intensities may lead to an increased rate of droplet coalescence (Jafari et al. 2006; Li and Chiang 2012). On the other hand, in an O/W emulsion system, sonication time, owing to thermodynamic equilibrium, has paramount effect upon the adsorption rate of surfactant to the surface of the droplets and size distribution of newly formed droplets (Li and Chiang 2012). Therefore, longer sonication (above 138 s) may lead to formation of larger droplets mainly because of coalescence (Jafari et al. 2006; Li and Chiang 2012).
Fig. 3.
Response surface plots of the Z-average (a, b, and c) and the polydispersity of the nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) as a function of time and amplitude, temperature and amplitude, temperature and time
The effect of amplitude and temperature in the fixed time (120 s) on the Z-average value of nanoemulsions is also shown in Fig. 3b. As can be seen, by increasing the temperature (up to 25 °C), the Z-average increased, but at higher temperatures it decreased. These findings mean that at a constant temperature (25 °C), increasing the intensity of sonication can result in smaller particle size. Furthermore, our results showed that the Z-average value of nanoemulsions was minimum at 37 °C. Thus, it appears that the temperature can be very effective on the emulsion droplet size because of its impact on viscosity and interfacial tension of oil and water phases (Yuan et al. 2008).
Figure 3c also shows the effect of sonication time and temperature (constant sonication intensity of 85 %) on the Z-average value. At constant temperature (25 °C), increasing sonication time can result in smaller particle sizes.
Polydispersity
Three-dimensional response surface plots for polydispersity index variable are shown in Fig. 3d–f. As can be seen, with increasing intensity and duration of sonication, PDI is increased.
Optimization of conditions for producing nanoemulsions
One of the main objectives of this study was to determine the optimal values of the independent variables to generate nanoemulsions with minimum droplet size. Hence, numerical optimization method was used to achieve the optimum process conditions. In this method, the optimization goals were specified, the levels of the response and independent variables were adjusted, and the best responses were obtained using fine tuning technique. The optimum range of independent variables including sonication amplitude, sonication time and process temperature to achieve the best-predicted values of Z-average (∼19.85 nm) were 94 %, 138 s, and 37 °C, respectively. It should be noted that the desirability value of the predicted zone was equivalent to 0.965 to 0.975. On the other hand, according to Table 2, the Z-average value of nanoemulsions, produced under the optimum conditions, was equivalent to 18.16 nm. Therefore, this indicates that a very good correlation existed between the results calculated and estimated values of statistical methods.
Flow behavior
Based on our rheological measurements, the Newtonian model was the most appropriate model to determine the flow behavior of nanoemulsions (Fig. 4a). As can be seen, there is a linear relationship between shear rate and shear stress. In addition, in the laminar flow range, the viscosity is independent of shear rate, which confirms its Newtonian behavior (Fig. 4b). Meanwhile, no hysteresis loop was observed in shear stress vs. shear rate curves (Barnes 2000; Bourne 2002). Figure 4c also shows that in constant shear rate, viscosity remains constant despite increased shear time. It should be noted that such behavior was observed in all the nanoemulsions even after 3 months of storage at 5, 25 and 45 °C.
Fig. 4.
Flow curves a shear stress/shear rate, b viscosity/shear rate and c viscosity/time of nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) prepared by sonication (94 %, 138 s, 37 °C)
Storage stability
Colloidal dispersions and emulsions normally need to be stored at different temperatures for long time for commercial and industrial applications. Accordingly, in order to evaluate the effect of storage time and temperature on the stability, nanoemulsions (including 1 % OPEO and 2 % Tween 80) were produced at optimum emulsification conditions (sonication amplitude 94 %, sonication time 138 s, and temperature 37 °C). Then, they were kept at 5, 25 and 45 °C for 12 weeks, and their mean droplet size, particle size distribution and the flow behavior were evaluated at 4-week intervals. It should be noted that the droplet diameter and size distribution are important parameters affecting emulsion stability (Cheong et al. 2008). Based on statistical analysis (Table 5), the effect of storage time, storage temperature and their interaction on the Z-average value was significant (P < 0.0001). Whereas, regarding the PDI, only the storage period showed a significant effect (P < 0.0001) and the temperature was not effective (P > 0.05).
Table 5.
ANOVA of the storage time and temperature for the Z-average and PDI value of nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) prepared by sonication (94 %, 138 s, 37˚C)
| Source | Z-average (nm) | PDI | ||
|---|---|---|---|---|
| F-value | P-value | F-value | P-value | |
| Time | 29.189 | <0.0001 | 15.037 | <0.0001 |
| Temperature | 658.357 | <0.0001 | 3.737 | 0.055 |
| Time*Temperature | 82.326 | <0.0001 | 2.243 | 0.110 |
| Model | 172.567 | <0.0001 | 6.004 | 0.02 |
| R 2 | 0.994 | 0.846 | ||
The comparison of the measured variables (Table 6) showed that Z-average value was in its minimum level after 4 and 8 weeks of storage and at its maximum on the first day and after 12 weeks. Meanwhile, at low storage temperature (5 and 25 °C) the Z-average was lower than the one stored at 45 °C.
Table 6.
Effect of storage time and temperature on the Z-average and PDI values of nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) prepared by sonication (94 %, 138 s, 37 °C)
| Time (week) | Z-average (nm) | PDI |
| 0 | 20.55 b | 0.753 b |
| 4 | 17.149 a | 0.411 a |
| 8 | 17.416 a | 0.481 a |
| 12 | 21.755 b | 0.521 a |
| Temperature (°C) | ||
| 5 | 14.114 a | 0.593 b |
| 25 | 13.451 a | 0.470 a |
| 45 | 30.078 b | 0.562 ab |
Various superscript letters show significant difference at P < 0.05
PDI of the samples had the highest value at zero time. Meanwhile, the samples stored at 25 °C showed the lowest values of PDI.
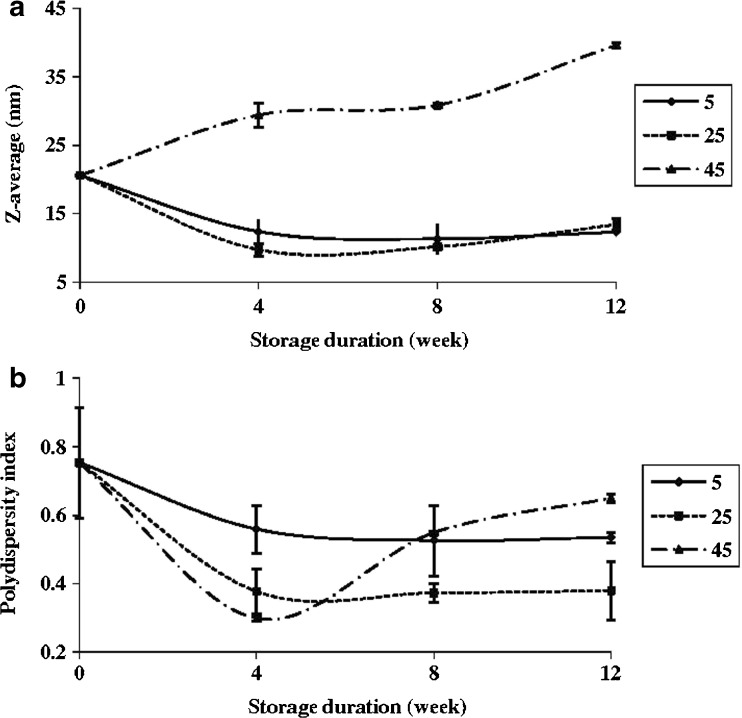
The influence of storage on Z-average and PDI is shown in Fig. 5. As can be seen, the Z-average value of the samples stored at 5 and 25 °C within the first 4 weeks showed a downward trend, after which it was increased with a much lower slope. It seems that the downward trend of Z-average during the first 4 weeks is due to a gradual reduction in kinetic energy barrier in the system, subsequent to which the samples gradually reach kinetic equilibrium. In the systems including oil, water and surfactant at ambient temperature, there is a kinetic energy barrier preventing these systems from reaching the highest kinetic equilibrium status (Rao and McClements 2011a). Reduction of this barrier over time probably enhances the kinetic equilibrium of the system. The upward trend of Z-average after the first 4 weeks is likely due to droplets collision and phenomena such as coalescence and Ostwald ripening, which subsequently lead to an increase in the size of the droplets (Jafari et al. 2007b; Rao and McClements 2011a). In contrast, at 45 °C the OPEO nanoemulsions were highly unstable and faced with an increasing trend in the average size of the droplets. This trend could be due to the collision rate and coalescence of droplets at higher temperatures, which subsequently lead to an increase in emulsion droplet size (Rao and McClements 2011b). The small difference (although not statistically significant) which was observed on the Z-average value at 5 and 25 °C can be likely related to higher Ostwald ripening rate at lower temperatures (Li and Chiang 2012). That is why the Z-average value at 5 °C was slightly higher than the one at 25 °C.
Fig. 5.
Effect of storage (time and temperature) on a Z-average and b PDI of nanoemulsions (1 wt% OPEO, 2 wt% Tween 80) prepared by sonication (94 %, 138 s, 37 °C)
In addition, during the first 4 weeks of storage (at 5 and 25 °C), the PDI showed a downward and then an almost steady trend (Fig. 5b). It appears that during this storage period, the nanoemulsion system has progressed towards more kinetically balance due to the interactions occurring in the system. It should be noted that similar trend, although with greater slope, was clearly seen at 45 °C. But during the following weeks, it seems that high temperature has increased the coalescence rate and the subsequent decrease in kinetic equilibrium led to the further increase of PDI.
Conclusions
The results of this study showed that the application of response surface method in finding optimum conditions of ultrasonic emulsification process to produce OPEO nanoemulsions is a very effective and reliable method (Desirability = 0.975). According to our findings, the sonication amplitude, sonication time, process temperature and the interaction of first two parameters were effective on energy consumption during emulsification process and Z-average value. Meanwhile, the effect of sonication amplitude and time on PDI was significant. Moreover, the optimum condition for production of nanoemulsion (1 % OPEO, 2 % Tween 80, Z-average 19.36 nm) was equivalent to 94 %, sonication amplitude, 138 s, sonication time, and 37 °C, temperature. In addition, the nanoemulsions showed Newtonian behavior and were physically stable at 5 and 25 °C over 3 months of storage. These results elucidate the potential capability of ultrasonic technique for production of nano-scale emulsions of essential oils with reasonably long term kinetic stability which can be used in food and pharmaceutical products.
References
- Abismail B, Canselier JP, Wilhelm AM, Delmas H, Gourdon C. Emulsification by ultrasound: drop size distribution and stability. Ultrason Sonochem. 1999;6(1–2):75–83. doi: 10.1016/S1350-4177(98)00027-3. [DOI] [PubMed] [Google Scholar]
- Acosta E. Bioavailability of nanoparticles in nutrient and nutraceutical delivery. Curr Opin Colloid Interface Sci. 2009;14(1):3–15. doi: 10.1016/j.cocis.2008.01.002. [DOI] [Google Scholar]
- Anton N, Benoit JP, Saulnier P. Design and production of nanoparticles formulated from nano-emulsion templates—a review. J Control Release. 2008;128(3):185–199. doi: 10.1016/j.jconrel.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Barnes HA. A handbook of elementary rheology. Wales: The University of Wales Press; 2000. [Google Scholar]
- Bouchemal K, Briancon S, Perrier E, Fessi H. Nano-emulsion formulation using spontaneous emulsification: solvent, oil and surfactant optimization. Int J Pharm. 2004;280(1–2):241–251. doi: 10.1016/j.ijpharm.2004.05.016. [DOI] [PubMed] [Google Scholar]
- Bourne MC. Food texture and viscosity: concept and measurement. 2. California: Academic; 2002. [Google Scholar]
- Cheong JN, Tan CP, Che Man YB, Misran M. α-tocopherol nanodispersions: preparation, characterization and stability evaluation. J Food Eng. 2008;89:204–209. doi: 10.1016/j.jfoodeng.2008.04.018. [DOI] [Google Scholar]
- Delmas T, Piraux H, Couffin AC, Texier I, Vinet F, Poulin P, Cates ME, Bibette J. How to prepare and stabilize very small nanoemulsions. Langmuir. 2011;27(5):1683–1692. doi: 10.1021/la104221q. [DOI] [PubMed] [Google Scholar]
- Duke JA, Bogenschutz-Godwin MJ, Cellier J, Duke PAK. Handbook of medicinal herbs. London: CRC Press; 2002. [Google Scholar]
- Gutierrez JM, Gonzalez C, Maestro A, Sole I, Pey CM, Nolla J. Nano-emulsions: new applications and optimization of their preparation. Curr Opin Colloid Interface Sci. 2008;13:245–251. doi: 10.1016/j.cocis.2008.01.005. [DOI] [Google Scholar]
- Izquierdo P, Esquena J, Tadros TF, Dederen JC, Garcia MJ, Azemar N. Formation and stability of nano-emulsions prepared using the phase inversion temperature method. Langmuir. 2001;18(1):26–30. doi: 10.1021/la010808c. [DOI] [Google Scholar]
- Jafari SM, He Y, Bhandari B. Nano-emulsions production by sonication and microfluidization—a comparison. Int J Food Prop. 2006;9(3):475–485. doi: 10.1080/10942910600596464. [DOI] [Google Scholar]
- Jafari SM, He Y, Bhandari B. Production of sub-micron emulsions by ultrasound and microfluidization techniques. J Food Eng. 2007;82:478–488. doi: 10.1016/j.jfoodeng.2007.03.007. [DOI] [Google Scholar]
- Jafari SM, He Y, Bhandari B. Effectiveness of encapsulating biopolymers to produce sub-micron emulsions by high energy emulsification techniques. Food Res Int. 2007;40:862–873. doi: 10.1016/j.foodres.2007.02.002. [DOI] [Google Scholar]
- Kentish SE, Wooster TJ, Ashokkumar M, Balachandran S, Mawson R, Simons L. The use of ultrasonics for nanoemulsion preparation. Innov Food Sci Emerg. 2008;9:170–175. doi: 10.1016/j.ifset.2007.07.005. [DOI] [Google Scholar]
- Li PH, Chiang BH. Process optimization and stability of D-limonene-in-water nanoemulsions prepared by ultrasonic emulsification using response surface methodology. Ultrason Sonochem. 2012;19:192–197. doi: 10.1016/j.ultsonch.2011.05.017. [DOI] [PubMed] [Google Scholar]
- Madene A, Jacquot M, Scher J, Desobry S. Flavor encapsulation and controlled release—a review. Int J Food Sci Technol. 2006;41(1):1–21. doi: 10.1111/j.1365-2621.2005.00980.x. [DOI] [Google Scholar]
- Mason TJ. Sonochemistry. 1. New York: Oxford University Press Inc; 1999. [Google Scholar]
- McClements DJ. Food emulsions: principles, practices, and techniques. 2. Boca Raton: CRC Press; 2005. [Google Scholar]
- McClements DJ, Decker EA. Lipid oxidation in oil-in-water emulsions: impact of molecular environment on chemical reactions in heterogeneous food systems. J Food Sci. 2000;65(8):1270–1282. doi: 10.1111/j.1365-2621.2000.tb10596.x. [DOI] [Google Scholar]
- Peter S, Given JR. Encapsulation of flavors in emulsions for beverages. Curr Opin Colloid Interface Sci. 2009;14:43–47. doi: 10.1016/j.cocis.2008.01.007. [DOI] [Google Scholar]
- Rao J, McClements DJ. Formation of flavor oil microemulsions, nanoemulsions and emulsions: influence of composition and preparation method. J Agric Food Chem. 2011;59:5026–5035. doi: 10.1021/jf200094m. [DOI] [PubMed] [Google Scholar]
- Rao J, McClements DJ. Food-grade microemulsions, nanoemulsions and emulsions: fabrication from sucrose monopalmitate & lemon oil. Food Hydrocoll. 2011;25:1413–1423. doi: 10.1016/j.foodhyd.2011.02.004. [DOI] [Google Scholar]
- Sanguansri P, Augustin MA. Nanoscale materials development—a food industry perspective. Trends Food Sci Technol. 2006;17:547–556. doi: 10.1016/j.tifs.2006.04.010. [DOI] [Google Scholar]
- Silva HD, Cerqueira MN, Vicente AA. Nanoemulsions for food applications: development and characterization. Food Bioprocess Technol. 2012;5:854–867. doi: 10.1007/s11947-011-0683-7. [DOI] [Google Scholar]
- Solans C, Izquierdo P, Nolla J, Azemar N, Garcia-Celma MJ. Nano-emulsions. Curr Opin Colloid Interface Sci. 2005;10:102–110. doi: 10.1016/j.cocis.2005.06.004. [DOI] [Google Scholar]
- Tadros T, Izquierdo P, Esquena J, Solans C. Formation and stability of nanoemulsions. Adv Colloid Interf Sci. 2004;108–109:303–318. doi: 10.1016/j.cis.2003.10.023. [DOI] [PubMed] [Google Scholar]
- Tang SY, Manickam S, Wei TK, Nashiru B. Formulation development and optimization of a novel cremophore EL-based nanoemulsion using ultrasound cavitation. Ultrason Sonochem. 2012;19:330–345. doi: 10.1016/j.ultsonch.2011.07.001. [DOI] [PubMed] [Google Scholar]
- Teixeira MI, Andrade LR, Farina M, Rocha-Leao MHM. Characterization of short chain fatty acid microcapsules produced by spray drying. Mater Sci Eng C. 2004;24:653–658. doi: 10.1016/j.msec.2004.08.008. [DOI] [Google Scholar]
- Uson N, Garcia MJ, Solans C. Formation of water-in-oil (W/O) nano-emulsions in a water/mixed non-ionic surfactant/oil systems prepared by a low-energy emulsification method. Colloids Surf A. 2004;250(1–3):415–421. doi: 10.1016/j.colsurfa.2004.03.039. [DOI] [Google Scholar]
- Yuan Y, Gao Y, Mao L, Zhao J. Optimization of conditions for the preparation of β-carotene nanoemulsions using response surface methodology. Food Chem. 2008;107:1300–1306. doi: 10.1016/j.foodchem.2007.09.015. [DOI] [Google Scholar]