Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Apr 15;5:9590. doi: 10.1038/srep09590

High-order localized spoof surface plasmon resonances and experimental verifications

Zhen Liao 1, Yu Luo 2,3, Antonio I Fernández-Domínguez 3,4, Xiaopeng Shen 1, Stefan A Maier 3, Tie Jun Cui 1,5,a
PMCID: PMC4397533  PMID: 25873523

Abstract

We theoretically demonstrated and experimentally verified high-order radial spoof localized surface plasmon resonances supported by textured metal particles. Through an effective medium theory and exact numerical simulations, we show the emergence of these geometrically-originated electromagnetic modes at microwave frequencies. The occurrence of high-order radial spoof plasmon resonances is experimentally verified in ultrathin disks. Their spectral and near-field properties are characterized experimentally, showing an excellent agreement with theoretical predictions. Our findings shed light into the nature of spoof localized surface plasmons, and open the way to the design of broadband plasmonic devices able to operate at very different frequency regimes.

Surface plasmons (SPs), coherent electronic oscillations at the interface of materials with permittivities of opposite sign (typically metals and dielectrics), have been intensively investigated in recent years1,2. At optical and infrared frequencies, light can couple to SPs and create propagating electromagnetic (EM) waves confined at metal-dielectric interfaces, the so-called surface plasmon polaritons (SPPs)3. There is another family of plasmonic modes, termed localized surface plasmons (LSPs), which originate from the optical excitation of SPs in finite metallic nanoparticles4. At LSP resonance, EM field amplification occurs both inside and in the near-field of the nanoparticle, leading as well to a significant increase of its extinction cross section4. Taking advantage of these features, LSPs have been exploited in a broad range of technological areas, such as chemical and biological sensing5,6, Raman sensors7, and plasmonic antennas8,9. When plasmonic nanoparticles are much smaller than the wavelength of light, the quasi-static approximation is valid and only dipolar LSP modes are active. However, when for increasing particle size, multipolar resonances emerge10,11,12,13,14,15,16.

At regimes of the EM spectrum far lower than the plasma frequency (such as far infrared, terahertz, and microwave frequencies), metals behave as perfect conductors, which prevents them from supporting SP modes. To transfer the capabilities of SPPs to these frequency ranges, spoof (or designer) surface plasmons have been proposed17,18,19,20. These geometrically-originated modes mimic the dispersion characteristics and confinement properties of SPPs in perfect conducting surfaces structured at a sub-wavelength scale. The spoof plasmon concept has made possible the design and realization of SPP-components21,22,23,24,25 operating at low spectral ranges. Lately, corrugated metallic strips with nearly zero thickness have been shown to support highly-confined conformal SPP waves, which open the way to the design of compact, ultrathin, microwave and terahertz plasmonic functional devices26,27,28,29. Unlike spoof SPPs, which have been widely studied in the past decade, spoof LSPs have been theoretically proposed30 and experimentally tested only very recently31. Specifically, the occurrence of microwave multipolar spoof LSPs was demonstrated in metallic cylinders and disks decorated by periodic one-dimensional (1D) groove arrays.

The analogy between conventional SP modes at optical frequencies and low-frequency spoof plasmons is not complete. Contrary to two-dimensional (2D) corrugations (such as holes or dimples), the spoof plasmon fields inside 1D apertures (such as grooves or slits) is always propagating17,32. This establishes a fundamental difference between spoof and conventional SPs, whose tail inside the supporting metal is always evanescent. Importantly, although 1D spoof plasmon structures were firstly associated with positive effective permittivity parameters33, it has been shown recently that there are also significant discrepancies between spoof SP and dielectric resonators34. There exist, though, a common feature shared by dielectric and spoof SPP waveguides. Both support high-order modes, associated with Fabry-Perot-like cavity resonances within the plane normal to the direction of propagation. Several theoretical studies have predicted the existence of these high-order spoof SPPs32,33,35,36, which have been also recently reported experimentally37.

In this article, we introduce and verify experimentally the emergence of high-order radial spoof LSPs in periodically corrugated metal particles. These modes resemble the optical whispering gallery modes38 sustained by dielectric resonators, whose high Q-factor characteristics are currently being exploited in a wide range of technologies39,40. We provide analytical and numerical insights into the emergence of these high-order radial resonances for different azimuthal dependencies (hexa-, octo-, deca-, dodeca-, tetradeca-, and hexadeca-pole modes). Finally, we design, fabricate and characterize an ultrathin corrugated mm-sized spoof plasmon disk. Our microwave experiments demonstrate that this structure supports second-order radial octopole and decapole LSPs.

Results

Theory and analysis

First, we investigate theoretically the LSPs supported by the textured 2D perfectly conducting cylinder (with radius R) shown in Fig. 130,41. The structure consists of an inner core of radius r surrounded by periodic array of grooves of pitch d = 2πR/N (where N is the number of grooves), height h = R − r, and width a. For simplicity, we assume that the dielectric constant filling grooves is n = 1. The system is excited under TM plane wave illumination. Using Mie scattering and an effective medium approach (see the method section), an analytical expression for the scattering cross section (SCS) of the corrugated cylinder can be expressed as 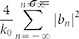Inline graphic. The spoof LSP resonances supported by the structure are given by the singularities in the Mie expansion coefficients, bn(where n labels the azimuthal characteristics of the LSP mode). The vanishing condition for the denominator of the n-coefficient can be expressed as

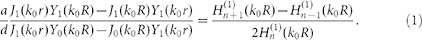graphic file with name srep09590-m1.jpg

where Jn() and Yn() are Bessel functions of the first and second kind, respectively and 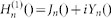Inline graphic.

Figure 1.

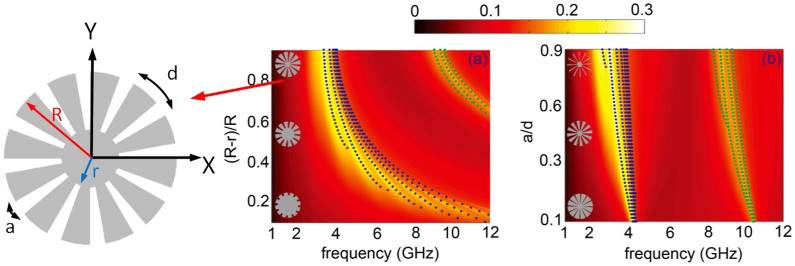
Figure 1

Open in a new tab

(a) Normalized scattering cross section of textured perfect conducting 2D cylinders as a function of the frequency and the ratio (R − r)/R. The geometrical parameters are set as R = 25 mm and a = 0.5d. (b) Normalized scattering cross section as function of the frequency and a/d. The geometrical parameters are set as R = 25 nm and r = 2 nm. The left sketch and insets show the geometric parameters of the structure. The blue and green dots are plotted using Eq. (3)

We can gain physical insight into Equation (1) by taking the limit k0R, k0r ≫ 1, in which the asymptotic form of the Bessel functions can be used. In this limit, Equation (1) can be rewritten as

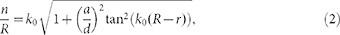graphic file with name srep09590-m2.jpg

which identifying the right hand side with the propagating wavevector, k = n/R (note that the azimuthal index n gives the number of modal wavelengths which fit within the cylinder perimeter), recovers the spoof SPP dispersion relation in a 1D array of grooves17. Despite their approximate character (the effective medium approximation is only valid in the limit a, d ≪ λ), Equation (2) establishes a clear analogy between spoof SPs in corrugated flat surfaces and spoof LSPs in textured cylinders. Note that the structures we consider here do not fulfil the conditions which led to Equation (2). However, an equivalent relation can be obtained from Equation (1) in the most realistic configuration, k0R ≫ 1, k0r ≪ 1 (small core radius), having

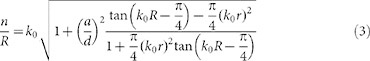graphic file with name srep09590-m3.jpg

Figure 1a depicts the scattering cross section (SCS) for a corrugated cylinder of outer radius R = 25 mm versus the incident frequency and h/R = (R − r)/R for a groove width a = 0.5d. Note that the cross sections are normalized to the structure physical cross section. The contour plot was calculated using the effective medium approach described above, and the blue dots render the resonant condition obtained from Equation (3). The spectra show a prominent scattering maximum band which redshifts with increasing groove depth. This band comprises several LSP resonances30,41, as reflected by our analytical predictions. Importantly, Fig. 1a shows another set of SCS peaks for large groove depths and high frequencies (green dots). The effective medium field maps evaluated at the various SCS maxima for r = 2 mm are rendered in Fig. 2. These results show that the modes within each scattering band share the same radial characteristics, but present different azimuthal properties. Importantly, whereas the LSPs in the first band have been investigated in the past30,41, to the best of our knowledge, the high frequency resonances, whose fields exhibit a node along the groove depth, had not been observed yet. It is the aim of this work to characterize in detail these high, second order radial modes.

Figure 2. Effective medium field distributions evaluated at different frequencies for a corrugated perfect conducting cylinder with R = 25 mm, r = 2 mm, and a = 0.5d.

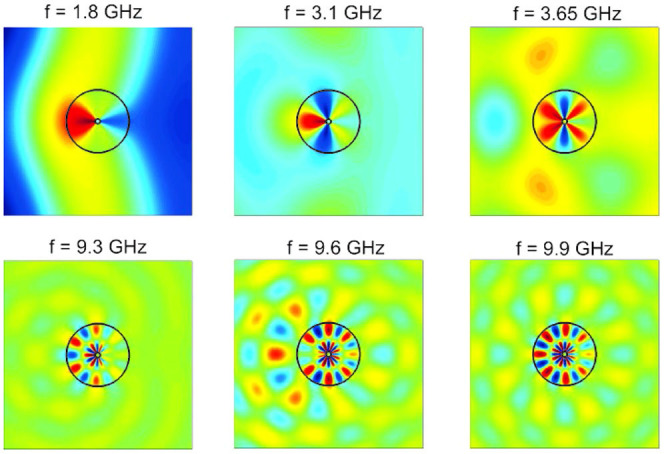
Figure 2

Open in a new tab

Figure 1a indicates that in order to design a spoof SP resonator supporting high-order radial LSPs at lower frequencies, deep grooves must be carved at the cylinder surface. Thus, we fix the outer and inner radii to R = 25 mm and r = 2 mm. Fig. 1b illustrates how, within the effective medium approximation, the ratio a/d affects slightly the scattering properties of the structure, yielding a small redshift of the LSP resonances with increasing groove width. In the following, we set a/d = 0.5 for a feasible, three-dimensional full electromagnetics numerical design and characterization of our spoof LSP resonators.

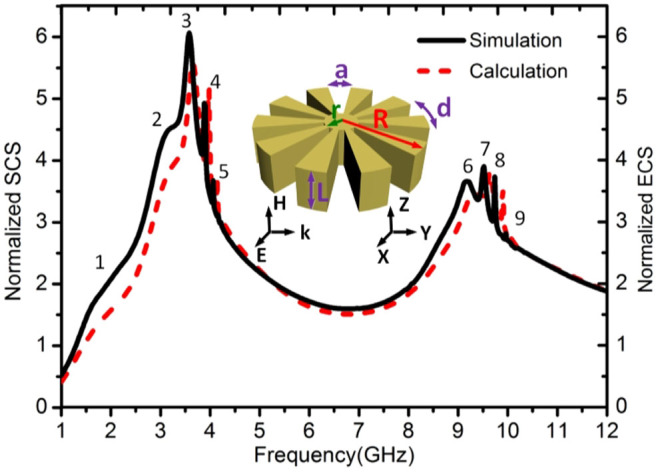
In order to retain the EM properties of the previous 2D textured cylinders, we consider thick disks with a thickness-to-radius aspect ratio L/R = 10. The extinction cross section (ECS) of a representative textured cylinder, simulated using the full-wave commercial software CST Microwave Studio, is shown in Fig. 3 (black solid line). The parameters of the structure are in which the parameters are chosen as R = 25 mm, r = 2 mm, L = 250 mm, N = 60 (d = 2.6 mm), and a = 0.5d = 1.3 mm (see inset of Fig. 3). From the simulation results, we observe that the 3D ECS contains two well-separated bands as well, both of which have multiple peaks. As discussed above, we expect the lower (higher) extinction band to encompass spoof LSP modes presenting zero (one) field nodes along the radial direction inside the grooves. The first (second) set of modes are labelled as 1 to 5 (6–9). The SCS obtained from our effective mode theory for a textured 2D cylinder with the same geometric parameters is plotted in red dashed line. Note that whereas the theoretical SCS has been normalized to the 2D cylinder diameter 2R, the numerical ECS value has been normalized to the disk side area 2RL. Remarkably, both normalized spectra are in excellent agreement (note that the absorption cross section of both structures vanishes, as we are using a perfect conducting model for the metal permittivity).

Figure 3. Simulated ECS (black solid line) and theoretically calculated SCS (red dashed line) for a corrugated metallic disk (see inset) with R = 25 mm, r = 2 mm, L = 250 mm (note that the structure is 2D in the theoretical calculations), N = 60 (d = 2.6 mm), and a = 0.5d = 1.3 mm.

Figure 3

Open in a new tab

The numbers indicate the LSP resonance ordering.

To further confirm the nature of the spoof LSP modes governing the EM response of 3D our textured metal disk, Fig. 4 shows the near electric field patterns for the 9 cross section maxima identified in Fig. 3. Specifically, the z-component of the electric field is plotted within the x-y plane 1.5 mm above the disk upper surface. In all panels, the colour scale has been saturated to show clearly the mode profile, ranging from red (positive) to blue (negative). Fig. 4 demonstrates that the corrugated disks supports two kinds of LSP modes. The first five LSPs (panels a–e) do not present radial nodes, and correspond to fundamental dipole to decapole modes. These were evaluated at the frequencies labelled as 1 to 5 in Fig. 3, and have been reported earlier in theory30 and experiments31. Importantly, the dipole (a) and quadrupole (b) LSPs are resonances are not evident in the ECS spectrum (see Fig. 3), which is consistent to what observed in Ref. 30. Equation (3) sheds light into this observation. It is straightforward to show that it cannot be satisfied for n = 1 (dipole) and n = 2 (quadrupole) for the geometric parameters of the structure. Thus, the spectral shoulders labelled as 1 and 2 in Fig. 2 emerge due to a maximum, rather than a divergence, in the corresponding Mie scattering coefficient.

Figure 4. Simulated near-field maps showing the z-component of the electric field within the x-y plane 1.5 mm above the upper surface of the corrugated metallic disk considered in Fig. 2.

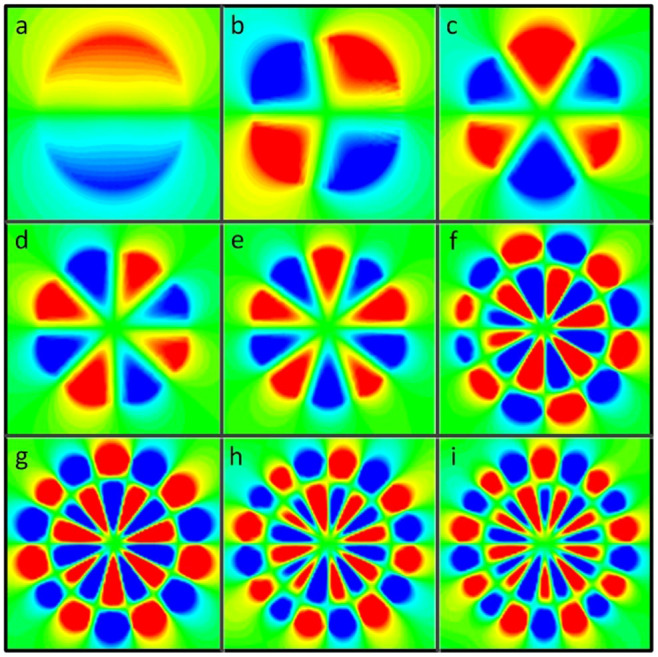
Figure 4

Open in a new tab

Panels a to e (f to i) show the fundamental (second-order) spoof LSPs labelled as 1 to 5 (6 to 9) in Fig. 3. The colour scales are saturated in each case to make the field profiles more apparent.

The last four electric field maps in Fig. 4 (panels f–i) correspond to the cross section maxima 5 to 9 in Fig. 3 and show azimuthal characteristics corresponding to dodeca to octadecapole modes. However, all these field profiles present a radial node along the grooves, and can be identified as second-order radial spoof LSPs. It is noteworthy that all these patterns are in accordance with the field distributions based on effective medium theoretical results shown in Fig. 2. Whereas the first set of resonances could be related to the LSPs sustained by metallic nanoparticles, the emergence of these high-order radial modes indicates that the analogy with optical whispering gallery modes in dielectric resonators38 is more appropriate.

Recently, it has been reported that fundamental spoof LSP resonances (whose electric field does not exhibit radial nodes) are significantly altered when the disk thickness is reduced to values much smaller than R31. In the ultrathin limit, the dipole and quadrupole resonances became clearly apparent (note that this cannot be reproduced by Equation (3), as it is valid only for large L). In Fig. 5, the dependence of second-order radial spoof LSPs on the disk thickness is analysed. This figure shows that, for the geometric parameters considered in Fig. 3, reducing the disk thickness from L = 25 mm to L = 0.018 mm the ECS maxima experience a moderate red-shift, while the most apparent resonance shifts from a second-order radial dodeca to a decapole LSP mode. This observation can be understood through the analogy that Equation (2) establishes between spoof LSPs and spoof SPPs26 (see Fig. 6). In accordance with the previous study34, we find that that localized spoof plasmon resonances can present different physical features in 2D and 3D systems. Specifically, the spectral ordering of magnetic and electric modes can change.

Figure 5. Simulated ECS spectra (between 8 and 11 GHz) showing the signature of various second-order spoof LSPs for L = 25, 12.5, 6, 3 and 0.018 mm (panels from top to bottom.

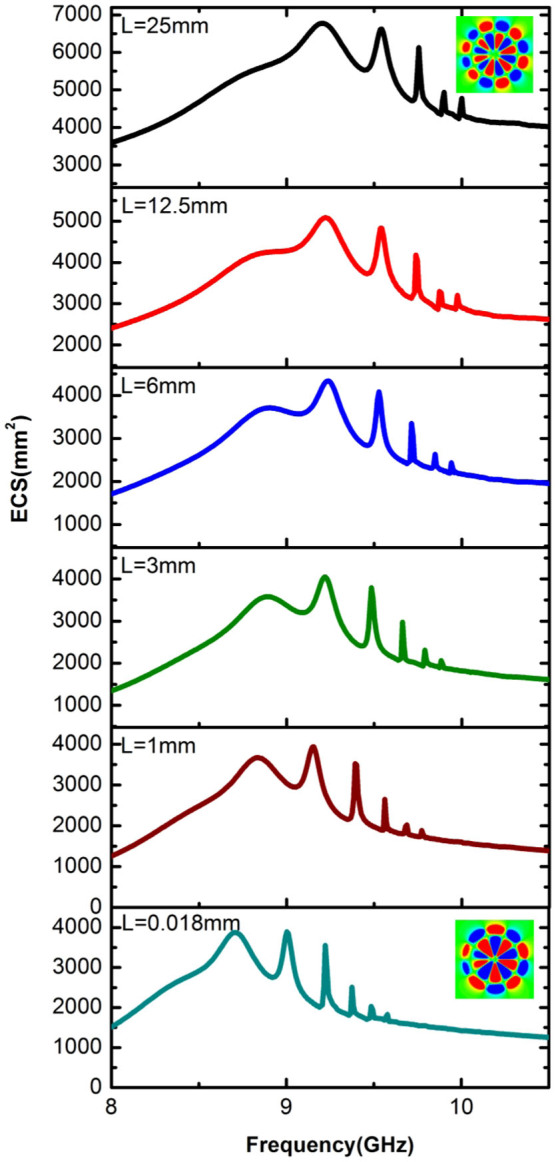
Figure 5

Open in a new tab

The insets in the top and bottom panels render the most intense resonance: dodecapole (decapole) LSP for L = 25 mm (L = 0.018 mm).

Figure 6. Spoof SPP dispersion bands for groove arrays of different thicknesses, L, and a = 0.5d, h = 23 mm,and d = 1.4 mm (parameters equivalent to the texture in Fig. 5).

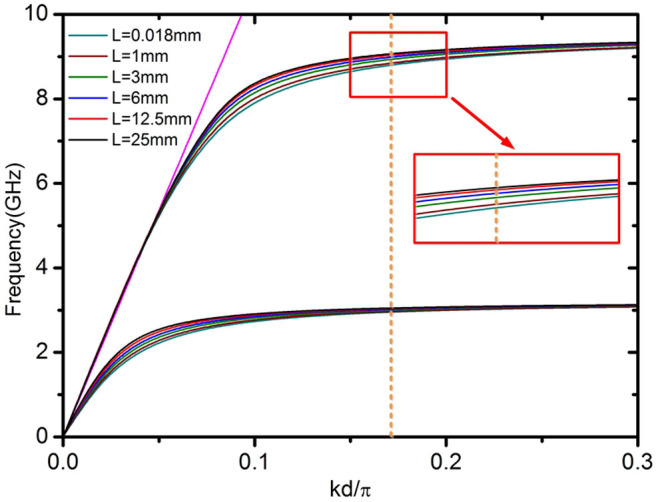
Figure 6

Open in a new tab

Two different set of modes can be observed, each of which can be associated with a different divergences for the tangent function in Eq. (2). The lower (upper) band is linked to the resonant condition k0h = π/2 (k0h = 3π/2), and correspond to the fundamental (second order) spoof SPP mode. The orange dashed line shows the resonance condition (k = n/R) for the decapole resonance in Fig. 5. The inset shows an enlargement of the second-order dispersion, which explains qualitatively the LSP red-shifting with decreasing L observed in Fig. 5.

Figure 7 shows the ECS spectrum between 7.5 and 10 GHz for an ultrathin corrugated metallic disk with nearly zero thickness (see inset), with geometric parameters R = 25 mm, r = 2 mm, L = 0.018 mm, N = 60, d = 2.61 mm, and a = 0.5d. The emergence of second-order radial spoof LSP resonances translates into various extinction maxima. In order to reveal the nature of the LSPs, we simulate the near electric fields at the frequencies labelled as 1 to 6, and shown in the right panels of Fig. 7. We clearly observe second-order radial hexa-, octo-, deca-, dodeca-, tetradeca-, and hexadecapole spoof LSP modes. Note that the lowest second-order radial modes (hexa- and octopole), labelled as 1 and 2, are not apparent in the extinction spectrum, in a similar way as it was observed for thick disks in Figs. 3 and 4. Fig. 7 shows that, as we already mentioned, the most intense spoof second-order radial LSP in thin disks is a decapole mode, whereas it was a dodecapole mode in the case of thick cylinders.

Figure 7. Normalized ECS spectrum for an ultrathin corrugated metallic disk with R = 25 mm, r = 2 mm, L = 0.018 mm, N = 60, d = 2.61 mm, and a = 0.5d.

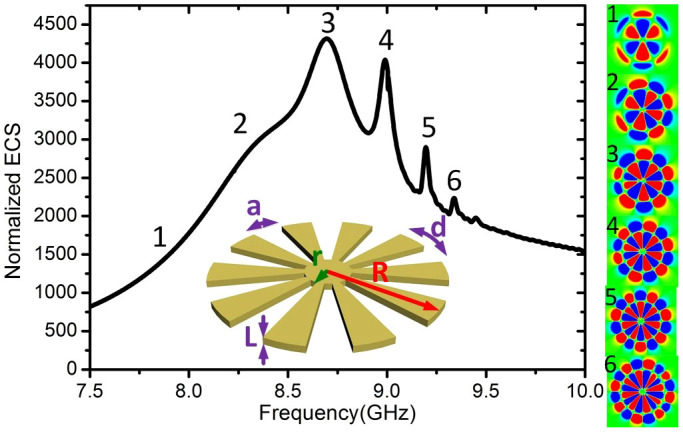
Figure 7

Open in a new tab

The right panels display the near electric-field distributions on the x-y plane which is 1.5 mm above the upper surface of the disk at the resonant frequencies, corresponding to the second-order hexa-, octo-, deca-, dodeca-, tetradeca-, and hexadecapole modes, respectively.

Experimental results

We fabricate an ultrathin (L = 0.018 mm) corrugated cooper disk for the sake of experimental verification of the second-order radial LSPs predicted by theory and numerical calculations. The structure is shown in the Fig. 8a, whose geometric parameters are chosen to be the same as in Fig. 7 (r = 2 mm, R = 25 mm, L = 0.018 mm, N = 60, a = 0.5d). The cooper disk is etched on a 0.2 mm-thick substrate with dielectric constant 3.5 and loss tangent 0.02. In order to investigate the influence of the dielectric substrate on the high-order radial spoof LSPs supported by the system, we performed CST Microwave Studio simulations in which both cooper and dielectric losses were considered to match the experimental conditions. The system is excited using a linearly polarized plane wave. The numerical ECS spectrum is plotted in black solid line in Fig. 8a. The comparison with Fig. 7 (without substrate) shows that the effect of the dielectric substrate is a slight redshifting of the spoof LSP frequencies. On the other hand, the introduction of dielectric and metal losses translates into the degradation of the spoof LSPs quality factor. Thus, the dominant, low frequency, resonance peaks (1–3 in Fig. 7) have been broaden, and the sharp, high frequency modes (4–6 in Fig. 7) have vanished. Fig. 8b render the simulated near electric-field patterns at the frequencies indicated in panel (a). As expected, the modes 1 and 2 can be clearly identified with second-order radial octopole and decapole spoof LSP resonances, respectively.

Figure 8. Simulation and experimental results of the extinction properties (a) and near electric-field characteristics (b and c) of the fabricated ultrathin corrugated disk sample (placed on the top of a thin dielectric substrate, see inset in panel (a).

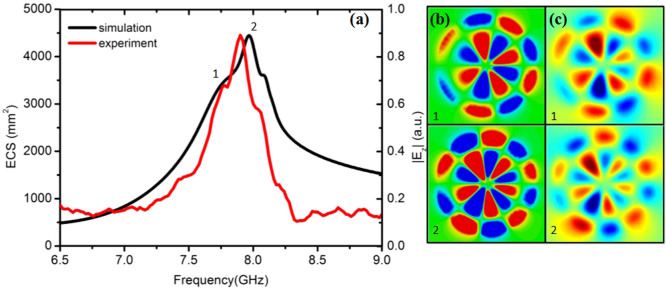
Figure 8

Open in a new tab

The parameters of the sample are:R = 25 mm, r = 2 mm, L = 0.018 mm, d = 2.6 mm (N = 60) and a = 1.3 mm The numerical (b) and experimental (c) near-field maps can be identified with second-order octopole (top) and decapole (bottom) spoof LSP resonances.

To demonstrate the predicted ECS spectrum experimentally, we measured the near field response of the fabricated LSP structure, as presented in Fig. 8a (the red line). Fig. 8a shows the excellent agreement between experiment and simulations, and the measured spectrum exhibits extinction peaks at 7.75 GHz and 7.96 GHz very close to the numerical spoof LSP resonances.

Figure 8c renders the measured near-field maps at 7.75 GHz and 7.96 GHz, which are the resonant frequencies identified from the measured spectrum. These maps are in very good agreement with the full-wave simulations in panel (b), which demonstrates experimentally the emergence of second-order radial spoof octopole and decapole LSPs in our corrugated cooper disk sample.

Conclusion

In summary, we have introduced the concept of high-order radial spoof localized surface plasmon resonances. Using an effective medium theory, we have provided analytical insight into the properties of these electromagnetic modes in corrugated perfect metal cylinders. Through numerical simulations, we have showed their emergence in thick and ultrathin disks at microwave frequencies. Finally, we have verified experimentally the occurrence of second-order radial octo- and decapole spoof plasmon resonances, showing an excellent agreement between numerical predictions and measurements for both spectral and near-field characteristics. Our findings shed light into the actual nature of spoof localized surface plasmons, and open the way to the design of plasmonic broadband devices, which exploiting high-order radial resonances, can be able to operate efficiently at very different frequency ranges (from the microwave to the terahertz regime).

Methods

Experimental setup and measurement

The near electric-field response of the spoof LSP sample is measured by means of two monopole antennas. First, a transmitter antenna placed 3 mm away from the disk plane is used to excite the spoof LSP modes. Second, a receiving antenna, able to move freely within the plane 1.5 mm above the sample, is used to probe the near-field response of the system, as illustrated in Fig. 9. Both monopole antennae are connected to an Agilent vector network analyser.

Figure 9. Photograph of the experimental set up used to measure the near-field characteristics of the spoof LSPs supported by an ultrathin corrugated cooper disk.

Figure 9

Open in a new tab

To map the near spoof LSP electric-field distributions experimentally, we make use a metamaterial-based Vivaldi antenna42 to produce quasi-plane waves in the ultrathin corrugated disk plane. A coaxial probe is used to record the z-component of the electric field (out of the disk plane) at different locations within a plane 1.5 mm above the sample surface. The experimental setup is shown in Fig. 10.

Figure 10. Photograph of the experimental platform used to measure the spoof LSP near electric-field distributions.

Figure 10

Open in a new tab

The set up consists in a metamaterial Vivaldi antenna as the source, a vector network analyser, a monopole antenna with a 0.2-mm-diameter inner conductor as the detector, and a motion controller.

Theoretical derivations based on Mie-Lorentz theory

Within the effective medium approximation, and using Mie scattering theory, the fields inside and outside the cylinders can be written as

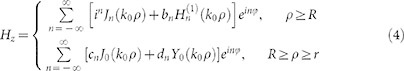graphic file with name srep09590-m4.jpg

where Jn, Yn, and 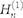Inline graphic are Bessel function, Neumann function, and Hankel function of the first kind. The unknown coefficients can be obtained through the following matching equations at the interface ρ = R:

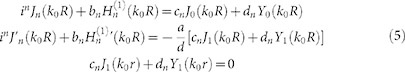graphic file with name srep09590-m5.jpg

from which, we obtain

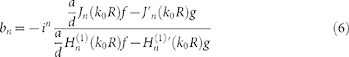graphic file with name srep09590-m6.jpg
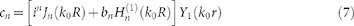graphic file with name srep09590-m7.jpg
graphic file with name srep09590-m8.jpg

where f and g are defined as:

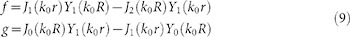graphic file with name srep09590-m9.jpg

Author Contributions

Z.L. and Y.L. contribute equally in this work. Z.L., X.S. and T.J.C. conducted the experiment, Y.L., A.I.F.D. and S.A.M. performed the theoretical calculation, Z.L., A.I.F.D. and T.J.C. wrote the manuscript, all the authors discussed the results and edited the manuscript.

Acknowledgments

Z.L. and Y.L. contribute equally in this work. This work was supported in part by the National Science Foundation of China (60990320, 60990321, 60990324, 61171024, 61171026, and 61138001), in part by the National High Tech (863) Projects (2012AA030402 and 2011AA010202), in part by the 111 Project (111-2-05), in part by the Scientific Research Foundation of Graduate School of Southeast University (Grant No. YBJJ1436), in part by the Program for Postgraduates Research Innovation in University of Jiangsu Province (Grant No. 3204004910) and in part by the Fundamental Research Funds for the Central Universities. Y.L. and S.A.M. are supported by the Leverhulme trust. Y.L. would like to acknowledge the funding support from NTU-A*STAR Silicon Technologies Centre of Excellence under the program grant No. 11235150003.

References

  1. Harvey A. F. Periodic and Guiding Structures at Microwave Frequencies. IRE Trans. Microw. Theory Tech. 8, 30–61 (1960). [Google Scholar]
  2. Barnes W. L., Dereux A. & Ebbesen T. W. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003). [DOI] [PubMed] [Google Scholar]
  3. Maier S. A. Plasmonics: Fundamentals and Applications: Fundamentals and Applications. (Springer Science & Business Media, 2007). [Google Scholar]
  4. Kreibig U. & Vollmer M. Optical properties of metal clusters. (Springer-Verlag, 1995). [Google Scholar]
  5. Khlebtsov B. N. & Khlebtsov N. G. Biosensing potential of silica/gold nanoshells: Sensitivity of plasmon resonance to the local dielectric environment. J. Quant. Spectrosc. Radiat. Transf. 106, 154–169 (2007). [Google Scholar]
  6. Fang J., Yi Y., Ding B. & Song X. A route to increase the enhancement factor of surface enhanced Raman scattering (SERS) via a high density Ag flower-like pattern. Appl. Phys. Lett. 92, 131115 (2008). [Google Scholar]
  7. Jackson J. B., Westcott S. L., Hirsch L. R., West J. L. & Halas N. J. Controlling the surface enhanced Raman effect via the nanoshell geometry. Appl. Phys. Lett. 82, 257–259 (2003). [Google Scholar]
  8. Cubukcu E., Kort E. A., Crozier K. B. & Capasso F. Plasmonic laser antenna. Appl. Phys. Lett. 89, 093120 (2006). [Google Scholar]
  9. Schnell M. et al. Controlling the near-field oscillations of loaded plasmonic nanoantennas. Nat. Photonics 3, 287–291 (2009). [Google Scholar]
  10. Hao F., Larsson E. M., Ali T. A., Sutherland D. S. & Nordlander P. Shedding light on dark plasmons in gold nanorings. Chem. Phys. Lett. 458, 262–266 (2008). [Google Scholar]
  11. Evlyukhin A., Reinhardt C. & Chichkov B. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Phys. Rev. B 84, 235429 (2011). [Google Scholar]
  12. Sonnefraud Y., Leen Koh A., McComb D. W. & Maier S. A. Nanoplasmonics: Engineering and observation of localized plasmon modes. Laser Photonics Rev. 6, 277–295 (2012). [Google Scholar]
  13. You E.-A., Zhou W., Suh J. Y., Huntington M. D. & Odom T. W. Polarization-Dependent Multipolar Plasmon Resonances in Anisotropic Multiscale Au Particles. ACS Nano 6, 1786–1794 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li K. et al. Multiple Surface Plasmon Resonances and Near-Infrared Field Enhancement of Gold Nanowells. Anal. Chem. 80, 4945–4950 (2008). [DOI] [PubMed] [Google Scholar]
  15. Shuford K. L., Ratner M. A. & Schatz G. C. Multipolar excitation in triangular nanoprisms. J. Chem. Phys. 123, 114713 (2005). [DOI] [PubMed] [Google Scholar]
  16. Oldenburg S. J., Jackson J. B., Westcott S. L. & Halas N. J. Infrared extinction properties of gold nanoshells. Appl. Phys. Lett. 75, 2897–2899 (1999). [Google Scholar]
  17. Garcia-Vidal F. J., Martín-Moreno L. & Pendry J. B. Surfaces with holes in them: new plasmonic metamaterials. J. Opt. Pure Appl. Opt. 7, S97 (2005). [Google Scholar]
  18. Pendry J. B., Martín-Moreno L. & Garcia-Vidal F. J. Mimicking Surface Plasmons with Structured Surfaces. Science 305, 847–848 (2004). [DOI] [PubMed] [Google Scholar]
  19. Hibbins A. P., Evans B. R. & Sambles J. R. Experimental Verification of Designer Surface Plasmons. Science 308, 670–672 (2005). [DOI] [PubMed] [Google Scholar]
  20. Williams C. R. et al. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat. Photonics 2, 175–179 (2008). [Google Scholar]
  21. Navarro-Cía M. et al. Broadband spoof plasmons and subwavelength electromagnetic energy confinement on ultrathin metafilms. Opt. Express 17, 18184–18195 (2009). [DOI] [PubMed] [Google Scholar]
  22. Martin-Cano D. et al. Domino plasmons for subwavelengthterahertz circuitry. Opt. Express 18, 754–764 (2010). [DOI] [PubMed] [Google Scholar]
  23. Ma Y. G., Lan L., Zhong S. M. & Ong C. K. Experimental demonstration of subwavelength domino plasmon devices for compact high-frequency circuit. Opt. Express 19, 21189–21198 (2011). [DOI] [PubMed] [Google Scholar]
  24. Yu N. et al. Designer spoof surface plasmon structures collimate terahertz laser beams. Nat. Mater. 9, 730–735 (2010). [DOI] [PubMed] [Google Scholar]
  25. Ng B. et al. Spoof Plasmon Surfaces: A Novel Platform for THz Sensing. Adv. Opt. Mater. 1, 543–548 (2013). [Google Scholar]
  26. Shen X., Cui T. J., Martin-Cano D. & Garcia-Vidal F. J. Conformal surface plasmons propagating on ultrathin and flexible films. Proc. Natl. Acad. Sci. 110, 40–45 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Gao X. et al. Ultrathin dual-band surface plasmonic polariton waveguide and frequency splitter in microwave frequencies. Appl. Phys. Lett. 102, 151912 (2013). [Google Scholar]
  28. Shen X. & Cui T. J. Planar plasmonic metamaterial on a thin film with nearly zero thickness. Appl. Phys. Lett. 102, 211909 (2013). [Google Scholar]
  29. Ma H. F., Shen X., Cheng Q., Jiang W. X. & Cui T. J. Broadband and high-efficiency conversion from guided waves to spoof surface plasmon polaritons. Laser Photonics Rev. 8, 146–151 (2014). [Google Scholar]
  30. Pors A., Moreno E., Martin-Moreno L., Pendry J. & Garcia-Vidal F. Localized Spoof Plasmons Arise while Texturing Closed Surfaces. Phys. Rev. Lett. 108, 223905 (2012). [DOI] [PubMed] [Google Scholar]
  31. Shen X. & Cui T. J. Ultrathin plasmonic metamaterial for spoof localized surface plasmons. Laser Photonics Rev. 8, 137–145 (2014). [Google Scholar]
  32. Maradudin A. A. Structured Surfaces as Optical Metamaterials. (Cambridge University Press New York, NY, 2011). [Google Scholar]
  33. Shen J., Catrysse P. & Fan S. Mechanism for Designing Metallic Metamaterials with a High Index of Refraction. Phys. Rev. Lett. 94, 197401 (2005). [DOI] [PubMed] [Google Scholar]
  34. Huidobro P. A. et al. Magnetic Localized Surface Plasmons. Phys. Rev. X 4, 021003 (2014). [Google Scholar]
  35. Fernandez-Dominguez A. I., Martin-Moreno L., Garcia-Vidal F. J., Andrews S. R. & Maier S. A. Spoof Surface Plasmon Polariton Modes Propagating Along Periodically Corrugated Wires. IEEE J. Sel. Top. Quantum Electron. 14, 1515–1521 (2008). [Google Scholar]
  36. Jiang T., Shen L., Zhang X. & Ran L.-X. High-order modes of spoof surface plasmon polaritons on periodically corrugated metal surfaces. Prog. Electromagn. Res. M 8, 91–102 (2009). [Google Scholar]
  37. Liu X., Feng Y., Zhu B., Zhao J. & Jiang T. High-order modes of spoof surface plasmonic wave transmission on thin metal film structure. Opt. Express 21, 31155–31165 (2013). [DOI] [PubMed] [Google Scholar]
  38. Oraevsky A. N. Whispering-gallery waves. Quantum Electron. 32, 377–400 (2002). [Google Scholar]
  39. Kippenberg T. J. & Vahala K. J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 321, 1172–1176 (2008). [DOI] [PubMed] [Google Scholar]
  40. Del'Haye P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214–1217 (2007). [DOI] [PubMed] [Google Scholar]
  41. Noh H., Chong Y., Stone A. & Cao H. Perfect coupling of light to surface plasmons by coherent absorption. Phys. Rev. Lett. 108, 186805 (2012). [DOI] [PubMed] [Google Scholar]
  42. Zhou B., Li H., Zou X. & Cui T.-J. Broadband and high-gain planar Vivaldi antennas based on inhomogeneous anisotropic zero-index metamaterials. Prog. Electromagn. Res. 120, 235–247 (2011). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES