Abstract
Movement science is driven by observation, but observation alone cannot elucidate principles of human and animal movement. Biomechanical modeling and computer simulation complement observations and inform experimental design. Biological models are complex and specialized software is required for building, validating, and studying them. Furthermore, common access is needed so that investigators can contribute models to a broader community and leverage past work. We are developing OpenSim, a freely available musculoskeletal modeling and simulation application and libraries specialized for these purposes, by providing: musculoskeletal modeling elements, such as biomechanical joints, muscle actuators, ligament forces, compliant contact, and controllers; and tools for fitting generic models to subject-specific data, performing inverse kinematics and forward dynamic simulations. OpenSim performs an array of physics-based analyses to delve into the behavior of musculoskeletal models by employing Simbody, an efficient and accurate multibody system dynamics code. Models are publicly available and are often reused for multiple investigations because they provide a rich set of behaviors that enables different lines of inquiry. This report will discuss one model developed to study walking and applied to gain deeper insights into muscle function in pathological gait and during running. We then illustrate how simulations can test fundamental hypotheses and focus the aims of in vivo experiments, with a postural stability platform and human model that provide a research environment for performing human posture experiments in silico. We encourage wide adoption of OpenSim for community exchange of biomechanical models and methods and welcome new contributors.
Keywords: neuromusculoskeletal biomechanics, biological joints, musculotendinous actuators, neuromuscular control, gait simulation, Simbios biocomputation, SimTK Simbody
1. Introduction
Musculoskeletal modeling and simulation has tremendous potential to improve patient care and reduce treatment costs by elucidating cause and effect relationships in individuals with neurological and musculoskeletal impairments and by predicting effective surgical and rehabilitation treatments. Experiments alone cannot identify the sources of abnormal movement and design of treatments remains limited because important variables, such as muscle forces, are generally not measurable. Muscle-actuated dynamic simulations are becoming a viable approach for determining how the elements of the musculoskeletal system interact to produce movement. To apply this emerging technology, to identify which elements impact an individual’s movement disorder (e.g., bone deformities, abnormal muscle excitations, or muscle weakness) and to evaluate potential treatments, we need three-dimensional, muscle-actuated simulations that accurately reproduce the gait and other movement dynamics of individual patients. Furthermore, simulation technology must be scalable and reusable for a variety of models and movements, and these models and data should be transferable and their results reproducible.
As the NIH national center for physics-based simulation of biological structures (Simbios) our mandate is to develop and disseminate a simulation tool-kit (SimTK) to lower barriers to the adoption of simulation as a tool for advancing biomedical research. In particular, we introduced OpenSim [1] as a community resource to enable individual investigators to model and simulate neuromusculoskeletal dynamics for the purpose of understanding gait in unimpaired and patient populations.
In this paper we begin with a brief overview of OpenSim. In section 2, we describe our approach to modeling key musculoskeletal elements and performing analyses that distinguish biomechanical simulation from industrial and mechanical engineering problems for which there exist ample tools. In section 3 we report how OpenSim’s architecture addresses the implementation of musculoskeletal models in a reusable and extensible simulation framework to construct system equations and manage model states during computation. In the subsequent sections we describe three studies that apply OpenSim. Section 4 demonstrates the use of a complex musculoskeletal model to gain insight into normal and pathological gait. Section 5 describes using the OpenSim framework to perform posture and balance experiments in simulation. We conclude with a discussion of the current limitations and challenges facing musculoskeletal modeling and the exciting opportunities for innovation and community collaboration to impact the standard of care and improve human motor performance. To meet these challenges we require greater engagement with the broader scientific community in terms of adoption, feedback and contributions so that all can gain from a common infrastructure for modeling and simulating human and animal movement.
1.1. OpenSim overview
“OpenSim” encompasses a software framework for the human movement scientist, biomechanist, roboticist, neuroscientist, orthopaedic surgeon, or any human or animal movement enthusiast wanting to build musculoskeletal models, simulate movement, and analyze resulting behaviors. This framework includes 1) an end-user application with a graphical user interface (GUI), 2) a set of command-line utilities, 3) a software development kit (SDK) including application programming interfaces (APIs) and corresponding libraries, 4) a standardized set of file formats for defining and sharing neuromusculoskeletal models and related data, and 5) a growing set of reusable musculoskeletal models in these formats, developed and published by various researchers [2, 1, 3, 4]. Although most users are served by the OpenSim GUI for access to existing tools, command line executables facilitate batch processing and data management via third-party programs and shell scripts.
Extending the capabilities of OpenSim programmatically requires a modest level of C++ programming skill and knowledge of the OpenSim API. Extensions take two forms: 1) “plugins” that extend the existing set of tools and can be used, for example, from within the OpenSim GUI, and 2) new programs that make use of the OpenSim API, such as special-purpose GUIs or additional command-line utilities. OpenSim plugins make user extensions easy when new functionality falls into one of two categories: a new model element, or a method to extract states or measurements from a model or simulation. An example of a user extension might be a command-line program that determines subject-specific musculoskeletal model parameters from experimental data using a novel algorithm. OpenSim’s own command-line tools are implemented the same way; they use the OpenSim API to load a specified model, execute a sequence of solvers, and report results.
The OpenSim libraries are written in C++ and accessed through an object-oriented API. A modular design helps to keep the casual plugin programmer focused on the creation of a single class or method without having to master the inner workings behind the OpenSim API. This design is discussed in section 3 below. OpenSim’s API and libraries are in turn built on Simbody, also part of SimTK, which provides an extensive API for assembling and managing the underlying multibody system and performing multibody dynamics computations and other numerical operations. Simbody is described in a companion paper in these proceedings [5]. OpenSim API programmers have full access to the Simbody API as well.
1.2. OpenSim’s capabilities
OpenSim enables the construction of musculoskeletal models, the visualization of their motion, and a set of tools for extracting meaningful information. These tools include inverse kinematics, to resolve internal coordinates from available spatial marker positions corresponding to known landmarks on rigid segments; inverse dynamics to determine the set of generalized forces necessary to match estimated accelerations; static optimization [6, 7] to decompose net generalized forces amongst redundant actuators (muscles); and forward dynamics to generate trajectories of states by integrating system dynamical equations in response to input controls and external forces. Specialized tools are provided for generating patient-specific simulations. These include scaling of an existing model to match patient-specific measurements [8], and determination of dynamic muscle activations that cause the model to track experimental data [9].
OpenSim models consist of several elements (components) that have computational counterparts in the underlying Simbody multibody system. These include: bones (rigid bodies), joints (mobilizers, constraints and forces), contact elements (rigid constraints and compliant forces), as well as ligaments and muscle actuators (forces). The representation of neural commands originating in the central nervous system that control muscle activity and thus muscle force generation is central to neuromusculoskeletal simulation. Therefore, OpenSim also provides a controller element that can consist of user-defined functions, canonical feedback control, optimal control, as well as simplified surrogate models for the estimation of feed forward control.
2. Modeling the kinematics, dynamics and control of the human musculoskeletal system
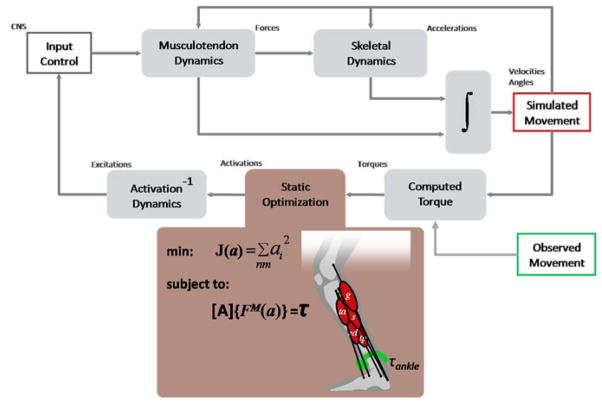
Movement in animals and humans is a result of a cascade of neurological and muscle physiological processes that lead to forces on bones that generate reaction forces and accelerate joints. Multibody dynamics plays a key role by providing a physical basis for transforming physiological forces to movement according to Newton’s laws of motion. The dominant forces driving the skeletal system are musclulotendinous forces. Muscle forces arise from protein interactions that cause muscle-fibers to contract in response to the electrical state of the muscle-fiber. The electrical state of a muscle (its activation) is modulated by neural inputs from the central nervous system (CNS) also known as muscle excitations [10]. As movement scientists we are interested in understanding the control of musculoskeletal dynamics to produce coordinated movement. Thus the controller in the canonical model (Fig. 1) provides a conceptual framework for testing models of the CNS with regards to movement generation.
Fig. 1.
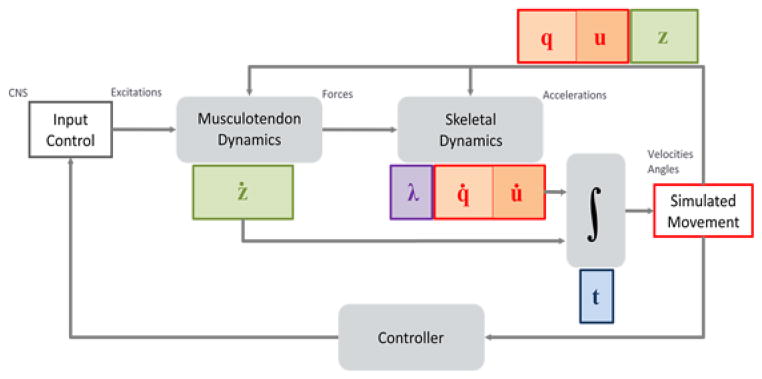
A canonical block-diagram of the dynamical musculoskeletal system. Inputs are muscle excitation or more generally actuator controls, and the outputs are trajectories for generalized coordinates, q, and speeds, u, as well as muscle states, z, as a function of time, t. The primary sources of system dynamics are musculotendinous actuators and the skeletal multibody dynamics. Controllers may also introduce dynamics to simulate signal transmission delay and other physiological behaviours.
2.1. Biological joints
Biological joints are unlike human engineered joints and are underserved by the set of revolute, slider, universal, planar, and ball-and-socket joints available in mechanical simulators. Since every biological joint is unique the modeler using computer-aided design tools for industrial machines is faced with making unnecessary assumptions and simplifications or sacrificing performance.
Take for example the shoulder’s scapulothoracic joint. It has been described by an ellipsoid thoracic surface upon which the scapula (shoulder blade) rotates and translates [11]. It can be modeled by 6 generalized coordinates and 3 constraint equations, for 3 degrees-of-freedom (dof), or 9 generalized coordinates and 5 constraints for a 4 dof shoulder complex [12]. The internal coordinate joint representation in Simbody, termed a mobilizer, can specify any continuous permissible-motion manifold parameterized by 1 through 6 generalized coordinates [13]. We can exploit the generality of a mobilizer to define joints that better serve the needs of biomechanical modelers, such as an EllipsoidJoint.
An EllipsoidJoint parameterizes the relative motion of a mobile body with respect to a parent body such that the joint frame on the mobile body traces the surface of an ellipsoid affixed to the parent. The surface motion is parameterized by 2 rotational coordinates (analogous to latitude and longitude on a globe) and a 3rd rotation is about the Z-axis of the mobile body, which is defined to remain normal to the ellipsoid surface (Fig. 2a). The EllipsoidJoint adds 3 ordinary differential equations opposed to the conventional 9 differential algebraic equations. We have demonstrated that an EllipsoidJoint performs comparably to a ball-and-socket mobilizer and is 10× faster to solve than the equivalently constrained system generating identical motion [13].
Fig. 2.
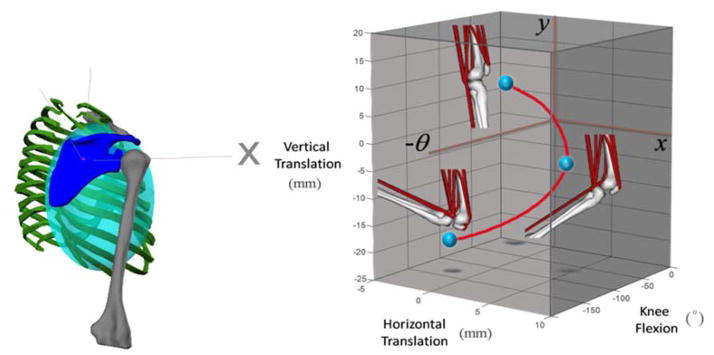
(a) A 3-dof internal coordinate model of the scapulo-thoracic joint modelled with an ellipsoid mobilizer. The scapula (blue) is the child body who’s joint origin translates on the surface of an ellipsoid (shaded) fixed in the thorax body (green) and is able to spin about its z-axis, which remains normal to the ellipsoid surface. (b) The permissible-motion manifold (red curve) of a user-specified custom joint used to model the knee includes the planar (x, y) displacements of the tibia with respect to the femur as a function of the knee-flexion angle, θ (extension is positive) with the position of the knee presented at 0, 60 and 120° of knee flexion.
Custom joints in OpenSim enable experimental data describing the coupled translations of a planar knee (Fig. 2b) [2] to be modeled as a 1-dof joint with no constraints. With increasing data to describe the coupled-motion in healthy lower extremity joints these data can be embedded as differentiable splines in the definition of a custom joint to provide stereotypical kinematics for human joints. Custom paths obtained from imaging technology can be used to define patient-specific joints [14]. The formulation of mobilizers to enable user-defined manifolds and their property of being reversible (to describe parent motion in the child body) is described in detail by [13].
In OpenSim joints (as underlying mobilizers) provide dofs whereas constraints are responsible for removing them. As a result, constraints primarily serve two purposes. First, constraints are necessary for loop closure in the multibody tree. Each body (excluding ground) has a single “inboard” mobilizer that enables its dofs with respect to a parent, forming a tree-structured connectivity graph. Any additional connection that forms a loop in the connectivity graph must be made via a constraint. Constraints such as a weld, point-to-point, distance, point-on-line, point-on-plane, and fixed-orientation are available.
The second case is to couple motion between joints. For example, the spine is comprised of 24 articulating vertebrae, with each vertebral joint contributing to the flexion/extension of the spine. In this case a constraint can be applied to distribute the total flexion of the spine to fractional rotations (flexion) across all the individual vertebrae [4].
2.2. Interaction with the environment (Contact and constraints)
Several approaches for modeling external forces are possible with OpenSim. In one case, measured forces and center-of-pressure data can be applied to specified bodies, with the force and point of application vectors prescribed as functions of time.
In the absence of experimental data, or to try to predict new motions, contact with the environment (e.g. ground) must be modeled. OpenSim implements two contact force formulations using Simbody that are described in detail in a companion paper [5]. The first is the HuntCrossleyForce [15], which is based on Hertz contact theory [16]. This method analytically computes deformations from linear elasticity theory, and is currently limited to planes, spheres, and ellipsoid geometries. The second is the elastic-foundation model [17], which uses a mesh to represent arbitrary surfaces in contact, but calculates deformations and forces using a simplified bed-of-springs elastic model.
The third option is to model interaction with the environment via constraints. OpenSim provides a rolling on surface constraint consisting of four constraint equations: no surface penetration; two no slip constraints of the contact point on the surface, and a no twist constraint about the surface normal at the experimentally measured point of contact [18].
2.3. Passive structures and physiological actuators
Forces in OpenSim include springs, dampers, bushings, and ligaments, all of which compute force as a function of positions and velocities from the state. Actuators are forces and can be dependent on the state, but unlike passive forces, an actuator must be dependent on a control value, like the current to a motor.
OpenSim supplies multiple muscle models based on formulations of muscle dynamics described by Zajac [10], which we summarize here. Muscles are, in fact, musculotendinous actuators with a contractile muscle-fiber and compliant tendon in series. The muscle contractile dynamics observed by Hill [19], relating muscle force to activation, muscle-fiber length and contractile velocity are generalized to a model of whole muscle contraction dynamics (Fig. 4).
Fig. 4.
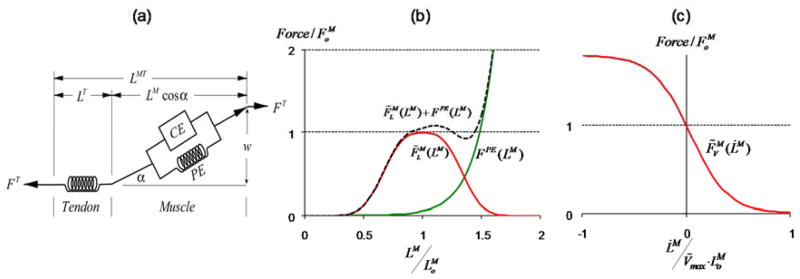
(a) Schematic of the elements of a musculotendinous actuator as a single muscle in series with an elastic tendon. F, is the scalar force or tension, and L is length with superscripts referring to muscle, M, tendon, T, or the complete musculotendinous actuator, MT. The pennation angle, α, represents the mean orientation of muscle fibers in a muscle with respect to the line of action, and changes as function of LM in order to maintain a constant muscle width, w. Phenomenological curves describe the force generating capacity of the muscle’s contractile element (CE, in red) and passive elastic element (PE, green) as a function of normalized muscle-fiber length (b) and shortening velocity (c). Fiber length is normalized by the optimal-fiber length, which is the length at which the muscle can generate its maximum active force isometrically (zero velocity) and its velocity is normalized by optimal fiber length and a maximum shortening rate, Vmax.
We formulate the musculotendinous dynamic equations by first assuming that muscle, FM, and tendon, FT, forces are in equilibrium at all times (1), and that muscle activation, a, and muscle-fiber length, LM, are the two state variables of the actuator.
| (1) |
| (2) |
| (3) |
| (4) |
where kT and LST are the tendon stiffness and slack length properties, and fl and fv are the physiological force-length and force-velocity relationships of the contractile element (red curves, Fig. 4b,c) and fPE is the passive-element force-length curve (green curve, Fig. 4b) for inputs that are not normalized.
Activation describes the overall electrical state of a muscle resulting from muscle-fiber depolarizations and the release of calcium ions. The electrical activity of a muscle-fiber relates to tension production in the muscle and is described by (3). Activation dynamics capture the charge and discharge rates of the muscle-fiber membrane and internal structures that sequester and release calcium ions that lead to electromechanical delay. The onset and offset rates of activation can therefore be expressed as a differential equation of the muscle excitation, x, [20]:
| (5) |
Muscle excitations, x, represent the neural signals from the CNS and can be viewed as the “controls” to the musculoskeletal system. Muscle excitations are continuous variables bounded, 0 < x ≤ 1, and account for the minimum and maximum firing rates of motor neurons. Subsequently, activation also ranges from zero to one corresponding to polarized muscle-fiber membrane (inactive state) to fully depolarized (electrically activated) fiber.
Muscles apply forces to bones as a tension along a muscle’s path. A tensile path (e.g. a rope) can pass through specified via points attached to bones and wrap over a variety of geometrical objects, such as cylinders, ellipsoids and through toroids [2]. Tensile forces are applied at each point directed along the line-segment connecting to an adjacent point on the path. Consequently all intermediate (via) points have two forces applied (two adjacent points) while the path’s origin (first) and insertion (and last) points having one applied force. In the case of wrapping (Fig. 5) intermediate points are populated onto a geodesic, with the number of points added proportional to the geodesic length, and forces are applied to these points in the same manner.
Fig. 5.
Gastrocnemii (calf) muscle paths wrapping over a wrap-cylinder affixed to the tibia [3].
Ligaments and muscles share the same path description to apply their computed forces to bones. Unlike a muscle, the tension generated by ligament is dependent only on path length and velocity.
2.4. Neuromuscular control
Given a musculoskeletal model with joints and muscles, how are realistic movements synthesized? No amount of anatomical detail in a model will produce human like behavior (besides collapsing like a rag-doll or standing with stiff joints) without a controller. The model is a complex plant that must be controlled to cause muscles to contract and pull on bones in a coordinated way to produce the desired motion.
In some cases it is plausible to manually prescribe excitation patterns to a limited number of muscles in order to perform simple tasks like an arm-curl or to simulate the non-weight bearing leg during the swing phase of gait. In general, however, the transformation from muscle excitation to bone movement is too complex to be adjusted by hand. Optimization provides a conceptual framework for solving for the inputs (controls) to produce the desired movement (Fig. 1). Discretizing continuous control signals in time and solving a nonlinear parameter optimization problem [21] for the control nodal values for every instant is an extremely high-dimensional problem. Some success has been achieved to simulate maximum height jumping [22, 23, 24], however simulating three-dimensional gait using this approach has yet to deliver robust and repeatable controls for multiple gait cycles. Even half a gait cycle has shown to be practically intractable requiring over 10,000 CPU hours on a 32-CPU super-computer [25].
Tracking controllers have recently become successful at reproducing model kinematics that are close to experimentally collected kinematics and with modeled muscle activity in good agreement with experimental muscle electromyogram (EMG) data [26, 27]. The computed muscle control algorithm [9] is implemented in OpenSim as a specialized Controller and described in Fig. 6. Unlike, a parameter-optimization problem, however, the muscle controls are computed during a single forward integration of the system, where optimization is performed at every instant to estimate muscle forces that produce the required moment (from method of computed torque) that take into account force-length and force-velocity relationships. Computed muscle control on a model with 23 dofs and 92 muscles requires computation times of 5–15 minutes on typical desktop computers to track a complete gait cycle, which is in stark contrast to the parameter optimization solution. Actual times can vary by several minutes due to the desired integration accuracy and the agreement of the model with experimental kinematics.
Fig. 6.
Schematic of the computed muscle control algorithm implemented as a controller. The Controller from Fig. 1 has been expanded into three stages. First, a method of computed torques determines the generalized forces (joint torques) necessary to track observed kinematics with experimental ground reaction forces applied to the model’s feet. The static optimization stage distributes the joint torques to muscle forces based on minimizing the sum of activations squared, subject to muscles forces generating equivalent generalized forces, with A being the moment-arm matrix. Third, the necessary excitation to produce the computed activations is determined by root-solving the inverse of the activation dynamics.
2.5. Analyses for extracting insights from models and simulations
OpenSim provides a variety of analyzing and reporting tools that describe the kinematics (internal or spatial) and dynamics (body forces, generalized forces, and muscle and ligament tensions) of the model. These tools are vital for comparing model results with all experimental measurements to gain confidence in the model and simulation results. However, reporting every force or the positions of every marker can obscure insights into the actions and effects of muscles on movement and on other tissues, like bones and cartilage. Synthesis of simulation results into more salient information for treatment and understanding is the purpose of analyses in OpenSim. Two examples are joint reactions and induced acceleration analyses.
Joint and constraint reactions forces are necessary to quantify bone on bone forces. OpenSim leverages Simbody to yield joint reaction forces, which represent the non-working forces that enforce the relative motion allowed by a mobilizer (e.g. the bearing loads of a revolute mobilizer). These forces can be resolved to a net reaction force acting on either parent or child joint frames and expressed in parent, child, or ground reference frames. Joint reactions are a first order approximation of the loading conditions (e.g. contact pressures) within a joint and can be used to assess implant and joint replacement loads [28] as well as loading conditions in patients with varying severity of oseteoarthritis [29].
Muscle forces themselves do not directly provide insight into their actions during movement. In particular in locomotion, where the task is to support and move the center-of-mass, knowledge about individual muscle contributions to joint or center-of-mass accelerations can be very informative for targeting treatment. A force’s contribution to the total system acceleration has been coined as its “induced acceleration” [30]. For a given configuration (position and velocity) of the system, the equations of motion are linear in forces and accelerations. Thus, a simple test for validity is to sum the individual contributions, and they must total the actual system accelerations when all forces are applied, since the linear system must satisfy the property of superposition. One complication to this analysis arises when the acceleration of the center-of-mass during a simulation is due external forces (e.g. from force-plate measurements or modeled with compliant contact). In the simulation, all the internal forces (including muscle forces) must balance the measured ground reaction force in such a way as to produce the desired model kinematics. Thus, when a single actuator force is applied to determine its contribution to the system acceleration, the problem is ill-posed since the corresponding ground reaction force is unknown. It is impossible to record the reaction load on a force-plate due to a single muscle’s force, which would be necessary to evaluate the induced accelerations of that muscle. Instead, we apply a suitable constraint (that reacts instantaneously) that can generate reaction loads that accelerate the center-of-mass due to the application of a single force (muscle, gravity, etc.) in the model. The test for validity is that the induced reaction loads of the constraint should total the measured ground reaction force and moment.
In this section we highlighted some of the capabilities of OpenSim for modeling, controlling and analyzing musculoskeletal systems. In the following section we will discuss how OpenSim implements a framework to: represent complex musculoskeletal models, formulate and solve model dynamics that ensures simulation correctness, provide high-level analysis and graphical tools, and enable extensibility.
3. OpenSim architecture
3.1. Objectives
The primary objective of the OpenSim software is to enable the individual investigator to develop subject-specific musculoskeletal simulations and establish the desired mix between model complexity, accuracy, and performance that are appropriate for his/her study of human, animal, or robot movement. To facilitate this goal, we must ensure that the individual components of a computational model can be combined to represent a wide variety of physical attributes and behaviors including pathology. Furthermore, we aim to reduce the likelihood of generating incorrect simulations by maintaining rigorous separation between the model and its set of state values by exploiting Simbody’s System-State-Study architecture [5]. That is not to say that all OpenSim models accurately represent human or animal behavior, but rather whatever model has been constructed will behave in accordance with Newton’s laws of motion and the physiological dynamics as specified by the modeler.
3.2. Organization
The OpenSim framework is organized into computational and functional layers (Fig. 7). OpenSim relies on the computational infrastructure provided by Simbody, particularly for creating and solving the multibody dynamics System, which is a domain-agnostic computational layer. Refer to the companion article in these Procedia [5] for details regarding the Simbody architecture and its formulation of the multibody system. The OpenSim code base provides two additional layers, specialized for neuromuscular biomechanics, which are the modeling and analysis layers.
Fig. 7.
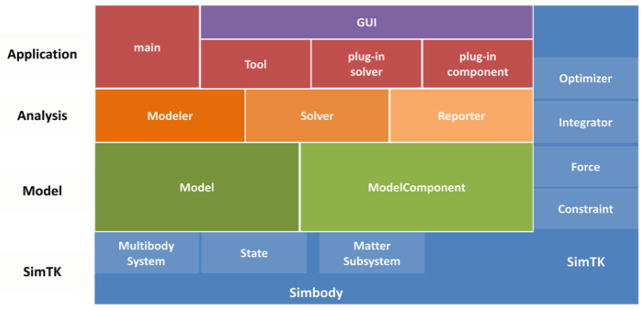
OpenSim Layers. The base layer is the computational layer provided by Simbody (in blue). Simbody components, numerical methods (e.g. integrators, optimizers) and other computational resources are available to all levels within the OpenSim API, and to users of the OpenSim API (right-hand side). The next layer up is the modelling layer (green), this defines the model and all its components. A model component is any part of the model that contributes to the system equations, which include degrees of freedom, constraints, forces, and user defined components (e.g. sensors) with their own dynamics and state variables. The modeling layer is followed by the analysis layer (orange), which is an abstraction for any algorithm that creates or modifies models (a modeler), solves the model system of equations for particular values (solver, e.g. an inverse dynamics solver) and/or collects and writes values from a model (with or without the help of a solver) to file or display (a reporter). The top layer is the application layer (red) which does not provide an API but is a consumer of the OpenSim API to generate applications like the OpenSim GUI or dynamic libraries (plugins) encapsulating model components and/or analyses that are loaded and executed by the GUI at run-time.
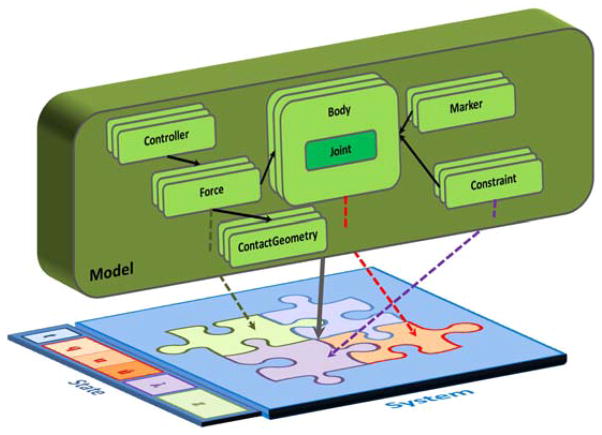
The OpenSim modeling layer comprises two main classes, Model and ModelComponent, which are responsible for representing the physical parts of a model (each in a ModelComponent) and assembling them to form a coherent and consistent whole (the Model). Model components include bodies, joints, constraints, forces, actuators and controllers, each of which can have several subtypes. From the Model a corresponding computational representation can be generated as a Simbody System object, with a corresponding State object for managing the model’s variables and parameters. Once a computational System is constructed, it is ready for use by the analysis layer.
The analysis layer comprises a set of analyses, which fall into three categories: modeler, solver, and reporter. A modeler generates or modifies models according to some criteria. For example, it might scale a generic model to fit a particular patient’s data. A solver solves a set of equations presented by a model, which include solving the model’s equations of motion to generate a trajectory of model kinematics, or solving the inverse dynamics equations to determine joint moments. A reporter simply records or displays values of interest, perhaps with some filtering or other processing.
Above the layers provided by the OpenSim API is the application layer, containing a growing variety of applications. The primary application is the OpenSim GUI, providing a visual interface to the OpenSim tools, including animation of motion, plotting, and detailed model exploration capabilities. This layer also includes command-line OpenSim utilities, as well as user-defined “main()” C++ programs that exercise the OpenSim API directly.
New Tools and plugins can be written to add functionality to the OpenSim GUI. A Tool is a kind of OpenSim “applet” that bundles a model, one or more solvers, and one or more reporters to display or store results. The InverseKinematicsTool and InverseDynamicsTool are primary examples. A Tool is generally not user-defined, but acts as the delivery vehicle for OpenSim developers to expose new algorithms to end-users. To augment the behavior of existing models and/or Tools, users can write plugins, which are dynamically-linked libraries (DLLs) that are loaded at run-time by an existing OpenSim application.
Plugins contain new classes, for model components, solvers, modelers, reporters or even tools. The most common use of a plugin is to extend a particular component, like a muscle, by augmenting its dynamics (perhaps including new states) in a derived subclass. Changing identifiers in the model file to use the augmented class name, then allows the augmented class to be used instead by the GUI and existing Tools. For example, a muscle class can be augmented to include an energy state and substituted in the place of existing muscles in the model so that running a forward simulation (ForwardTool) now reports an energy state as part of the reporting of all states.
3.3. Use of Simbody System and State objects
OpenSim is built on Simbody which rigorously defines a computational System and distinct State objects. A System object is an embodiment of all the equations that govern the behavior of a physical system being modeled. The State object can contain a value for each of the variables in the system equations and includes: time, coordinates, speeds, auxiliary states of forces, user-defined states for custom components, modeling options to enable/disable components like constraint and force elements, and model parameters such as masses and dimensions. Therefore, a State contains the complete set of values required to fully and identically recover the response of the System. The state (i.e. the collection of all system variables) is isolated from the system (i.e. equations) and anything computed from the state (e.g., spatial locations, distances, applied forces, accelerations, reaction forces) is also cached within the state. See the companion paper [5] for details about the Simbody System and State design, including how the cache is managed automatically to prevent references to out-of-date computations.
At the level of modeling with OpenSim, users simply name the state variables of components they include and supply the equations that govern their derivatives. The book-keeping and validity of the state are managed by the underlying computational system. For programmers, OpenSim provides an API to create state and cache entries and to specify the conditions for which a cache entry must be invalidated due to state changes.
OpenSim is a unique musculoskeletal simulation framework that treats bodies, joints, constraints, contact, muscles, ligaments, controllers and all user customizable components as part of a single computational system of equations, with all variables and model parameters treated as one composite state. More commonly, multibody codes are used to compute accelerations given applied generalized forces, while the user’s program computes forces and integrates resultant accelerations, generalized speeds and any other variable derivatives. In this case, it is up to the user’s program to manage the multitude of variables that capture the state of the entire system. In that case, it is far too easy for the user to change the state intentionally or accidentally, not realizing that Newton’s laws have been violated. For example, a muscle path wrapping over geometry is an expensive computation dependent only on generalized coordinate values, so it is typically saved to avoid recomputation. If an integrator subsequently rejects those generalized coordinates due to an excessive error estimate, the saved muscle path computation must be forgotten. If not, the next calculation based on the muscle path will not reflect the correct generalized coordinates, although typically it will not be qualitatively different from the correct result. It is nearly impossible to detect these errors from simulation results, especially as model complexity increases, intuition is insufficient, and benchmarks are unavailable. Unfortunately, it is precisely when complexity is high when “lazy” calculations (only recalculating a variable’s value when a dependency has changed) are most beneficial, yet the risk of stale calculations contaminating the solution is greatest. These issues are paramount to the design of OpenSim and Simbody and, therefore, Model and State abstractions comprise the most fundamental layer of modeling and simulation in OpenSim and a strict API enforces a careful discipline that prevents these errors.
3.4. Modeling context vs. computational implementation
OpenSim purposefully distinguishes between the model representation and its computational implementation (Fig. 8) because models contain a rich set of useful information (e.g. names, component relations, visual geometry) that are unnecessary for computation. Complex models have a natural hierarchy between their constituent parts, which provides a “modeling context.” For example, a bone is connected to the skeleton by a joint, a joint has coordinates, coordinates have limits, and all of these are named. So a coordinate (e.g. degree-of-freedom) value can be interpreted in this context as describing the relative angle between two bones, rather than seen only as one of many values in a vector of generalized coordinates used for computation.
Fig. 8.
A conceptual model with hierarchically arranged components vs. the flat underlying computational representation (system of equations). An OpenSim ModelComponent corresponds to a conceptual model, and embeds the logic to automatically create its computational counterparts in the system. These counterparts occupy different (even multiple) subsystems (multi-coloured puzzle pieces) in the underlying multibody system. System equations give rise to state variables (colours correspond to the subsystem that allocated the variables in the State). Model components maintain a reference (an index) to their computational counterparts in the corresponding subsystem (dashed-lines). All calculations are performed with the resulting System, then results are mapped back to the Model.
Furthermore, a human joint connects two bones via several interacting passive structures involving the bone cartilaginous surfaces, ligaments, bursa, and a joint capsule, and from an anatomical point of view these structures all belong to the context of a joint. From the multibody system perspective, a joint in internal coordinates is a grantor of degrees-of-freedom to a body relative to another; applied forces map to equivalent generalized forces, constraints yield Lagrange multipliers, and there is no hierarchy—the mathematical formulation is “flat” and needs to be for efficient computation (Fig. 8).
The biomechanics researcher is primarily concerned with capturing joint kinematics that match experimental data and secondarily with performance, but not whether mobilizers, constraints, or forces are used to permit this motion. Any of these might reasonably be used to model behaviorally equivalent joints, stops, and passive elements with different detail and performance. An OpenSim joint model, therefore, is free to choose and mix the finite set of multibody system (computational) implementations to satisfy musculoskeletal modeling needs. For example, locking joints can add constraint equations to the underlying system dynamics, but rather than treat these constraints as separate components (e.g. as in a flat list) they are attributes of the joint and its coordinates in the Model. The OpenSim Joint is therefore responsible for creating both the underlying degrees-of-freedom with an internal coordinate mobilizer as well as the constraint equation(s) to lock it if necessary.
3.5. The modeling layer
The modeling layer is charged with implementing the variety of model components that comprise a musculoskeletal model. A ModelComponent’s responsibility is to create its constituent part(s) (system generalized coordinates, constraint equations, etc…) in the underlying Simbody System via the Simbody API. A Model object consists of ModelComponents and the resulting System, after each component has contributed its equations and parameters. ModelComponent derived classes: Body, Joint, Constraint, Force, ContactGeometry, and Controller define an API that components of these types (subclasses) must satisfy. For example, a Force must implement computeForce() and a Controller implements computeControls(). OpenSim provides several subclasses of Force, such as Ligament, Actuator and its Muscle subclass to provide the common modeling abstractions for a musculoskeletal model. A model can be written to/read from an XML file to be archived or loaded according to the properties associated with the model and its components and their subcomponents and so on and so forth. A ModelComponent is also responsible for defining its properties (attributes) to be archived or read from the XML model file.
3.6. The analysis layer
As described earlier, the analysis layer is responsible for creating new models, solving system equations, and reporting useful information about a model. Thus, its main classes are Modeler, Solver, and Reporter. The task of creating a new model or set of models is performed by a Modeler. An example is a ModelScaler that takes as input an existing generic model and outputs a new model scaled to an individual subject based on anthropometric measurements.
Second, a Solver computes values of interest from the model, which includes its underlying computational system. An example of a Solver is the InverseDynamicsSolver, which takes as inputs a State and target generalized accelerations and uses the underlying system to apply model forces (e.g. measured external loads) and then to solve for the additional generalized forces required to generate the target accelerations.
Third, a Reporter records/outputs values of interest to a file, output window, or graphic display, for storage and interpretation of results arising from a solver or probing the model directly. An example of a Reporter is a ForceReporter, which queries each Force in a model for its force expressed as body forces, generalized force, or as scalar values for the tension in a Ligament or Muscle. It is up to the individual Force to define what output it produces.
3.7. OpenSim plugins
It is expected that the standard set of model components will not meet the needs of every user. In this case, user-derived classes for a Joint, Constraint, Force, etc. are necessary. Additionally, we want users to easily utilize these custom elements in the OpenSim API and GUI without having to rebuild all the OpenSim libraries from source code. Therefore, we support a plugin mechanism for user code to be compiled separately as a loadable dynamically linked library (DLL), and then loaded at run time as additional functionality for the API or GUI. A plugin can contain any number of user-defined classes that are exported by the DLL. Model files using the tags for a user-defined class will automatically cause OpenSim to create instances of the new class, as long as the plugin is loaded in OpenSim first.
Several now built-in ModelComponents, such as Ligament and EllipsoidJoint, were first introduced as plugins to meet a particular user need. Plugins enable valuable yet focused contributions with minimal investment. Plugins also serve as an easy way to share innovations with colleagues and the field.
4. Insights from muscle actuated simulations of human gait
4.1. Objective
The objective of this section is to demonstrate how movement scientists can leverage existing OpenSim models to generate and gain insights from muscle actuated simulations for varying individuals and types of gait. Models allow us to obtain access to internal variables not accessible in experimental studies. The examples here use Induced Acceleration Analysis to explore the otherwise-inaccessible contributions of individual muscles to gait.
4.2. Model and methods overview
In the studies that follow, a generic musculoskeletal model (lower extremities from [2] and torso from [24]) with 19 degrees of freedom and 92 musculotendon actuators was scaled to subjects according to their anthropometric measurements from static trials. The degrees of freedom included a ball-and-socket joint located at approximately the third lumbar vertebra between the pelvis and torso, ball-and-socket joints at each hip, the knee was modeled as a custom joint with 1 generalized coordinate (section 2.1), and revolute joints at each ankle.
Collected experimental data consisted of marker data from the lower extremities and ground reaction forces from force-plates over-ground (crouch gait) and treadmill (running).
Subject-specific simulations were then generated in OpenSim. The computed muscle control (CMC) algorithm was incorporated into a specialized controller (Fig. 6). The CMC controller was used to compute individual muscle excitations that generated motion in a forward dynamics simulation that tracked experimental kinematics when experimental ground reaction forces were applied [26].
Modeling contact with the ground with appropriate constraints was necessary to compute muscle induced accelerations (section 2.5). The rolling on surface constraint (section 2.2) was applied at the center-of-pressure at each time-frame of the analysis, located according to force-plate measurements.
4.3. Muscle function in crouch gait versus unimpaired gait
Muscle induced acceleration analysis was used with muscle actuated simulations of nine subjects walking at four different speeds to determine which muscles contribute to support and progression in unimpaired gait [31]. More recently we analyzed the muscle induced acceleration of a group of 10 children with crouch gait resulting from cerebral palsy [32].
The muscle induced acceleration results indicate that subjects with crouch gait utilized the same muscle groups to support the body as unimpaired gait; however, they employed a different support strategy during single-limb stance. In unimpaired subjects the action of supporting the body shifts from the vasti (quadriceps) in early stance to the calf muscles (gastroc and soleus) in late stance. In stark contrast, during crouch gait, the support muscles were active throughout single-limb stance and generated relatively constant accelerations of the mass center. Subjects with crouch gait also used a different strategy to move the mass center forward during single-limb stance, relying more on proximal muscles than the unimpaired subjects (Fig. 9).
Fig. 9.
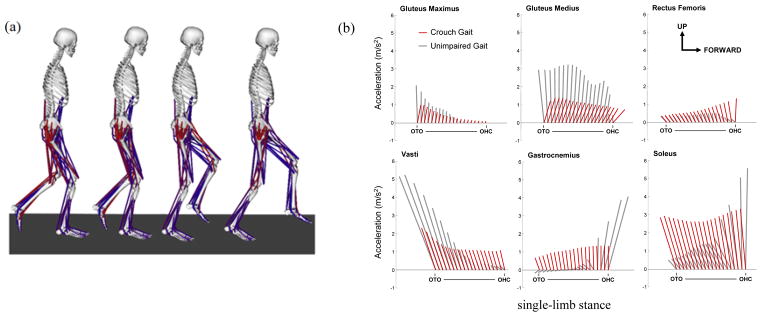
(a) Crouch gait model and simulation of single-limb stance from opposite limb toe-off (OTO) to opposite limb heel-contact (OHC). (b) Muscle contributions to center-of-mass acceleration in impaired (crouch) and unimpaired gait, where each ray is the acceleration vector of the center-of-mass in the sagittal plane due to the indicated muscle. Results from Steele et al. 2010 [32]
4.4. Muscle function during human running
In this study we were interested in identify the primary contributors to propulsion and support during running at a steady state long distance speed (3.96 m/s). The generic musculoskeletal gait model was augmented by torque actuated arms to consider the effects of arm-swing on total body accelerations during running. Each arm consisted of 5 degrees-of-freedom; the shoulder was modeled as a ball-and-socket joint (3 dofs), and the elbow and forearm rotation were each modeled with revolute joints (1 dof) [33]. A muscle induced acceleration was performed with the rolling on surface constraint enforced at every time-frame applied at the center-of-pressure.
The horizontal and vertical mass center accelerations (i.e., propulsion and support) during running were generated primarily by muscles, as skeletal structure contributed very little to support (Fig. 10, see “all muscles”). Muscles accelerated the mass center backward during the first 60% of stance phase (i.e., the braking phase) and the muscles accelerated the mass center forward during the remaining 40% of the stance phase (i.e., propulsion phase). During the braking phase, the primary contributor to both braking and support was the quadriceps muscle group, which contributed twice the peak braking acceleration and nearly half of the peak vertical support of the body mass center (Fig. 10, see quadriceps).
Fig. 10.
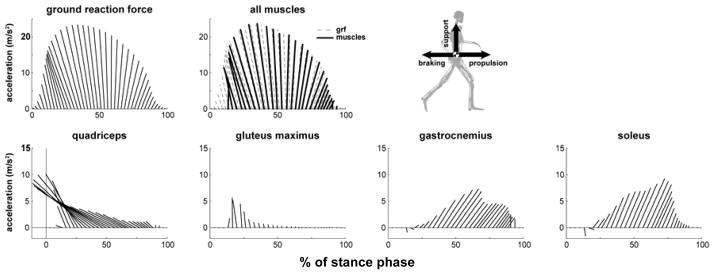
Top four muscle contributions to support and propulsion during running. Muscle contributions are to center-of-mass acceleration where each ray is the acceleration vector of the center-of-mass in the sagittal plane due to the indicated muscle. Results from Hamner et al. 2010 [18]
During the propulsion phase of stance (i.e., late stance), soleus and gastrocnemius were the two main contributors to propulsion and support; together they provided over twice the peak forward acceleration and over half of the peak vertical support of the body mass center (Fig. 10). During the propulsive phase, the quadriceps continued to oppose forward motion. The hamstrings, tibialis anterior, and iliopsoas slightly accelerated the mass center downward at the end of stance.
The arms did not contribute substantially to either propulsion or support, with a maximum contribution of less than 1% of both the peak horizontal and vertical mass center accelerations. However, the angular momentum of the arms about a vertical axis passing through the center of mass counterbalanced (i.e., was equal and opposite to) the angular momentum of the lower extremities about the vertical axis).
Interestingly, the quadriceps (the vasti and rectus femoris) and plantar-flexor muscles (soleus and gastrocnemius) contribute most significantly to vertical and horizontal accelerations during running as well as during unimpaired gait and show similar patterns of quadriceps early and plantar-flexors late with a smooth transition between (compare Fig. 9b and Fig. 10). This suggests common muscle recruitment and muscle actions for both running and walking.
5. Applying OpenSim to perform in silico experiments
5.1. Objective
In this section we demonstrate how movement scientists can design and build their own virtual experimental setup with OpenSim. Simulations offer numerous advantages such as safety, especially for delicate patients; exploration of failure modes via loading and perturbations; the removal of confounding factors that may mask fundamental characteristics of a model, and cost savings in terms of personnel time and capital resources. This is not to say that simulations can replace physical experiments, but rather simulations can complement experiments, help refine research questions and target experimental protocols.
5.2. What is a posture perturbation platform experiment?
Subjects stand on an actuated 6dof platform with various visual and other potentially altered feedback cues while the platform is moved in any direction. Subject kinematics and foot reaction forces from the platform are recorded. This test is used to determine deficits in balance recovery [34]. Varying the direction of the perturbation and available feedback (e.g. with vision and without) yield different responses from which clinicians can identify plausible causes of deficits, such as cerebellar dysfunction [35].
5.3. Platform and balance subject model
In our initial experiment, the perturbation platform is modeled as a box-like rigid body with 3 translational dofs that are prescribed as functions of time. The subject is represented by the standard gait model without arms (section 4.2) and 5 HuntCrossleyForce contact spheres on the major flesh pads of the foot and the surface of the platform represented as a half-plane.
5.4. What is the effect of skeletal posture on stability?
In vivo, it is impossible to isolate the effect of posture from other elements in the neuromuscular system, such as passive muscle forces, spinal reflexes, as well as cerebellar and cortical control that me be triggered or enhanced by postural changes. Although we are ultimately interested in the interaction of these systems, it is necessary to decouple their effects to gain a clear understanding of the role of posture in maintaining stability.
To understand the effect of posture, muscles and all passive joint structures were removed. The model was perturbed by anterior and posterior disturbances (i.e. translations of the platform) and the time to fall recorded. During the perturbation simulation, joint motion was modeled in one of two ways: (1) the joints were free to move while constant torques necessary to maintain the model posture in quiet standing were applied, and (2) all the joints of the legs and back were locked.
Postural simulations confirmed that crouch postures are more resistant to disturbances than an upright posture. The model with joints free was unstable for all postures, but greater instability resulted from less crouch and anterior platform displacements (Fig. 12a). Locking the joints created stable regions for each posture and stability progressively improved with increasing knee-flexion (Fig. 12b). In the absence of control, these results clearly indicate a performance advantage to crouch for rejecting disturbances.
Fig. 12.
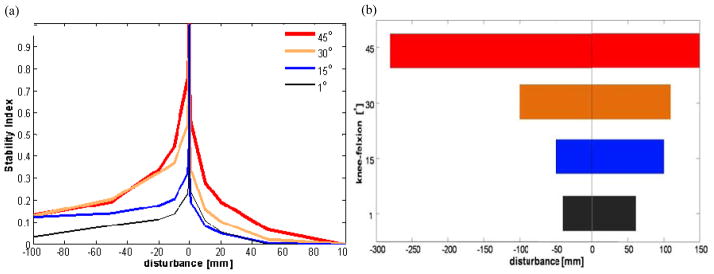
The effects on stability for varying degrees of crouch with (a) joints free and (b) joints locked. The stability index = 1–e−T2, where T is the time to fall. An index of 1 means the model does not fall for that disturbance. In (b) the range of disturbances for which the model is stable (index = 1) is presented. Anterior disturbances are positive.
6. Limitations, challenges and opportunities
The accuracy of a simulation depends on the fidelity of the underlying mathematical model of the neuromusculoskeletal system to reproduce the behaviors of the subject being studied. Many assumptions are made in the development of musculoskeletal models, and some of these assumptions are based on limited experimental evidence. To improve the accuracy of musculoskeletal models, more in vivo measurements of musculoskeletal geometry and joint kinematics are needed to understand how variations due to size, age, deformity, or surgery influence the predictions of a model, and to determine the conditions under which simulations based on a generic model are applicable to individual subjects. Given that simulations include assumptions and approximations, it is critically important that each simulation be tested to establish its limitations. As more investigators use musculoskeletal simulations, it is essential that scientists individually test for accuracy in the context of their specific scientific study.
It remains a major challenge to demonstrate that simulation can improve treatment outcomes for individuals with movement disorders. The potential to use subject-specific simulations to understand the causes of movement deviations and to assess treatment options is exciting, but has not been fully realized. Future studies, in which simulations of many subjects are conducted, are needed to determine if general principles for treatment planning can be elucidated from the insights gained by analyzing simulations. Studies that retrospectively compare predictions from subject-specific simulations to the subjects’ actual outcomes are also needed to evaluate whether existing musculoskeletal models are sufficiently accurate, and to establish the conditions under which the results of simulations are applicable. OpenSim provides a simulation framework that makes such large-scale studies possible, though more development is needed to streamline the process of creating and validating simulations of individuals with impairments.
The prediction of outcome due to treatment or intervention (surgery, physical training, biofeedback, etc.) remains the ultimate goal of musculoskeletal modeling and simulation. The biggest limitation to prediction remains computational performance especially as models begin to resemble biological complexity. For example, there is no muscle-actuated model of the upper-extremity including the kinematics of the shoulder girdle that is capable of running a forward simulation in real-time. Sensitivity analyses to test model assumptions and optimizations to predict new behaviors becomes daunting if individual forward simulations cannot run at or faster than real-time. It is common for model moments and moment-arms to be compared to experimental data and values reported in the literature to assess model accuracy, but the computational performance of models has not received the same level of scrutiny in biomechanics. Exciting opportunities for theoretical and technical innovations exist to represent muscle dynamics and geometry in new ways to bolster both computational performance and accuracy.
Muscle-driven simulations generate a wealth of data. Using simulations to uncover the principles that govern muscle coordination and to achieve improved clinical outcomes requires tools that can help interpret simulations. Developing and disseminating analysis and visualization tools that provide new insights poses an important challenge for advancing biomechanical simulation. Our goal is to provide OpenSim as a platform upon which the broader scientific community can build tools that help to uncover principles of human movement and design better treatments for individuals with physical disabilities.
OpenSim provides new opportunities for collaboration and peer review. The code that comprises OpenSim is being tested, analyzed, and improved through a multi-institutional collaboration. Users are encouraged to modify models, create plugins, and augment the code to suit their applications and to share their contributions with others. As a result, simulation-based studies can now be reproduced and tested outside the institution where the simulation is first developed. Such rigorous tests are essential if biomechanical simulation is to become more of a science and less of an art.
We envision a future in which simulations maximize treatment efficacy, limit undesired consequences and reduce costs. To accomplish this will require the scientific and clinical community to contribute and refine musculoskeletal models and their analyses. Towards this end OpenSim provides a free and open musculoskeletal modeling and simulation environment that combines the efficient formulation and solution of system dynamics with high fidelity graphics and analysis tools. It is our hope that OpenSim will act as a catalyst to promote model exchange and ignite modeling innovation to be shared by all.
Fig. 3.
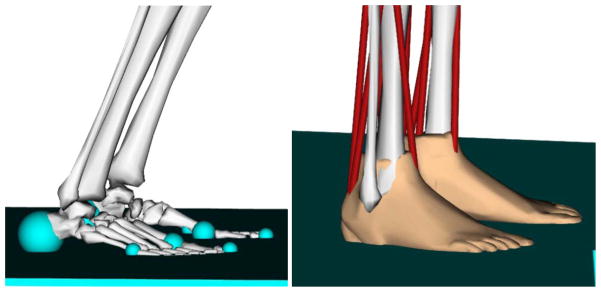
(a) Hunt and Crossley force spheres and (b) Elastic Foundation mesh-based forces for representing foot-floor contact in OpenSim.
Fig. 11.

Postural model at 1, 15, 30 and 45°of knee flexion. Spheres on the feet are in contact with the moveable platform.
Acknowledgments
The authors are grateful to Ayman Habib, Peter Eastman, Samuel Hamner, Katherine Steele, Edith Arnold, Matt Demers, Peter Loan, and Clay Anderson for their contributions and pioneering work. This work was supported by NIH grants U54 GM072 970 and R24 HD065 690.
References
- 1.Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. Opensim: Open-source software to create and analyze dynamic simulations of movement. IEEE Transactions on Biomedical Engineering. 2007;54(11):1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 2.Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37(8):757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- 3.Arnold E, Ward S, Lieber R, Delp S. A model of the lower limb for analysis of human movement. Annals of Biomedical Engineering. 2010;38:269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Christophy M, Faruk Senan N, Lotz J, O’Reilly OM. A musculoskeletal model for the lumbar spine. Biomechanics and Modeling in Mechanobiology. 2011:1–16. doi: 10.1007/s10237-011-0290-6. [DOI] [PubMed] [Google Scholar]
- 5.Sherman MA, Seth A, Delp SL. Simbody: multibody dynamics for biomedical research. In: McPhee J, Kövecses J, editors. Procedia IUTAM, International Union of Theoretical and Applied Mechanics. Elsevier Science; 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Crowninshield RD. Use of optimization techniques to predict muscle forces. Journal of Biomechanical Engineering. 1978;100(2):88–92. [Google Scholar]
- 7.Crowninshield RD, Brand RA. A physiologically based criterion of muscle force prediction in locomotion. Journal of Biomechanics. 1981;14(11):793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- 8.Delp S, Loan J. A computational framework for simulating and analyzing human and animal movement. Computing in Science & Engineering. 2000;2(5):46–55. [Google Scholar]
- 9.Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. Journal of Biomechanics. 2003;36:321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- 10.Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Critical Reviews in Biomedical Engineering. 1989;17(4):359–411. [PubMed] [Google Scholar]
- 11.van der Helm FCT. Analysis of the kinematic and dynamic behavior of the shoulder mechanism. Journal of Biomechanics. 1994;27(5):527–550. doi: 10.1016/0021-9290(94)90064-7. [DOI] [PubMed] [Google Scholar]
- 12.De Sapio V, Holzbaur K, Khatib O. The control of kinematically constrained shoulder complexes: physiological and humanoid examples. Robotics and Automation, 2006. ICRA 2006. Proceedings 2006 IEEE International Conference on; 2006. pp. 2952–2959. [Google Scholar]
- 13.Seth A, Sherman M, Eastman P, Delp S. Minimal formulation of joint motion for biomechanisms. Nonlinear Dynamics. 2010;62:291–303. doi: 10.1007/s11071-010-9717-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Draper C, Besier T, Santos J, Jennings F, Fredericson M, Gold G, Beaupre G, Delp S. Using real-time mri to quantify altered joint kinematics in subjects with patellofemoral pain and to evaluate the effects of a patellar brace or sleeve on joint motion. Journal of orthopaedic research: official publication of the Orthopaedic Research Society. 2009;27(5):571. doi: 10.1002/jor.20790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hunt KH, Crossley FRE. Coefficient of restitution interpreted as damping in vibroimpact. ASME Journal of Applied Mechanics. 1975;42:440–445. [Google Scholar]
- 16.Hertz H. On the contact of elastic solids. J Reine Angew Math. 1882;92:156–171. [Google Scholar]
- 17.Pérez-González A, Fenollosa-Esteve C, Sancho-Bru JL, Sánchez-Marín FT, Vergara M, Rodríguez-Cervantes PJ. A modified elastic foundation contact model for application in 3d models of the prosthetic knee. Medical Engineering & Physics. 2008;30(3):387–398. doi: 10.1016/j.medengphy.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 18.Hamner SR, Seth A, Delp SL. Muscle contributions to propulsion and support during running. J Biomech. 2010;43(14):2709–2716. doi: 10.1016/j.jbiomech.2010.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hill AV. The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of Biology. 1938;126:136–195. [Google Scholar]
- 20.Thelen DG. Adjustment of muscle mechanics model parameters to simulate dynamic contractions in older adults. Journal of Biomechanical Engineering. 2003;125(1):70–77. doi: 10.1115/1.1531112. [DOI] [PubMed] [Google Scholar]
- 21.Pandy MG, Anderson FC, Hull DG. A parameter optimization approach for the optimal control of large-scale musculoskeletal systems. ASME Journal of Biomechanical Engineering. 1992;114(4):343–363. doi: 10.1115/1.2894094. [DOI] [PubMed] [Google Scholar]
- 22.Pandy MG, Zajac FE, Sim E, Levine WS. An optimal control model for maximum-height human jumping. Journal of Biomechanics. 1990;23(12):1185–1198. doi: 10.1016/0021-9290(90)90376-e. [DOI] [PubMed] [Google Scholar]
- 23.van Soest AJ, Schwab AL, Bobbert MF, van Ingen Schenau GJ. The influence of the biarticularity of the gastrocnemius muscle on vertical-jumping performance. Journal of Biomechanics. 1993;26:1–8. doi: 10.1016/0021-9290(93)90608-h. [DOI] [PubMed] [Google Scholar]
- 24.Anderson FC, Pandy MG. A dynamic optimization solution for vertical jumping in three dimensions. Computer Methods in Biomechanics and Biomedical Engineering. 1999;2:201–231. doi: 10.1080/10255849908907988. [DOI] [PubMed] [Google Scholar]
- 25.Anderson FC, Pandy MG. Dynamic optimization of human walking. Journal of Biomechanical Engineering. 2001;123:381–90. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- 26.Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. Journal of Biomechanics. 2006;39:1107–1115. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
- 27.Seth A, Pandy MG. A neuromusculoskeletal tracking method for estimating individual muscle forces in human movement. Journal of Biomechanics. 2007;40:356–366. doi: 10.1016/j.jbiomech.2005.12.017. [DOI] [PubMed] [Google Scholar]
- 28.Bergmann G, Deuretzbacher G, Heller M, Graichen F, Rohlmann A, Strauss J, Duda GN. Hip contact forces and gait patterns from routine activities. Journal of Biomechanics. 2001;34(7):859–871. doi: 10.1016/s0021-9290(01)00040-9. [DOI] [PubMed] [Google Scholar]
- 29.Richards C, Higginson J. Knee contact force in subjects with symmetrical oa grades: Differences between oa severities. Journal of Biomechanics. 2010;43(13):2595–2600. doi: 10.1016/j.jbiomech.2010.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zajac FE, Gordon ME. Determining muscle’s force and action in multi-articular movement. Exrercise Sport Science Review. 1989;17(1):187–230. [PubMed] [Google Scholar]
- 31.Liu M, Anderson F, Schwartz M, Delp S. Muscle contributions to support and progression over a range of walking speeds. Journal of Biomechanics. 2008;41(15):3243–3252. doi: 10.1016/j.jbiomech.2008.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Steele KM, Seth A, Hicks JL, Schwartz MS, Delp SL. Muscle contributions to support and progression during single-limb stance in crouch gait. Journal of Biomechanics. 2010;43(11):2099–2105. doi: 10.1016/j.jbiomech.2010.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Holzbaur KRS, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of Biomedical Engineering. 2005;33:829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- 34.Nashner LM, McCollum G. The organization of human postural movements: A formal basis and experimental synthesis. Behavioral and Brain Sciences. 1985;8(01):135–150. [Google Scholar]
- 35.Morton SM, Bastian AJ. Cerebellar control of balance and locomotion. The Neuroscientist. 2004;10(3):247–259. doi: 10.1177/1073858404263517. [DOI] [PubMed] [Google Scholar]