Subthalamic Nucleus Local Field Potential Activity Helps Encode Motor Effort Rather Than Force in Parkinsonism

Abstract

Local field potential (LFP) recordings from patients with deep brain stimulation electrodes in the basal ganglia have suggested that frequency-specific activities correlate with force or effort, but previous studies have not been able to disambiguate the two. Here, we dissociated effort from actual force generated by contrasting the force generation of different fingers while recording LFP activity from the subthalamic nucleus (STN) in patients with Parkinson's disease who had undergone functional surgery. Patients were studied while on their normal dopaminergic medication. We investigated the relationship between frequency-specific oscillatory activity in the STN and voluntary flexion of either the index or little finger at different effort levels. At each tested effort level (10%, 25%, and 40% of the maximal voluntary contraction force of each individual finger), the index finger generated larger force than the little finger. Movement-related suppression of beta-band power in the STN LFP was significantly modulated by effort, but not by which finger was used, suggesting that the beta suppression in the STN LFP during sustained contraction serves as a proxy for effort. The absolute force scaled with beta power suppression, but with the scaling determined by the maximal voluntary contraction force of the motor effector. Our results argue against the hypothesis that the basal ganglia are directly involved in the parameterization of force during movement and support a role of the STN in the control of motor effort to be attributed to a response.

Introduction

How do we scale our movements? The simplest policy would be to parameterize absolute force directly, but psychophysical arguments (Carson et al., 2002; Simon and Ferris, 2008) and some computational models (Guigon et al., 2007; Baraduc et al., 2013) suggest that we might scale movements by coding a more complex construct termed motor effort or sometimes vigor (Mazzoni et al., 2007). This can be considered to determine the gain of the motor command. Ordinarily, the dynamic range of motor effort will correspond to the range of strength of a given muscle group or effector, from no effort and no contraction to maximal effort and maximal voluntary contraction. Therefore, exerting a given force with a weaker digit such as the little finger requires more effort than exerting the same force with a stronger digit such as the index finger. The actual force generated scales with effort, but the slope of this relationship will vary with changes in maximal voluntary contraction strength due to changes in effector, fatigue, disease, or injury. But is there any evidence for a central signal that behaves in such a way, varying with effort rather than effector or absolute force?

Here, we demonstrate such neural activity in the subthalamic nucleus (STN) of the basal ganglia. The basal ganglia have long been associated with the scaling of effort or force. Imaging studies in healthy humans have suggested that basal ganglia nuclei, in particular the internal portion of the globus pallidus and the subthalamic nucleus (STN), are involved in encoding gripping force amplitude and rate (Spraker et al., 2007; Prodoehl et al., 2009). Neuronal recordings in monkeys have also suggested that the basal ganglia play an important role in the control of the scaling of motor responses measured in terms of their amplitude or velocity (DeLong et al., 1984; Turner and Anderson, 1997). More recently, direct recordings from humans suggest that power suppression in the beta band and power increase in the gamma band of the local field potential (LFP) picked up from the STN may correlate with forces or efforts made over the lower and higher effort ranges, respectively (Tan et al., 2013b). Other investigators have also reported that STN LFP activity is modulated by movement amplitude and velocity, but mainly in the gamma frequency band (Anzak et al., 2012; Brücke et al., 2012; Joundi et al., 2012), perhaps because the tasks tested required higher effort levels over which gamma-band changes may be more evident in the STN LFP. Moreover, in the paradigms studied thus far, the absolute force and other biomechanical parameters have not been disambiguated from motor effort. Here, we explore whether task-related beta-band desynchronization in the STN LFP scales with motor effort during low-intensity contractions and if this can be disambiguated from a scaling with force per se through the selection of different motor effectors. Our findings have significant implications for the understanding of the normal functioning of the basal ganglia and for theoretical accounts of motor impairment in disorders such as Parkinson's disease (PD).

Materials and Methods

Subjects.

Eleven patients with idiopathic PD (mean disease duration of 10 years, mean age 56.6 years, range 44–71 years, eight males) provided written informed consent to take part in this study, which was approved by the local ethics committees. Nine patients underwent bilateral and two patients underwent unilateral implantation deep-brain stimulation (DBS) electrodes into the STN as a prelude to therapeutic high-frequency stimulation for advanced idiopathic PD with motor fluctuations and/or dyskinesia. These offered access to 20 STNs in total. Techniques to target and implant electrodes in the STN have been described previously (Foltynie and Hariz, 2010). Microelectrode recordings were not made during surgery. The permanent quadripolar macroelectrode used was Model 3389 from Medtronic Neurologic Division featuring four platinum-iridium cylindrical surfaces. Its contacts are numbered 0, 1, 2, and 3, with 0 being the most caudal and 3 the most cranial. Localization was supported by the effects of direct stimulation (sites 1 and 3) intraoperatively and by immediate postoperative stereotactic imaging (site 2). DBS electrode extension cables were externalized through the scalp to enable recordings before connection to a subcutaneous DBS pacemaker implanted in a second operative procedure up to 7 d later. Clinical details of the patients are given in Table 1. The patients showed 61.2 ± 4.4% (p < 0.001) improvement in the motor section of the Unified Parkinson's Disease Rating Scale (UPDRS) on treatment with levodopa, indicating good responsiveness to this drug.

Table 1.

Clinical details of patients

Case	Site	Age	Disease duration	UPDRS III On	UPDRS III Off	First symptom	Primary reason for DBS	Medication (daily dose in mg)
1	1	63	14	24	35	Right hand tremor	Tremor	Levodopa 150, ropinirole 23
2	1	50	9	23	58	Right shoulder stiffness	On/off fluctuations and tremor	Levodopa 800
3	1	50	4	N/A	N/A	Right arm tremor	Tremor	Rotigotine 16, levodopa 300, entacapone 600
4	2	71	16	13	32	Loss of dexterity and reduced arm swing	Off period bradykinesia	Levodopa 600, amantadine 200, ropinirole 24, rasagiline 1
5	2	48	7	13	58	Dragging left leg	Tremor and gait difficulty	Levodopa 1300
6	2	44	14	11	34	Left arm bradykinesia	Motor fluctuations and dyskinesia	Levodopa 350, pramipexole 1.05, amantadine 300
7	2	66	9	24	63	Shoulder pain/stiffness	Motor fluctuations	Levodopa 650, pergolide 9
8	3	62	2.5	8	18	Left side tremor, rigidity	Left sided tremor, rigidity	Levodopa 800
9	3	58	10	20	42	Leg cramp	Tremor	Trihexyphenidyl 2, levodopa 450, rasagline 1, amantadine 100
10	3	62	10	8	20	Left side tremor and bradykinesia	On off fluctuations, tremor and impulse control disorder	Levodopa 1000, trihexyphenidyl 6
11	3	49	10	6	42	Tremor in right hand	Tremor	Levodopa 300, trihexyphenidyl 2

Surgical sites: (1) Kings College Hospital, London; (2) National Hospital for Neurology and Neurosurgery, London, United Kingdom; (3) John Radcliffe Hospital, Oxford. Cases 8 and 11 underwent unilateral implantation. Cases 10 and 11 were excluded from the final analysis because they made more than 20% invalid trials per session. N/A, Not available.

Experimental paradigm.

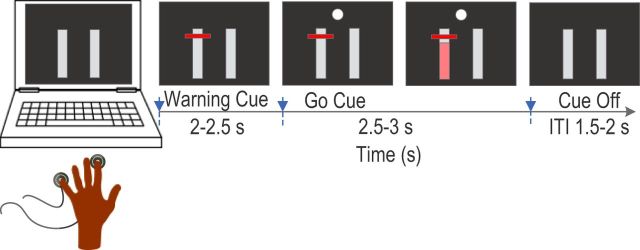
LFPs were recorded while patients engaged in a task in which they were requested to press a force-sensitive device (Precision Pinchmeter P200; Biometrics) with different fingers at different effort levels after imperative visual cues. Subjects were seated in a comfortable chair in front of computer monitor with their shoulders adducted and their elbows flexed at ∼90°. Subjects were asked to place their pronated hand flat on top of a desk with the flexor surface of the forearm and wrist touching the desk. All fingers were kept naturally extended and with a force-sensitive device under the index finger and little fingers. The experiment started with separately measuring the maximal voluntary contraction (MVC) pressing force of the index and little finger. The subjects were asked to press the force-sensitive device using the corresponding finger as hard as they could while keeping the position of the hand, wrist, and forearm relatively stable and touching the desk. Three attempts were recorded and the average of the maximal force achieved was used as the MVC for that finger. In the formal experiment, subjects were presented with a series of visual cues displayed on the monitor indicating which finger to press and the effort level that should be applied. These visual cues included two vertical bars that corresponded to the pressing force of the index and little fingers according to the position of the bars: for the right hand, the bar on the left side corresponded to the index finger and the bar on the right corresponded to the little finger. The converse was true for the left hand (Fig. 1). The pressing force of each finger was measured and displayed in real time as a filled pink color of the corresponding bar, with 50% of the MVC of that finger displayed as a completely pink bar. At the beginning of each individual trial, a horizontal line appeared on one of the vertical bars at one of the three vertical locations corresponding to 10%, 25%, and 40% of MVC, indicating which finger should be pressed and the effort level to apply. Subjects were asked to prepare to press with the correct finger at the appropriate effort level once they saw the horizontal line, but only start to press once a circular white imperative signal appeared. The filled pink color in the vertical bar indicated whether pressing force reached the required level and subjects were asked to continue pressing until the imperative signal went off (Fig. 1). There were 100 trials in each session and the warning cues randomly changed in the six experimental conditions with ∼16 trials in each condition: little finger at 10% of MVC, little finger at 25% of MVC, little finger at 40% of MVC, index finger at 10% of MVC, index finger at 25% of MVC, and index finger at 40% of MVC.

Figure 1.

Experimental paradigm. Two vertical bars were presented, with the left and right denoting the little and index finger of the left hand or the index and little finger of the right hand. Filled pink color indicated the pressing force of the responding finger, where a completely filled pink bar indicated 50% of MVC of that finger. The warning cue was a red horizontal line at one of three locations (corresponding to 10%, 25%, and 40% of MVC) on one of the vertical bars, indicating which finger to press and the effort level required. Subjects were asked to press with the correct finger with the appropriate level of effort at the onset of the filled circle go cue and to hold the force until the circle was extinguished.

Recordings.

Recordings were made when the patients were on their usual dopaminergic medication 3–6 d postoperatively while electrodes were externalized and before implantation of the pulse generator. Both hands were tested for patients who underwent bilateral implantation, with the order in which the left and right hands were tested counterbalanced across subjects. For patients who underwent unilateral implantation, only the hand contralateral to the side of electrode implantation was tested. Monopolar LFPs were recorded with a TMSi porti (TMS International) and its respective software. They were high- and low-pass filtered at 0.5 and 300 Hz, respectively. Force was low-pass filtered at 200 Hz. LFPs and force were sampled at 2048 Hz.

Analysis.

Analyses of both behavioral and LFP data were performed in MATLAB (version 2012b; The MathWorks). The finger-pressing force trajectory of each individual trial of each hand was normalized against the average MVC force of the index finger of that hand for easier comparison across subjects. The subjects were asked not to press until the visual “Go” white circle cue appeared so as to have a “preparation” phase between the warning cue and the go cue. Trials with muscle activation in this phase, measured as a pressing force >3 times the SD of the baseline, were rejected. Sessions with >20% invalid trials were excluded and this afforded 16 hands from nine subjects for the final analysis. The majority of invalid trials were due to premature responses in the preparation phase. The mean number (± SEM) of remaining trials per hand per condition was 14.0 ± 0.5. The force trajectories were differentiated against time and then low-pass filtered at 40 Hz to calculate the rate of change in force. Force initiation was defined as the time when the rate of change in force crossed a threshold of three times the SD of the signal (and its noise) at “rest” and was sustained above this threshold for at least 100 ms. Reaction time was calculated as the interval between the Go cue and force initiation; the time to peak force rate was calculated as the interval between the force initiation and the time when the rate of change in force reached its maximum. Stable force was calculated as the average force during a second in each trial when the force was stable. All of these parameters were calculated for each individual trial and averaged within each experimental condition before averaging across subjects.

LFP data were converted offline to give three bipolar contact pairs (01, 12, and 23) per electrode. A time-frequency decomposition based on the continuous wavelet transform was then applied to the LFP recordings from each trial to analyze changes in LFP activity in the time-frequency domain. Event related LFP power change (ERPC) was subsequently normalized relative to the average power during the one second before the warning cue so that a value higher than zero indicated power higher than before the cue and vice versa. The normalized power of each bipolar contact pairs was aligned to either the warning cue (to calculate ERPC in the preparation phase) or the Go cue (to calculate ERPC in the pressing phase) and subsequently averaged across the three bipolar contacts for each STN lead contralateral to the gripping hand. Analysis of the LFP from the STN focused on the side of the STN that was contralateral to the hand used to perform the task. Of the three bipolar channels from each STN, the channel with the largest event-related power change in the beta-band (13–30 Hz)—that is, the largest difference between the trough of event-related desynchronization during the sustained contraction phase and the peak synchronization during a second after movement in the beta band (Devos et al., 2006)—was selected for further analysis. Postoperative MRI scans were available for coregistration with preoperative MRI in 12 of 16 STNs included in the final analysis. Within this group, the bipolar channels that showed the largest movement-related modulation in the beta-band either had one contact inside STN (7 of 12, with the other contact either above or lateral to STN) or had both contacts inside STN (5 of 12). In two of the STNs without postoperative MRI, the bipolar channels chosen for final analysis included one of the contacts used for chronic clinical stimulation. In a further patient (1 STN) without postoperative imaging, follow-up chronic stimulation details were unavailable. In the remaining STN, the lower most bipolar contact pair was used for analysis and the electrode subsequently repositioned by advancing it 5 mm deeper before connection to the subcutaneous pulse generator.

Statistics.

Repeated-measure ANOVAs were used to examine the effect of effort level and the pressing finger on the force and LFP measurements. Correlation and partial correlation were used to investigate the relationship between normalized force and LFP measurements across subjects. These statistical tests were performed in SPSS Statistics 19. Independent software (G*power 3.1.9.2; Erdfelder et al., 1996; Faul et al., 2007) was used to calculate statistical power. Means ± SEM are presented throughout the text unless otherwise specified.

A multilevel multivariate regression modeling approach (Hox, 2002) was used to investigate whether the frequency-specific STN LFP activity was related to required effort, actual effort, or exerted force and to identify the relationship between frequency-specific LFP activities and absolute exerted force within subjects and how this relationship changed with the motor effector (index or little finger). The multilevel multivariate regression modeling approach used here has the advantage of taking into account the dependency in the data caused by repeated measurements within subjects, which makes it possible to investigate within-subject correlations that are consistent across subjects. Multilevel modeling was performed using the nlme package (Pinheiro et al., 2013) in R (R Development Core Team, version 2.13.2). In the modeling, the absolute pressing force was the dependent variable, LFP measurements were the continuous independent variables, and the motor effector (index finger or little finger) was treated as a categorical independent variable. The effects of all of the predictors were treated as fixed effects (consistent across subjects) and the baseline difference between individual hands was treated as a random effect. The normality assumption of the modeling was assessed by visually inspecting the Q-Q plot of the residuals of the modeling; the residues were also plotted against the fitted values and a uniform distribution was used to assess the validity of the modeling. The fit of different models was compared using the likelihood-ratio test. For variables with a significant effect, the estimated regression coefficient (mean ± SEM) and the p- value are reported.

Akaike information criterion (AIC) analysis was used to compare the different models used to describe the relationship between frequency-specific LFP activities and effort and absolute force. The AIC value was first calculated for each model and the best candidate model with minimal AIC was identified. The differences in AIC with respect to the AIC of the best candidate model (Δ_i(AIC) = AIC_i − min(AIC)) and the Akaike weight for a model $\left(w_i\left(AIC\right)=\frac{\exp \left\{-\frac{1}{2}{\Delta }_i\left(AIC\right)\right\}}{{\displaystyle {\sum }_{k=1}^k\exp \left\{-\frac{1}{2}{\Delta }_k\left(AIC\right)\right\}}}\right)$ were then calculated and used to evaluate the probability that the ith model was the best model in the AIC sense given the data and the set of candidate models (Burnham and Anderson, 2002; Wagenmakers and Farrell, 2004). The likelihood of the other models relative to the best candidate model was also evaluated using the relative Akaike weight $\frac{w_i\left(AIC\right)}{w_{bst}\left(AIC\right)}$, where w_bst(AIC) was the Akaike weight of the best candidate model.

Results

Index finger generates larger force compared with little finger for a similar effort level

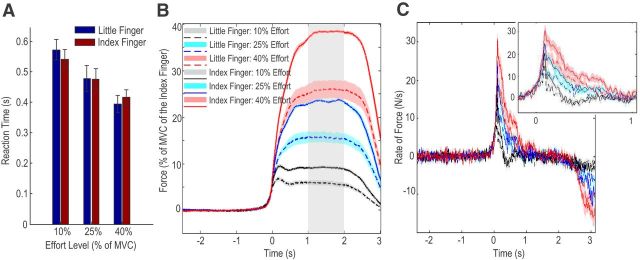
The mean MVC of the index finger (30.4 ± 3.14 N) was significantly larger than the mean MVC of the little finger (20.6 ± 1.87 N, t₁₅ = 4.255, p = 0.001), with the index finger 53.7 ± 14.6% stronger than the little finger. The average reaction times for different experimental conditions are shown in Figure 2A. Two-way ANOVA with the effect of factors of finger (index or little) and effort level (10%, 25%, and 40% of the MVC of individual fingers) on the reaction time identified a significant effect of effort level (F_(2,30) = 12.728; p < 0.001), but no effect of finger (F_(1,15) = 0.122; p = 0.732). The reaction time averaged across fingers reduced with increasing effort and was 556 ± 31, 477 ± 37, and 405 ± 25 ms at effort levels of 10%, 25%, and 40%, respectively.

Figure 2.

Behavioral results. A, Reaction time reduced with increasing effort level, but was independent from motor effector. B, Exerted force aligned to force onsets in different experimental conditions. The actual exerted force was modulated by the effort level required. At each effort level tested, the force achieved by the index finger was significantly larger than that achieved by the little finger, confirming successful dissociation between effort and actual force in this paradigm. C, The rate of force development aligned to force onsets in different experimental conditions. The inset shows that the time to peak force rate was constant across all experimental conditions, but the peak force rate changed with effort and motor effector. Group mean ± SEM (error bars in A and colored shaded areas in B and C) are shown. Gray band in B is the period taken as stable force.

The force trajectory of each finger at different effort levels was normalized to the MVC force achieved by the index finger of the same hand and aligned to force onset for easier comparison across subjects (Fig. 2B). Similar results were seen if absolute force was also used (data not shown). Average normalized force during the second over which force was stable (during sustained contraction in the middle of the gripping phase) was calculated for each condition. The “actual effort” measured as the average exerted force during the sustained contraction as a percentage of the MVC of the activated effector, closely matched the “required effort” set by the cue (r = 0.978, p < 0.001 considering all individual trials from all subjects). Two-way ANOVA with the factors of finger (index or little) and effort level (10%, 25%, and 40% of the MVC of individual fingers) applied on the exerted force identified significant effects of finger (F_(1,15) = 31.182, p < 0.001) and effort (F_(2,30) = 789.28, p < 0.001), together with a significant interaction between these two factors (F_(2,30) = 35.811, p < 0.001). The force exerted by the index finger was significantly larger than that exerted by the little finger at each effort level: 9.02 ± 0.35% vs 5.82 ± 0.48%, t₁₅ = 4.808, p < 0.001 at effort level of 10%; 23.43 ± 0.31% vs 16.01 ± 1.16%, t₁₅ = 5.446, p < 0.001 at effort level of 25%; 38.11 ± 0.27% vs 26.54 ± 1.95%, t₁₅ = 5.827, p < 0.001 at effort level of 40%. Therefore, effort and the actual exerted force were successfully dissociated in this paradigm.

The rate of the rise of force peaked shortly after force onset and then fell back to zero within one second of force onset, as shown in Figure 2C. The time interval between force onset and peak force rate (108 ± 8 ms) was constant across all experimental conditions and a two-way ANOVA showed no effect of finger: F_(1,15) = 0.098; p = 0.758; no effect of effort: F_(2,30) = 0.419; p = 0.662; nor an interaction: F_(2,30) = 2.659; p = 0.086. A two-way ANOVA of peak force rate with factors of finger and effort level identified a significant effect of finger (F_(1,15) = 40.745, p < 0.001) and of effort (F_(2,30) = 58.006, p < 0.001), but no interaction between these two factors (F_(2,30) = 2.857, p = 0.073). The maximal force rate achieved significantly correlated with the sustained stable force across subjects and across experimental conditions (r = 0.8230, p < 0.001, n = 64).

LFP beta activity increased after the warning cue and premovement beta ERPC positively correlated with reaction time

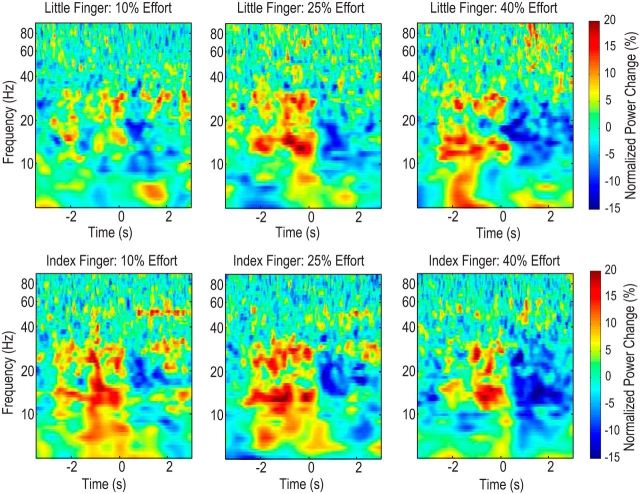
The average power changes during the preparation and movement relative to the average power before the warning cue are shown for different experimental conditions in Figure 3. The power in the beta-band (13–30 Hz) increased to above baseline after the warning cue (average ERPC = 5.45 ± 1.99, t₁₅ = 2.739, p = 0.015 vs zero for the little finger across different efforts, average ERPC = 8.89 ± 1.56, t₁₅ = 3.476, p = 0.003 vs zero for the index finger, one-sample t test) and then reduced to below baseline after the Go cue (average ERPC = −10.42 ± 1.72, t₁₅ = −6.057, p < 0.001 for the little finger across different efforts, average ERPC = −9.85 ± 1.32, t₁₅ = −1.52, p < 0.001 for the index finger, one-sample t test).

Figure 3.

Average power changes aligned to the Go cue in the different experimental conditions. Power in the beta-band (13–30 Hz) first increased after the warning cue (from minus 2.5 to 2.0 s) and then reduced after the Go cue (time 0 in the figure). Both the increase and the decrease were significant with respect to baseline. Note line noise at 50 Hz in bottom panels.

Two-way ANOVA applied on the beta-band ERPC during the preparation phase (between the warning cue and the Go cue) identified a significant effect of the finger (F_(1,15) = 5.696, p = 0.031), but no effect of effort levels (F_(2,30) = 1.245; p = 0.302) nor interaction between these factors (F_(1,15) = 0.502, p = 0.610). The average beta ERPC was significantly larger when the index finger would be activated after the Go cue (8.89 ± 1.56 ca 5.45 ± 1.99 when little finger would be activated, t₁₅ = 2.387, p = 0.031). There was a positive correlation between the beta ERPC during the preparation phase and the reaction time after the Go cue across subjects and across experimental conditions (r = 0.4158, p < 0.001, n = 64).

We also calculated average beta power during the time between the Go cue and force onset and between force onset and the time to peak force rate, but there was no significant modulation effect of either effort or effector on the beta desynchronization during these periods of time and there was no consistent correlation between the beta desynchronization during these periods of time and the rate of the rise of muscle force.

LFP beta activity during sustained contraction was modulated by the effort level not by which finger was activated

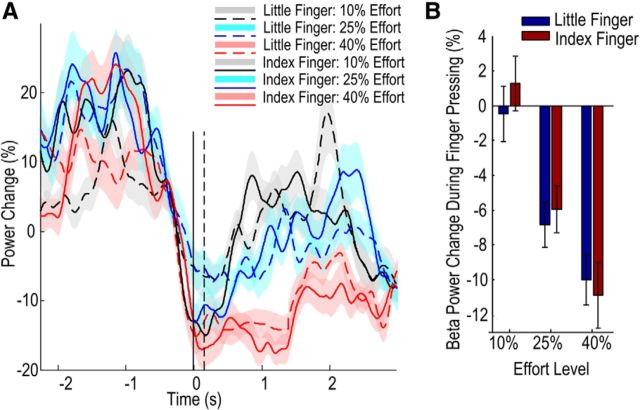
Comparison of the event-related power change in different frequency bands for different experimental conditions revealed that LFP activity in the beta-band during a sustained contraction phase was suppressed as effort level increased (Fig. 4). Two-way ANOVA with the factors of finger (index or little) and effort level (10%, 25%, and 40% of MVC of that finger) was applied to the average beta relative power change during the second in the middle of the finger press when force was stable. This identified a significant effect of effort (F_(2,30) = 9.276, p = 0.001, η² = 0.333) and a lack of effect of finger (F_(1,15) = 0.110, p = 0.745, η² = 0.006) and no interaction between the finger and effort level (F_(2,30) = 1.774, p = 0.187, η² = 0.106). In particular, the observed effect size of the effort level was 55.5 times that of the finger. Given the observed effect size for the finger, the statistical power for the finger would only increase by 0.002 even if the sample size were 10 times that of the current study. This indicates that the nonsignificant results for the effect of “finger” were not due to small sample size, but rather to the minute or negligible effect size.

Figure 4.

Beta activity during sustained contraction was modulated by effort level and not by the motor effector. A, Group mean ± SEM (colored shaded areas) time evolving beta power aligned to force onset (0 s). The solid and dashed vertical lines indicate the time of force onset and the time to peak force rate, respectively. B, Group mean ± SEM beta power during the period of sustained contraction (taken from 1 to 2 s after the force onset; see Fig. 2).

Furthermore, multilevel linear modeling was applied to the data from all valid trials of all subjects, with the LFP beta activity during sustained contraction as the dependent variable, and the required effort (determined by the cue), actual effort (the average force during the sustained contraction phase as a percentage of the MVC of the specific effector), or the “absolute exerted force” as the predictor in different models. AIC analysis was used to evaluate different models (results in Table 2). This identified the model based on the actual effort as the best candidate model with the minimal AIC value, closely followed by the model with required effort as the predictor. Both models had significantly higher probability of being better, in terms of AIC, than the model using actual force as predictor. This is despite the observation that the absolute force by itself had a significant effect on the STN beta activity (k = −0.0159 ± 0.007, p = 0.021). Modeling using the z-score of absolute force as the predictor showed that 1 SD of increase in the absolute force led to a significant reduction (4.266 ± 0.574, p = 0.020) in the STN beta ERS during movement. The significance of this effect was further confirmed by examining surrogate data. The model with absolute force had a significantly lower AIC value than the same model in which randomly permuted force was used as the predictor (p = 0.005; AIC = 11501.99 ± 0.45 for 1000 surrogates). Critically, though, the actual or required effort (the two being indistinguishable in the current paradigm) was a better predictor of LFP beta activity than the absolute exerted force in terms of AIC.

Table 2.

AIC analysis results for different regression models for LFP beta activity during sustained contraction

Model	Predictor	Effect of the predictor	AIC	Δi(AIC)	wi(AIC)	$\frac{w_i\left(AIC\right)}{w_2\left(AIC\right)}$
1	Required effort	k = −0.278 ± 0.043, p < 0.001	11453.9	3.2	0.168	p = 0.202
2	Actual effort	k = −0.283 ± 0.041, p < 0.001	11450.7	0	0.832	—
3	Absolute force	k = −0.0159 ± 0.007, p = 0.021	11472.2	21.5	1.78e-5	p < 0.001

The model with actual effort as predictor was the best candidate model with minimal AIC. The Akaike weight (w_i(AIC)) and the relative Akaike weight $\frac{w_i\left(AIC\right)}{w_3\left(AIC\right)}$ showed that this model had significantly higher likelihood of being the better model than the model with absolute force as the predictor. However, the model with actual effort as predictor proved not to be significantly better than that with required effort.

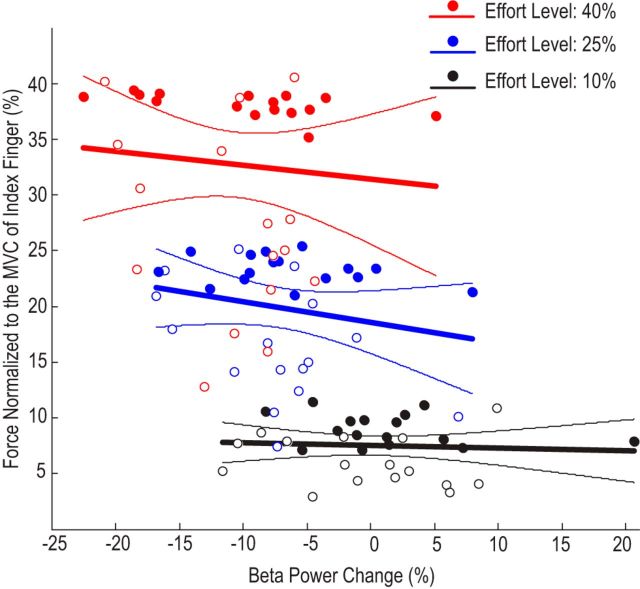
Consistent with this, considering the forces generated by different fingers together when the effort level was fixed, there was no significant correlation between the beta power change and force (normalized to index finger) achieved across subjects at any of the tested effort levels: r = −0.0629, n = 32, p = 0.732 at the effort level of 10% of MVC of individual finger; r = −0.2118, n = 32, p = 0.245 at the effort level of 25% of MVC; r = −0.0944, n = 32, p = 0.608 at the effort level of 40% of MVC (Fig. 5). Similar results were seen if absolute force was used instead of force normalized to the index finger (data not shown).Therefore, our results indicated a significant effect of effort level with large effect size and statistical power, but little evidence for any effect of the finger used or the actual force generated in the modulation of the beta power during movement. The same analysis applied to relative gamma-band power during finger press failed to show any effect of effort (F_(2,30) = 1.197, p = 0.316), or finger (F_(1,15) = 0.019, p = 0.892) or their interaction (F_(2,30) = 2.230, p = 0.125).

Figure 5.

No significant correlation between normalized force and average beta power change during movement at each effort level when forces from different fingers were considered together. Regression lines and their respective 95% confidence limits are shown. Filled circles are data points from the index fingers; unfilled circles are data from little fingers.

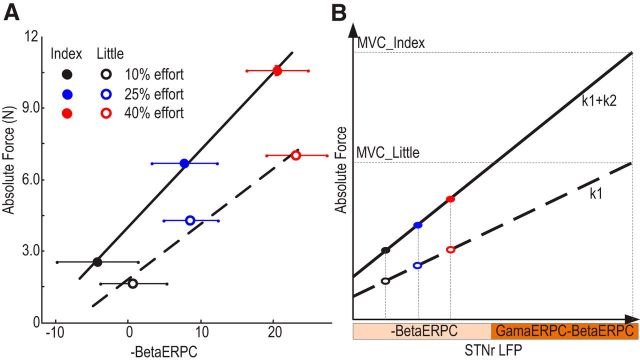
Relationship between STN beta activity during sustained contraction and absolute force changed with motor effector

The dependency of the relationship between STN beta power suppression (−BetaERPC) during sustained contraction and absolute force upon motor effector is illustrated for an exemplar subject in Figure 6A. Multilevel linear modeling was applied to the data from all valid trials of all subjects to test different hypotheses about the relationship of STN beta activity, motor effector, and the absolute exerted force. Four models were compared. The first (Equation 1) assumed that the absolute exerted force scaled with beta power suppression (−BetaERPC) with a constant regression coefficient and that any effect exerted by the different effectors consisted of an intercept shift. The second model (Equation 2) differed from the first model in the inclusion of an additional term of interaction between the relative beta suppression and the motor effector. This term modeled the effects of different motor effectors as changing the regression coefficient, with this change constant across all subjects. In the third model (Equation 3), the absolute force scaled with the beta power suppression and the regression coefficient scaled with the MVC of the motor effector. The intercept shift introduced by different effectors remained. The fourth model (Equation 4) tested whether an extra interaction term between the relative beta suppression and motor effector could further improve the prediction of exerted force if the slope between the force and the beta change was modeled as scaling with the MVC of the motor effector as in Model 3.

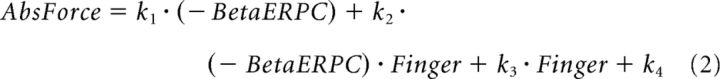Model 2 identified a significant effect of relative beta LFP power (k₁ = 0.027 ± 0.0065, p < 0.001) and a significant interaction between the beta power and motor effector (k₂ = 0.033 ± 0.010, p = 0.0017) in predicting the absolute force generated. This suggests that the regression coefficients relating relative beta LFP power suppression to the absolute force generated were significantly different for the two fingers, with the regression coefficient having larger absolute values for the index finger. Model 3 identified a significant effect of the MVC_i · (− BetaERPC) (k₁ = 0.013 ± 0.001, p < 0.001), confirming that the regression coefficients between beta power suppression and the absolute force k₁ · MVC_i scaled with the MVC of the motor effector. Model 4 showed that the interaction between the motor effector and the beta suppression was no longer necessary for the prediction of exerted force (k₂ = 0.0056 ± 0.0037, p = 0.418) once the regression coefficients between the beta power suppression and force was modeled as scaling with the MVC of the effector. The AIC analysis (results shown in Table 3) identified Model 3 to be the more compact and accurate representation of the relationship between the beta ERPC and exerted force and to have significantly higher probability of being the better model than the other two in terms of AIC. Therefore, absolute force scaled with beta power suppression but with the scaling determined by the MVC of the motor effector, which is consistent with our hypothesis that it is effort (i.e., force as a fraction of the total force achievable by the corresponding effector) that is indexed by beta LFP power suppression.

Figure 6.

Dependency of force generation on finger in an exemplar subject (A) and in a schematic of modeling (B). A, Data from case 7 (right hand). The solid and dashed line show the regression lines for the absolute force of the index and little fingers, respectively. The dots with horizontal bars show the means and SEMs across trials for different conditions. Note that in A and B, the sign of the event-related LFP power change is reversed (−BetaERPC) for convenience of viewing; therefore, more positive values represent increasing beta suppression. B, Actual exerted force scales with STN LFP beta power suppression relative to baseline and the maximal capacity of the effector adopted in the task. Thick solid line and dashed line in the figure show the force generation from effectors of different MVCs. The basal ganglia help determine the effort or vigor to be attributed to a response, with beta suppression operationalizing, or providing a proxy for, effort during sustained finger pressing. Note that gamma-band power increases in the STN LFP relative to baseline (GammaERPC) may be enlisted in coding effort at stronger effort levels (as suggested by Tan et al., 2013b). When different effectors are adopted, beta modulation is similar at the same effort level, but the actual force generated is different (compare colored filled circles with unfilled circles).

Table 3.

AIC analysis results for different models describing how absolute force relates to LFP beta activity during sustained contraction

Model	Predictor	Effects	df	AIC	Δi(AIC)	wi(AIC)	$\frac{w_i\left(AIC\right)}{w_3\left(AIC\right)}$
1	Beta + finger	Beta: k = 0.039 ± 0.005, p < 0.001; finger: k = 2.626 ± 0.203, p < 0.001	5	7183.41	29.76	2.081e-7	p < 0.001
2	Beta + finger + beta*finger	Beta: k = 0.027 ± 0.006, p < 0.001; finger: k = 2.593 ± 0.203, p < 0.001; beta*finger: k = 0.033 ± 0.010, p = 0.0017	6	7175.52	21.87	1.076e-5	p < 0.001
3	Beta*MVC + finger	Beta*MVC: k = 0.013 ± 0.001, p < 0.001; finger: k = 2.609 ± 0. 202, p < 0.001	5	7153.65	0	0.604	—
4	Beta*MVC + finger + beta*finger	Beta*MVC: k = 0.013 ± 0.001, p < 0.001; finger: k = 2.609 ± 0. 202, p < 0.001; beta*finger: k = 0.0056 ± 0.0037, p = 0.418	6	7154.49	0.84	0.396	0.656

Model 3 was the model with the minimal AIC value and the extra interaction term in Model 4 did not further increase the prediction power of the model. The Akaike weight (w_i(AIC)) and the relative Akaike weight $\frac{w_i\left(AIC\right)}{w_3\left(AIC\right)}$ showed that Model 3 had the highest probability of being the best model.

Discussion

The basal ganglia motor cortical circuit, including its dopaminergic innervation, has been suggested to regulate response vigor or effort (Niv and Rivlin-Etzion, 2007; Salamone et al., 2009; Turner and Desmurget, 2010). Previous studies have shown that frequency-specific LFP activities in the STN and globus pallidus correlate with effort and force in manual actions over the full range of contraction strengths in patients with PD or dystonia (Brücke et al., 2012; Tan et al., 2013b). Using motor effectors of different capacities for force generation, we dissociated effort from the actual force of the motor response. In particular, we show that beta power changes in the STN LFP negatively correlate with effort level independently of the motor effector or the actual force that was exerted when the effort level was stable. Our results support the hypothesis that the basal ganglia help determine the effort or vigor to be attributed to a response rather than being directly involved in the parameterization of the motor response in terms of absolute force. The results suggest that the beta suppression in the STN LFP during sustained contraction serves as or provides a proxy for effort (albeit at low effort levels) and that actual force scales with the effort signal from the basal ganglia and the maximal capacity of the effector adopted in the task in the manner schematically illustrated in Figure 6B. At stronger efforts, STN gamma power increases are enlisted in coding effort (Anzak et al., 2012; Tan et al., 2013b).

Before considering the significance of the findings in greater detail, we should acknowledge some significant limitations of the present study. First, participants were necessarily PD patients who had undergone surgery, so inferences with regard to normal functioning must be circumspect (Williams et al., 2002). That said, recordings were made on levodopa while patients' behavioral state was as near normal as possible, albeit not normal. Second, we limited maximal effort level to 40% of the MVC of individual fingers to limit fatigue. We have previously shown that force or effort correlate with beta band desynchronization over this range (Tan et al., 2013b). Higher forces or efforts were not tested and it is under these conditions that gamma synchronization may play a role in encoding force or effort. Therefore, the current study was focused on lower effort levels where beta desynchronization preferentially scales with effort, but was not designed to explore gamma power changes. Third, because visual feedback of exerted effort and required effort were simultaneously presented and veridical, we cannot dissociate between these two aspects of effort and any distinction remains an interesting research question for further study. However, we could show that the beta synchronization was not modulated by effort during the preparation phase between the warning cue and the go cue, providing some evidence that the correlation between beta activity and effort was related to motor performance rather than elicited by signaling of the required effort level. Fourth, the multilevel linear modeling combined with model comparison and selection approach based on AIC used in part here, as with any other model-based approach, can select the most compact and accurate description of the relationship of interest, but only from among presented candidate models. Finally, by only recording from the locality of the STN we can only assert that this nucleus may help to determine the effort or vigor to be attributed to a motor response because this function may be underpinned by a more extensive circuit that includes, but is not limited to, the STN.

The current study provides evidence for a contribution of the basal ganglia to encoding effort rather than actual force. Interestingly, this function was manifest during sustained contraction and not before even though subjects were presented with predictive information about the task. Indeed, once this predictive information was presented beta activity rose, rather as seen in no-go tasks (Kühn et al., 2004), and perhaps indicating the need to suppress intercurrent processing in readiness for the imperative cue. This change in beta activity during a period without movement underscores the fact that changes in beta synchrony do not themselves exclusively code for any single parameter or function. Rather, they may be better conceptualized as a property of basal ganglia circuits that sets the performance of circuit elements (Brittain and Brown, 2014). Beta synchronization may also be modulated when independent or overlapping circuits are engaged in other functions, such as offline error correction mechanisms (Tan et al., 2014) or the suppression of conflicting choices affecting behavior (Brittain et al., 2012). In this schema, beta synchrony is a generic feature of basal ganglia circuits, which is then modulated according to the recruitment of specific network elements that are necessary in the delivery of the task at any given moment in time. Such a schema therefore also allows for changes in beta activity to be a composite of several simultaneously active lines of processing.

The notion that one of the functions of the basal ganglia is to encode effort rather than force is consistent with findings from previous studies in which subjects were required to match different levels of absolute force or torque between two limbs with asymmetric maximum strength whether this was induced by fatigue (Carson et al., 2002; Weerakkody et al., 2003; Proske et al., 2004) or naturally present (Simon and Ferries, 2008). These studies showed that, without visual feedback, subjects attempting to produce equal forces between limbs actually produce equal relative forces (i.e., scaled to the instantaneous maximum strength of the muscle groups), consistent with an interpretation based on a matching of effort rather than absolute force or torque and consistent with our hypothesis about the central encoding of effort as opposed to absolute force. In addition, the current results have two interesting implications. First, our results suggested that the basal ganglia help to determine the effort to be attributed to a motor response, with such effort being related to the current maximal capacity of the motor effector. The relationship between motor effort and absolute force may change when tasks are executed with different effectors, such as the index and little finger as tested here, and due to fatigue, illness, or trauma. Therefore, to generate the most appropriate motor response required for a certain task, the required effort and underpinning frequency-specific basal ganglia activities need to be adjusted and to take into account the current state of available effectors. This adjustment may depend on peripheral feedback revealing unexpected changes in the properties of motor effectors and/or on an internal forward model that includes representation of the dynamic range of forces generated by different effectors given a certain effort level. Such an internal forward model, which generates predictions of the state of the system given current motor commands and permits compensation for instabilities due to feedback delays and uncertainty, is assumed to be a central feature in motor control, particularly during ballistic movements (Wolpert and Miall, 1996; Todorov and Jordan, 2002; Diedrichsen et al., 2010). This implies that the function of the basal ganglia in optimal control might not be limited to learning costs and rewards (Shadmehr and Krakauer, 2008), but might also extend to updating the required motor effort based on predictions from internal forward models. Second, the present findings may provide insight into the pathophysiology of bradykinesia in PD. Previous work has shown that, off of dopaminergic medication, the power suppression in the beta-band, especially that in the low-beta-band (13–23 Hz), was attenuated in patients with PD during movement initialization (Doyle et al., 2005; Devos et al., 2006; Androulidakis et al., 2007; Anzak et al., 2012) and when a constant force was meant to be sustained (Tan et al., 2013a). Such a diminished range of beta-band suppression during movement may restrict the dynamic range of the coding of effort (contracting the x-axis in Fig. 6B) and contribute to underscaled, bradykinetic movements. This is consistent with previous observations that untreated PD patients produce normal muscle activation patterns, but that muscle activity is not adequately scaled to produce the required force (Berardelli et al., 1986; Turner and Desmurget, 2010), and that PD patients show an increased probability of selecting slow movement speeds (Mazzoni et al., 2007). The relative reversibility of these motor deficits and improvement in motor-related beta reactivity with dopaminergic therapy further implicates the dopaminergic system in transcribing behavioral expediency into motor effort (Schmidt et al., 2008), a process that seems to involve, or be indexed by, beta-band suppression.