Predictors of Abstinence from Heavy Drinking During Treatment in COMBINE and External Validation in PREDICT

Abstract

Background

The goal of the current study was to use tree-based methods (Zhang and Singer, 2010) to identify predictors of abstinence from heavy drinking in COMBINE (Anton et al., 2006), the largest study of pharmacotherapy for alcoholism in the United States to date, and to validate these results in PREDICT (Mann et al., 2012), a parallel study conducted in Germany.

Methods

We compared a classification tree constructed according to purely statistical criteria to a tree constructed according to a combination of statistical criteria and clinical considerations for prediction of no heavy drinking during treatment in COMBINE. We considered over one-hundred baseline predictors. The tree approach was compared to logistic regression. The trees and a deterministic forest identified the most important predictors of no heavy drinking for direct testing in PREDICT.

Results

The tree built using both clinical and statistical considerations consisted of four splits based on consecutive days of abstinence (CDA) prior to randomization, age, family history of alcoholism (FHAlc) and confidence to resist drinking in response to withdrawal and urges. The tree based on statistical considerations with four splits also split on CDA and age but also on GGT level and drinking goal. Deterministic forest identified CDA, age and drinking goal as the most important predictors. Backward elimination logistic regression among the top 18 predictors identified in the deterministic forest analyses identified only age and CDA as significant main effects. Longer CDA and goal of complete abstinence were associated with better outcomes in both data sets.

Conclusions

The most reliable predictors of abstinence from heavy drinking were CDA and drinking goal. Trees provide binary decision rules and straightforward graphical representations for identification of subgroups based on response and may be easier to implement in clinical settings.

Introduction

Most statistical analyses of randomized clinical trials focus on between-group comparisons, however it is also important to identify predictors of good outcome regardless of treatment. A systematic literature review (Adamson et al., 2009) identified dependence severity, psychopathology ratings, alcohol-related self-efficacy, motivation and treatment goal as the most consistent predictors of alcohol treatment outcome. Furthermore, dependence severity together with baseline alcohol consumption accounted for the greatest variance in predictive models. However, potentially important variables (e.g. social support, alcoholism typology) were considered in too few studies to allow for meaningful analysis and many studies considered predictors one at a time and ignored the relationships among predictor variables. Since classical regression approaches are often limited to testing main effects and lower order interactions of limited number of predictors, a more powerful approach may be based on classification and regression trees.

Tree-based methods originated with the development of automatic interaction detection (AID) algorithms by Morgan and Sonquist (1963), Morgan and Messenger (1973) (THAID) and Kass (1980) (CHAID). Classification And Regression Tree (CART) methods were formalized by Breiman et al. (1984). Modern developments include deterministic and random forests (Zhang and Singer, 2010) and take full advantage of the computational power available today. The basic goals of tree-based methods are to produce good classification algorithms and to estimate the predictive structure of the data (i.e. identify which variables interact with one another to produce a certain classification). This is done by the method of recursive partitioning on a learning sample with the goal of validating the algorithm on an independent sample and prediction of future cases.

The learning sample is recursively divided into groups that are most homogeneous with respect to the outcome and most different from one another. Different versions of the algorithm incorporate different statistical criteria for splitting the sample and determining the optimal size of the tree (Breiman et al, 1984; Zhang and Singer, 2010).

Tree-based methods are appealing alternatives to standard linear model techniques when assumptions of additivity of the effects of explanatory variables, normality and linearity are untenable. Tree-based and forest-based methods are nonparametric computationally intensive algorithms that can be applied to large data sets and are resistant to outliers. They allow consideration of a large pool of predictor variables and can discover predictors that even experienced investigators may have overlooked (Zhang et al., 2010). These methods are most useful for identification of variable interactions and may be easier to use in clinical settings because they require evaluation of simple decision rules rather than mathematical equations (James et al, 2005; Zhang and Singer, 2010).

However, due to their focus on interactions, tree-based methods can lead to idiosyncratic results that fail to replicate. This problem has plagued the field since the inception of tree-based algorithms especially earlier versions of the methods. In order for tree-based methods to be used in clinical practice, clinical and practical considerations may need to be taken into account in order to avoid deriving trees with splitting variables that may be difficult to use by clinicians and that are unlikely to replicate in other studies.

In alcohol research, tree-based techniques have been used only in epidemiological studies for prediction (Vik et al., 2006; Muller et al., 2008). The potential of these methods to inform clinical decisions in treatment studies and ultimately in clinical practice has not been explored. The goal of the current study was to use tree-based methods to identify groups of subjects with good drinking outcomes during treatment in COMBINE (Anton et al., 2006) and to validate these results in PREDICT (Mann et al., 2012).

The COMBINE Study evaluated the benefits of combining pharmacotherapy treatment (naltrexone, acamprosate) and behavioral interventions (Medication Management (MM) (Pettinati et al., 2004), Combined Behavioral Intervention (CBI), (Miller, 2004)) in alcohol dependent patients. The PREDICT Study adopted the methodologies, assessment and behavioral interventions used in the COMBINE Study to allow for direct comparisons of the findings between the two studies (Mann et al., 2009).

A number of summary drinking outcomes have been considered in alcohol research (e.g. percent drinking or heavy drinking days, total abstinence). In COMBINE we focus on abstinence from heavy drinking following a grace period of eight weeks, which has been recommended as an outcome measure for clinical trials because it is associated with reduced risk of alcohol related consequences while allowing for improvements in drinking short of abstinence (Falk et al., 2010). This binary measure is also convenient to use with the classification approach as it provides an easily ascertained outcome and an easily interpreted decision.

2. Materials and Methods

2.1. The study samples

In COMBINE, eight groups received medical management (MM) with 16 weeks of naltrexone (100 mg/day) or acamprosate (3 g/day), both, and/or both placebos, with or without CBI. Our analysis focused on subjects who had any drinking data during treatment (N=1220). A small percentage of subjects had received inpatient treatment in the 30 days prior to enrollment (7.7%) and the majority was recruited from the community.

In PREDICT, 426 subjects were recruited from inpatient facilities and were randomly assigned to naltrexone (50 mg/day), acamprosate (2g/day) or placebo. Pharmacotherapy was given for 12 weeks combined with MM. Following the first day of heavy drinking, subjects were detoxified and randomized to augmentation with CBI in another protocol.

2.2. Drinking outcome

The outcome measure in COMBINE was no heavy drinking during the last eight weeks of double-blind treatment. Seventy subjects (5.74%) were coded as heavy drinking due to missing values. In PREDICT once subjects relapsed to heavy drinking they were switched to another protocol (Berner et al., 2013); therefore, the outcome variable in PREDICT was whether subjects relapsed to heavy drinking during double-blind treatment.

2.3. Predictors

We considered over one hundred baseline predictors in COMBINE that had less than 15% missing values. Categorical predictors with missing values had an additional missing category created. Continuous predictors had missing values imputed using PROC MI in SAS. Predictors are shown by domain in Table 1 and described in detail in Appendices 1 and 2.

Table 1.

Predictors in tree and forest analyses in COMBINE.

DOMAIN	VARIABLES
Baseline:
Demographics	Age, Gender, Race, Marital Status, Education, Employment, Family Income
Alcohol Consumption	% heavy days, % abstinent days, consecutive days abstinent, peak BAC, trajectories of any drinking and heavy drinking
Alcohol Severity	SCID symptom count, CIWA, DRINC Total, Age of Onset
Prior Alcohol Treatment	Detox, AA attendance, any treatment
Drinking Goal	Complete abstinence, conditional abstinence, controlled drinking, other
Family History	Alcohol, Smoking
Craving	OCDS Total Score
Smoking	Current smoker
Drug use	Cannabis Use
Physical Exam	Weight, Height, Pulse, Blood pressure
Laboratory Analysis	Urine and blood test results
Alcohol Abstinence Self-Efficacy	Total and Subscale Scores
URICA	Overall Readiness and 4 Subscale scores
WHO Quality of Life	Environment, Physical, Psychological, Social Relationships
SF12	Physical health
Profile of Mood States	Tension, Depression, Anger, Vigor, Fatigue, Confusion
Perceived Stress	PSS total
Important People	Number of in-network daily drinkers
Legal Problems	Arrested
Treatment:
Treatment Condition	Acamprosate, Naltrexone, COMBINE Behavioral Intervention

2.4. Training and validation samples

A random two thirds of the COMBINE data (N=809) was used for tree development and the remaining one third (N=411) for tree validation. The whole PREDICT sample (N=426) was used for external validation.

2.5. Tree construction

Two approaches to tree construction were undertaken: one based on purely statistical criteria, and another based on statistical and practical considerations.

Purely statistical approach

The Willows program (Zhang et al., 2009) was used to construct a tree to predict the outcome in COMBINE using recursive partitioning.

Tree growing

A node was split into two daughter nodes so that each daughter node was as homogeneous as possible with respect to the outcome, while the two nodes were as different from each other as possible on outcome. At each step the predictor variable and threshold of that variable that led to the best split in terms of entropy was selected. That is, for each node in the tree, the program assessed all potential predictors and all possible splits of values on these predictors (multiple possible thresholds for continuous and ordinal variables and combinations of categories for nominal variables) and identified the variable and split that was associated with the largest difference in proportions of heavy drinking in the two daughter nodes. The algorithm proceeded recursively until no further splits were possible. We imposed the restriction of at least 20 subjects in each node to avoid unstable splits.

Tree pruning

Once the full tree was grown, the chi-square statistic for 2x2 contingency tables was calculated for each split. Using a pre-selected alpha level (p = .0001), nodes whose chi-square values as well as the chi-square values of subsequent splits did not exceed the predetermined threshold were pruned to avoid over-fitting. That is, splits for which the proportions of subjects without heavy drinking in the two daughter nodes were not significantly different were removed from the tree.

Performance of the algorithm on was assessed using Area under the Curve (AUC) of the Receiver Operating Curves (ROC) showing sensitivity vs. 1-specificity for the classification of subjects in outcome categories. Values close to 1 reflect near perfect classification while values around 0.5 reflect random classification.

Approach based on statistical and clinical considerations

Tree growing

A tree was constructed in steps using recursive partitioning in JMP (SAS Institute, 2010) since in JMP the user can control the final choice of splitting variables. For each split, the top three candidates based on the log-worth statistic were considered. Two of the authors (RG and RW) prepared a table with information about the top three candidates (an example is presented in Table 2) for splitting a node and asked the remaining co-authors to rank-order the predictors based on the practical utility of each candidate. The number 1 ranks were counted and the predictor that collected the most number 1 ranks was selected. In case of a tie, a discussion among the voting members of the team resolved the tie. For continuous predictors, the optimal split was allowed to be adjusted slightly based on clinical considerations. For example, a GGT cutoff of 193 IU/L in a tree based on practical and statistical considerations was lowered to 189 IU/L which is three times the upper limit of the normal range. Tree growing proceeded until the group voted to stop splitting because the splitting paths became too complicated.

Table 2.

Top three candidates for splitting the root node of the tree predicting no heavy drinking during the last eight weeks of treatment in the training sample in COMBINE.

Predictor	Categories	Number in category	Percent without heavy drinking	Statistical Criteria (Log worth)
CDA before treatment	>14 days	120	70%	10.35
	<=14 days	689	38%
Age	>45 years	373	54%	8.38
	<=45 years	436	34%
Drinking goal	Complete abstinence or missinga	318	54%	5.62
	Othersb	491	35%

^aComplete Abstinence: “I want to quit using alcohol once and for all, to be totally abstinent, and never use alcohol ever again for the rest of my life”

^bOthers: this grouping contains all of the other responses including: 1) no goal; 2) controlled use;3) abstinence but may drink later; 4) occasional use; 5) want to quit but realize might slip.

Tree pruning

The constructed tree with 10 splits was evaluated on the validation sample in COMBINE. Splits for which the percentage of subjects with no heavy drinking in the two daughter nodes were different by less than 5% and/or the differences were not in the same direction in the validation data set as in the training data set were pruned.

Performance of the algorithm on each sample was assessed using AUC (Table 3).

Table 3.

Areas Under the Curve (AUC) showing the predictive ability of each of the considered trees and models in COMBINE and in PREDICT.

	Predictors	COMBINE Training Sample	COMBINE Validation Sample	PREDICT
Tree based on purely statistical approach	CDA	69%	61%	57%
	Age (within CDA)
	GGT (within Age)
	GOAL (within GGT)
Tree based on statistical and clinical considerations	CDA	68%	61%	57%
	Age (within CDA)
	CWITHDR (within Age)
	FH (within CWITHDR)
Tree with only the two top splits	CDA	66%	60%	57%
	Age (within CDA)
Full tree (22 splits)		78%	64%	--
Final model from logistic regression after backward elimination with 2-way interactions in both training and validation sample	CDA continuous	68%	62%	56%
	Age continuous
Logistic regression with robust predictors identified in trees	CDA	66%	60%	57%
	Age
	CDA*Age
Logistic regression with predictors identified in deterministic forest	CDA	69%	62%	60%
	Age
	GOAL

2.6. Deterministic forest

Since different combinations of predictors may lead to similar prediction, we also constructed deterministic forest in the training sample to identify the strongest predictors of the outcome. A deterministic forest consists of trees of similar structure based on the best set of splits for predicting the outcome. We applied the approach of Zhang et al (2003) and considered the top 20 splits of the root node and the top 3 splits of the two daughter nodes of the root node, giving rise to 180 (20 × 3 × 3) trees in the forest.

2.7. Logistic regression in COMBINE

We performed backward elimination logistic regression analysis with main effects and two-way interactions among the predictors identified as splitters at least 20% of the time in the deterministic forest. We limited the number of predictors because it was not possible to consider simultaneously all possible two-way interactions. At each step of the backward elimination procedure, the effect with the least significant p-value larger than 0.05 was dropped so that at each step the model was hierarchically well-formulated. Only effects that were significant in both the training and validation data sets were selected for further testing in PREDICT. We also performed logistic regression with the top categorized predictors identified from the trees and their interactions to estimate odds ratios and associated 95% confidence intervals. Backward elimination logistic regression was used to assess all possible interactions and main effects among the top three predictors identified in deterministic forests.

2.8. External validation in PREDICT

We reconstructed the trees identified in COMBINE, in the PREDICT sample. We also fit the final logistic regression models identified after backward elimination algorithms in COMBINE and tested the main effects and interactions corresponding to the trees that validated internally in COMBINE to assess effect sizes in PREDICT. The predictive abilities of the trees and logistic regression models were evaluated using AUCs.

3. Results

3.1. Classification trees

Tree based on purely statistical approach

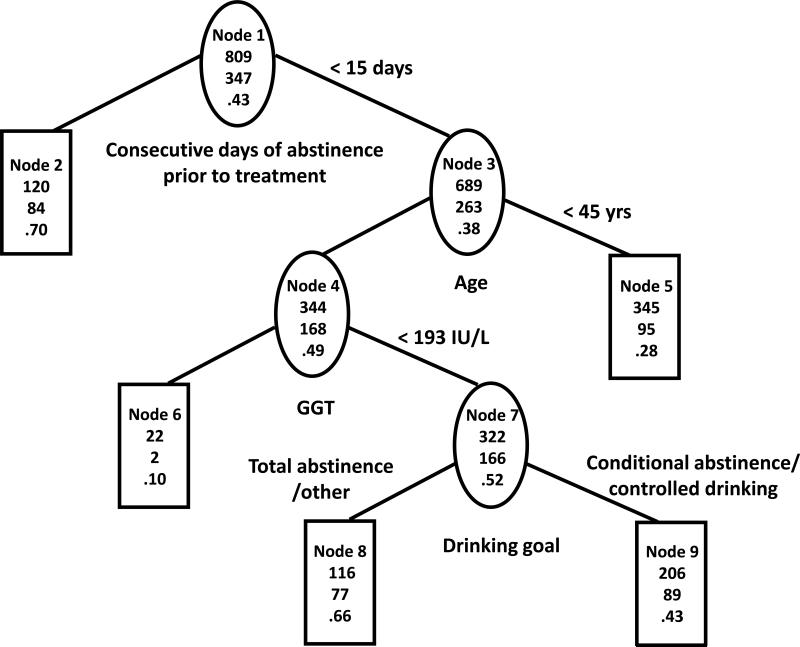
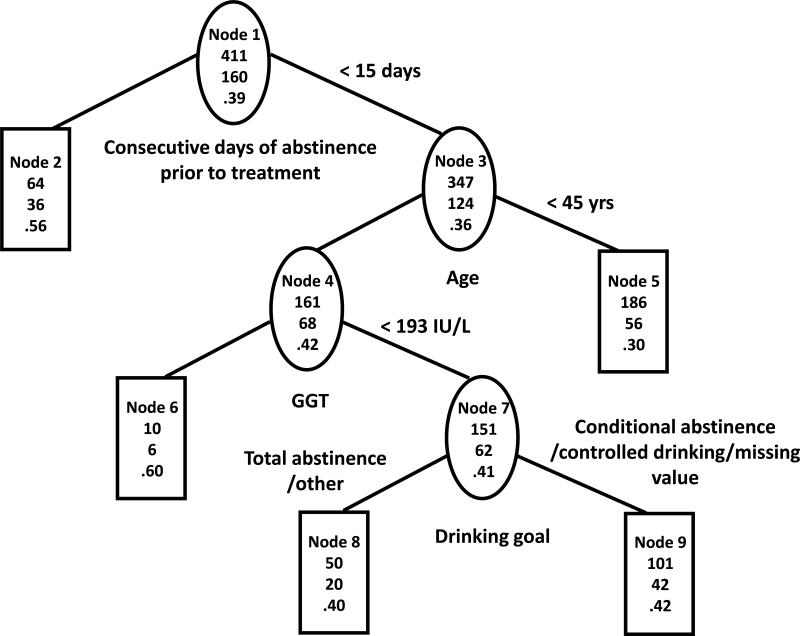
The constructed tree on the training sample (TS) is shown in Figure 1a and the same tree on the validation sample (VS) is shown in Figure 1b. The first splits of the trees show that a high proportion of subjects with more than two consecutive weeks of continuous abstinence (CDA) prior to randomization (N=120 in TS, N=64 in VS, nodes 2) abstained from heavy drinking in the last eight weeks of treatment (P = 70% in TS, 56% in VS). The second splits show that among those who had two weeks or fewer CDA prior to randomization, younger subjects (age < 45 years, nodes 5) were less likely to abstain from heavy drinking (P = 28% in TS, P = 30% in VS). The remaining two splits were based on high GGT (>=193) and on drinking goal, and did not replicate in VS. The AUC for was 69% in TS vs. 61% in VS.

Figure 1a. Tree based on statistical considerations in COMBINE training sample.

The three numbers from top to bottom in each node of the tree are total number of subjects, number of subjects with no heavy drinking during the last eight weeks of treatment and percent of subjects with no heavy drinking during the last eight weeks of treatment.

Figure 1b. Tree based on statistical considerations in COMBINE validation sample.

The three numbers from top to bottom in each node of the tree are total number of subjects, number of subjects with no heavy drinking during the last eight weeks of treatment and percent of subjects with no heavy drinking during the last eight weeks of treatment.

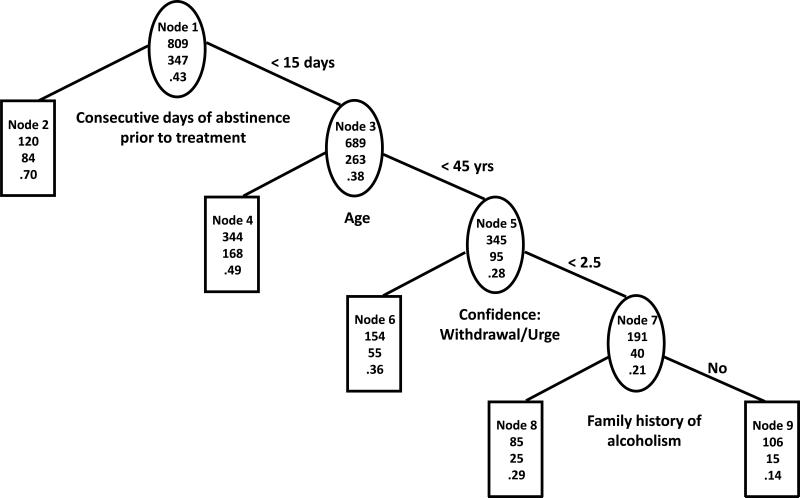
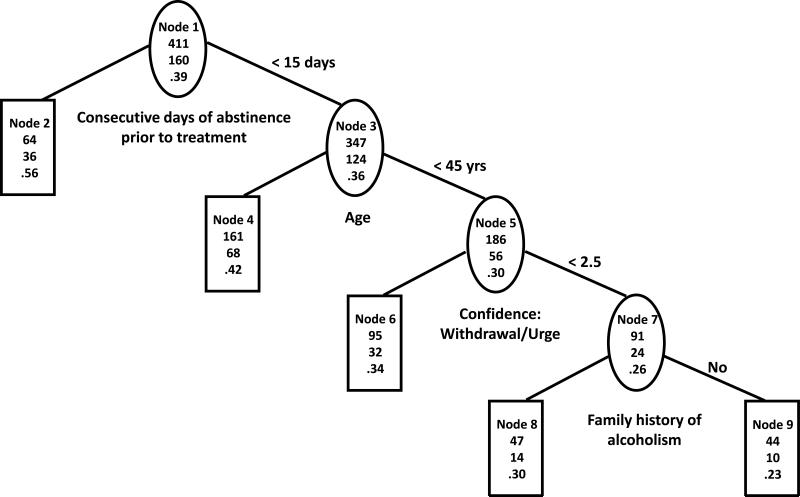
Tree based on statistical and clinical considerations

The first two splits of the trees based on statistical and practical considerations (Figures 2a and 2b) were exactly the same as the first two splits of the trees based on statistical considerations only. However, the third split was for subjects who abstained from drinking for two weeks or less prior to randomization and were younger (less than 45 years old) and was based on the withdrawal/urge sub-score on the Alcohol Abstinence Self-Efficacy (AASE) confidence scale. Subjects with higher confidence that they could resist drinking in response to withdrawal and urges (CWITHDR>=2.5, nodes 6) had higher chance of abstaining from heavy drinking (P=36% in TS, P=34% in VS) than subjects with lower confidence (P=21% in TS, P=26% in VS, nodes 7). Positive compared to negative family history of alcoholism in the group with lower confidence was associated with better outcome (P=29% vs. P=14% in TS, P=30% vs. P=23% in VS, nodes 8 vs. 9). The predictive ability of the tree was fair in TS (AUC=68%) but was substantially lower in VS (AUC=61%).

Figure 2a. Tree based on statistical and clinical considerations in COMBINE training sample.

The three numbers from top to bottom in each node of the tree are total number of subjects, number of subjects with no heavy drinking during the last eight weeks of treatment and percent of subjects with no heavy drinking during the last eight weeks of treatment.

Figure 2b. Tree based on statistical and clinical considerations in COMBINE validation sample.

The three numbers from top to bottom in each node of the tree are total number of subjects, number of subjects with no heavy drinking during the last eight weeks of treatment and percent of subjects with no heavy drinking during the last eight weeks of treatment.

Since the first two splits coincide for the two approaches, a tree with only these two splits was evaluated and had AUC=66% in TS and AUC=60% in VS. For comparison purposes, the largest tree that was constructed on TS (prior to pruning of branches) had 22 splits, AUC=78% on TS and AUC=64% on VS. These represent the upper limits of achievable prediction accuracy with the tree approach for these data.

3.2. Deterministic forest

The deterministic forest identified 94 variables that were used to split nodes in at least one of the 180 trees in the forest. Of these, 18 variables were used for node splitting at least 36 times, which corresponds to about 20% of the trees in the forest (Table 4). The top three predictors (CDA, age and drinking goal) occurred in all trees in the forest. The treatments occurred less often than 20% of the time as splitting variables in the trees and thus did not appear to be strong predictors of outcome (naltrexone – 29 times, acamprosate – 24 times, CBI – 21 times).

Table 4.

Top predictors used in node splitting in the forest and how often they were used to split a tree in the forest.

VARIABLE in COMBINE	Number of times as splitters1	Available in PREDICT
CDA prior to treatment	300	Yes
Age	300	Yes
Drinking goal	229	Yes
Baseline trajectory of heavy drinking	125	No
AASE total confidence score	105	Yes
Self-report ordinal health measure	105	No
POMS fatigue scale	87	No
Baseline trajectory of any drinking	79	No
AASE total temptation score	51	Yes
OCDS total score	51	Yes
WHO QoL psychological domain	45	Yes
AASE confidence: withdrawal/urge	39	Yes
Family history: 2 or more members	38	Yes
POMS depression scale	36	No
Perceived stress score	36	Yes2
Potassium	36	No2
Baseline smoking (yes/no)	36	Yes2
AST(SGOT)	36	Yes2

¹A predictor can be used more than once in splitting the nodes of a tree in the forest.

²These predictors were not used in the external validation logistic regression analyses due to different ranges or categories between the two data sets.

3.3. Logistic regression

Backward elimination with the top predictors identified in the deterministic forest analysis resulted in only two continuous predictors: CDA and age (Table 3). The predictive ability of this analysis was fair in TS (AUC=68%) and substantially lower in VS (AUC=62%).

Logistic regression analyses with CDA (<=14 days, >14 days), age (<=45 years, > 45 years) and the interaction had slightly worse predictive ability (AUC=66% in TS and AUC=60% in VS, Table 3). The estimates in Table 5 suggest that longer abstinence was associated with significantly higher odds of abstinence from heavy drinking in TS (OR=3.97, 95% CI: (2.59, 6.09)) and in VS (OR=2.39, 95% CI: (1.37, 4.15)). Older age was also associated with better outcome in TS (OR=2.08, 95% CI: (1.36, 3.20)) and in VS (OR=1.70, 95% CI: (1.09, 2.64)). In TS, the age effect was more significant among those with shorter abstinence (OR=2.51, 95% CI: (1.83, 3.45)) than among those with longer abstinence (OR=1.61, 95% CI: (0.58, 4.43)).

Table 5.

Odds ratios and 95% confidence intervals for the effects of predictors on abstinence from heavy drinking in logistic regression analyses in COMBINE and in PREDICT.

	Predictor	Categories	COMBINE TS	COMBINE VS	PREDICT
Predictors from tree analyses	CDA	Longer vs. Shorter1	3.97 (2.59, 6.09)*	2.39 (1.37, 4.15)*	1.60 (1.09, 2.35)*
	Age	Older vs. Younger2	2.08 (1.36, 3.20)*	1.70 (1.09, 2.64)*	1.21 (0.82, 1.78)
	Age (among shorter abstinence)	Older vs. Younger2	2.51 (1.83, 3.45)*	1.61 (0.58, 4.43)	1.13 (0.65, 1.97)
	Age (among longer abstinence)	Older vs. Younger2	1.73 (0.78, 3.83)	1.65 (0.95, 2.87)	1.29 (0.76, 2.20)
Predictors from deterministic forest analyses	CDA	Longer vs. Shorter1	3.73 (2.40, 5.78)*	2.18 (1.24, 3.81)*	1.63 (1.11, 2.40)*
	Age	Older vs. Younger2	2.43 (1.80, 3.28)*	1.40 (0.92, 2.13)	1.16 (0.75, 1.65)
	Drinking goal	Complete abstinence vs. other goals	1.97 (1.45, 2.66)*	1.71 (1.14, 2.57)*	1.71 (1.14, 2.55)*

¹In COMBINE “longer” means “> 14 days”, in PREDICT “longer” means “> 21 days”.

²In both data sets “older” means “> 45 years”.

^*Effects are significant at 0.05 level.

Backward elimination logistic regression with the top three categorized predictors identified in deterministic forest analyses (CDA, age and drinking goal) resulted in only a main effects model that had fair classification accuracy in TS (69%) and lower classification accuracy in VS (62%). As in the previous logistic regression analysis longer abstinence was associated with better outcome in both TS and VS. Goal of complete abstinence or other was associated with significantly better outcome in both TS (OR=1.97, 95% CI: (1.45, 2.66)) and VS (OR=1.71, 95% CI: (1.14, 2.57)). However, the effect of age was significant only in the TS (OR=2.43, 95% CI: (1.80, 3.28)) and not in the VS (OR=1.40, 95% CI: (0.92, 2.13)).

3.4. External validation of the results in PREDICT

Subjects in PREDICT had longer pre-randomization abstinence (median=22 days, IQR (interquartile range): 20-25 days) than subjects in COMBINE (median=5 days, IQR: 4-10 days) since COMBINE required 4 days of abstinence whereas PREDICT required two weeks of abstinence. Therefore, the cutoff for CDA in the external validation analyses was raised from two weeks (14 days) to three weeks (21 days).

We then reconstructed the trees built in COMBINE, using PREDICT. All three trees (not shown) had the same classification accuracy (57%) in PREDICT, corresponding to slightly better classification accuracy than random classification. Logistic regression analysis with CDA (<=21 days, >21 days), age (<=45 years, > 45 years) and the interaction showed that the odds of abstinence from heavy drinking during treatment were higher by about 60% among subjects with more than 3 weeks of abstinence prior to treatment (OR=1.60, 95% CI: (1.09, 2.35), Table 5). The AUC based on this model was also 57%.

The logistic regression model with age (<=45 years, > 45 years), CDA (<=21 days, >21 days) and drinking goal (total abstinence vs. all other goals) showed that longer abstinence and goal of total abstinence was associated with significantly higher odds of abstinence from heavy drinking (OR = 1.63, 95% CI: (1.10, 2.40) and OR=1.71, 95% CI: (1.14, 2.55)). Age, however, did not have a significant effect on the outcome. This model achieved 60% classification accuracy, the highest achieved classification accuracy in.

4. Discussion

Both tree-based and logistic regression analyses showed at best fair classification accuracy in the data sets. This suggests that the signal-to-noise ratios in these data sets are small and that even with multiple variables accurate prediction of abstinence from heavy drinking during treatment is difficult. Nevertheless, a couple of predictors of good outcome emerged from all analyses, namely abstinence prior to treatment and drinking goal.

The capacity to sustain abstinence prior to treatment significantly decreased the likelihood of heavy drinking. Two weeks of abstinence was the optimal split in COMBINE which is consistent with prior work by Stout (2000). In PREDICT, CDA was defined as more than three weeks of abstinence due to the differences in the data ranges between COMBINE and PREDICT, but this different categorization also showed that longer pre-treatment abstinence predicted a good response. Thus individuals with less abstinence prior to entering treatment may need additional support to improve their odds of a good outcome.

Drinking goal also emerged as an important variable in the deterministic forest analyses. In both data sets a goal of total abstinence was associated with significantly lower likelihood of heavy drinking. Subjects with goals of conditional abstinence or controlled drinking may require additional monitoring and interventions specifically designed to teach moderate drinking skills in order to achieve better outcome. In COMBINE, individuals with controlled drinking goals have more daily drinkers in their social networks suggesting that efforts to incorporate non-drinkers in their network might be worth exploring (DeMartini et al., in press).

The treatments did not appear in our individual trees and were very infrequently selected as splitting variables in the deterministic forest. However, we performed sensitivity analyses when forcing the first split to be on treatment in order to assess how robust the identified predictors are in the context of treatment. Results when naltrexone was forced to be the first splitting variable are presented in Supplemental Figures 1a and 1b. It appears that the identified predictors (consecutive days of abstinence, age) are robust across treatments but it is possible that within a particular treatment stronger predictors may be identified (e.g. lower BAC peak levels may be a slightly better predictor of outcome than older age for subjects on naltrexone with shorter abstinence). While the question of which predictors are associated with good outcome within a treatment group is of interest, identifying subgroups of subjects for whom a particular treatment is better than another is the more challenging and potentially more important question. The latter goal may be achieved by modifying the splitting criterion (Zhang et al, 2010; Lipkovich et al, 2014) so that subjects are divided into subgroups with the greatest difference in treatment response rather than forcing the first split. Approaches based on counterfactual outcomes (Foster et al., 2011) are also possible. Systematic exploration of moderator effects in COMBINE and PREDICT is a topic of future research.

The purely statistical approach of tree building performed comparably to the approach based on statistical and practical considerations on TS but did not replicate as well on VS. It identified splitting variables (e.g. GGT) with cutoffs that are difficult to apply due to differences in lab reference values. In analyses with multiple predictors, the best splitting variable may only be marginally better than another more practically useful variable that is either more robust across samples (i.e. absolute values are more comparable across samples) or is easier to implement in a clinical setting. When due consideration to practical utility is given in the statistical analysis and different alternatives are evaluated in parallel, the results are more likely to be both nearly optimal in terms of statistical performance and translate more easily into clinical practice.

Tree-based methods have potential advantages over classical statistical methods because they rely on fewer assumptions and are useful for identification of interactions. Although logistic regression can also be used to test interactions, usually the number of predictors and the order of the considered interactions is limited (only up to two-way or three-way). Furthermore, there are no automatic procedures for cutoff selection on continuous variables and although usually power is greater with continuous predictors, when the relationship between the predictor and the outcome is non-linear, or when a simple decision rule is necessary, logistic regression may not be very practical. In contrast, trees automatically present in the form of simple decision rules and can be easier to adapt for use in clinical settings.

However, extra caution needs to be used to perform both internal and external validation of trees since interactions replicate less frequently than main effects. In particular, trees can identify splitting variables that are idiosyncratic to the particular data set more often than classical methods that focus on main effects (Hastie et al., 2009; Zhang and Singer, 2010). Due to the performed internal and external validation of our analyses, our results can be considered stable in similar samples of patients.

Tree-based methods can discover important predictors and combinations of predictors among a large pool of covariates. However, in this particular application tree-based methods did not identify strong predictors of outcome and had slightly worse performance to logistic regression in terms of classification accuracy on VS. This is probably due to lack of important multi-way interactions in the data set and to a set of predictors that is not prohibitively large to be handled by classical methods.

Our conclusions are limited because the COMBINE and PREDICT samples are not necessarily representative of the patient populations treated for alcohol dependence. Programs may vary in the requirements for abstinence, patients may have comorbidities, such as drug dependence, which were exclusionary criteria in COMBINE and PREDICT.

Furthermore, while the three best predictors (length of pre-treatment abstinence, age and drinking goal) can be easily assessed, the cutoffs on abstinence and age are sample-dependent. PREDICT was designed to allow direct comparisons to COMBINE but differences in some of the inclusion/exclusion criteria, the study populations, the treatment length and the outcome definitions hampered the external validation process. In particular, the two study samples differed on CDA, which turned out to be the most important predictor. In PREDICT, subjects were required to have at least 2 weeks of inpatient hospitalization prior to enrollment and thus had significantly longer CDA than subjects in COMBINE who achieved abstinence primarily as outpatients. Our decision to increase the cutoff from 2 weeks in COMBINE to 3 weeks in PREDICT was meant to assure that sufficient sample sizes were available in each group in PREDICT and may appear somewhat arbitrary. However, since fluctuations in drinking follow a weekly pattern, by increasing the cutoff by one week, we were able to minimize the effect of such fluctuations on the results.

We also used two different periods to define “no heavy drinking”: eight weeks in COMBINE following a grace period of eight weeks and twelve weeks in PREDICT. We could have used the first twelve weeks of the 24-week study period in COMBINE in order to achieve complete comparability of outcome, however we chose to focus in COMBINE on no heavy drinking following a grace period in order to identify strongest predictors of this clinical outcome recommended by the FDA. Ideally, the same outcome should have been used in PREDICT but it was not possible since after relapse to drinking, individuals were randomized to CBI.

We coded missing heavy drinking data as heavy drinking in the analyses. This approach could produce biased estimates when the proportion of missing data is large and/or the assumptions that dropouts have relapsed to heavy drinking is untenable. To investigate the sensitivity of our conclusions, we performed alternative analyses on completers only and when subjects with missing drinking data were coded as not heavy drinking. The results were very similar, that is the first two splits of all trees were exactly the same, deterministic forests identified the same top three predictors and there was significant overlap in the remaining top predictors (Supplemental Table 3). This is probably due to the small proportion of subjects with missing data but speaks to the robustness of our conclusions. In studies with larger proportion of missing data, multiple imputation may be considered (Hapfelmeier et al., 2012).

Although we did not identify unexpected or surprising predictors, our results have clinical and research utility. In particular, our finding that longer abstinence prior to treatment is a reliable predictor of treatment response can help with the design of future studies. Subjects who are able to maintain abstinence for two weeks or more are likely to have good outcome regardless of treatment and hence assessment of novel treatments for alcoholism could focus on subjects who do not achieve this level of abstinence. In clinical settings with tight resources, more intensive counseling could be allocated to those with less abstinence at evaluation time. Our forest analyses identified the most important predictor variables associated with good outcome and thus our findings could guide instrument selection for future studies. Further external validation of the results in other data sets will be beneficial. The PROJECT MATCH data could be particularly informative because it contains two arms, an aftercare arm following inpatient treatment and an outpatient arm (The project MATCH research group, 1997).