Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2015 Jan 5;593(Pt 4):763–774. doi: 10.1113/jphysiol.2014.282723

Silicon central pattern generators for cardiac diseases

Alain Nogaret 1,✉, Erin L O'Callaghan 2, Renata M Lataro 3, Helio C Salgado 3, C Daniel Meliza 4, Edward Duncan 5, Henry D I Abarbanel 6, Julian F R Paton 2
PMCID: PMC4398520  PMID: 25433077

Abstract

Cardiac rhythm management devices provide therapies for both arrhythmias and resynchronisation but not heart failure, which affects millions of patients worldwide. This paper reviews recent advances in biophysics and mathematical engineering that provide a novel technological platform for addressing heart disease and enabling beat-to-beat adaptation of cardiac pacing in response to physiological feedback. The technology consists of silicon hardware central pattern generators (hCPGs) that may be trained to emulate accurately the dynamical response of biological central pattern generators (bCPGs). We discuss the limitations of present CPGs and appraise the advantages of analog over digital circuits for application in bioelectronic medicine. To test the system, we have focused on the cardio-respiratory oscillators in the medulla oblongata that modulate heart rate in phase with respiration to induce respiratory sinus arrhythmia (RSA). We describe here a novel, scalable hCPG comprising physiologically realistic (Hodgkin–Huxley type) neurones and synapses. Our hCPG comprises two neurones that antagonise each other to provide rhythmic motor drive to the vagus nerve to slow the heart. We show how recent advances in modelling allow the motor output to adapt to physiological feedback such as respiration. In rats, we report on the restoration of RSA using an hCPG that receives diaphragmatic electromyography input and use it to stimulate the vagus nerve at specific time points of the respiratory cycle to slow the heart rate. We have validated the adaptation of stimulation to alterations in respiratory rate. We demonstrate that the hCPG is tuneable in terms of the depth and timing of the RSA relative to respiratory phase. These pioneering studies will now permit an analysis of the physiological role of RSA as well as its any potential therapeutic use in cardiac disease.

An unmet clinical need

Heart failure affects around 900,000 people in the UK, accounts for 5% of emergency hospital admissions and utilises 2% of all NHS hospital bed days (Cleland et al. 2012). In the USA, over 1 million patients are admitted to hospital for congestive heart failure (Hall et al. 2012). Despite use of the optimal medical therapy available, the prognosis remains poor for this group of patients who also have a high symptom burden. Patients in whom symptoms are refractory to medical therapy may be considered for cardiac resynchronisation therapy (CRT) using biventricular pacemakers. Unfortunately, these devices are only appropriate in a minority of patients with a left bundle branch block pattern (LBBB) ECG (25% of the total heart failure population). Furthermore, amongst recipients of CRT, 30% of patients do not respond clinically (Jeevanathan et al. 2009). Thus, there remains a substantial unmet clinical need in the heart failure population and new interventional therapies are required. An early prognosis indicator of heart disease is loss of respiratory sinus arrhythmia and this raises the question as to its physiological role and whether reinstatement could provide therapeutic benefit.

Respiratory sinus arrhythmia (RSA) and its loss in cardiovascular disease

The healthy heart is subjected to chronotropic modulation by the respiratory cycle (Anrep et al. 1936); this is respiratory sinus arrhythmia (RSA). RSA is a naturally occurring arrhythmia that is prominent at birth and in athletes but is lost with ageing and cardiovascular disease. RSA is brought about by a combination of afferent feedback (pulmonary lung inflation, baroreceptors) and central coupling between medullary respiratory and cardiac vagal motor neurones (McAllen & Spyer, 1978; McAllen et al. 2011). Despite RSA being highly preserved during evolution (cartilaginous fish, amphibians, reptiles) its functional significance remains both incompletely understood and controversial (Larsen et al. 2010). It has been suggested that the physiological function of RSA is to match ventilation and perfusion in the lungs thereby optimising oxygen uptake and carbon dioxide removal (Hayano et al. 1996). In dogs, Giardino et al. (2002) showed that dead space-to-tidal volume ratio and intrapulmonary shunt fraction decreased and that oxygen uptake was enhanced. They measured the ventilatory equivalents of CO2 and O2 during paced breathing in healthy humans and concluded that gas exchange efficiency increased with RSA. In contrast, Sin et al. (2010) concluded that the improvements in gas exchange efficiency were unrelated to RSA in humans. Additionally, Elstad has reported a role for RSA in stabilising blood pressures generated from the left and right ventricles (Elstad, 2012). Finally, Grossman & Taylor (2007) discussed the importance of RSA for optimising energy use by cardio-respiratory synchronisation, consistent with the idea that RSA saved heart beats.

Recently, we built a mathematical model to understand the functional role of RSA and to address the inconsistencies of previous reports (Ben-Tal et al. 2012, 2014). We demonstrated that although gas exchange efficiency can improve with both slow and deep breathing, and increased mean heart rate, this was all unrelated to RSA. Rather, we showed that RSA minimises the work done by the heart, so saving energy and making it more efficient, while maintaining physiological levels of arterial carbon dioxide. Given that poor control of arterial CO2 (hypocapnia) contributes to central sleep apnoea in ∼45% of patients with heart failure (Javaheri et al. 1995), RSA may, via its ability to regulate 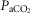Inline graphic, reduce incidence of central sleep apnoea and provide therapeutic benefit for a failing heart. Consistent with this notion is the finding that RSA may increase cardiac efficiency by saving energy (Ben-Tal et al. 2012, 2014). This result has led to the notion that in heart failure, a condition when heart rate variability is diminished, re-instatement of RSA could provide therapeutic benefit to cardiac pumping (Mortara et al. 1994). To begin to address this, we have designed and tested a silicon hardware central pattern generator (hCPG) based on realistic neurones with Hodgkin–Huxley kinetics.

Why biological central pattern generators (bCPGs) are better than digital electronics for rhythm generation

The study of bCPGs of invertebrates (Kristan et al. 2005; Marder et al. 2005; Selverston, 2009) has shown why neural networks are better suited than digital electronics for generating biological rhythms. First, neurons are intrinsically non-linear devices. Non-linearity, which is often an undesirable property in conventional electronic design, is the property that enables bCPGs to integrate their motor output based on incoming biological stimuli (Rabinovich et al. 2000). Second, bCPGs are able to maintain the precise timing of burst discharges within the rhythmic cycle by adapting neuron phase lag to changes in rhythm frequency. Marder et al. (2005) have ascribed this property to frequency-dependent synaptic depression or activation of transient outward potassium current on release from a hyperpolarised membrane potential, for example. These mechanisms are essential for maintaining the correct sequence of motor signals as the rhythmic frequency increases (Mamiya & Nadim, 2004). For instance, the neuromeres of leech maintain the sequence of contraction of body wall segments as the swimming rate increases (Kristan et al. 2005). This approach could conceivably be used to maintain the contraction of the four chambers of the heart during tachycardia, for example. However, existing cardiac resynchronisation pacemakers have fixed timings which are adjusted by the practitioner and cannot adapt when heart rate increases. An hCPG, however, would provide beat-to-beat instantaneous adjustment of the inter-ventricular (τVV) and atrio-ventricular (τAV) delays.

The basic building block of a bCPG is the half-oscillator which consists of two neurons inhibiting each other (Varona et al. 2001). This elementary circuit has been thoroughly studied in the leech where it acts as a two phase cardiac pacemaker (De Schutter et al. 1993; Marder & Calabrese, 1996) producing fundamental heartbeat. The inhibitory pair is surrounded by four pairs of interneurons whose role is to switch motor drive between the two hearts of the leech in cycles lasting 20–40 beats (Norris et al. 2006). Three-phase bCPGs are found in the stomatogastric ganglion of the lobster and the respiratory pattern generator of Lymnaea (Taylor & Lukowiak, 2000; Selverston, 2009). They incorporate a third neuron which interacts with the others via mutually inhibitory links. In mammals, respiratory rhythms are equally generated by a three phase bCPG located in the brainstem (Fig. 1). This consists of three neurons: early-I (early inspiration), post-I (post inspiration) and aug-E (late inspiration) (Richter, 1982; Smith et al. 2007; Abdala et al. 2009). These neurones are considered by us to be connected together via reciprocal inhibitory synapses (Smith et al. 2007, 2013). It has been argued that the coupled respiratory oscillators, which are active in the expiratory phase and located in the Bötzinger complex (BötC: post-I and aug-E neurons) and in the inspiratory phase in the pre-Bötzinger complex (pre-BötC: early-I), derive from the gill and lung oscillators of earliest air breathers (Vasilakos et al. 2005). Neurocircuitry in the ventrolateral medulla oblongata couples the respiratory oscillator with both cardiac vagal preganglionic motoneurones, which slow the heart rate in expiration, and the diaphragm, to inflate lungs (Fig. 1). The amplitude and phase of heart rate modulation depend on physiological feedback (blood pressure, lung inflation, hormonal release) which is integrated, in part, by the circuit in Fig 1. It is this function that we would ideally wish to replicate to either boost or restore naturally occurring RSA.

Figure 1. Regulation of the cardio-respiratory system by biological CPGs (bCPGs) in the brainstem.

Figure 1

Open in a new tab

The respiratory bCPG is based on a group of three mutually inhibitory neurons named post-I, aug-E and early-I which generate a three phase rhythm in the following sequence: inspiration (early-I fires), post-inspiration (post-I fires) and expiration (aug-E fires). Pulmonary lung inflation stimulates vagal feedback that inhibits inspiratory neurons. By projecting excitatory synapses to post-I neurons, arterial baroreceptors provide part of the feedback responsible for respiratory sinus arrhythmia. The central coupling between post-I and cardiac vagal motoneurones (cVN) contributes to respiratory sinus arrhythmia (RSA) also. Inspiration is driven by the activation of the pre-I and early-I neurons that via aug-I neurones send signals to inhibit cVN and excite phrenic motoneurones that innervate the diaphragm. cVN activity has the effect of slowing heart rate. This depressive action is balanced by rostral ventrolateral medulla (RVLM) neurons that accelerate heart rate and increase the force of contraction via sympathetic innervation. Figure based on circuits described in Smith et al. 2007 and Smith et al. 2013. Abbreviations: VRC, ventral respiratory group; PN, phrenic nerve; cVN, cardiac vagus nerve; SN, sympathetic nerve; VN, vagus nerve; GPN, glossopharyngeal nerve; RTN, retro-trapezoid nucleus; Inline graphic, excitatory link; Inline graphic, inhibitory link.

Generalising this to networks of N neurons reciprocally connected by inhibitory synapses gives so-called Winnerless dynamics (Laurent et al. 2001). As neurons compete for firing, electrical activity ‘bounces’ from one neuron to another along closed loop trajectories producing competition without a winner (Rabinovich et al. 2001, 2006). Theoretical studies of these inhibitory networks have demonstrated two more properties of CPGs. The firing sequence of neurons along these trajectories generates motor patterns which are extremely stable with respect to noise yet very sensitive to changes in input signal. The reason for this is that neurons that compete via mutually inhibitory connections develop mildly chaotic dynamics characterised by attractors surrounded by basins of attraction. Assuming moderate noise is present in the system, its effect is only to perturb the oscillations of the CPG about the attractor. The CPG then returns to the stable oscillatory mode when the perturbation has been removed. In contrast, a pulsed input, which unlike noise has non-zero time average, may kick the CPG state from one basin of attraction to another by moving across dynamic saddle points. This has the advantage that pacing devices based on neural electronics will be inherently safer because they are not easily perturbed when set into a given mode of oscillation. The CPG theoretically behaves like an associative memory with (N−1)! attractors where the same circuit will produce different modes of oscillation in response to a given stimulus (Bick & Rabinovich, 2009). Lastly, CPGs are very robust. The natural life span of the lobster is 25 years and the rhythmic patterns of the stomatogastric ganglion must be preserved over this time despite changes in neurotransmitter production. This bCPG has been shown to restore the original modes of oscillation even after the structure of the network had been impaired (Thoby-Brisson & Simmers, 2002). In Drosophila, the connectivity of CPGs is present at birth and this enables the correct motor patterns to be generated innately (Suster & Bate, 2002). The mammalian respiratory rhythm generator is another good example of the robustness of the bCPG despite constant state changes during exertion, speech, swallowing and sleep states. The addition of bCPG-like technology to pacemakers, which are known to be affected by parasitic electromagnetic fields in the leads (e.g. within magnetic resonance scanners), would improve the safety of cardiac rhythm management. hCPGs emulating the neuro-circuitry of the brainstem (Fig. 1) have the potential to restore a number of important cardiac functions (Fig. 2). These include: RSA, adaptation of heart rate to effort and beat-to-beat adaptation of atrio-ventricular and inter-ventricular delays in cardiac resynchronisation.

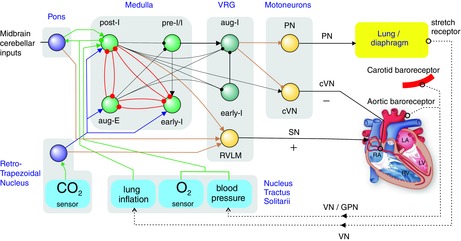
Figure 2. Challenges for hCPG pacemaker: adaptation of the heart to physiological feedback.

Figure 2

Open in a new tab

A, vagus nerve (cVN) activity modulates heart rate across the respiratory cycle to produce respiratory sinus arrhythmia (RSA). The phase (and amplitude) of heart rate modulation could be shifted to any part of the respiratory cycle using a hCPG. RSA arises from the respiratory bCPG oscillator depicted in Fig. 1. B, heart rate (HR) correlates to the breathing rate to provide adaptation that is proportional to the increase in physical effort. This coupling is again based on brainstem circuitry (Fig. 1). C, the atrio-ventricular delay (τAV) and inter-ventricular delays (τVV) also adapt to heart rate. Beat-to-beat adaptation of these delays can be integrated in pacing by hCPGs. Abbreviations: AV, atrio-ventricular; f, frequency; PN, phrenic nerve (diaphragm); SN, sympathetic nerve; VV, inter-ventricular; ϕ, phase.

The limitations of software neuron CPGs

CPGs have been modelled using computational neuron models to investigate network dynamics (Rabinovich et al. 2001, 2006). Computer simulations of these networks (sCPGs), however, rely on increasingly reductive neuron models as network size increases. One reason for this is that large systems of Hodgkin–Huxley equations (Hodgkin & Huxley, 1952) develop stiffness as a result of incorporating multiple time constants. The accurate integration of stiff systems of equations causes computer processing time to rise exponentially with the size of the network. Wojcik et al. (2011) and Zhao & Nogaret (2014) have mapped the dynamics of three Hodgkin–Huxley neurons that interact through mutually inhibitory synapses. The time required for integrating the output of such an elementary network or even a single neuron with seven ion channels (Meliza et al. 2014) is of the order of several minutes. Digital technology is therefore inadequate for making cardiac implants that must integrate physiological feedback in real time. Approximate neuron models are not suitable either as neurons must produce motor signals with the same degree of realism as complex mammalian neurons, which host a wide range ion channels. In contrast, software neurons have the advantage of flexibility and have been successfully interfaced with bCPGs to substitute one bCPG neuron with a software neuron model running on digital processing board. In this way, Olypher et al. (2006) and Sorensen et al. (2004) have controlled the burst duty cycle of the leech heart bCPG by artificially changing calcium and h-current properties in the model neuron. Prinz et al. (2004) and Sharp et al. (1993) have developed computer controlled conductances that inject specific time-dependent currents in order to tune the coupling between neurons. This has enabled Pinto et al. (2001) to change the firing sequence of stomatogastric neurons in the lobster. To meet the demands of greater performance for neural model simulation and dynamic clamps, several groups are turning to field programmable gate arrays (Graas et al. 2004; Mak et al. 2006).

Hardware implementations – the analog way

Analog neural computation is the approach needed for generating accurate motor patterns in real time with instantaneous response time irrespective of the size of the network or the complexity of the neuron models. To date, technologists have only implemented hCPGs for engineering applications such as modelling the gait of robots (Briggman & Kristan, 2008), the walking and swimming motions of the salamander (Ijspeert et al. 2013) or the undulation of robotic fish (Lee et al. 2007). However, neurons used in these studies are simplified models based on various degrees of approximation, which would be unsuitable for driving physiological systems that need to integrate afferent feedback signals in vivo. Lee et al. (2007) used the Hindmarsh–Rose neuron (Hindmarsh & Rose, 1984) which models bursting dynamics but is constrained by a stiff parameter space that cannot be easily adjusted to fit real neurons. Nakada et al. (2003) have proposed an hCPG that generates the motor sequences of different horse gaits: walk, trot and gallop. Switching from one gait to another, however, involved a physical reconfiguration of the network rather than the application of the appropriate stimulus to switch from one oscillator (attractor) mode to another (Zhao & Nogaret, 2014). To our knowledge hCPGs have not yet been developed for neuro-stimulation. Our interests are in building hCPGs for naturalistic and adaptive pacing of cardiac function, as described in Fig. 2.

In Table1, we list the advantages of hCPGs for medical devices. Analog circuits are simpler than digital ones due to the elimination of analog-to-digital conversion, microprocessor and memory. Thus, they are easier to scale down on a silicon chip for implanting. They have lower power requirements that increases battery lifetime beyond the lifetime of the patient. They integrate input signals in real time and with perfect accuracy irrespective of the number of channels or compartments in the neurons, and of the number of neurones in the network. However, analog hCPGs are difficult to program not least because of their chaotic dynamics.

Table 1.

Comparative merits of sCPGs and hCPGs

Digital/software CPGs (sCPGs) Analog/hardware CPGs (hCPGs)
Cons Analog (in) → ADC → CPU → DAC → Analog (out) Pros Analog (in) → Analog neurons → Analog (out)
Clocked digital electronics (CPU, ADC, DAC) Asynchronous electronics capable of responding to stimuli in real time
Slow numerical integration of real stimuli by Hodgkin–Huxley-like models Instantaneous integration of stimuli
Accuracy and speed of computation decreases when the network size increases Accuracy and speed is independent of the size of the network
Increasingly simple neuron approximations need to be considered as the network size increases to keep integration tractable Realistic multichannel neurons can be integrated in networks of arbitrary size
Hard to scale down Easy to scale down to a few square millimetres (no ADC, DAC or CPU needed)
Battery lifetime: 10 years Battery lifetime >> patient life
Pros Ease and flexibility of programming software Cons Complex programming of analog chips
Open in a new tab

Abbreviations: ADC, analog-to-digital converter; CPU, central processing unit; DAC, digital-to-analog converter.

The challenge in engineering neural networks for medicine therefore lies in finding the network parameters (neuronal and synaptic conductances, channel gate and kinetic parameters) that enable the network to emulate the bCPG. For the simplest networks such parameters can be obtained by trial and error (Nogaret et al. 2013). For more complicated networks such as the mammalian respiratory CPG in Fig. 1, analytical techniques must be devised to generate these parameters automatically. Such techniques exist and have been developed in recent years to infer the parameters of systems of non-linear differential equations from the assimilation of electrophysiological data (Vanier & Bower, 1999; Jolivet et al. 2008; van Geit et al. 2008). It is therefore conceivable that if the activity of the PN, cVN and RVLM output neurons can be measured as a function of the electrical activity of the inputs, over a wide dynamic range of inputs (e.g. sensory feedback), a quantitative model of the respiratory CPG can be inferred and tested. Data assimilation methods have been used to build quantitative neuron models and this is what we describe in the next section.

Data assimilation – a novel automated method for building biologically accurate hCPGs

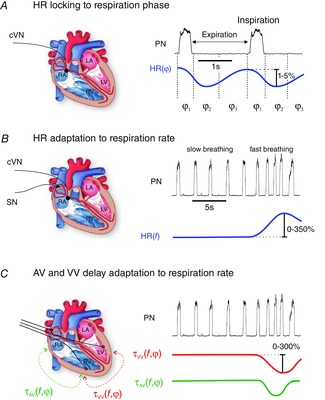
Mathematical tools that infer hidden parameters from experimental data are routinely used by medical practitioners when reconstructing internal organs with computer tomography. Inverse methods of this kind generally rely on the knowledge of a mathematical model (describing how X-rays interact with biological tissue) together with the measurement of a model variable (the intensity of scattered photons) to infer parameters inaccessible to the experimenter (the volume density of biological tissue). Inferring the internal parameters of neurons and networks, however, requires a more sophisticated algorithm that accounts for the non-linear nature of the models (Abarbanel, 1993). This methodology is based on Takens’ embedding theorem that states that, under certain conditions, a non-linear system can be reconstructed from a sequence of observations of the state of a dynamic system (Takens, 1981). If the observation is the recording of a neuron membrane voltage, all internal parameters of the neuron (channel conductances, gate threshold voltages and kinetic parameters) may be inferred from the time series data as long as the current waveform stimulating the neuron is sufficiently varied to activate every time constant of the neuron. In this case, the inverse problem is fully constrained meaning that data assimilation yields a single value for each parameter of the model. These theoretical premises have in recent years spurred the search for parameter extraction methods capable of constructing quantitative neuron models by assimilation of the electrophysiological recordings of biological neurons (Vanier & Bower, 1999; Jolivet et al. 2008; van Geit et al. 2008). One approach started from semi-empirical Hodgkin–Huxley (Hodgkin & Huxley, 1952) models incorporating tabulated values for channel activation, inactivation and kinetic parameters and extracting the ion channel conductances. The problem of fitting these conductances to the electrophysiological data is essentially a linear one. Optimal conductances have been inferred from random parameter search (Tuckwell & Richter, 1978; Baldi et al. 1998; Goldman et al. 2001; Golowasch et al. 2002; Prinz et al. 2003; Huys et al. 2006; Lepora et al. 2012), evolutionary (Eiben & Smith, 2003; Hobbs & Hooper, 2008) and genetic algorithms (Achard & De Schutter, 2006; Druckmann et al. 2007; Kobayashi et al. 2009; Buhryet al. 2011; Hendrickson et al. 2011; Marasco et al. 2012;), gradient descent methods (Reid et al. 2007) and simulated annealing (Pospischil et al. 2008; Brookings et al. 2014). A second category of methods has been developed to infer the non-linear parameters that control the time dependence and voltage dependence of channel conductances. Vavoulis et al. (2012) have extracted activation thresholds, time delays and ion channel conductances from Lymnaea motoneurons by performing time series analysis with Kitagawa's self-organising state space approach (Kitagawa, 1998) and the Kalman filter (Evensen, 2009). Kostuk et al. (2012) have demonstrated Monte Carlo path integral methods and Meliza et al. (Toth et al. 2012; Meliza et al. 2014) have modelled different populations of neurons from the songbird high vocal centre using interior point optimisation, a non-linear convex optimisation method (Gill et al. 2005; Wächter & Biegler, 2006). In a first step, the interior point filter automatically generates the parameters (i.e. membrane ionic conductances and their kinetics) that best synchronise the model to the experimental time series data (Fig. 3). In a second step, the completed neuron model is validated by comparing its response to any current waveform with experimental observation (Fig. 3). Neuron models built from data assimilation are remarkably accurate at making quantitative predictions of voltage oscillations elicited by arbitrary current waveforms (Meliza et al. 2014). This approach may now be extended to finding the parameters of networks to build hCPGs that accurately reproduce the behaviour of bCPGs.

Figure 3. Construction of quantitative neuron models.

Figure 3

Open in a new tab

Top, neuron parameters including the channel conductances, gate thresholds and kinetic parameters are extracted by assimilating electrophysiological recordings of interneurons of the songbird high vocal centre with interior point optimisation (green curve). The current protocol used to stimulate the neuron was generated by the chaotic Lorenz system. Bottom, predicted response made by integrating the experimental current protocol with the completed neuron model (red curve). The prediction is compared with the observed membrane voltage (black curve). This demonstrates the power of data assimilation for constructing predictive neuron (and network) models (after Meliza et al. 2014).

Besides building predictive models, data assimilation offers a novel route for categorising neuron types and neuron functions based on the types of ion channels expressed in electrophysiological experiments. Provided the electrical parameters of ion channels can be extracted with sufficient accuracy, the method may identify subunits of ion channels based on the different conformal properties of their constituting proteins. Through assimilation of electrophysiological data, Meliza et al. (2014) have succeeded in identifying neurons projecting to different cortices of the songbird high vocal centre. Given the one-to-one correspondence between ion channels and genes (Warren et al. 2010; Lovell et al. 2013) data assimilation may also reveal the genes expressed in different categories of neurons. In summary, non-linear optimisation enables the construction of both neurons and neural network models that accurately emulate the response of biological CPGs. This recent work has removed a major obstacle to the engineering of efficient implantable hCPGs.

Proof of concept – artificially inducing respiratory sinus arrhythmia with two/three phase hCPG

The neuronal hCPG we have built is based on analog neurons which integrate the Hodgkin–Huxley equations in real time that is suitable for neuro-stimulation (Nogaret, 2012; Nogaret et al. 2013; Fig. 4). Our hCPG applies biphasic neuron bursts of controlled duration and timing to the vagus nerve, which we stimulate unidirectionally using selective anodal block clamp (Jones et al. 1995) to slow the heart rate. The stimulation can be phase tuned to target any point within the respiratory cycle with pulses of amplitude varying between 0 and 4.3 V (Fig. 5). Our hCPG synchronises heart rate modulation to the respiratory cycle by receiving signals from either the phrenic nerve or diaphragmatic electromyographic activity. Switching the timing of stimulation from inspiration to expiration affected the amplitude of heart rate modulation (Nogaret et al. 2013). The sensitivity of the heart rate response to stimulation in the different respiratory phases was found to vary (Nogaret et al. 2013) as shown in Fig. 5.

Figure 4. Slowing down of the heart rate in phase with respiration (in vitro).

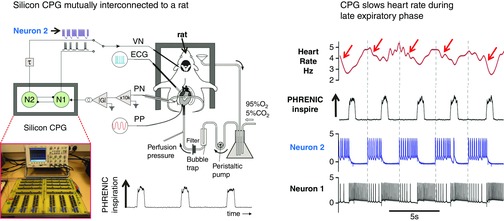
Figure 4

Open in a new tab

The analog hCPG receives respiratory feedback from the phrenic nerve via filters, amplifiers and a rectifying transconductance amplifier |G| (conductance modulus). The r.m.s. amplitude of the raw phrenic signal (not show) is 60–100 μV. Using this information, the central pattern generator (CPG) stimulates the vagus nerve with neuron bursts in phase or out of phase with inspiration recorded from the phrenic nerve (PN). Neuron 2 is connected to the vagus nerve (VN) and slows down the heart rate by ∼40% during the expiratory phase. Note: Neuron 1 is not connected to any output but is reciprocally connected to Neuron 2 to produce a two phase oscillator. Current work is to build a three neuron CPG to generate a three phase rhythm to emulate breathing in vivo. Abbreviation: ECG, electrocardiogram.

Figure 5. RSA induced by stimulating the vagus nerve in phase and out of phase with inspiration.

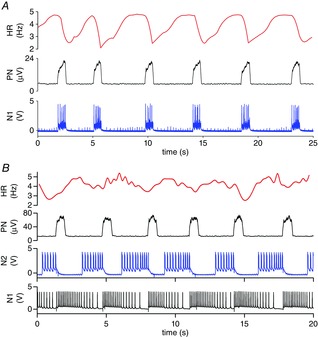
Figure 5

Open in a new tab

The flexibility of the hCPG allows cardiac RSA pacing during either inspiration coincident with phrenic nerve activity (stimulation by Neuron 1 of hCPG -N1: 80 Hz; A) or during the latter part of the expiratory pause (stimulation by N2: 58 Hz; B). Abbreviations: HR, heart rate; PN, phrenic nerve; N1, Neuron 1 of hCPG; N2, Neuron 2 of hCPG (after Nogaret et al. 2013).

To test the adaptive ability and robustness of our hCPG, we changed respiratory rate and found that stimulation naturally synchronises to respiration even at high breathing rates (Fig. 6). This novel analog hCPG now provides us with the ability to induce RSA in rats and mimic some functional aspects generated within the cardio-respiratory networks of the ventrolateral medulla.

Figure 6. Adaptive response of the hCPG to variation in respiratory frequency.

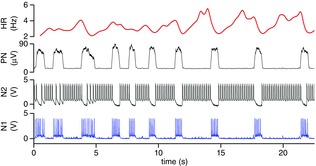
Figure 6

Open in a new tab

The dynamic response of the hCPG to a change in respiratory frequency is shown. Note how the hCPG tracks the change in respiratory rate precisely to maintain respiratory sinus arrhythmia. The reduction in RSA amplitude at the faster respiratory frequency reflects a lack of time for the full bradycardia to develop prior to the next inspiration. Abbreviations: HR, heart rate; PN, phrenic nerve; N1, Neuron 1 of hCPG; N2, Neuron 2 of hCPG (after Nogaret et al. 2013).

Future applications for bioelectronic medicine

Because of their stability and ability to integrate incoming physiological signals in real time, implantable analog hCPGs are likely to have numerous applications in both basic science and medical therapeutics where the endogenous rhythmic drive required by a biological system is suppressed or lost in disease. Table1 emphasises the unique and potentially game changing advantages that analog hCPGs have over digital devices. Analog hCPGs will provide novel and more naturalistic ways to modulate body systems because of their adaptive characteristics allowing them to respond to changes in the environment. They can integrate incoming sensory information and provide an appropriate effective output dependent upon behavioural state.

An application we are exploring is cardiac pacemaking and the generation of RSA for improving cardiac function; the latter is based on a prediction we made using a new mathematical model (Ben-Tal et al. 2012, 2014). Current cardiac pacemakers are pre-set and although some have the ability to respond to acceleration or movement or body temperature this is limited and restrictive. The adaptive properties of hCPGs can be harnessed with data assimilation to provide heart rate adaptation to the rate of respiration and beat-to-beat adaptation of τVV and τAV delays in cardiac resynchronisation therapy, for example. This would, for the first time, provide physiological pacing and physiological gearing of the degree of exertion (as detected from changes in respiratory rate) with appropriate levels of cardiac pacing. This could include, for example, appropriate post-exercise pacing which is likely to be important in protecting a failing heart. Given the possibility for modulation of synaptic transmission at the level of the cardiac vagal ganglion McAllen et al. (2011), the data from Bibevski & Dunlap (1999) is most pertinent: synaptic transmission efficacy at the pre-ganglionic to post-ganglionic synapse (within the cardiac vagal ganglia) was depressed in a canine heart failure model. Clearly this would compromise the efficacy of such a device in heart failure, at least in dogs. However, recent data from the rat indicate no such loss of transganglionic transmission for controlling cardiac vagal activity up to 4 h post myocardial infarction (Passamani et al. 2014). Nevertheless, any application to a model (or human) in which transmission through the cardiac ganglion is suppressed in disease states can be circumvented by stimulating the SA node directly via the right atrium. This would also alleviate issues of vagus-induced negative ionotropism, which may compromise any beneficial effects of vagal-induced respiratory sinus arrhythmia pacing in the failing heart. Finally, other applications might include generation of respiratory and locomotor rhythmicity following spinal cord injury but this all remains a challenge for the future.

Glossary

Abbreviations

ADC

analog-to-digital converter

bCPG

biological central pattern generator

BötC

Bötzinger complex

CPG

central pattern generator

CPU

central processing unit

CRT

cardiac resynchronisation therapy

cVN

central vagus nerve

DAC

digital-to-analog converter

hCPG

hardware central pattern generator

HR

heart rate

GPN

glossopharyngeal nerve

LBBB

left bundle branch block

NHS

National Health Service (UK)

PN

phrenic nerve

r.m.s

root mean square

RSA

respiratory sinus arrhythmia

RTN

retro-trapezoid nucleus

RVLM

rostral ventro lateral medulla

sCPG

software central pattern generator

SN

sympathetic nerve

τAV

atrioventricular delay

τVV

interventricular delay

VN

vagus nerve

VRG

ventral respiratory group

Biography

Inline graphic Alain Nogaret is a physicist with interest in building and studying artificial neurons and networks that make constructive use of the principles of nonlinear science to develop novel therapies for chronic diseases. He has demonstrated enhanced transmission of electric pulses by stochastic resonance in semiconductor neurons that have dendrites, soma and axon compartments. He has also demonstrated the coexistence of multiple motor patterns in central pattern generator hardware and their activation by command neuron signals. Erin O'Callaghan, Renata Lataro (research fellows) and Julian Paton are all experimental physiologists interested in neural control systems of arterial pressure and respiration.

Additional information

Competing interests

None declared.

Authors contributions

A.N. and J.F.R.P. have written the manuscript. All authors have commented on specific sections.

Funding

E.L.O. and J.F.R.P. are supported by the British Heart Foundation. The support of the National Institutes of Health is acknowledged (R01 NS069220). R.M.L. is supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP).

References

  1. Abarbanel HDI, Brown R, Sidorowich JJ. Tsimring LSh. The analysis of observed chaotic data in physical systems. Rev Mod Phys. 1993;65:1331. [Google Scholar]
  2. Abdala APL, Rybak IA, Smith JC. Paton JFR. Abdominal expiratory activity in the rat brainstem-spinal cord in situ patterns, origins and implications for respiratory rhythm generation. J Physiol. 2009;587:3539–3559. doi: 10.1113/jphysiol.2008.167502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Achard P. De Schutter E. Complex parameter landscape for a complex neuron model. PLoS Comp Biol. 2006;2:e94. doi: 10.1371/journal.pcbi.0020094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Anrep GV, Pascual W. Rossler R. Respiratory variations of the heart rate II. The central mechanism of the respiratory arrhythmia and the inter-relations between the central and the reflex mechanisms. Proc Roy Soc. 1936;119:218–230. [Google Scholar]
  5. Baldi P, Vanier MC. Bower JM. On the use of Bayesian methods for evaluating compartmental neural models. J Comput Neurosci. 1998;5:285–314. doi: 10.1023/a:1008887028637. [DOI] [PubMed] [Google Scholar]
  6. Ben-Tal A, Shamailov SS. Paton JFR. Evaluating the physiological significance of respiratory sinus arrhythmia: looking beyond ventilation-perfusion efficiency. J Physiol. 2012;590:1989–2008. doi: 10.1113/jphysiol.2011.222422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ben-Tal A, Shamailov SS. Paton JF. Central regulation of heart rate and the appearance of respiratory sinus arrhythmia: New insights from mathematical modelling. Math BioSci. 2014;255C:71–82. doi: 10.1016/j.mbs.2014.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bibevski S. Dunlap ME. Ganglionic mechanisms contribute to diminished vagal control in heart failure. Circulation. 1999;99:2958–63. doi: 10.1161/01.cir.99.22.2958. [DOI] [PubMed] [Google Scholar]
  9. Bick C. Rabinovich MI. Dynamical origin of the effective storage capacity in the brain's working memory. Phys Rev Lett. 2009;103:218101. doi: 10.1103/PhysRevLett.103.218101. [DOI] [PubMed] [Google Scholar]
  10. Briggman KL. Kristan WB., Jr Multifunctional pattern-generating circuits. Ann Rev Neurosci. 2008;31:271–294. doi: 10.1146/annurev.neuro.31.060407.125552. [DOI] [PubMed] [Google Scholar]
  11. Brookings T, Goeritz ML. Marder E. Automatic parameter estimation of multicompartmental models via minimization of trace error with control adjustment. J Neurophysiol. 2014;112:2332–2348. doi: 10.1152/jn.00007.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Buhry L, Pace M. Saighi S. Global parameter estimation of an Hodgkin–Huxley formalism using membrane voltage recordings: Application to neuro-mimetic analog integrated circuits. Neurocomp. 2011;81:75–85. [Google Scholar]
  13. Cleland J, Dargie H, Hardman S. McDonagh T. National Heart Failure Audit. British Society for Heart Failure; 2012. [Google Scholar]
  14. De Schutter E, Simon TW, Angstadt JD. Calabrese RL. Modeling a neural oscillator that paces heart beat in the medicinal leech. Amer Zool. 1993;33:16–28. [Google Scholar]
  15. Druckmann S, Banitt Y, Gidon A, Schürmann F, Markram H. Segev I. A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front Neurosci. 2007;1:7. doi: 10.3389/neuro.01.1.1.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eiben AE. Smith JE. Introduction to Evolutionary Computing. Heidelberg: Springer; 2003. [Google Scholar]
  17. Elstad M. Respiratory variations in pulmonary and systemic blood flow in healthy humans. Acta Physiol (Oxf) 2012;205:341–348. doi: 10.1111/j.1748-1716.2012.02419.x. [DOI] [PubMed] [Google Scholar]
  18. Evensen G. Data Assimilation: The Ensemble Kalman Filter. 2nd edn. Berlin: Springer; 2009. [Google Scholar]
  19. Giardino ND, Glenny RW, Borson S. Chan L. Respiratory sinus arrhythmia is associated with efficiency of pulmonary gas exchange in healthy humans. Am J Physiol Heart Circ Physiol. 2002;284:H1585–H1591. doi: 10.1152/ajpheart.00893.2002. [DOI] [PubMed] [Google Scholar]
  20. Gill PE, Murray W. Saunders MA. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005;47:99–131. [Google Scholar]
  21. Goldman MS, Golowasch J, Marder E. Abbott LF. Global structure, robustness and modulation of neuronal models. J Neurosci. 2001;21:5229–5238. doi: 10.1523/JNEUROSCI.21-14-05229.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Golowasch J, Goldman MS, Abbott LF. Marder E. Failure of averaging in the construction of a conductance-based neuron model. J Neurophysiol. 2002;87:1129–1131. doi: 10.1152/jn.00412.2001. [DOI] [PubMed] [Google Scholar]
  23. Graas EL, Brown EA. Lee RH. An FPGA-based approach to high speed simulation of conductance-based neuron models. Neuroinformatics. 2004;2:417–435. doi: 10.1385/NI:2:4:417. [DOI] [PubMed] [Google Scholar]
  24. Grossman P. Taylor EW. Toward understanding respiratory sinus arrhythmia: relations to cardiac vagal tone, evolution and biobehavioral functions. Biol Psychol. 2007;754:263–85. doi: 10.1016/j.biopsycho.2005.11.014. [DOI] [PubMed] [Google Scholar]
  25. Hall MJ, Levant S. DeFrances CJ. Hospitalization for Congestive Heart Failure: United States, 2000–2010. NCHS Data Brief. 2012;108 [PubMed] [Google Scholar]
  26. Hayano J, Yasuma F, Okada A, Mukai S. Fujinami T. Respiratory sinus arrhythmia. A phenomenon improving pulmonary gas exchange and circulatory efficiency. Circulation. 1996;94:842–847. doi: 10.1161/01.cir.94.4.842. [DOI] [PubMed] [Google Scholar]
  27. Hendrickson EB, Edgerton JR. Jaeger D. The use of automated parameter searches to improve ion channel kinetics. J Comput Neurosci. 2011;31:329–346. doi: 10.1007/s10827-010-0312-x. [DOI] [PubMed] [Google Scholar]
  28. Hindmarsh JL. Rose RM. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc London B. 1984;221:87–102. doi: 10.1098/rspb.1984.0024. [DOI] [PubMed] [Google Scholar]
  29. Hobbs KH. Hooper SL. Using complicated, wide dynamic range driving to develop models of single neurons in single recording sessions. J Neurophysiol. 2008;99:1871–1883. doi: 10.1152/jn.00032.2008. [DOI] [PubMed] [Google Scholar]
  30. Hodgkin AL. Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Huys QJM, Ahrens MB. Paninski L. Efficient estimation of detailed single neuron models. J Neurophysiol. 2006;96:872–890. doi: 10.1152/jn.00079.2006. [DOI] [PubMed] [Google Scholar]
  32. Ijspeert AJ, Crespi A, Ryczko D. Cabelguen J-M. From swimming to walking with a salamander robot driven by a spinal cord model. Science. 2013;315:1416–1420. doi: 10.1126/science.1138353. [DOI] [PubMed] [Google Scholar]
  33. Javaheri S, Parker TJ, Wexler L, Michaels SE, Stranberry E, Nishyama H. Roselle GA. Occult sleep-disordered breathing in stable congestive heart failure. Ann Intern Med. 1995;122:487–492. doi: 10.7326/0003-4819-122-7-199504010-00002. [DOI] [PubMed] [Google Scholar]
  34. Jeevananthan V, Daubert JP. Zareba W. Cardiac resynchronization therapy in heart failure patients: An update. Cardiol J. 2009;16:197–209. [PubMed] [Google Scholar]
  35. Jolivet R, Schürmann F, Berger TK, Naud R, Gerstner W. Roth A. The quantitative single-neuron modeming competition. Biol Cybern. 2008;99:417–426. doi: 10.1007/s00422-008-0261-x. [DOI] [PubMed] [Google Scholar]
  36. Jones JFX, Wang Y. Jordan D. Heart rate response to selective stimulation of cardiac vagal C fibres in anaesthetized cats, rats and rabbits. J Physiol. 1995;489.1:203–214. doi: 10.1113/jphysiol.1995.sp021042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Kitagawa G( A self-organizing state-space model. J Am Stat Assoc. 1998;93:1203–1215. [Google Scholar]
  38. Kobayashi R, Tsubo Y. Shinomoto S. Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold. Front Comput Neurosci. 2009;3:9. doi: 10.3389/neuro.10.009.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kostuk M, Toth BA, Meliza CD, Margoliash D. Abarbanel HDI. Dynamical estimation of neuron and network properties II: path integral Monte Carlo methods. Biol Cyb. 2012;106:155–167. doi: 10.1007/s00422-012-0487-5. [DOI] [PubMed] [Google Scholar]
  40. Kristan WB, Jr, Calabrese RL. Friesen WO. Neuronal control of leech behaviour. Prog Neurobiol. 2005;76:279–327. doi: 10.1016/j.pneurobio.2005.09.004. [DOI] [PubMed] [Google Scholar]
  41. Larsen PD, Tzeng YC, Sin PYW. Gallety DC. Respiratory sinus arrhythmia in conscious humans during spontaneous respiration. Respir Physiol Neurobiol. 2010;174:111–118. doi: 10.1016/j.resp.2010.04.021. [DOI] [PubMed] [Google Scholar]
  42. Laurent G, Stopfer M, Friedrich R, Rabinovich M, Volkovskii A. Abarbanel H. Odor encoding as an active, dynamical process: experiments computation and theory. Ann Rev Neurosci. 2001;24:263–297. doi: 10.1146/annurev.neuro.24.1.263. [DOI] [PubMed] [Google Scholar]
  43. Lee YJ, Lee J, Kim KK, Kim Y-B. Ayers J. Low power CMOS electronic central pattern generator design for a biomimetic underwater robot. Neurocomp. 2007;71:284–296. [Google Scholar]
  44. Lepora NF, Overton PG. Gurney K. Efficient fitting of conductance-based model neurons from somatic current clamp. J Comput Neurosci. 2012;32:1–24. doi: 10.1007/s10827-011-0331-2. [DOI] [PubMed] [Google Scholar]
  45. Lovell PV, Carleton JB. Mello CV. Genomics analysis of potassium channel genes in songbirds reveals molecular specializations of brain circuits for the maintenance and production of learned vocalizations. BMC Genomics. 2013;14:1–28. doi: 10.1186/1471-2164-14-470. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. McAllen RM. Spyer KM. The baroreceptor input to cardiac vagal motoneurones. J Physiol. 1978;282:365–74. doi: 10.1113/jphysiol.1978.sp012469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. McAllen RM, Salo LM, Paton JF. Pickering AE. Processing of central and reflex vagal drives by rat cardiac ganglion neurones: an intracellular analysis. J Physiol. 2011;589:5801–18. doi: 10.1113/jphysiol.2011.214320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Mak TST, Rachmuth G, Lam K-P. Poon C-S. A component-based FPGA design framework for neuronal ion channel dynamics simulations. IEEE Trans Neur Sys Rehab Eng. 2006;14:410–418. doi: 10.1109/TNSRE.2006.886727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Mamiya A. Nadim F. Dynamic interaction of oscillatory neurons coupled with reciprocally inhibitory synapses acts to stabilize rhythm period. J Neurosci. 2004;24:5140–5150. doi: 10.1523/JNEUROSCI.0482-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Marasco A, Limongiello A. Migliore M. Fast and accurate low-dimensional reduction of biophysically detailed neuron models. Sci Rep. 2012;2:928. doi: 10.1038/srep00928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Marder E, Bucher D, Schulz D. Taylor AL. Invertebrate central pattern generation moves along. Curr Biol. 2005;15:R685–R699. doi: 10.1016/j.cub.2005.08.022. [DOI] [PubMed] [Google Scholar]
  52. Marder E. Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
  53. Meliza CD, Kostuk M, Huang H, Nogaret A, Margoliash D. Abarbanel HDI. Estimating parameters and predicting membrane voltages with conductance based models. Biol Cyb. 2014;108:495–516. doi: 10.1007/s00422-014-0615-5. [DOI] [PubMed] [Google Scholar]
  54. Mortara A, La Rovere MT, Signorini MG, Pantaleo P, Pinna G, Martinelli L, Ceconi C, Cerutti S. Tavazzi L. Can power spectral analysis of heart rate variability identify a high risk subgroup of congestive heart failure patients with excessive sympathetic activation? A pilot study before and after heart transplantation. Br Heart J. 1994;71:422–430. doi: 10.1136/hrt.71.5.422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Nakada K, Asai T. Amemiya Y. An analog CMOS central pattern generator for interlimb coordination in quadruped locomotion. IEEE Trans Neur Net. 2003;14:1356–1365. doi: 10.1109/TNN.2003.816381. [DOI] [PubMed] [Google Scholar]
  56. Nogaret A( Central pattern generator. 2012. . Patent GB1209174.0.
  57. Nogaret A, Zhao L, Moraes DJA. Paton J. Modulation of respiratory sinus arrhythmia in rats with central pattern generator hardware. J Neurosci Meth. 2013;212:124–132. doi: 10.1016/j.jneumeth.2012.09.024. [DOI] [PubMed] [Google Scholar]
  58. Norris BJ, Weaver AL, Morris LG, Wenning A, Garcia PA. Calabrese RL. A central pattern generator producing alternative outputs: temporal pattern of premotor activity. J Physiol. 2006;96:309–326. doi: 10.1152/jn.00011.2006. [DOI] [PubMed] [Google Scholar]
  59. Olypher A, Cymbalyuk G. Calabrese RL. Hybrid systems analysis of the control of burst duration by low-voltage-activated calcium current in leech heart interneurons. J Neurophysiol. 2006;96:2857–2867. doi: 10.1152/jn.00582.2006. [DOI] [PubMed] [Google Scholar]
  60. Passamani LM, Abdala AP, Moraes DJ, Sampaio KN, Mill JG. Paton JF. Temporal profile and mechanisms of the prompt sympathoexcitation following coronary ligation in Wistar rats. PLoS One. 2014;9:e101886. doi: 10.1371/journal.pone.0101886. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Pinto RD, Elson RC, Szücs A, Rabinovich MI, Selverston AI. Abarbanel HDI. Extended dynamic clamp: controlling up to four neurons using a single desktop computer and interface. J Neurosci Meth. 2001;108:39–48. doi: 10.1016/s0165-0270(01)00368-5. [DOI] [PubMed] [Google Scholar]
  62. Pospischil M, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Frégnac Y, Markram H. Destexhe A. Minimal Hodgkin–Huxley type models for different classes of cortical and thalamic neurons. Biol Cybern. 2008;99:427–441. doi: 10.1007/s00422-008-0263-8. [DOI] [PubMed] [Google Scholar]
  63. Prinz AA, Abbott LF. Marder E. The dynamic clamp comes of age. Trends Neurosci. 2004;27:218–24. doi: 10.1016/j.tins.2004.02.004. [DOI] [PubMed] [Google Scholar]
  64. Prinz AA, Billimoria CP. Marder E. Alternative to hand-tuning conductance-based models: Construction and analysis of databases of model neurons. J Neurophysiol. 2003;90:3998–4015. doi: 10.1152/jn.00641.2003. [DOI] [PubMed] [Google Scholar]
  65. Rabinovich MI, Varona P, Abarbanel HDI. Nonlinear cooperative dynamics of living neurons. Int J Bifurcation & Chaos. 2000;10:913–933. [Google Scholar]
  66. Rabinovich MI, Varona P, Selverston AI. Abarbanel HDI. Dynamical principles in neuroscience. Rev Mod Phys. 2006;78:1213–1265. [Google Scholar]
  67. Rabinovich M, Volkovski A, Lecanda P, Huerta R, Abarbanel HDI. Laurent G. Dynamical encoding by networks of competing neuron groups: Winnerless competition. Phys Rev Lett. 2001;87:068102. doi: 10.1103/PhysRevLett.87.068102. [DOI] [PubMed] [Google Scholar]
  68. Reid MS, Brown EA. De Weerth SP. A parameter-space search algorithm tested on a Hodgkin–Huxley model. Biol Cybern. 2007;96:625–634. doi: 10.1007/s00422-007-0156-2. [DOI] [PubMed] [Google Scholar]
  69. Richter DW( Generation and maintenance of the respiratory rhythm. J Exp Biol. 1982;100:93–107. doi: 10.1242/jeb.100.1.93. [DOI] [PubMed] [Google Scholar]
  70. Selverston AI( Invertebrate central pattern generator circuits. Phil Trans R Soc B. 2009;365:2329–2345. doi: 10.1098/rstb.2009.0270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Smith JC, Abdala APL, Koizumi H, Rybak IA. Paton JFR. Spatial and functional architecture of the mammalian brain stem respiratory network: a hierarchy of three oscillatory mechanisms. J Neurophysiol. 2007;98:3370–3387. doi: 10.1152/jn.00985.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Smith JC, Rybak IA, Borgmann A, Abdala AP. Paton JFR. Brainstem respiratory networks: building blocks and microcircuits. Trends Neurosci. 2013;36:152–162. doi: 10.1016/j.tins.2012.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Sharp AA, O'Neil MB, Abbott LF. Marder E. Dynamic clamp: Computer generated conductances in real neurons. J Neurophysiol. 1993;69:992–995. doi: 10.1152/jn.1993.69.3.992. [DOI] [PubMed] [Google Scholar]
  74. Sin PYW, Webber MR, Gallety DC, Ainslie PN, Brown SJ, Willie CK, Sasse A, Larsen PD. Tzeng Y-C. Interactions between heart rate variability and pulmonary gas exchange efficiency in humans. Exp Physiol. 2010;95:788–797. doi: 10.1113/expphysiol.2010.052910. [DOI] [PubMed] [Google Scholar]
  75. Sorensen M, De Weerth S. Cymbalyuk G. Calabrese RL. Using a hybrid neural system to reveal regulation of neuronal network activity by an intrinsic current. J Neurosci. 2004;24:5427–5438. doi: 10.1523/JNEUROSCI.4449-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Suster ML. Bate M. Embryonic assembly of a central pattern generator without sensory input. Nature. 2002;416:174–178. doi: 10.1038/416174a. [DOI] [PubMed] [Google Scholar]
  77. Takens F. Detecting strange attractors in turbulence. In: Young L-S, editor; Rand DA, editor. Dynamical Systems and Turbulence. Vol. 898. 1981. pp. 366–381. Lect Notes Math. [Google Scholar]
  78. Taylor BE. Lukowiak K. The respiratory central pattern generator of Lymnaea: a model, measured and malleable. Rep Physiol. 2000;122:197–207. doi: 10.1016/s0034-5687(00)00159-6. [DOI] [PubMed] [Google Scholar]
  79. Thoby-Brisson M. Simmers J. Long term neuro-modulatory regulation of a motor pattern-generating network: Maintenance of synaptic efficiency and oscillatory properties. J Neurophysiol. 2002;88:2942–2953. doi: 10.1152/jn.00482.2001. [DOI] [PubMed] [Google Scholar]
  80. Toth BA, Kostuk M, Meliza CD, Margoliash D. Abarbanel HDI. Dynamical estimation of neuron and network properties I: variational methods. Biol Cyb. 2012;105:217–237. doi: 10.1007/s00422-011-0459-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Tuckwell HC. Richter W. Neuronal interspike distribution and the estimation of neurophysiological and neuroanatomical parameters. J Theor Biol. 1978;71:167–183. doi: 10.1016/0022-5193(78)90265-5. [DOI] [PubMed] [Google Scholar]
  82. van Geit W, Schutter ED. Achard P. Automated neuron model optimization techniques: a review. Biol Cybern. 2008;99:241–251. doi: 10.1007/s00422-008-0257-6. [DOI] [PubMed] [Google Scholar]
  83. Vanier MC. Bower JM. A comparative survey of automated parameter-search methods for compartmental models. J Comput Neurosci. 1999;7:149–171. doi: 10.1023/a:1008972005316. [DOI] [PubMed] [Google Scholar]
  84. Varona P, Torres JJ, Abarbanel HDI, Rabinovich Elson RC. Dynamics of two electrically coupled chaotic neurons: Experimental observations and model analysis. Biol Cybern. 2001;84:91–101. doi: 10.1007/s004220000198. [DOI] [PubMed] [Google Scholar]
  85. Vasilakos K, Wilson RJA, Kimura N. Remmers JE. Ancient gill and lung oscillators may generate the respiratory rhythms of frogs and rats. J Neurobiol. 2005;15:369–85. doi: 10.1002/neu.20102. [DOI] [PubMed] [Google Scholar]
  86. Vavoulis DV, Straub VA, Aston JAD. Feng J. A self-organizing state-space-model approach for parameter estimation in Hodgkin–Huxley-type models of single neurons. PLoS Comp Biol. 2012;8:e1002401. doi: 10.1371/journal.pcbi.1002401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Wächter A. Biegler LT. On the implementation of an interior-point filter line search algorithm for large-scale nonlinear programming. Math Program Ser A. 2006;106:25–57. [Google Scholar]
  88. Warren WC, Clayton DF, Ellegren H, Arnold AP, Hillier LDW, Künstner A, Searle S, White S, Vilella AJ, Fairley S, et al. The genome of a songbird. Nature. 2010;464:757–762. doi: 10.1038/nature08819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Wojcik J, Clewley R. Shilnikov A. Order parameter for bursting polyrhythms in multifunctional central pattern generators. Phys Rev E. 2011;83:056209. doi: 10.1103/PhysRevE.83.056209. [DOI] [PubMed] [Google Scholar]
  90. Zhao L. Nogaret A. Stimulus-dependent polyrhythms of central pattern generator hardware. Int J Math Comput Phys Quant Eng. 2014;8:721. [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES