Abstract
In surgical planning of the Fontan connection for single ventricle physiologies, there can be differences between the proposed and implemented options. Here, we developed a surgical planning framework that determines the best performing option and ensures that the results will be comparable if there are slight geometrical variations.
Eight patients with different underlying anatomies were evaluated in this study; surgical variations were created for each connection by changing either angle, offset or baffle diameter. Computational fluid dynamics were performed and the energy efficiency (indexed power loss-iPL) and hepatic flow distribution (HFD) computed. Differences with the original connection were evaluated: iPL was not considerably affected by the changes in geometry. For HFD, the single superior vena cava (SVC) connections presented less variability compared to the other anatomies. The Y-graft connection was the most robust overall, while the extra-cardiac connections showed dependency to offset. Bilateral SVC and interrupted inferior vena cava with azygous continuation showed high variability in HFD. We have developed a framework to assess the robustness of a surgical option for the TCPC; this will be useful to assess the most complex cases where pre-surgery planning could be most beneficial to ensure an efficient and robust hemodynamic performance.
Key terms: Congenital heart defects, Computational fluid dynamics, Fontan procedure, Surgical planning
Introduction
The staged Fontan procedure has been the method of choice in single ventricle (SV) congenital heart defect palliation for many years1. In this procedure, the superior and inferior vena cava (SVC and IVC, respectively) are anastomosed to the pulmonary arteries, bypassing the heart. The IVC is connected via the Fontan pathway (FP) in the final stage, creating the total cavopulmonary connection (TCPC)2. Although short-term outcomes are acceptable, there are still many long-term complications that affect these patients3, 4. An example of these is pulmonary arteriovenous malformations (PAVM); these are characterized by the formation of arterial to venous shunts in the lungs, which bypass the pulmonary gas exchange unit, resulting in decreased oxygen saturation. The origin of this complication is unknown, but previous studies have shown that factors present in the hepatic venous blood prevent the formation of these shunts5–8. Decreased exercise capacity is another morbidity that affects SV patients; elevated TCPC energy loss and increased workload on the functional ventricle are hypothesized to contribute to this decreased capacity9–11.
Surgical planning has been used in the most anatomically complex and high-risk cases in order to design a TCPC that can provide the best hemodynamic conditions12, 13. While this framework has been used in over 30 patients to date, there are still geometrical discrepancies between the proposed and implemented option14. The cause of these differences can be multifactorial: i) the surgeon is only given a visual representation of the proposed option, and the actual surgical implementation is an interpretation of this; ii) the reconstruction and modeling could also differ from the actual physiology. As a result, the connection’s angle and exact placement (offset with respect to the proposed attachment point) will not be exactly the same as the one proposed.
To address this issue, de Zelicourt and colleagues12 proposed general guidelines on what connections should be avoided in the most complex cases. While there have been efforts to systematically evaluate the variability of a surgical option15, further studies are needed to develop a framework in which this can be applied in more single ventricle cases. We hypothesize that quantifying the changes in the hemodynamics between the proposed connection and its variations can assess the robustness of a surgical connection. With this, we will be able to ensure that the proposed hemodynamic performance will be maintained even if small changes in the implementation are present. In other terms, robustness is inversely proportional to the (partial) derivatives of the performance indicators with respect to the design parameters. Thus, we created a collection of surgical variations by changing the FP baffle’s diameter, offset and connection angle, then performed computational fluid dynamics simulations to obtain the hemodynamic metrics of interest, and finally compared the results to the original (i.e. the connection implemented in surgery) connection. Even without a rigorous evaluation of the derivatives of the performances indexes with respect to the design parameter (mathematically more challenging, being based on the concept of shape derivative), this sensitivity analysis allows one to assess the robustness of the different surgical options.
Materials and Methods
Patient-specific data reconstruction
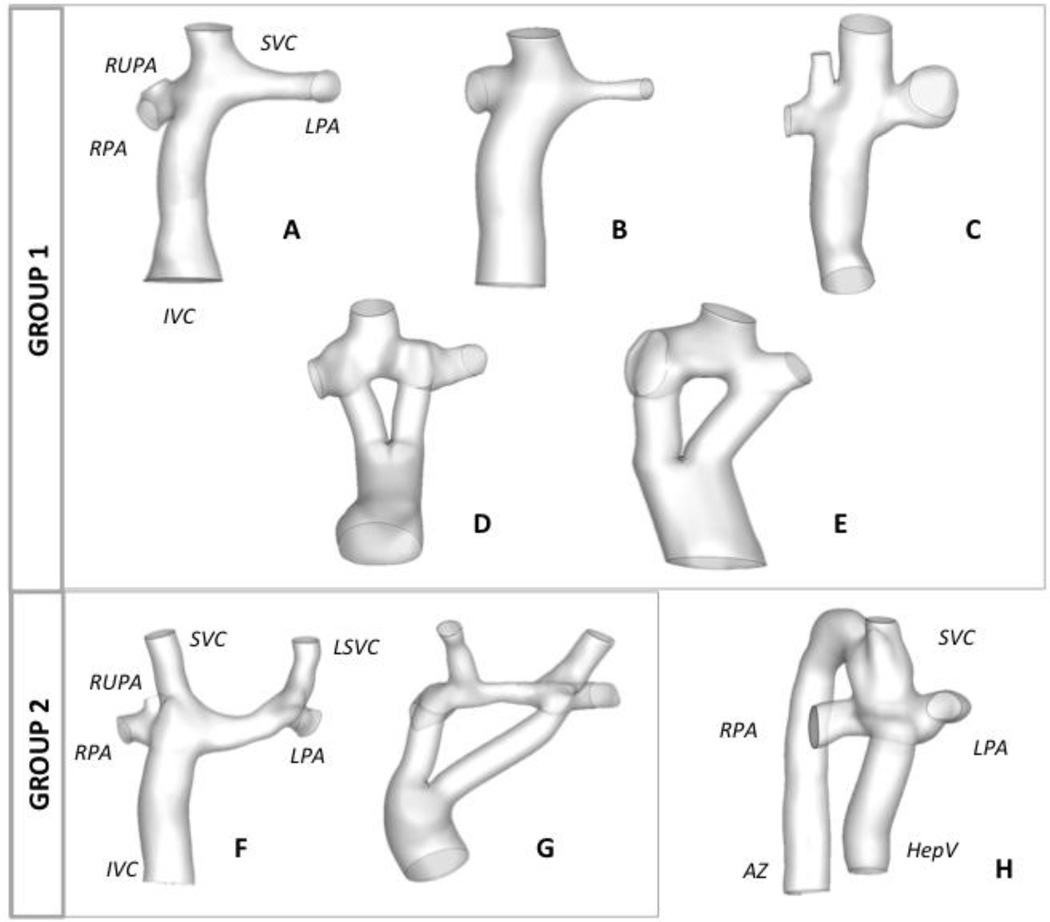
Fontan Patients with a post-operative cardiac magnetic resonance (CMR) scan were included in this study. Retrospective data sets were acquired at the Children’s Hospital of Philadelphia (CHOP) and Children’s Healthcare of Atlanta (CHOA). Patients were selected if they had either an extra-cardiac (EC) or a Y-graft Fontan connection. The Institutional Review Boards of the institutions involved approved this study. Patients were separated into different groups as follows (Figure 1): Group 1, 5 patients with a single SVC (n=3 EC and n=2 Y-graft connections); Group 2, 2 patients with bilateral SVCs (one EC and one Y-graft); Patient H was analyzed independently because it has an interrupted IVC with azygous continuation.
Figure 1.
Reconstructed anatomies for all patients included in this study; Group 1 includes all patients with a single SVC and Group 2 are all with bilateral SVC. Patient H is not grouped because it is the only patient with AZ continuation. IVC: inferior vena cava; SVC: superior vena cava, LSVC: left superior vena cava; AZ: azygous vein; LPA: left pulmonary artery; RPA: right pulmonary artery; RUPA: right upper pulmonary artery; HepV: hepatic vein
Patient-specific anatomies were reconstructed from axial CMR images using previously developed and validated methods16, 17. Geomagic Studio® (Geomagic, 3D Systems, Rock Hill, SC) was used to fit a 3D surface around the reconstructed point-cloud. All TCPC vessels were cut before the closest branching point and these planes were used to impose the inlet and outlet boundary conditions for the computational fluid dynamic simulations. However, for Patients A, C and F, the first branching vessel on the RPA (right upper pulmonary artery – RUPA) was included due to the proximity it had to the SVC anastomosis site. Velocities were extracted from the phase contrast CMR images; all vessels of interest, including IVC, SVC, LPA and RPA (left SVC –LSVC- and Azygous-AZ- vein if present) were segmented using previous methods18, 19.
Surgical Connection Generation
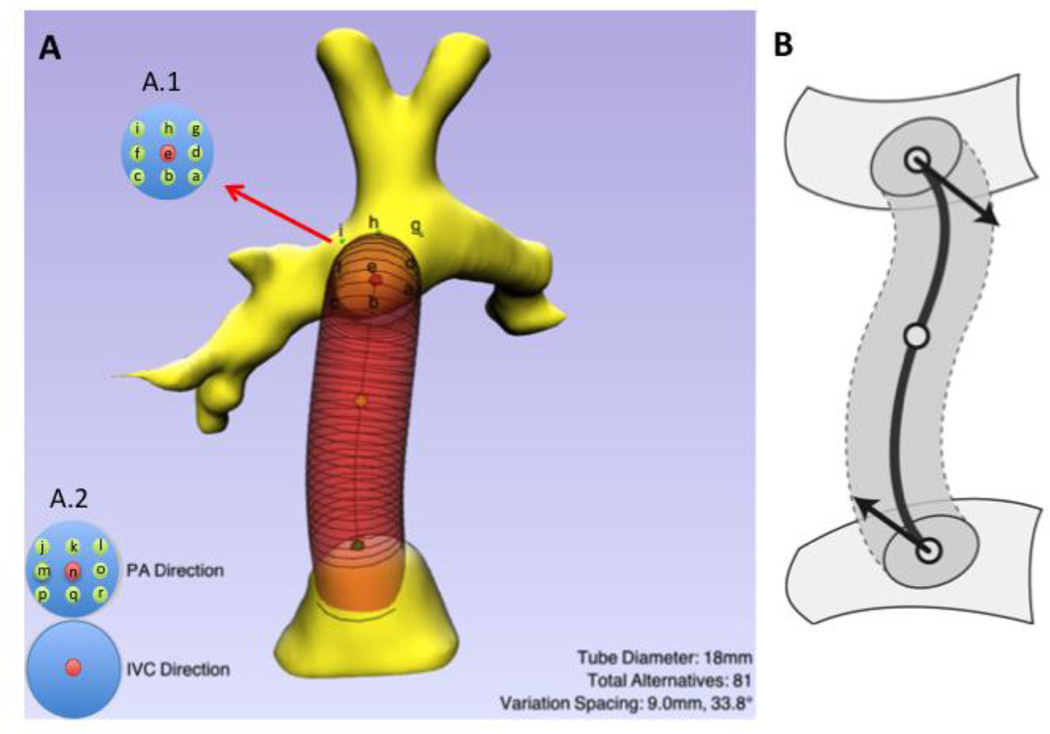
SURGEM III (Figure 2), an in-house developed surgical planning platform, is used to design and edit a baffle using the patient’s anatomy to create various surgical options. The original baffle geometry created matches the one present in the connection at the time the retrospective scan was performed. The baffle is defined by the radius and vessel centerline. This last one is a smooth, non-planar, quartic polynomial curve that is controlled by its two endpoints, by the tangent directions at these endpoints, and by a third mid-course point. The user can modify the baffle’s geometry with three points. The two endpoints have been constrained to lie on the surface, either the IVC or the pulmonary arteries. The range of the parameters that will be considered for the parametric evaluation (diameter, angle and offset) can be also modified in the interface. The points defined for the offset variations (Figure 2 – A.1) lie on top of the pulmonary arteries surface and can be displaced in any direction (coronal, sagittal or axial) with respect of the original point.
Figure 2.
A) Screen shot of the surgical planning tool, SURGEM. The parameters for the baffle displayed are shown in the bottom right. The controls on the bottom left allow for adjusting the baffle vectors to modify the connection angles at the IVC confluence and at the pulmonary arteries (PA). A.1: shows the control points for the parametric variations for the offset: possible positions range from a through g; A.2: shows the possible angle variations, which range from j through r. B) Diagram showing the baffle and control points, as well as the vectors.
For all patients analyzed in this study we varied the parameters as follows: i) diameter was changed by ±2mm from the original value; ii) the offset was changed by half a diameter of the original baffle; and iii) angle was changed by 33 degrees in different directions. Table 1 shows the variations selected for the EC baffles (10 variations per patient) and Table 2 the variations for the Y-grafts (18 variations per patient)
Table 1.
Diameter, angle and offset location for the Original configuration and all surgical variations for the EC baffles generated. The letters in italics correspond to those in Figure 2 (A.1 and A.2) and refer to specific parametric variations; n: original angle location; e: original offset location; 0.5D: offset distance of half a diameter from original value.
| Surgical variation |
Diameter (mm) | Angle location (degrees) |
Offset location (0.5 diameter in mm) |
|---|---|---|---|
| Original | 18 or 20 | n | e |
| 1 | +2mm | n | e |
| 2 | −2mm | n | e |
| 3 | - | n | 0.5D top left (i) |
| 4 | - | n | 0.5D top right (g) |
| 5 | - | n | 0.5D bottom left (c) |
| 6 | - | n | 0.5D bottom right (a) |
| 7 | - | 33° top left (j) | e |
| 8 | - | 33° top right (l) | e |
| 9 | - | 33° bottom left (p) | e |
| 10 | - | 33° bottom right (r) | e |
Table 2.
Diameter, angle and offset location for the Original configuration and all surgical variations for the Y-graft baffles generated. The letters in italics correspond to those in Figure 2 (A.1 and A.2) and refer to specific parametric variations; n: original angle location; e: original offset location; 0.5D: offset distance of half a diameter from original value.
| Surgical variation |
Diameter (D) |
Branch 1 | Branch 2 | ||
|---|---|---|---|---|---|
| Angle (degrees) |
Offset (mm) | Angle (degrees) |
Offset (mm) | ||
| Original | 18-9-9 or 20- 10-10 |
n | e | n | e |
| 1 | +2mm | n | e | n | e |
| 2 | −2mm | n | e | n | e |
| 3 | - | n | 0.5D top left (i) | n | e |
| 4 | - | n | 0.5D top right (g) | n | e |
| 5 | - | n | 0.5D bottom left (c) | n | e |
| 6 | - | n | 0.5D bottom right (a) | n | e |
| 7 | - | n | e | n | 0.5D top left (i) |
| 8 | - | n | e | n | 0.5D top right (g) |
| 9 | - | n | e | n | 0.5D bottom left (c) |
| 10 | - | n | e | n | 0.5D bottom right (a) |
| 11 | - | 33° top left (j) | e | n | e |
| 12 | - | 33° top right (l) | e | n | e |
| 13 | - | 33° bottom left (p) | e | n | e |
| 14 | - | 33° bottom right (r) | e | n | e |
| 15 | - | n | e | 33° top left (j) | e |
| 16 | - | n | e | 33° top right (l) | e |
| 17 | - | n | e | 33° bottom left (p) | e |
| 18 | - | n | e | 33° bottom right (r) | e |
Mesh preparation and computational fluid dynamic simulations
All geometries generated were imported into GAMBIT (ANSYS Inc., Lebanon, NH) to generate the unstructured surface meshes. Extensions were added to inlets (10mm) and outlets (50mm) to reduce the impact of the uncertainty of the boundary conditions on the region of interest and for enhancing the stability of the solver at the outflows. A previously developed in-house immersed boundary solver was used for the fluid simulations20. The grid resolution used for all the models was h=0.016DIVC, based on de Zelicourt et al20, where is the equivalent hydraulic diameter of the IVC cross-section at the inflow. This resulted in mesh sizes in the order of 2 million nodes depending on the geometry analyzed.
The inlet boundary conditions were imposed as time averaged flow rates (computed from the velocity segmented data) based on the study presented by Khiabani et al.21: most cases had low weighted pulsatility index (below 50%), except Patient E. Nonetheless, this case was also simulated with steady flow to be consistent between the cases analyzed. In addition, the selection of time-averaged boundary conditions allowed the authors to optimize the CPU time used in over 100 CFD simulations performed. Parabolic velocity profiles were imposed at the inlets of the connections.
Average flow rates were computed from the velocity data segmented and imposed in the inlets.
The outflows were imposed as percentage of cardiac output as measured from PC-MRI.
The power loss (PL) of the connection was computed as follows:
where p is the static pressure relative to the inlet, ρ is the blood density; A is area of the inlet/outlet, and v the velocity. Power loss was indexed (iPL) as ()22, where Qs is the systemic venous flow (here, in units of L·s−1), BSA is the body surface area [m2], and ρ is the blood density [kg·m−3].
The hepatic flow distribution, HFD, is defined as the amount of IVC flow going to each one of the pulmonary arteries. To obtain it, streamlines were seeded into the IVC cross-section and then classified as going to either LPA or RPA. The fluxes of the streamlines (p) are computed based on the velocity (u) of the IVC seed point and the differential area23:
The relative distribution is then quantified:
Finally, The percentage change on all metrics obtained from each surgical variation were computed with respect to the original connection as follows:
where X is each one of the surgical variations generated in SURGEM III.
Results
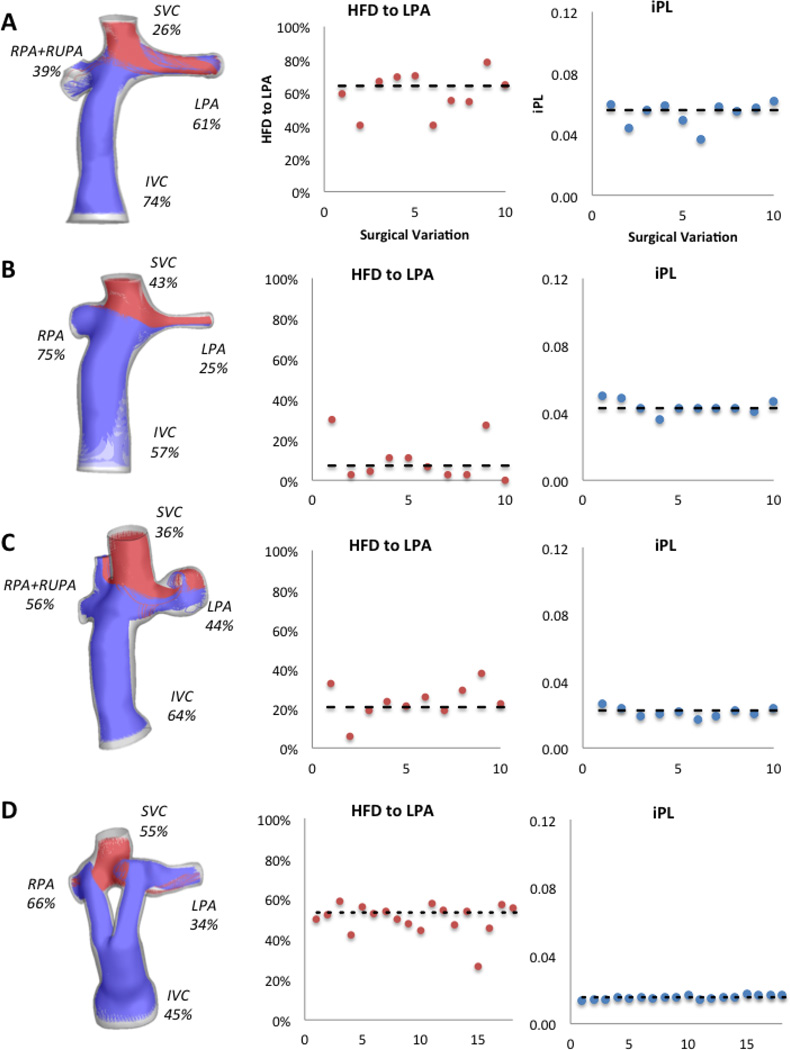
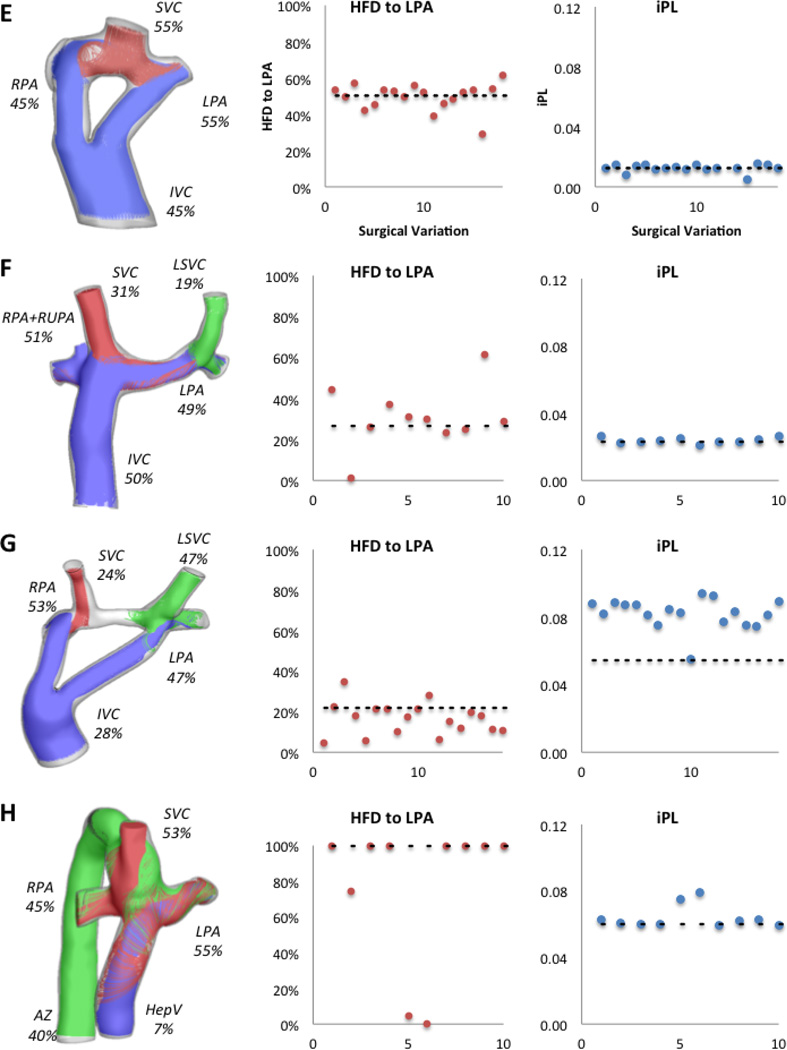
Figure 3 shows the hemodynamic results for the original configuration in all patients and the values for iPL and HFD for all the surgical variations evaluated. In general, all iPL values fall close to the original configuration’s value (dashed line), except for Patient G where only one surgical variation was similar. The HFD values vary greatly with respect to the original.
Figure 3.
Hemodynamic results for all patients in the study; left column shows the percentage of cardiac output through each vessel and the streamtraces color-coded by vessel of origin (IVC/HepV: blue, SVC: red, AZ/LSVC: green). Middle column shows the HFD to the LPA and the right column shows the iPL for all surgical variations per patient; the dashed line shows the value for the original option. X-axis corresponds to each surgical variation.
Given the inherent anatomical differences present in the patients analyzed in this study, patients are analyzed in groups based on the anatomy and surgical Fontan connection.
Group 1: Patients with a single superior vena cava (N=5)
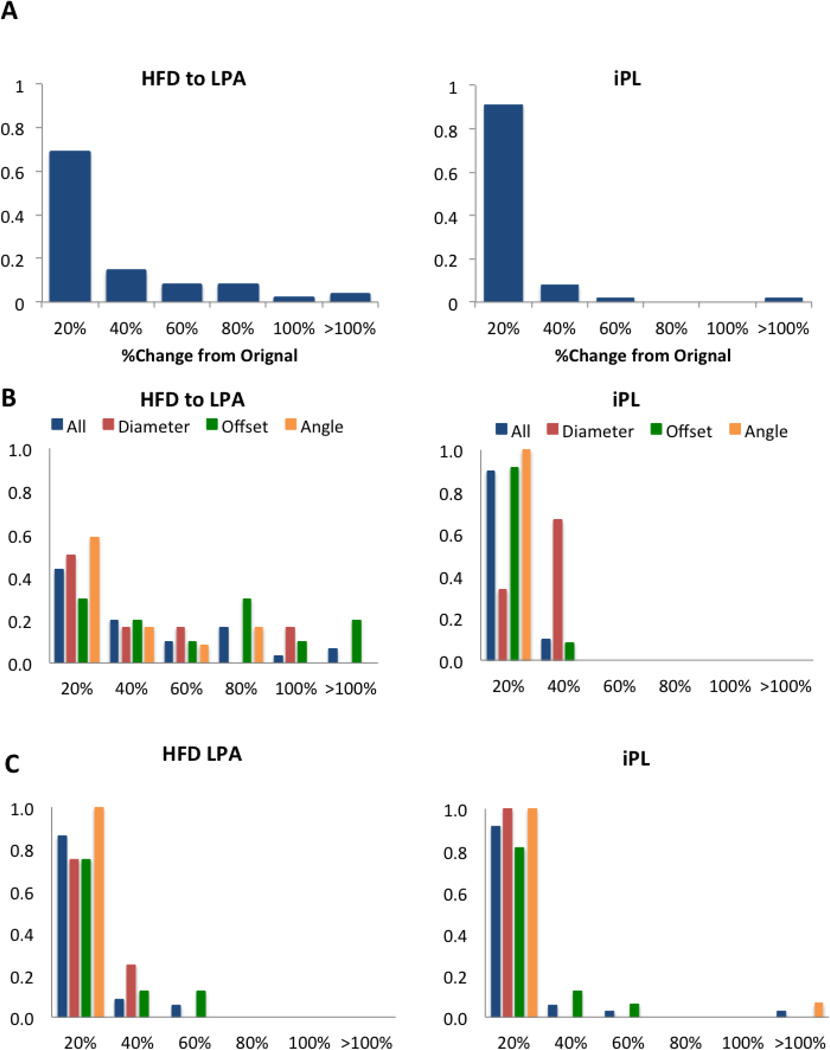
Figure 4 shows the results for all surgical variations in Group 1. The percentage change for the metrics analyzed is presented as normalized histogram, where the X-axis is divided in intervals of X=20% from 0–100%, and then a final interval for all changes greater than 100%. For a given X, the cumulative reading of these diagrams (i.e. the sum of all the histograms for x ≤ X) represent the total percentage of surgical options with changes below X. The Y-axis represents the percentage of incidence in each one of the bins defined in the X-axis. In Figure 4A the results for all patients in Group 1 and the FP variations are combined: the normalized histogram for the HFD and for iPL are both skewed towards the left, showing that most surgical variations resulted in less than a 20% change in these metrics. However, when we look at the subdivisions within this group, these trends are not maintained. The HFD in patients with an EC connection (Figure 4B) is affected by the surgical variations, as shown by the spread in the normalized histogram. Parameters such as offset, angle and diameter result in changes greater than 80% in this metric compared to the original. This behavior is not observed in the iPL, where all values remained within 40% of the original.
Figure 4.
Normalized histogram for the HFD to the LPA and IP for Group 1: A) all patients (N=5); B) patients with an extra-cardiac connection (N=3); C) patients with a Y-graft Fontan (N=2). X-axis shows the percentage change from the original results. For B and C the normalized histograms show all parameters combined (blue) and each one independently: diameter (red), offset (green) and angle (orange).
Patients with a Y-graft in this group (Figure 4C) present less variability on HFD (most values within 40%); however, changes in offset may increase this variability up to 60%. Similar to the EC patients, the iPL normalized histogram is skewed towards the left, although offset and angle may produce changes up to 60 and over 100%, respectively.
Group 2: Patients with bilateral superior vena cava (N=2)
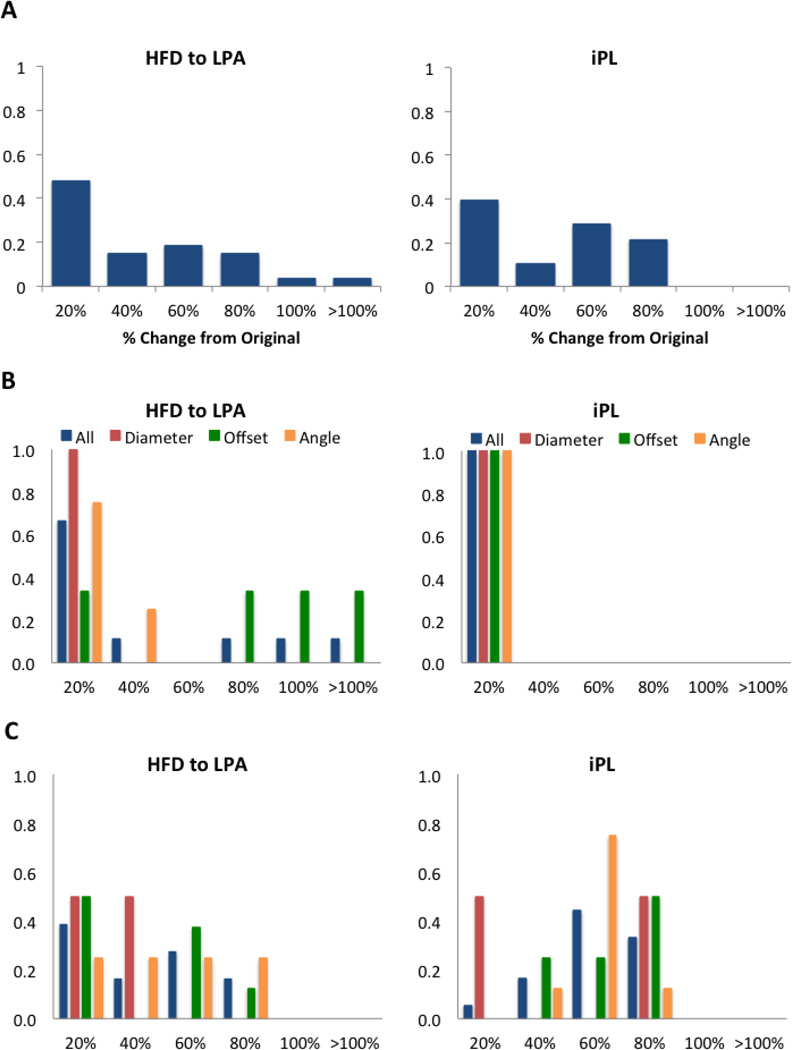
Figure 5A shows the combined normalized histogram for the two patients in this group. Compared to Group 1, the normalized histogram for iPL has a larger spread, meaning that geometrical parameters have a larger impact on this parameter. The results for Patient F (Figure 5B) show that while iPL remained within 20% of the original, the HFD is affected by offset changes altering values by over 80% of the original. For Patient G (Figure 5C) changes in offset, angle and diameter result in large differences in the HFD as well as iPL.
Figure 5.
Group 2: A) combined HFD and iPL normalized histogram for all patients (N=2), Patient F (B) and Patient G (C). X-axis shows the percentage change from the original results. For B and C the normalized histograms show all parameters combined (blue) and each one independently: diameter (red), offset (green) and angle (orange).
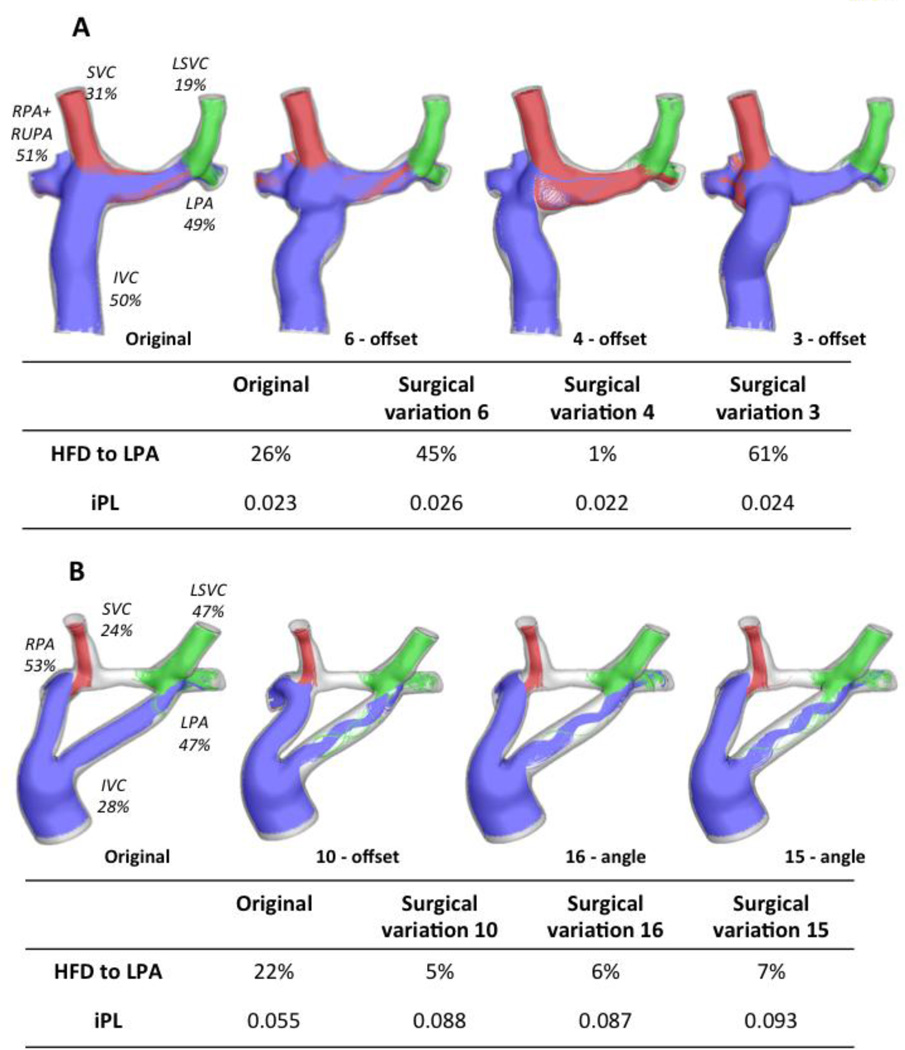
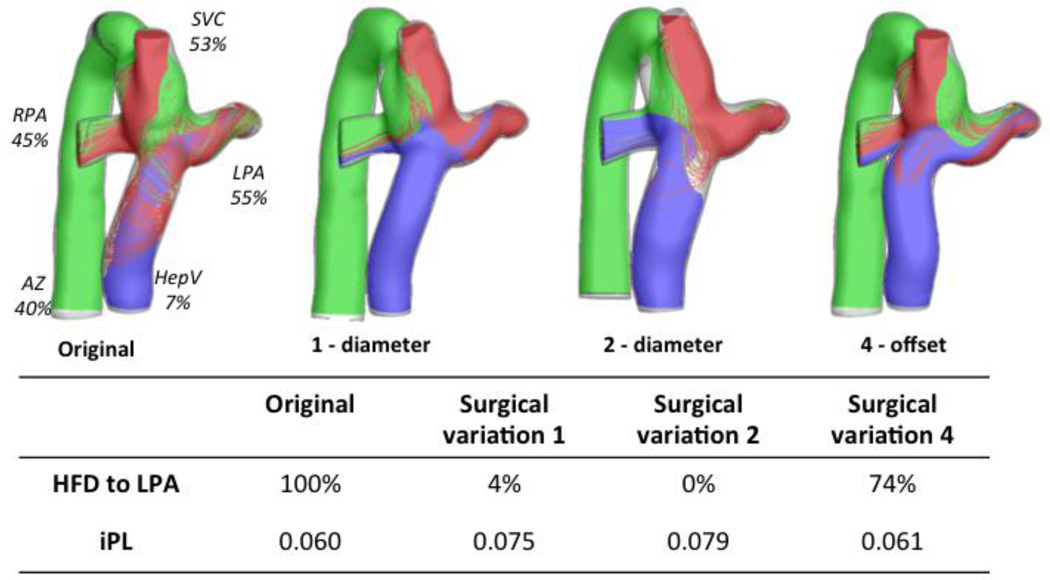
Figure 6A shows the geometries and the flow streamtraces for Patient F’s original configuration, as well as for the three surgical variations that resulted in the largest HFD differences. The FP offset variations affect the interaction between the IVC (blue) and the SVC (red): in the surgical variation 6, as the FP is connected closer to the LPA, the IVC flow towards the left lung increases. However, in the surgical variation 4 as the FP is moved towards the RPA, the SVC flow supplies all the LPA flow demand, because the LSVC is only providing 19% of the cardiac output (CO). Similarly, Figure 6B shows the surgical variations that differed the most from the original connection for Patient G: since the LSVC is already supplying most of the flow necessary for the LPA, the variations result in even less IVC flow to the left lung.
Figure 6.
Worst performing surgical variations for the patients with bilateral SVC; A) Patient F: left figure is the original configuration, and the three variations correspond to offset changes (surgical variations 6, 4 and 3); HFD and iPL values are reported on the table. B) Patient G: original is shown on the left, and one offset (Surgical variation 10) and two angle variations are also shown (Surgical variations 16 and 15); iPL and HFD values reported in the table. Streamtraces are color coded by vessel of origin: IVC (blue), SVC (red), LSVC (green).
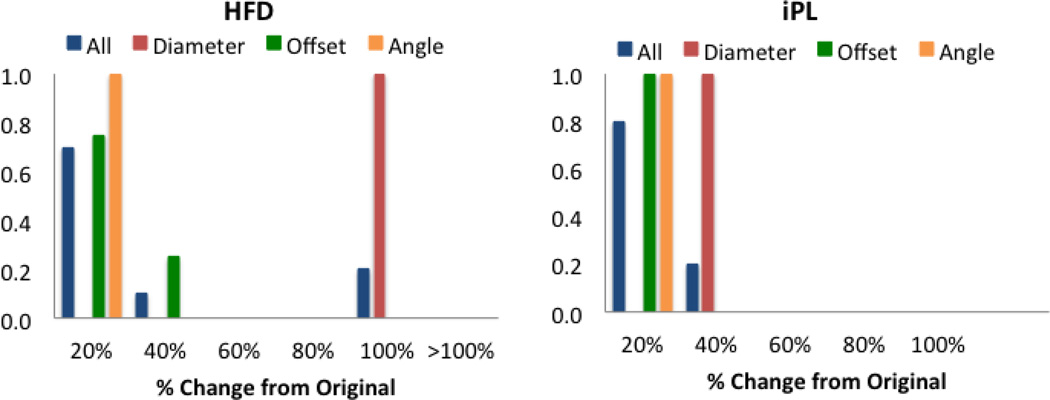
Patient H: interrupted IVC with Azygous continuation
The angle and offset variations in Patient H did not affect the HFD or iPL for more than 40% as shown in Figure 7. However, variations in baffle diameter change the HFD by up to100%. Given the low percentage of CO going through the hepatic vein (7%), any small variations on the FP connection result in large changes, as shown in Figure 8. The diameter variations (surgical variation 1, −2mm, and surgical variation 2, +2mm) change the momentum of the hepatic/IVC flow (mean velocity magnitude values were 4.00m/s in the original, 4.44cm/s in surgical variation 1 and 3.85cm/s in surgical variation 2), which alter the interaction between the superior and the inferior flow streams: in the Original model, the SVC flow (in red) impinges in the HepV due to the low flow present in this vessel; with this interaction, the superior and inferior flows mix resulting in an almost even HFD. In surgical variation 1, since the baffle diameter is smaller, the inferior flow has more momentum and the mixing is reduced. On the other hand, in surgical variation 2 the dominant SVC flow does not allow the passage of the inferior flow to the LPA.
Figure 7.
HFD and IP probability density function for Patient H. X-axis shows the percentage change from the original results. Normalized histograms show all parameters combined (blue) and each one independently: diameter (red), offset (green) and angle (orange).
Figure 8.
Surgical variations for Patient H that resulted in the highest differences from the original configuration (left); Surgical variation 1 represents a decrease in the FP baffle (−2mm), and Surgical variation 2 an increase (+2mm); Surgical variation 4 is a change in offset. Table shows the HFD and iPL values. Streamtraces are color coded by vessel of origin: hepatic vein (blue), SVC (red), AZ (green).
Discussion
In the TCPC studies to date, many have analyzed the effect that different geometric parameters have on the hemodynamic performance of the connection, ranging from simplified geometries to more complex patient-specific models24, 25. For example, Yang et al26 looked into the hemodynamic optimization of the Fontan Y-graft by using a complex framework in which geometrical parameters where varied until the best performing option was found. This study provided sufficient information to elucidate the complexities present in these connection types. However, due to the inherent complexities present in all SV vascular anatomies a patient-specific approach is needed to understand how the geometrical variations may affect the connections’ hemodynamic performance. While previous studies have related the hemodynamic performance and geometrical parameters, this is the first time that offset, angle and baffle diameter are assessed in a series of different geometries.
De Zelicourt et al12 performed surgical planning on complex Fontan cases with an interrupted IVC. In that study several guidelines were proposed: first, for patients with a single SVC the EC Fontan should be avoided due to the low robustness of the resulting HFD results, and instead proceed with a hepatic to azygous connection or a Y-graft to avoid mixing. In our study we further confirmed this with Patient H. Here, the IVC flow was so low compared to the superior venous returns, which not only the original connection was under-performing in terms of HFD, but also any small variation resulted in metric variability. In addition, De Zelicourt et al12 showed that for bilateral SVC patients the robustness of the connection depended not only on the geometry but also on the percentage of cardiac output going through all vessels involved. We confirmed the offset dependency of these connections with the results shown for patients F and G. While the results for patients with bilateral SVC and AZ continuation agree with previous studies12, 13, the sample sizes are not large enough to draw conclusions for the overall population with these characteristics.
In this study, we were able to parametrically evaluate the influence of different geometric variables, such as baffle diameter, offset and angle, on the hemodynamic performance of the TCPC. This analysis allows for the evaluation of the robustness of a connection by assessing the variability of the results. Overall, results showed that the energy efficiency of the connection, in the form of iPL, did not change considerably with respect to the original connection. The clinical benefit of this is that even if the surgical implementation is not identical to the one proposed the energy efficiency will not change substantially. These results also agree with what was previously reported by Tang et al23, where they demonstrated that iPL was affected mostly by vessel stenosis and not by caval offsets. Nonetheless, since the TCPC resistance accounts between 15–20% of the total pulmonary vascular resistance27–29, it is important to ensure that the proposed surgical connection will result in low variability even if geometrical perturbations occur in the implementation.
The HFD results varied considerably with the geometrical variations, which agree with previous studies discussed here. The Fontan Y-graft on single SVC patients was the only case where these variations did not affect the resulting HFD. However, the robustness of the Y-graft may not be extended to the bilateral SVC due to the aforementioned dependency on vessel flow splits (as shown on Patient G).
Limitations
The authors acknowledge that this study is based in a diverse and small sample size, for which the conclusions from it are formulated as observations for the specific patients and should not be generalized for the entire Fontan population. From a modeling standpoint, steady flow boundary conditions have been assumed, which differs from the in-vivo physiology. Furthermore, outflow boundary conditions were imposed at the outlets in the CFD models, modeling the immediate peri-operative status in the TCPC, and not the longer-term adaptation of the single ventricle physiology using resistances or lumped parameter networks in the boundary conditions as shown in10, 30–32. Finally, rigid walls simulations and circular baffles were also assumed in the computational modeling, which differs from the compliant vessel walls present in the patient.
Conclusions
In this study we developed a framework to assess the robustness of a given surgical option to measure the variability of the outcome metrics when the parameters of the connection design are perturbed locally. This sensitivity analysis to geometrical variants represents a first contribution for the quantification of the effects of uncertainties in surgical implementation on clinically relevant indexes. Furthermore, it highlights the importance of the relationships between geometrical configuration and hemodynamic performance. This further strengthens the importance of assessing the geometries and flows prior to surgery, and highlights the need to perform surgical planning with a robustness analysis on the most complex cases. With this, we will be able to provide the clinical team with an option that will maintain the optimal performance even if changes occur during implementation.
Overall, the energetic efficiency was not significantly affected by the minor geometrical changes, while the HFD did. Based on the anatomical configurations analyzed on this study, the Y-graft Fontan in single SVC patients demonstrated to be the most robust connection, while the geometries with bilateral SVC and AZ continuation revealed low robustness in the selected baffle placements.
Acknowledgments
The authors would like to acknowledge Dr. Mark Fogel from the Children’s Hospital of Philadelphia and Dr. Timothy Slesnick from the Children’s Healthcare of Atlanta for the CMR data. This work was made possible thanks to the American Heart Association Pre-Doctoral Fellowship Award13PRE14580005, NHLBI grants HL67622 and HL098252, and the Petit Undergraduate Research Scholarship from the Georgia Institute of Technology.
References
- 1.Fontan F, Baudet E. Surgical repair of tricuspid atresia. Thorax. 1971;26:240–248. doi: 10.1136/thx.26.3.240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.de Leval MR, Kilner P, Gewillig M, Bull C. Total cavopulmonary connection: A logical alternative to atriopulmonary connection for complex fontan operations. Experimental studies and early clinical experience. J Thorac Cardiovasc Surg. 1988;96:682–695. [PubMed] [Google Scholar]
- 3.Burkhart HM, Dearani JA, Mair DD, Warnes CA, Rowland CC, Schaff HV, Puga FJ, Danielson GK. The modified fontan procedure: Early and late results in 132 adult patients. J Thorac Cardiovasc Surg. 2003;125:1252–1259. doi: 10.1016/s0022-5223(03)00117-x. [DOI] [PubMed] [Google Scholar]
- 4.Chowdhury UK, Airan B, Kothari SS, Talwar S, Saxena A, Singh R, Subramaniam GK, Pradeep KK, Patel CD, Venugopal P. Specific issues after extracardiac fontan operation: Ventricular function, growth potential, arrhythmia, and thromboembolism. Ann Thorac Surg. 2005;80:665–672. doi: 10.1016/j.athoracsur.2005.02.024. [DOI] [PubMed] [Google Scholar]
- 5.Duncan B, Desai S. Pulmonary arteriovenous malformations after cavopulmonary anastomosis. The Annals of Thoracic Surgery. 2003;76:1759–1766. doi: 10.1016/s0003-4975(03)00450-8. [DOI] [PubMed] [Google Scholar]
- 6.Pandurangi UM, Shah MJ, Murali R, Cherian KM. Rapid onset of pulmonary arteriovenous malformations after cavopulmonary anastomosis. Ann Thorac Surg. 1999;68:237–239. doi: 10.1016/s0003-4975(99)00407-5. [DOI] [PubMed] [Google Scholar]
- 7.Pike NA, Vricella LA, Feinstein JA, Black MD, Reitz BA. Regression of severe pulmonary arteriovenous malformations after fontan revision and "hepatic factor" rerouting. Ann Thorac Surg. 2004;78:697–699. doi: 10.1016/j.athoracsur.2004.02.003. [DOI] [PubMed] [Google Scholar]
- 8.Shinohara T, Yokoyama T. Pulmonary arteriovenous malformation in patients with total cavopulmonary shunt: What role does lack of hepatic venous blood flow to the lungs play? Pediatr Cardiol. 2001;22:343–346. doi: 10.1007/s002460010243. [DOI] [PubMed] [Google Scholar]
- 9.Whitehead KK, Pekkan K, Kitajima HD, Paridon SM, Yoganathan AP, Fogel MA. Nonlinear power loss during exercise in single-ventricle patients after the fontan: Insights from computational fluid dynamics. Circulation. 2007;116:I165–I171. doi: 10.1161/CIRCULATIONAHA.106.680827. [DOI] [PubMed] [Google Scholar]
- 10.Baretta A, Corsini C, Marsden AL, Vignon-Clementel IE, Hsia TY, Dubini G, Pennati G . Respiratory effects on hemodynamics in patient-specific cfd models of the fontan circulation under exercise conditions. European Journal of Mechanics-B/Fluids. 2012;35 [Google Scholar]
- 11.Marsden AL, Vignon-Clementel IE, Chan FP, Feinstein JA, Taylor CA. Effects of exercise and respiration on hemodynamic efficiency in cfd simulations of the total cavopulmonary connection. Annals of biomedical engineering. 2007;35:250–263. doi: 10.1007/s10439-006-9224-3. [DOI] [PubMed] [Google Scholar]
- 12.de Zelicourt DA, Haggerty CM, Sundareswaran KS, Whited BS, Rossignac JR, Kanter KR, Gaynor JW, Spray TL, Sotiropoulos F, Fogel MA, Yoganathan AP. Individualized computer-based surgical planning to address pulmonary arteriovenous malformations in patients with a single ventricle with an interrupted inferior vena cava and azygous continuation. J Thorac Cardiovasc Surg. 2011;141:1170–1177. doi: 10.1016/j.jtcvs.2010.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sundareswaran KS, de Zelicourt D, Sharma S, Kanter KR, Spray TL, Rossignac J, Sotiropoulos F, Fogel MA, Yoganathan AP. Correction of pulmonary arteriovenous malformation using image-based surgical planning. JACC Cardiovasc Imaging. 2009;2:1024–1030. doi: 10.1016/j.jcmg.2009.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haggerty CM, de Zelicourt DA, Restrepo M, Rossignac J, Spray TL, Kanter KR, Fogel MA, Yoganathan AP. Comparing pre- and post-operative fontan hemodynamic simulations: Implications for the reliability of surgical planning. Ann Biomed Eng. 2012 doi: 10.1007/s10439-012-0614-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sankaran S, Marsden AL. A stochastic collocation method for uncertainty quantification and propagation in cardiovascular simulations. J Biomech Eng. 2011;133:031001. doi: 10.1115/1.4003259. [DOI] [PubMed] [Google Scholar]
- 16.Frakes DH, Conrad CP, Healy TM, Monaco JW, Fogel M, Sharma S, Smith MJ, Yoganathan AP. Application of an adaptive control grid interpolation technique to morphological vascular reconstruction. IEEE transactions on bio-medical engineering. 2003;50:197–206. doi: 10.1109/TBME.2002.807651. [DOI] [PubMed] [Google Scholar]
- 17.Frakes DH, Dasi LP, Pekkan K, Kitajima HD, Sundareswaran K, Yoganathan AP, Smith MJ. A new method for registration-based medical image interpolation. IEEE Trans Med Imaging. 2008;27:370–377. doi: 10.1109/TMI.2007.907324. [DOI] [PubMed] [Google Scholar]
- 18.Frakes D, Smith M, de Zelicourt D, Pekkan K, Yoganathan A. Three-dimensional velocity field reconstruction. J Biomech Eng. 2004;126:727–735. doi: 10.1115/1.1824117. [DOI] [PubMed] [Google Scholar]
- 19.Sundareswaran KS, Frakes DH, Fogel MA, Soerensen DD, Oshinski JN, Yoganathan AP. Optimum fuzzy filters for phase-contrast magnetic resonance imaging segmentation. J Magn Reson Imaging. 2009;29:155–165. doi: 10.1002/jmri.21579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zélicourt Dd, Ge L, Wang C, Sotiropoulos F, Gilmanov A, Yoganathan A. Flow simulations in arbitrarily complex cardiovascular anatomies – an unstructured cartesian grid approach. Computers & Fluids. 2009;38:1749–1762. [Google Scholar]
- 21.Khiabani RH, Restrepo M, Tang E, De Zelicourt D, Sotiropoulos F, Fogel M, Yoganathan AP. Effect of flow pulsatility on modeling the hemodynamics in the total cavopulmonary connection. J Biomech. 2012;45:2376–2381. doi: 10.1016/j.jbiomech.2012.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dasi LP, Pekkan K, de Zelicourt D, Sundareswaran KS, Krishnankutty R, Delnido PJ, Yoganathan AP. Hemodynamic energy dissipation in the cardiovascular system: Generalized theoretical analysis on disease states. Ann Biomed Eng. 2009;37:661–673. doi: 10.1007/s10439-009-9650-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tang E, Restrepo M, Haggerty CM, Mirabella L, Bethel J, Whitehead KK, Fogel MA, Yoganathan AP. Geometric characterization of patient-specific total cavopulmonary connections and its relationship to hemodynamics. JACC Cardiovasc Imaging. 2014;7:215–224. doi: 10.1016/j.jcmg.2013.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hsia TY, Migliavacca F, Pittaccio S, Radaelli A, Dubini G, Pennati G, de Leval M. Computational fluid dynamic study of flow optimization in realistic models of the total cavopulmonary connections. The Journal of surgical research. 2004;116:305–313. doi: 10.1016/j.jss.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 25.Ensley AE, Lynch P, Chatzimavroudis GP, Lucas C, Sharma S, Yoganathan AP. Toward designing the optimal total cavopulmonary connection: An in vitro study. Ann Thorac Surg. 1999;68:1384–1390. doi: 10.1016/s0003-4975(99)00560-3. [DOI] [PubMed] [Google Scholar]
- 26.Yang W, Feinstein JA, Shadden SC, Vignon-Clementel IE, Marsden AL. Optimization of a y-graft design for improved hepatic flow distribution in the fontan circulation. J Biomech Eng. 2013;135:011002. doi: 10.1115/1.4023089. [DOI] [PubMed] [Google Scholar]
- 27.Haggerty CM, Restrepo M, Tang E, de Zelicourt DA, Sundareswaran KS, Mirabella L, Bethel J, Whitehead KK, Fogel MA, Yoganathan AP. Fontan hemodynamics from 100 patient-specific cardiac magnetic resonance studies: A computational fluid dynamics analysis. J Thorac Cardiovasc Surg. 2013 doi: 10.1016/j.jtcvs.2013.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Khairy P, Fernandes SM, Mayer JE, Jr, Triedman JK, Walsh EP, Lock JE, Landzberg MJ. Long-term survival, modes of death, and predictors of mortality in patients with fontan surgery. Circulation. 2008;117:85–92. doi: 10.1161/CIRCULATIONAHA.107.738559. [DOI] [PubMed] [Google Scholar]
- 29.Sundareswaran KS, Pekkan K, Dasi LP, Whitehead K, Sharma S, Kanter KR, Fogel MA, Yoganathan AP. The total cavopulmonary connection resistance: A significant impact on single ventricle hemodynamics at rest and exercise. Am J Physiol Heart Circ Physiol. 2008;295:H2427–H2435. doi: 10.1152/ajpheart.00628.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Baretta A, Corsini C, Yang W, Vignon-Clementel IE, Marsden AL, Feinstein JA, Hsia TY, Dubini G, Migliavacca F, Pennati G. Virtual surgeries in patients with congenital heart disease: A multi-scale modelling test case. Philos Transact A Math Phys Eng Sci. 2011;369:4316–4330. doi: 10.1098/rsta.2011.0130. [DOI] [PubMed] [Google Scholar]
- 31.Corsini C, Baker C, Kung E, Schievano S, Arbia G, Baretta A, Biglino G, Migliavacca F, Dubini G, Pennati G, Marsden A, Vignon-Clementel I, Taylor A, Hsia TY, Dorfman A. An integrated approach to patient-specific predictive modeling for single ventricle heart palliation. Comput Methods Biomech Biomed Engin. 2014;17:1572–1589. doi: 10.1080/10255842.2012.758254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kung E, Baretta A, Baker C, Arbia G, Biglino G, Corsini C, Schievano S, Vignon-Clementel IE, Dubini G, Pennati G, Taylor A, Dorfman A, Hlavacek AM, Marsden AL, Hsia TY, Migliavacca F Modeling Of Congenital Hearts Alliance I. Predictive modeling of the virtual hemi-fontan operation for second stage single ventricle palliation: Two patient-specific cases. J Biomech. 2013;46:423–429. doi: 10.1016/j.jbiomech.2012.10.023. [DOI] [PubMed] [Google Scholar]