Fluid shear, intercellular stress, and endothelial cell alignment

Abstract

Endothelial cell alignment along the direction of laminar fluid flow is widely understood to be a defining morphological feature of vascular homeostasis. While the role of associated signaling and structural events have been well studied, associated intercellular stresses under laminar fluid shear have remained ill-defined and the role of these stresses in the alignment process has remained obscure. To fill this gap, we report here the tractions as well as the complete in-plane intercellular stress fields measured within the human umbilical vein endothelial cell (HUVEC) monolayer subjected to a steady laminar fluid shear of 1 Pa. Tractions, intercellular stresses, as well as their time course, heterogeneity, and anisotropy, were measured using monolayer traction microscopy and monolayer stress microscopy. Prior to application of laminar fluid flow, intercellular stresses were largely tensile but fluctuated dramatically in space and in time (317 ± 122 Pa). Within 12 h of the onset of laminar fluid flow, the intercellular stresses decreased substantially but continued to fluctuate dramatically (142 ± 84 Pa). Moreover, tractions and intercellular stresses aligned strongly and promptly (within 1 h) along the direction of fluid flow, whereas the endothelial cell body aligned less strongly and substantially more slowly (12 h). Taken together, these results reveal that steady laminar fluid flow induces prompt reduction in magnitude and alignment of tractions and intercellular stress tensor components followed by the retarded elongation and alignment of the endothelial cell body. Appreciably smaller intercellular stresses supported by cell-cell junctions logically favor smaller incidence of gap formation and thus improved barrier integrity.

perhaps the most well-known morphological response of the endothelial cell to laminar fluid flow is elongation and alignment of the cell body along the direction of flow. Laminar fluid shear activates a cascade of biochemical (30) and genetic (30) signaling events, including activation of the Rho family small GTPases (49) and upregulation of intercellular adhesion molecule (30). These events are associated with structural reorganization and translocation of the cytoskeleton (16), cell-cell junctions (35), focal adhesions (29), and transmembrane proteins (49). Although these events within a confluent monolayer have been associated with alignment and function of endothelial cells, the underlying tractions exerted by each cell upon its substrate (48), and intercellular stresses exerted by each cell upon its immediate neighbors (43), have remained largely unobservable experimentally, and for that reason, their roles in signaling, structure, and alignment have remained ill-defined.

Of the few studies in the literature regarding endothelial cells and their associated intercellular stresses under laminar fluid shear, the evidence is conflicting. Shiu et al. (40) demonstrated that the individual adherent endothelial cell subjected to laminar fluid flow exerts Rho-dependent increases in tractions and, almost a decade later, Ting et al. (45) and Hur et al. (22) used elastomeric microposts and three-dimensional (3-D) intercellular force microscopy, respectively, in the confluent endothelial monolayer to demonstrate that both tractions and intercellular stresses increase. However, the validity of those findings was soon challenged by Conway et al. (10), who used Förster resonance energy transfer (FRET) to reason that laminar fluid flow causes intercellular stresses to decrease, not increase. They argued that this decrease in intercellular stress occurs through decreased tension on VE-cadherin along with increased tension on PECAM-1 (10), and in independent experiments they used elastomeric microposts to confirm that tractions and intercellular stresses decrease. As such, the time course of tractions and in-plane intercellular stresses, as well as the heterogeneity and anisotropy of those stresses under laminar fluid flow conditions, remain equivocal. Consequently, a well-defined physical picture illustrating how endothelial cells align under laminar fluid flow remains elusive.

To fill this gap and thus resolve these conflicting findings, we developed a novel method that consists of a parallel plate flow chamber integrated with monolayer traction microscopy to measure tractions (7, 48) and monolayer stress microscopy to measure the complete in-plane intercellular stress tensor (43). With regard to the latter we used micropatterned cellular monolayers to secure precise boundary conditions and thus avoid errors attributable to unbalanced forces caused by cells outside the optical field-of-view (42). Using these methods we found an unexpected biphasic response. This response consisted of an early phase characterized by rapid alignment of the traction forces and intercellular stresses along the fluid flow direction within 1 h, followed by a late phase in which the cell body exhibited a more gradual and less precise alignment after 12 h.

MATERIALS AND METHODS

Cell culture.

Cells and cell culture reagents were purchased from Life Technologies unless noted otherwise. Human umbilical vein endothelial cells (HUVECs) were cultured in Medium 200 cell culture media supplemented with Large Vessel Endothelial Supplement on 0.1% gelatin (Sigma-Aldrich)-coated cell culture flasks at 37°C and 5% CO₂. All experiments were done using cells from passages 3–5.

Preparation of polyacrylamide gels.

Polyacrylamide gels (Young's modulus; 1.2 kPa) were prepared as previously described (5) with the following modifications: 1) 1 M NaOH was used to cover the glass surface in step 1; 2) 80 μl of an acrylamide/bis-acrylamide mixture was dissolved in ultrapure water containing 0.4% of 0.5 μm diameter red fluorescent carboxylate-modified beads (Fluospheres, Invitrogen) in step 3; and 3) the gel surface was activated using 0.4 μM sulfosuccinimidyl-6-(4-azido-2-nitrophenylamino)hexanoate (Sulfo-SANPAH; Pierce) dissolved in 0.1 M HEPES buffer, also in step 3. The gel height was ∼100 μm, as confirmed by fluorescence microscopy.

Fabrication of polydimethyl siloxane membrane micropatterns.

A thin layer of polydimethyl siloxane (PDMS; 20:1 base-to-curing agent ratio) was cured in a petri dish for 3 h at 75°C. After curing, a rectangular PDMS section was removed and a 1.5 mm diameter biopsy punch was used to pattern circular holes in the membrane.

Cellular monolayer micropatterning on polyacrylamide gels.

Prior to cell seeding, a polyacrylamide gel was air-dried for 10 min. PDMS membranes were washed twice with 70% ethanol and PBS and subsequently were air-dried for 10 min as well. The PDMS membranes were then carefully placed on top the polyacrylamide gel surface and incubated with 5 ml of collagen I (0.1 mg/ml) overnight at 4°C. After this time, undeposited collagen was removed and a small volume of cell suspension (25 μl of a 4 × 10⁶ solution) was deposited on the top surface of the PDMS membrane, which was incubated at 37°C and 5% CO₂ for 1 h. At this time a confluent monolayer was observed and the PDMS membrane was carefully removed so as not to disturb the underlying monolayer. The gel was then hydrated with cell culture media and incubated at 5% CO₂ and 37°C 36 h prior to experimentation.

Steady laminar fluid shear stress.

A 25 mm × 75 mm glass slide (VWR) containing micropatterned HUVEC monolayers attached to a polyacrylamide gel was attached to a sticky-Slide I Luer flow chamber (Ibidi). This laminar flow chamber (height, 400 μm; width, 5 mm, length, 50 mm) contained an adhesive that formed a watertight seal with the glass slide upon attachment. A peristaltic flow pump (Monostat) circulated cell culture media bubbled with 5% CO₂ through the flow chamber (Fig. 1A). Pulsatile flow was dampened by introducing the fluid through a damper prior to its arrival to the flow chamber inlet, producing a steady flow rate of 6.3 ml/min. Utilizing this steady flow rate, the manufacturer's instructions, and a corrected chamber height of 300 μm (to account for gel height), the laminar fluid shear stress was calculated to be ∼1 Pa. An in-solution flow heater (Harvard Apparatus) heated cell culture media to 37°C prior to its arrival to the flow chamber inlet. The entire flow chamber was maintained at 37°C during experiments.

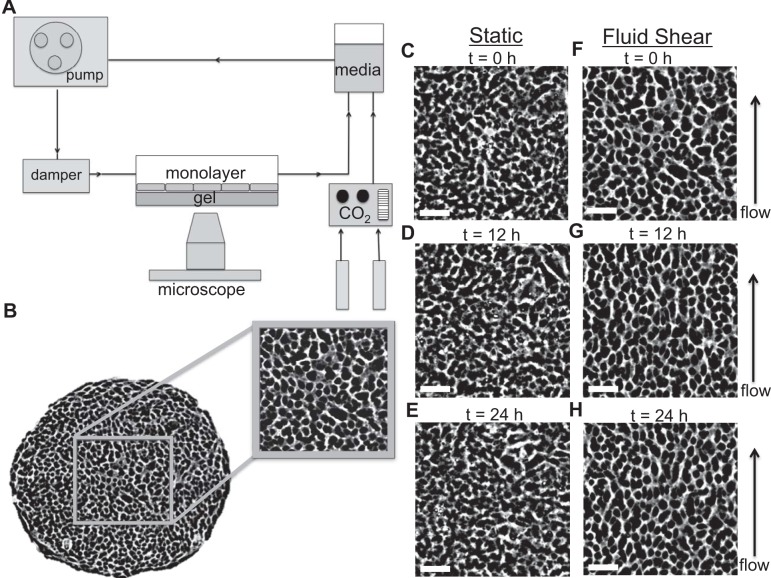
Fig. 1.

Experimental setup and human umbilical vein endothelial cell (HUVEC) morphology. A: schematic of the experimental system used to exert a steady laminar fluid flow of 1 Pa on HUVEC monolayers. B: phase-contrast image of a representative micropatterned HUVEC monolayer (1.5 mm diameter). Within the interior of this monolayer, a 500 × 500 μm square area was used to analyze cell body and intercellular stress orientations. C–E: phase-contrast images of HUVECs in static conditions at 0 h (C), 12 h (D), and 24 h (E) display a cobblestone morphology with no preferred orientation. F–H: HUVEC morphology at the onset of laminar fluid shear displayed a cobblestone morphology with no preferred orientation (F); however, cell body elongation and alignment along the fluid flow direction was observed between 12 h (G) and 24 h (H) of steady laminar fluid shear. Scale bars, 100 μm.

Time-lapse microscopy.

Experiments were conducted on an automated inverted microscope (Leica, DMI 6000B). Image acquisition began ∼10 min after application of steady laminar fluid shear stress. Fluorescence and phase-contrast images were taken in 10-min intervals for 24 h using a ×5 objective. To view the entire monolayer, four images were acquired at each time interval. After image acquisition, all four images were stitched in ImageJ (National Institutes of Health, Bethesda, MD) using a custom-written macro, which utilized an algorithm that allowed for image stitching with subpixel resolution (37).

Measurements of gel displacement.

The direct effect of fluid shear on gel displacement is negligible. For example, if the uniform fluid shear stress is 1 Pa, the gel stiffness is 1,000 Pa, and gel height is 100 μm, then the uniform displacement of the top surface of the gel will be 0.1 μm. By contrast, beneath cells we find root mean square (RMS) traction values on the order of 100 Pa and peak values on the order of 1,000 Pa, with proportionally larger gel displacements (data not shown). Accordingly, fluid shear-induced gel deformation is much smaller than the cell-induced gel deformations, as we have reported in the past (7), suggesting the direct effects of fluid shear on gel deformation in the presence of cells to be negligible. This estimate is in keeping with the model of Dabagh and coworkers (12), who predicted stress amplification at focal adhesions close to 200-fold. Experimental comparison of gel deformations with cells in the presence and absence of fluid flow confirm that fluid flow has minimal direct influence on gel deformation (data not shown). Similarly, the direct effect of fluid shear on cell deformation is negligible. During cell realignment, the cell strains are of order unity. With a fluid shear of 1 Pa and a cellular shear modulus of order 100–1,000 Pa (8, 20), the direct physical influence of fluid shear would cause strains that are 2–3 orders of magnitude smaller.

Gel displacement measurements were made by comparing a fluorescent bead image from any experimental time point with a reference fluorescent bead image obtained after monolayer trypsinization using particle image velocimetry (PIV). The PIV cross-correlation window size was 32 × 32 pixels and the overlap window was 24 pixels. Using this method we measured the in-plane gel displacements; errors associated with ignoring out-of-plane displacements are negligible (42).

Calculation of tractions and intercellular stresses.

Tractions and intercellular stresses were calculated using monolayer traction microscopy (48) and monolayer stress microscopy (43), respectively. In brief, we computed the monolayer tractions from the gel displacements. We next utilized the tractions in a rigorous, straightforward force balance as demanded by Newton's laws to calculate the two-dimensional stress tensor within the entire monolayer (42, 43). By rotating the coordinate system at every point within the monolayer we computed the maximum principal stresses (σ_max) and minimum principal stresses (σ_min), and their corresponding orientations.

To represent the complete state of local tensorial intercellular stress within the endothelial monolayer, we used a stress ellipse in which the ellipse major axis represents the maximum principal stress, the ellipse minor axis represents the minimum principal stress, the ellipse shape departure from circularity provides a measure of local stress anisotropy, and the ellipse orientation defines the local principal stress orientation, referred to as intercellular stress orientation in this paper (23). In addition, at each point within the monolayer we computed the average normal stress (σ_max + σ_min)/2 and the maximum shear stress (σ_max − σ_min)/2.

Boundary conditions.

Computation of the intercellular stress tensor was done using a force balance between each cell and its neighbors and between each cell and its underlying substrate as required by Newton's laws (23, 43, 47). When the entire monolayer boundary falls within the field-of-view, bounded only by a cell-free region, we term this a free-edge boundary condition (42) (data not shown). Computation of the intercellular stresses using free-edge boundary conditions is precise since the intercellular stresses at the monolayer boundary are known; boundary stresses are zero. By contrast, when the field-of-view is bounded by cells inside the field-of view on one side and cells outside the field-of-view on the other side, we term this an optical-edge boundary condition (42) (data not shown). Computation of the intercellular stresses using optical-edge boundary conditions is less precise since the contributions of intercellular stresses from cells outside the field-of-view are unknown, and assumptions about their nature can cause errors (42). We utilized the free-edge boundary condition in this study, which has no cells outside the field-of-view, and therefore avoid associated errors in our intercellular stress calculations.

Eliminating boundary effects.

Along the boundary of the micropatterned, circular monolayer, one to two rows of HUVECs tend to align and elongate parallel to the local edge. To eliminate any potential influences that these aligned cell rows might have on our analysis of orientations of the cell body or orientations of the intercellular stress, these regions were cropped using a square, 500 × 500 μm area within the interior of the monolayer, and thus excluding all cells outside this area (Fig. 1B). In the remainder of this paper we show only this cropped interior region.

Cell orientation measurements.

Cell orientations were measured using the method of Serra-Picamal et al. (39) with the modification of cell body segmentation being based on phase-contrast images.

Statistical analysis.

Statistical analysis was performed using a paired Student's t-test; P < 0.05 was considered statistically significant.

RESULTS

Laminar fluid flow causes alignment of the cell body.

In the absence of laminar fluid flow, phase-contrast images of HUVECs revealed a cobblestone morphology with no preferred orientation (Fig. 1C). This unbiased cell orientation persisted in culture for at least 24 h (Fig. 1, D and E). With the onset of laminar fluid shear (Fig. 1F), by contrast, HUVEC alignment and elongation along the direction of fluid flow became evident within 12 h (Fig. 1G). This alignment and elongation were enhanced after 24 h (Fig. 1H). These findings are consistent with previous reports (16, 33).

Laminar fluid flow attenuates tractions and intercellular stresses.

We next considered the local tractions exerted by the cells on their substrate. Tractions occur primarily through myosin-generated tension on the actin cytoskeleton in both the presence and absence of laminar fluid shear (6, 45, 48). In the absence of laminar fluid flow the underlying y-component tractions were strongly heterogeneous in space and in time in the absence of flow (Fig. 2, A and B), fluctuating between −100 Pa and +100 Pa. The scale of these fluctuations was similar to that reported previously in both endothelial cells and epithelial cells (43, 48). With the onset of laminar fluid flow, tractions decreased slightly from the beginning (Fig. 2C) to end (Fig. 2D) of experimentation, being on average ∼6% lower than traction forces under static conditions.

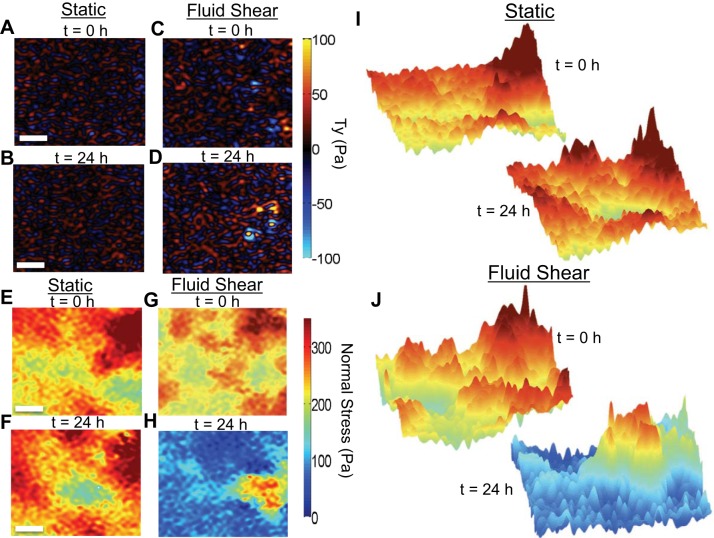
Fig. 2.

Average normal intercellular stress and traction maps in the presence and absence of steady laminar fluid shear. A and B: y-component traction (Ty) maps in static conditions at 0 h (A) and 24 h (B). C and D: y-component traction (Ty) maps immediately after the onset of laminar fluid shear (C) and 24 h later (D). E and F: average normal intercellular stress maps in static conditions at 0 h (E) and 24 h (F). G and H: application of steady laminar fluid shear induced a rapid reduction in the average normal intercellular stress between 0 h (G) and 24 h (H). I and J: the average normal intercellular stress landscape was appreciably rugged and spatial heterogenous in both static (I) and steady laminar fluid shear stress conditions (J). Scale bars, 100 μm.

According to Newton's laws, the local tractions described above must be balanced by local intercellular stresses transmitted within cells through the cytoskeleton and between cells across cell-cell junctions, yielding a tug-of-war within the monolayer (43, 48). Using this force balance, we have previously shown the intercellular stresses to be cooperative across roughly 10–20 cell diameters and be characterized by a rugged stress landscape (43). Although the biological molecules responsible for intercellular stresses remain uncertain, prior studies by us and others have suggested this to in part be dependent on actomyosin activity (32, 34, 45) and intercellular calcium (43). To determine the intercellular stresses within the monolayer, we used monolayer traction microscopy (48) and monolayer stress microscopy (43). The average normal intercellular stress is a scalar that corresponds to monolayer tension or compression. In the absence of laminar fluid shear, the average normal intercellular stresses were largely tensile, severely heterogeneous in space and in time, and fluctuated around 310 ± 81 Pa (P < 0.05) (Fig. 2E and Supplemental Video S1; Supplemental Material for this article is available online at the Journal website); the stress landscape in the absence of laminar fluid flow was rugged (Fig. 2I), and dramatic fluctuations in the intercellular stresses continued for the duration of the experiment (24 h; Fig. 2F). In the presence of laminar fluid flow, by comparison, the average normal intercellular stresses remained severely heterogeneous in space and in time but decreased within 12 h from 317 + 122 Pa (P < 0.05) to 142 + 84 Pa (P < 0.05), and within 24 h decreased to 128 + 49 Pa (P < 0.05) (Fig. 2, G, H, and J and Supplemental Video S2). The maximum shear intercellular stress exhibited behavior equivalent to the average normal intercellular stress (data not shown).

Laminar fluid flow causes strong anisotropy and alignment of intercellular stresses.

We depicted the local state of intercellular stress and its anisotropy using a stress ellipse as described above. In the absence of laminar fluid flow, stress ellipses were mostly circular in shape, thus showing little anisotropy and no preferred orientation (Fig. 3, A, B, E, and F). In contrast, within 1 h of the onset of laminar fluid flow the stress ellipses became strongly and systematically anisotropic and strongly aligned along the direction of fluid flow (90°) (Fig. 3, I and J). At 12 h this alignment became even more prominent (Fig. 3, M and N).

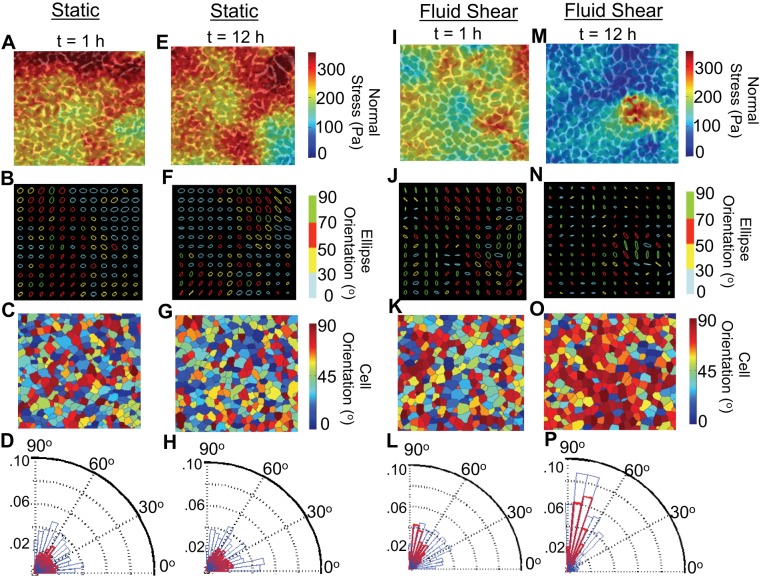
Fig. 3.

Cell body and intercellular stress orientations in the absence and presence of steady laminar fluid shear. A and E: overlay of average normal intercellular stress maps on phase contrast images after 1 h (A) and 12 h (E) of static conditions. B and F: corresponding stress ellipses displayed little anisotropy. C and G: cellular orientations were broadly distributed between 0° and 90°. D and H: angular distributions of intercellular stress orientations (red bars) and cell body orientations (blue bars) both exhibited no preferred orientations after 1 h (D) and 12 h (H) of static conditions. I: within 1 h of steady laminar fluid shear the average normal intercellular stress has already begun to decrease. J and K: stress ellipses (J) are anisotropic, while the cell body displays no preferred orientation (K). L: angular distributions of the intercellular stress (red bars) and cell body (blue bar) shows the intercellular stress to primarily align along the direction of fluid flow (90°), while cell orientations remain broadly distributed between 0° and 90°. M: after 12 h of steady laminar fluid shear the average normal intercellular stress has decreased substantially. N and O: stress ellipses are even more anisotropic (N), and most of the endothelial cells are oriented along the direction of fluid flow (90°) (O). P: angular distributions of the intercellular stress and cell body have both now aligned along the direction of fluid flow (90°).

Cell body alignment lags intercellular stress alignment.

In the absence of laminar fluid flow (Fig. 3, C and G), and with the onset of laminar fluid flow (Fig. 3K), cellular orientations were disorganized and unbiased, but cells progressively elongated and aligned along the direction of fluid flow within 12 h (Fig. 3O). We quantified the progressive alignment of the cell bodies and intercellular stresses using a histogram depicting their rose of directions. This histogram shows the angular distributions of cell body orientations (blue bars) overlapped with angular distributions of intercellular stress orientations (red bars). In the absence of laminar fluid shear, cellular orientations and intercellular stress orientations were unbiased and broadly distributed between 0° and 90° over 24 h (Fig. 3, D and H and Supplemental Video S3). However, in the presence of laminar fluid shear the intercellular stresses aligned along the direction of fluid flow quite early (within 1 h) (Fig. 3L), followed by the delayed alignment of the endothelial cell body within 12 h (Fig. 3P and Supplemental Video S4).

Tractions align along the direction of fluid flow.

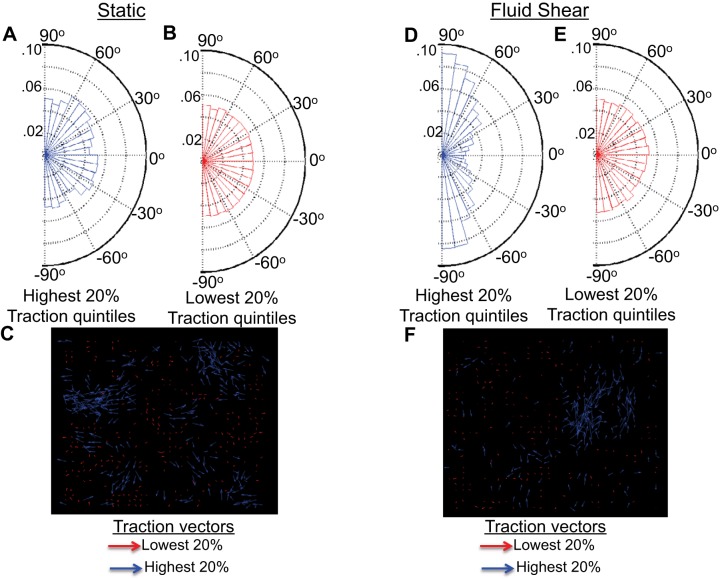
Total tractions (x- and y-components) were rank-ordered into quintiles to determine orientations of tractions largest and smallest in magnitude. In the absence of fluid shear the 20% highest tractions (Fig. 4A) and 20% lowest tractions (Fig. 4B) showed no preferred orientations and spanned all angles from 90° to −90°. Traction vectors representing the lowest 20% tractions (red arrows) and highest 20% tractions (blue arrows) show tractions pulling in all directions (Fig. 4C). In the presence of laminar fluid shear the 20% highest tractions were aligned mostly parallel to the fluid flow direction at either 90° or −90° (Fig. 4D), while the 20% lowest tractions were broadly oriented in all directions from 90° to −90° (Fig. 4E). Corresponding traction vectors show the highest 20% tractions (blue arrows) to pull mostly north or south (along the fluid flow direction) while the lowest 20% tractions (red arrows) pull in all directions (Fig. 4F).

Fig. 4.

Traction orientations in the absence and presence of steady laminar fluid shear. A and B: the highest 20% (A) and lowest 20% (B) traction quintiles show no preferred orientation after 12 h of static conditions. C: traction vectors show the lowest 20% (red arrows) and highest 20% (blue arrows) tractions to pull in all directions. D and E: after 12 h of steady laminar fluid shear the highest 20% tractions (D) are primarily aligned along the fluid flow direction (90° and −90°), while the lowest 20% tractions show no preferred orientation (E). F: traction vectors under laminar fluid shear show the lowest 20% tractions (red arrows) to pull in all directions, while the highest 20% tractions (blue arrows) primarily pull north and south.

DISCUSSION

In the confluent endothelial monolayer, steady laminar fluid shear causes constituent endothelial cells to align along the direction of fluid flow, but underlying changes in associated intercellular stresses —and even the sign of those changes—have until now remained unclear. Using a novel approach, we show here that laminar fluid flow triggers prompt alignment and then slow attenuation of those intercellular stresses, followed by the delayed and less precise alignment of the endothelial cell body itself. Laminar fluid shear is known to be atheroprotective and therefore essential to vascular homeostasis (3, 30, 46). As such, these findings are important because the effects of fluid shear are often described as a culmination of signaling and structural events, whereas underlying changes in the tractions and intercellular stresses that drive those structural rearrangements have remained poorly characterized and understood.

This poor understanding stems in part from conflicting reports in the literature (10, 22, 45), with even the sign of the stress change being a matter of dispute. While these discrepancies might be attributable in part to the different endothelial cell types studied, they are more likely attributable to methodological limitations that were not fully appreciated. On the one hand, 3-D intercellular force microscopy as used by Hur et al. (22) rests on the assumption of spatial homogeneity of the intercellular stress field, but it has been shown by us previously (42, 43), and again here, that the assumption of intercellular stress homogeneity is not supported by our observations; in fact, the intercellular stress field is strongly heterogeneous, highly dynamic, and markedly anisotropic. On the other hand, the discontinuous surface topography experienced by cells attached to spaced vertical microposts as used by Ting et al. (45) and Conway et al. (10) may not best represent the continuous surface topography of the native underlying endothelial matrix. Moreover, the micropost assay is strictly locally reacting since it is designed to prevent any stress or strain transmission within the underlying elastic matrix; each individual post responds locally and independently of forces applied at a distance. By contrast, the constituent cell in a monolayer adherent to a continuous elastic matrix responds to stresses and strains generated by other cells at great distances (2, 43).

FRET as used by Conway et al. (10) is an elegant new molecular approach to measure stretch of single reporter molecules, but FRET too has its innate limitations. For example, any FRET probe reports the stretch of the reporter molecule but does not distinguish greater stretch per molecule versus greater proportion of molecules under stretch. And because the FRET output is a scalar, the resulting FRET signal is neither a tensorial quantity, as is a stress, nor a vectorial quantity, as is a force (17). As such, the relationship of the scalar FRET signal to the local stress tensor is at best unclear. Moreover, the scalar stretch reported by any particular FRET probe represents only one of the multiple molecular species that might support the overall local mechanical stress (17), some of which might act mechanically in parallel to support the local load. In such circumstances there is no reason to believe that mechanical support of this load would be equally distributed among different stress-bearing molecular species. And given the strong nonlinear behavior of most biological molecules and their potential for low yield stresses (26, 36), detachment (9), or depolymerization (11, 36), it cannot be ruled out that as one molecular species becomes increasingly loaded and stretched that others might become progressively unloaded and recoiled, thus leading to an ambiguous interpretation of the FRET signal magnitude and even its sign. As such, there is cause for ambiguity in interpretation of FRET signals in terms of the magnitude and even the sign of mechanical stress changes. Similarly, the use of DNA-based molecular tension probes for optically reporting cellular traction forces provides high spatial resolution of tractions (5) but is a scalar output that cannot resolve direction or sign; as such, the resulting information is incomplete and cannot be used in conjunction with monolayer stress microscopy to measure intercellular stresses.

To avoid these limitations, we used micropatterned monolayers in conjunction with monolayer traction force microscopy and monolayer stress microscopy to calculate explicitly the tractions and the complete in-plane intercellular stress tensor. Compared with other existing methodologies, this approach has two major advantages. First, monolayer traction microscopy and monolayer stress microscopy rely only on the force balances implied by Newton's laws and are almost model independent. Therefore, results are insensitive to assumptions regarding monolayer material properties (42, 43, 51). Second, we avoid boundary artifacts (42) from cells outside the optical field of view through the use of micropatterned monolayers. Micropattern shape and area have both been shown to affect cellular migration (15, 25, 28), a process essential to endothelial cell alignment under fluid flow (1, 13, 21, 44), but here we have cropped the region of interest so as to avoid the influence of distant boundaries. In addition, this approach is insensitive to out-of plane stresses and strains (42). As such, our findings remain robust and help to resolve existing conflicts in the literature.

What are the physiological implications of these findings? The classical view of mechanical regulation of endothelial barrier permeability, barrier leakage, and wound repair emphasizes the role of the paracellular transport pathway and its reliance on the balance between stresses exerted across the cell-cell junction and stresses exerted at the cell-substrate interface (14, 50). Intercellular stresses increase in the presence of barrier-disruptive compounds such as histamine or thrombin, and they decrease in the presence of barrier-protective compounds such as sphingosine 1-phosphate or hepatocyte growth factor (18, 31, 32, 41). However, the addition of laminar fluid shear reduces both the intercellular stresses and tractions; these magnitudes are similar in scale to the stresses estimated to occur across adherens junctions and focal adhesions (12). While the mechanisms by which laminar fluid shear reduces tractions and intercellular stresses are unknown, previous experimental studies have suggested the dynamic remodeling, disassembly, and translocation of focal adhesions, the cytoskeleton, and cell-cell junctions to play a pivotal role (32, 45). Because the Piezo1 (Fam38a) channel has been shown to sense fluid shear stress and determine vascular structure (27), it is plausible to suspect that Piezo1 may also be responsible for the shear-induced attenuation of intercellular stresses and tractions reported here. If so, then the tug-of-war phenomenon we have described in the past (43), and again here, would complement the Piezo1 mechanism because reduced tractions would be balanced by reduced intercellular stresses, possibly through Piezo1.

Because laminar fluid shear appreciably reduces these tractions and intercellular stresses (Fig. 2, C and D and Fig. 2, G and H), it is appealing to ask whether laminar fluid shear is therefore barrier protective and might reduce barrier permeability, possibly through the reduction of stress-induced paracellular gap formation. This notion leads to other important unanswered questions and unresolved issues. For example, in the presence of inflammatory mediators, does laminar fluid shear decrease tractions and intercellular stresses and thus act by that mechanism to maintain barrier integrity? The answer is presently unknown.

In this regard, distributions of tractions and intercellular stresses have been shown previously, and shown again here, to have non-Gaussian exponential tails (38, 48). Does the persistence of such heterogeneity suggest that endothelial barrier permeability might depend not so much on the average stress magnitude of intercellular stresses, but depend more so on peak stresses? Observation of these peak stresses have only recently been accessible within the past few years; as such, their underlying signaling and structural underpinnings have yet to be discovered. Moreover, these intercellular stress fluctuations and their dynamic heterogeneities are a signature of glassy dynamics and cell jamming (4, 19, 43, 47, 48). We have previously shown reorientation of the isolated endothelial cell under mechanical stimulation to be guided by alternating periods of fluidization and resolidification (24), a common signature of glassy dynamics. What roles do glassy dynamics and jamming play in the process of cellular reorientation and vascular homeostasis in the confluent monolayer? These questions remain unanswered, but, as shown here, the experimental tools are now in hand to answer them.

In conclusion, for the confluent HUVEC monolayer under laminar fluid shear, we find the prompt reduction and alignment of the tractions and intercellular stress tensor components followed by the retarded and less precise alignment of the endothelial cell body. These events seem to be a fundamental physical feature of endothelial cell alignment under laminar fluid shear and imply that intercellular stresses guide alignment of the endothelial cell body and are fundamental to vascular homeostasis.

GRANTS

This research was supported by the National Heart, Lung, and Blood Institute Grants T32HL007118, R01HL107561, and P01HL120839.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

R.S.J., D.T., and J.J.F. conception and design of research; R.S.J. performed experiments; R.S.J. analyzed data; R.S.J. and J.J.F. interpreted results of experiments; R.S.J. prepared figures; R.S.J. drafted manuscript; R.S.J., D.T., C.C.H., R.K., and J.J.F. edited and revised manuscript; R.S.J., D.T., C.C.H., R.K., and J.J.F. approved final version of manuscript.