Abstract
We present and characterize a multi-host epidemic model of Rift Valley fever (RVF) virus in East Africa with geographic spread on a network, rule-based mitigation measures, and mosquito infection and population dynamics. Susceptible populations are depleted by disease and vaccination and are replenished with the birth of new animals. We observe that the severity of the epidemics is strongly correlated with the duration of the rainy season and that even severe epidemics are abruptly terminated when the rain stops. Because naturally acquired herd immunity is established, total mortality across 25 years is relatively insensitive to many mitigation approaches. Strong reductions in cattle mortality are expected, however, with sufficient reduction in population densities of either vectors or susceptible (ie. unvaccinated) hosts. A better understanding of RVF epidemiology would result from serology surveys to quantify the importance of herd immunity in epidemic control, and sequencing of virus from representative animals to quantify the realative importance of transportation and local reservoirs in nucleating yearly epidemics. Our results suggest that an effective multi-layered mitigation strategy would include vector control, movement control, and vaccination of young animals yearly, even in the absence of expected rainfall.
Keywords and phrases: epidemiology, rift valley fever, mitigation, vaccination, geography, weather, network model
1. Introduction
Vector-borne diseases cause significant human and animal morbidity and mortality. Their complex, multi-host disease transmission cycle makes predicting their spread and assessment of control mechanisms complex. Mathematical models can account for this complexity and assess the effectiveness of control measures, including vector control, vaccination, culling, quarantine, and movement control of animal hosts. Non-uniformity of control measures and natural fluctuations in the density of vectors and susceptible hosts can lead to complicated variations in both the temporal and geographic distribution of epidemic severity. A comprehensive model can reproduce patterns of change of epidemic severity and provide understanding of transmission mechanisms, the impact of changes in the host-range of a reservoir species or vector, and the value of various mitigation strategies. As the fraction of animals that are not susceptible to disease changes, either from vaccination or infection, a model can account for the importance of herd immunity in keeping the disease in check. A validated model can predict the extent that a newly introduced disease will penetrate a geographical area.
Rift Valley fever (RVF) is a significant cause of animal mortality and is capable of causing severe disease in humans [6, 47]. Recent large epidemics have raised concerns of the disease significantly expanding its geographic range. Treatment for illness caused by RVF virus consists primarily of supportive care for both infected humans and animals [5]. Although vaccination of cattle can control epidemics, the live vaccine causes spontaneous abortions while the inactivated vaccine requires multiple inoculations to provide protection from disease. In both cases, disease can be inadvertently spread from animal to animal during vaccination through multiple usages of needles [47].
Models of RVF have been aimed at addressing two primary concerns [34]. First, what is the risk of disease resurgence and spread in endemic regions? Second, what is the risk of RVF introduction into disease-free regions? Anyamba et al. [2] used GIS and weather data to create risk maps that change with time. Hightower et al. [25] also use geography and climate data to model outbreaks, predicting that RVF is more likely in lower elevations, on the plains, and in the bush. They point out that although geography and climate can be good predictors, other factors such as susceptibility and availability of hosts could also be important. Gaff et al. [19] designed a compartmental SIR differential equation model for RVF with one host species and two mosquito species. This model was later extended to include mitigation strategies [19, 28]. Mpeshe et al. [36] analyzed an SIR model for RVF with one mosquito species, livestock, and humans [36]. Xue et al. [49] extended the SIR models to include spatial heterogeneity via patch models, using data from South African outbreaks to parameterize and validate the model. Chitnis et al. [10] modeled RVF with vertical transmission in mosquitoes including marked seasonality and storage of infected eggs during the dry season to explore the role of vertical transmission in interepidemic persistence. Manore and Beechler [16] extended this work to model RVF spread and persistence in buffalo herds in Kruger National Park, South Africa. Soti et al. observed that while RVF prevalence correlated well with rainfall in East Africa, it was necessary to examine ground water hydrology and incorporate a more detailed model of Aedes and Culex mosquito lifecycles to reproduce observations in West Africa [41].
RVF prevalence data are sparse and contain numerous systematic biases which can discourage construction of more realistic and detailed models. For example, the models described above that focus on spatial aspects of RVF epidemiology (climate and geography) are coupled with host susceptibility and availability while models that focus on temporal aspects of RVF epidemiology, account for vaccines, transmission chains, and immune history, but do not explicitly include climate and geography. Long-range transport of infected animals requires details of both spatial and temporal aspects that are difficult to treat when either effect is approximated. Technical innovations in sequencing and high throughput characterization systems have raised the possibility of new types of global biosurveillance data. Many aspects of infectious disease monitoring, such as presence in a particular host or diversity of strains present in a particular region could be addressed with such technologies [29]. For example, sequence data was used during the avian influenza outbreaks in Nigeria in 2007 to show that multiple introductions, rather than intra-country transport, was responsible for introduction of the disease in Lagos [13, 37]. Detailed studies of such well-known pathogens as HIV or influenza also show that it is possible to utilize phylogenetic analyses of pathogen sequences to quantitatively relate disease correlates and transmission modalities to observed patterns in pathogen spread [23]. Such considerations motivate us in the daunting task of constructing a realistic model of RVF spread. In this modality, a detailed epidemiology model is not constructed by fitting detailed prevalence data, but rather by systematically examining mechanisms and observing trends, with a goal of shedding insight into how better practices can reduce the disease burden from RVF and other emerging zoonotic infections.
In this work, we explore and combine aspects of both spatial and temporal models using geography and weather together with temporal models that track mosquito, livestock, wildlife, and human populations with rule-based mitigations. This hybrid model allows us to incorporate rainfall, land use, animal and human populations, susceptibility via changes in herd immunity, the mosquito life cycle (including vertical transmission), and movement of hosts between regions. Although we still find empirical data lacking to constrain such a complex model, we are still able to identify numerous threshhold points, where each of the complexities becomes qualitatively important. The network aspect of the problem (geography), in particular, greatly increases the demands upon both validation and constraint of epidemiological modes, since distinct effects are often at work in different areas. Identifying and understanding these complexities, however, will be essential to effectively control these diseases and optimize resource allocation [38]. This point was particularly emphasized in Fenner’s book about the eradication of smallpox [18].
2. Methods
Careful observation of how a disease progresses through different populations and the effectiveness of mitigation strategies at minimizing impact are essential components of successful disease control programs. Our hybrid deterministic and stochastic multi-host RVF epidemiological model with explicit geography as a network of locations and mitigation measures is an expanded version of our Multi-Scale Epidemiological model (MuSE), developed to describe rinderpest spreading across livestock in the United States [32]. Geographic spread across the network was modeled with a deterministic, SIR-like model of the epidemic spread within counties (nodes) and a stochastic spread between counties (across edges). Although country-level data does exist for long-range transport of livestock [46], in this work we relied on spatially-defined short-range geographic spread between nodes. Our hybrid model retains much of the computational rapidity of homogeneously mixed (SIR) models, while allowing for explicit, rule-based mitigations and explicit incorporation of any geographically dependent variable, such as population density, rainfall, income, or a locally defined replicative number, often denoted as R0. We assume that within the determined regions (40 km squares for these simulations), transmission in animals, humans, and mosquitoes can be represented by standard SIR differential equations. Tildesely et al. [43] have described the appropriateness of such ‘coarse-grained’ models for agricultural diseases.
Multiple mitigations of RVF have occurred in East Africa, including vaccination, vector control, and movement restrictions. We assumed quarantine and culling of susceptible cattle and wildlife did not occur, and implemented vaccination and movement controls by specifying how long after detection in a particular grid square such measures became effective. We did not explicitly include vector control, but instead investigated the dependence of epidemic severity on the density of susceptible hosts and vectors.
2.1. Mathematical Model
The disease states for the animals are shown in Figure 1a, and are similar to those in our previous studies, except that birth and death rates are added, replenishing the supply of susceptible hosts over time. Each species category has a constant per-capita birth rate and death rate based on the average lifespan of each category and a carrying capacity for each category assigned to each region based on population data for cattle, and inferred from land use for wildlife.
Figure 1.
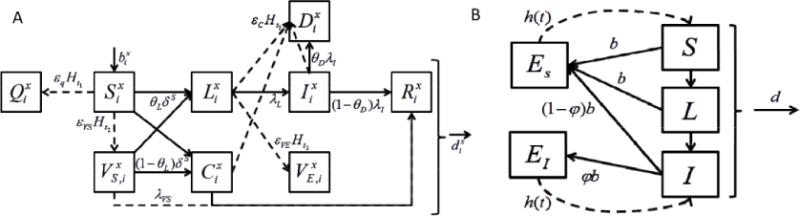
Dynamic states of model for (a) cattle, wildlife, and humans, and (b) Aedes and Culex mosquitoes. For both models, S denotes Susceptible, D denotes Dead, and I denotes Infected. Additionally, for the animal and human model, Q denotes Quarantine, VS denotes Vaccinated susceptible, VE denotes Vaccinated exposed, L denotes Latent infection (incubating), C denotes Carrier, and R denotes Recovered. In (a), dashed lines represent mitigations. For the mosquito model, ES denotes Susceptible Eggs, EI denotes Infected Eggs, and the dashed lines indicate a hatching rate that explicitly incorporates a waiting-time before new mosquitoes can hatch. Equations describing the model are provided in text and parameters are provided in Table 1.
Our model of RVF disease progression and mitigation used three different animal hosts: cattle or livestock, wildlife, and humans. Cattle provide an important economic concern (consequence metric) during RVF outbreaks, while wildlife are likely the major portion of the viral reservoir. Even though humans serve as a dead-end host in the epidemiology of RVF, they are included in the model to predict the impact of mitigation strategies on protecting humans from disease. The disease progression and transition probabilities for the three representative hosts, cattle and other livestock, wildlife, and humans, are shown in Fig. 1a. To the standard Susceptible, Infected, and Recovered states, we add Dead to track consequence, Latent and Carrier to describe asymptomatic disease states, and two Vaccinated states to account for the imperfect aspects of vaccines. The Quarantined state, defined as a way to protect susceptible populations, is shown in Fig. 1a, but considered ineffective for combating RVF in East Africa.
Vector dynamics are essential determinants of the time and place of RVF outbreaks, and we include both Aedes mosquitoes and Culex mosquitoes. Mosquitoes can become infected by biting an infected animal; humans and animals can become infected by being bitten by an infected mosquito, and humans can also become infected, at a reduced rate, by direct contact with infected animals. While it is possible to model human RVF by simply changing the parameters of the animal model, incorporation of mosquitoes into MuSE required adding a mosquito lifecycle model coupling hatching of eggs to rainfall data and including vertical transmission of RVF virus by Aedes mosquitoes. The assumed lifecycle of the mosquito is shown in Figure 1b, including a larval state by forcing a minimum stay in the egg state before hatching is allowed (similar to the mosquito portion of the RVF larvae models of Chitnis et al. [10] or Soti et al. [41]). The hatching process requires the presence of rainfall in our model, and Figure 2 shows monthly totals for ten years of rainfall from the Serengeti wildlife reserve, taken from Holdo et al [26]. Although rainfall data are available across East Africa at high spatial resolution in 10-day intervals [48], we chose to stochastically generate rainfall patterns with a time-course similar to that in Figure 2. These dynamics generate the rapid expansion and contraction of the mosquito populations with the coming and going of the rainy season, from November to May of each year, and illustrate the non-trivial problem of how RVF emerges at the begining of each rainy season. We explicitly include the egg → larvae → mosquito → death cycle illustrated in Fig. 1b in the model. The time-course of yearly epidemics is affected by incubation times and vertical transmission rates. These are shown in Fig. 1b and parameters are provided in Table I, below for two representative genera of mosquitoes, Aedes and Culex. We assume that only Aedes mosquitoes transmit RVF virus transovarially.
Figure 2.
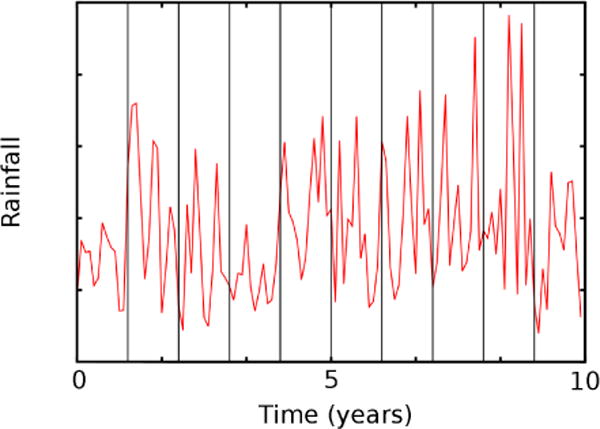
Ten years of rainfall in the Serengeti wildlife refuge, taken from Reference [26]. Vertical lines designate the start of November of each year. Both the duration of rainy seasons and the monthly total vary significantly from year to year.
TABLE 1.
Parameters in the model
| Aedes | Culex | Cattle | Wildlife | Human | |
|---|---|---|---|---|---|
| Susceptibility, si | 58 | 58 | 20 | 20 | 20 |
| Transmissibility a (10−8), , | 11.5 | 11.5 | 11.5 | 11.5 | 11.5 |
| Transmissibility i (10−7), | 7 | 7 | 3 | 3 | 11.5 |
| Transmissibility l (10−8), | 11.5 | 11.5 | 11.5 | 11.5 | 11.5 |
| Birth time (days), 1/bi | 10 | 10 | 1000 | 1000 | 18,250 |
| Death time (not RVF, days), 1/di | 10 | 10 | 1000 | 1000 | 18,250 |
|
| |||||
| Vertical transmission rate of RVF (fraction), ϕ | 0.07 | 0 | 0 | 0 | 0 |
| Maturation time for mosquito eggs (days) | 14 | 14 | – | – | – |
| Hatch rate for mosquito eggs (1/days) | 0.3 | 0.03 | – | – | – |
| Duration of immunity | – | – | Life | Life | Life |
|
| |||||
| Asymptomatic stage residence time (days), 1/λL | 7–15 | 7–15 | 2–4 | 2–4 | 2–4 |
| Symptomatic stage residence time (days), 1/λI | Life | Life | 4–8 | 4–8 | 4–8 |
| Duration of carrier state (days), 1/λC, | – | – | 10–20 | 10–20 | 10–20 |
| Time to build immunity after vaccination, | – | – | 5–15 | 5–15 | 5–15 |
| Fraction infected who progress to symptoms, θL | 1 | 1 | 0.8–0.9 | 0.8–0.9 | 0.2–0.7 |
| Fraction infected who die (case fatality rate), θD | – | – | 0.1–0.5 | 0.1–0.5 | 0.0–0.05 |
| Fraction vaccinated who are protected | – | – | 0.6–0.95 | 0.6–0.95 | 0.6–0.95 |
|
| |||||
| Short-range movement control efficacy, χS | – | – | 0.1–0.9 | 0.1–0.9 | – |
| Long-range movement control efficacy, χL | – | – | – | – | – |
| Time between detection and mvmnt cntrls (days) | – | – | 1–14 | – | – |
| Time between detection and vaccination (days) | – | – | 20–40 | – | 20–40 |
| Time between detection and culling (days) | – | – | 1–3 | – | 1–3 |
Explicit, rule-based models of surveillance, quarantine, culling, vaccination, and movement control are implemented as in the rinderpest study [32], although only to the applicable hosts, and quarantine, culling, and long-range transport were not explored. We assume once a region has more than 50 infectious livestock or humans, an alarm will be raised and mitigation strategies will begin with appropriate delays. Vaccination, the primary mitigation strategy considered here, has a lag time after detection ranging from days to weeks in our model. Regions immediately surrounding an infected region were assumed to implement surveillance, resulting in faster response time when disease is detected in the simulation, and disease spread to regions adjacent to infected areas was implemented.
The geography was defined by conditions in each cell of a 100 by 60 grid of well-mixed compartments 40 kilometers on a side. This resolution was chosen by our estimate of the spatial extent of isolated outbreaks, balanced by our desire to enable thousands of decade-long simulations to be run overnight on a desktop computer. While all of the parameters listed in Table 1 could be made explicit functions of geography, we chose to allow only the density of hosts and vectors in the various disease compartments, rainfall, and the status of the various mitigation measures to vary. The importance of GIS correlates is emphasized in Reference [2]. The geographic spread of RVF was assumed to occur through a short-range mechanism with an exponential dependence on distance.
Short range movement rates are based on Euclidean distance with probability of movement and infection of a nearby area governed by an exponential distribution in distance from the infected region. Long range transportation would be governed by a matrix specifying movement rates between regions based on known livestock trade, wildlife migrations, or human movement, as in our rinderpest study [32]. We assume that mosquitoes do not move from their home region. For each run of the model, we choose randomly from a distribution of the parameters outlined in Table 1. During a particular run, the chosen parameters remain the same, while probability of spreading the infection due to movement of infected hosts is implemented stochastically, changing with density of infected organisms, movement control, vaccination, and availability of susceptible hosts during the run [32]. We ran the mitigation scenarios 75 times each, sampling along the range of possible parameter values in order to understand the full spectrum of possible outcomes and the uncertainty inherent in such models.
The differential equations used to model within-patch spread of the disease are:
| (2.1) |
| (2.2) |
| (2.3) |
| (2.4) |
| (2.5) |
| (2.6) |
| (2.7) |
| (2.8) |
where
and
| (2.9) |
| (2.10) |
are the force of infection terms, and with a constant per-capita death rate, , for every compartment except the death due to disease compartment and a birth rate, , increasing occupation of susceptible compartments (except for Aedes mosquitoes which exhibit vertical transmission). Transmission within a patch, x, depends on density of animals and mosquitoes within the patch. The contact rate is denoted e−r(x)/a where , Nx is to total number of animals and mosquitoes in the patch, Ax is the area of the patch, and a is the characteristic length of local spread (about 5 miles). In this case, the transmission rates are where is the infectiousness of species i at stage n and is the susceptibility of species i at stage m. Susceptibility at stages where the virus is already incubating, shedding, or cleared is assumed to be zero (i.e. complete immunity). At low host and vector density, transmission is density-dependent and at high density it is constant, while for mid ranges of host and vector density, transmission rates fall between the two. For species categories where particular mitigation strategies are not appropriate, we set the corresponding parameter to zero (e.g. we set εq = 0 since animal quarantine is not considered effective for vector-borne diseases). See Reference [32] for a full description of the model and parameters.
For the mosquito categories, an extra compartment for egg and larvae aquatic stages was added and the mosquito birth term is directed into this compartment before hatching at a weather-dependent percapita hatch rate into the susceptible adult compartment. For Aedes mosquitoes, it is possible for a certain fraction (ϕ) of eggs laid by infected mosquitoes to be infected, so some Aedes mosquitoes in the aquatic compartment hatch directly into the infected adult mosquito category and only progress through the latent incubation and infectious stages. Mosquitoes do not recover once infected.
Between-patch disease transmission occurs at rate depending on Euclidean distance and on long range transport. Long range transport would determined by the user and entered as a matrix indicating rates of movement between patches or regions; it was not modeled in the present work. The probability that a susceptible patch X will be infected is
| (2.11) |
| (2.12) |
where κs is a short range distance kernel and κL is a long range distance kernel determined by the matrix entry corresponding to transport for patch y to patch x. The terms χS and χL represent short and long distance movement control implemented after detection. Similar long/short range transmission terms are used for a model of foot and mouth spread in the U.K. [42] and are described in detail in Manore et al. [32].
2.2. Parameters and their Variation in the Model
Exploring the interplay of herd immunity, pathogen variability, host and vector population density, rainfall patterns, disease progression parameters, and mitigation strategies can be complex. Simplified model systems can lack elements necessary to capture realism, yet the simultaneous treatment of all sources of variability in epidemic progression can make it difficult to quantify sensitivities and characterize and visualize results. In this work, we present historical rainfall data [26,48] and produce a minimal model of how this couples to mosquito density. Similarly, we present actual cattle [17], human [7], and land use data [24], and infer wildlife and vector carrying capacities from land use data. In keeping with the observed usefulness of patch-models of disease, we explore fluctuations of epidemic severity and the dependence of epidemic severity on host and vector population density, rainfall, and movement and vaccination control measures on a simplified 30 × 30 square patch with uniform initial host and vector populations, driven by stochastically generated rainfall data derived from observations at the Serengeti wildlife reserve. Since one important goal of this study is to characterize the importance and potential coupling of the effectiveness of various mitigation strategies, we used uniform distributions across plausible ranges for these parameters, as indicated in Table 1.
Considerable uncertainty surrounds the parameters describing disease progression and transmission as well as population movements and dynamics. These uncertainties reflect both a lack of knowledge and intrinsic variability among outbreaks. To capture these uncertainties and enable the above sensitivities to be more robustly computed, we judiciously used uniform distributions for several of the parameters describing our disease progression and transmission.
Table 1 lists all of the parameters necessary to define the model. Some parameters were taken from observations of disease progression ([10,16] and references therin), while others were taken by identifying attributes from isolated historical epidemics (e.g. [5,35,38]), and comparing to overall system dynamics in the present model simulations. Vertical transmission of RVF virus in mosquitos is discussed in Refs. [8,9,33]
3. Results
We consider the results in the order of multi-host dynamics, population density, saturation, herd immunity, and mitigations.
3.1. Multi-host dynamics
An important aspect of our model is the mosquito population dynamics, which have been observed to depend on temperature, photoperiod, and rainfall (among other environmental factors) [3,12]. Rainfall can lead to mosquito population increases which can lead to increased biting intensities. More mosquitoes successfully feeding on blood can lead to more eggs and an increase in immature stages of mosquitoes [30,40]. Temperature can affect the development of the immature stages of mosquito growth (egg, larva, pupae). Among the dependencies on temperature, the virus incubation period for mosquitoes tends to decrease with increases in temperature (up to a point) [44] and the mosquito life span is longer in temperate regions compared to very hot or cold regions [11,30]. We are modeling an African region close to the equator with nearly constant temperature and daylight so rainfall is the dominant environmental forcing term for our model (as in Schaeffer et al. [39]). Figure 2 shows a time-series of rainfall amounts in the middle of our simulation region. An additional sensitivity of the epidemic progression on the rainfall history occurs because subsequent generations of RVF require alternating incubation times in the host and the vector, which slows the establishment of RVF virus in the host and vector populations.
Figure 3 shows a typical time-series from the RVF model showing the appearance of disease in a naive population on a 30×30 grid with 100,000 cattle in each of the 900 46×46 km grid squares. The dynamics of a single epidemic are shown with an expanded temporal scale, while the recurrent epidemics over 25 years are shown to the right. Displayed populations are aggregated across the geographic region. Susceptible populations are in the tens of millions, and are thus at the top of Figure 3, while infected populations are much smaller, and thus at the bottom. Rainfall is indicated by the magenta squares in arbitrary units. Note that since only a small portion of the entire region is, in general, infected, an epidemic can be saturating one region while the ratio of infected to total population in Figure 3 is only a few percent. Although the 900 geographic regions have uniform initial communities and applied rainfall patterns, the strong inhibition of disease provided by prior exposure (herd immunity) creates a strong and enduring spatial heterogeniety in disease prevalence.
Figure 3.
Epidemic timelines for populations (top) and infected populations (bottom) of Aedes and Culex mosquito, and cattle versus time. On the left, one cycle of an epidemic is shown, while in the right are shown the sporadic epidemics over 25 years. Rainfall is modulated stochastically in a rough approximation to the patterns shown in Figure 2, and is shown in squares with an arbitrary scale.
The rapid rise of susceptible Aedes mosquitoes and slower rise of Culex mosquitoes is in keeping with the hatch rates in Table 1, and is readily visible at the left of Figure 3 starting promptly at the beginning of each rainy season. A short time later, the populations of infected mosquitoes and cattle begin to increase. This increase is much slower than that of mosquito populations, as it requires alternate incbuation times in hosts and vectors to establish the epidemic. The mosquito populations track closely with rain, and when the rain stops, there is a rapid exponential decline in the Aedes mosquito population. In addition to the rainfall, the epidemic is most sensitive to the incubation time for the virus in the mosquitoes. Later we examine in more detail how rainfall, vaccination, and movement control are important in determining the severity of the epidemics.
The recurring epidemic predictions shown on the right half of Figure 3 are correlated with the mosquito population and the seasonal rainfall. Year-to-year fluctuations in mosquito populations vary by approximately a factor of three, while the peak number of infected animals fluctuates by almost an order of magnitude. It takes approximately ten years for the epidemics to equilibrate in scale across the geographic area. This happens when a rainy season is long enough for a large epidemic to spread across the entire geographic region. It is likely that long-range transport of animals, which we do not consider, will significantly impact the details of how epidemics spread across East Africa, although in our uniform patch, short range transport is fully capable of spreading RVF across the entire region. Another significant time-scale observed in the simulations is the replenishment of susceptible cattle, which occurs with a rate of 33 % per year in our simulations. Because we assume that the cattle do not migrate between the regions, the herd immunity can be analyzed locally. When we remove the variability in duration of rainfall (without changing the overall amplitude), the epidemic eventually extinguishes itself.
3.2. Population density, saturation, and herd immunity
We next examine the geographic dependence of our inputs. Figure 4 shows four inputs needed for our model as a contour map overlaid on East Africa, with country borders in black and rivers in cyan. The Indian Ocean and Lake Victoria are white in all four maps. Cattle density [17], land use [24] (from which initial mosquito populations are linearly estimaed), human population density [7], and cumulative rainfall over the first ten days of 2007 [48], are each indicated in coutour maps in Figure 4. The data were aggregated to 40 km × 40 km squares, and the 25 × 15 degree area is covered by a 100 × 60 grid of squares. Color range scales for the four plots are logarithmic, and correspond to factor three changes between adjacent colors for each figure, with specific values for all four plots provided in the caption.
Figure 4.
Spatial distribution of hosts and risk factors, geographic data for cattle populations [17], land use [24], human populations [7], and rainfall for January 1–10, 2007 [48]. For cattle, red indicates densities > 1,000 per km2; for land use, red indicates broad-leaf trees, green indicates mixed forests and grasslands, and blue desert (details of classification are provided in [24]; for human populations, red indicates densities > 100 per km2; for rainfall in the first ten days of 2007, red indicates > 10 cm.
Two salient features in Figure 4 inform our choice of simulations to investigate. First, our choice of 40 km squares are large enough to cover several large countries with a few thousand regions, while small enough to capture spatial dependencies of host populations, changes in land-use, and regional rainfall patterns. While there are undoutably numerous important local variations of importance to disease progression, such as contact terms between people and animals, the presence of standing water, and local concentrations of animals, it appeares that even a hundred-fold increase in the number of geographic regions would fail to capture these changes. Additionally, the data in Figure 4 derived from sources which are largely available for regions throughout the world, while the more local data would require significantly more effort to obtain. Secondly, regions of high human and cattle populations largely cooccur, around Lake Victoria and at the north of this area, in southern Ethiopia. The land use data, from which mosquito and wildlife carrying capacities were inferred, shows a relatively smooth progression from rainforest on the west side of our region to desert to the east. The spatial and temporal patterns of the weather are only hinted at in Figures 2 and 4, but clearly contain important aspects on the regional length scale and yearly time scales, respectively.
Although we have run simulations using the actual inputs shown in Figure 4, more insight into the disease dynamics can be obtained by considering a simpler patch, 30 squares on a side, with uniform initial host and mosquito populations, and rainfall data. Even in such a system, the role of the spatial network enters in a non-trivial manner and important insights into the real-world impacts of population density, duration of the rainy season, and the impacts of vaccination and movement controls can be understood.
To illustrate the role of population density (and thus also transmissibility) in determining epidemic severity, we plot the total number of cattle dying from RVF as a function of both mosquito population and cattle population in Figure 5a. For simplicity, we used identical parameters for cattle and wildlife distributions in these simulations. For our choice of epidemic parameters, epidemics are capable of spreading across the entire 1380 km region in a (particularly lengthy) single rainy season, if they are broadly seeded with infected animals and mosquitoes at the start of the season. In the typical example shown in Figure 3, it took a full decade for this to occur. Eventually, herd immunity limits the spread of the virus. Consequently, increases in the transmissibility do not greatly increase the consequence, when averaged across a 25-year period.
Figure 5.
Important drivers of RVF epidemic severity. (a) Population density dependence of consequence over 25 years for cattle and mosquitoes. (b) Total deaths in a given year vs. the duration of the rainy seasons for the indicated mosquito densities of 0.4 (red +), 0.6 (magenta line), 0.8 (green line), 1.0 (cyan line), and 1.9 (blue x) times that of baseline case. The smoothing spline was a heavily smoothed cubic spline, as implemented with the Gnuplot function acspline and a weighting parameter of 0.001; in the limit of zero weighting, this function provides a simple linear least squares fit to the data. Since the individual years were sampled from a 25 year simulation, the curves sample over not only the range of rainfall durations, but also the variety of possible sequences of wet and dry years.
The transmissibility is lower in regions with either lower mosquito or cattle densities. These low population regions can create geographic barriers that the epidemics are unable to propagate across in the timescale of animal lifetimes and cattle in the protected regions have a significant likelihood of never encountering the disease during their lifetimes. Nevertheless, increasing the density of susceptible hosts above the baseline case does not lead to a similar order-of-magnitude increase in consequence. This is because, at the baseline case, each subregion of our simulated area is typically impacted by an epidemic during the lifetime of the hosts. Effectively, this means naturally acquired herd immunity is built up in every region. The raw value of our transmissibility for RVF was, of course, not determined by experiments on contagious spread, but by our desire to have our model reproduce the observed timescale of RVF to spread across wide regions of East Africa. Further observations, such as serological studies or selective sequencing of viruses, could be used to determine epidemiological linkages among regions will be required to further refine the relative importance of long range transport of livestock, vertical transmission in mosquitoes, and pathogen variability in the appearance of epidemics across the region.
This dependence can be used to guide the potential impact of vaccination of newborn livestock and mosquito control mitigation in areas of varying cattle density. The strong non-linearities observed in the simulations suggest the importance of serological surveys for prevalence of exposure in deciding which areas will benefit from mosquito control programs.
To illustrate the role of lengthy rainy seasons on epidemic scale, Figure 5b shows the total number of dead cattle in a single season as a function of the duration of the rainy season for different assumed values of the initial mosquito population and associated carrying capacities. From Figure 5a, we expect the dependence on cattle populations to be similar to the dependence on mosquito population. Since the consequence also depend on other randomly sampled variables (Table 1) we use smoothing splines to summarize the prediction trends for the different cases of mosquito density, and show the complete variablity for only two of the simulations, as symbols. Once again, the epidemic size reaches the saturation value after the rainfall of longest duration (note, we used the same scaling factor of 1.0 as in Figure 5a). For higher mosquito densities, this saturation value is reached in half the time, but the same maximal consequence occurs. Cutting the mosquito populations by a factor of 2.5, however, reduces the number of dead cattle 10-fold. Although much of the variance is due to variability in disease progression and severity parameters, much is also due to the interplay of geographic heterogeniety and herd immunity.
3.3. Mitigations
This same interplay of geographic heterogeniety and herd immunity complicates the assessment of the impact of mitigative measures. In Figure 6, we explore the impact of two such measures, short-range movement control and vaccination, for different values of vector density.
Figure 6.
Mitigation strategies. Smoothing splines indicating deaths per individual epidemic, aggregated over 25 year simulations, as a function of (a) fraction of normal movement, and (b) vaccine response times, for different mosquito densities, with values of 0.4, 0.6, 0.8, 1.0, 1.3, 1.6, and 1.9 indicating the fraction of the baseline mosquito population used, from bottom to top. For the basline case, (green, labeled 1.0), symbols are shown for each run determining the spline. Both plots were made from the same set of runs with both variables sampled over the indicated uniform distributions. The smoothing spline was a heavily smoothed cubic spline, as implemented with the Gnuplot function acspline and a weighting parameter of 0.001; in the limit of zero weighting, this function provides a simple linear least squares fit to the data. Most of the impact of vaccination occurs in subsequent years.
Restricting cattle movement is a common mitigation measure to prevent the spread of epidemics. For the uniformly distributed populations considered in these simulations, no long-range transport was included and the movement restrictions were applied to the distance dependent spread between nearby geographic units. As with Figure 5b, the solid lines indicate smoothing splines that indicate the trend in a considerable background of other, significant, dependencies. For the base case mosquito population, labeled 1.0 in Figure 6a, the data points that the approximating spline is derived from are also shown. Movement controls make the most difference when the transmissibility is higher and the geographic spread is greatest.
For a 45 day rainy season, we see that there is only a 3 week window of opportunity to vaccinate in time to impact an ongoing epidemic for the baseline case. Since vaccination continues until the epidemic is extinguished, the overall consequence in Figure 6b is nearly an order of magnitude below the single-season consequence from Figure 5b; the benefits of vaccination primarily occur in years subsequent to the vaccination effort. The dependencies between the variables, shown in Fig. 6a, provide insight into the value of such vaccination programs when applied locally or with sub-optimal coverage of susceptible.
Including spatial heterogeneity and explicit time-dependence in the epidemiology model captures important and realistic effects. The most important effects are the relatively large year-on-year fluctuations in epidemic size and the likelihood that herd immunity in densely populated areas impacts the severity of epidemics at other locations.
4. Discussion
We present a model of RVF spread which incorporates interdependencies of the most important determinants of disease range and severity (host and vector population density; duration of rainy seasons). We quantified the impact of three important mitigative measures, vector control, vaccination, and movement restriction. The presence of geographic heterogeniety and herd immunity complicates our ability to understand the value of local (temporal and spatial) application of such controls in any particular region, although their overall value when applied consistently was clearly evident. Knowledge gaps exist in both our understanding of the geographic dependence and temporal dependence of RVF progression.
4.1. Geographic uncertainties
The density of susceptible hosts is of primary importance in determining epidemic severity and geographic range of RVF disease; a factor 2.5 reduction in density of susceptible hosts or mosquitoes is observed in Figure 5a to result in a factor ten or more reduction in consequence, averaged over 25 years. Examination of the cattle population density in Figure 4 already allows one to see that the epidemics will be centered primarily in two locations: Ethiopia to the north and the regions surrounding Lake Victoria in the southwest of the East African region shown. Both the human populations and land use (and, by assumption, mosquito population) correlate reasonably well with the cattle populations, meaning that it should be possible to model some of the effects of geographic heterogeneity with an implicit vector model. Recent work has modeled the yearly changes in cattle populations, as impacted by rainfall, climate change, and human behaviors [31].
Further examination of Figure 4 suggests short-range transport alone will not allow the epidemic to spread from Lake Victoria to Ethiopia. Consequently, a realistic model will likely require an explicit long-range transport of cattle between countries. Reference [46] suggests that a value of 200,000 cattle transported each year among countries represented in East Africa (Kenya, Tanzania, Rwanda, Burundi, Uganda, and Sudan) is reasonable.
In this work, we somewhat arbitrarily placed the transmissibility at the level needed to cause shortrange spread to take the disease across our simplified geographic region during one of the longer rainy seasons. Although in reasonable agreement with observation, specific efforts to characterize the level of naturally occurring herd immunity (fraction seropositive) as a function of geography and time would enable a better understanding of where the transmissibility lies [14].
Although reasonable sources of data exist for human and cattle populations, specifying the regional carrying capacity for competent vectors and relevant wildlife reservoirs is more problematic. Not only are the particular species-dependencies of competence not understood, but the population densities and disease-carrying attributes of each are also, in general, unknown. A recent study [15] documents the incidence of wildlife in mosquito meals in Uganda, suggesting that possible vector-wildlife reservoir relationship for several arboviruses, including Rift Valley fever virus. Similarly, investigation of the role of various wildlife hosts in re-seeding RVF epidemics in Kruger National Park, South Africa has suggested the wildlife must be considered for proper treatment [16].
While we kept a wildlife compartment in our model for completeness, we have left exploration of the wide variety of potential carrier states, long range transportation terms, and potentially complex spatial distributions for a subsequent work. It appears likely to us that land-use data, such as that shown in Figure 4 will be a necessary intermediate step to inform detailed models and guide collection of the relevant data. The principal aspect of our study relevant to these considerations are the impact of the 3 year replacement time of cattle in re-seeding the susceptible population for epidemics and the dependence of the yearly epidemic size on the duration of the rainy season.
In picking a granularity of 40 km, we were able to simulate multi-year epidemics across much of East Africa in a few minutes of time on a single computer processor, and compare to similarly aggregated data on epidemic progressions. In doing so, we have necessarily aggregated mosquito populations and rainfall to a similar spatial scale. The observation that human, cattle, and land use correlate will likely need refinement at higher level of spatial resolution, as local heterogeneities in the distributions of animal and human hosts and the vectors are resolved.
4.2. Temporal uncertainties
Numerous RVF epidemics have been characterized over the past three decades [1,35]. The strong correlation of RVF epidemics with rainfall has previously been noted [2]; consequently we used rainfall as the temporal variable driving our simulation. Other choices, such as temperature [22] or estimated area of standing water [41] can be incorporated to improve the correlation between model and observation. At least two types of problems are impacted by the choice of temporal drivers of epidemics. First is how the epidemic severity depends on the amplitude of the forcing term (Does doubling the rainfall double the hatch rate of mosquitoes?) or the duration over which this term is applied. Second is how the seeding of subsequent epidemics occurs, such as survival of infected mosquito eggs through the dry season, a reservoir in wildlife, chronic-carrier cattle or wildlife, or long-range transport terms.
A decade is required in our simulations for a newly introduced RVF strain to equilibrate into the mosquito populations and spread across the geographic region and define appropriate, near steady state, initial conditions for the simulations. This initialization requires a few heavy rainfall years, because of the highly non-linear dependence of epidemic size on the duration of the rainy season. Targeted strain tracking would provide much-needed constraint on the relative importance of animal reservoirs of RVF and long- and short-range transportation of animals in spreading RVF throughout East Africa.
Although the yearly cycle of rainfall is immediately recognizable in Figure 2, the presence of two distinct rainy seasons per year, the spatial and temporal heterogeniety and ambiguity in this quantity is also evident. It is clear from our simulations that the consequence in any given epidemic will depend on the level of seropositive animals, the spatial-temporal profile of the rainfall, details of the lifecycle parameters describing the vectors, as well as assumed mitigations [27].
Even though there are over 30 species of mosquitoes that are vectors for RVF virus [38,45], we consider two representative types of mosquitoes: Aedes, or floodwater, mosquitoes and Culex mosquitoes. As mentioned earlier we use rainfall as the main driving factor of the populations. Aedes eggs must be dry for at least 6 days before they can mature. After they mature, they hatch during the next flooding event large enough to cover them with water. The eggs can survive dry and dormant for months to years [9,21]. At the beginning of the rainy season, the Aedes mosquitoes quickly ramp up to very large numbers and then decline due to the need of dry conditions for egg maturation. There can be a second increase at the end of the rainy season if it stops raining for several days and then rains again. Culex mosquitoes, on the other hand, prefer water that has been standing for a while. Their eggs require water to mature and hatch. They survive the dry season in adult form. During the rainy season, Culex mosquitoes ramp up to a maximum toward the end of the season.
Distinguishing among the above possibilities will be useful in guiding particular decisions surrounding local disease control efforts, and incorporation of these refinements will undoubtably improve the fidelity of modeling efforts such as ours. In particular, serology studies of areas of differing host and vector population density could provide an important constraint on our model by measuring the extent to which naturally acquired herd immunity limits epidemics of RVF [14]. Nevertheless, the particular mechanistic choices we made reporoduced widely-observed empirical features of RVF epidemiology, and should suffice for our intent – to explore the interplay of vector-host dynamics, weather, geography, and mitigation measures.
4.3. Recommendations for control
Several observations appear robust enough (and plausible enough) to impact control measures. The observation of the benefits of vaccination in years subsequent to the vaccination program, when taken together with the problems of spontaneous abortion and spread of RVF virus through re-use of needles suggest an optimal mitigation strategy would consist of regular vaccination of cattle during their first year of life. Comparison of unmitigated epidemics in Figure 5 with mitigated epidemics in Figure 6 show an aproximately 30-fold reduction in mortality associated with relatively slow vaccination programs (with a much greater reduction for vaccination progams taking less than two weeks). The extent to which vaccination reduces impact in subsequent years will depend primarily on the birth/death rate of susceptible cattle, which was assumed to occur in 1,000 days. Since the epidemics occur yearly, it is relatively straightforward to imagine how changes in this value will impact the value of such a vaccination program. The 30-fold reduction in mortality by reducing the susceptible pool by a factor of three is in keeping with the sensitivity observed in Figure 5a, and emphasizes the tremendous value of vaccination programs, provided they can establish herd immunity. We have modeled RVF epidemics and found the periodic rainfall and high sero-positive prevalence suggests self-limited epidemics. This leads to vaccination as the most robust mitigation, and it could be done annually in young animals, rather than under the severe time constraints that occur after an epidemic has begun.
Much more understanding of the role of ungulate wildlife and details of mosquito population dynamics will be necessary to fully characterize and realistically simulate RVF epidemics. Our model has identified some of the key quantities and data such as serological studies and sequencing, that are needed for validating improved mathematical models and future extensions of RVF simulations.
The potential importance of herd immunity has been highlighted in this work, but the potential of multiple co-circulating strains of RVF virus has not been considered in detail. As climate change, economic patterns, and population densities of hosts and vectors have all co-occurred in conjunction with increasing geographic range and severity of epidemics in the past decade, the likelihood of a virulent or vaccine-evading strain emerging must be considered, especially in regard to potential mitigation programs.
Acknowledgments
We thank Dennis Powell, Leslie Moore, Mac Brown, Joel Berendzen, and Mary Green for assistance with data collection and analysis. This work was performed in part by Defense Threat Reduction Agency (DTRA) CBT-09-IST-05-1-0092. Los Alamos National Security, LLC, is operator of the Los Alamos National Laboratory (LANL) under Contract No. DE-AC52-06NA25396 with the US Department of Energy. This work was also supported in part by an NIH/NIGMS grant in the Models of Infectious Disease Agent Study (MIDAS) program, U01-GM097661-01 and by the NSF MPS Division of Mathematical Sciences NSF/MPS/DMS grant DMS-1122666.
References
- 1.Andriamandimby SF, Randrianarivo-Solofoniaina AE, Jeanmaire EM, Ravololomanana L, Razafimanantsoa LT. Rift Valley Fever during Rainy Seasons, Madagascar, 2008 and 2009. Emerging Infectious Diseases. 2010;16(6):963–970. doi: 10.3201/eid1606.091266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anyamba A, Chretien JP, Small J, Tucker CJ, Formenty PB. Prediction of a Rift Valley fever outbreak. PNAS USA. 2009;106(3):955–959. doi: 10.1073/pnas.0806490106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ba Y, Diallo D, Dia I, Diallo M. Feeding pattern of Rift Valley Fever virus vectors in Senegal. Implications in the disease epidemiology. Bull Soc Pathol Exot. 2006;99:283–9. [PubMed] [Google Scholar]
- 4.Ba Y, Diallo D, Kebe CMF, Dia I, Diallo M. Aspects of bioecology of two rift valley fever virus vectors in Senegal (West Africa): Aedes vexans and Culex poicilipes (Diptera : Culicidae) Journal of Medical Entomology. 2005;42:739–750. doi: 10.1603/0022-2585(2005)042[0739:aobotr]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 5.Bird BH, Ksiazek TG, Nichol ST, Maclachlan NJ. Rift Valley fever virus. J Am Vet Med Assoc. 2009;234:883–893. doi: 10.2460/javma.234.7.883. [DOI] [PubMed] [Google Scholar]
- 6.Boshra H, Lorenzo G, Busquets N, Brun A, Rift A. Valley Fever: Recent Insights into Pathogenesis and Prevention. J of Virol. 2011;85:6098–6105. doi: 10.1128/JVI.02641-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Center for International Earth Science Information Network (CIESIN)/Columbia University, and Centro Internacional de Agricultura Tropical (CIAT) Gridded Population of the World, Version 3 (GPWv3): Population Density Grid, Future Estimates. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC); 2005. http://sedac.ciesin.columbia.edu/data/set/gpw-v3-population-density-future-estimates. Accessed October, 2010. [Google Scholar]
- 8.Chevalier V, De La Rocque S, Baldet T, Vial L, Roger F. Epidemiological processes involved in the emergence of vector-borne diseases: West Nile fever, Rift Valley fever, Japanese encephalitis and Crimean-Congo haemorrhagic fever. Revue scientifique et technique. 2004;23:535–555. doi: 10.20506/rst.23.2.1505. [DOI] [PubMed] [Google Scholar]
- 9.Chevalier V, Pepin M, Plee L, Lancelot R. Rift Valley fever – a threat for Europe? Eurosurveillance. 2010;15(10):18–28. [PubMed] [Google Scholar]
- 10.Chitnis NC, Hyman JM, Manore CA. Modelling vertical transmission in vector-borne diseases with applications to Rift Valley fever. J of Biol Dyn. 2013;7:11–40. doi: 10.1080/17513758.2012.733427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Depinay JM, Mbogo CM, Killeen G, Knols B, Beier J. A simulation model of African Anopheles ecology and population dynamics for the analysis of malaria transmission. Malaria Journal. 2004;3:29. doi: 10.1186/1475-2875-3-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Diallo M, Nabeth P, Ba K, Sall AA, Ba Y. Mosquito vectors of the 1998–1999 outbreak of Rift Valley Fever and other arboviruses (Bagaza, Sanar, Wesselsbron and West Nile) in Mauritania and Senegal. Medical and Veterinary Entomology. 2005;19:119–126. doi: 10.1111/j.0269-283X.2005.00564.x. [DOI] [PubMed] [Google Scholar]
- 13.Ducatez MF, Olinger CM, Owoade AA, De Landtsheer S, Ammerlaan W. Multiple introductions of H5N1 in Nigeria – Phylogenetic analysis reveals that this deadly virus first arrived in Africa from different sources. Nature. 2006;442:37–37. doi: 10.1038/442037a. [DOI] [PubMed] [Google Scholar]
- 14.Evans A, Gakuya F, Paweska JT, Rostal M, Akoolo L. Prevalence of antibodies against Rift Valley fever virus in Kenyan wildlife. Epidemiology and Infection. 2008;136:1261–1269. doi: 10.1017/S0950268807009806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Crabtree MB, Kading RC, Mutebi JP, Lutwama JJ, Miller BR. Identification of host blood from engorged mosquitoes collected in western Uganda using cytochrome oxidase I gene sequences. J Wildlife Dis. 2013;49:611–626. doi: 10.7589/2012-08-213. [DOI] [PubMed] [Google Scholar]
- 16.Manore CA, Beechler BR. Interepidemic persistence of Rift Valley fever: vertical transmission or cryptic cycling? Transboundary and Emerging Diseases. 2013 doi: 10.1111/tbed.12082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.FAO, Geonetwork. Predicted global cattle density (2005), corrected for unsuitability, adjusted to match observed totals. avalable at http://www.fao.org/geonetwork/srv/en/metadata.show?id=12713, accessed October 2010.
- 18.Fenner F, Henderson DH, Arita I, Jezek Z, Ladnyi IA. Smallpox and its Eradication. World Health Organization; Geneva: 1988. freely available at http://biotech.law.lsu.edu/blaw/bt/smallpox/who/red-book/index.htm. [Google Scholar]
- 19.Gaff H, Burgess C, Jackson J, Niu T, Papelis Y. Mathematical model to assess the relative effectiveness of Rift Valley Fever countermeasures. Int J Artificial Life Res. 2011;2(2):1–18. [Google Scholar]
- 20.Gao D, Cosner C, Cantrell RS, Beier JC, Ruan S. Modeling the Spatial Spread of Rift Valley Fever in Egypt. Bul Math Biol. 2013;75:523–542. doi: 10.1007/s11538-013-9818-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gargan TP, 2nd, Jupp PG, Novak RJ. Panveld oviposition sites of floodwater Aedes mosquitoes and attempts to detect transovarial transmission of Rift Valley fever virus in South Africa. Med Vet Entomol. 1998;2:231–236. doi: 10.1111/j.1365-2915.1988.tb00189.x. [DOI] [PubMed] [Google Scholar]
- 22.Goswami P, Murty US, Mutheneni SR, Kukkuthady A, Krishnan ST. A model of malaria epidemiology involving weather, exposure, and transmission applied to North East India. PLOS ONE. 2012;7:e49713. doi: 10.1371/journal.pone.0049713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Graw F, Leitner T, Ribeiro RM. Agent-based and phylogenetic analyses reveal how HIV-1 moves between risk groups: injecting drug users sustain the heterosexual epidemic in Latvia. Epidemics. 2012;4(2):104–116. doi: 10.1016/j.epidem.2012.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hansen M, DeFries R, Townshend JRG, Sohlberg R. Global land cover classification at 1km resolution using a decision tree classifier. Int J Rem Sens. 2000;21:1331–1365. Accessed from http://www.landcover.org/data/landcover/in October, 2010. [Google Scholar]
- 25.Hightower A, Kinkade C, Nguku PM, Anyangu A, Mutonga D, Omolo J, Kariuki Njenga M, Feikin DR, Schnabel D, Ombok M, Breiman RF. Relationship of Climate, Geography, and Geology to the Incidence of Rift Valley Fever in Kenya during the 2006–2007 Outbreak. Am J Trop Med Hyg. 2012;86(2):373–2380. doi: 10.4269/ajtmh.2012.11-0450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holdo RM, Holt RD, Fryxell JM. Opposing rainfall and plant nutritional gradients best explain the wildebeest migration in the Serengeti. Am Nat. 2009;173:431–445. doi: 10.1086/597229. [DOI] [PubMed] [Google Scholar]
- 27.Hoogstraal H, Meegan JM, Khalil GM, Adham FK. Rift-valley fever epizootic in Egypt 1977–78.2. ecological and entomological studies. Transactions of the Royal Society of Tropical Medicine and Hygiene. 1979;73(6):624–629. doi: 10.1016/0035-9203(79)90005-1. [DOI] [PubMed] [Google Scholar]
- 28.Hughes-Fraire R, Hagerman A, McCarl B, Gaff H. Rift Valley Fever: An Economic Assessment of Agricultural and Human Vulnerability. presented at the Southern Agricultural Economics Association Annual Meeting; Corpus Christi, TX. February 5–8, 2011. [Google Scholar]
- 29.Ikegami T. Molecular biology and genetic diversity of Rift Valley fever virus. Antiviral Research. 2012;95:293–310. doi: 10.1016/j.antiviral.2012.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kasari TR, Carr DA, Lynn TV, Weaver JT. Evaluation of pathways for release of Rift Valley fever virus into domestic ruminant livestock, ruminant wildlife, and human populations in the continental United States. Javma-Journal of the American Veterinary Medical Association. 2008;232(4):514–529. doi: 10.2460/javma.232.4.514. [DOI] [PubMed] [Google Scholar]
- 31.Lund TM, Lindtjorn B. Cattle and climate in Africa: How climate variability has influenced national cattle holdings from 1961–2008. PeerJ. 2013;1:e55. doi: 10.7717/peerj55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Manore CA, McMahon BH, Fair JM, Hyman JM, Brown M. Disease properties, geography, and mitigation strategies in a simulation spread of rinderpest across the United States. Vet Res. 2011;42:1–55. doi: 10.1186/1297-9716-42-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Martin V, Chevalier V, Ceccato PN, Anyamba A, De Simone L, Lubroth J, de La Rocque S, Domenech J. The impact of climate change on the epidemiology and control of Rift Valley fever. Revue Scientifique et Technique. 2008;27:413–426. [PubMed] [Google Scholar]
- 34.Metras R, Collins LM, White RG, Alonso S, Chevalier V. Rift Valley Fever Epidemiology, Surveillance, and Control: What Have Models Contributed? Vector-borne and Zoonotic Diseases. 2011;11:761–771. doi: 10.1089/vbz.2010.0200. [DOI] [PubMed] [Google Scholar]
- 35.MMWR. Rift Valley fever outbreak: Kenya, November, 2006 – January, 2007. Ma M Report. 2007:73–76. [PubMed] [Google Scholar]
- 36.Mpeshe SC, Haario H, Tchuenche JM. A mathematical model of Rift Valley Fever with human host. Acta Biotheoretica. 2011;59:3–4. 231–250. doi: 10.1007/s10441-011-9132-2. [DOI] [PubMed] [Google Scholar]
- 37.Pattnaik B, Pateriya AK, Khandia R, Tosh C, Nagarajan S. Phylogenetic analysis revealed genetic similarity of the H5N1 avian influenza viruses isolated from HPAI outbreaks in chickens in Maharashtra, India with those isolated from swan in Italy and Iran in 2006. Current Science. 2006;91:77–81. [Google Scholar]
- 38.Pepin M, Bouloy M, Bird BH, Kemp A, Paweska J. Rift Valley fever virus (Bunyaviridae: Phlebovirus): an update on pathogenesis, molecular epidemiology, vectors, diagnostics and prevention. Vet Res. 2010;41(6):61. doi: 10.1051/vetres/2010033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schaeffer B, Mondet B, Touzeau S. Using a climate dependent matrix model to predict mosquito abundance: Application to Aedes (Stegomyia) africanus and Aedes (Diceromyia) furcifer (Diptera : Culicidae), two main vectors of the yellow fever virus in West Africa. Infection Genetics and Evolution. 2008;8(4):S45–S45. doi: 10.1016/j.meegid.2007.07.002. [DOI] [PubMed] [Google Scholar]
- 40.Shaman J, Day JF. Reproductive Phase Locking of Mosquito Populations in Response to Rainfall Frequency. PLoS ONE. 2007;2(3):e331. doi: 10.1371/journal.pone.0000331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Soti V, Tran A, Degenne P, Chevalier V, Seen DL. Combining hydrology and mosquito population models to identify the drivers of Rift Valley Fever emergence in semi-arid regions of West Africa. PLOS Negl Trop Diseases. 2012;6:e1795. doi: 10.1371/journal.pntd.0001795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tildesley MJ, Savill NJ, Shaw DJ, Deardon R, Brooks SP. Optimal reactive vaccination strategies for a foot-and-mouth outbreak in the UK. Nature. 2006;440(7080):83–86. doi: 10.1038/nature04324. [DOI] [PubMed] [Google Scholar]
- 43.Tildesley MJ, House TA, Bruhn MC, Curry RJ, O’Neil M. Impact of spatial clustering on disease transmission and optimal control. PNAS USA. 2010;107:1041–1046. doi: 10.1073/pnas.0909047107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Turell MJ, Rossi CA, Bailey CL. Effect of extrinsic incubation-temperature on the ability of Aedes taeniorhynchus and Culex pipiens to transmit Rift Valley fever virus. Am J of Trop Med and Hyg. 1985;34(6):1211–1218. doi: 10.4269/ajtmh.1985.34.1211. [DOI] [PubMed] [Google Scholar]
- 45.Turell MJ, Dohm DJ, Mores CN, Terracina L, Wallette DL., Jr Potential for North American mosquitoes to transmit Rift Valley fever virus. J Am Mosq Cont Ass. 2008;24(4):502–507. doi: 10.2987/08-5791.1. [DOI] [PubMed] [Google Scholar]
- 46.USAID, Food security and nutrition working group. East Africa cross-border trade bulletin: October–December 2011. 2012:1–4. [Google Scholar]
- 47.WHO. Rift Valley Fever Factsheet. 2013 Available from: http://www.who.int/mediacentre/factsheets/fs207/en/
- 48.Xie P, Arkin PA. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bul Am Met Soc. 1997;78(11):2539–2558. Data set available at http://earlywarning.usgs.gov/fews/africa/index.php and accessed in October, 2010. [Google Scholar]
- 49.Xue L, Scott HM, Cohnstaedt LW, Scoglio C. A network-based meta-population approach to model Rift Valley fever epidemics. Journal of Theoretical Biology. 2012;306:129–144. doi: 10.1016/j.jtbi.2012.04.029. [DOI] [PubMed] [Google Scholar]


