Multiple Acquisition of Magic Angle Spinning Solid-State NMR Experiments Using One Receiver: Application to Microcrystalline and Membrane Protein Preparations

Abstract

Solid-State NMR spectroscopy of proteins is a notoriously low-throughput technique. Relatively low-sensitivity and poor resolution of protein samples require long acquisition times for multidimensional NMR experiments. To speed up data acquisition, we developed a family of experiments called Polarization Optimized Experiments (POE), in which we utilized the orphan spin operators that are discarded in classical multidimensional NMR experiments, recovering them to allow simultaneous acquisition of multiple 2D and 3D experiments, all while using conventional probes with spectrometers equipped with one receiver. POEs allow the concatenation of multiple 2D or 3D pulse sequences into a single experiment, thus potentially combining all of the aforementioned advances, boosting the capability of ssNMR spectrometers at least two-fold without the addition of any hardware. In this Perspective, we describe the first generation of POEs, such as dual acquisition MAS (or DUMAS) methods, and then illustrate the evolution of these experiments into MEIOSIS, a method that enables the simultaneous acquisition of multiple 2D and 3D spectra. Using these new pulse schemes for the solid-state NMR investigation of biopolymers makes it possible to obtain sequential resonance assignments, as well as distance restraints, in about half the experimental time. While designed for acquisition of heteronuclei, these new experiments can be easily implemented for proton detection and coupled with other recent advancements, such as dynamic polarization, to improve signal to noise. Finally, we illustrate the application of these methods to microcrystalline protein preparations as well as single and multi-span membrane proteins reconstituted in lipid membranes.

1. Introduction

Magic angle spinning solid-state NMR (MAS ssNMR) spectroscopy is emerging as a unique method for the atomic resolution structure determination of biomacromolecules, such as membrane proteins and fibrils that are recalcitrant to crystallization. Recent reviews have illustrated the most important achievements in this field [1-3]. The advancements of this spectroscopy are due to the concomitant developments in high-field magnet technology, advances in probe design, isotopic-labeling schemes, and sample preparations, as well as pulse sequence design. However, sensitivity and resolution of the ssNMR spectra still limit the routine application of these techniques, particularly for membrane proteins, where lipids are used in the preparations to maintain the native conditions of the proteins.

There is no doubt that ssNMR structure determination of biomacromolecules is time consuming. Many hours or several days of signal averaging are required for a series of multidimensional experiments. In the classical experiments used for membrane proteins, low gyromagnetic ratio nuclei ¹³C and ¹⁵N are acquired, which are intrinsically insensitive. In the past few years, several approaches have been introduced to speed-up ssMAS NMR experiments, including dynamic nuclear polarization (DNP) at ultra-low temperatures[4-6], paramagnetic relaxation enhancement (PRE)[7-9], and ¹H detection using ultra-fast MAS probes with or without perdeuteration [10, 11]. However, all these methods rely on sample modifications such as doping the samples with chemical compounds with unpaired electrons, use of low temperatures, and ultra-fast spinning speeds. While these methods have been successfully used for crystalline proteins, their application to membrane proteins is limited. To maintain their tertiary fold and function, membrane proteins need to be reconstituted in lipid membranes in a liquid crystalline phase[12, 13]. Lipid types as well as lipid to protein ratio are crucial parameters to maintain their functional integrity[12, 13]. Also, high spinning speeds can in several cases limit the application of ssMAS techniques[14]. For instance, enzyme function can be significantly reduced in the case of high spinning rates, although moderate spinning speeds can still be used to analyze the structural features of these enzymes.

In recent years, our group has been revisiting the classical NMR experiments for resonance assignment and distance determination in biological solids. Inspired by the previous work of Pines and Waugh [15], we asked ourselves: how much of the polarization generated by the experiments is actually converted into observable signals? Can we optimize the pulse sequences by recovering the orphan spin operators that are neglected or purged by the current pulse schemes?

Toward this goal, we developed a class of new experiments called Polarization Optimized Experiments (POE) that utilize orphan spin operators to generate multiple NMR spectra from one pulse sequence[16-19]. These experiments are carried out using commercial solid-state NMR probes for bio-solids and require only one receiver. To accomplish this task, we worked on the three main building blocks of the pulse sequences, including creation of the polarization, evolution, and detection. To generate extra operators to be utilized during the experiments, we introduced simultaneous cross polarization (SIM-CP)[18], generating multiple spin operators to be utilized in the generation of additional experiments. We introduced the concept of bidirectional specific cross polarization[17], and the use of long-living ¹⁵N z-polarization[20] to generate parallel pathways of spin operators to detect several (up to four) multidimensional spectra[17], with at least two-fold time saving.

In this Perspective, we describe the most common experiments, such as dual acquisition MAS (DUMAS)[18, 19] and MEIOSIS (Multiple ExperIments via Orphan SpIn operatorS)[17], that enable the recording of three to four multi-dimensional experiments, explaining the principles and the technical details for concatenating multiple experiments together. We also project the use of these experiments in conjunction with other techniques, including ¹H detection experiments. In the following synopsis, we will illustrate the optimization of the various steps and the implementations that make possible the simultaneous acquisition of multiple 2D, 3D, and 4D spectra.

2. Simultaneous cross-polarization

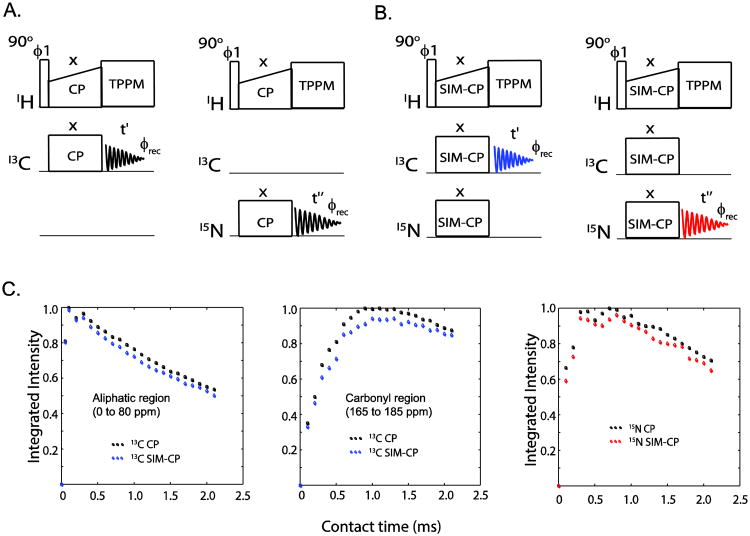
A central element in an MAS ssNMR experiment is the Hartmann-Hahn (HH) cross-polarization (CP)[21], which enables the polarization transfer from high (¹H) to low gyromagnetic ratio nuclei (¹³C or ¹⁵N) (Figure 1A). The optimization of this first step is crucial for enhancing the sensitivity of the ssNMR experiments. For the POE experiments such as DUMAS and MEIOSIS, we create the initial polarization using a SIM-CP on three different channels. This scheme makes it possible to create both ¹³C and ¹⁵N polarization by satisfying the Hahn-Hartmann conditions for ¹H and ¹³C as well as ¹H and ¹⁵N (Figure 1B). The rotating frame radio frequency (RF) amplitudes for SIM-CP transfer are given by ω₁ ± n.ω_r, ω₁,ω₁ for ¹H, ¹³C, and ¹⁵N, respectively, where ω₁ is ¹³C and ¹⁵N RF amplitudes, ω_r is MAS spinning frequency, and n is set to ±1 or ±2 to satisfy first or second sideband matching conditions, respectively. To test the efficiency of polarization transfer during SIM-CP, we performed a series of experiments on microcrystalline protein preparations or membrane proteins, varying spinning speeds and RF amplitudes. The ¹³C and ¹⁵N spectra are acquired separately using a single receiver. Importantly, we found that the ¹³C sensitivity is almost identical for CP and SIM-CP, whereas for ¹⁵N we observed ∼5-10% loss. Moreover, the HH matching conditions for SIM-CP are identical to those of conventional CP. Therefore, the experimental setup for the SIM-CP is relatively straightforward. As an example, we report a comparison of CP and SIM-CP optimization profiles carried out with U-¹³C,¹⁵N ubiquitin (Figures 1C-D). The data points indicate the normalized integrated intensities of ¹³C and ¹⁵N at a spinning rate of 12 kHz. Notably, the build-up rates of the polarization transfer for both CP and SIM-CP are very similar, with SIM-CP showing only marginal loss (less than 10%) of sensitivity for ¹⁵N spectra with respect to conventional CP.

Figure 1.

Pulse sequences utilized for the optimization of (A) ¹H-¹³C CP, and ¹H-¹⁵N CP, and (B) simultaneous CP (SIM-CP). (C) Comparison of ¹³C and ¹⁵N sensitivity for CP and SIM-CP for a sample of U-¹³C,¹⁵N microcrystalline ubiquitin. The sensitivity is almost identical for CP and SIM-CP for the aliphatic region, whereas for the carbonyl region and ¹⁵N a minimal loss of sensitivity (less than 10%) is observed using SIM-CP sequence.

3. Bidirectional Specific-CP and Residual Polarization

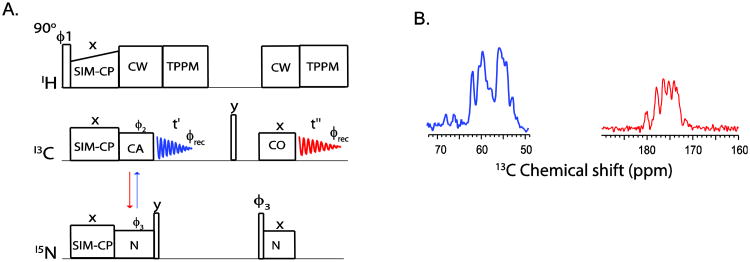
In the conventional ssNMR pulse sequences for resonance assignments, ¹H-¹³C or ¹H-¹⁵N double resonance CP creates the initial ¹³C or ¹⁵N polarization, respectively. Thereafter, a specific-CP scheme[22] transfers the polarization between ¹⁵N and ¹³C from N to CA or CA to N in a unidirectional manner. We discovered that, using SIM-CP followed by specific-CP, it is possible to obtain a bidirectional polarization transfer between ¹³C (either CA or CO) and ¹⁵N. This additional polarization can be detected using the sequence shown in Figure 2A, in which, after SIM-CP, the polarization is transferred from N to CA and, simultaneously, from CA to N. The CA polarization is detected in the first acquisition (blue FID); while the ¹⁵N polarization is stored along z-direction and then transferred to ¹³CO for a second acquisition (red FID). Figure 2B shows the two spectra obtained for U-¹³C,¹⁵N ubiquitin using the dual acquisition pulse sequence reported in Figure 2A, which utilizes SIM-CP and the bidirectional specific-CP for NCA and CAN transfers.

Figure 2.

(A) Pulse sequence to measure the bidirectional polarization transfer from N to CA and vice- versa. The CA polarization is acquired in the first acquisition, whereas 15N polarization transferred to CO and detected during the second acquisition. (B)1D spectra originating from the bidirectional polarization transfer on U-¹³C,¹⁵N crystalline ubiquitin using the pulse sequence shown in (A). The spectra were acquired with 32 scans and 3 ms contact periods for both NCA and NCO. The integrate intensity of carbonyl spectrum (red) is 48% of the CA spectrum (blue) due to two NC transfer periods.

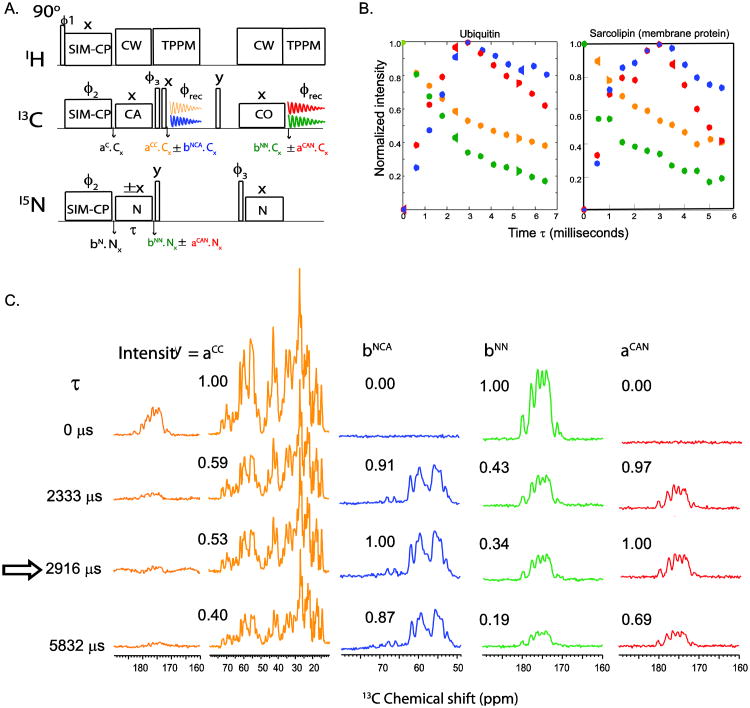
Similarly, it is possible to achieve bidirectional NCO and CON transfers using NCO specific-CP prior to first acquisition. In fact, the ¹⁵N polarization from a CON transfer can be stored during first acquisition and subsequently transferred to CA for a second acquisition time. For the optimization of the N-C specific-CP experiments, we utilize the 1D pulse sequences reported in Figure 2A. These sequences are used as building blocks for the 3D DUMAS experiments [19] that we will describe below. To cancel the residual polarization of ¹³C and ¹⁵N, we implemented a specific-CP sequence with a four-step phase cycle on ¹³C and ¹⁵N spin-lock pulse phases (see ϕ₂ and ϕ₃ in Figure 2A). Later on, we found that the residual polarization of ¹³C and ¹⁵N along with bidirectional polarization transfer creates four different polarization transfer pathways. These new coherences can also be detected and utilized to generate additional 2D and 3D experiments. This represented the genesis of MEIOSIS, a pulse scheme that enables one to detect four FIDs simultaneously. The one-dimensional experiment is shown in Figure 3A. Although conceptually similar to the experiment depicted in Figure 2A, the MEIOSIS pulse sequence has phase ϕ₂ of the specific-CP set to x and ϕ₃ switched between x and −x. This phase scheme enables one to decode the polarization into four data sets that are then stored into separate files representing four different polarization pathways: NCA, NN, CAN, and CC, where NCA and CAN refer to polarization transfer from N to Cα and vice versa, and NN and CC refer to the residual magnetization on ¹⁵N and ¹³C that is not transferred to ¹³C and ¹⁵N during specific-CP. The first acquisition gives the ¹³C spectrum resulting from the NCA and CC pathways (Figure 3A). The ¹⁵N polarization resulting from the other two pathways (i.e., CAN and NN) is stored along the z direction, and at the end of the first acquisition, is transferred to ¹³CO. At this point, a second acquisition records the coherences resulting from the CAN and NN pathways. In order to decode the two pathways in each acquisition, we switch the specific-CP ¹⁵N spin-lock phase between +x and −x in alternate scans. The resultant time domain data for +x and −x phases are then separated prior to processing. Since the NCA and CAN transfers occur in a doubly tilted rotating frame, the phase switching of ¹⁵N spin-lock during specific-CP will invert the sign of the NCA and CAN transfer, whereas the residual CC or NN magnetization will not be affected by the phase switching. If the two data sets of the first acquisition with phases +x and −x are added, the CC transfer is summed, while the NCA transfer cancels out. On the other hand, if the two data sets are subtracted the NCA transfer is summed while the CC transfer cancels out, resulting into two different spectra. Similarly, the addition and subtraction of two data sets for the second acquisition will give magnetization resulting from NN and CAN pathways, respectively. Figure 3B shows the polarization build-up and decay of four pathways as a function of specific-CP contact period τ, on U-¹³C,¹⁵N microcrystalline ubiquitin and a single-pass membrane protein, sarcolipin[16, 23-26]. At optimal polarization transfer (∼2800 or 3100 μs) from N to CA and vice versa, the residual polarization of ¹³C and ¹⁵N is approximately 55 and 35%, respectively.

Figure 3.

(A) Pulse sequence to measure the signal intensity of four polarization pathways resulting from NCA specific-CP. The ¹⁵N spin lock phase is set to +x and −x in alternate scans. The data are then decoded into four spectra using the procedure described within the text. (B) Experimental curves for the build-up of the four polarization pathways for a microcrystalline U-¹³C-¹⁵N ubiquitin sample and a DMPC reconstituted sarcolipin sample. Normalized signal intensities were plotted as a function of specific-CP contact period τ. (C) Representative 1D spectra obtained from pulse sequence (A) on a U-¹³C,¹⁵N microcrystalline ubiquitin sample shown in (B).

4. 2D DUMAS experiments

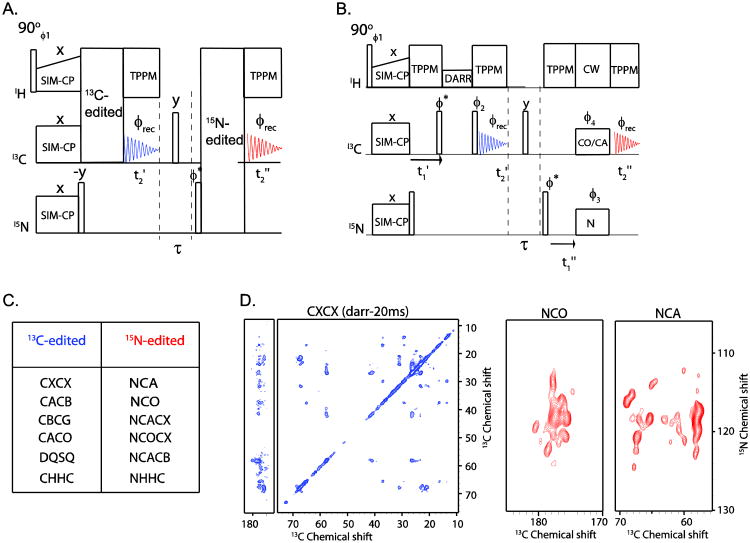
In the 2D DUMAS scheme, a ¹³C-edited experiment is concatenated with a ¹⁵N-edited experiment. Figure 4A shows a typical DUMAS pulse sequence where the ¹³C-edited CXCX experiment is combined with ¹⁵N-edited NCA experiment. The pulse sequence starts with SIM-CP to create an initial polarization for both ¹³C and ¹⁵N nuclei. In the first acquisition, the ¹³C-edited 2D experiment is recorded, while the ¹⁵N polarization is stored along the z-direction. The ¹⁵N polarization is then transferred to ¹³C and detected during the second acquisition giving the ¹⁵N-edited spectrum. As mentioned above, there are several different possibilities to combine ¹³C- and ¹⁵N-edited experiments using the DUMAS scheme. A non-comprehensive list of the most popular experiments is given in Figure 4C.

Figure 4.

(B) A general schematic of 2D DUMAS for simultaneous acquisition of ¹³C- and ¹⁵N-edited experiments, as shown in (C). (B) An example of 2D DUMAS that combines a CXCX with an NCA or NCO experiment. (D) CXCX, NCA, and NCO spectra of sarcolipin obtained from 2D DUMAS in 10 hours of total experimental time. This experiment is divided into two parts, where CXCX and NCO are acquired in the first 6 hours using 16 scans, and another identical CXCX and NCA are acquired in the last 6 hours. The two CXCX data sets are then added before processing, whereas NCO and NCA are processed separately. The t₁ evolution parameters are according to table 1, in which the number of increments for ¹³C evolution is 256, C is set to 8, ¹³C and ¹⁵N t₁ dwell times are 30 and 300 μs respectively.

5. On choosing the right combination of 2D DUMAS experiments

Although it is possible to concatenate several different experiments, it is critical to select ¹³C and ¹⁵N-edited experiments that maximize the sensitivity via dual acquisition. The ¹³C-edited experiments can be divided into two main categories. The first category includes the CXCX correlation experiments that make use of homonuclear polarization transfer among ¹³C nuclei. Typical experiments are DARR and PDSD, where shorter mixing periods (∼15 to 30 ms) correlate intra-residue ¹³C chemical shifts, and longer mixing periods (∼50 to 300 ms) correlate inter-residue ¹³C resonances at medium- and long-range distances. The second category is represented by selective homonuclear polarization transfer experiments such as CACB or CACO. These experiments use DREAM[27], SPC5[28], or R2TR mixing periods to correlate ¹³C resonances[29]. The ¹⁵N-edited experiments use NC specific-CP sequence for heteronuclear polarization transfer from ¹⁵N nuclei to CA or CO, giving NCA or NCO, respectively. Usually, the NC transfer is followed by CACX, COCX, CACB, or CACO mixing periods to obtain the classical 2D NCACX, NCOCX, NCACB, or NCACO experiments [30]. One has to consider that the relative sensitivity for these experiments depends on the nature and length of heteronuclear or homonuclear mixing periods as well as T₁ρ and T₂ relaxation times. Notably, these features are quite different for membrane proteins and microcrystalline proteins. Although it is not possible to accurately predict the relative sensitivity of these multidimensional experiments based only on the 1D spectrum, one can roughly estimate the relative sensitivity from the 1^st increment of the DUMAS experiments and follow the guidelines suggested by Wagner and co-workers[31]. Also, a major advantage of this method is that the building-block architecture of the DUMAS experiments make it possible to rearrange the pulse sequence and change the ¹⁵N-edited experiment to a different one, while continuing acquiring the ¹³C-edited experiment in the first acquisition.

As a case study, consider the combination of CXCX with NCA and NCO experiments. In general, NCA and NCO experiments are relatively shorter than the CXCX experiments, which require 20-40 ms of mixing periods. Therefore, it is convenient to set the 2D DUMAS experiments to acquire the CXCX experiment in the first part of the pulse sequence (i.e., first acquisition period) with n scans, and the NCA and NCO experiments in the second part of the pulse sequence (i.e., second acquisition) with n/2 scans for each experiments. In other words, two pulse programs are encoded with CXCX-NCA and CXCX-NCO combinations, with identical CXCX block followed by NCA and NCO, respectively. The resulting data sets (the first for CXCX-NCA, and the second for CXCX-NCO) are stored in separate memory locations. The CXCX acquisitions are added prior to processing, whereas the NCA and NCO spectra are processed separately.

Another important aspect is the optimization of the t₁ evolution parameters. While the t₂ acquisition parameters are identical for both acquisitions, the t₁ evolution parameters need to be optimized. In a typical ¹³C-edited experiment, a full ¹³C spectral width of 180 ppm is used in the indirect dimension. On the other hand, ¹⁵N-edited experiments require only about one tenth of the ¹³C spectral width or ten times the ¹³C dwell time (t₁). Since the t₁ evolution periods of ¹³C and ¹⁵N dimensions are coded separately for the 2D DUMAS pulse sequence, it is possible to choose two different dwell times and numbers of increments for ¹³C and ¹⁵N while satisfying the maximum t₁ evolution time and number of scans as shown in table 1. The integer ‘C’ dictates the dwell time and maximum t₁ evolution time for an ¹⁵N-edited experiment. Of course, depending on the desired spectral width, it is possible to choose other combinations of ¹³C and ¹⁵N dwell times by adjusting the ‘C’ value. The value of ‘C’ ranges from 3 to 10, depending on the ratio of ¹³C and ¹⁵N increments (see Table 1). Figure 4D shows the simultaneous acquisition of 2D CXCX-NCA DUMAS experiments on a U-¹³C,⁵N-labeled membrane protein, phospholamban.

Table 1.

Criteria for t₁ acquisition parameters for 2D DUMAS experiments. Here ni(t₁′).ns(t₁′)=ni(t₁″)*ns(t₁″), and ‘C’ is an integer.

Parameter	t1′ (t1 evolution of an 13C edited experiment)	t1″ (t1 evolution of an 15N edited experiment)
dw (dwell time)	dw (t1′)	dw (t1″)
ni (number of increments)	ni(t1′)	$\text{ni}({{\mathrm{t}}_1}^{″})=\left(\frac{1}{C}\right).\text{ni}({{\mathrm{t}}_1}^{\prime })$
t1max (Maximum t1 evolution)	t1max′ =dw(t1′).ni(t1max′)	t1max″ =dw(t1″).ni(t1max″)
ns (number of scans)	ns(t1′)	nt(t1″)=C. ns(t1′)

6. One experiment gives four spectra: MEIOSIS

Several multidimensional ¹³C-edited experiments, including CA(N)CO, CO(N)CA, CA(N)COCX, and CO(N)CACX, make use of two heteronuclear (NC) polarization transfer steps with or without CC mixing sequence. In these experiments, the first NC transfer step corresponds to NCA and second NCO (or vice-versa). We will refer to them as CNC- or CNCC-type experiments[32]. These experiments detect the inter-residue correlations between CA and CO resonances and are used as a complement to the CXCX-type of experiments, though they are less sensitive due to the double NC transfer steps. Nonetheless, unlike CXCX experiments they offer unambiguous one-to-one correlations for assigning the backbone of medium-sized proteins. Using similar principles to the DUMAS experiments, we developed new pulse sequences that combine one CNCC, one CC, and two ¹⁵N-edited experiments. Referencing the biological concept of meiosis, we called these experiments MEIOSIS. In fact, by combining bidirectional polarization transfer with residual polarization, we were able to create four polarization pathways that are then used for recording four different 2D experiments. Figure 5A shows the general scheme for the 2D MEIOSIS experiments. Briefly, the pulse sequence starts with SIM-CP to create initial ¹³C- and ¹⁵N- polarization, followed by a t₁ evolution period. During the subsequent NC transfer, four polarization pathways are created, namely CC, NC, NN, and CN pathways. The residual ¹³C and ¹⁵N polarization results from CC and NN transitions, whereas NC and CN are the transferred polarization from ¹⁵N to ¹³C (CA or CO) and vice versa. At this point, the ¹³C polarization resulting from CC and NC pathways undergoes homonuclear polarization transfer during a CC mixing period, followed by t₂ acquisition, while the ¹⁵N polarization from the NN and CN pathways is stored along the z direction. Based on the mixing sequence, the first acquisition can give either CXCX and NCC or CACB and NCACB spectra. After the first acquisition, ¹⁵N polarization from NN and CN pathways is transferred to ¹³C, followed by homonuclear CC mixing and the acquisition time (t₂), at the same time the NN and CN pathways generated are converted into the NCC and CNCC spectra, respectively. We have analyzed both the residual and transferred polarizations of NCA and NCO resulting from the specific-CP for microcrystalline as well as membrane proteins. At optimal NCA or CAN specific-CP mixing time, we detected approximately 50-55% residual ¹³C polarization and 30-35% ¹⁵N polarization (Figure 3).

Figure 5.

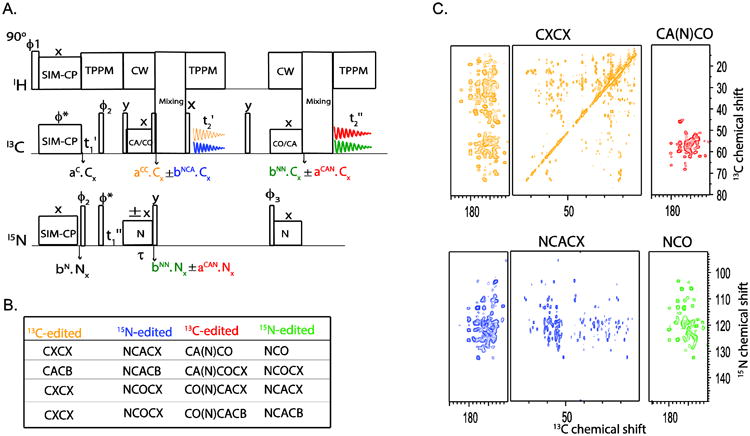
(A) 2D MEIOSIS method for simultaneous acquisition of four 2D experiments that are listed in (B). An example of 2D MEIOSIS is method is demonstrated on U-¹³C,¹⁵N microcrystalline ubiquitin sample.

As for the DUMAS experiments, it is important to select and concatenate the appropriate pulse sequences to yield the highest possible sensitivity. In fact, the choice of the CNCC experiment will dictate the possible combinations of the three other experiments. In the typical MEIOSIS scheme, the first and second specific-CP transfers are set to NCA and NCO, or vice versa, whereas the first and second mixing periods are set for CXCX or CACB homonuclear transfer. By permuting these NC and CC mixing periods, it is possible to obtain multiple combinations of these experiments (Figure 5B). For example, the CA(N)CO experiment can be combined with CXCX, NCACX, and NCO, with CXCX and NCACX acquired during the first acquisition period and the CA(N)CO and NCO experiments during the second acquisition period. The latter is accomplished by setting the second mixing period in the pulse sequence to zero. Note that the spectra resulting from the second acquisition are relatively insensitive with respect to those from the first acquisition period. To optimize the acquisition of CACB or CXCX spectra, we usually set the second mixing time to zero. Alternatively, longer mixing periods (∼100-200 ms) prior to the first acquisition and shorter mixing periods (∼20 to 40 ms) during the second acquisition can be used to obtain comparable sensitivity for both acquisitions.

Unlike the DUMAS schemes, the t₁ evolution periods in the MEIOSIS experiments for the two ¹³C-edited experiments and the corresponding ¹⁵N-edited experiments are time-shared. Although CNC experiments require a smaller spectral width in the indirect dimension (i.e., approximately 30-40 ppm), the dwell time (t₁′) is set to cover approximately 185 ppm. The latter makes the spectral width in the indirect dimension compatible with the acquisition of a CC-type experiment. As for the 2D DUMAS, ¹⁵N evolution time (t_1^″) and the effective number of scans are chosen according to Table 1. Figure 5C shows the simultaneous acquisition of CXCX, NCACX, CA(N)CO and NCO 2D spectra on U-¹³C,¹⁵N labeled microcrystalline ubiquitin.

7. 3D DUMAS experiments

The ¹³C-detected 3D ssNMR experiments can be divided into two main categories: A) ¹³C- and ¹⁵N-edited (CNC or CNCC), and B) ¹⁵N- and ¹³C-edited (NCC) experiments, which start with a ¹H-¹³C and ¹H-¹⁵N double resonance cross polarization sequence[33]. After the initial CP, these pulse sequences comprise two heteronuclear and homonuclear polarization transfer periods sandwiched between two evolution periods (t₁ and t₂) followed by the acquisition period for the third dimension (t₃). Several of these 3D experiments can be concatenated into one multiple spectra-generating experiment using the DUMAS approach.

A typical 3D DUMAS experiment (Figure 6A) starts with SIM-CP to create the initial ¹³C and ¹⁵N polarization that can be exploited to obtain NCC and CNC (or CNCC) experiments simultaneously. The NCC experiment is recorded in the first acquisition period, whereas the CNC experiment is recorded in the second. Specific-CP is used for heteronuclear transfer between ¹⁵N and ¹³CA (or ¹³CO), whereas CC (or alternatively CACB or CACO) homonuclear transfer is obtained using mixing sequences such as DREAM, SPC5, and R2TR. Both NCC and CNC polarization pathways originate from the same NC or CN specific-CP period via a bidirectional transfer followed by a t₁ evolution period. The NCC experiment, which is preceded by a t₂ evolution period and ¹³C homonuclear mixing, is recorded during the first acquisition period (t₃′), while the ¹⁵N polarization is stored along the z-direction. After the first acquisition, a 90° degree pulse brings the ¹⁵N polarization in the transverse plane, which is then allowed to evolve under during an evolution period t₂. An NC specific-CP transfers the polarization from ¹⁵N to CA/CO and, after a mixing period, the CNC experiment is acquired during the t₃ period. Alternatively, the homonuclear mixing can be applied prior to the second acquisition period to obtain a CNCC experiment. The first and second specific-CP sequences are optimized for NCA and NCO transfer, giving ¹⁵N-, ¹³Ca-edited and ¹³Ca-, ¹⁵N-edited experiments in the first and second acquisitions, respectively. Sometimes, however, it is advantageous to evolve ¹³CO in the indirect evolution periods. In this case, it is possible to obtain ¹³CO-edited DUMAS experiments by switching the specific-CP periods. During the mixing period, the non-selective CXCX transfer is obtained via DARR [34] or PDSD [35] sequences, whereas the selective CACB (or CACO) transfer is achieved using DREAM or R2TR sequences. The t₁ and t₂ dwell times for ¹³Cα (¹³CO) and ¹⁵N are set to cover the required spectral widths. Typically the dwell time for ¹³Cα is set to 0.5 to 0.7 times that of ¹⁵N, whereas the dwell time for ¹³CO is set equal to that of ¹⁵N. Depending on the type and length of CC mixing period, several pairs of NCC and CNCC experiments can be combined in the 3D DUMAS experiments. For instance, NCACX or NCACB can be combined with CANCO or CAN(CO)CX experiments. Similarly, NCOCX can be combined with CONCA, CONCACX, or CONCACB. For CACB or CACO selective transfers, mixing times of 5 to 10 ms are generally used. In contrast, for non-selective CACX or COCX transfers, several mixing times are used to obtain sequential, medium, and long-range correlations. While longer mixing times result in more correlations in the spectra, they also lower the overall sensitivity of the experiment. Additionally, the presence of two specific-CP periods for the CNCC experiment lowers its sensitivity by about 30-50% as compared to the NCC experiment. For this reason, we usually run this experiment without, or with a very short, mixing period prior to the second acquisition. In the absence of a mixing period, the second acquisition gives CANCO or CONCA, whereas the incorporation a CC mixing period yields CANCOCX or CONCACX. Figure 6c shows an example of simultaneous acquisition of NCACX and CANCO on a U-¹³C,¹⁵N microcrystalline ubiquitin sample.

Figure 6.

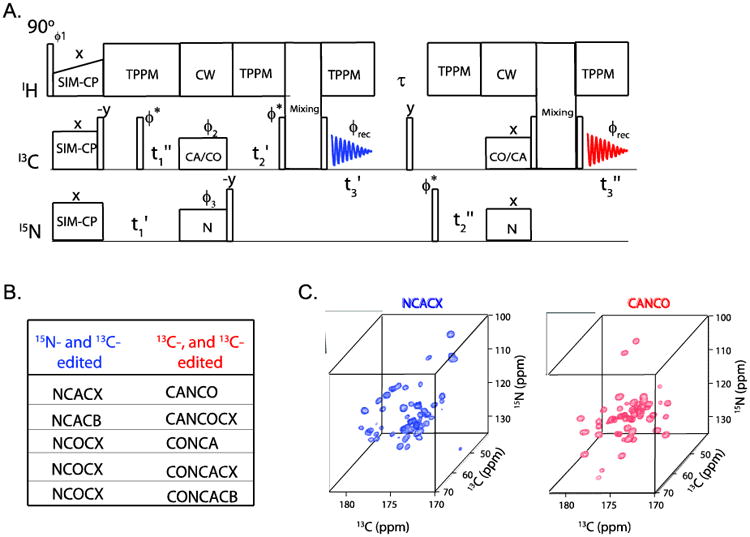
A general pulse sequence diagram for 3D DUMAS for combing a pair of 3D experiments shown in (B). (C) Simultaneous acquisition of NCACX and CANCO on U-13C-15N ubiquitin using 3D DUMAS.

8. 3D Meiosis

The combination of residual and transferred polarization of specific-CP can be used for acquiring multiple three-dimensional experiments [17]. The general protocol of 3D MEIOSIS is shown in Figure 7. The 3D experiments originate from the 2D MEIOSIS pulse sequence (Figure 5A), with the addition of an evolution period (t₂′ and t₂″) prior to the mixing periods. The pulse sequence starts with SIM-CP to create the initial ¹³C and ¹⁵N polarization, which is then evolved during the t₁′ and t₁″ evolution periods, then followed by an NC/CN specific-CP transfer. The NC/CN transfer creates four polarization pathways, including bidirectional transfer from N to C (CA or CO) and C to N, as well as residual polarization (CC and NN pathways) of ¹³C and ¹⁵N nuclei. The ¹⁵N polarization resulting from the NN and CN pathways is stored along the z-direction; whereas the ¹³C polarization from NC and CC pathways is evolved during t₂, followed by a mixing period and the t₃′ acquisition period, which corresponds to the sum of the NCC and CCC 3D experiments, respectively. After the first acquisition, the ¹⁵N polarization is transferred to CO or CA, then evolved during t₂ followed by the mixing period and t₃″ acquisition. This second acquisition is the sum of two 3D experiments, C(N)CC and NCC, resulting from the CN and NN pathways, respectively. As with the 2D MEIOSIS, two data sets are recorded with the ¹⁵N spinlock phase of the first specific-CP set to +x and −x, and stored in separate memory locations. The phase switching of the ¹⁵N spinlock will not affect the residual polarization, but it will invert the phase of the transferred polarization from the NC and CN pathways. The sum of these two data sets will give CCC and NCC experiments in the first and second acquisitions, respectively, cancelling out the NCC and CNCC coherences; whereas the difference of the two data sets will give NCC and C(N)CC experiments. The t₁ and t₂ evolution of the CCC experiment are identical, giving an aliased DARR spectrum along the F1-F2 diagonal; therefore, this data set is discarded. According to the scheme in Figure 6, the 3D MEIOSIS method combines a C(N)CC experiment with two ¹⁵N- and ¹³C-edited experiments for the simultaneous acquisition of three 3D experiments. As with the 2D MEIOSIS, the sensitivity of the C(N)CC and NCC experiments that are acquired during the second acquisition is lower compared to the NCC experiment recorded in the first acquisition. This is expected since the C(N)CC experiment requires two specific-CP periods, while the NCC experiment of the second acquisition utilizes the ¹⁵N residual polarization, which is typically 30-35% of the absolute intensity. However, the sensitivity of both acquisitions can be optimized by using different lengths of mixing periods as explained in the 2D MEIOSIS section. Depending on the choice of C(N)CC experiment, two other NCC experiments can combined using 3D MEIOSIS method. For example CA(N)COCX is combined with NCACX and NCOCX, similarly CO(N)CACX is combined with NCOCX and NCACX. The 3D C(N)CC and NCC experiments resulting from the second acquisition are relatively insensitive compared to NCC experiment of the first acquisition. As for the 2D MEIOSIS, the sensitivity is optimized by choosing a longer (50 to 100 ms) and shorter (20 to 30 ms) mixing times prior to the first and second acquisitions, respectively. Similarly other two combinations of 3D MEIOSIS can be obtained by using selective CACB transfer prior to the first or second acquisition. Examples of 3D NCACX-CA(N)COCX-NCOCX MEIOSIS spectra are reported in Figure 7C.

Figure 7.

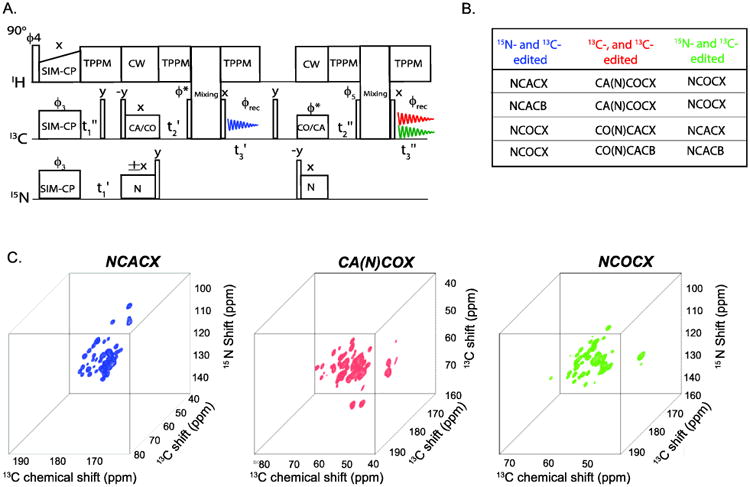
Protocol of 3D MEIOSIS for simultaneous acquisition of three 3D experiments that are listed in (B), the first and second NC transfer are respectively set to NCA and NCO or vice versa. Two data sets are recorded with 15N spin lock phase set to +x and −x. Sum of the two data sets of the second acquisition gives the NCC experiment (shown in green), whereas the difference of two data sets gives NCC (shown in blue) and C(N)CC (shown in red) associated with the first and second acquisitions, respectively. (C) Simultaneous acquisition of NCACX, CA(N)COCX and NCOCX on U-13C,15-N ubiquitin using 3D MEIOIS shown in (A).

9. Sequential assignment of soluble and membrane bound proteins using POEs

Sequential assignment of chemical shifts is the first step towards the structure determination of proteins. For a number of reasons, protein assignment concepts in solid-state NMR are intrinsically different to those known from solution NMR triple resonance experiments involving 1H detection. Proton detection in solid-state NMR is still challenging, even with high-frequency MAS. Here we show the application of DUMAS and MEIOSIS based ¹³C-detected experiments for the assignment of uniformly ¹³C- and ¹⁵N-labeled ubiquitin and sarcolipin proteins. In both cases, sequential assignment was achieved by using a single experiment, namely DUMAS-NCACX-CANCO. While for ubiquitin 56 out of 76 residues were assigned, for sarcolipin the entire transmembrane region (22 out of 31 residues) was assigned (Figure 8).

Figure 8.

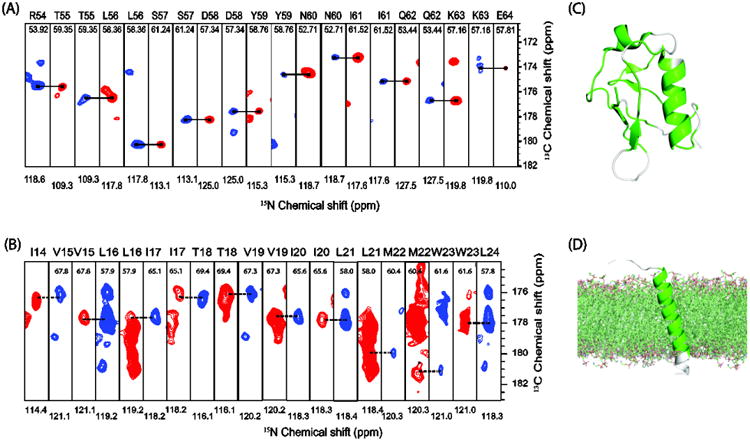
Sequential assignment of (A) ubiquitin, and (B) the membrane protein sarcolipin using the 3D DUMAS-NCACX-CANCO experiment shown in figure 6. Assigned residues from the 3D DUMAS experiment are highlighted in green on the secondary structure of ubiquitin (C), and sarcolipin (D).

10. Discussion

Rather than a suite of new pulse sequences, POE illustrates a novel approach to optimize the existing experiments using the classical setup of NMR spectrometers and acquire multiple 2D and 3D experiments, reducing by half the experimental time. In the most favorable cases, this approach enables spectroscopists to double the capacity of the spectrometer; while in other cases the additional spectra can be stored and summed later on with other acquisitions. The overall philosophy of the approach is to make the best out of the polarization generated. The existence of unused polarization that was not converted into observable coherences (orphan spin operators) was pointed out by Pines and Waugh [15]. Historically, the solution NMR community has been the most attentive to detect multiple spin operators for simultaneous acquisition of 2D experiments such as COSY-NOESY [36] and COCONOSY [37] and/or enhance the signal [38]. More recently, the afterglow phenomenon exploited by Kay and co-workers opened up the possibility for the acquisition of multidimensional NMR spectra of proteins in parallel [39]. The latter approach has been implemented with either one or multiple receivers [40-42]. Sensitivity enhanced experiments in solids have also been proposed by Tycko and co-workers [43] and been implemented in a manner similar to the sensitivity enhancement for solution NMR experiments. Moreover, Takegoshi and co-workers have implemented the equivalent of COCONOSY for solids [44] as well as the double acquisition using discarded coherences in 2D spectra with the States method [45], paving the way for multiple acquisition in biological solids.

For POE, the creation of two polarization transfer pathways via SIM-CP in which the relatively long-living ¹⁵N polarization allows one to acquire additional NMR experiments. Another important property we discovered is the bidirectional ¹⁵N-¹³C polarization transfer, which enables one to rescue the orphan spin operators resulting from residual polarization and obtain multiple 2D and 3D experiments to be detected simultaneously.

In the past few year, the POE family has expanded. It now includes the ¹H detected experiments under fast MAS conditions [46], the afterglow sequence developed by Traaseth and coworkers [47, 48], the simultaneous acquisition of PAIN and PAR experiments discovered by Meier and coworkers [49] as well as the more recent pulse sequences that are the dipolar-edited versions of DUMAS methodology [50]. These experiments reinforce the importance of developing pulse sequences that exploit as many orphan operators as possible to enhance the NMR signal in solids and enable multiple acquisitions.

11. Conclusions and Perspectives

Sensitivity and resolution are the two devils that pester NMR spectroscopy. However, we believe that there is a lot of room for new developments in solid-state NMR of biomacromolecules. While we (as researchers) have the tendency to reassure our audience that all of the methods are in place, in actuality, there are plenty of improvements that must be done to make this technique flourish. It is hard to predict whether the current methods will survive the rapid progress of many groups in this field. Our contribution, however, underscores the fact that even the most robust experiments used for the routine resonance assignment of biopolymers can be improved. The techniques that we reviewed in this paper can be implemented in commercially available spectrometers without additional hardware. Commercial probes for biomacromolecules can be utilized with only a single receiver, effectively doubling the capacity of the spectrometer. Given the long-living nature of ¹⁵N polarization, we expect that several other groups will take on this approach, which in our opinion represents a totally new way to speed up solid-state NMR data acquisition. An obvious extension of this approach is inverse detection experiments, which will enable higher sensitivity and the possibility to recover even more orphan operators to give additional spectra. Another development includes the possibility of using double receivers, optimizing data collection and processing. Finally, our methods do not preclude other approaches to be implemented. In fact, when applied in concert with other fast acquisition and sensitivity enhancement techniques (e.g., Dynamic Nuclear Polarization and/or Paramagnetic Relaxation Enhancements), our methods will increase the throughput of high-resolution structure determination by MAS NMR.

Highlights.

• Acquisition of multiple solid-state NMR experiments using only one receiver

• DUMAS enables the simultaneous acquisition of two MAS NMR spectra

• 3D DUMAS: acquisition of two 3D spectra simultaneously

• MEIOSIS make it possible to acquire four 2D spectra or three 3D spectra simultaneously