Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jan 5.
Published in final edited form as: Cold Spring Harb Protoc. 2015 Jan 5;2015(1):pdb.top083519. doi: 10.1101/pdb.top083519

Single and Multiphoton Fluorescence Recovery after Photobleaching

Kelley D Sullivan 1, Ania K Majewska 2, Edward B Brown 3,✉
PMCID: PMC4399237  NIHMSID: NIHMS678033  PMID: 25561627

Abstract

Fluorescence recovery after photobleaching (FRAP) is a microscopy technique for measuring the kinetics of fluorescently labeled molecules, and can be applied both in vitro and in vivo for two-and three-dimensional systems. This chapter discusses the three basic FRAP methods: traditional FRAP, multi-photon FRAP (MPFRAP), and FRAP with spatial Fourier analysis (SFA-FRAP). Each discussion is accompanied by a description of the appropriate mathematical analysis appropriate for situations in which the recovery kinetics are dictated by free diffusion. In some experiments, the recovery kinetics are dictated by the boundary conditions of the system, and FRAP is then used to quantify the connectivity of various compartments. Since the appropriate mathematical analysis is independent of the bleaching method, the analysis of compartmental connectivity is discussed last, in a separate section.

Introduction

Since its introduction in the 1970's (Peters et al. 1974; Axelrod et al. 1976), FRAP has been used to measure the diffusion coefficient (or analogous transport parameters) of labeled molecules in both two-dimensional systems, such as cell membranes, small regions of cells, and lamellipodia (Feder et al. 1996; Braga et al. 2007), and in three-dimensional systems, such as tumor tissue or cell bodies (Chary and Jain 1989; Berk et al. 1997; Pluen et al. 2001; Stroh et al. 2004; Chauhan et al. 2009). Each of the three FRAP techniques are performed by first photobleaching a small region of interest within a sample, then monitoring the region as still fluorescent molecules from outside the region diffuse in to replace the photobleached molecules. The original “spot” FRAP technique has undergone a variety of modifications to accommodate different photobleaching methods, including patterned (Abney et al. 1992), continuous (Wedekind et al. 1996), line (Braeckmans et al. 2007), and disc-shaped (Mazza et al. 2008) photobleaching. Modifications to the recovery analysis have also expanded FRAP as a tool to analyze binding kinetics (Kaufmann and Jain 1991; Berk et al. 1997; Schulmeister et al. 2008), to quantify the connectivity of compartments (Majewska et al. 2000; Cardarelli et al. 2007), and to investigate polymer structure-property relationships (Li et al. Submitted).

FRAP and MPFRAP

In a FRAP experiment, a focused laser beam bleaches a region of fluorescently labeled molecules in a thin sample of tissue (Axelrod et al. 1976). The same laser beam, greatly attenuated, then generates a fluorescence signal from that region as unbleached fluorophores diffuse in. A photomultiplier tube, or similar detector, records the recovery in fluorescence signal, producing a fluorescence versus time curve. In a conventional (one-photon) FRAP experiment, simple analytical formulas can be fit to the fluorescence recovery curve in order to generate the two-dimensional diffusion coefficient of the fluorescent molecule, but only if the sample is sufficiently thin (see FRAP Diffusion Analysis). If the sample is not thin enough for the analytical solution to hold, the diffusion coefficient can be estimated by comparing the recovery time to that of molecules with known diffusion coefficients in samples of identical thickness.

In an MPFRAP experiment, a focused beam from a mode-locked laser provides both bleaching and monitoring, generating fluorescence and photobleaching via multi-photon excitation (Brown et al. 1999). The intrinsic spatial confinement of multi-photon excitation means that the bleaching/monitoring volume is three-dimensionally resolved (Denk et al. 1990); consequently, there is no upper limit on the sample thickness. Simple analytical formulas can be applied to the fluorescence recovery curve to generate the three-dimensional diffusion coefficient of the fluorescent molecule.

FRAP Instrumentation

The primary instrumentation of one-photon FRAP consists of a laser source, an acoustooptic modulator (AOM), a dichroic mirror, an objective lens, a gated photomultiplier tube (PMT), and a data recording system such as an analog-to-digital (A/D) board or scaler (photon counting device) (Fig. 1A). The laser source is directed through the AOM to the dichroic mirror and objective lens and into the fluorescent sample.

Figure 1.

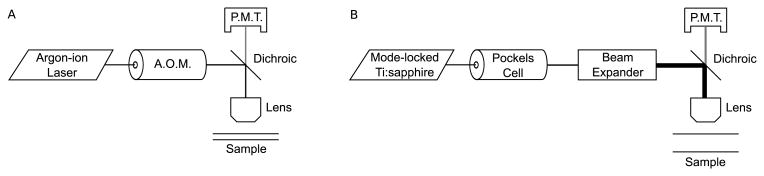
Figure 1

Open in a new tab

(A) Equipment for fluorescence recovery after photobleaching. (B) Equipment for multi-photon fluorescence recovery after photobleaching.

The laser is typically an argon ion laser operating in TEM00 mode to produce a Gaussian transverse intensity profile, suitable for analysis of recovery curves (see FRAP Diffusion Analysis). The laser must be modulated on a much faster timescale than the diffusive recovery time of the system, often requiring modulation times of fractions of a msec. This necessitates the use of an AOM as the beam modulation device because of its fast response time. To generate significant variation in transmitted intensity, the first diffraction maximum of the AOM should be used, not the primary transmitted beam.

MPFRAP Instrumentation

The primary instrumentation of MPFRAP consists of a laser source, Pockels Cell, beam expander, dichroic mirror, objective lens, gated photomultiplier tube (PMT), and a data recording system (Fig. 1B). The laser source is directed through the Pockels cell to the beam expander, dichroic mirror, and objective lens and into the fluorescent sample.

The laser is typically a mode-locked (100-fsec pulses) Ti:sapphire laser. This beam is expanded to overfill the objective lens (Zipfel et al. 2003), thereby producing a uniformly illuminated back aperture, resulting in the formation of the highest resolution spot in the plane of the sample (Born and Wolf 1980). The intrinsic spatial confinement of multi-photon excitation produces a three-dimensionally defined bleach volume, whose size depends on the numerical aperture (NA) and wavelength of excitation light, and is typically ∼0.5 × 0.5 × 1 <micro>m. This extremely small bleached volume dissipates rapidly (hundreds of <micro>secs for smaller fluorescently labeled molecules such as FITC-bovine serum albumin [BSA] or green fluorescent protein [GFP]). Consequently, MPFRAP requires a beam-modulation system with response times as fast as 1 <micro>sec. The AOM traditionally used in one-photon FRAP relies on diffraction of the laser beam to achieve intensity modulation, whereas 100-fsec pulses, typical of a mode-locked Ti:sapphire laser used in multi-photon FRAP, have a bandwidth of 15 nm. Different wavelengths of light will diffract in different directions; therefore, the nondiffractive Pockels Cell is often used for MPFRAP beam modulation instead of an AOM. A Pockels Cell operates by passing a beam through a crystal, across which a voltage is applied. Varying the voltage rotates the plane of polarization of the incident light. Before exiting the Pockels Cell, the beam passes through a polarizer, which converts the rotation in plane of polarization to a variation in intensity.

Procedure

  1. The laser modulator (AOM or Pockels cell) is set to a low transmission state, producing the “monitor” beam<!> and generating fluorescence from the sample, which is collected by the objective lens and detected by the PMT. The scaler monitors the output of the PMT for a short duration (tens of <micro>secs to msecs), recording the “prebleach signal.”

  2. The laser power modulator is switched to a high transmission level, producing the “bleach” beam, which photobleaches a fraction of the fluorophores within the sample. The modulator is returned rapidly to the low monitoring state (after a total bleach time that depends on the sample dynamics). If possible, the PMT is gated during the bleach pulse to avoid damage to the PMT.

  3. The fluorescence generated by the monitor beam is then recorded continuously. As unbleached fluorophores diffuse into the region excited by the laser beam, the fluorescence signal recovers to equilibrium levels.

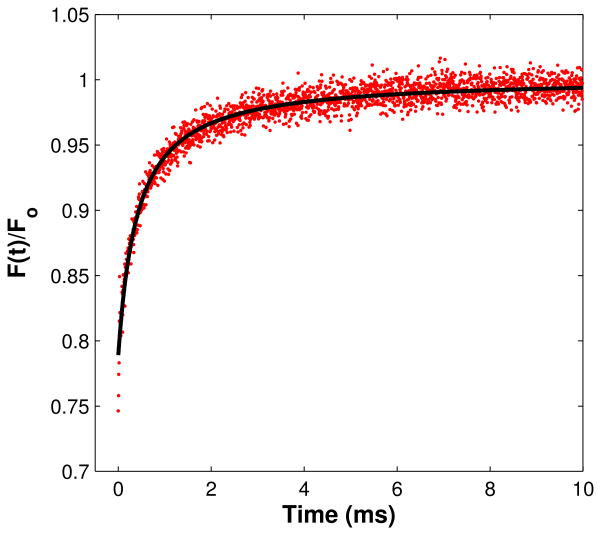
  4. The fluorescence recovery curve is analyzed to yield diffusion coefficients or analogous parameters, as well as the fraction of immobile fluorophores (Fig. 2).

Figure 2.

Figure 2

Open in a new tab

MPFRAP recovery curve. MPFRAP was performed on FITC-BSA in free solution. (Solid line) Least chi-squared fit, producing a diffusion coefficient at 22°C of 52.2 um2/s.

Caution: See Appendix 3 for appropriate handling of materials marked with <!>.

Limitations

A number of steps must be taken to ensure accurate determination of the diffusion parameters.

  • 1

    The power of the monitoring beam must be high enough to generate sufficient fluorescence signal but not so high as to cause significant photobleaching. The generation of photobleaching by the monitoring beam can be detected easily by photon counting over an integration time much larger than the expected recovery time for a range of typical monitoring powers. For MPFRAP, a reduction from a slope of two on a log-log plot of photon counts as a function of power indicates the presence of photobleaching. For FRAP, a deviation from a slope of one on a linear plot of photon counts as a function of power indicates the presence of photobleaching. This is because fluorescence scales as intensity to the nth power, where n is the number of photons absorbed during excitation. In a one-photon FRAP experiment, if the resultant monitoring power is too low to allow a sufficient signal-to-noise ratio, the monitoring beam can be repeatedly cycled between zero and a high power that causes some limited photobleaching, allowing intermittent recording of the fluorescence recovery at higher signal rates, while limiting the total photobleaching by the monitoring beam (Waharte et al. 2005).

  • 2

    The duration of the bleaching flash must be short enough that no significant diffusion (i.e., recovery in fluorescent signal) occurs during the bleach pulse. A rule of thumb is that the bleach pulse should be less than 1/20th of the half-recovery time of the subsequent recovery curve.

  • 3

    If the acquisition of the fluorescence recovery curve does not occur for a long enough period, overestimation of the immobile fraction and underestimation of the diffusion recovery time can result. A rule of thumb is that the recovery curve should be visibly flat (i.e., any systematic change in signal is less than shot noise) for the latter half of the recording time.

  • 4a

    In FRAP and MPFRAP, the fluorescence excitation rate is assumed to scale as Rate ∼<sigma><Ib>, where <sigma> is the absorption cross section (units of cm2 for one-photon excitation and cm2s for two-photon excitation), I is the intensity of the bleach beam, b is the number of photons absorbed in a bleaching event, and <> denotes a time average. There is an upper limit to the excitation rate of a fluorescent molecule, however, because fluorescent molecules have excited-state lifetimes of tL ≈10−15 nsec and hence cannot be excited at a faster rate than 1/tL. Furthermore, the pulsed lasers used in MPFRAP have a duty cycle of tD = 12.5 nsec. Consequently, when the excitation rate of fluorophores during the bleaching pulse approaches a significant fraction of 1/tL or 1/tD, the rate of excitation will deviate from ∼<sigma><Ib> and will asymptotically approach a limiting value, which depends on 1/tL or 1/tD. This phenomenon is known as excitation saturation. FRAP or MPFRAP curves generated in the saturation regime, where the photobleaching rate does not scale as ∼<sigma><Ib>, will produce erroneously low diffusion coefficients.

  • 4b

    To avoid excitation saturation, a series of FRAP or MPFRAP curves must be generated at increasing bleach powers. The curves are then analyzed (see Diffusion Analysis below) using the bleach depth parameter and the diffusive recovery time as the fitting parameters. The bleach depth parameter of a FRAP or MPFRAP curve is proportional to the bleaching rate and will scale as <sigma><Ib> when the curve is not in the excitation saturation regime. When the bleach depth parameter measurably deviates from a <sigma><Ib> dependence, the bleaching is subject to excitation saturation and the diffusion coefficients will be erroneously low. A good rule of thumb is that the fractional deviation of the bleach depth parameter from <sigma><Ib> dependence should be less than 10%.

  • 5

    To convert a measured diffusive recovery time to a diffusion coefficient, the characteristic size of the bleached region must be known. In both FRAP and MPFRAP, the excitation probability as a function of position transverse to the beam axis at the focal spot (i.e., the transverse beam intensity profile to the nth power) can be well represented by a Gaussian function (see below), whose characteristic half-width at e-2 must therefore be determined in order to convert recovery times to diffusion coefficients. In the case of one-photon FRAP, the e-2 half-width of the excitation probability must be measured transverse to the beam axis only, whereas in MPFRAP, the 1/e half-width in both the transverse and axial directions must be measured. This is typically accomplished by scanning the focus of the laser beam across a subresolution (∼10 nm or less) fluorescent bead and recording the fluorescent signal versus position of the bead. Unless the excitation beam of a one-photon FRAP system is provided by a confocal laser-scanning microscope, there is no mechanism for easily altering the position of the laser focus in the sample plane, so a simple method to measure the excitation probability is to scan a sub-resolution bead transversely across the stationary beam focus with a stepper motor or piezoelectric motor (Schneider and Webb 1981). In an MPFRAP system, the laser position is usually governed by galvanometers and stepper motors as part of a multi-photon laser-scanning microscope system. Consequently, it is relatively easy to scan the laser across a stationary sub-resolution fluorescent bead to determine the transverse e-2 half-width, whereas the axial e-2 half-width can be determined by scanning the bead across the focus, using the focus stepper motor that accompanies most laser-scanning microscope systems.

Diffusion Analysis: Conventional (One-photon) FRAP

If the sample thickness in a FRAP experiment is sufficiently thin, the complex three-dimensional hourglass shape of the focused bleaching beam (Born and Wolf 1980) can be ignored. This is because the bleaching only occurs in a thin slice at the focus of the beam, and the postbleach recovery kinetics occur laterally in a two-dimensional system. If the excitation laser is operating in TEM00 mode and significantly underfills the objective lens (i.e., the beam is significantly smaller than the back aperture of the objective lens), then the transverse intensity profile is a simple Gaussian, and an analytical formula for the fluorescence recovery curve can be derived. For a Gaussian laser beam, the fluorescence recovery curve describing free diffusion in a two-dimensional system is given by (Axelrod et al. 1976)

F(t)=F∞∑n=0∞(−β)nn!1(1+n+2nt/τD)

where F∞ is the t = ∞ fluorescence signal, beta is the bleach depth parameter, and <tau>D is the two-dimensional diffusion recovery time. The fraction of immobile fluorophores in the sample is given by (F0-F∞)/F∞, where F0 is the pre-bleach fluorescence signal and “immobile” is defined as having a diffusive mobility significantly slower than the timescale of the experiment. The diffusion coefficient is given by D = w2/4<tau>D, where w is the transverse e-2 half-width of the laser beam at the sample.

FRAP can be extended to thicker samples, but analytic derivations of the diffusion coefficient become problematic due to the complex nature of the hourglass-shaped focus laser distribution. Furthermore, the fluorescence recovery time becomes dependent on the thickness of the sample, which may or may not be known. In these cases, the FRAP technique is often limited to a simple comparison of recovery times between samples of unknown diffusion coefficients and samples with known diffusion coefficients that have been measured with analytical techniques such as those described above.

Diffusion Analysis: MPFRAP

In an MPFRAP experiment, the highest spatial resolution is achieved by overfilling the objective lens, producing a diffraction-limited intensity distribution at the beam focus. The square (or higher power) of this intensity profile is well approximated by a Gaussian distribution, both transverse to and along the optical axis, although the half-width at e-2 is typically longer in the axial dimension than in the transverse dimension (Born and Wolf 1980). For an overfilled objective lens inducing two-photon fluorescence and photobleaching, the fluorescence recovery curve describing free diffusion in a three-dimensional system is given by (Brown et al. 1999)

F(t)=F∞∑n=0∞(−β)nn!1(1+n+2nt/τD)11+n+2nt/(RτD)

Where F∞ is the t = ∞ fluorescence signal, beta is the bleach depth parameter, and <tau>D is the three-dimensional diffusion recovery time. Because the signal is limited by restrictions on the bleaching and monitoring powers (as described in “Limitations” above), MPFRAP experiments are generally performed with a series of bleach/monitor sequences at a location of interest, and the resultant curves averaged together to improve the signal-to-noise ratio. Therefore, MPFRAP is insensitive to immobile fluorophores, as they are bleached out during repeated flashes and do not contribute to recovery kinetics. The diffusion coefficient is given by D = wr2/8<tau>D, where wr is the transverse e-2 half-width of the laser beam at the sample and R is the square of the ratio of the axial (wz) to the radial (wr) e-2 half-width (Fig. 2).

In some experiments it may be the case that the mobility of the fluorophore of interest is influenced by convective flow, as well as diffusion. In this case, the shape of the fluorescence recovery curve changes, and so must the mathematical model describing the recovery. By introducing a simple coordinate shift into the derivation of the equation immediately above, the new derivation yields (Sullivan et al. 2009)

F(t)=Fo∑n=0∞(−β)nn!exp[4nt(1/τvx2+1/τvy2)1+n+2nt/τD]exp[4nt/τvz21+n+2nt/RτD](1+n+2nt/τD)(1+n+2nt/RτD)1/2

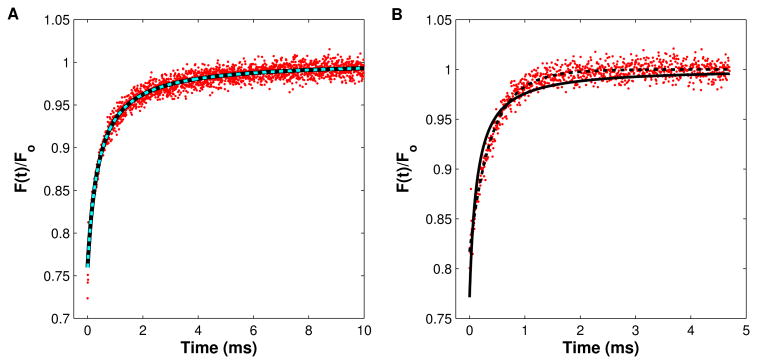
where <tau>vx = wr/vx, <tau>vy = wr/vy, and <tau>vz = wz/vz; and v2 = vx2 + vy2 + vz2 is the speed of the convective flow. All other variables are defined as above. With this “diffusion-convection” model, accurate values for the diffusion coefficient can be obtained even under the influence of moderate flows, defined by a dimensionless speed parameter, vs = v(wr/8D) ≤ 3 (Fig.3) (Sullivan et al. 2009).

Figure 3.

Figure 3

Open in a new tab

Equipment for FRAP with spatial Fourier analysis.

SFA-FRAP

In a FRAP experiment with spatial Fourier analysis, a focused laser beam is used to bleach a region of fluorophore, as in the FRAP described above. Unlike conventional FRAP, however, the evolution of the bleached region is imaged repeatedly using a CCD camera with wide-field illumination provided by a mercury lamp. The sequential images of the recovery of the bleached spot are Fourier-transformed, and the decay of selected spatial frequency components produces the diffusion coefficient of the diffusing fluorophore, without requiring knowledge of the details of the bleaching distribution or sample thickness (Tsay and Jacobson 1991; Berk et al. 1993). Consequently, SFA-FRAP can be performed in thick samples, although its reliance upon epifluorescence means that the diffusion coefficients it measures are averages over the entire depth of view of the microscope and are not three-dimensionally resolved.

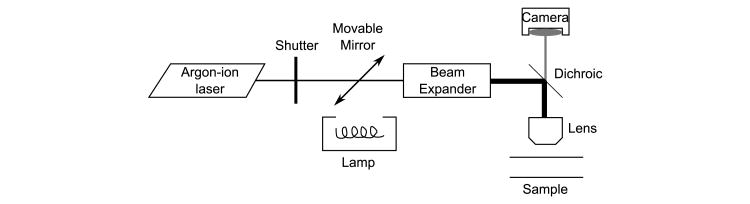
Instrumentation

The primary instrumentation of conventional SFA-FRAP consists of a laser source, dichroic mirror, two fast shutters, a galvanometer-driven movable mirror, an objective lens, a CCD camera and mercury arc lamp, and an image recording system such as a frame grabber card (Fig. 4). The laser source is directed through one shutter and dichroic mirror to the objective lens and into the fluorescent sample, whereas the lamp is directed by the movable mirror to be colinear with the laser.

Figure 4.

Figure 4

Open in a new tab

MPFRAP recovery curves. In both (A) and (B) MPFRAP was performed on FITC-BSA in free solution, and the data was fit to both the conventional “diffusion only” (solid line) and “diffusion-convection” (dashed line) models. (A) Solution exhibits no convective flow. Both fits yield a diffusion coefficient at 22°C of 52.9 <micro>m2/s. (B) Solution exhibits convective flow with a scaled speed of 0.8. The diffusion-only model fits the data poorly and yields a diffusion coefficient at 22°C of 160 <micro>m2/s. The diffusion-convection model fits the data well and yields a diffusion coefficient of 51.9 <micro>m2/s, in good agreement with the value determined in the absence of convective flow.

The laser is typically an argon ion laser, as in FRAP. SFA-FRAP is traditionally used in thick (many hundreds of microns) tissues, and the imaged bleach spot is several tens of microns wide. Consequently, the diffusive recovery times can be relatively slow (several tens of msecs to many mins), and the laser modulation rate does not have to be as rapid as in FRAP. Furthermore, the laser modulation is binary, with a bright bleaching flash and zero power being the only required states, and no intermediate power monitoring beam is needed. Therefore, a fast shutter is generally sufficient for SFA-FRAP, instead of a rapid (and more expensive) analog device such as the AOM or Pockels cell.

Procedure

  1. The laser is shuttered and the movable mirror directs the mercury lamp illumination into the sample. The CCD records a few prebleach images.

  2. The CCD is shuttered to avoid damage, and the movable mirror is moved out of the laser path. The laser shutter opens briefly, allowing the bleaching flash through. The laser shutter closes again, ending the bleaching flash, and the CCD is unshuttered.

  3. The movable mirror periodically shifts back into the light path, directing the mercury arc lamp illumination into the objective lens and allowing epifluorescence images to be captured as the bleached distribution recovers to equilibrium levels and the bleached spot disappears.

  4. The series of images of the evolution of the bleached spot are Fourier-transformed, and six of the lowest spatial frequencies are plotted. The exponential decay of the spatial frequencies yields the diffusion coefficient of the labeled molecule, as well as the fraction of immobile fluorophores.

Limitations

A number of steps must be taken to ensure accurate determination of the diffusion parameters.

  1. The epifluorescence lamp must be bright enough to generate sufficient signal, but not so bright as to cause significant photobleaching. Photobleaching due to the lamp can be easily detected by performing a test SFA-FRAP experiment with no bleach pulse. If the fluorescence signal decays significantly over the course of the image series, the epifluorescence lamp must be attenuated. Additionally, the duty cycle of the monitoring pulses can be altered, thereby reducing the total exposure time of the sample during the recovery period.

  2. The duration of the bleaching flash must be short enough that no significant diffusion (i.e., recovery in fluorescent signal) occurs during the bleach pulse. A rule of thumb is that the bleach pulse must be less than 1/20th of the half-recovery time of the subsequent spatial frequency decay curve.

  3. If the acquisition of the fluorescence recovery images does not occur for a long enough period, overestimation of the immobile fraction and underestimation of the diffusion recovery time can result. A rule of thumb is that the decay curve of the spatial frequencies (see below) should be visibly flat (any change is less than shot noise) for the latter half of the recording time.

Diffusion Analysis

After a photobleaching pulse, the concentration distribution of unbleached fluorophores c(x,y,t) evolves according to the diffusion equation. If the concentration distribution is first Fourier-transformed with respect to x and y, the solution to this differential equation is a simple exponential (Berk et al. 1993)

C(u,v,t)=C(u,v,0)e−4π2(u2+v2)Dt

where u and v are the spatial frequencies and D is the diffusion coefficient. The relationship between dye concentration at the sample and intensity at the corresponding location in the CCD image may vary in space, but is expected to be constant in time. Therefore, the Fourier transform of the CCD images also decays with a simple exponential, where the exponential decay time of a given pair of spatial frequencies is 1/(4pi2(u2 + v2)D). To analyze SFA-FRAP data, the series of CCD images of the evolving dye distribution are each Fourier-transformed, and the exponential decay of a number (typically six) of selected spatial frequency pairs is analyzed to produce the exponential decay time, which directly yields the diffusion coefficient. Unlike FRAP or MPFRAP, no knowledge of the initial spatial distribution of photobleaching is required. Note that this analysis ignores diffusion along the optical axis and furthermore uses epifluorescence images of the diffusing system, therefore generating a diffusion coefficient that is an average over the visible depth of the system. In other words, any depth-dependent differences in the diffusion coefficient will be averaged out to a single value (Berk et al. 1993).

Compartmentalization Analysis

Single-photon and multi-photon FRAP can also be used to measure the diffusional coupling between two connected compartments. A characteristic time course for the diffusion or transport of different fluorescent molecules can be obtained by bleaching one compartment and monitoring the fluorescence recovery curve as it is refilled with fluorophore from the unbleached compartment. This information can then be used to determine parameters such as resistivity and pore size of the separating barrier. MPFRAP has been used to examine diffusion of dyes between the excitatory synapse (dendritic spine) and its parent dendrite (Svoboda et al. 1996; Majewska et al. 2000; Sobczyk et al. 2005), and between plant plastids (Kohler et al. 1997). FRAP has examined the cell cytoplasm and the nucleus (Wei et al. 2003), as well as the turnover of fluorescently tagged actin filaments between the spine and dendrite (Star et al. 2002).

Instrumentation

A FRAP or MPFRAP instrument (described above) can be used for compartmentalization analysis. Since diffusion between compartments tends to be slower than diffusion within a compartment, these experiments can often be performed in line-scan mode on a laser-scanning microscope. In line-scan mode, the excitation beam is scanned repeatedly along a single line that intersects an object of interest, and a position versus time curve of the fluorescence is generated. The line-scan mode utilizes the acquisition electronics of the laser-scanning microscope and obviates the need to purchase a separate photon-counting device. This mode can limit the acquisition speed, however, depending on the design of the microscope.

Procedure

  1. One of the compartments is chosen for bleaching and monitoring (typically the smaller compartment). The laser modulator (AOM or Pockels cell) is set to a low transmission state, producing the “monitor” beam and generating fluorescence from a region of interest (ROI) within the sample, which is collected by the objective lens and detected by the PMT as a measure of the prebleach fluorescence.

  2. The PMT is then gated (i.e., the dynode voltage is set to zero) to avoid damage, and the laser modulator is switched to a high transmission level, producing the “bleach” beam, which photobleaches a fraction of the fluorophores within the ROI. The modulator rapidly returns to the low monitor state (after a total bleach time that depends on the sample dynamics, as described above), and the PMT is subsequently ungated.

  3. The fluorescence generated in the ROI by the monitor beam is then recorded continuously. As unbleached fluorophores diffuse in from the unbleached compartment, the fluorescence signal recovers back to equilibrium levels.

  4. The fluorescence recovery curve is analyzed to yield the characteristic coupling time, as well as the fraction of immobile fluorophores.

Limitations

  1. Bleaching during the monitoring phase, bleach duration, and total acquisition time must be evaluated as in points 1–3 in FRAP and MPFRAP “Limitations,” described above.

  2. Diffusional coupling is typically studied between two well-mixed compartments, i.e., where the timescale of diffusional equilibrium within the compartments is much faster than between compartments. This can be verified by spot bleaching within each of the compartments to determine the diffusion characteristics for fluorophores in each of the compartments.

  3. Because the communicating compartments are well-mixed, the initial spatial distribution of bleached molecules is irrelevant because the bleached compartment undergoes diffusive mixing before significant communication with other compartments can occur. Consequently, neither the bleach spot profile nor excitation saturation are significant concerns. However, it is important to determine that bleaching occurs in only one compartment. This can be done by performing a line scan that intersects both compartments, while restricting the bleaching pulse to a single compartment. In this case, both compartments can be monitored to ensure that bleaching is spatially restricted.

Compartmentalization Analysis

The fluorescence recovery curve in a well-mixed, photobleached compartment diffusionally coupled to larger well-mixed compartments is given by (Svoboda et al. 1996; Majewska et al. 2000)

F(t)=F(∞)−ΔF0e−t/τ

where F(∞) is the fluorescence at t = ∞, deltaF0 is the change in fluorescence level following the bleach pulse, and <tau> is the timescale of diffusion between the two compartments. The timescale, <tau>, of recovery between compartments provides insight into the characteristic resistivity of the coupling pathway, the number of coupling pathways, the diffusion coefficient of the tracer, etc., depending on the geometry of the system (Majewska et al. 2000; Wei et al. 2003).

References

  1. Abney JR, Scalettar BA, Thompson NL. Evanescent interference patterns for fluorescence microscopy. Biophysical Journal. 1992;61:542–552. doi: 10.1016/S0006-3495(92)81858-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Axelrod D, Koppel DE, Schlessinger J, Elson E, Webb WW. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophysical Journal. 1976;16:1055–1069. doi: 10.1016/S0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berk DA, Yuan F, Leunig M, Jain RK. Fluorescence photobleaching with spatial Fourier analysis: Measurement of diffusion in light-scattering media. Biophysical Journal. 1993;65:2428–2436. doi: 10.1016/S0006-3495(93)81326-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berk DA, Yuan F, Leunig M, Jain RK. Direct in vivo measurement of targeted binding in a human tumor xenograft. Proceedings of the National Academy of Sciences. 1997;94:1785–1790. doi: 10.1073/pnas.94.5.1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Born M, Wolf E. Principles of optics: Electromagnetic theory of propagagtion, interference and diffraction of light. Pergamon Press; New York: 1980. [Google Scholar]
  6. Braeckmans K, Remaut K, Vandenbroucke RE, Lucas B, De Smedt SC, Demeester J. Line FRAP with the confocal laser scanning microscope for diffusion measurements in small regions of 3-D samples. Biophysical Journal. 2007;92(6):2172–2183. doi: 10.1529/biophysj.106.099838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Braga J, McNally JG, Carmo-Fonseca M. A reaction-diffusion model to study RNA motion by quantitative fluorescence recovery after photobleaching. Biophysical Journal. 2007;92(8):2694–2703. doi: 10.1529/biophysj.106.096693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Brown EB, Wu ES, Zipfel W, Webb WW. Measurement of molecular diffusion in solution by multiphoton fluorscence photobleaching recovery. Biophysical Journal. 1999;77:2837–2849. doi: 10.1016/S0006-3495(99)77115-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cardarelli F, Serresi M, Bizzarri R, Giacca M, Beltram F. In vivo study of HIV-1 Tat arginine-rich motif unveils its transport properties. Mol Ther. 2007;15(7):1313–1322. doi: 10.1038/sj.mt.6300172. [DOI] [PubMed] [Google Scholar]
  10. Chary SR, Jain RK. Direct measurement of interstitial convection and diffusion of albumin in normal and neoplastic tissues by fluorescence photobleaching. Proceedings of the National Academy of Sciences. 1989;86:5385–53989. doi: 10.1073/pnas.86.14.5385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chauhan VP, Lanning RM, Diop-Frimpong B, Mok W, Brown EB, Padera TP, Boucher Y, Jain RK. Multiscale measurements distinguish cellular and interstitial hindrances to diffusion in vivo. Biophysical Journal. 2009;97(1):330–336. doi: 10.1016/j.bpj.2009.03.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Denk W, Strickler JH, Webb WW. Two-photon laser scanning microscopy. Science. 1990;248:73–76. doi: 10.1126/science.2321027. [DOI] [PubMed] [Google Scholar]
  13. Feder TJ, Brust-Mascher I, Slattery JP, Baird B, Webb WW. Constrained diffusion or immobile fraction on cell surfaces: A new interpretation. Biophys J. 1996;70:2767–2773. doi: 10.1016/S0006-3495(96)79846-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kaufmann EN, Jain RK. Measurement of mass transport and reaction parameters in bulk solution using photobleaching. Reaction limited binding regime. Biophysical Journal. 1991;60(60):596–610. doi: 10.1016/S0006-3495(91)82089-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kohler RH, Cao J, Zipfel WR, Webb WW, Hanson MR. Exchange of protein molecules through connections between higher plant plastids. Science. 1997;276:2039–2042. doi: 10.1126/science.276.5321.2039. [DOI] [PubMed] [Google Scholar]
  16. Li J, Sullivan KD, Brown EB, Anthamatten M. Thermally Activated Diffusion in Reversibly Associating Polymers Submitted. [Google Scholar]
  17. Majewska A, Brown E, Ross J, Yuste R. Mechanisms of calcium decay kinetics in hippocampal spines: Role of spine calcium pumps and calcium diffusion through the spine neck in biochemical compartmentalization. Journal of Neuroscience. 2000;20:1722–1734. doi: 10.1523/JNEUROSCI.20-05-01722.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Mazza D, Braeckmans K, Cella F, Testa I, Vercauteren D, Demeester J, De Smedt SS, Diaspro A. A new FRAP/FRAPa method for three-dimensional diffusion measurements based on multiphoton excitation microscopy. Biophys J. 2008;95(7):3457–3469. doi: 10.1529/biophysj.108.133637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Peters R, Peters J, Tews K, Bahr W. Microfluorimetric study of translational diffusion of proteins in erythrocyte membranes. Biochimica et Biophysica Acta. 1974;367:282–294. doi: 10.1016/0005-2736(74)90085-6. [DOI] [PubMed] [Google Scholar]
  20. Pluen A, Boucher Y, Ramanujan S, McKee TD, Gohongi T, Tomaso Ed, Brown EB, Izumi Y, Campbell RB, Berk DA, et al. Role of tumor-host interactions in interstitial diffusion of macromolecules: Cranial vs. subcutaneous tumors. Proceedings of the National Academy of Sciences. 2001;98:4628–4633. doi: 10.1073/pnas.081626898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Schulmeister S, Ruttorf M, Thiem S, Kentner D, Lebiedz D, Sourjik V. Protein exchange dynamics at chemoreceptor clusters in Escherichia coli. Proc Natl Acad Sci U S A. 2008;105(17):6403–6408. doi: 10.1073/pnas.0710611105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Sobczyk A, Scheuss V, Svoboda K. NMDA receptor subunit-dependent [Ca2+] signaling in individual hippocampal dendritic spines. J Neurosci. 2005;25(26):6037–6046. doi: 10.1523/JNEUROSCI.1221-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Star EN, Kwiatkowski DJ, Murthy VN. Rapid turnover of actin in dendritic spines and its regulation by activity. Nature Neuroscience. 2002;5:239–246. doi: 10.1038/nn811. [DOI] [PubMed] [Google Scholar]
  24. Stroh M, Zipfel WR, Williams RM, Ma SC, Webb WW, Saltzman WM. Multiphoton microscopy guides neurotrophin modification with poly(ethylene glycol) to enhance interstitial diffusion. Nature materials. 2004;3(7):489–494. doi: 10.1038/nmat1159. [DOI] [PubMed] [Google Scholar]
  25. Sullivan KD, Sipprell WH, 3rd, Brown EB, Jr, Brown EB., 3rd Improved model of fluorescence recovery expands the application of multiphoton fluorescence recovery after photobleaching in vivo. Biophys J. 2009;96(12):5082–5094. doi: 10.1016/j.bpj.2009.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Svoboda K, Tank DW, Denk W. Direct measurement of coupling between dendritic spines and shafts. Science. 1996;272:716–719. doi: 10.1126/science.272.5262.716. [DOI] [PubMed] [Google Scholar]
  27. Tsay TT, Jacobson KA. Spatial Fourier analysis of video photobleaching measurements. Principles and optimization. Biophys J. 1991;60(2):360–368. doi: 10.1016/S0006-3495(91)82061-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Waharte F, Brown CM, Coscoy S, Coudrier E, Amblard F. A two-photon FRAP analysis of the cytoskeleton dynamics in the microvilli of intestinal cells. Biophys J. 2005;88(2):1467–1478. doi: 10.1529/biophysj.104.049619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wedekind P, Kubitscheck U, Heinrich O, Peters R. Line-scanning microphotolysis for diffraction-limited measurements of lateral diffusion. Biophysical Journal. 1996;71:1621–1632. doi: 10.1016/S0006-3495(96)79366-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wei X, Henke VG, Strubing C, Brown EB, Clapham DE. Real-time imaging of nuclear permeation by EGFP in single intact cells. Biophysical Journal. 2003;84:1317–1327. doi: 10.1016/S0006-3495(03)74947-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zipfel WR, Williams RM, Christie R, Nikitin AY, Hyman BT, Webb WW. Live tissue intrinsic emission microscopy using multiphoton-excited native fluorescence and second harmonic generation. Proc Natl Acad Sci U S A. 2003;100(12):7075–7080. doi: 10.1073/pnas.0832308100. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES