Kernel regression based segmentation of optical coherence tomography images with diabetic macular edema

Abstract

We present a fully automatic algorithm to identify fluid-filled regions and seven retinal layers on spectral domain optical coherence tomography images of eyes with diabetic macular edema (DME). To achieve this, we developed a kernel regression (KR)-based classification method to estimate fluid and retinal layer positions. We then used these classification estimates as a guide to more accurately segment the retinal layer boundaries using our previously described graph theory and dynamic programming (GTDP) framework. We validated our algorithm on 110 B-scans from ten patients with severe DME pathology, showing an overall mean Dice coefficient of 0.78 when comparing our KR + GTDP algorithm to an expert grader. This is comparable to the inter-observer Dice coefficient of 0.79. The entire data set is available online, including our automatic and manual segmentation results. To the best of our knowledge, this is the first validated, fully-automated, seven-layer and fluid segmentation method which has been applied to real-world images containing severe DME.

1. Introduction

Diabetic retinopathy is the leading cause of blindness among working-aged adults in the United States [1]. Among those affected, approximately 21 million people develop diabetic macular edema (DME) [2]. DME results from the breakdown of the blood-retinal barrier as retinal vascular endothelial and mural cells become damaged from chronic hyperglycemia [3]. Retinal hypoxia results in increased production of vascular endothelial growth factors (VEGF) and other signaling cascades [3–5]. These further progress DME through mechanisms such as cytotoxic damage to retinal fluid transport cells [6–9]. Ultimately, the imbalance between vascular leakage and fluid transport leads to retinal edema and vision loss.

While clinical trials of several treatment modalities have been conducted for therapies for DME [10–19], the significant proportion of subjects that fail to respond to any single therapy suggests that DME pathophysiology is multifactorial, and unfortunately no consensus yet exists for determining which patients are likely to respond to specific therapies. This may be due to the absence of a standard method for stratifying patients based on disease mechanisms [20, 21]. In recent years, the additional depth-resolved dimension of data provided by optical coherence tomography (OCT) imaging has prompted groups to correlate morphological patterns of the retina on OCT with DME and vision outcomes [22–26]. For clinical trials, the most commonly used quantitative imaging biomarker of DME severity is currently central subfield thickness, which does not capture details such as edema volume or changes in specific retinal layers. We expect that these parameters will provide valuable prognostic information to guide treatment decisions. However, despite the development of automated retinal layer segmentation methods applicable to normal eyes or eyes with limited pathological deformation or loss of retinal structures [27–42], most DME studies require either manual [22, 24–26, 43] or semi-automatic [44] evaluation of OCT images. Currently few automated algorithms exist to quantify morphological or pathological features on images with DME [43, 45–51].

Furthermore, while averaging-based denoising methods enhance image quality and improve the performance of automated image segmentation algorithms [52], they also result in drastic increases in image acquisition times, which may not be tolerated by ill or uncooperative patients, especially when capturing dense volumetric scans. It is therefore desirable to develop automatic OCT segmentation algorithms which can be applied to lower quality images captured using fast-image scanning protocols, as these are often required in real-world, clinical settings.

Finally, while a few state-of-the-art algorithms provide combined fluid and layer segmentation methods [47, 48, 50], to the best of our knowledge, no fully-automated algorithm has been validated to identify all retinal layers and fluid-filled regions. Furthermore, there is limited rigorous analysis of layer-specific changes in retinal thickness following therapy. As such, the selection of personalized therapeutic strategies for patients remains subjective. As a step towards this goal, we present a fully automated algorithm based on kernel regression (KR) [53] and our previously described graph theory and dynamic programming (GTDP) framework [46, 54, 55] to identify fluid-filled regions and seven retinal layers on spectral domain (SD)-OCT images of eyes with DME. In the first phase of developing our algorithm, we created KR-based classifiers to estimate fluid and retinal layer positions. We then used these classification estimates in the second phase to guide GTDP segmentation for a more accurate result.

In Section 2, we provide an introduction to KR, and in Section 3 we present our new general purpose KR-based classification method. We then combine our KR-based classification method with GTDP segmentation in Section 4 and describe our implementation on OCT images of eyes with DME in Sections 5 and 6. Finally, we validate the performance of our algorithm in Sections 7 and 8.

2. Kernel regression review

KR is a non-parametric method for deriving local estimates of a function using a kernel that weighs the relative importance of nearby points [53]. While traditional KR-based applications include image denoising and interpolation [53], deblurring [56], and object detection [57], we use KR to improve image classification and segmentation. In this section, we provide an overview on the second order iterative Gaussian steering KR method for image denoising as introduced and described in detail in [53].

2.1 Problem formulation

Looking at a small patch of $P$ pixels on a noisy image $I\in {\Re }^{M\times N},$ the intensity $y_p$ of a pixel can be described by

$$y_p=f({\mathit{z}}_p)+n_p,p=1,\dots ,P,$$ (1)

where ${\mathit{z}}_p={[i_p,j_p]}^T$ is the $p^{th}$ pixel located at row $i$ and column $j$ on $\mathit{I}$, $f(\cdot )$ is an unspecified (non-parametric) regression function, and $n_p$ is an independent and identically distributed zero-mean noise value at ${\mathit{z}}_p$. Using this formulation, we would like to obtain a local estimate of the regression function $\hat{f}({\mathit{z}}_p)$ to generate a denoised image $\hat{\mathit{I}}$ can approximate $f({\mathit{z}}_p)$ using the second order Taylor series expansion about a point $\mathit{z}$ near ${\mathit{z}}_p$ following

$$f({\mathit{z}}_p)\approx {\beta }_0+{\mathit{\beta }}_1{}^T({\mathit{z}}_p-\mathit{z})+{\mathit{\beta }}_2{}^T\text{vech}\hspace{0.17em}\left[({\mathit{z}}_p-\mathit{z}){({\mathit{z}}_p-\mathit{z})}^T\right],$$ (2)

$$\text{where} {\beta }_0=f(\mathit{z}),{\mathit{\beta }}_1={\left[\begin{array}{cc}\frac{\partial f(\mathit{z})}{\partial i}& \frac{\partial f(\mathit{z})}{\partial j}\end{array}\right]}^T,$$

$${\mathit{\beta }}_2=\frac{1}{2}{\left[\begin{array}{ccc}\frac{{\partial }^{2}f(\mathit{z})}{\partial i^2}& \frac{{\partial }^{2}f(\mathit{z})}{\partial ij}& \frac{{\partial }^{2}f(\mathit{z})}{\partial j^2}\end{array}\right]}^T,$$

$$\text{vech}\hspace{0.17em}\left(\left[\begin{array}{cc}a& b\\ b& d\end{array}\right]\right)={\left[\begin{array}{ccc}a& b& d\end{array}\right]}^T.$$

We next solve for the unknowns ${\beta }_0,$ ${\mathit{\beta }}_1,$ and ${\mathit{\beta }}_2$ in Eq. (2) using the weighted linear least squares formulation [53, 58] following

$$\hat{\mathit{b}}=\underset{b}{\arg \min }\left[{\left(\mathit{y}-\mathit{Z}\mathit{b}\right)}^T\mathit{D}\left(\mathit{y}-\mathit{Z}\mathit{b}\right)\right],$$ (3)

$$\text{where} \mathit{y}={\left[y_1,y_2,\dots ,y_P\right]}^T,$$

$$\mathit{b}={\left[{\beta }_0,{\mathit{\beta }}_1{}^T,{\mathit{\beta }}_2{}^T\right]}^T,$$

$$\mathit{D}=\text{diag}\left[\hat{\mathit{K}}({\mathit{z}}_1-\mathit{z}),\hat{\mathit{K}}({\mathit{z}}_2-\mathit{z}),\dots ,\hat{\mathit{K}}({\mathit{z}}_P-\mathit{z})\right],$$

$$\mathit{Z}=\left[\begin{array}{ccc}1& {({\mathit{z}}_1-\mathit{z})}^T& \text{vech}({\mathit{z}}_1-\mathit{z}){({\mathit{z}}_1-\mathit{z})}^T\\ 1& {({\mathit{z}}_2-\mathit{z})}^T& \text{vech}({\mathit{z}}_2-\mathit{z}){({\mathit{z}}_2-\mathit{z})}^T\\ ⋮& ⋮& ⋮\\ 1& {({\mathit{z}}_P-\mathit{z})}^T& \text{vech}({\mathit{z}}_P-\mathit{z}){({\mathit{z}}_P-\mathit{z})}^T\end{array}\right],$$

and “diag” defines a diagonal matrix and $\hat{\mathit{K}}(\cdot )$ is a linearly normalized kernel function used to weigh the $P$ observations such that ${\displaystyle {\sum }_{p=1}^P\hat{\mathit{K}}({\mathit{z}}_P-\mathit{z})=1}$. Since Eq. (3) is a linear least squares formulation, the solution can be given by Eq. (4), where the first element in $\hat{\mathit{b}}$ is the denoised image $\hat{I}.$

$$\hat{\mathit{b}}={({\mathit{Z}}^T\mathit{D}\mathit{Z})}^{-1}{\mathit{Z}}^T\mathit{D}\mathit{Z}\mathit{y}$$ (4)

2.2 Adaptive iterative Gaussian steering kernel

In order to perform KR as described in Section 2.1, an appropriate kernel must be selected. In this section, we describe the popular adaptive iterative Gaussian steering kernel $\left({\mathit{K}}_{iGS}\right)$ [53]. To summarize, this kernel can be described as a Gaussian function that is elongated $\left(\sigma \right)$, rotated $\left(\theta \right)$, and scaled $\left(\gamma \right)$ based on the local data to reduce edge blurring.

To compute the Gaussian steering kernel for a pixel $\mathit{z},$ we first smooth the image using a linear Gaussian filter with standard deviations of $h_i$ and $h_j$ along the $i$ and $j$ dimensions, and then we compute the image gradients ${\mathit{G}}_i$ and ${\mathit{G}}_j\in {\Re }^{M\times N}.$We then calculate the truncated singular value decomposition following Eq. (5) [53, 59, 60].

$$\mathit{U}\mathit{S}{\mathit{T}}^T=\left[\begin{array}{cc}{\mathit{G}}_i({\mathit{z}}_1)& {\mathit{G}}_j({\mathit{z}}_1)\\ {\mathit{G}}_i({\mathit{z}}_2)& {\mathit{G}}_j({\mathit{z}}_2)\\ ⋮& ⋮\\ {\mathit{G}}_i({\mathit{z}}_P)& {\mathit{G}}_j({\mathit{z}}_P)\end{array}\right],\hspace{1em}\text{where}\hspace{1em}\mathit{S}=\left[\begin{array}{cc}{\mathit{S}}_{11}& 0\\ 0& {\mathit{S}}_{22}\end{array}\right],\mathit{T}=\left[\begin{array}{cc}{\mathit{T}}_{11}& {\mathit{T}}_{12}\\ {\mathit{T}}_{21}& {\mathit{T}}_{22}\end{array}\right].$$ (5)

Second, we compute the steering parameters $\sigma ,$ $\theta ,$ and $\gamma$ as described in Eq. (6), where $\lambda \prime$ and $\lambda \prime \prime$ are parameters that prevent undefined or zero values for $\sigma$ and $\gamma .$ We then denoise $\mathit{z}$ following Eq. (4) using a linearly normalized version of the kernel defined Eq. (7), where $h$ is the global smoothing parameter.

$$\theta =\text{arc tan}\hspace{0.17em}\left(\frac{{\mathit{T}}_{12}}{{\mathit{T}}_{22}}\right),\sigma =\frac{{\mathit{S}}_{11}+\lambda \prime }{{\mathit{S}}_{22}+\lambda \prime },\gamma ={\left(\frac{{\mathit{S}}_{11}{\mathit{S}}_{12}+\lambda \prime \prime }{P}\right)}^{\frac{1}{2}}.$$ (6)

$${\mathit{K}}_{\mathit{G}S}({\mathit{z}}_p-\mathit{z})=\exp \left[-\frac{{({\mathit{z}}_p-\mathit{z})}^T\Sigma ({\mathit{z}}_p-\mathit{z})}{2h^2}\right],$$ (7)

$$\text{where} \Sigma =\gamma {\mathbf{\Theta }}^T\mathbf{\Lambda }\mathbf{\Theta },\mathbf{\Theta }=\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right],\mathbf{\Lambda }=\left[\begin{array}{cc}\sigma & 0\\ 0& {\sigma }^{-1}\end{array}\right]\text{.}$$

Third, we iteratively improve the denoised image ( ${\hat{\beta }}_0$) by recalculating the steering parameters and kernel using the denoised image gradients ( ${\hat{\mathit{\beta }}}_1$) [53].

An example image and its Gaussian steering KR denoised result are shown in Fig. 1(a) and 1(f), respectively. Figure 1(c) and 1(e) are the iterative Gaussian steering kernels for Fig. 1(b) and 1(d), respectively. The kernel in Fig. 1(c) is wider and more isotropic since its corresponding image patch does not contain strong edges, while the kernel in Fig. 1(e) is narrower and oriented along the image edge. In Fig. 1(f), the regions external to the retina (black) were not denoised with the exception of a padded boundary surrounding the retina. The thickness of this boundary is half the kernel size to encapsulate all pixels required for feature vector computation in Sections 3.2 and 5.8. Parameter values used to generate Fig. 1(f) were chosen empirically using the training data set and include a kernel size of 73.7 × 147.4 µm (11 × 11 pixels, $P$ = 121), 3 iterations for ${\hat{\mathit{K}}}_{iGS}$, $h_i=1$, $h_j=3$, $h=3$, $\lambda \prime =0.1$, and $\lambda \prime \prime =1.$

Fig. 1.

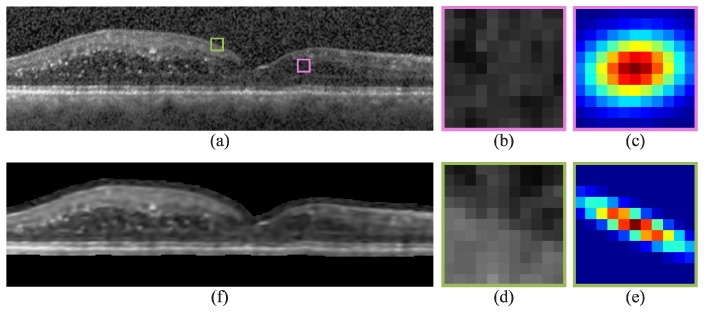
Second order iterative Gaussian steering KR of an SD-OCT image with DME. a) Automatically flattened image, b,d) zoomed-in images of the pink and green boxes in (a), c,e) Gaussian steering kernels used to denoised the central pixel of (b) and (d), and f) KR-denoised image of (a). In (f), regions external to the retina (black) were not denoised with the exception of a padded boundary surrounding the retina required for feature vector computation.

3. Kernel regression-based classification

In this section, we integrate KR with supervised classification [61, 62] to classify noisy images. The following subsections describe our novel, general purpose KR-based classification method. Specific application of this method for segmenting retinal layers is discussed in Sections 5 and 6.

3.1 Steering kernel regression estimation

Since pixels within an image are individually classified, the presence of noise worsens classification results. Thus, the first step is to use the KR method described in Eq. (4) to denoise the image and obtain: 1) direct estimates for the noise-free first and second derivatives ( ${\hat{\mathit{\beta }}}_1$ and ${\hat{\mathit{\beta }}}_2$), and 2) adaptive directional kernels $(\hat{\mathit{K}})$ for each pixel.

3.2 Computing features

To classify a pixel $\mathit{z}$, the pixel needs associated descriptors called features. Each feature $v$ is a scalar value used to describe the pixel, and $L$ features comprise a feature vector $\mathit{v}=\left[v_1,v_2,\dots ,v_L\right].$ Basic features include pixel intensity, gradient, and location. Other feature types include textural features such as Laws’ Texture Energy Measures [63, 64].

To mitigate the effects of noise on feature computation, we perform weighted averaging. Since the steering kernels in Section 2.2 adapt to the shape of the underlying structure, we use the kernels from Section 3.1 to filter the features following

$${\hat{v}}_l(\mathit{z})={\displaystyle \sum _{p=1}^P{v}_l({\mathit{z}}_p)}\hat{\mathit{K}}({\mathit{z}}_p-\mathit{z}),$$ (8)

where $v_l({\mathit{z}}_p)$ is the $l^{th}$ feature for pixel ${\mathit{z}}_p$ and ${\hat{v}}_l(\mathit{z})$ is the $l^{th}$ (now denoised) feature for pixel $\mathit{z}.$ We also use the kernels themselves as features (e.g. kernel height, width, and area) to reveal more indistinct information. Specific feature examples are defined in Section 5.8.

3.3 Defining the true (training) classes

In supervised classification, a set of classes (categories) $\mathit{c}={\left\{c_k\right\}}_{k=1}^K$ is pre-defined for a given classifier [62]. Given a training data set, we manually identify the true class $c$ for each training pixel $\mathit{z}$ such that $c\in \mathit{c}.$ Specific examples of these classes are given in Section 5.2.

3.4 Defining the classifier function

For an image $\mathit{I},$ we define a classifier $\phi (\cdot )$ which estimates the class $\hat{c}\in \mathit{c}$for a pixel $\mathit{z}$ following

$$\hat{c}=\phi (\mathit{v}).$$ (9)

Provided that the training data set is composed of $R$ total training pixels, we first combine the feature vectors for all $R$ pixels into the feature vector set $\mathit{V}={\left[{\mathit{v}}_1{}^T,{\mathit{v}}_2{}^T,\dots ,{\mathit{v}}_R{}^T\right]}^T\in {\Re }^{R\times L},$ where ${\mathit{v}}_r$ is the feature vector for the $r^{th}$ training pixel. For each class $c_k$, we then create a feature vector subset ${\mathit{V}}_k\subseteq \mathit{V}$ where ${\mathit{V}}_k=\left\{\mathit{v}\in \mathit{V}|c=c_k\right\}\in {\Re }^{R_k\times L}$ and $R_k$ is the number of training pixels with $c_k$ as the true class. From this definition, it can be seen that ${\displaystyle {\sum }_{k=1}^K{R}_k=R}$.

We next define the classifier function used to estimate the class. To take into consideration the typical spread of feature values, we use a weighted negative Gaussian classifier function following Eq. (10), where ${\mathit{\mu }}_{\text{k}}\in {\Re }^{1\times L}$ is the mean feature vector across the training feature vector subset ${\mathit{V}}_k,$ ${\epsilon }_k\in {\Re }^{1\times L}$ is the element-wise reciprocal of the variance feature vector for ${\mathit{V}}_k,$ $\mathit{\omega }\in {\Re }^{1\times L}$ is a set of constant weights used to alter the relative importance of features, and $\circ$ is the Hadamard product, an element-wise multiplication operation for vectors and matrices. Selection of these weights is described in Section 3.5.

$${\phi }_{wN\mathit{G}}(\mathit{v})=\left\{c_k|\underset{k}{\arg \min }{\left[1-\exp \left(\frac{1}{2}\left[{\epsilon }_k\circ \mathit{\omega }\circ \left(\mathit{v}-{\mathit{\mu }}_k\right)\right]{\left[{\epsilon }_k\circ \mathit{\omega }\circ \left(\mathit{v}-{\mathit{\mu }}_k\right)\right]}^T\right)\right]}^{\frac{1}{2}}\right\}$$ (10)

3.5 Weighted sequential forward feature selection

Since not all features in $\mathit{v}$ may be useful for predicting the true class $c$, we reduce the dimension of $\mathit{v}$ by defining a subset $\mathit{v}\prime \subseteq \mathit{v}$ of length $L\prime \le L$ containing the most relevant features [65–67]. We achieve this by performing weighted sequential forward feature selection (wSFFS), a variation of the classic SFFS method [66] that simultaneously selects features and their corresponding weights. In the classic SFFS method, $\mathit{v}\prime$ begins as a null set and features are added to it sequentially [66] by minimizing a predefined criterion function $E(\cdot )$ (e.g. misclassification rate).

A limitation of the SFFS method is that it weighs each feature equally. As a result, we use the wSFFS method to select features along with their optimal weight. Given a set of $A$ possible weight values $\mathit{a}=\left[a_1,a_2,\dots ,a_A\right],$ we create a new set of weighted feature vectors ${\mathit{V}}_A=\left[a_1\mathit{V},a_2\mathit{V},\dots ,a_A\mathit{V}\right]\in {\Re }^{R\times LA}.$ We then perform SFFS on ${\mathit{V}}_A$ to find the most relevant weighted feature. After sequentially adding weighted features, the result is a subset of features $\mathit{v}\prime$ and corresponding weights $\omega \prime =\left[{\omega }_1,{\omega }_2,\dots ,{\omega }_{L\prime }\right]$ where the $l^{th}$ weight ${\omega }_l\in \mathit{a}.$ We subsequently use this new set of reduced features and weights in Eq. (10) to classify the pixel in place of the full, non-weighted feature vector $\mathit{v}.$

Finally, to reduce classifier overfitting, we use K-fold cross-validation [68] during feature selection. We also increase the classification accuracy by using K-means clustering [69] to divide $\mathit{V}$ into $K$ clusters. We then perform wSFFS on each of the clusters to generate $K$ sets of selected feature vectors and weights. When classifying a pixel, the set that minimizes the criterion function is used to determine the final class.

4. Classification-based GTDP segmentation

To improve the KR-based classification method from Section 3, we apply our GTDP segmentation framework introduced in [54] to more accurately isolate class boundaries. This section provides an overview of our GTDP method and describes how the classification results can be used to both improve and simplify GTDP segmentation.

4.1 GTDP layer segmentation review

We represent an image $\mathit{I}\in {\Re }^{M\times N}$ as a graph, where each pixel is a node on the graph and adjacent nodes are connected by edges. To create a path preference, we assign positive weights to the edges based on features such as image intensity or gradient, where ultimately the lowest weighted path is preferred. For example, to segment the darkest path across an image, we assign weights based on image intensity, where the weight $w_{ab}$ of the edge connecting nodes $a$ and $b$ following

$$w_{ab}=I_a+I_b+w_{\min },$$ (11)

where $I_n$ is the intensity of $\mathit{I}$ at node $n$ and $w_{\min }$ is a positive number specifying the minimum weight of an edge since a weight equal to zero indicates two unconnected nodes. We also specify that $w_{ab}=w_{ba}$ for all node pairs, as this generates an undirected graph with half as many weight values.

To segment a horizontal layered structure, we add an additional node to either side of the graph to automatically initialize the start and end nodes of our path. The additional node on the left is connected to all nodes in the leftmost column of the graph, and the right additional node has edges connecting it to all nodes in the rightmost column. These additional edges are assigned a weight of $w_{\min }.$ We then apply Dijkstra’s algorithm [70] to find the shortest path from the start node to the end node, which corresponds to our desired segmentation. For more details referring to our GTDP segmentation algorithm, refer to [54, 55].

4.2 Classification-based search region limitation

For scenarios in which multiple similar features are to be segmented within a given image (e.g. retinal layer boundaries), the graph may be isolated to a smaller region containing only one of the features. This may be done using a priori knowledge of the feature to segment. For example, to segment the inner plexiform layer (IPL) / inner nuclear layer (INL) boundary, we can set all edge weights in the outer half of the retina to zero. This prevents the algorithm from segmenting outer retinal features such as the outer segment (OS) / retinal pigmented epithelium (RPE) boundary. Implementation examples of these types of search region limitation can be found in [45, 46, 54, 55, 71].

To simplify and reduce the complexity of search region limitation, we can modify the edge weights of the graph to emphasize a particular region. For example, let us extend our example in Section 4.1 to segment the darkest path across an image. Given an image $\mathit{I}$ and its classification result $\mathit{C}\in {\Re }^{M\times N}$ where $\mathit{C}[i,j]\in \mathit{c}$ is the estimated class of $\mathit{I}[i,j]$, we would like to segment the darkest path across the portion of the image where $\mathit{C}[i,j]\in c_k.$ To do this, we compute the edge weights for $n=\left\{a,b\right\}$ following

$$w_{ab}=I_a+I_b+\#\left\{n|C_n\ne c_k\right\}+w_{\min },$$ (12)

where $C_n$ is the class at node $n$ and $\#\left\{n|C_n\ne c_k\right\}$ represents the number of nodes not equal to $c_k.$ From Eq. (12), it can be seen that edges connecting nodes with class $c_k$ are given lower weights than edges connecting nodes assigned to other classes. The advantage of this method is that far fewer a priori rules are required to isolate the desired region, as the classification method automatically generates estimates of region locations. Furthermore, hard limits are not set on the search region, as portions of the graph are not excluded.

5. Training the DME classifier

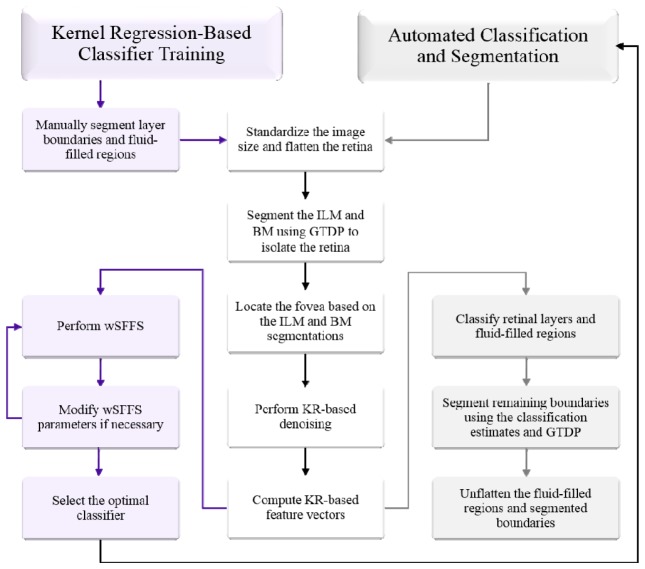
In this Section, we describe an implementation of our KR-based classification method to generate a DME classifier to identify fluid-filled regions and seven retinal layers on SD-OCT images of eyes with DME. An outline of our method is shown on the left side of Fig. 2 . All parameter values were either selected empirically based on the training data set or were extensions from our previous segmentation algorithms [45, 54, 55].

Fig. 2.

Flowchart of the KR-based classification and GTDP-based segmentation algorithm for identifying fluid-filled regions and eight retinal layer boundaries on images with DME pathology.

5.1 DME training data set

To learn our DME classifier, we obtained training data separate from our validation data set. We used the Duke Enterprise Data Unified Content Explorer search engine to retrospectively identify patients within the Duke Eye Center Medical Retina practice with a billing code for DME (ICD-9 362.07) associated with their visit. An ophthalmologist then identified six patients imaged in clinic using the standard Spectralis (Heidelberg Engineering, Heidelberg, Germany) 61-line volume scan protocol with severe DME pathology and varying image quality. Averaging of the B-scans was determined by the photographer, and ranged from 9 to 21 raw images per averaged B-scan. The volumetric scans were $Q=$61 B-scans × $N=$768 A-scans with an axial resolution $r_i=3.87$ µm/pixel, lateral resolution $(r_j)$ ranging from 11.07 – 11.59 µm/pixel, and azimuthal resolution $(r_k)$ ranging from 118 – 128 µm/pixel.

5.2 Target classes

To generate the target classes for classifier training, we manually segmented fluid-filled regions and semi-automatically segmented all eight retinal layer boundaries following the definitions in Fig. 3 . This was done for 12 B-scans within the training data set (two from each volume). The B-scans selected consisted of six images near the fovea (B-scan 31 for all volumes) and six peripheral images (B-scans 1, 6, 11, 16, 21, and 26, one for each of the six volumes). We then used the manual segmentations to assign the true class for each pixel, with a total of eight possible classes defined in Table 1 and the classified result shown in Fig. 4(a) .

Fig. 3.

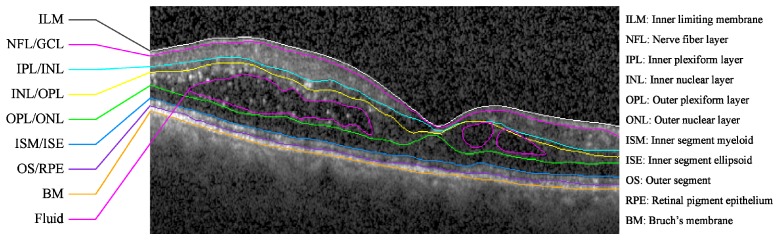
Target retinal layer boundaries and fluid to segment on an SD-OCT B-scan of an eye with DME. A flattened version of the image without markings is shown in Fig. 1(a).

Table 1. DME classes.

Class	Description	Color
$c_1$	Fluid	Blue
$c_2$	NFL	Light Blue
$c_3$	GCL-IPL	Cyan
$c_4$	INL	Green
$c_5$	OPL	Yellow
$c_6$	ONL-ISM	Orange
$c_7$	ISE	Red
$c_8$	OS-RPE	Dark Red

Fig. 4.

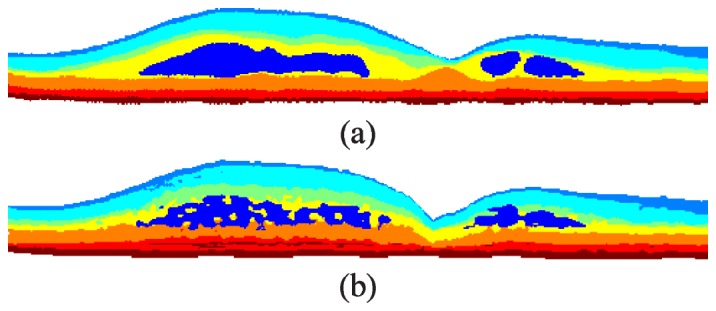
KR-based classification of retinal layers and fluid-filled regions. a) Manual classification of the image in Fig. 1(a) with the classes defined in Table 1. b) Automatic classification using the merged DME classifier.

5.3 Pre-processing the image

Prior to training the classifier, we perform image pre-processing steps for all B-scans within a volume following our validated DME algorithm described in [45]. To summarize, we first remove Spectralis registration boundaries by replacing them with the mirror image of the valid image regions. To standardize the images following [45] and [55], we resize the image to a lateral and axial resolution of $r_j=13.4$µm/pixel and $r_i=6.7$µm/pixel, respectively, and then linearly normalize the image to range from 0 to 1.

5.4 Flattening the retina

Next, we flatten the curved retina to obtain a shorter path for GTDP segmentation. Following [45], we achieve this by first heavily filtering each image using a 40.2 µm × 80.4 µm Gaussian with $\sigma =73.7$µm × 147.4 µm. We then threshold the filtered image at 0.5 to extract the inner and outer hyper-reflective complexes. We refine the hyper-reflective mask by 1) opening any gaps in the clusters using a 33.5 µm × 40.2 µm rectangular structuring element, 2) removing all clusters less than 0.018 mm² in size, and 3) closing any remaining gaps using the same structuring element. Using GTDP, we segment the boundaries of the hyper-reflective complexes as described in [55] which obtains estimates at the middle of the ONL and RPE.

Unlike our previous algorithms which flattened the retina on B-scans individually [45, 54, 55], in this algorithm we perform the above steps for all images in the volume to generate 2D map estimates ( $\in {\Re }^{Q\times N}$) of the OPL and RPE surfaces. Using the map of the RPE, we linearly interpolate any missing A-scans and B-scans. We then search for outliers by computing the absolute second derivative in the vertical direction and isolating all values greater than three standard deviations above the mean. Outlier clusters within each B-scan are then linearly interpolated, and the map of the RPE is smoothed using a 500 µm Gaussian filter with $\sigma =250$µm. Finally, for each B-scan, we circularly shift the A-scans until the RPE estimate is flat. Since the ONL boundary no longer aligns with the flattened RPE and image, we also flatten the ONL using the same flattening transformation.

5.5 Segmenting the total retina

To isolate the retina from the vitreous and choroid, we implement our GTDP layer segmentation framework described in Section 4.1 to segment the ILM using the dark-to-light gradient weights computed following

$$w_{ab}=\text{LinNorm}\left(-G_a^{DL}-G_b^{DL},0,1\right)+w_{\min },$$ (13)

where $G_n^{DL}$ is the maximum of the dark-to-light vertical (filter $={[1,-1]}^T$) and diagonal gradients of $\mathit{I}$ at node $n$ after filtering the image using a Gaussian (20.1 µm × 67 µm, $\sigma =13.4$µm × 26.8 µm), $w_{\min }=1\times {10}^{-5},$ and $\text{LinNorm}\left(x,y,\mathit{z}\right)$ is a linear normalization of $x$ to range from $y$ to $\mathit{z}.$ While using Dijkstra’s algorithm to segment the ILM, we limit the search region to span from the top of the image down to the RPE estimate generated in Section 5.4. To ensure that hyper-reflective spots or detachments internal to the ILM are not segmented, we re-segment the boundary using the weights in Eq. (14) where $D_{ab}$ is the Euclidean distance from node $a$ to node $b.$ We also limit the search region to span from the initial ILM estimate to 67 µm below the ILM.

$$\begin{array}{cc}{w}_{ab}=& \text{LinNorm}\left(-G_a^{DL}-G_b^{DL},0,1\right)+\text{LinNorm}\left(-D_{ab},0,0.1\right)+w_{\min }\end{array}$$ (14)

To segment BM, we compute weights following Eq. (15) where $G_n^{LD}$ is the light-to-dark equivalent of $G_n^{DL}$ and $I_n$ is the intensity of the filtered image at node $n$. We also set the top boundary of the search region to the mean location between the ONL estimate and 100.5 µm below the ILM, and we set the bottom boundary to the bottom of the image.

$$\begin{array}{ll}{w}_{ab}=& \text{LinNorm}\left(-G_a^{LD}-G_b^{LD},0,1\right)+\text{LinNorm}\left(-D_{ab},0,0.4\right)+\\ & \text{LinNorm}\left(-I_a-I_b,0,0.4\right)+w_{\min }\end{array}$$ (15)

5.6 Locating the fovea

To compute the features in Section 5.8 and gauge the location of the optic nerve and merged retinal layers, we first identify the location of the fovea on the volumetric macular scan. Upon segmenting the ILM and BM across all B-scans, we locate the fovea based on the 2D total retinal thickness (TRT) map computed by subtracting the ILM from BM. To do this, we first filter the TRT map ( $\in {\Re }^{Q\times N}$) using a Gaussian (120 µm × 89.8 µm and σ = 18.95 µm × 85.8 µm). We then narrow our search region to the central 3 mm of the volumetric macular scan and find all local extrema with a depth greater than 13.4 µm. If the extremum with the lowest or highest TRT resides closest to the center of the volume, then we assign that location as the fovea. Otherwise, we create a summed voxel projection (SVP) by summing pixels ranging from the ILM to 33.5 µm below the ILM across all B-scans. As with the TRT, we smooth the SVP, locate the extrema, and computed distances from the fovea. Looking at the five extrema closest to the center of the volume, we set the extremum with the lowest intensity as the fovea.

5.7 Kernel regression-based denoising

We next perform iterative Gaussian steering KR on each training image as described in Section 2 to 1) extract the normalized kernels ${\hat{\mathit{K}}}_{iGS}$ for every pixel $\mathit{z}$ in the retina, and 2) recover $\hat{\mathit{b}}$ defined in Eq. (4) which contains the denoised image and its first and second order derivatives. Parameter values are listed in Section 2.2, and since only the pixels within the retina need to be classified, we do not denoise pixels within the vitreous and choroid.

5.8 Computing DME training features

To learn the DME classifier, we computed feature vectors for the 12 training images manually segmented in Section 5.2. We generated a total of 22 features ( $v_1-v_{22}$) for each vector, and only pixels within the retina were processed. The nine KR-based features are defined in Table 2 , the four position-related features are listed in Table 3 , and the nine Laws’ Texture Energy Measure features [63, 64] are listed in Table 4 . We then enhance the texture features in Table 4 using Eq. (8) and further enhance all features except $v_7-v_{13}$ using adaptive histogram equalization [72]. Finally, we normalize all features to match the range of the training features. Figure 5 shows Laws’ $E{5}^{T}E5$ feature computed with and without KR-based denoising. As can be seen from Fig. 5, utilizing KR reduced the amount of noise present within the feature.

Table 2. Kernel regression-based DME training features.

Definition	Description
$v_1=f(\mathit{z})$	KR denoised pixel
$v_2=\frac{\partial f(\mathit{z})}{\partial i}$	KR denoised vertical first derivative
$v_3=\frac{\partial f(\mathit{z})}{\partial j}$	KR denoised horizontal first derivative
$v_4=\frac{{\partial }^{2}f(\mathit{z})}{\partial i^2}$	KR denoised vertical second derivative
$v_5=\frac{{\partial }^{2}f(\mathit{z})}{\partial i\partial j}$	KR denoised diagonal second derivative
$v_6=\frac{{\partial }^{2}f(\mathit{z})}{\partial j^2}$	KR denoised horizontal second derivative
$\begin{array}{l}{v}_7=\#\{p|{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})>\frac{{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})}{2}\\ \begin{array}{c}\\ \end{array}\text{and}(i_p-i)=0\},p=1,\dots ,P\end{array}$	Horizontal kernel full width at half max
$\begin{array}{l}{v}_8=\#\{p|{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})>\frac{{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})}{2}\\ \begin{array}{c}\\ \end{array}\text{and}(j_p-j)=0\},p=1,\dots ,P\end{array}$	Vertical kernel full width at half max
$\begin{array}{l}{v}_9=\#\left\{p|{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})>\frac{{\hat{\mathit{K}}}_{iGS}({\mathit{z}}_p-\mathit{z})}{2}\right\},\\ p=1,\dots ,P\end{array}$	Kernel half max area

Table 3. Position-based DME training features.

Definition	Description
$v_{10}=\{\begin{array}{c}j-j_{fov},\hspace{1em}\text{right eye}\\ j_{fov}-j,\hspace{1em}\text{left eye}\end{array}$	Horizontal distance from the fovea, where $j_{fov}$ is the foveal A-scan
$v_{11}=\frac{i-i_{ILM}}{i_{BM}-i_{ILM}}$	Vertical distance from the fovea, where $i_{ILM}$ and $i_{BM}$ are the vertical positions of the ILM and BM for column $j$determined in Section 5.5.
$v_{12}=\sqrt{{[r_j(j-j_{fov})]}^2+{[r_k(k-k_{fov})]}^2}$	Radial distance from the fovea, where $r_j$ and $r_k$ are the lateral and azimuthal resolutions, and $k$ is the B-scan number of the image within the volumetric scan
$v_{13}=i_{BM}-i_{ILM}$	Retinal thickness

Table 4. Laws’ texture training features.

$v_{14}=\text{Laws'}L{5}^{T}E5/E{5}^{T}L5\text{filter}$
	$v_{19}=\text{Laws'}E{5}^{T}R5/R{5}^{T}E5\text{filter}$
$v_{15}=\text{Laws'}L{5}^{T}S5/S{5}^{T}L5\text{filter}$
	$v_{20}=\text{Laws'}S{5}^{T}S5\text{filter}$
$v_{16}=\text{Laws'}L{5}^{T}R5/R{5}^{T}L5\text{filter}$
	$v_{21}=\text{Laws'}S{5}^{T}R5/R{5}^{T}S5\text{filter}$
$v_{17}=\text{Laws'}E{5}^{T}E5\text{filter}$
	$v_{22}=\text{Laws'}R{5}^{T}R5\text{filter}$
$v_{18}=\text{Laws'}E{5}^{T}S5/S{5}^{T}E5\text{filter}$

Fig. 5.

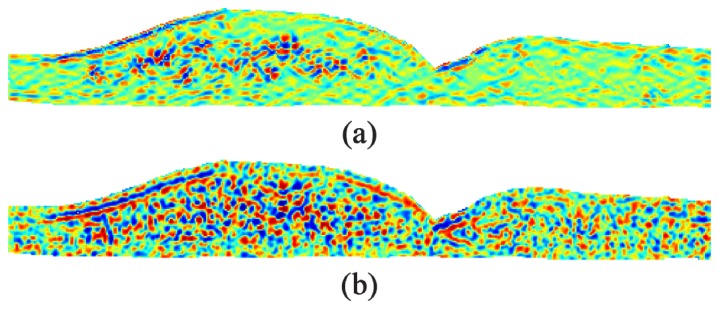
Laws’ $E{5}^{T}E5$ texture feature computed for the image in Fig. 1(a) with (a) and without (b) KR-based denoising. Both feature images have been enhanced using adaptive histogram equalization.

5.9 Selecting relevant features and weights

To select the most relevant features and weights for fluid and layer classification, we implemented our wSFFS method described in Section 3.5. We used ten-fold cross-validation [73] during this process and adjusted selection parameters until we achieved the desired classification result. During feature selection, we set the maximum number of features in $\mathit{v}\prime$ to 10, $\mathit{a}$ ranged from 0.1 to 1 in 0.1 increments, used the classifier function defined in Eq. (10), and allowed a maximum of three clusters.

Next, we defined three types of DME classifiers: 1) a layer classifier ( ${\phi }_l$) for segmenting layer boundaries, 2) a fluid classifier ( ${\phi }_f$) for identifying fluid-filled regions, and 3) a layer + fluid classifier ( ${\phi }_{l+f}$) used to remove false positive fluid detected by the fluid classifier. For each classifier type, we defined the criterion function following Eqs. (16) and (17), where $\mathit{V}\prime ={\left[\mathit{v}{\prime }_1{}^T,\mathit{v}{\prime }_2{}^T,\dots ,\mathit{v}{\prime }_R{}^T\right]}^T\in {\Re }^{R\times L\prime }$ is the set of reduced feature vectors for all training data, $c_r$ is the true class for $\mathit{v}{\prime }_r,$ and $c_k$ is the class that is being analyzed. For the fluid classifier, $k=1$ so only the fluid class is evaluated by the criterion function. For the layer classifier, $k=2,\dots ,8$ so only the layers are analyzed, and $k=1,\dots ,8$ for the layer + fluid classifier so all classes are analyzed. The resulting feature and weights are shown in Table 5 and Fig. 6 , where ${\phi }_l$ is a 3-cluster classifier, and ${\phi }_f$ and ${\phi }_{l+f}$ are 1-cluster classifiers.

Table 5. Selected DME classifier features and weights.

Layer			Fluid			Layer + Fluid
Feature	Weight		Feature	Weight		Feature	Weight
v11	1.5		v1	2.7		v11	1.4
v12	0.9		v3	1.9		v13	0.8
v10	0.8		v11	1.8		v1	0.5
v6	0.8		v13	1.0		v14	0.5
v13	0.6		v17	1.0		v10	0.3
v14	0.5		v9	0.6		v12	0.3
v1	0.4					v9	0.3
v15	0.3					v15	0.2
v7	0.3					v7	0.2

Fig. 6.

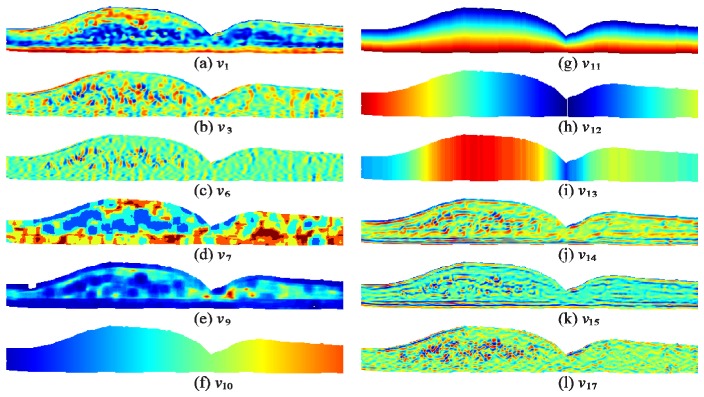
Visual example of features selected for the DME classifiers. a-l) Features computed for the image in Fig. 1(a).

$$E(\mathit{V}\prime )=\begin{array}{ll}\{\begin{array}{l}2-\frac{1}{\mathit{K}}{\displaystyle \sum _{k\subseteq \left\{1\dots \mathit{K}\right\}}\frac{T{N}_k}{T{N}_k+F{P}_k}}\\ 2-\frac{1}{\mathit{K}}{\displaystyle \sum _{k\subseteq \left\{1\dots \mathit{K}\right\}}\left(\frac{T{N}_k}{T{N}_k+F{P}_k}+1\right)}\\ 2-\frac{1}{\mathit{K}}{\displaystyle \sum _{k\subseteq \left\{1\dots \mathit{K}\right\}}\left(\frac{T{N}_k}{T{N}_k+F{P}_k}+\frac{T{P}_k}{T{P}_k+F{N}_k}\right)}\end{array}& \begin{array}{l}\begin{array}{l}\text{if}T{P}_k=0,F{P}_k>0,F{N}_k=0\\ \end{array}\\ \text{if}T{P}_k=0,F{P}_k=0,F{N}_k=0\\ \begin{array}{l}\\ otherwise\end{array}\end{array}\end{array}$$ (16)

$$\begin{array}{c}T{P}_k=\#\left\{r|\phi (\mathit{v}{\prime }_r)=c_k \text{and} c_k=c_r\right\},r=1,\dots ,R\\ T{N}_k=\#\left\{r|\phi (\mathit{v}{\prime }_r)\ne c_k \text{and} c_k\ne c_r\right\},r=1,\dots ,R\\ F{P}_k=\#\left\{r|\phi (\mathit{v}{\prime }_r)=c_k \text{and} c_k\ne c_r\right\},r=1,\dots ,R\\ F{N}_k=\#\left\{r|\phi (\mathit{v}{\prime }_r)\ne c_k \text{and} c_k=c_r\right\},r=1,\dots ,R\end{array}$$ (17)

5.10 Merged DME classifier

Given three classification images ${\mathit{C}}_l$, ${\mathit{C}}_f$, and ${\mathit{C}}_{l+f}\in {\Re }^{M\times N}$ output by the layer, fluid, and layer + fluid classifiers developed in Section 5.9, we next merge the results to create a single classification result. We achieve this by first setting all regions in ${\mathit{C}}_f$ and ${\mathit{C}}_{l+f}$ to zero if it is not classified as fluid. Next, we remove all fluid clusters in ${\mathit{C}}_f$ that do not overlap with the fluid in ${\mathit{C}}_{l+f}$. We also examine the shape of the fluid clusters and remove any that are abnormally wide and thin. More specifically, if a cluster is more than 536 µm wide and less than 33.5 µm tall, then we consider the cluster as a false positive. Finally, we generate the merged classification image $\mathit{C}$ by setting $\mathit{C}={\mathit{C}}_l$ and subsequently assigning all pixels in $\mathit{C}$ to $c_1$ (fluid) where ${\mathit{C}}_f>0$. Figure 4 shows an example training image comparing the true classes (Fig. 4(a)) to the automatically generated classes output by our algorithm (Fig. 4(b)).

6. Automatic classification-based GTDP segmentation algorithm for DME

We next leveraged the classification results from Section 5 to create a fully automatic GTDP segmentation algorithm to identify fluid-filled regions and seven retinal layers on SD-OCT images with DME. An outline of the algorithm is shown on the right side of Fig. 2 and explained in detail in the following subsections.

6.1 Pre-processing, flattening, and segmenting the retina

We pre-process all images in a volumetric scan, flatten the entire retina based on estimates of the RPE, and use GTDP to segment the ILM and BM following Sections 0 – 5.5.

6.2 Classification of fluid and retinal layers

To classify the images, we locate the fovea and perform second order iterative Gaussian KR as described in Sections 5.6 and 5.7, respectively. We then compute the 12 features listed in Table 5 for all pixels residing within the retina following Section 5.8. Finally, we classify the feature vectors using the three classifiers from Section 5.9, and merge the results following Section 5.10 to generate the final image $\mathit{C}$ containing the fluid and layer class estimates.

6.3 GTDP segmentation of intraretinal layers

To segment the six remaining intraretinal layer boundaries, we begin by creating a binary mask of the OS/RPE boundary based on the layer classification image ${\mathit{C}}_l.$ To generate the binary image $\mathit{B},$ we set all pixels from the bottom of the classified ISE layer to the bottom of the classified RPE layer to 1. We then segment the OS/RPE boundary using the weights in Eq. (18) and a search region extending from the ILM to BM, where $B_n$ is the value of $\mathit{B}$ at node $n,$ $d_{\max }=0.5,$ and $b_{\max }=\mathrm{0.5.}$ Furthermore, for Eq. (18) and for all subsequent weight calculations, we compute $G_n^{DL}$ using the denoised image ${\hat{\beta }}_0$ generated in Section 6.2.

$$\begin{array}{ll}{w}_{ab}=& \text{LinNorm}\left(-G_a^{DL}-G_b^{DL},0,1\right)+\text{LinNorm}\left(-D_{ab},0,d_{\max }\right)+\\ & \text{LinNorm}\left(-B_a-B_b,0,b_{\max }\right)+w_{\min }\end{array}$$ (18)

Next, we segment the ISM/ISE by setting all pixels in $\mathit{B}$ ranging from the bottom of the classified ONL-ISM to the bottom of the classified ISE. We then segment the boundary using Eq. (18) where $d_{\max }=0.5,$ $b_{\max }=0.1,$ and the search region extends from halfway between the classified ILM and OS/RPE to13.4 µm above the OS/RPE.

The third intraretinal boundary we segment is the NFL/GCL. Since the ILM is oftentimes significantly brighter and creates a pseudo light-dark transition within the NFL, we take the pixel-wise square root of $\hat{\mathit{I}}$ and use the resulting image to compute the light-to-dark gradient image of the NFL/GCL boundary, generating ${\mathit{G}}^{sqLD}$. We then compute the graph weights following

$$\begin{array}{ll}{w}_{ab}=& \text{LinNorm}\left(-G_a^{sqLD}-G_b^{sqLD},0,1\right)+\text{LinNorm}\left(-D_{ab},0,0.1\right)+\\ & \text{LinNorm}\left(-B_a-B_b,0,0.1\right)+w_{\min },\end{array}$$ (19)

where $G_n^{sqLD}$ is the light-to-dark gradient of ${\mathit{G}}^{sqLD}$ at node $n$ and values in $\mathit{B}$ ranging from the middle of the classified NFL to the bottom of the GCL-IPL are set to 1. We then set the search region to range from the ILM to the ISM/ISE. However, since the thickness of the NFL varies more than all other layers and is oftentimes very faint on the temporal side, we provide additional search region steps as follows: 1) the bottom boundary for A-scans less than 1 mm from the fovea is set to the ILM plus 40.2 µm times the distance from the fovea (in mm), 2) the top boundary for A-scans between 1.5 and 3 mm nasal to the fovea is set to the ILM plus 6.7 µm times the distance from the fovea, and 3) the bottom boundary for A-scans greater than 1 mm temporal to the fovea is set to a third of the distance between the ILM and ISM/ISE.

Next, we segment the OPL/ONL using Eq. (20) where $b_{\max }=0.5,$ $i_{\max }=0.5,$ and the binary image is set to 1 between the top of the classified OPL and the middle of the classified ONL. We then set the top of the search region to either the NFL/GCL plus the NFL thickness, or 67 µm below the NGL/GCL, whichever is closer to the NFL/GCL. Finally, the bottom of the search region is set to the ISM/ISE.

$$\begin{array}{ll}{w}_{ab}=& \text{LinNorm}\left(-G_a^{LD}-G_b^{LD},0,1\right)+\text{LinNorm}\left(-D_{ab},0,0.1\right)+\\ & \text{LinNorm}\left(-B_a-B_b,0,b_{\max }\right)+\text{LinNorm}\left(I_a+I_b,0,i_{\max }\right)+w_{\min }\end{array}$$ (20)

To segment the INL/OPL, we set values in $\mathit{B}$ extending from the top of the classified INL to the bottom of the classified OPL to 1. We also morphologically dilate the edges of the fluid in $\mathit{C}$ using a disk structuring element with a radius of 2 pixels. The dilated edges are also set to 1 in $\mathit{B}$. We then use Eq. (18) with $d_{\max }=0.1$ and $b_{\max }=0.1$ to compute graph weights, and we limit the search region extent from 13.4 µm below the NFL to the OPL/ONL.

With the IPL/INL being the last boundary to segment, we set values in $\mathit{B}$ ranging from the bottom of the classified GCL-IPL to the bottom of the INL to 1. To discourage the IPL/INL from running through fluid regions, we set fluid regions to a negative value in $\mathit{B}.$ We then compute graph weights following Eq. (20) with $b_{\max }=0.4$ and $i_{\max }=0.$ Finally, we limit the search region to range from the a third of the distance between the NFL/GCL and INL/OPL, to the INL/OPL.

7. Algorithm validation

7.1 DME validation data set

We obtained our validation data set by identifying ten patients with DME that were not included in the training data set. The method for selecting these data sets is described in Section 5.1, with the difference that the images had to be of adequate quality (i.e. layer and fluid boundaries needed to be visible). The image acquisition parameters were consistent with the training data set, and lateral and azimuthal resolutions ranged from 10.94 – 11.98 µm/pixel and 118 – 128 µm/pixel, respectively. We made the entire data set available online, including the training and validation data sets and their corresponding automatic and manual segmentation results. This data set can be found at www.duke.edu/~sf59/Chiu_BOE_2014_dataset.htm.

7.2 Automatic versus manual segmentation

Two ophthalmologists manually segmented all fluid-filled regions and eight retinal layer boundaries using custom software (DOCTRAP V50.9) for 110 images (11 per patient). The images selected consisted of the foveal scan $k_{fov}$ and scans $k_{fov}$ ± 2, $k_{fov}$ ± 5, $k_{fov}$ ± 10, $k_{fov}$ ± 15, and $k_{fov}$ ± 20. The graders worked in a dimly lit room alone and free of other distractions. A tablet computer was used to allow the grader to utilize a stylus to mark or draw the segmentation as if writing on a flat surface. While marking the images, the ophthalmologists were able to use either a freeform (drawing) or connect-the-dots (piecewise cubic-interpolated clicking) method. They also had the options to hide/show other markings, erase/add/correct markings, and pin/unpin adjacent layer boundaries. The graders first segmented the retinal layers using predominantly the connect-the-dots function with freehand segmentation reserved for particularly complex contours such as those encountered when retinal layers are severely disrupted by edema. In cases where boundaries between layers were completely obscured or lost, the graders made their best estimate. The retinal layer segmentation could then be hidden to allow segmentation of edema without influence by retinal layer segmentation. The graders segmented retinal edema using the freehand function, and all edema was segmented whether it was cystic or non-cystic in nature. Cysts were segmented individually, whereas non-cystic edema was segmented according to the contour of thickening and the perceived location of the edema with respect to the retinal layers. The expert graders (MJA and PSM) are both fellowship-trained medical retina specialists on the faculty at the Duke Eye Center. They each have over five years of clinical experience working with diabetic subjects and reading OCT images. Both have prior experience with manual OCT grading and have each published two manuscripts involving OCT analysis and grading. Outside consultation and discussion between graders was prohibited.

To validate our algorithm, we compared our fully automatic KR + GTDP segmentation to our pre-determined primary grader (MJA) within a 6-mm lateral radius from the fovea. We then measured the Dice coefficient [74, 75] for retinal layer and fluid classification. We also measured the mean layer thickness difference between automatic and manual segmentation for each B-scan, and computed the absolute mean error across all 110 B-scans. To realize the improvement of our new KR + GTDP segmentation algorithm compared to existing methods that do not consider the presence of fluid, we also evaluated the performance of our GTDP algorithm developed for normal eyes on the DME data set. This Normal GTDP algorithm is a modified version of our 2010 algorithm described in [54], where enhancements had been made following our 2010 publication to improve segmentation results and address issues such as registration artifacts seen on Spectralis SD-OCT images. Finally, we computed the mean Dice coefficient and thickness difference for each layer for a given patient and performed the Wilcoxon matched-pairs test across all patients for each automated algorithm compared to the inter-manual results, as well as the Normal and DME algorithms compared to each other.

8. Experimental results

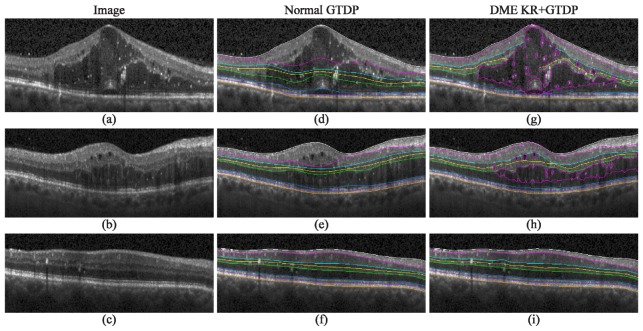
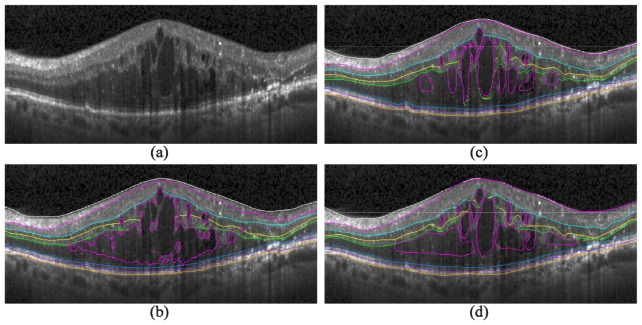
Figure 7 (right) shows the qualitative results of our automatic KR + GTDP segmentation algorithm for varying amounts of edema, including cases where there was no fluid present (Fig. 7(f)). This is in comparison to the automatic GTDP results using the normal algorithm (Fig. 7, middle). Table 6 and Table 7 report quantitative results comparing automatic and manual segmentation, with an overall mean Dice coefficient and thickness difference of 0.78 ± 0.10 and 5.22 ± 5.81 µm, respectively, for our proposed KR + GTDP algorithm. This is comparable to the inter-manual results which yielded an overall mean Dice coefficient and thickness difference of 0.79 ± 0.09 and 4.30 ± 2.38 µm, respectively. On the other hand, our popular GTDP algorithm developed for eyes without pathology had mean overall values of 0.70 ± 0.19 and 11.39 ± 19.11 µm. Table 8 shows the resulting p-values when comparing a) the mean patient Dice and thickness difference values between the automated and gold standard methods, to b) the inter-manual (Columns 1 and 2) or Normal GTDP (Column 3) results. An insignificant result against the inter-manual results indicates that the automated algorithm performed comparably to a second expert grader, while a significant result against the Normal algorithm indicates an improvement in the segmentation algorithm. Finally, Fig. 8 is an example comparison of the segmentations completed by the algorithm (Fig. 8(b)) and by the two graders (Fig. 8(c) and 8(d)), and Fig. 9 shows example errors in automatic segmentation (Fig. 9, bottom) when compared to a manual grader (Fig. 9, middle). The performance of the algorithms in MATLAB (MathWorks, Natick, MA) were 1.8 seconds per image on average for the Normal GTDP algorithm and 11.4 seconds for the KR + GTDP algorithm. This is in comparison to the 5.5 minutes required per image for manual segmentation.

Fig. 7.

Qualitative results for the identification of fluid and eight retinal layer boundaries on SD-OCT images of eyes with DME. a-c) Images with significant, moderate, and no visible fluid, respectively, d-f) their corresponding automatic segmentation result using the GTDP algorithm developed for normal eyes, and g-i) the automatic KR + GTDP segmentation result.

Table 6. Dice coefficients for DME segmentation.

Class	Inter-Manual			Normal GTDP Automatic vs Manual			DME KR + GTDP Automatic vs Manual
	Mean	SD		Mean	SD		Mean	SD
Fluid	0.58	0.32		N/A	N/A		0.53	0.34
NFL	0.86	0.06		0.78	0.19		0.86	0.05
GCL-IPL	0.89	0.05		0.74	0.25		0.88	0.06
INL	0.77	0.07		0.63	0.22		0.73	0.08
OPL	0.72	0.08		0.63	0.19		0.73	0.09
ONL-ISM	0.87	0.06		0.86	0.09		0.86	0.08
ISE	0.85	0.05		0.85	0.06		0.86	0.05
OS-RPE	0.82	0.05		0.79	0.06		0.80	0.06

Table 7. Layer thickness differences for DME segmentation in µm.

Class	Inter-Manual			Normal GTDP Automatic vs Manual			DME KR + GTDP Automatic vs Manual
	Mean	SD		Mean	SD		Mean	SD
Fluid	N/A	N/A		N/A	N/A		N/A	N/A
NFL	4.02	3.30		25.83	50.42		3.68	4.13
GCL-IPL	4.91	6.74		11.90	20.33		4.84	5.12
INL	6.04	8.48		9.91	20.40		7.90	11.92
OPL	4.21	3.74		6.50	5.90		6.35	6.11
ONL-ISM	4.93	5.25		19.58	32.29		6.80	8.37
ISE	3.03	2.11		2.53	2.00		2.88	2.28
OS-RPE	2.99	2.30		3.51	2.39		3.61	2.47

Table 8. Wilcoxon matched-pairs test p-values.

Class	Normal GTDP vs Manual			DME KR + GTDP vs Manual			DME KR + GTDP vs Normal GTDP
	Dice	Thickness		Dice	Thickness		Dice	Thickness
Fluid	N/A	N/A		0.432	N/A		N/A	N/A
NFL	0.014*	0.014*		0.695	0.557		0.049*	0.027*
GCL-IPL	0.002*	0.004*		0.432	0.557		0.010*	0.006*
INL	0.006*	0.557		0.027*	0.275		0.014*	> 0.999
OPL	0.002*	0.037*		0.322	0.084		0.004*	0.922
ONL-ISM	0.557	0.010*		0.193	0.049*		0.275	0.004*
ISE	0.695	0.084		0.322	0.275		0.770	0.232
OS-RPE	0.106	0.275		0.846	0.065		0.193	0.695

* indicates statistical significance

Fig. 8.

Automatic and manual segmentation comparison. a) An SD-OCT B-scan with DME pathology, b) the fully automatic segmentation result, and c-d) the segmentation results completed by two different graders.

Fig. 9.

Automatic fluid detection errors. Top) Cropped portions of SD-OCT B-scans with DME, middle) manual segmentation of fluid-filled regions by a grader, and bottom) automatic fluid-filled classification. a) An image with hyper-reflective deposits, b) a dim image with a hyper-reflective outlier, and c) a high quality image.

9. Discussion

Despite having two qualified graders to manually mark the validation data sets, their results did not overlap with high accuracy (Table 6). This is likely due to the lower image quality and severe DME pathology present within the data set, as we deliberately chose to use real-world, clinical images in our study. While not necessarily a representative example for all graded images, Fig. 8 shows the challenge faced by both expert and automatic graders when confronted with an image from clinical practice that is affected by severe DME. The massive retinal thickening and punctate inner retinal hyper-reflectivity results in shadowing and loss of detail in the outer retinal layers. While some cysts are well-delineated hypo-reflective spaces in Fig. 8(a), others are minimally hypo-reflective compared to the surrounding tissue and create a judgment call for the grader. In this case, one grader perceived some non-cystic edema (Fig. 8(d)) while the other identified primarily cystic edema (Fig. 8(c)). The subjective nature of complex image segmentation by humans is thus one of the major obstacles to generating robust imaging-based biomarkers and is the primary unmet scientific and clinical need that is addressable using automated algorithms.

Despite the difficulty in managing such a challenging data set, Table 6 indicates that our fully automatic KR + GTDP algorithm generated results with an error close to the inter-observer variability (Dice coefficient of 0.78 versus 0.79). Furthermore, this was a significant improvement from previous algorithms developed by us, as our Normal GTDP method was tested on images without the significant pathology as seen on our DME data set. KR + GTDP classification of fluid-filled regions yielded the lowest Dice coefficient with errors similar to those shown in Fig. 9. In Fig. 9(a), false positives were detected near areas containing hyper-reflective deposits. Since the training data set did not include images with these hyper-reflective spots, the algorithm perceived these areas as “normal” and its surrounding regions as hypo-reflective, thus resulting in false positive classifications. Future versions of the algorithm can include the deposits as an additional class. Figure 9(b), in contrast, is a very dim image. Since the image contained a single hyper-reflective spot, the rest of the image remained dark after linear normalization. In future versions, the image can instead be non-linearly normalized (e.g. histogram equalization) prior to using the DME classifier. Finally, Fig. 9(c) shows the algorithm’s tendency to identify more regions of the ONL as fluid compared to the grader. This may be partially due to the small training data set size of 12 images.

Classification-based GTDP segmentation includes embedded denoising which is advantageous for reducing the noise present within the classification feature vectors (Fig. 5). While many different denoising methods may be also used to reduce the noise, the exciting properties of KR include its direct estimation of the denoised first and second order derivatives ( ${\hat{\mathit{\beta }}}_1$ and ${\hat{\mathit{\beta }}}_2$), as well as the generation of locally-weighted kernels which can be used directly as features or reused for non-linear feature denoising. A limitation of KR is the dependence of parameter values on the image noise level. Thus in order to optimally denoise images of varying scan types, future versions of the algorithm should adapt the KR parameter values based on the estimated noise level. Adapting alternative image representation models such as sparsity-based techniques, shown to be very efficient in representing retinal OCT images [76], may also improve the performance and is part of our ongoing work.

The need for GTDP segmentation is a limitation to this study, as the KR-based classification method was not sufficient to accurately identify retinal layers as a standalone method. While K-means clustering helped improve the classification of layers with varying thicknesses and positions (e.g. a thicker NFL on the nasal side versus a thinner NFL on the temporal side as shown in Fig. 4(b), the classified intraretinal layers did not merge at the fovea. Furthermore, three separate classifiers were required to achieve the final classification result. While ${\mathit{C}}_{l+f}$ provided a balance in accuracy between the layer and fluid classifiers, ${\mathit{C}}_l$ generated the most accurate layer classifications and ${\mathit{C}}_f$ achieved better fluid classifications but with more false positives. We therefore merged all three classifiers to achieve the best possible classification result. Finally, since there was no hard constraint on layer ordering, Fig. 4(b) shows the OS-RPE layer sometimes appearing above the ISE. Nevertheless, the classification example shown in Fig. 4(b) shows that our method provides a significant starting point that is helpful in simplifying the GTDP search region step. Other more advanced classification methods (e.g. support vector machines) may also be implemented in place of our described method to possibly improve the classifier performance.

The classifier features and weights shown in Fig. 6 and Table 5 provide insight into the characteristics that are important for fluid and layer identification. For example, the denoised intensity feature ( $v_1$) was the most important feature for identifying fluid, likely due to the dark intensity exhibited by fluid. In contrast, for both cases where the classifier was required to identify layers, the vertical position within the retina ( $v_{11}$) was most important. This is due to the layered nature of the retina. Adapting alternative image representation models such as sparsity-based techniques, shown to be very efficient in representing retinal OCT images [76], may improve the performance and is part of our ongoing work.

Finally, our randomly selected validation data set did not include many images with subretinal fluid, a relatively uncommon feature in DME. Thus, its performance for such images is unknown. Furthermore, our algorithm does not yet distinguish between cystic and non-cystic fluid. Incorporating the ability to identify and categorize different types of fluid (e.g. subretinal, cystic, non-cystic) is a necessary step in our future work, as this will enable rigorous DME subtyping. While the correlation between DME subtype and response to therapy is still unknown, the potential clinical implications of personalized therapy and improved treatment outcomes are vast.

10. Conclusion

We developed a fully automatic algorithm to identify fluid and eight retinal layer boundaries on SD-OCT images with DME pathology. Results showed that our automatic algorithm performed comparably to manual graders. This is the first validated, fully-automated, and multi-layer segmentation method which has been applied to real-world, clinical images containing severe DME. Accurate identification of DME imaging biomarkers is extremely important, as it will facilitate the quantification and understanding of DME.