Characterizing the beam steering and distortion of Gaussian and Bessel beams focused in tissues with microscopic heterogeneities

Abstract

Bessel beams have recently been investigated as a means of improving deep-tissue microscopy in highly scattering and heterogeneous media. It has been suggested that the long depth-of-field and self-reconstructing property of a Bessel beam enables an increased penetration depth of the focused beam in tissues compared to a conventional Gaussian beam. However, a study is needed to better quantify the magnitude of the beam steering as well as the distortion of focused Gaussian and Bessel beams in tissues with microscopic heterogeneities. Here, we have developed an imaging method and quantitative metrics to evaluate the motion and distortion of low-numerical-aperture (NA) Gaussian and Bessel beams focused in water, heterogeneous phantoms, and fresh mouse esophagus tissues. Our results indicate that low-NA Bessel beams exhibit reduced beam-steering artifacts and distortions compared to Gaussian beams, and are therefore potentially useful for microscopy applications in which pointing accuracy and beam quality are critical, such as dual-axis confocal (DAC) microscopy.

1. Introduction

In recent years, there has been a renewed interest in exploiting Bessel beams as a form of illumination for deep-tissue laser-scanning microscopy [1–7]. The irradiance profile of an ideal Bessel beam is described by a zero-order Bessel function of the first kind in which the narrow main lobe of a Bessel beam is surrounded by a decaying set of “side-lobe” rings [8–10]. There are two prominent features of a Bessel beam: its “non-diffracting” and “self-reconstructing” properties. These features have been shown to benefit laser-scanning microscopy in large specimens with micro-architectural heterogeneities, such as cell clusters or embryos [1, 2]. The “non-diffracting” property of a Bessel beam refers to its ability to propagate over a long distance along the optical axis without exhibiting any broadening or bending of its main lobe [1–3]. The “self-reconstructing” property refers to the ability of this main lobe to propagate through highly heterogeneous media, even in the presence of obstructions that may block or distort the main lobe temporarily [2, 4, 11]. This self-healing behavior is aided by the fact that each side lobe of a Bessel beam carries approximately the same amount of energy as the main lobe and continuously acts to reconstruct the main lobe as it propagates [12–14]. As a consequence, the irradiance of the main lobe is preserved as well as its position and shape. Unfortunately, the large side lobes of a Bessel beam also contribute out-of-focus background that can reduce image contrast, which is a major trade-off when implementing Bessel beams in various optical microscopy applications [1,2].

Numerous groups have recently explored the use of Bessel beams in light-sheet-based microscopy [1, 2, 4–6]. When performing light-sheet microscopy with conventional Gaussian illumination in tissues, the field of view (FOV), within which the thickness of the light sheet is fairly uniform, is restricted and may be approximated by the confocal parameter, or twice the Rayleigh range of the Gaussian beam [2, 5, 6]. In addition, tissue-heterogeneity-induced light-sheet distortions have been shown to diminish the contrast and resolution in Gaussian light-sheet-based microscopy [1, 11]. The “non-diffracting” and “self-reconstructing” characteristics of a Bessel beam have shown promise for reducing the limitations mentioned above [1–6]. For example, some have explored the “non-diffracting” property of Bessel beams to generate an extended FOV, which is advantageous for imaging relatively large biological samples such as whole embryos [2, 6]. Other groups have utilized the “self-reconstructing” property of Bessel beams to improve image contrast and resolution when performing deep-tissue light-sheet microscopy within highly heterogeneous samples [1, 4]. Many of these groups have also explored various strategies such as structured illumination, confocal line detection, as well as two-photon excitation, to mitigate the background caused by the diffraction side lobes of Bessel beams, providing further improvements for deep-tissue imaging with Bessel light-sheet microscopy [6, 15–17].

In summary, a major challenge for optical microscopy in tissues is that micro-architectural heterogeneities can cause spatial variations of the beam foci in terms of position and shape [1–6]. These heterogeneity-induced beam-steering artifacts and distortions tend to deteriorate the image resolution of laser-scanned microscopes designed to visualize and monitor cellular structures in thick tissues at a large depth [1–6]. A notable example is dual-axis confocal (DAC) microscopy [18], which achieves improved spatial-filtering and optical-sectioning performance over conventional confocal microscopy through off-axis illumination and collection of light with low-numerical aperture (NA) objectives [19, 20]. This unique architecture requires a pair of illumination and collection beams to intersect at their foci within tissues, thus causing the DAC imaging performance to be highly sensitive to any positional changes and distortions of these foci [21–23]. In previous studies with tissue-like phantoms, our group and others have observed that heterogeneity-induced beam steering leads to a degradation in spatial resolution for DAC microscopy [24, 25]. Furthermore, our group has also demonstrated that the signal collected by a DAC microscope is significantly reduced when the alignment of the illumination and collection beams is spatially modulated at the micron scale [26].

Although the fundamental principles of “self-reconstructing” Bessel beams have been extensively studied previously [8–10], there is a need to quantitatively assess this “self-reconstructing” property of low-NA Bessel beams compared to conventional Gaussian beams in tissues. In particular, while previous studies focused on the irradiance of a Bessel beam, and its preservation through scattering tissues, less attention has been given to the positional stability and shape of the Bessel beam, which are of great importance in DAC microscopy. Therefore, in this study, we developed an experimental strategy (section 2.1) and a quantitative metric (section 2.2) to evaluate the motion (heterogeneity-induced beam steering) of focused Gaussian and Bessel beams in water, heterogeneous phantoms, and mouse esophagus tissues. We also developed a quantitative metric (section 2.3) to evaluate the beam distortion of focused Gaussian and Bessel beams in these same media. While acknowledging the presence of diffraction side lobes, which must be mitigated in order to achieve high-contrast imaging, here we limited our characterization of Bessel beams to their main lobes alone. In particular, since the spatial resolution of a DAC microscope is directly related to the spot size of its intersecting illumination and collection beams [20, 21], we compared a low-NA Gaussian and Bessel beam with matching spot sizes (i.e. the full width at half maximum (FWHM) Gaussian beam waist diameter matches the FWHM diameter of the main lobe of the Bessel beam).

2. Methods

2.1 System architecture

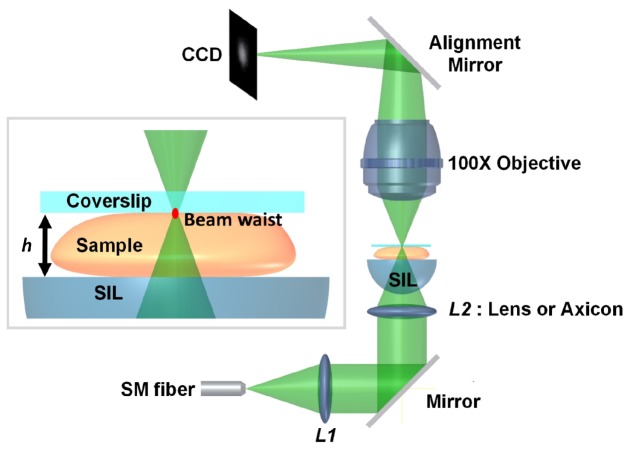
The imaging system used in this study is shown in Fig. 1 . For both Gaussian and Bessel illumination, the light source was a diode-pumped solid-state laser (Coherent Laser, Inc.) at 550 nm. For Gaussian illumination, a beam with a low numerical aperture, NA = 0.12 (prior to the solid immersion lens, SIL) was imaged without magnification into different samples (water, heterogeneous phantoms containing silica beads of various concentrations, and fresh mouse esophagus tissues) though a pair of matched aspheric lenses with a 25-mm focal length (NT49-660, Edmund Optics, Barrington, NJ). For Bessel illumination, an axicon with a 20-deg base angle (Thorlabs AX2520-A) was utilized instead of the second aspheric lens (L2) in the illumination path. The FWHM spot size (diameter) at the sample was 1.2 µm for the Gaussian beam waist and 1.0 µm for the main lobe of the Bessel beam [14]. The samples were placed on a SIL with a refractive index of n = 1.45, which provided index matching to allow the focused beams to enter into tissue-like samples with minimal aberrations. The use of a SIL also matched the design of dual-axis confocal (DAC) microscopes that have been previously developed by our group and others [19, 20]. A 100x microscope objective (Nikon, PN: 79235, NA = 0.9, WD = 1 mm) was utilized to image the beam foci onto a CCD camera (PointGrey, GRAS-14S5M-C with 6.45-µm pixel spacing). An alignment mirror was utilized to direct the beam foci to the same detector region for all measurements (i.e. the same group of CCD pixels). This was done to ensure a uniform detector response for all experiments. In order to fill the 8-bit dynamic range of the CCD for each experiment and to minimize the effects of detector background, we deliberately changed the laser power for each experimental condition. Experiments were performed in a dark room to eliminate the ambient background. In the absence of laser illumination, the dark background count from the CCD was less than 1 count out of 256. Therefore, no background subtraction was necessary.

Fig. 1.

The imaging system for quantifying both beam steering and distortion of Gaussian and Bessel beams focused in heterogeneous media. The beam focus (and CCD imaging plane) is positioned at the coverslip interface at the top (far end) of each sample. The distance between the coverslip and the SIL (solid immersion lens), h, was 250 µm.

2.2 Motion quantification

The motion of Gaussian and Bessel beam foci was quantified in MATLAB (Mathworks Inc, Natick, Massachusetts). Figure 3(a) illustrates the calculation of “beam motion”, which is defined as the standard deviation in the random “displacement” of n snap-shot images of a focused beam taken at different times. The “displacement” refers to the distance between the centroid of each image snap shot and the centroid of an unperturbed beam. The centroids were determined in MATLAB with the “weightedcentroid” measurement in the “regionprops” function. For example, A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) are the centroid coordinates of a focused beam imaged at different times. $M(\overline{x},\overline{y})$ represents the average centroid position (the unperturbed beam location) from n images of the same focused beam, in which n images is sufficient to capture the fully randomized motion of the beam (see Appendix for details). The distance between point $M(\overline{x},\overline{y})$ (the unperturbed beam location) and each individual centroid position (x_i, y_i) is calculated as:

Fig. 3.

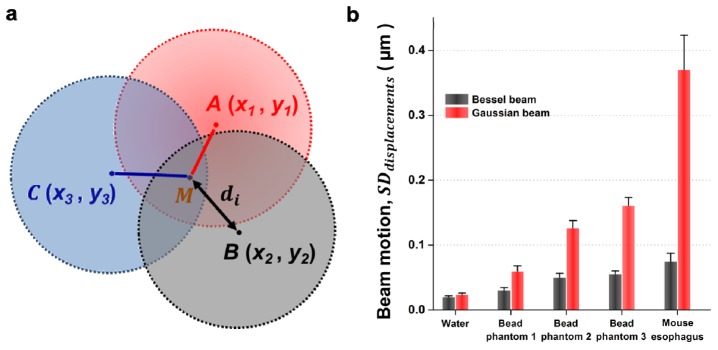
(a) A depiction of how “d_i” is calculated, where d_i is the displacement between the position of individual snap-shot images of beam foci (A,B,C,…) and the average position (unperturbed beam position), M. See Methods for additional details. (b) The standard deviation in the displacement of focused Gaussian and Bessel beams in water, bead phantoms and fresh mouse esophagus tissues. Each set of data contains 100 successive snap-shot images of a beam focus. Error bars represent the variability between five sets of data. Bead phantoms 1, 2, and 3 are at concentrations of 0.25 mg/mL, 0.50 mg/mL and 1.00 mg/mL, respectively.

$$d_i=\sqrt{{\left(x_i-\overline{x}\right)}^2+{\left(y_i-\overline{y}\right)}^2}$$ (1)

The standard deviation of the individual displacements for a set of n images is therefore calculated as:

$$S{D}_{displacements}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(di)}^2}}$$ (2)

2.3 Distortion quantification

We also quantified the distortion of the main lobe of the focused Gaussian and Bessel beams. In this study, “beam distortion” was defined as the standard deviation of a “distortion residual” between each snap-shot image of a beam with respect to an unperturbed beam profile, as described below:

• 1.
  For each individual image of a focused beam, a 2D Gaussian fit was performed utilizing a least-squares fitting algorithm. Here, we assumed an isotropic Gaussian beam since this fitting function was intended to model an ideal focused beam in the absence of heterogeneity-induced distortions. The fitting function was expressed as:

  $$f_i\left(x,y\right)=f_0{e}^{\left(-\left(\frac{{\left(x-{\mu }_x\right)}^2+{\left(y-{\mu }_y\right)}^2}{2{\sigma }_i^2}\right)\right)}$$ (3)

  The three fitting parameters in this function were: the centroid location of the focused beam, (µ_x, µ_y), and the isotropic beam width, σ_i.

• 2.
  For each set of n images, an average “best-fit” Gaussian surface, $\overline{f}\left(x,y\right)$, was used to approximate an unperturbed beam based on the average beam width, $\overline{\sigma }$:

  $$\overline{f}\left(x,y\right)=e^{\left(-\left(\frac{{\left(x-{\mu }_x\right)}^2+{\left(y-{\mu }_y\right)}^2}{2{\overline{\sigma }}^2}\right)\right)},\text{with}\overline{\sigma }=\frac{{\displaystyle \sum _{i=1}^n{\sigma }_i}}{n}$$ (4)
• 3.Each image (from a set of n individual images) was normalized by dividing the original pixel intensities by f₀ (determined from step 1) to form a new normalized image, $I_i\left(x,y\right)$. Since each image, $I_i\left(x,y\right)$, had a unique position (center coordinate) due to beam steering, we aligned each image such that the center coordinate of each image snapshot, $I_i\left(x,y\right)$, matched the center coordinate of the unperturbed beam, $\overline{f}\left(x,y\right)$, as depicted in Fig. 4(a).
• 4.By subtracting $\overline{f}\left(x,y\right)$ from $I_i\left(x,y\right)$, a two-dimensional matrix (R_i) was created to represent the absolute value of the difference (“residual”) between $I_i\left(x,y\right)$ and $\overline{f}\left(x,y\right)$ on a pixel-by-pixel basis.
• 5.A region of interest (ROI), defined by the full-width-at-10%-maximum irradiance of $f_i\left(x,y\right)$, was applied for both Gaussian and Bessel beams in order to focus our analysis on the main lobe itself and to reject beam distortions due to system noise and side-lobe aberrations. The distortion quantification was not strongly dependent on our choice of the threshold.
• 6.For each individual image, a “distortion residual” metric, r_i, was calculated by averaging all elements in matrix R_i within the ROI.
• 7.
  The standard deviation of the distortion residuals was calculated as:

  $$S{D}_{residuals}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(ri)}^2}}$$ (5)

Fig. 4.

(a) Contour plots (irradiance isolines) of an unperturbed beam focus (black), and one individual image (red) that is centered with respect to the unperturbed beam. See Methods for additional details. (b) The standard deviation in the “distortion residual,” r_i, which quantifies the beam distortion of focused Gaussian and Bessel beams in water, bead phantoms and fresh mouse esophagus tissues. Each set of data contains 100 successive snap-shot images of a beam focus. Error bars represent the variability between five sets of data.

2.4 Phantom preparation

Based on previous work [24], a polydisperse silica-bead mixture (MIN-U-SIL^®40, U.S. Silica, Berkeley Springs, WV) was suspended in water to produce a heterogeneous phantom for characterizing the beam steering and distortion of focused Gaussian and Bessel beams. This mixture contains silica beads over a distribution of sizes (a median diameter of 10.5 µm and a maximum bead diameter of 40 µm), which can simulate the size of different heterogeneities in tissues, such as subcellular organelles (<10 µm), cell bodies (10–50 µm) and microvasculature (>10 µm). We prepared phantom concentrations at 0.25 mg/mL, 0.50 mg/mL and 1.00 mg/mL to mimic biological samples with different densities of heterogeneities.

2.5 Mouse esophagus preparation

This study was performed in accordance with an animal use protocol approved by Institutional Animal Care and Use Committees (IACUC) at Stony Brook University. Small segments (~2-mm length) of full-thickness epithelium of the mouse esophagus (mucosa and submucosa, 50- to 100-µm thick [27, 28]), were obtained from a euthanized mouse and rinsed thoroughly with 1 × PBS. We utilized thin mouse esophagus tissues in order to minimize background due to tissue scattering (the typical scattering coefficient of esophagus tissues, μ_s, is 7 to 14 mm⁻¹ [29–31]). This ensured that speckle noise and background (due to scattering) did not overwhelm our ability to discern and quantify the main lobe of the beams. Tissues were dissected from mouse esophagi that were cut open. The lumenal surfaces of the mouse esophagus specimens were placed towards the incident beams. As shown in Fig. 1, these fresh tissues were flattened and adhered to the bottom of the coverslip by surface tension, such that we could image the foci of Gaussian and Bessel beams after the beams propagated through the tissue. The gap between the SIL surface and the coverslip was filled with saline buffer.

3. Results

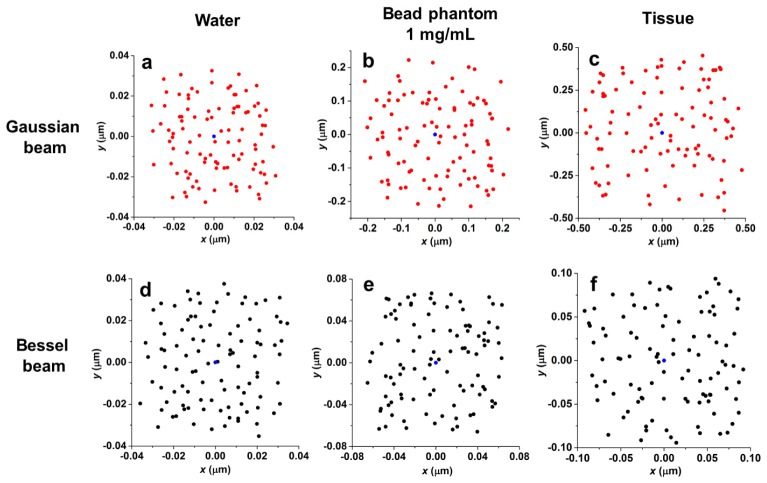
Representative images of Bessel or Gaussian beam foci are shown in Fig. 2 . The freshly isolated mouse esophagus tissues, which contain a large number of micro-architectural heterogeneities, created more severe beam distortion than the silica-bead phantoms. However, the Bessel beams exhibited less heterogeneity-induced distortions compared to the Gaussian beams in all cases.

Fig. 2.

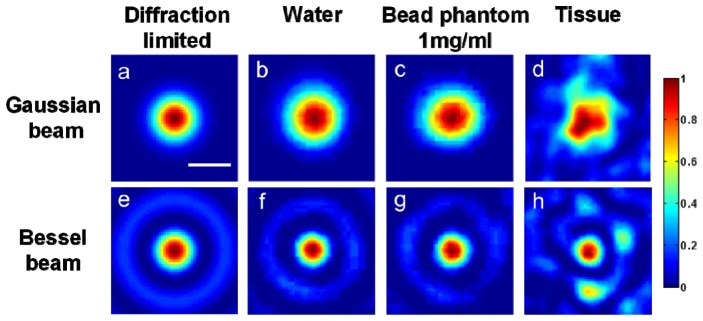
The normalized irradiance of focused Gaussian and Bessel beams. From left to right, the columns represent: (a,e) simulations of diffraction-limited beam foci, (b,f) beam foci imaged in water, (c,g) beam foci imaged in bead phantoms (1 mg/ml concentration), and (d,h) beam foci imaged in fresh mouse esophagus tissues. The scale bar measures 1 µm.

3.1 Quantification of beam motion

In this study, “beam motion” was defined as the standard deviation in the displacement of n = 100 snap-shot images of beam foci compared to the position of an unperturbed beam (see Section 2.2 and Appendix). The entire process of quantifying the beam motion of focused Gaussian and Bessel beams in different types of media was repeated five times to ensure statistical significance (calculated by a two-sample t-test, P < 0.01) and to demonstrate that our results were reproducible (indicated by the error bars in Fig. 3(b) ). Figure 3(b) displays the average beam displacement of focused Gaussian and Bessel beams in water, heterogeneous silica-bead phantoms at 0.25 mg/mL, 0.50 mg/mL and 1.00 mg/mL concentration, as well as fresh mouse esophagus tissues. When imaging beam foci within phantoms and fresh tissues, the motions of the Bessel beams were significantly reduced as compared to the Gaussian beams, indicating that Bessel beams are less sensitive to the heterogeneity-induced beam steering generated by these samples. The beam motions observed for water samples were due to mechanical vibrations from the environment.

3.2 Quantification of beam distortion

Snap-shot images were obtained of the foci of Gaussian or Bessel beams in various media (water, phantoms and tissues). A 2D “residual” matrix, R_i, was calculated to quantify the deviation in the shape of individual snap-shot images of focused beams compared to an unperturbed beam (see Section 2.3 and Appendix). Then, for each individual image, a “distortion residual” metric, r_i, was calculated by averaging all elements in matrix R_i within a region of interest (see section 2.3 for details). By computing the standard deviation of r_i for 100 snap-shot images, we could compare the beam distortion of focused Gaussian and Bessel beams in different types of media. As shown in Fig. 4(b) , focused Gaussian beams exhibited more distortion than focused Bessel beams. The beam distortions observed for water samples were due to aberrations and mechanical vibrations.

4. Discussion

This study focused on characterizing the “self-reconstructing” property of Bessel beams in heterogeneous media in comparison with conventional Gaussian beams. Previous studies have demonstrated that Bessel beams are capable of preserving the peak irradiance of their main lobe even in the presence of small obstructions [1, 4]. Here, we optimized our experiments to characterize two other parameters that are of particular importance for certain imaging applications: the positional stability and distortion of the main lobe of a Bessel beam, in comparison to a Gaussian beam, when propagating through heterogeneous media. In order to achieve this, we have developed an experimental method to accurately image the foci of low-NA beams in heterogeneous tissues, and have defined two metrics to quantify beam steering and beam distortion, respectively. By quantifying the beam steering and distortion of low-NA focused Gaussian and Bessel beams in different media, our results suggest that Bessel illumination is superior for maintaining the position and shape of a focused beam, which has implications for laser-scanning microscopy within highly scattering and inhomogeneous samples.

Our motivation for performing this study was the observation that DAC microscopy imaging performance is sensitive to positional changes and distortions at the foci of the low-NA illumination and collection beams utilized in the DAC configuration. In previous studies with tissue-like phantoms, our group and others have observed that heterogeneity-induced beam steering leads to a degradation in spatial resolution in DAC microscopy [24, 25]. Note that a single-axis illumination/collection architecture (e.g. optical coherence tomography and conventional confocal microscopy) is likely to be less sensitive to tissue heterogeneities due to the common path traversed by the incoming and outgoing ballistic photons. In the future, we plan to apply Bessel beams to enhance DAC microscopy in heterogeneous tissues and to explore various approaches to mitigate the out-of-focus background caused by the Bessel side lobes, and thereby to improve deep-tissue optical-sectioning performance.

5. Appendix

5.1 Optimization of imaging parameters

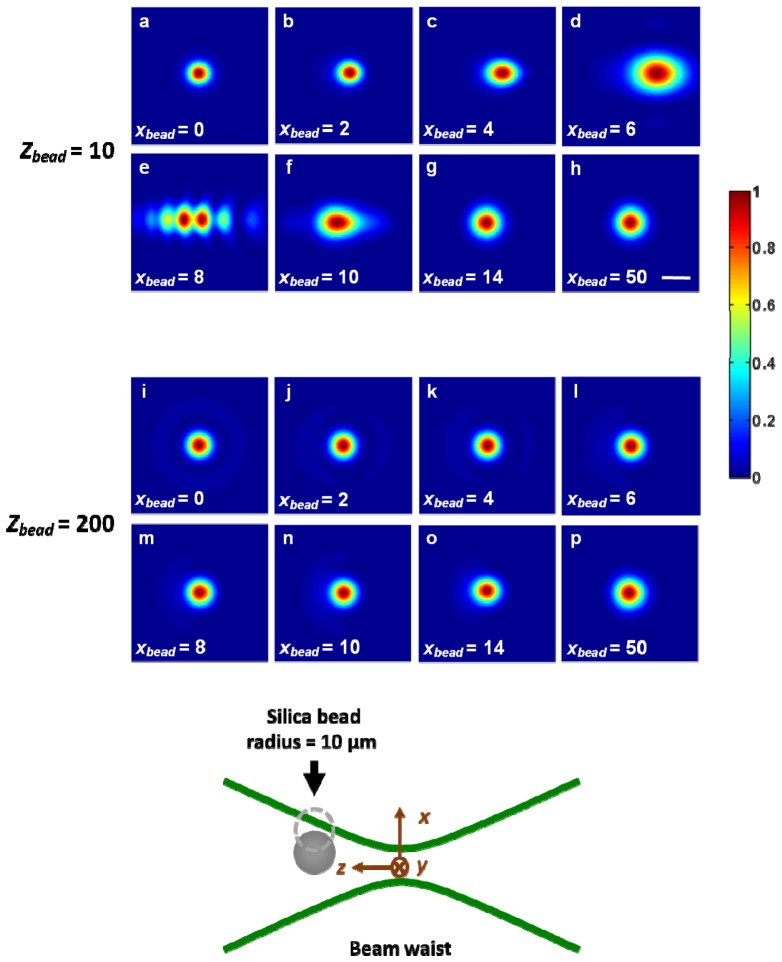
In order to provide a physical understanding of the beam-steering phenomenon, and to explain certain aspects of our experimental setup, we performed basic simulations using FRED ray-tracing software (Photon Engineering, Tucson, AZ). These simulations utilized the same Gaussian illumination conditions that were applied in our experiments and involved placing a single silica bead (10-µm radius) at various locations (x_bead = 0, 2, 4… 50 µm; z_bead = 10, 200 µm) near the focus (z = 0) of a diffraction-limited Gaussian beam (Fig. 5

Fig. 5.

Normalized lateral irradiance profiles at the focus (z = 0) of a Gaussian beam (diffraction-based simulations) when a single silica bead with a 10-µm radius was placed at various locations (x_bead = 0, 2, 4… 50 µm; z_bead = 10, 200 µm) near the focus of the beam. Significant beam steering and distortion of the Gaussian beam focus was observed when the bead was positioned near the focus (z_bead = 10 µm); however, negligible beam steering and distortion were observed when the bead was positioned further from the focus (z_bead = 200 µm). The scale bar measures 1 µm.

). As shown in Fig. 5, the magnitude of beam steering and distortion is maximized when the beads are positioned near the focus of the beam: z_bead = 10 instead of z_bead = 200 µm. Therefore, we took care in our experiments to image and quantify beam motions and distortions due to heterogeneities near the beam focus – this was achieved by positioning the focus (as well as CCD imaging plane) at the coverslip interface at the top (far end) of each sample, as shown in the inset of Fig. 1. If the beam focus was located beyond the sample (within or above the coverslip), the measured motion and distortion of the focus was significantly reduced due to a lack of heterogeneities near the focus. If, on the other hand, the beam focus was located deep within the sample (well below the coverslip interface), then the CCD would not be able to accurately image the beam focus due to light scattering (in tissues) between the focus and the camera.

Another experimental detail of critical importance was the choice of a proper integration time for the CCD camera. Due to the time scale of the random motions within the experimental phantoms and tissue samples, long integration times would cause beam distortion and motions to average away, whereas short integration times would require us to acquire an extremely large number of images in order to determine a best-fit shape or an average position of successive beam foci. By plotting the relationship between beam motion and CCD integration time (from 0.1 ms to 1 s), it was found that an integration time of < 1 ms was required to avoid averaging out the motion of the beams in our phantoms (Fig. 6

Fig. 6.

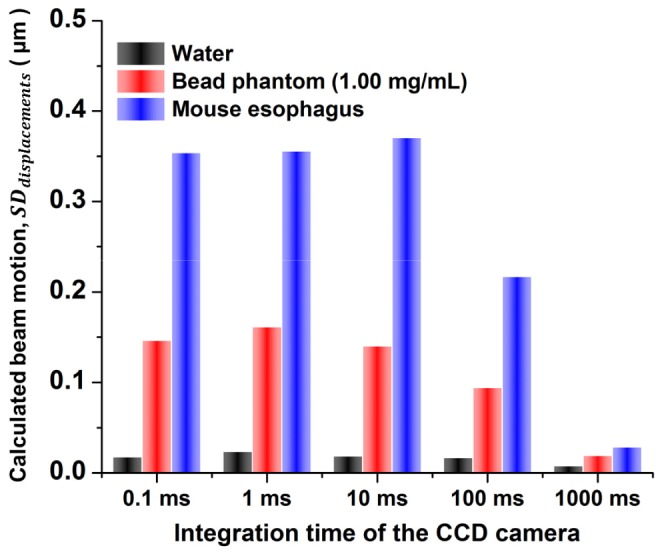
The relationship between beam motion and CCD integration time (from 0.1 ms to 1 s). The calculated beam motion of focused Gaussian beams in different media is constant when short CCD integration times are used to “freeze” the motion during each image “snapshot.” At longer integration times, the beam motion is averaged out during each image snapshot, resulting in erroneous (under-estimated) beam-motion calculations.

). However, a longer integration time (10 ms) could be applied for measurements in tissues due to an increased decorrelation time that is consistent with previous reports on the decorrelation time of focused light in fresh tissues [32, 33]. Since Bessel beams exhibited less beam motion compared to Gaussian beams, we only characterized the relationship between integration time and beam motion for focused Gaussian beams (Fig. 6) and utilized the same integration time for both Gaussian and Bessel beams.

We also determined the total imaging duration required to capture the full extent of the beam motion (Fig. 7

Fig. 7.

The total imaging duration required to capture the full extent of the beam motion in various media. Panels (a)-(f) demonstrate that the calculated beam motions of focused Gaussian and Bessel beams in different media are only accurate when the imaging duration is sufficiently long to randomize the motions of the beam foci (see Fig. 8). At short imaging durations, the motions are not randomized enough to provide an accurate quantification of beam steering, thus under-estimating the motion.

). Results show that the beam motion for both focused Gaussian and Bessel beams in water and bead phantoms was maximized (fully randomized) when the imaging duration reached 50 ms or longer (50 or more successive images acquired at a 1-ms integration time). Therefore, we applied an imaging duration of 100 ms or longer (n = 100 images acquired at a 1-ms integration time) to evaluate the full extent of beam steering and distortion in water and phantoms. According to Fig. 6 and Fig. 7, a longer imaging duration of 1 sec (n = 100 images acquired at a 10-ms integration time) was required to image the fully randomized motions of focused Gaussian and Bessel beams in fresh tissues.

Figure 8

Fig. 8.

The centroid distributions from 100 images of a focused beam in different media. Panels (a)-(f) illustrate how the motions of a focused beam are randomized in all directions when the imaging duration is sufficiently long (see Figs. 6 and 7). For water and phantoms, the imaging duration is 100 ms (100 images acquired at a 1-ms integration time); for tissues, the imaging duration is 1 sec (100 images acquired at a 10-ms integration time). Blue dots represent the positions of the unperturbed beam in different types of media.

shows that the acquisition of images (n = 100) was sufficient to completely randomize the motions of a focused Gaussian beam in all directions.

5.2 Modulation transfer functions (MTF)

MTFs were calculated at the beam focus of the Gaussian and Bessel beams used in this study. Because of the symmetry of Gaussian and Bessel beams, their spatial frequency in both transverse directions (x and y) are identical. As shown in Fig. 9

Fig. 9.

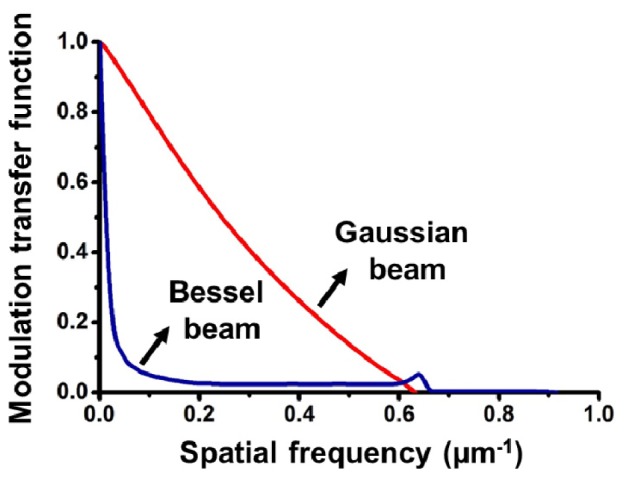
Modulation transfer functions of the Bessel beam and focused Gaussian beam that were used in these experiments. The Gaussian MTF were calculated at the focus.

, the Gaussian beam exhibits superior contrast compared to the Bessel beam at the focal plane. This is because the side lobes of a Bessel beam contribute out-of-focus background that reduces image contrast. As a result, we limited our characterization of Bessel beams to their main lobes alone, and utilized a Bessel beam with a main lobe diameter (FWHM) that matched the FWHM beam-waist diameter of the focused Gaussian beam used in this study. This was done because the spatial resolution of DAC microscopes is directly related to this parameter [20, 21].