A non-canonical secondary structure stabilizes mitochondrial tRNA^Ser(UCN) by reducing the entropic cost of tertiary folding

Abstract

Mammalian mitochondrial tRNA^Ser(UCN) (mt-tRNA^Ser) and pyrrolysine tRNA (tRNA^Pyl) fold to near-canonical three-dimensional structures despite having non-canonical secondary structures with shortened interhelical loops that disrupt the conserved tRNA tertiary interaction network. How these non-canonical tRNAs compensate for their loss of tertiary interactions remains unclear. Furthermore, in human mt-tRNA^Ser, lengthening the variable-loop by the 7472insC mutation reduces mt-tRNA^Ser concentration in vivo through poorly understood mechanisms, and is strongly associated with diseases such as deafness and epilepsy. Using simulations of the TOPRNA coarse-grained model, we show that increased topological constraints encoded by the unique secondary structure of wild-type mt-tRNA^Ser decrease the entropic cost of folding by ~2.5 kcal/mol compared to canonical tRNA, offsetting its loss of tertiary interactions. Further simulations show that the pathogenic 7472insC mutation disrupts topological constraints and hence destabilizes the mutant mt-tRNA^Ser by ~0.6 kcal/mol relative to wild-type. UV melting experiments confirm that insertion mutations lower mt-tRNA^Ser melting temperature by 6–9°C and increase the folding free energy by 0.8–1.7 kcal/mol in a largely sequence- and salt-independent manner, in quantitative agreement with our simulation predictions. Our results show that topological constraints provide a quantitative framework for describing key aspects of RNA folding behavior and also provide the first evidence of a pathogenic mutation that is due to disruption of topological constraints.

INTRODUCTION

Mammalian mitochondrial tRNAs (mt-tRNAs), along with the mitochondrial ribosome, are responsible for translating thirteen proteins encoded by the mitochondrial DNA that are central to oxidative phosphorylation.⁴ In order to fulfill this essential biological role, mt-tRNAs must fold to the well known L-shaped tRNA 3D structure, and mutations to mt-tRNA genes that disrupt folding have been implicated in a growing number of human diseases.⁴

Compared to canonical cytosolic tRNAs (cc-tRNAs), mt-tRNA folding thermodynamics remains poorly understood. Many mt-tRNAs possess “bizarre” secondary structures that deviate significantly from the canonical tRNA cloverleaf, characterized by shortened interhelical linkers and apical loops, lengthened helices, and sometimes lacking entire helical domains.^5,6 Furthermore, mt-tRNAs frequently lack otherwise universally conserved tertiary interactions important for stabilizing the tRNA 3D fold.^5,6 Understanding how mt-RNAs fold to near-canonical 3D structures despite their non-canonical morphologies has the potential to provide broader insights into the design principles of RNA tertiary folding.

Recent studies of canonical tRNA by our groups led us to hypothesize that the non-canonical secondary structures of mt-tRNAs may be central to their tertiary structure stability.⁷ Due to the hierarchical nature of the RNA free energy landscape, tertiary structure folding generally proceeds from a state that consists of prefolded secondary structure helices.^8,9 Using simulations of cc-tRNAs, we showed that so-called topological constraints posed by the connectivity and sterics of prefolded secondary structure impose large free energy costs on adopting different 3D conformations, contributing to the specificity, stability, and cooperativity of cc-tRNA tertiary folding.⁷ Furthermore, evolutionary conservation of cc-tRNA secondary structure was correlated with conservation of topological constraints. Due to their uniquely shortened interhelical linkers, mt-tRNAs should experience significantly greater topological constraints than cc-tRNA. This additional constraining of the unfolded conformational space may in turn reduce the entropic penalty of 3D folding, potentially explaining how mt-tRNAs fold despite possessing fewer tertiary interactions.

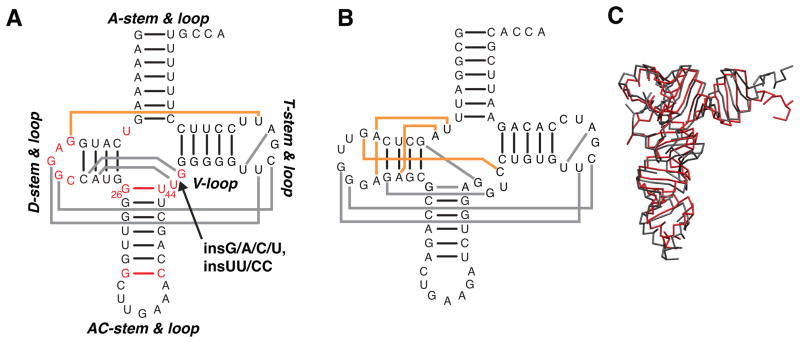
A good system for exploring this hypothesis is human mt-tRNA^Ser(UCN) (hereafter referred to as mt-tRNA^Ser),^3,10 which has an identical secondary structure and similar sequence as the rare cytosolic pyrolysine tRNA (tRNA^Pyl) species.^11,12 In mt-tRNA^Ser, the A/D-loop is only one nucleotide (nt) long, compared to 2-nts in all other tRNA species (Figure 1A, B).^13,14 The non-canonical base pair atop the AC-stem is also typically replaced with a canonical base pair, and the V-loop is shortened from five to three nucleotides.^5,12,13 This unique secondary structure precludes formation of several normally critical tertiary pairs (Figure 1A, B). Nevertheless, while less stable than cc-tRNAs, mammalian mt-tRNA^Ser and archaeal tRNA^Pyl transcripts fold to near canonical 3D structures (Figure 1C).^11,15–17

Figure 1.

(A) Secondary structure of human mt-tRNA^Ser(UCN) and the location of the insertion mutations. Secondary structure features that differ from cc-tRNA are indicated by red. Gray and orange lines indicate tertiary interactions inferred from the tRNA^Pyl crystal structure.¹⁵ Tertiary interactions shared by cc-tRNA are shown in gray, and novel interactions are shown in orange. (B) Secondary structure of yeast tRNA^Phe (cc-tRNA). Conserved tertiary interactions missing in mt-tRNA^Ser are shown in orange. (C) Superposition of TOPRNA representations of the cc-tRNA²² (gray) and tRNA^Pyl; ¹⁵ (red) crystal structures.

Intriguingly, a mutation expected to disrupt the topological constraints of mt-tRNA^Ser is also pathogenic in humans (Figure 1A). The 7472insC mutation, hereafter referred to as the insG mutation, lengthens the polyG tract that terminates in the V-loop of human mt-tRNA^Ser (Figure 1A), and has been strongly implicated as a cause of deafness, progressive encephalomyopathy, and MERFF (myoclonic epilepsy with ragged red fibers).^10,18–20 Consistent with pathogenesis arising from destabilized tertiary structure, the insG mutation does not alter the folded structure but impairs transcript processing and decreases the concentration of mature mt-tRNA^Ser by 65%.^1,3,21 One proposal is that the inserted G is accommodated into the T-loop, destabilizing the tertiary pairs formed with the D-loop.¹⁸ However, the T-loop is highly conserved and disrupting its local structure may be expected to cause a more severe phenotype.^5,14 Alternatively, the inserted G could be accommodated into the V-loop. This would give the V-loop a similar length to that found in cc-tRNA but would increase the topologically available conformational space relative to wild-type (WT) mt-tRNA^Ser.

In this study we explore the role of topological constraints in mt-tRNA^Ser folding using simulations of the specialized TOPRNA coarse-grained model.²³ TOPRNA specifically isolates the effects of topological constraints on the RNA free energy landscape by treating base-paired regions as permanent A-form helices, single-stranded nucleotides as freely rotatable chains, and ignores both electrostatic and attractive interactions. Consistent with our hypothesis, our simulations indicate that secondary structure plays a critical role in reducing the entropic cost of WT mt-tRNA^Ser folding, and that the pathogenic insG mutation destabilizes mt-tRNA^Ser by increasing the size of the accessible unfolded conformational space. These results provide the first example of a topological-constraint-based disease mechanism and suggest that topological constraints are a key design principle of RNA tertiary folding.

RESULTS

Topological constraints stabilize WT mt-tRNA^Ser(UCN)

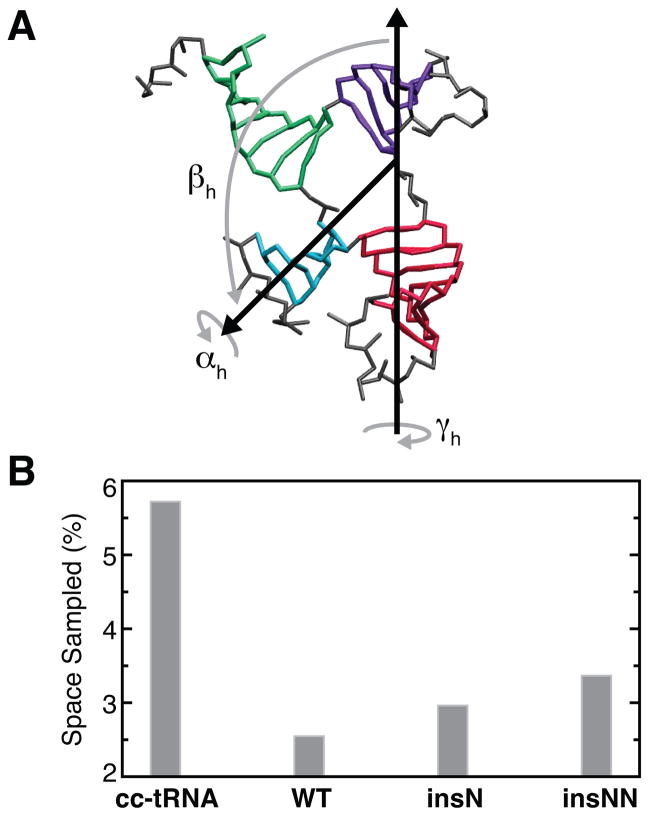
To determine whether increased topological constraints from the non-canonical secondary structure of WT mt-tRNA^Ser help stabilize tertiary structure, we performed extensive temperature replica exchange simulations of mt-tRNA^Ser using an updated version of the TOPRNA²³ coarse-grained model (Supplementary Information, Figure S1). We quantified whether mt-tRNA^Ser is more topologically constrained than cc-tRNA by counting the number of unique global conformations sampled by the simulations, using Euler angles, (α_h, β_h, γ_h), to measure the relative orientation of two helices, where α_h and γ_h describe the helical twists and β_h the interhelical bend (Figure 2A).^24,25 Three sets of Euler angles measured between the A-, D-, and T-stems relative to the AC-stem in turn provide a nine-dimensional description of global tRNA 3D conformation that can be discretized onto a finite grid.⁷ Consistent with our expectations, the shorter A/D- and V-loops of mt-tRNA^Ser reduce the number of interhelical conformations sampled by mt-tRNA^Ser by two-fold relative to cc-tRNA (2.5% vs. 5.7%; Figure 2B). We previously showed that one of the primary mechanisms through which topological constraints restrict cc-tRNA conformation is by coupling the orientation of all four tRNA helices together, giving rise to long-range correlated motions that contribute to folding cooperativity.⁷ Consistent with this explanation, we find that helices in mt-tRNA^Ser are 10–90% more correlated than in cc-tRNA (Figure S2).

Figure 2.

(A) Representative snapshot from a TOPRNA simulation of mt-tRNA^Ser illustrating the Euler angle representation of the conformation between the AC-stem (red) and D-stem (blue). Loops, which are treated as freely rotatable chains by TOPRNA, are colored gray. (B) The fraction of theoretically possible interhelical (α_h, β_h, γ_h) conformations sampled by TOPRNA simulations.

To quantify the extent to which the increased topological restriction of WT mt-tRNA^Ser biases the molecule towards native-like conformations, we computed the probability P_nat of mt-tRNA^Ser and cc-tRNA sampling native-like 3D conformations in our simulations, which we directly ascribe to the topological constraint contribution to the free energy of folding through

$$\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}=-\mathit{RT}ln\left(\frac{P_{\mathit{nat}}}{1-P_{\mathit{nat}}}\right).$$ [1]

As TOPRNA lacks attractive interactions, our simulations spend the majority of their time sampling extended conformations and P_nat is exceedingly small; depending on the metric used to define native-like structure, P_nat ranged from 10⁻² to 10⁻⁵. $\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ is hence large and positive for both molecules, reflecting the entropic penalty of folding that must be offset by favorable tertiary interactions. Strikingly, however, we find that the $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ (T = 300 K) between cc-tRNA and mt-tRNA^Ser is 1.5–2.5±0.1 kcal/mol (Figure 3, S3; see discussion below), indicating that topological constraints can stabilize mt-tRNA^Ser by as much as this amount. Notably, this is comparable to the favorable free energy provided by one to two base pairs,²⁶ and strongly supporting that topological constraints provide compensation for the decreased number of tertiary interactions in mt-tRNA^Ser.

Figure 3.

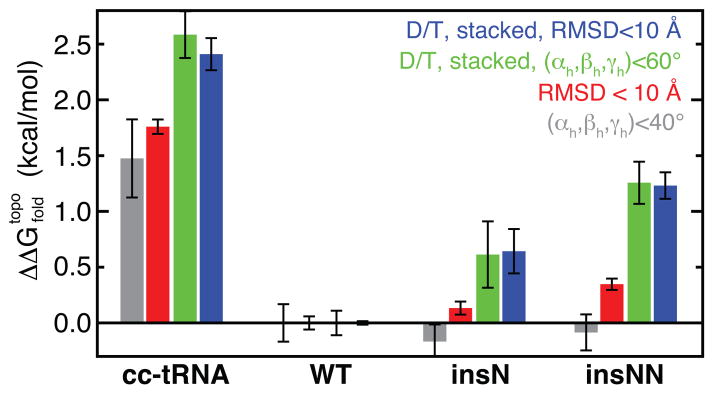
Differences in the topological constraint contribution to the folding free energy ΔΔG_{fold, topo} = ΔG_{fold, topo}(i) - ΔG_{fold, topo}(WT). Values and error bars represent the mean and standard deviation of the ΔΔG computed by block averaging over thirds of the simulations.

In theory, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ between mt-tRNA^Ser and cc-tRNA should be independent of the metric used to compute P_nat. Specifically, while P_nat itself will vary with the definition of native structure, it should vary proportionally for both tRNAs. Interestingly, however, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ varies significantly based on the native metric. To measure global structure, we required tRNA conformations to have <10 Å RMSD from their respective crystal structure. Alternatively, we required all interhelical (α_h, β_h, γ_h) angles to be within 40° of their crystal structure values. Both of these global definitions yielded $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ estimates of 1.5–1.7 kcal/mol (Figure 3). By contrast, when P_nat was recomputed also requiring that the tRNAs possess contacts between the D- and T-loops and both of the native interhelical stacks, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ increased to ~2.5 kcal/mol (Figure 3). This suggests that topological constraints stabilize mt-tRNA^Ser by two mechanisms. First, as captured by global metrics alone, the cost of forming near-native interhelical orientations is reduced relative cc-tRNA. Second, the shorter connecting loops of mt-tRNA^Ser further restrict the translational freedom of the helices, reducing the entropic cost of forming D and T-loop and stacking contacts (Figure S3).

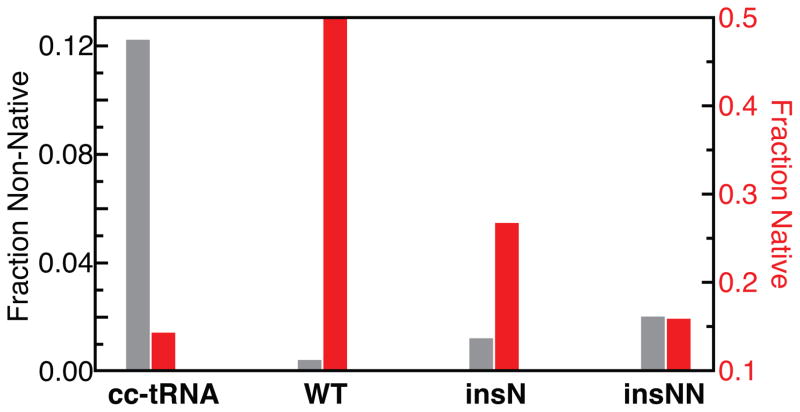
The above analysis reports on the free energy cost of each tRNA forming the native structure. Another important aspect of the energy landscape is whether or not the tRNAs can form competing tertiary folds, or in other words, the specificity of the folding landscape. We previously found that topological constraints prevent cc-tRNA from forming non-native tertiary folds,⁷ and thus we assessed whether topological constraints also increase mt-tRNA^Ser folding specificity. As before,⁷ we identified the 500 conformers sampled by TOPRNA that have the best inter-loop packing (and thus potential to form putative tertiary interactions). Notably, only 0.4% of mt-tRNA^Ser compared to ~12% of cc-tRNA best-packed conformers possess non-native contacts (Figure 4). The degree to which individual conformers are close in structure to other best-packed conformers also provides a measure of their relative conformational entropy.²⁷ Compared to cc-tRNA, near-native 3D conformations of mt-tRNA^Ser have significantly higher entropies (Figure S4), which is summarized in Figure 4 as the entropy-weighted fraction of best-packed conformers that possess D-to-T-loop contacts and both interhelical stacks. Thus, mt-tRNA^Ser topological constraints both lower the cost of forming native interactions ( $\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$) and increase the energy gap between native and non-native folds.²⁸

Figure 4.

Fraction of the 500 best-packed conformations of each tRNA that have non-native loop-loop contacts (gray), or that have D-to-T-loop contacts and both interhelical stacks (red). The fraction of conformers with both native contacts is weighted by entropy. Note that the third conformational possibility – lacks stacking or D-T-loop contacts – is not shown.

The mt-tRNA^Ser simulation analyzed above treated the G26-U44 base pair as a permanent feature of secondary structure (Figure 1A). This pair is conserved as either a GU or AU pair in humans,²⁹ and as canonical pair in the majority of mt-tRNA^Ser and tRNA^Pyl species. However, A⁺C, AA, or GA pairs at this position are also observed in other species.^5,12,13 To determine the contribution of intact G26-U44 pairing to our observations we performed an additional TOPRNA simulation of mt-tRNA^Ser where these residues were treated as single strands (mt-tRNA^Ser_noBP). Compared to when G26-U44 is paired, the mt-tRNA^Ser_noBP simulation samples ~50% more interhelical conformations, $\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ is increased by ~1 kcal/mol, and folding specificity is reduced ~5% (Figure S5). This decrease in stability provides a feasible explanation for the evolutionary preference for WC/GU pairs between residues 26 and 44; for species without canonical pairing, other sequence changes in the D- and T-loops may serve to strengthen the tertiary interaction network. Significantly, however, $\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ in mt-tRNA^Ser_noBP is still ~1.5 kcal/mol more favorable than in cc-tRNA.

The insG mutation destabilizes mt-tRNA^Ser by disrupting its topological constraints

We next explored whether the insG mutation disrupts the ability of topological constraints to stabilize mt-tRNA^Ser, thereby potentially explaining its pathogenicity (Figure 1A). Consistent with our hypothesis, a TOPRNA simulation of mt-tRNA^Ser with an insN mutation in the V-loop samples ~16% more interhelical conformations than the WT simulation (Figure 2B). (We use the insN notation to denote that our simulations are independent of inserted nucleotide identity). Likewise, the interhelical correlations of the insN mutant are decreased ~1–20% compared to WT (Figure S2).

Significantly, this reduction in topological constraints is accompanied by a ~0.6 kcal/mol increase in the $\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ of the insN mutant compared to WT, and a 50% decrease in folding specificity (Figure 3, 4, S3, S4). This is a consequential destabilization of mt-tRNA^Ser given its expected instability.¹⁶ Near the melting temperature, a 0.6 kcal/mol increase in folding energy should decrease the folded population by ~40%, in reasonable qualitative agreement with the 65% decrease in insG mutant concentration observed in cells.²¹ An analogous insA mutation in the related tRNA^Pyl reduces its translational activity by a similar amount (83%),³⁰ consistent with the insN mutation being destabilizing in a sequence independent manner. This destabilization arises from an increased cost of forming tertiary contacts, as near-native global 3D conformations are formed with similar energies (Figure 3). Consistent with the insN mutant’s decreased interhelical correlations (Figure S2), ~0.2 kcal/mol of this increase is due to a loss of cooperativity among interhelical stacking and D-to-T-loop contacts (Figure S3). Thus, in part due to decoupling of the helices, greater conformational freedom near the native-state increases the entropic cost of forming tertiary interactions in the mutant. Simulations of the insN mutant without a G26-U44 base pair also demonstrated similar decreases in topological confinement, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ between mutant and WT, and folding specificity (Figure S5).

To further establish the trend between topological constraints and folding, we also performed simulations of an insNN V-loop mutant of mt-tRNA^Ser (Figure 1A). As expected, these simulations indicated that the insNN mutant has the effect of further decreasing topological confinement and folding specificity, and increasing the free energy cost of folding (Figures 2–4, S2–S4). Similar results were also observed for an insNN simulation performed without a G26-U44 base pair (Figure S5).

Melting experiments reveal destabilization of insertion mutants in quantitative agreement with TOPRNA predictions

Our simulations make several strong predictions regarding mt-tRNA^Ser stability: (i) Single and double insertions in the V-loop should destabilize tertiary structure by ~0.6 kcal/mol and ~1.2 kcal/mol at 300 K, respectively. (ii) This destabilization should be independent of the inserted nucleotide(s) identity, assuming that, like the insG mutation,³ the insertions do not cause secondary structure misfolding. (iii) This destabilization should be attributable to an increase in the entropic cost of folding for the mutants. Notably, from this last prediction we can estimate the expected decrease in melting temperature (T_m) of the mutants. As detailed in Supporting Information, isolated changes in the entropy of the unfolded state will cause, to a first-order approximation, proportional changes in T_m through

$$T_m^{WT}\mathrm{\Delta }{S}_{\mathit{fold},3\mathit{Dconf}}^{WT}\approx T_m^{\mathit{mut}}\mathrm{\Delta }{S}_{\mathit{fold},3\mathit{Dconf}}^{\mathit{mut}}.$$ [2]

Estimating the change in 3D conformational entropy upon folding, ΔS_{fold, 3Dconf}, from our simulations, and setting T_m^WT=45° C, we predict that the T_m of the insN and insNN mutants should be decreased by 8° C and 15° C, respectively (Figure S6).

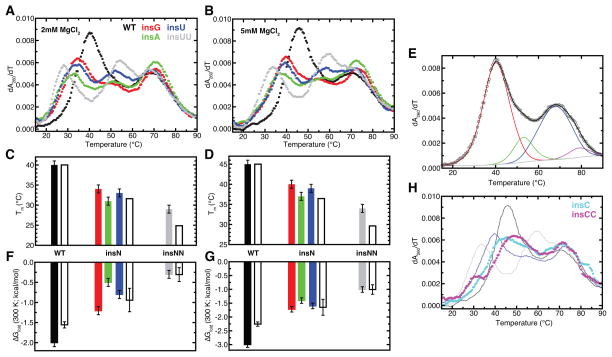
To test these predictions, we used in vitro transcription to prepare WT, insG, insC, insU, insA, insCC, and insUU human mt-tRNA^Ser constructs and characterized their folding stabilities by UV melting experiments. Experiments were done at both near-physiological (2 mM MgCl₂; 150 mM NaCl) and “stabilizing” (5 mM MgCl₂; 150 mM NaCl) solution conditions. At both conditions, the WT tRNA^Ser exhibits a pronounced cooperative melting transition at 40 or 45°C followed by multiple broad transitions at higher temperatures (Figure 5A, B). The increase in melting temperature to 45°C at higher MgCl₂ concentration is consistent with the expected stabilizing effects of MgCl₂, and both the shape and T_m of these transitions are in good agreement with prior UV melting studies of bovine mt-tRNA^Ser(UCN) transcripts.¹⁶ NMR melting studies of the bovine transcript further demonstrated that the first transition corresponds to tertiary structure melting coupled with some loss of D-stem and T-stem structure.¹⁶ We thus also assign the low T_m=40 or 45°C to tertiary structure melting and the higher temperature transitions to unfolding of the remaining secondary structure stems.

Figure 5.

(A, B) Derivative of absorbance at 260 nm of mt-tRNA^Ser species in the presence of 2 mM MgCl₂ (A, C, F) or 5 mM MgCl₂ (B, D, G). All melts were performed in a background of 20 mM sodium cacodylate (pH 7.2) and 150 mM NaCl. Curves of different molecules are colored according to the key in (A). (C, D) Tertiary structure melting temperatures determined from van’t Hoff fits to melting curves. Error bars represent estimated 1 °C error (see methods). Bars are colored by mutant according to (A). TOPRNA predicted values, in reference to the WT T_m, are shown with open bars and represent the mean of the different ΔT_m estimates in Figure S6. (E) Example van’t Hoff fit to the WT transcript at 2 mM MgCl₂. The different transitions are shown in color, the baseline in gray, and the overall fit in black. (F, G) ΔG_fold determined from van’t Hoff fits extrapolated to 300 K. Color scheme is the same as in (C, D). TOPRNA predictions are referenced to the insUU ΔG_fold. (H) Melting curves of insC and insCC mutants at 5 mM MgCl₂. WT, insG, and insUU melting curves are shown by lines colored according to the key in (A) for reference.

The insG, insA, and insU mutants exhibit similar melting curves at both MgCl₂ concentrations, yet the T_m of the first transition is decreased by 6–9(±1)°C compared to WT, and decreased by 11±1°C in the insUU mutant (Figure 5A, B). Strikingly, these observed decreases closely match the 8°C and 15° C ΔT_m predictions of our simulations (Figure 5C, D); we consider differences of a few degrees to be within the expected accuracy of our approximated ΔT_m predictions. While we cannot unequivocally assign the first transition in the mutants to tertiary structure melting, several observations beyond the gross similarities of the melting curves support the assumption that the mutants adopt a native-like tertiary fold. First, prior enzymatic probing studies found no structural differences between mature WT and insG mt-tRNA^Ser purified from cells.³ insG pre-tRNA transcripts are also processed by nuclear RNase P and mitochondrial tRNAse Z under solution conditions highly comparable to those used here,¹ indicative of the formation of native structure. Finally, the observed sensitivity of T_m to Mg²⁺ concentration³¹ and the incremental decrease in T_m between the insU and insUU mutants argues against the first transition only representing secondary structure unfolding. Combined, these data support the proposal that changes in topological constraints are responsible for destabilizing the tertiary structure of the mutant transcripts.

Interestingly, the insG/A/U and insUU mutants also melt less cooperatively than the WT transcript (reflected by lower maximum derivatives and greater transition widths in Figure 5A, B), suggesting that the unfolding enthalpies are different. Indeed, van’t Hoff analysis confirms that the unfolding enthalpy is typically lower in the mutants (see below; Tables S1, S2). While this decrease is qualitatively consistent with our prediction that tertiary structure should fold less cooperatively in the mutants (Figure S3), it is more likely that the decrease reflects differential hydration and ion interactions with the folded state, and/or differences in base stacking cooperativity. Note that because of potential entropy-enthalpy compensation effects, this does not necessarily contradict that an increased entropic cost of folding is primarily responsible for decreased stability of the mutants.

We further used a van’t Hoff analysis to extract thermodynamic parameters of the first melting transition for the WT, insA, insU, insG, and insUU constructs.³² Each melting curve was globally fit using a four-state sequential unfolding model (Figure 5E). While fitting generally yielded multiple solutions, all curves shared a “parsimonious” fit that gave similar thermodynamic parameters for each of the four unfolding transitions (Figure 5E; Table S1, S2). As alternative fits varied between melting curves, or were inconsistent with NMR data collected on the bovine mt-tRNA^Ser transcript,¹⁶ we restricted our analysis to the parsimonious fit (Supporting Information). Depending on the mt-tRNA and MgCl₂ concentration, the unfolding enthalpy of the first transition varied between 40±5 and 54±3 kcal/mol (Table S1, S2), consistent with melting of tertiary structure and some D-stem base pairs.¹⁶ Notably, when used to derive ΔG_fold,vH(300 K), the van’t Hoff analysis indicates that the insG/A/U mutants are destabilized by 0.8–1.7(±0.1) kcal/mol relative to WT, and the insUU mutant by 1.7–2.0(±0.1) kcal/mol (Figure 5F, G). Again, these values are remarkably close to our TOPRNA predictions of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ kcal/mol and 1.2±0.1 kcal/mol, respectively. The ΔΔG_fold,vH=0.6 kcal/mol between the insN and insUU mutants exactly matches our prediction. Disruptions of Mg²⁺ interactions or tertiary structure hydrogen bonding caused by the insN mutations, which are not included in our TOPRNA model, can explain the variable and larger than predicted ΔΔG_fold,vH between the WT and insN mutants.

By contrast, the insC and insCC mutants lack a well-defined tertiary structure melting transition (Figure 5H). Both mutants appear to exhibit small shoulders near the predicted T_m’s of the insN and insNN mutants, but these shoulders were poorly fit by a van’t Hoff analysis (not shown). We propose this different melting behavior is due to secondary structure misfolding, perhaps involving mispairing between the inserted C and the complementary Gs atop the AC-stem (Figure 1A).

DISCUSSION

How mt-tRNA^Ser(UCN) and tRNA^Pyl stably to fold to near-canonical 3D structures despite their non-canonical architectures has long been poorly understood. Our results indicate that these tRNAs employ a novel mechanism where the entropic cost of folding is reduced by a more constrained secondary structure, thereby compensating for a fewer number of tertiary interactions. In particular, our simulations predict that increased topological constraints stabilize the WT mt-tRNA^Ser 3D structure by as much as −2.5 kcal/mol and also substantially increase folding specificity compared to cc-tRNA. In the insA, insU, and insG mutants, lengthening the V-loop by a single nucleotide destabilizes mt-tRNA^Ser by 0.8–1.7 kcal/mol, leading to a 6–9° C decrease in melting temperature. A two nt insertion destabilizes the insUU mutant by 1.7–2.0 kcal/mol and decreases T_m by 11° C. The agreement between these experimentally measured values and those predicted by our simulations, as well as the sequence and salt independence of the mutant destabilization, provide strong evidence that topological constraints are indeed responsible for these changes.

Importantly, our results provide a potential explanation for why the insG mutation is pathogenic. Prior studies found that mt-tRNA^Ser concentration is decreased 65% in mitochondria when all mt-DNA plasmids contain the insG mutation, which presumably disrupts mitochondrial protein synthesis and hence cellular respiration.²¹ This decrease is primarily due to fast degradation of misprocessed and/or unprocessed transcripts.^1,3 However, why the mutant was specifically degraded was unclear. Our data show that WT mt-tRNA^Ser transcripts are only marginally stable, such that the destabilized insG mutant is primarily unfolded at physiological temperatures (T_m<37° C at near-physiological MgCl₂ concentrations). We propose that this shift in folding equilibrium results in increased flux through degradative pathways that compete with maturation (Figure 6). Notably, the 65% decrease of mature insG mt-tRNA^Ser in cells²¹ is similar to the ~50% decrease in folding equilibrium expected from a 0.8 kcal/mol higher folding free energy. For the mutant transcripts that enter the maturation pathway, nucleotide modifications likely help stabilize the tertiary structure, explaining the similar cellular half-life of mature insG and WT mt-tRNA^Ser.³ Interestingly, recent studies have shown that unstable cytosolic tRNAs are rapidly degraded by a rapid tRNA decay (RTD) surveillance pathway.² We speculate that a similar RTD pathway may exist in mitochondria. Although mt-tRNA^Ser lacks consecutive 5’-Gs shown to be important for cytosolic RTD, it possesses the requisite unstable acceptor stem.² In support of an RTD mechanism, destabilizing mutations to the mt-tRNA^Ser acceptor stem cause similar decreases in mitochondrial concentration and pathogenic phenotypes.^33,34 Finally, we note that the appearance of insG and not insA/U/C mutations in the human population does not necessarily indicate that the former is more tolerable; insG mutations are naturally expected at a much higher frequency due to the adjacent G-tract in the T-stem.^18,35

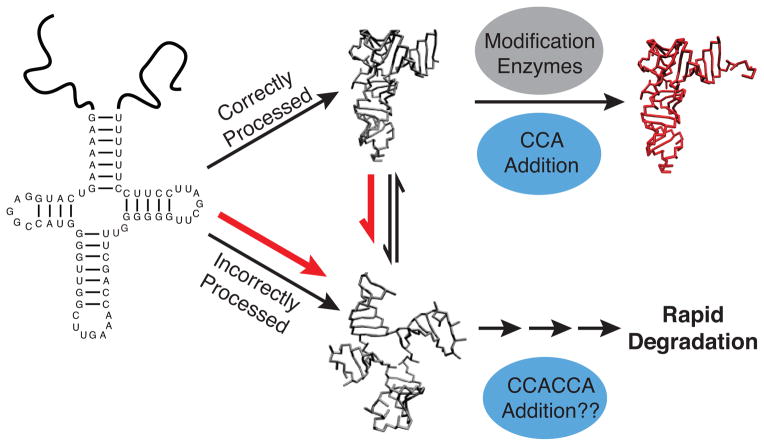
Figure 6.

Proposed pathogenic mechanism of the insG mutation. The unstable transcript exists in equilibrium between folded and unfolded tertiary conformations, with only the folded conformation likely efficiently processed into mature tRNA. In competition with maturation is a degradation pathway that degrades unfolded and misprocessed tRNAs. The insG mutation shifts the transcript equilibrium towards unfolded conformations (red arrows), leading to increased misprocessing and degradation.¹ Degradation may be promoted by 3′-CCACCA addition as in cytosolic rapid decay.² Once modified, insG mt-tRNA^Ser molecules have similar stabilities as WT.³

Inspection of other mt-tRNAs suggests that topological constraints may broadly compensate for non-canonical tertiary interaction networks. Of particular note, in mt-tRNA^Ser(AGY) the entire D-stem and loop is replaced with a 3–5 nt single-strand linker between the A- and AC-stems.⁵ This short linker, along with its shorter 3-nt V-loop, should place substantially greater constraints on the A-, AC-, and T-stems compared to cc-tRNAs. More generally, the significant majority of mt-tRNAs possess 4-nt V-loops compared to the 5-nt V-loops found in most cc-tRNAs.^5,7 mt-tRNA mutations that disrupt secondary structure are also particularly likely to be pathogenic.³⁶ However, the few insertion mutations comparable to 7472insC observed in other mt-tRNAs with more canonical secondary structures are benign polymorphisms,²⁹ indicating that the pathogenic mechanism we observe here is likely unique to the particular architecture of mt-tRNA^Ser(UCN).

We emphasize that the true measure of our simulations lies in their ability to predict overall destabilization trends rather than their exact quantitative agreement with experiment. Clearly, forces ignored in our model, such as electrostatics and sequence specific attractive interactions, play crucial roles in RNA tertiary folding.^37,38 It is also worth noting that the inherent instability of mt-tRNA^Ser – T_m for cc-tRNAs is generally >60° C¹⁶ compared to 45° C measured here – makes it clear that greater topological constraints are insufficient to fully offset the significant loss of tertiary interactions in mt-tRNA^Ser. A full understanding of RNA tertiary folding requires accounting for all aspects of the RNA free energy landscape, including secondary structure misfolding, which we propose occurs in the insC and insCC mutants. Given these facts, we note that our near quantitative prediction of the mutant ΔT_m is likely partially due to offsetting errors in our analysis, as we assumed that the conformational distribution sampled by TOPRNA directly matches that of real mt-tRNA^Ser. Nevertheless, we stress that our $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{fold}}^{\mathit{topo}}$ estimates are assumption free, and due to the additivity of free energy, reflect a real component of the RNA free energy landscape.^7,23

A growing body of literature has suggested that secondary structure, and topological constraints in particular, plays an important role in RNA tertiary folding.^{7,23–25,39–43} Significantly, our study is the first to experimentally measure the contribution of such topological constraints to the folding free energy of a complex RNA molecule. Indeed, to our knowledge, our study is the first to quantitatively predict a priori the destabilizing effect that a secondary structure mutation will have on RNA tertiary folding. The magnitude of the free energy differences we observe indicates that topological constraints play a comparable role to tertiary interactions in determining RNA tertiary stability. Notably, our study only explored small variations of the optimized tRNA secondary structure scaffold; more significant deviations from this scaffold would likely prohibitively increase the entropic penalty of tertiary folding. Extensive work on the hairpin ribozyme has demonstrated that its evolutionarily selected secondary structure reduces the entropic cost of folding,^44–47 although the origins of this entropic stabilization were unclear. Combined with our results, we propose that entropic stabilization by topological constraints may be a general design principle of RNA folding. Such a mechanism may be a critical bridge towards understanding tertiary structure stability, specificity, and ultimately rationally designing novel RNA folds.

MATERIALS AND METHODS

TOPRNA model

As described elsewhere,²³ TOPRNA uses three beads to represent the sugar (S), base (B), and phosphate (P) moieties of each nucleotide. GC, AU, and GU paired B beads are permanently bonded together and contiguously paired regions are parameterized to adopt A-form helical structure. Single-stranded nucleotides are freely rotatable and do not experience attractive interactions. Paired B beads experience small attractive interactions to one another, which is meant to simulate intra-helical stacking, but also marginally favors inter-helical stacking. However, no other beads experience this attractive term. All electrostatic forces are ignored.

Simulation Details

All simulations were performed using the updated force field described in Supplementary Methods. Initial coordinates of WT, insN, and insNN mt-tRNA^Ser were obtained by assembling the molecules from initially linear chains using the init option of toprnaCreate.pl (brooks.chem.lsa.umich.edu). Langevin dynamics temperature replica exchange simulations were performed in CHARMM⁴⁸ using the MMTSB toolset⁴⁹ for a total of 10⁹ dynamics steps, using a 20 fs timestep, 5 ps⁻¹ friction coefficient, and 8 temperature windows spanning 300 to 450 K. The first 2× 10⁶ simulations steps were discarded as equilibration. Exchanges were attempted every 2000 dynamics steps, with exchange rates varying between 42–45% for all simulations. All other simulation parameters were set as previously described.²³

Simulation Analysis

Analysis was restricted to conformations sampled at 300 K. Interhelical Euler angles were measured as previously described;^7,24 for the AC-stem, the three base-pairs below G26-U44 were used for alignments to facilitate comparisons to cc-tRNA. The fraction of interhelical conformations sampled was computed by binning on a 60° grid, as described previously.⁷ Distances in Euler angle space were computed as the amplitude of the single axis rotation needed to convert a given interhelical (α_h, β_h, γ_h) angle to the value measured in the crystal structure.²⁴ The D- and T-loops were considered to be in contact if the S-beads from at least one pair of residues were within 14 Å.⁷ Interhelical stacking was evaluated using a modified version of the Tyagi and Mathews criteria as previously described.^7,50 RMSDs were computed using P-beads, excluding the 3′-A/GCCA and V-loops.

The 500 best-packed conformations sampled by each simulation were identified using the energy function E = n_lε_l + n_sε_s, with n_l corresponding to the number of contacts between loop residues, n_s the number of interhelical stacks, and ε_s and ε_l scaling parameters set to −3.5 and −0.6 kcal/mol.⁷ Stacking interactions were considered between the A- and D-stems, the D- and AC-stems, and T- and A-stems. The entropy of each best-packed conformation i was computed through

$$S_i=k_{B}ln\left[1+\sum _{j\ne i}exp\left(-\frac{{{\mathit{rmsd}}_{i,j}}^3}{{(10Å)}^3}\right)\right],$$ [3]

where the sum is done over all other best-packed conformations and rmsd_i,j is the P-bead RMSD computed excluding the V-loop and 3’-A/GCCA-loop.^7,27 The entropy weighted ensemble average was computed as

$$\langle N\rangle =\frac{{\sum }_i{N}_{i}exp\left(S_i/k_B\right)}{{\sum }_{i}exp\left(S_i/k_B\right)}.$$ [4]

UV melting experiments

RNA cloning and synthesis procedures are described in Supporting Information. Briefly, human mt-tRNA^Ser(UCN) was subcloned into a pUC18 plasmid and prepared by run-off transcription using T7 RNA polymerase. Mutants were obtained by site-directed mutagenesis and similarly prepared by run-off transcription. All DNA templates were verified by sequencing.

Concentrated tRNA was diluted into a lightly buffered water solution containing ~0.01 mM EDTA and ~0.1 mM Tris (pH 7.2), denaturated at 95° C for two minutes, refolded at room temperature for 15 minutes, followed by addition of folding buffer and incubation at room temperature for 30 minutes. Final solution conditions consisted of 0.5 μM RNA, 0.01 mM EDTA, 0.1 mM Tris, 150 mM NaCl, 20 mM Na-cacodylate (pH 7.2), and either 2 mM or 5 mM MgCl₂. The solution was placed in 1 cm capped quartz cuvettes and was topped with 50 μL of mineral oil to prevent evaporation. Melts were performed at a rate of 0.5°C/min from 15 to 90°C, monitoring absorbance at 260 nm on a Cary 100Bio UV/Vis spectrophotometer. Derivatives were obtained by subtracting the buffer baseline, normalizing to the absorbance at 15°C, and computing the slope of the linear least-squares fit to all data points within a ±3° C temperature window.³² Experimental replicates showed good agreement (not shown).

Global Melt Fit (GMF) provided by D.E. Draper (Johns Hopkins) was used to extract melting enthalpies and temperatures from the WT, insA, insU, insG, and insUU dAbs(260 nm)/dT melting data utilizing custom python wrapper scripts to interface with the GMF fitting routine.³² Scripts and documentation are available for download at brooks.chem.lsa.umich.edu. Curves were globally fit assuming three, four, or five sequential transitions, with ΔH and ΔAbs of all transitions required to be >0 for the fit to be considered successful. Three- and four-transition models successfully fit all curves, but five-transition models generally failed to converge. Four-transition models were selected because they yielded a total ΔH of unfolding consistent with expectations from nearest neighbor stacking parameters (200–260 kcal/mol), whereas three-transition models yielded lower estimates (<190 kcal/mol). As detailed in Supplementary Information, our analysis is based on the “parsimonious” four-state fit of each individual melting.

ΔG_fold,vH was computed from the fitted T_m and ΔH_vH of the first transition according to:

$$\mathrm{\Delta }{G}_{\mathit{fold},vH}(300K)=\mathrm{\Delta }{H}_{vH}(1-300K/T_m)$$ [5]

Errors of fitted parameters were computed for each melting curve by bootstrap analysis.³² However, in some cases the bootstrap estimated errors were smaller than the differences observed between the fits of experimental duplicates. Hence, we report the error as the larger of the two values.