A pharmacokinetic/viral kinetic model to evaluate the treatment effectiveness of danoprevir against chronic HCV

Abstract

Background

Viral kinetic models have proven useful to characterize treatment effectiveness during HCV therapy with interferon (IFN) or with direct acting antivirals (DAAs).

Methods

We use a pharmacokinetic/viral kinetic (PK/VK) model to describe HCV RNA kinetics during treatment with danoprevir, a protease inhibitor. In a phase 1 study, danoprevir monotherapy was administered for 14 days in ascending doses ranging from 200 to 600 mg per day to 40 patients of whom 32 were treatment-naïve and 8 were non-responders to prior PEG-IFN-α/ribavirin treatment.

Results

In most patients, a biphasic decline of HCV RNA during therapy was observed. A two-compartment PK model and a VK model that considered treatment effectiveness to vary with the predicted danoprevir concentration inside the second compartment provided a good fit to the viral load data. A time-varying effectiveness model was also used to fit the viral load data. The antiviral effectiveness increased in a dose-dependent manner, with a 14-day time-averaged effectiveness of 0.95 at the lowest dose (100 mg bid) and 0.99 at the highest dose (200 mg tid). Prior IFN non-responders exhibited a 14-day time-averaged effectiveness of 0.98 (300 mg bid). The second phase decline showed two different behaviors, with 30% of patients exhibiting a rapid decline of HCV RNA, comparable to that seen with other protease inhibitors (>0.3 d⁻¹), whereas the viral decline was slower in the other patients.

Conclusions

Our results are consistent with the modest SVR rates from the INFORM-SVR study where patients were treated with a combination of mericitabine and ritonavir-boosted danoprevir.

Introduction

Hepatitis C virus (HCV) can lead to chronic hepatitis, a disease that affects over 185 million people worldwide [1]. The goal of treatment is to achieve a sustained virologic response (SVR), defined as undetectable levels of HCV RNA in blood 24 weeks after cessation of treatment [2]. Direct acting antivirals (DAAs) represent a new step in anti-HCV therapy [3]. Within the class of DAAs, NS3/4A protease inhibitors (PIs) have been significantly effective in suppressing viral loads in HCV genotype 1 infected patients [4], and two PIs, telaprevir and boceprevir, have been approved for clinical use with pegylated interferon (PEG-IFN) and ribavirin (RBV) [5-8].

Danoprevir (also known as ITMN-191 or R7227), a non-covalent macrocyclic acyl-sulfonamide inhibitor of NS3/4A [9, 10], has shown potency and a high degree of specificity against HCV serine protease in genotypes 1-6 [10]. In the INFORM-1 study, danoprevir was administered to chronically infected patients in combination with mericitabine, a nucleoside inhibitor of the viral RNA dependent RNA polymerase, NS5B, for 14 days. This combination achieved 5 logs of viral RNA decline without any viral breakthrough [11], thus providing a proof-of-concept that a combination of different DAAs without PEG-IFN or RBV can potentially lead to sustained viral suppression. In order to optimize combination therapies, it is important to understand the treatment effectiveness of the individual DAAs used in combination.

One of the methods of evaluating the effectiveness of treatment against HCV using DAA monotherapy or combination therapy is through analysis of HCV viral kinetics (VK) using mathematical models [12]. Mathematical models for a number of DAAs have been developed [13-18], but no viral kinetic model of the response to danoprevir treatment has been reported. Here we introduce a combined pharmacokinetic (PK)/ viral kinetic (VK) model to analyze danoprevir monotherapy data during short term treatment.

Materials and Methods

Patients

We analyzed data from a previously published phase 1 single ascending dose study of danoprevir in 40 chronically HCV-infected patients [9], randomized to receive oral danoprevir or placebo for a period of 14 days. Patients were divided into 5 cohorts (Table 1). Each cohort comprised 10 patients, randomized in a ratio of 8:2 to receive danoprevir or a placebo equivalent. Cohorts 1, 2, 3 and 4, contained treatment-naïve patients, receiving danoprevir doses of 100 mg twice a day (bid), 100 mg three times a day (tid), 200 mg bid and 200 mg tid, respectively. Cohort 5 was comprised of non-responders to previous PEG-IFN-α/RBV treatment, i.e., patients who achieved <2 log₁₀ reduction in viral load at week 12 or failed to achieve undetectable HCV RNA at the end of treatment, who received 300 mg tid of danoprevir. Among the 40 patients, 30% were infected with genotype 1a, 55% with genotype 1b and 15% were genotype 1, but the subtype could not be identified. We did not find that the HCV genotype was significantly different between the cohorts (P=0.13, Chi-square test).

Table 1.

Baseline characteristics of the patients and total viral decline during therapy

Cohort	Dose (regimen)	Patient type	Genotype			Initial viral load Log10 IU/mL	Total viral decline Log10 IU/mL
			1a	1b	Missing value
1	100mg (bid)	Treatment-naïve (TN)	5	2	1	5.8	2.0
2	100mg (tid)	TN	2	6	0	6.2	2.7
3	200mg (bid)	TN	3	5	0	6.3	2.3
4	200mg (tid)	TN	1	6	1	6.4	3.9
5	300mg (bid)	Non responder	2	3	3	6.5	2.7

All the patients in cohorts 1-5 were allowed to start PEG-IFN-α/RBV treatment post day 14 [9]. We restrict the current analysis to the 14 days of danoprevir monotherapy and we excluded patients taking placebo.

Pharmacokinetics of danoprevir

Danoprevir concentrations measured in plasma prior to the first dose, at 0.5, 1, 1.5, 2, 2.5, 3, 4, 6, 8 and 12 hours after the first dose and 12 hours after the last dose were used for data fitting across all cohorts. The methods used to measure the danoprevir concentrations are summarized in [9, 19].

Viral kinetics in patients treated with danoprevir

HCV RNA levels were measured as previously described [9, 19] from blood samples obtained at 0, 2, 4, 6, 8, 12, 16, 24, 26, 28, 30, 48, 52 hours, and on days 6 and 8 pre- and post-dose and on day 13. We assume patients did not miss any doses as they were confined to a clinical research unit for the duration of the study, with all doses administered by study staff. For patients that exhibited viral rebound during therapy (≥log₁₀ 0.1 increase in HCV RNA/mL at 2 or more consecutive time points), a truncated data set with viral load data before rebound was used in order to exclude any major contribution from drug-resistant variants, which are likely to be the major cause of breakthrough during short term therapy.

Mathematical modeling of danoprevir PK/VK during monotherapy

Viral kinetic (VK) model

Due to the short duration of therapy and limited viral load data, models that include liver regeneration and parameters describing hepatocyte growth [20, 21] were considered not suitable. Instead, the kinetics of viral decline was assumed to follow the standard model developed by Neumann et al. [22], with target cells assumed to remain constant. Further, either a constant effectiveness, ε, or a time-varying effectiveness, ε(t), Eq. (1)-(2) in Supplementary Information, was used. When ε is taken to be a constant, this model has been called a constant effectiveness (CE) model [23]. Further details are given in the Supplementary Information.

Pharmacokinetic (PK) model

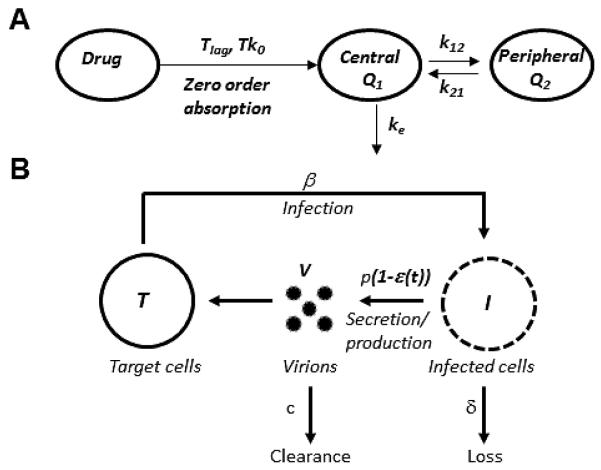
We tested models with one or two compartments and zero- or first-order absorption. We assume that after a lag-time, T_lag, danoprevir is absorbed into the first or central compartment (e.g. blood plasma plus tissues in rapid equilibrium with the plasma) following a zero order absorption law (Fig. 1A), with rate constant k₀, and is eliminated by a first order process with rate constant k_e. The zero order rate constant is given by $k_0=\frac{D}{T_{k0}}$, where D is the administered dose and is the time over which danoprevir is absorbed. The amounts of drug in the first and second compartments are denoted Q₁ and Q₂, respectively. Drug in the second compartment assumes distribution of danoprevir to the tissue compartment outside of the plasma, which includes the liver. We assume drug can move into and out of the second compartment with forward and backward rate constants, k₁₂ and k₂₁, respectively (Eq. (3)-(4) in Supplementary Information).

Figure 1. Combined PK/VK model used to describe viral kinetics during danoprevir monotherapy.

(A) Schematic of the two-compartment PK model following zero-order absorption of danoprevir. Danoprevir is absorbed, after a lag time T_lag into the central compartment/blood plasma (Q₁) following a zero order absorption law with rate constant Tk₀. Danoprevir is eliminated from the central compartment via a first order elimination process with rate constant k_e, and moves in to and out of the second compartment (Q₂) with forward and backward rate constant k₁₂ and k₂₁, respectively. (B) Schematic representation of the VK model. Danoprevir inside infected cells, I, is considered to partially block viral RNA production with a time varying effectiveness, ε(t), which depends on the danoprevir concentration. Target cells, T, are infected by virus, V, with rate constant β to produce infected cells, I. Infected cells, I, are lost with rate constant δ and virus, V, is cleared from the circulation with rate constant c. In the absence of drug infected cells produce virus with rate p per infected cell.

The plasma concentration is given by C₁₌ Q₁F₁/V₁, where V₁ is the volume of distribution of the drug in the first compartment and F₁ is the drug’s bioavailability. Here we incorporate into F₁ any loss of drug from the absorption site as well as any first-pass effects. Since F₁ is not known and cannot be identified from the available data, we redefine V₁ as V₁/F₁, i.e. as effective volume of distribution.

Danoprevir pharmacodynamics

We assume that the drug effectiveness ε(t) varies as a function of C₁, according to the E_max model shown in Eq. (1), where the maximum effectiveness is assumed to be 1. Here, EC₅₀ represents the concentration at which the effectiveness of danoprevir is 0.5 times its maximum, and h is the Hill coefficient, which determines how steeply the effectiveness varies with drug concentration.

$$\epsilon \left(t\right)=\frac{C_1{\left(t\right)}^h}{E{C}_{50}^h+C_1{\left(t\right)}^h}$$ (1)

Varying effectiveness (VE) modeling

In many situations PK data is not available or is not complete. In order to understand how our conclusions might change if we used VK data only, we fitted the VK model, Eqs. (3)-(4) in the Supplemental Information, to the VK data using a VE model [24]. The pharmacodynamic (PD) model [21] for the final effectiveness is ${\epsilon }_{final}=\frac{Dose}{E{D}_{50}+Dose}$ where Dose is the total amount of danoprevir received per day, ED₅₀ is the daily dose leading to 50% of the maximal effectiveness, allows one to describe the dose effect in the absence of PK data. We completed the effectiveness model with a time-varying component such that ${\epsilon }_{final}=\frac{Dose}{E{D}_{50}+Dose}(1-e^{-kt})$ where k is the rate constant, describing the change in treatment effectiveness from 0 to the final effectiveness.

Parameter estimation and statistical methods

Population estimates and inter-individual variability (IIV) estimates were obtained using a maximum-likelihood method implemented in MONOLIX version 4.2 (http://software.monolix.org). Further details about mixed effect models and the population approach used here, as well as other details about parameter estimation are given in the Supplementary Information.

Equations (1)-(4) in the Supplementary Information were fitted simultaneously to PK and VK data in order to estimate parameters in the PK/VK model, instead of fitting PK and VK separately, since simultaneous fitting provides more accurate fits [25, 26]. For the PK/VK model, the parameters estimated were Tk₀, k₁₂, k₂₁, k_e1, EC₅₀, V₀, c and δ, and the Hill coefficient was fixed to h=1, 2 or 3. For each parameter, we report the population estimates (fixed and random effects) and their standard errors. The PK/VK model was fit to log₁₀ viral load. HCV genotype was tested as a covariate in the model to study its effect on the PK/VK parameters.

Results

Among the patients not previously treated with anti-HCV drugs, the lowest (100 mg bid) and highest dose (200 mg tid) cohorts showed median viral load declines of 2.0 log₁₀IU/mL and 3.9 log₁₀IU/mL, respectively (Table 1). The prior IFN non-responder group (300 mg bid) had a median viral load decline of 2.7 log₁₀IU/mL. The viral decline was found to be higher in the tid groups, (2.7 log₁₀IU/mL and 3.9 log₁₀IU/mL for 100 and 200 mg tid, respectively) than the bid groups (2.0 log₁₀IU/mL and 2.3 log₁₀IU/mL for 100 and 200 mg bid, respectively) (Table 1).

Although the constant effective (CE) model provided good fits to the patient data (Fig. S1 and Table S1), it averages the treatment effectiveness and does not take into account its variations due to fluctuations in drug concentration. This is especially important since the danoprevir plasma concentration fluctuates between intakes (Fig. S2). These fluctuations appear to be coupled to fluctuations of viral load, which are more noticeable at lower doses (Fig. S1) [19]. Thus, we explored the possibility that the treatment effectiveness depends on danoprevir concentration by using a PK/VK model fitted to both PK and VK data and a VE model fitted to VK data alone to describe treatment effectiveness increase under danoprevir monotherapy.

PK/VK model

A one-compartment PK model using either zero-order (corrected Akaike information criterion, AICc=5911, Bayesian information criteria, BIC =5927 or first-order absorption (AICc=5967, BIC=5983), and a two-compartment PK model using either zero- (AICc=5652, BIC=5673) or first-order absorption (AICc=5685, BIC=5707) were fitted to the danoprevir plasma concentrations. The two-compartment PK model with zero-order absorption and first-order elimination provided the best model for the PK data, as evidenced by the lowest AICc and BIC [27]. A combined error model (see Supplemental Information) was found to best describe the residual error for the PK data with an additive error term (a=0.25± 0.012 ng/mL) and a proportional error term (b=0.61± 0.02). The high proportional error term can be explained by the wide range of C_max concentrations (2.67 to 589 ng/mL).

Consistent with the PK data, the PK model predicted plasma concentrations of danoprevir increase and then decrease within a dosing interval (Figs. S2 and S4A). Fitting the PK/VK model for h=1 (AICc=6097, BIC=6098), h=2 (AICc=6123, BIC=6154) and h=3 (AICc=6154, BIC=6182), showed that h=1 provided the best model, as evidenced by the lowest AICc and BIC [27]. Thus h=1 was used for all subsequent analyses. As summarized in Table 2, the fitting yielded estimates of a post-dose lag-time of 0.50 hr (inter-individual variability, IIV=64%), following which danoprevir was absorbed over a short period of time estimated as T_k0 = 0.58 hr (IIV=122%). The estimated first order drug elimination rate constant k_e = 1.02 hr⁻¹ (IIV=30%) for the central compartment. The rate constants for forward and backward movement of danoprevir between the two compartments were estimated as k₁₂=0.25 hr⁻¹ (IIV=79%) and k₂₁=0.81 hr⁻¹(IIV=89%), respectively. The EC₅₀ for danoprevir was estimated as 0.0082 ng/mL (IIV=152%), which is 2.6 to 7.7 time higher than C_min for the lowest dose cohort 1 and highest dose cohort 4, respectively, leading to a minimal effectiveness of 0.706 and 0.877 for cohorts 1 and 4, respectively. An additive error model was found to best describe the residual error for the VK data (a=0.29±0.0094 log₁₀(IU/mL). All the parameters were estimated with a good precision and the visual predictive check, which is a graphical comparison of the observations and simulated predictions [28], confirmed the accuracy of the model (Fig. S3.A).

Table 2.

Population parameter estimates obtained using the PK/VK model and the VE model

		PK/VK model
Cohort			PARAMETERS: Estimate±Standard error (P-value: Wald test)
		Tlag (hr)	Tk0 (hr)	V1 (L)	ke (hr−1)	k12 (hr−1)	k21 (hr-1)	V0 (IU/mL)	c (d−1)	δ (d−1)	EC50 (ng/mL)
Cohort 1: 100 mg bid, treatment- naïve (TN)*		0.50± 0.057	0.58± 0.13	2100± 360	1.02± 0.09	0.25± 0.08	0.81± 0.17	5.4×l05±2.4×l05 -	5.28± 0.38	0.18± 0.024	0.0082± 0.0024
Cohort 2: 100 mg tid, TN								1.9×l06±6.9×105 (P=0.08)
Cohort 3: 200 mg bid, TN								1.8×106±8×105 (P=0.048)
Cohort 4: 200 mg tid, TN								2.6×106±l.1×106 (P=0.012)
Cohort 5: 300 mg bid, Non- responder								2.7×106±1.2×106 (P=0.0092)
IIV ± S.E. (%)		63.5± 8.4	122±1 7	90±11	30.3± 6.8	79.4± 25	89.2± 16	118± 14	38.4±5 .8	55.9±1 3	152±22
	VE model
		k (d−1)		c (d−1)		V0 (IU/mL)		δ (d−1)	ED50 (mg/d)
PARAMETERS: Estimate±Standard error		29.1 ±13		7.25 ±0.59		1.93×106 ± 4.1 × 105		0.184 ± 0.03	4.85± 1.4
Inter-individual variability %		-		37 ± 5.9		124 ± 15		77 ± 13	170 ± 20

^*Reference: Cohort 1 was used as the reference group.

P-values were computed with a Wald test to assess the statistical difference between each cohort and the reference one.

Danoprevir effectiveness increases rapidly to reach 95% and 99% of its final effectiveness within 30 min and 36 min, respectively, of the first intake for the 100 mg bid dose. The effectiveness increases even faster with increasing dose (Fig. S4).

In the PK/VK model the drug effectiveness, ε, needs to be computed from the drug concentration and PD parameters. A useful way to summarize the drug effectiveness is to compute its time-average. Thus, we estimated the effectiveness averaged over the first 2 days of dosing, and the full 14 day dosing period, (Table 3) for each patient using their individual parameters and then averaging these values for all the patients in each cohort. For cohort 1, the lowest dose cohort, and , while for cohort 4, the cohort with the highest dose in treatment-naïve patients, the average effectiveness and . A useful way to evaluate the biological impact of these different effectiveness values is to compute the corresponding predicted first-phase log decline, i.e. −log₁₀(1- ε). For the lowest dose, corresponds to a 1.27 log₁₀ decline, while for the highest dose it corresponds to a 1.83 log₁₀ decline (Table 3). Overall the treatment effectiveness predicted by the PK/VK model increased in a dose-dependent manner attaining a 14-day average of 0.994 for the 200 mg tid dosing group (Table 3). All the parameters were estimated with a good precision and the visual predictive check confirmed the accuracy of the model (Fig. S3.B).

Table 3.

Average effectiveness over the first 2 days and the full 14-day dosing period estimated using the PK/VK and VE models

		Cohort 1: 100 mg bid, Treatment-naïve (TN)	Cohort 2: 100 mg tid, TN	Cohort 3: 200 mg bid, TN	Cohort 4: 200 mg tid, TN	Cohort 5: 300 mg bid, Non-responder
Average effectiveness over the first 2 days of dosing ${\stackrel{‒}{\epsilon }}_2$	PK/VK model	0.946	0.981	0.966	0.985	0.974
	VE model	0.973	0.982	0.985	0.990	0.990
Average effectiveness over the full 14-day dosing period ${\stackrel{‒}{\epsilon }}_{14}$	PK/VK model	0.953	0.990	0.974	0.994	0.982
	VE model	0.976	0.984	0.988	0.992	0.992
Predicted first-phase log decline, i.e. $-{\log }_{10}(1-{\stackrel{‒}{\epsilon }}_2)$	PK/VK model	1.27	1.72	1.47	1.83	1.58
	VE model	1.57	1.74	1.82	2.00	2.00

The viral clearance rate, c, was estimated to be 5.28 d⁻¹ (IIV=38%), which is similar to values estimated in patients treated with IFN [22] or PEG-IFN [21], but smaller than that estimated in patients treated with telaprevir [15] or daclatasvir [18], agents that may affect viral assembly or secretion [18, 29].

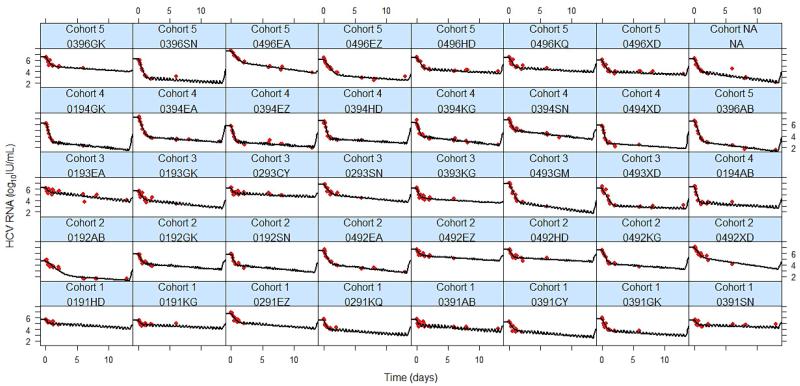
We found δ, which characterizes the slope of the second phase decline, to be patient specific, with 30% of patients showing a rapid second phase (δ > 0.3 d⁻¹) (Fig. 2). We used a mixture model to identify latent covariates. However, the results were inconclusive (P=0.17). Using the population approach, δ was estimated to be 0.18 d⁻¹ (IIV=56%) (Table 2). Using dose and patient type (treatment-naïve vs. non-responders) as covariates, their respective association with δ were not found to be statistically significant (P=0.91). A correlation between δ and the log₁₀ transformed final treatment effectiveness was not found, as a majority of patients have a low δ despite a high final effectiveness (Table S2). As discussed more fully below, the low value for δ found here may be due to the presence of resistant variants.

Figure 2. The viral kinetics of individual patients based on predictions of the PK/VK model during 14 days of treatment with danoprevir monotherapy.

The best-fit prediction of viral RNA decline is shown by the black curve, and the measured HCV RNA is shown by red dots.

VE model

PK data are not always available to study the effect of drug concentration on VK. In such cases it is necessary to use models adapted to VK data alone, such as the VE model [15, 24] that we combined with a PD model in which an ED₅₀ is estimated (see Methods). We found AICc=493 and BIC=508, lower than for the PD model with constant effectiveness (AICc =498, BIC =512). We found that ED₅₀= 4.85±1.4 mg/day (IIV=170%) and that the rate constant for effectiveness increase k = 29.1 ±13.0 d⁻¹ (Table 2). The average ED₅₀, was 41.2 to 123.7 times lower than the daily doses of 200 to 600 mg/day, suggesting that the drug effectiveness should be high and increase with drug dose. In fact, we predict a final population effectiveness of 0.976 for the lowest dose (cohort 1) and 0.992 for the highest dose given to treatment-naïve patients (cohort 4) (Fig. S5). As we did for the PK/VK model, we also estimated the effectiveness averaged over the first 2 days of dosing and over the full 14 day dosing period predicted by the VE model, both of which increased in a dose-dependent manner (Table 3).

Comparison of VE and PK/VK models

To assess the performance of the VE model relative to the PK/VK model, we computed the relative error (RE) as where is the effectiveness computed with the VE model and $RE=\frac{{\epsilon }_{PK∕VK}-{\epsilon }_{VE}}{{\epsilon }_{PK∕VK}}$ the effectiveness computed with the PK/VK model. The RE equals 0 when both models predict the same effectiveness. After the first intake but before the second, which is period during which the effectiveness increases to its steady state value, the RE between the VE and the PKVK models is between -2.0 and 0.3%. After day 1, the average RE, remained constant between -2.0 and 0.4% and overall the average effectiveness difference between both models is less than 2% (Fig. S6 and Table S4), suggesting that the VE model predictions cannot be distinguished from the PK/VK model predictions. We therefore conclude that the VE model predicts danoprevir’s antiviral effect nearly as accurately as the full PK/VK model but in the absence of PK data.

Discussion

In the past mathematical modeling has provided significant insights about the dynamics of hepatitis C under treatment, demonstrating the fast turnover of the virus [18] and providing a framework for understanding the rapid development of drug resistance observed during telaprevir monotherapy [30]. In addition, models have provided a means of assessing the in vivo drug effectiveness observed during PEG-IFN/RBV based therapy [22, 31], as well as for treatment with direct acting antivirals (DAAs) including the PI telaprevir [15, 32], the NS5A inhibitor daclatasvir [18] and the nucleoside polymerase inhibitor mericitabine [14]. Recently, Nguyen et al. [33], fitted a PK/VK model to data from a phase 1 study where patients were treated with alisporivir for 28 days and then used that model to successfully predict the SVR rate of a complex subsequent trial [34]. This is, to our knowledge, the first evidence that viral kinetic modeling can be used to predict SVR in a large population. Here we describe the first PK/VK model to estimate treatment parameters for monotherapy with danoprevir, although Adiwijaya et al. used a PK/VK model for the combination of telaprevir with PEG-IFN/RBV [16]. Analyzing danoprevir PK data, we found that a two-compartment model with zero-order absorption and first-order elimination provided the best fits. In the PK/VK model, we assumed that the effectiveness of danoprevir depended on the drug concentration in plasma. Also, because PK data are not always available for each patient in a VK study, we assessed the accuracy of a model that uses only VK data by fitting the VK data using a VE model with a dose effect. By fitting the same data using a PK/VK model we were able to quantitatively assess for the first time the utility of VE models for HCV. We found that the overall performance of this approximation was excellent with less than a 2% average error relative to the estimates made with the full PK/VK model. This analysis reveals that models without plasma PK can provide accurate information to understand the determinants of viral decline with robust parameter estimates. The usefulness of PK information in viral kinetic modeling may be drug-dependent and may not be critical for some drugs, such as protease inhibitors.

The danoprevir EC₅₀ in Huh-7 replicon cells with wild-type HCV genotype 1b ranges from 0.2 to 3.5 nM (0.15 to 2.6 ng/mL) [10], which is higher than our estimate of 0.0077 ng/mL. Our EC₅₀ estimate, which seems small compared to C_max, is only 2.6 to 7.7 times higher than the C_min of the cohort with the highest and lowest dose in treatment-naïve patients, respectively. This leads to a minimal effectiveness between 0.706 and 0.877 depending on the cohort. The difference between the in vivo and in vitro EC₅₀ estimates can be due to several factors such as protein binding (only free drug is active at the target), drug concentrations at the site of action, variability between in vitro viral growth characteristics and underlying variability in the viral drug susceptibility observed in different patients.

Similar to other PIs [15, 32, 35, 36], all patients treated with danoprevir monotherapy exhibited a biphasic viral load decline (Fig. 2). The model predicts that VK under danoprevir exhibits a rapid first phase decline within the first day, which is explained by a rapid increase of danoprevir effectiveness, with 99% of the final effectiveness reached within less than 1 hr. Unlike nucleoside polymerase inhibitors that need to be phosphorylated intracellularly, danoprevir, a PI, appears to become effective as soon as it is absorbed by the infected cells. Thus, as we have shown (Supplemental Information Table S1) the CE model with a dose-effect provides good fits to the data. However, due to the AICc and BIC being slightly lower for the VE model we only reported results for the VE model in the main text. Nonetheless, the population parameters estimates using the CE and VE models are similar being within one standard error of each other (compare Tables S1 and 2).

We found the second phase decline to be patient specific with nearly 30% of patients showing a flat second phase (Fig. 2). Using the population approach, δ was estimated to be 0.18 d⁻¹ (Table 2), which is slightly higher than that observed with IFN (0.14 d⁻¹) [22] and with Peg-IFN [21], suggesting that danoprevir may have an effect in increasing the loss rate of infected cells. However, the effect appears weaker than that seen with other PIs as higher estimates of δ have been obtained during monotherapy with ciluprevir (0.22-0.36 d⁻¹) at doses of 200 and 500 mg/day [35] and telaprevir (0.58 d⁻¹ estimated using the VE [15] model for doses ranging between 1350 and 2500 mg/day).

The clinical significance of the low δ estimate is unclear, as danoprevir has been shown in clinical trials to result in cure rates up to 85% in patients infected with genotype 1 in combination with IFN and ribavirin and up to 93% when the treatment was boosted with ritonavir [37]. Even though the data points at which viral rebound was observed were eliminated from the current analysis, undetected drug-resistant virus could still exist, which would lower the estimate of δ. Population-based sequence analysis of patients experiencing virologic plateau (low δ) indicate the presence of resistant virus at end of the treatment (day 14) with decreased susceptibility to danoprevir [38]. Patients were found to carry varied treatment-emergent substitutions in NS3/4A including R155R/K, V/I71I, R155Q, D168D/V, D168T, V/I71V and V170I/V [38].

Recently, a multiscale model has been introduced taking into consideration the replication, export and degradation of intracellular HCV RNA [18] and applied to the analysis of VK in the patients in cohort 4 [39]. Rong et al. [39] found that danoprevir at 200 mg tid blocked intracellular replication with an effectiveness of 99.2%, enhanced viral RNA degradation about 5-fold, and had a modest effect on viral secretion (mean effectiveness 56%). Because of the additional parameters in a multiscale model they were unable to incorporate PK and simultaneously fit PK/VK as was done here. Nonetheless, the results on blocking viral RNA replication are consistent with our finding here of a 99.4% final effectiveness of 200 mg danoprevir tid in blocking viral production.

Current DAA based therapy with the PIs telaprevir and boceprevir involve simultaneous administration of PEG-IFN and RBV, for both treatment-naïve and treatment-experienced patients [5, 6, 8, 40, 41]. To improve tolerability and treatment outcomes a number of IFN-free combination therapies are being developed [42-45]. The INFORM-1 study showed that a combination of two different DAAs, danoprevir and mericitabine, can successfully decrease HCV viral load by nearly 5 logs over a period of 14 days, with no viral breakthrough. However, our finding of a slow second phase viral decline with danoprevir and the result from a previous study showing the modest drug effect and slow second phase decline with mericitabine [14] are consistent the poor SVR rates in the INFORM-SVR study where patients were treated with a combination of mericitabine and ritonavir-boosted danoprevir for 24 weeks [46].