Robust optimization in intensity-modulated proton therapy to account for anatomy changes in lung cancer patients

Abstract

Background and Purpose

Robust optimization for IMPT takes setup and range uncertainties into account during plan optimization. However, anatomical changes were not prospectively included. The purpose of this study was to examine robustness and dose variation due to setup uncertainty and anatomical change in IMPT of lung cancer.

Material and Methods

Plans were generated with multi-field optimization based on planning target volume (MFO-PTV) and worst-case robust optimization (MFO-RO) on simulation computed tomography scans (CT0) for nine patients. Robustness was evaluated on the CT0 by computing the standard deviation of DVH (SD-DVH). Dose variations calculated on weekly CTs were compared with SD-DVH. Equivalent uniform dose (EUD) change from the original plan on weekly dose was also calculated for both plans.

Results

SD-DVH and dose variation on weekly CTs were both significantly lower in the MFO-RO plans than in the MFO-PTV plans for targets, lungs, and the esophagus (p < 0.05). When comparing EUD for ITV between weekly and planned dose distributions, three patients and 28% of repeated CTs for MFO-RO plans, and six patients and 44% of repeated CTs for MFO-PTV plans, respectively, showed an EUD change of > 5%.

Conclusions

RO in IMPT reduces the dose variation due to setup uncertainty and anatomy changes during treatment compared with PTV-based planning. However, dose variation could still be substantial; repeated imaging and adaptive planning as needed are highly recommended for IMPT of lung tumors.

Introduction

Intensity-modulated proton therapy (IMPT), which simultaneously optimizes the intensity and energy of proton beamlets using constraints for both targets and normal structures (similar to intensity-modulated photon radiotherapy), could reduce doses of radiation to normal tissues [1-5]. However, IMPT is sensitive to setup and range uncertainties and patient anatomy changes [6-9]. In recent years, robust optimization techniques have been developed to account for setup and range uncertainties [10]. Robustness in IMPT could be loosely viewed as the sensitivity of dose distribution to variations such as setup uncertainty, range uncertainty, and patient anatomy changes. In essence, robust optimization techniques employ extra criteria or constraints in conjunction with the normal objective functions during spot weight optimization to find the spot weight configuration that is least sensitive to the change in patient setup location or change in proton range inside of the patient. The ability of robustly optimized plans to retain intended dose distribution despite setup and range uncertainty has been validated for various cancer sites via planning studies [11-15].

However, unlike setup and range uncertainties, anatomy changes such as tumor shrinkage or patient weight loss are not usually prospectively taken into consideration in the planning process. In practice, repeated imaging and adaptive planning are used to account for anatomy changes in the patient [16-18], and clinically, the robustness of a treatment plan could be evaluated and quantified by the change of dose distribution and the need of adaptive planning through the course of treatment, i.e. a robust treatment plan will maintain the dose distribution in the patient throughout the course of the treatment. Even though the robust optimization method does not directly account for anatomy changes, it can be anticipated that the resulting spot weight configuration is in essence less sensitive to the change in the proton beam range along the ray lines regardless of what causes such change. In this study, we hypothesized that, in addition to the anticipated robustness against setup and range errors, robustly optimized plans can minimize the re-planning required to meet clinical goals.

The purpose of this study was to understand the relationship between robustness and the magnitude of dose variation through the course of patient treatment. Although the robust optimization technique incorporates only setup and range uncertainty, we also evaluated its effectiveness in making IMPT plans resilient to interfractional anatomical changes, in terms of the need for adaptive planning based on repeated computed tomography (CT) scans.

Material and Methods

Simulation and treatment planning

The records of nine consecutive lung cancer patients from an institutional review board-approved protocol who underwent IMPT at our institution between August 2012 and July 2013 were selected for this retrospective study. Table s1 in the supplement summarizes the pretreatment characteristics of the patients. Each patient underwent 4-dimensional (4D) CT simulation on a GE Lightspeed 16-slice CT scanner (GE Healthcare, Waukesha, WI). Each 4DCT dataset consisted of ten 3-dimensional image sets corresponding to the ten respiratory phases, along with maximum-intensity projection (MIP) and averaged-intensity projection (AVIP) datasets generated for planning purposes. To account for tumor motion, the internal gross tumor volume (IGTV) was contoured using either the union of the GTV on an individual phase or the contour of the GTV on MIP as verified through different breathing phases. The internal target volume (ITV) was defined as an 8 mm isotropic expansion of the IGTV and edited clinically. The planning target volume (PTV) was defined as an expansion of the ITV by 5 mm.

Respiratory motion is one of the major concerns in IMPT for patients with lung cancer. At our institution, currently only patients with minimum motion (< 5 mm) are considered for IMPT [19], and a separate study to minimize the dosimetric impact of respiratory motion is being performed [20]. For each patient in our study, motion analysis was performed on the acquired 4DCT before proceeding with IMPT planning, and an IGTV override technique was used for all patient planning [21]. Multi-field optimization (MFO) based on PTV (MFO-PTV) and robust optimization with respect to setup and range uncertainties (MFO-RO) were developed on a simulation averaged-intensity projection CT (CT0). The MFO-PTV plans were developed using a commercialized planning system (Eclipse v8.9, Varian Medical Systems, Palo Alto, CA), using PTV to account for setup uncertainties. The MFO-RO plans were developed using an in-house optimization system [14] with the dose calculated in Eclipse. The MFO-RO used ITV as the target volume of worst-case robust optimization, assuming ±3 mm setup uncertainties and ±3.5% range uncertainties [14, 15].

Three matched beam angles and similar planning constraints were used for the MFO-PTV and MFO-RO plans, with the exception of PTV, which was only used in MFO-PTV. Both plans were reviewed by the treating radiation oncologist, and the MFO-RO plans were used for patient treatment.

Robustness evaluation with setup and range uncertainties

Owing to the steep dose gradient of the proton beam, IMPT plans can be sensitive to both setup and range errors [7, 8] and can lead to a distorted dose distribution in the patient. Therefore, the robustness evaluation of an IMPT plan against setup and range uncertainty is an important component in the treatment planning process. Evaluation of the robustness of an IMPT plan is not straightforward. The conventionally used plan evaluation method based on enlarged volume (i.e. coverage of PTV in relation to true clinical target volume coverage) does not work well for proton therapy because of the non-static nature of dose distribution in and out of the volume being evaluated. The “worst-case scenario” method [15], in which the worst-case dose distribution is calculated as the voxel-by-voxel worst-case dose value that can occur when setup and range errors are introduced, was developed to evaluate the robustness of IMPT plans. Although the worst-case scenario evaluation has been shown to be a conservative bound on the real worst-case dose distribution [22], for our study the worst-case technique could be biased because the same technique was used in optimization. Therefore, we used a recently developed statistical technique [23] to evaluate the robustness of the IMPT plans. In this statistical technique, 600 combinations of setup and range uncertainties were introduced to the planning CT (CT0), and a fast dose calculation technique was used to calculate the dose distribution with the introduced uncertainties [24]. Dose-volume histograms (DVHs) of the target volumes and critical structures for each dose distribution were calculated. The mean DVH (E[DVH]) and the standard deviation of the DVH (SD-DVH), which represents the robustness of the plan under setup and range uncertainties, were calculated from the collection of the DVHs as follows:

$$E[\mathit{\text{DVH}}(d)]={\sum }_{i=1}^{n}P[d_i\ge d]{\nu }_i$$ (1)

where d is the dose in Gy, i indexes the voxels in a given ROI, n is the total number of voxels in the ROI, ν_i is the volume of voxel i, and d_i is the dose to voxel i.

$$\mathit{\text{SD}}[\mathit{\text{DVH}}(d)]=\sqrt{\frac{1}{N-1}{\sum }_{j=1}^N{({\mathit{\text{DVH}}}_j(d)-E[\mathit{\text{DVH}}(d)])}^2}$$ (2)

where j indexes the sampled setup and range uncertainties, and N is the total number of dose distributions sampled. The total dose variation (DV) of the plan for a structure was quantified using ±2σ (or 4σ) as in

$${\text{DV}}_{\text{SD}-\text{DVH}}={\int }_{d}4\ast \mathit{\text{SD}}[\mathit{\text{DVH}}(d)]$$ (3)

where the integral over dose (d) was calculated numerically by making 1000 equal spacing samples over 0 to the maximum dose among all scenarios. DV_SD-DVH could be visualized as the area of a DVH band with width of 2SD on each side of the E-DVH at dose level d, with a unit of dose * volume (Gy * cc). All DV data presented in the manuscript were normalized by the organ volume and prescription dose.

Robustness evaluation based on repeated CTs

CTs were taken approximately weekly during the course of treatment. For each patient, two to seven CTs were acquired, resulting in a total of 39 repeated CTs. Each repeated CT was registered with the planning CT using rigid registration of the bony anatomy to determine the isocenter. A new dose distribution was then calculated using the original MFO-PTV and MFO-RO plans' beam data using this isocenter. The original contours were deformed from the planning CT to the repeated weekly CTs using a commercial system (Velocity, Velocity Medical Solutions, Atlanta, GA). The accuracy and integrity of the newly deformed structures were visually assessed and approved by the treating physicians. Based on the newly created dose distribution and DVHs, adaptive planning was performed for selected patients as needed per the instruction of the treating physicians [16]. For adaptive planning, the same robust optimization and evaluation process was repeated on the repeated CT. It should be noted that even though the adaptive plans were generated and used for patient treatment, they were not evaluated in the current study because the purpose of the study was to evaluate the robustness of the original treatment plans.

To quantify the difference between the weekly dose distributions and the nominal dose distribution, the weekly dose distributions were deformed onto the CT0 coordinate by deformable image registration using Velocity. The dose was then accumulated on the CT0. Variation of weekly doses was calculated by accumulating the difference between maximum and minimum DVHs for weekly CTs and CT0:

$${\text{DV}}_{\text{weekly}}=\int d{max}_w({\mathit{\text{DVH}}}_w(d))-{min}_w({\mathit{\text{DVH}}}_w(d))$$ (4)

where DVH_w is the DVH calculated on CT w.

Dose variation of weekly doses (DV_weekly) and equivalent uniform dose (EUD) were compared on CT0 with the anticipated dose variations (DV_SD-DVH) predicted by the statistical plan robustness evaluation system. The EUD parameter a was collected from the literature [25-27]: for targets, a = -10; for the spinal cord, a = 20; for the lungs, a = 1.15; for the heart, a = 3; and for the esophagus, a = 16. Figure s1 in the supplement summarizes the process of evaluating the dose variation.

Statistical analysis

We used paired, two-sided Wilcoxon signed-rank tests to compare

1. DV_weekly between the MFO-PTV and MFO-RO plans

2. DV_SD-DVH between the MFO-PTV and MFO-RO plans

3. Accumulated EUD values for the target between the MFO-PTV and MFO-RO plans

4. DV_weekly and DV_SD-DVH of the MFO-PTV plan

5. DV_weekly and DV_SD-DVH of the MFO-RO plan

P values less than 0.05 were considered statistically significant.

We compared 1, 2, and 3 to determine whether the MFO-PTV or the MFO-RO plans performed better in terms of robustness.

We compared 4 and 5 to determine whether the DV_SD-DVH, which was calculated at the time of planning, was a good indicator of the dose variation throughout the course of the treatment. The correlation between DV_weekly and DV_SD-DVH was also calculated.

Results

Treatment plan parameters are summarized in Table s2 in the supplement for the MFO-RO and MFO-PTV plans. The nominal plan qualities for the MFO-RO plans were comparable or better than those of the MFO-PTV plans. Although both plans were clinically acceptable, the MFO-RO plans were used for patient treatment.

Example of different planning techniques

Figure 1 shows examples of nominal IMPT plans (patient 8) generated using MFO-PTV (Fig. 1a, left) and MFO-RO (Fig. 1a, right) techniques at the time of CT0. Targets were adequately covered for both plans, and efforts were made to spare the esophagus and spinal cord (as indicated by the arrows) in both plans. Figure 1b shows the same MFO-PTV (left) and MFO-RO (right) plans on one of the repeated CTs (day 50 from CT0). Coverage of the target area and sparing of the spinal cord and the esophagus deteriorated on the MFO-PTV plan but were maintained on the MFO-RO plan.

Fig. 1.

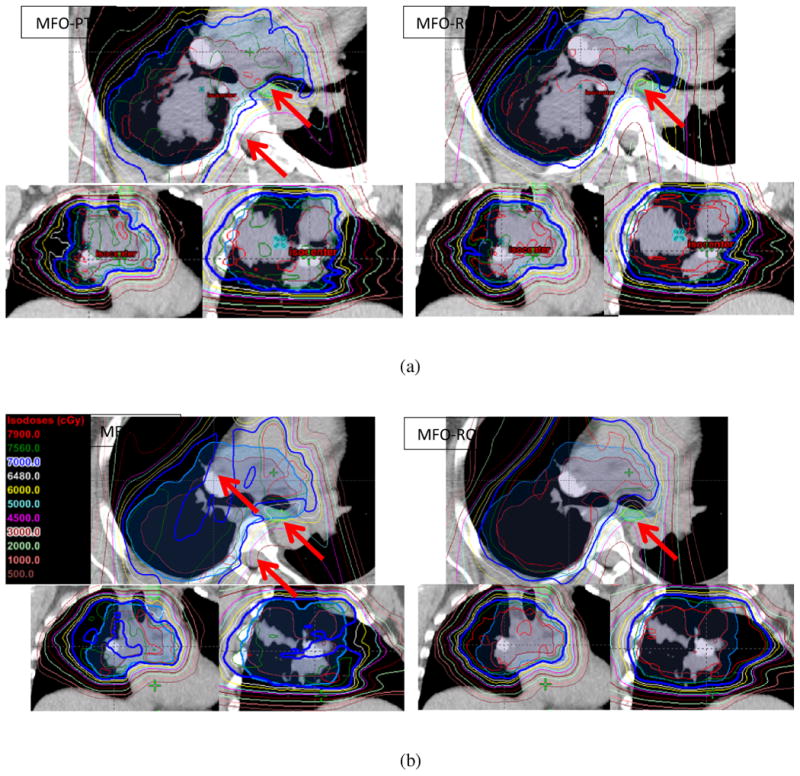
Examples of the multi-field optimized plan (MFO-PTV, left) and the robust-optimized MFO (MFO-RO, right) plan on the (a) original computed tomography (CT) scans and on the (b) verification CT scans. Note that owing to the anatomy changes, the prescription line was broken, and dose to the esophagus and the spinal cord was elevated on the repeated CT scan for the MFO-PTV plan (b, left), but the dose was maintained on the repeated CT scan for the MFO-RO plan (b, right).

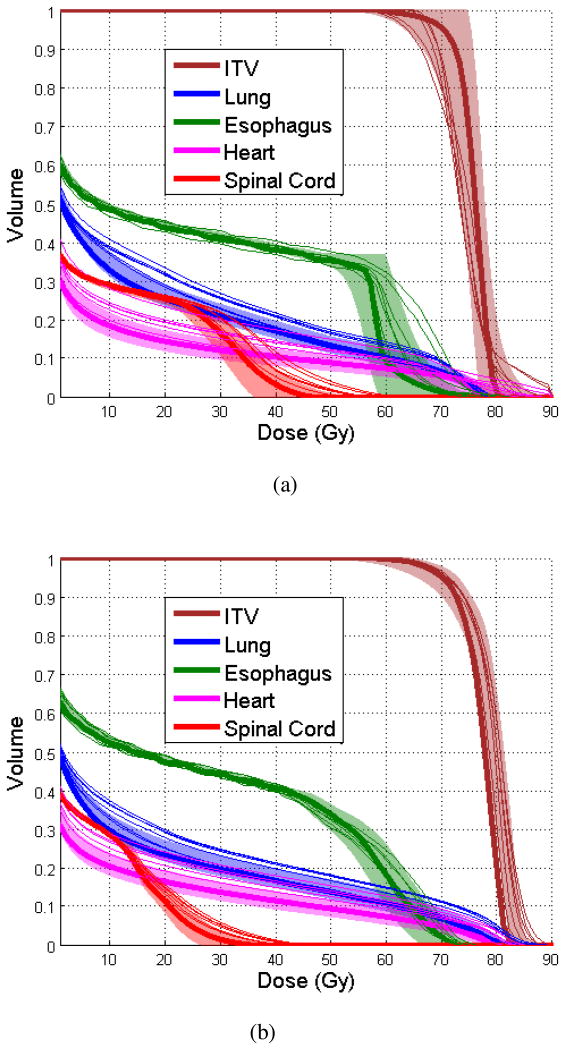
Figure 2 shows the nominal DVHs, SD-DVHs, and weekly DVHs of the same patient for the MFO-PTV (Fig. 2a) and MFO-RO plans (Fig. 2b) for the ITV, the lungs, the esophagus, the heart, and the spinal cord. The SD-DVH for the MFO-PTV plan was wider than that of the MFO-RO plan, indicating that the MFO-RO plan is more robust under the influence of setup and range uncertainty as expected. Moreover, the weekly DVHs for the ITV, the esophagus, and the spinal cord deviated from the nominal dose more on the MFO-PTV plan than on the MFO-RO plan, which is consistent with the findings shown in Fig. 2.

Fig. 2.

Nominal dose-volume histograms (DVHs; thick lines), standard deviation (SD)-DVHs (shaded areas, ±2σ), and weekly DVHs (thin lines) for (a) the multi-field optimized plan (MFO-PTV) and (b) the robust-optimized MFO (MFO-RO) plan for a patient. ITV, internal target volume.

Statistical analysis

DV_SD-DVH was calculated for each patient for both the MFO-RO and the MFO-PTV plans as an indicator of robustness against setup and range uncertainties for the GTV, the ITV, the lungs, the esophagus, the heart, and the spinal cord. A paired, two-sided Wilcoxon signed-rank test showed that DV_SD-DVH values were significantly lower in the MFO-RO plans than in the MFO-PTV plans for the GTV, the ITV, the lungs, and the esophagus (p < 0.05). Similarly, weekly dose variation (DV_weekly values), calculated for each patient using the MFO-RO and MFO-PTV plans on repeated CT scans, was significantly lower in the MFO-RO plans than in the MFO-PTV plans for the GTV, the ITV, the lungs, the esophagus, the heart, and the spinal cord (p <0.05).

However, the Wilcoxon signed-rank test did not show a significant difference between DV_SD-DVH and DV_weekly in either the MFO-RO or MFO-PTV plans for all structures. The correlation between DV_weekly and DV_SD-DVH was also calculated, and the correlation coefficient was 0.35 for ITV; similar coefficients were found for the other structures. A comparison of the ITV DV_SD-DVH and DV_weekly values for each patient is shown in Fig. 3a.

Fig. 3.

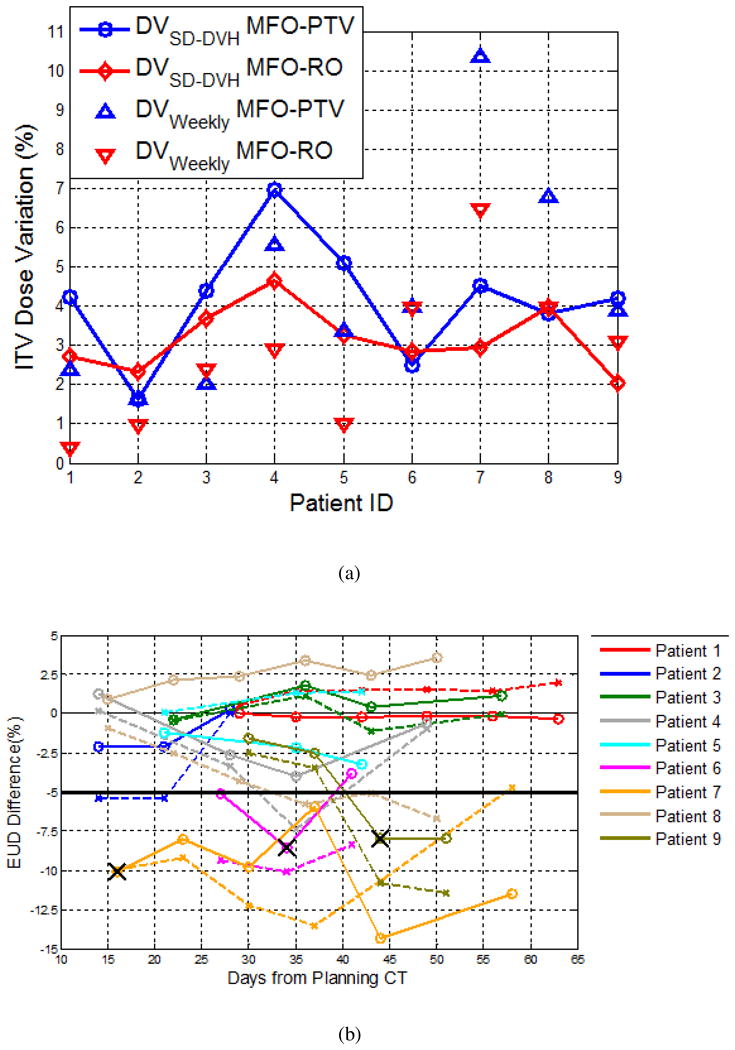
(a) Standard deviation of the dose variation (DV_SD-DVH) and weekly dose variation (DV_weekly) for the multi-field optimized plan (MFO-PTV) and the robust-optimized MFO (MFO-RO) plan evaluated for each patient. (b) Equivalent uniform dose (EUD) variation for the internal target volume (ITV) for different patients (shown in different colors) on the MFO-RO plans (solid lines) and MFO-PTV plans (dashed lines) as a function of time. X indicates adaptive planning.

Dose deviation from the original plan as a function of time

Figure 3b shows the EUD variation of the ITV for all patients as a function of time from the planning CT. For the MFO-RO plans, three of the nine patients required adaptive planning because of loss of coverage of the target volume on the weekly CT scans, identified by physician review (indicated by an X in Fig. 3b). Eleven of the 39 repeated CTs (for three patients, which is consistent with the physicians' review) showed an EUD change of > 5% for the ITV compared with the planned dose distribution. For the MFO-PTV plans, 17 of the repeated CTs (for six patients) showed an EUD change of > 5% for the ITV. As an example, no adaptive planning was necessary for patient 8 using MFO-RO (shown in Fig. 1 and 2); if the MFO-PTV plan had been used, adaptive planning would have been necessary after day 36 (EUD change > 5%; Fig. 3).

In 28 repeated CTs (seven patients), the ITV showed a higher EUD on the MFO-RO plan than that of the MFO-PTV plans. The accumulated GTV and ITV EUD was higher for the MFO-RO plans than for the MFO-PTV plans, and the Wilcoxon signed-rank test showed that the difference was statistically significant (p < 0.05).

Discussion

Robustness has been a major concern in IMPT. Robust optimization and robustness evaluation techniques have been developed to account for and evaluate the effect of setup and range uncertainties. However, these techniques were not designed to specifically account for anatomy changes, which could also lead to substantial change in dose distribution for IMPT. Therefore, it is important to evaluate the performance of robust optimization and robustness evaluation in a clinical setting. In our study, robustness of the treatment plan was quantified using DV_SD-DVH and DV_weekly, which can be visualized as the area of DVH bands defined by statistically simulated shifted dose distributions and by weekly dose distributions, respectively. They represent the predicted (DV_SD-DVH) and actual (DV_weekly) deviation from the nominal dose distribution. Robustness evaluation of the treatment plans using the statistical technique showed that, in general, the MFO-RO IMPT plans were more robust than the MFO-PTV IMPT plans. Evaluation of the dose variation during treatment showed that, compared with the MFO-PTV plans, the MFO-RO plans were less sensitive to setup uncertainties and anatomy changes. Although the robust optimization was not specifically designed to account for anatomy changes, because robust optimization in general forces the minimization of dose variation under different uncertainty scenarios, the robust optimized plan was less sensitive to anatomy changes as well.

The robustness of the plan as evaluated by SD-DVH generally encompassed the weekly dose, even though no significant differences were found (see Fig. 3a), indicating that SD-DVH could be an effective method to predict the robustness of an IMPT plan. While our Wilcoxon signed-rank test results indicated that MFO-RO plans are more robust compared to MFO-PTV plans, it is worth noting that in some instances the MFO-PTV plan could be more robust than the MFO-RO plan (see patient 2 and patient 6 in Fig. 3), suggesting a deficiency of the statistical analysis and discrepancy between the worst-case optimization and the statistical evaluation of the robustness. In addition, DV_weekly did not correlate well with DV_SD-DVH, with a correlation coefficient of 0.35 for ITV. The low correlation between DV_weekly and DV_SD-DVH indicates a discrepancy between the modeling of robustness in the optimization process (as range and setup uncertainties) and robustness evaluated as dose variation during treatment because of the change in patient setup or anatomy. Other quantities, such as dose variance across different volumes, could be investigated as alternative quantitative assessment of robustness. It appears from these results that if an ideal robustness evaluation tool that predicts the dose variation during patient treatment were used, the optimization technique that used during planning would become less relevant as long as robustness of the treatment plan used for patient treatment was acceptable. However, the ideal robustness evaluation tool and the level of acceptable robustness are yet to be defined, and studies with larger number of patients, and more statistical analyses are needed.

Deformable registration was used to deform weekly CTs to the simulation CT (CT0) and to enable dose comparison and accumulation. A recent study found that the mean 3D registration errors were 2.7 ± 0.8 mm for Velocity in thoracic images [28]. In the current study, the accuracy of each deformable registration was evaluated at landmark points and structures by a physician. EUD was calculated for each weekly dose distribution and was used to evaluate the dose variation. The results from EUD evaluation were highly consistent with those of the independent evaluation by the treating radiation oncologist in terms of the decision to use adaptive planning, as shown in Fig. 3b, thus confirming the validity of this technique. The MFO-RO plans were used to treat patients, and three of the nine patients required adaptive planning owing to loss of coverage in the ITV. In contrast, if the MFO-PTV plans had been used, six of the nine patients would have required adaptive planning, using the same criterion of an EUD change > 5%. These results indicate that although robust optimization reduces the sensitivity of the dose distribution to setup and range uncertainties, along with anatomy changes, the robustness of the plan still may not be adequate in some patients. Because anatomy changes are patient-dependent and no method can currently predict these changes, we highly recommend using repeated volumetric imaging to monitor the patient setup and/or anatomy changes during treatment. While the robustness and quality of an IMPT plan could be affected by different optimization techniques [29] and constraints, which are being investigated in a different study, our results indicate that accounting for anatomy changes directly during the planning process, by modeling tumor response in the optimization [30], might be more effective in minimizing the weekly dose variation for certain patients.

In conclusion, robust optimization in IMPT generates plans that are less sensitive to setup and range uncertainty and reduces the dose variation that is due to setup uncertainty and anatomy changes during treatment. Robust optimization substantially reduced the adaptive planning required during treatment. However, robust optimization alone may not be adequate to account for changes that occur during treatment, and we recommend repeated volumetric imaging along with adaptive planning as needed.