Estimating dead-space fraction for secondary analyses of ARDS clinical trials

Abstract

Objective

Pulmonary dead-space fraction is one of few lung-specific independent predictors of mortality from acute respiratory distress syndrome (ARDS). However, it is not measured routinely in clinical trials and thus altogether ignored in secondary analyses that shape future research directions and clinical practice. This study sought to validate an estimate of dead-space fraction for use in secondary analyses of clinical trials.

Design

Analysis of patient-level data pooled from ARDS clinical trials. Four approaches to estimate dead-space fraction were evaluated: three required estimating metabolic rate; one estimated dead-space fraction directly.

Setting

U.S. academic teaching hospitals.

Patients

Data from 210 patients across three clinical trials were used to compare performance of estimating equations with measured dead-space fraction. A second cohort of 3,135 patients from six clinical trials without measured dead-space fraction was used to confirm whether estimates independently predicted mortality.

Interventions

None.

Measurements and Main Results

Dead-space fraction estimated using the unadjusted Harris-Benedict equation for energy expenditure was unbiased (mean ± SD Harris-Benedict 0.59 ± 0.13; measured 0.60 ± 0.12). This estimate predicted measured dead-space fraction to within ± 0.10 in 70% of patients and ± 0.20 in 95% of patients. Measured dead-space fraction independently predicted mortality (OR 1.36 per 0.05 increase in dead-space fraction, 95% CI 1.10–1.68; p < .01). The Harris-Benedict estimate closely approximated this association with mortality in the same cohort (OR 1.55, 95% CI 1.21–1.98; p < .01) and remained independently predictive of death in the larger ARDSNet cohort. Other estimates predicted measured dead-space fraction or its association with mortality less well.

Conclusions

Dead-space fraction should be measured in future ARDS clinical trials to facilitate incorporation into secondary analyses. For analyses where dead-space fraction was not measured, the Harris-Benedict estimate can be used to estimate dead-space fraction and adjust for its association with mortality.

INTRODUCTION

Few lung-specific predictors of mortality from acute respiratory distress syndrome (ARDS) exist. Impaired oxygenation assessed by PaO₂:FiO₂ is a defining feature of ARDS, but severity inconsistently correlates with clinical outcomes (1–3). Oxygenation index, an alternative measure of oxygenation that includes mean airway pressure, may correlate with outcomes more reliably (2). In addition to measures of oxygenation, respiratory system compliance and pulmonary dead-space fraction have been found in multiple studies to predict mortality from ARDS (4–7). Yet while hypoxemia and compliance are commonly reported, dead-space fraction is rarely assessed in clinical trials.

Increased dead-space fraction occurs within hours of ARDS onset and independently predicts mortality, even after accounting for overall illness severity, hypoxemia, and compliance (4). Sustained elevation of dead-space fraction over the first week additionally identifies patients less likely to survive hospitalization (5, 8). Microvascular endothelial injury, microvascular thrombi, and derangements in pulmonary blood flow are characteristic features of ARDS that lead to increased dead-space fraction (9–11). Hyperinflation with excessive applied or intrinsic positive end-expiratory pressure (PEEP) may further increase dead-space fraction (12–14). Lowering tidal volume also increases dead-space fraction (15), an effect that may be offset partially by a brief end-inspiratory pause with each breath (16).

Determination of dead-space fraction requires measurement of expired carbon dioxide (CO₂) in a volume of expired gas. This volume is either derived by integrating flow or measured directly by collection in a Douglas bag. Expired CO₂ is measured only infrequently in routine clinical care and clinical trials of ARDS, contributing to underreporting of dead-space fraction.

Absent routine measurement or a reliable estimate, most studies do not account for dead-space fraction. Yet, such secondary analyses of clinical trials influence future research directions and, at times, even clinical decisions. Secondary analyses should account for known independent predictors of the outcome of interest to calculate a valid effect estimate, particularly when the analysis is not performed according to the groups to which patients were originally randomized. Otherwise, the calculated effect—benefit or harm—might be attributable to residual confounding, i.e. to other differences between groups that would explain the findings.

To address this gap, we evaluated the validity of four approaches to estimating dead-space fraction. Three approaches required predicting energy expenditure: the unadjusted Harris-Benedict estimate, which employs the eponymous formula for resting energy expenditure; the Siddiki estimate, which adjusts Harris-Benedict to account for hypermetabolic conditions often encountered in critical illness; and the Penn State estimate, which was derived specifically for use in critically ill patients. We also derived a novel approach to estimate dead-space fraction directly without requiring estimation of energy expenditure as an intermediate step. Dead-space fraction estimates were evaluated for their prediction of measured dead-space fraction and prediction of the association between measured dead-space fraction and mortality. We hypothesized that estimating dead-space fraction directly would yield the highest predictive validity.

METHODS

Study Design

De-identified patient-level data pooled from three randomized controlled trials of early ARDS (V_D/V_T cohort) were used to compare directly measured dead-space fraction with four methods for estimating dead-space fraction. To evaluate the association between estimated dead-space fraction and mortality in a larger population, a second cohort was created by pooling data from completed NHLBI ARDS Network trials in which dead-space fraction was not measured (ARDSNet Cohort). The study was exempt from review by the Institutional Review Board.

Subjects

Patients eligible for the V_D/V_T cohort had baseline measured dead-space fraction obtained within 24 hours of study enrollment and prior to any study interventions. Patients were enrolled in one of three randomized controlled trials testing therapies for early ARDS. These trials were chosen because dead-space fraction was reported in their primary publications. The ARDSNet ALTA trial (17) was a multicenter randomized, placebo-controlled trial in which patients with early ARDS were assigned to receive aerosolized albuterol (5 mg) or saline placebo every 4 hours for up to 10 days. The trial was stopped early for futility, with no significant difference in mortality or ventilator-free days between groups. EPVent (18) was a single-center randomized, controlled trial in which patients with early ARDS were assigned to undergo mechanical ventilation with PEEP adjustment guided by esophageal pressure or according to the ARDSNet PEEP titration table. The trial was stopped early for reaching the primary endpoint of improved PaO₂:FiO₂, with no significant difference in mortality or ventilator-free days in the unadjusted primary analysis. The APC trial (19) was a multicenter randomized, placebo-controlled trial in which patients with early ARDS were assigned to receive activated protein C (APC) 24 µg/kg/h or placebo for 96 hours. No significant difference in mortality or ventilator-free days was found.

For the ARDSNet cohort without measured dead-space fraction available, data were pooled from the ARMA (1) (low tidal volume group only), ALVEOLI (20), FACTT (21, 22), ALTA (17), OMEGA (23), and EDEN (24) trials. Inclusion and exclusion criteria for each trial are described in the original referenced publications.

Measurement of Physiological Dead-space Fraction

In the V_D/V_T cohort, physiological dead-space fraction was calculated by measuring mean expired CO₂ using volumetric capnography according to a validated protocol (25). An arterial blood gas was obtained at the time of expired gas analysis. Measured dead-space fraction was calculated using the Enghoff modification to the Bohr equation (26):

$$\frac{V_D}{V_T}=\frac{(PaC{O}_2-P_{E}C{O}_2)}{PaC{O}_2}$$

where PaCO₂ and P_ECO₂ represent partial pressure of CO₂ in arterial blood and expired gas, respectively. All measurements were made prior to study interventions.

Estimating Equations for Physiological Dead-space Fraction

Methods for estimating dead-space fraction that do not require measurement of expired CO₂ typically depend on the alveolar ventilation equation:

$$PaC{O}_2=\frac{\dot{V}C{O}_2\times 0.863}{{\dot{V}}_A}$$

where PaCO₂ is measured in mmHg, V̇CO₂ represents CO₂ production (mL/min), and V̇_A represents alveolar minute ventilation (L/min). Because V̇_A is defined as the difference between total minute ventilation and dead-space minute ventilation, this equation can be rewritten and, after solving for V_D/V_T, yields:

$$\frac{V_D}{V_T}=1-\frac{(0.863\times \dot{V}C{O}_2)}{(RR\times V_T\times PaC{O}_2)}$$

where RR is respiratory rate (breaths/minute) and V_T is tidal volume (liters). In this rearranged equation for dead-space fraction, the only variable not routinely available is V̇CO₂, which may be calculated from the resting energy expenditure (REE) using the rearranged Weir equation (27):

$$\dot{V}C{O}_2=\frac{REE}{(\frac{5.616}{RQ}+1.584)}$$

where RQ is the respiratory quotient, assumed to be 0.8 for this analysis.

In this study, four different strategies for estimating dead-space fraction were considered. All physiological measurements required for dead-space fraction estimates were obtained prior to study interventions associated with the clinical trial.

1. Unadjusted Harris-Benedict estimate: The original sex-specific Harris-Benedict equations (28) were used to estimate REE:

   $$\text{Males}:RE{E}_{HB}=66.473+13.752(Wt)+5.003(Ht)-6.755(\mathit{\text{age}})$$

   $$\text{Females}:RE{E}_{HB}=655.096+9.563(Wt)+1.850(Ht)-4.676(\mathit{\text{age}})$$

   with weight (Wt) in kg, height (Ht) in cm, and age in years. The value for REE_HB was inserted into the rearranged Weir equation to calculate V̇CO₂, which was then used to calculate dead-space fraction.
2. Siddiki estimate: Siddiki et al. (29) proposed using a modified Harris-Benedict equation to estimate REE. In this approach, REE_HB is adjusted to account for the hypermetabolic state resulting from certain clinical conditions:

   $$RE{E}_{\mathit{\text{Siddiki}}}=RE{E}_{HB}\times hf$$

   where hf is a unitless multiplier term for hypermetabolic factors with potential values of 1.13 per °C above 37°C, 1.2 for minor surgery, 1.35 for major trauma, and 1.6 for severe infection. The hypermetabolic factor yielding the highest value for hf is selected to calculate REE_Siddiki. The value for REE_Siddiki was inserted into the rearranged Weir equation to calculate V̇CO₂, which was then used to calculate dead-space fraction. In the original report of Siddiki et al. (29), the rearranged Weir equation for V̇CO₂ differs trivially from that above due to rounding.
3. Penn State estimate: An alternative formulation for estimating REE was derived previously by Frankenfield et al. (30, 31) specifically for critically ill patients. This approach uses the Mifflin-St. Jeor equation (32) to estimate REE for the patient in good health:

   $$\text{Males}:RE{E}_{MSJ}=10(Wt)+6.25(Ht)-5(\mathit{\text{age}})+5$$

   $$\text{Females}:RE{E}_{MSJ}=10(Wt)+6.25(Ht)-5(\mathit{\text{age}})-161$$

   with weight (Wt) in kg, height (Ht) in cm, and age in years. Additional clinical variables are then incorporated to yield the Penn State equations for REE in critical illness (30, 31):

   $$\text{If }\mathrm{B}\mathrm{M}\mathrm{I}<30\mathrm{k}\mathrm{g}/{\mathrm{m}}^2:RE{E}_{PSU}=0.96(RE{E}_{MSJ})+31(RR)(V_T)+167(T_{\mathit{\text{max}}})-6212$$

   $$\text{If }\mathrm{B}\mathrm{M}\mathrm{I}\ge 30\mathrm{k}\mathrm{g}/{\mathrm{m}}^2:RE{E}_{PSU}=0.71(RE{E}_{MSJ})+64(RR)(V_T)+85(T_{\mathit{\text{max}}})-3085$$

   where BMI is body mass index, RR is respiratory rate (breaths/minute), V_T is tidal volume (liters), and T_max is the maximum temperature (°C) over the last 24 hours.

4. Direct estimate from physiological variables: A novel alternative approach to estimate dead-space fraction directly was developed using least angle regression to derive a prediction model. Only variables with physiological plausibility were considered for inclusion in the model: anthropometrics (height, measured body weight, predicted body weight, body mass index, body surface area, sex, age, and race/ethnicity), respiratory variables (tidal volume, tidal volume per predicted body weight, respiratory rate, minute ventilation, minute ventilation per predicted body weight, PaCO₂, PaO₂:FiO₂, respiratory system compliance, PEEP, number of quadrants with infiltrates on chest imaging, and Murray lung injury score (33)), hemodynamic variables that may affect ventilation/perfusion matching (systolic blood pressure, mean arterial pressure, shock as defined by the Brussels criteria (34), heart rate, and rate-pressure product), primary cause of lung injury, and maximum temperature over the previous 24 hours. Clinically relevant multiplicative interaction terms were also considered, consisting of PaCO₂ and each of: minute ventilation, minute ventilation per predicted weight, body mass index, body surface area, measured body weight, height, sex, age, and temperature.

Model building employed least angle regression with five-fold cross-validation to minimize cross-validated mean squared prediction error. For parsimony, only the first five variables were retained in the final model since mean squared prediction error improved minimally with additional variables. The final model was refit using ordinary least squares to derive the reported coefficients:

$$V_D/V_T=0.1726+0.0059(RR)+0.0054(PEEP)+0.0293(LIS)+0.0036(PaC{O}_2\times {\dot{V}}_E)+0.000057(PaC{O}_2\times \mathit{\text{age}})$$

where RR is respiratory rate (breaths/minute), PEEP represents set PEEP (cmH₂O) on the mechanical ventilator, LIS is Murray lung injury score (33), PaCO₂ is measured in mmHg, and V̇_E represents total minute ventilation (liters/minute).

Comparison of Approaches

Dead-space fraction estimates were evaluated based on two overarching criteria: prediction of measured dead-space fraction and prediction of the association between measured dead-space fraction and mortality. Measured and estimated dead-space fraction were compared graphically using the Bland-Altman approach for assessing agreement between methods of clinical measurement (35). Quantitatively, methods were compared according to bias and accuracy. Bias describes whether the estimate systematically under-predicts or over-predicts measured dead-space fraction and was determined by comparing the difference in means between measurement and each estimating equation. A one-sample t-test was performed to determine if the mean difference was significantly different from zero. Accuracy describes how close each estimated value for dead-space fraction is to the true measured value and was calculated in two ways. First, the 95^th percentile of the absolute difference between measured and estimated values was calculated; the absolute difference was used to avoid canceling effects of negative and positive values. Second, the proportion of estimated dead-space fraction values that fell within ± 0.10 or ± 0.20 of measured dead-space fraction was calculated.

Measured and estimated dead-space fraction were also compared for their ability to predict 28-day mortality. Mortality per dead-space fraction quintile was used to evaluate whether the predictive ability of each dead-space fraction estimate varied by level. Simple logistic regression was used to compare the unadjusted association between each dead-space fraction estimate and mortality. In a sensitivity analysis, measured dead-space fraction was then added to each model to determine whether the association between estimated dead-space fraction and mortality included effects beyond that explained by measured dead-space fraction. Multivariable logistic regression was performed to evaluate the relationship between each dead-space fraction estimate and mortality. First, backward elimination (threshold p ≤ .05 to remain in model) was used to construct the best-fitting model of mortality with measured dead-space fraction, selecting from the following candidate predictors: age, shock, APACHE II, tidal volume per predicted body weight, PEEP, primary cause of lung injury, and respiratory system compliance. Berlin ARDS severity (3) and clinical trial enrolled were forced into the model as categorical variables for face validity. The selected covariates were then used to fit logistic models for each estimate of dead-space fraction. Finally, the area under the receiver operating curve (AUROC) for logistic regression models of mortality was used to determine whether measured dead-space fraction and the best-performing estimate improved predictive validity of the Berlin definition. Statistical analyses were performed using SAS 9.3 (Cary, NC). A two-sided p ≤ .05 was considered statistically significant.

RESULTS

A total of 210 patients in the V_D/V_T cohort were included in the primary analysis. In this cohort, measured dead-space fraction was markedly elevated (mean ± SD 0.60 ± 0.12). An additional 3,135 patients enrolled in the ARDSNet trials did not have measured dead-space fraction and were included in the second cohort. Patient characteristics for both cohorts are described in Table 1. Overall, mortality at 28 days was significantly lower in the V_D/V_T cohort (16% vs. 22%; p = .05).

Table 1.

Patient characteristics

	VD/VT Cohort				ARDSNet Cohort (n = 3,135)
	ALTA (n = 92)	EPVent (n = 57)	APC (n = 61)	Total (n = 210)
Demographics
Age	50 ± 17	54 ± 19	52 ± 18	52 ± 18	51 ± 16
Female	46 (50%)	22 (39%)	26 (43%)	94 (45%)	1,439 (46%)
Non-white race	28 (30%)	7 (12%)	18 (30%)	53 (25%)	871 (28%)
Body mass index (kg/m2)	29.0 ± 9.0	30.7 ± 9.3	28.3 ± 7.4	29.3 ± 8.7	28.7 ± 7.6
Clinical Characteristics
APACHE II	26 ± 7	26 ± 6	20 ± 7	25 ± 7	27 ± 7
Shock	59 (64%)	33 (58%)	16 (26%)	108 (51%)	1,733 (55%)
Primary cause of lung injury
Aspiration or pneumonia	50 (54%)	8 (14%)	44 (72%)	102 (49%)	1,952 (62%)
Sepsis	24 (26%)	14 (25%)	9 (15%)	47 (22%)	659 (21%)
Multiple transfusions	2 (2%)	0	0	2 (1%)	65 (2%)
Trauma	8 (9%)	15 (26%)	0	23 (11%)	223 (7%)
Other	8 (9%)	20 (35%)	8 (13%)	36 (17%)	235 (8%)
Respiratory Characteristics
Tidal volume (mL)	390 ± 70	493 ± 96	415 ± 92	425 ± 94	408 ± 94
Tidal volume (mL/kg PBW)	6.3 ± 0.9	7.7 ± 1.4	6.7 ± 1.4	6.8 ± 1.3	6.5 ± 1.4
Respiratory rate (breaths/min)	28 ± 7	25 ± 6	27 ± 7	27 ± 7	27 ± 7
PEEP (cmH2O)	9 ± 3	13 ± 4	9 ± 3	10 ± 4	10 ± 4
PaO2/FiO2	184 ± 63	148 ± 57	160 ± 63	167 ± 63	172 ± 76
PaCO2 (mmHg)	40 ± 8	41 ± 8	41 ± 11	41 ± 9	41 ± 10
Respiratory system compliance (mL/cmH2O)	32 ± 17	36 ± 11	31 ± 22	33 ± 17	32 ± 17
Murray lung injury score	2.4 ± 0.6	2.8 ± 0.6	2.6 ± 0.6	2.6 ± 0.6	2.6 ± 0.7
VD/VT measured	0.57 ± 0.12	0.67 ± 0.10	0.59 ± 0.12	0.60 ± 0.12	N/A
Clinical Outcomes
Mortality	12 (13%)	15 (26%)	7 (11%)	34 (16%)	693 (22%)
Vent-free days through day 28	16 ± 10	10 ± 9	15 ± 10	14 ± 10	14 ± 11

Data are reported as mean ± standard deviation or number (%).

Abbreviations: PEEP = positive end-expiratory pressure; V_D/V_T = dead-space fraction.

Performance of Estimating Equations

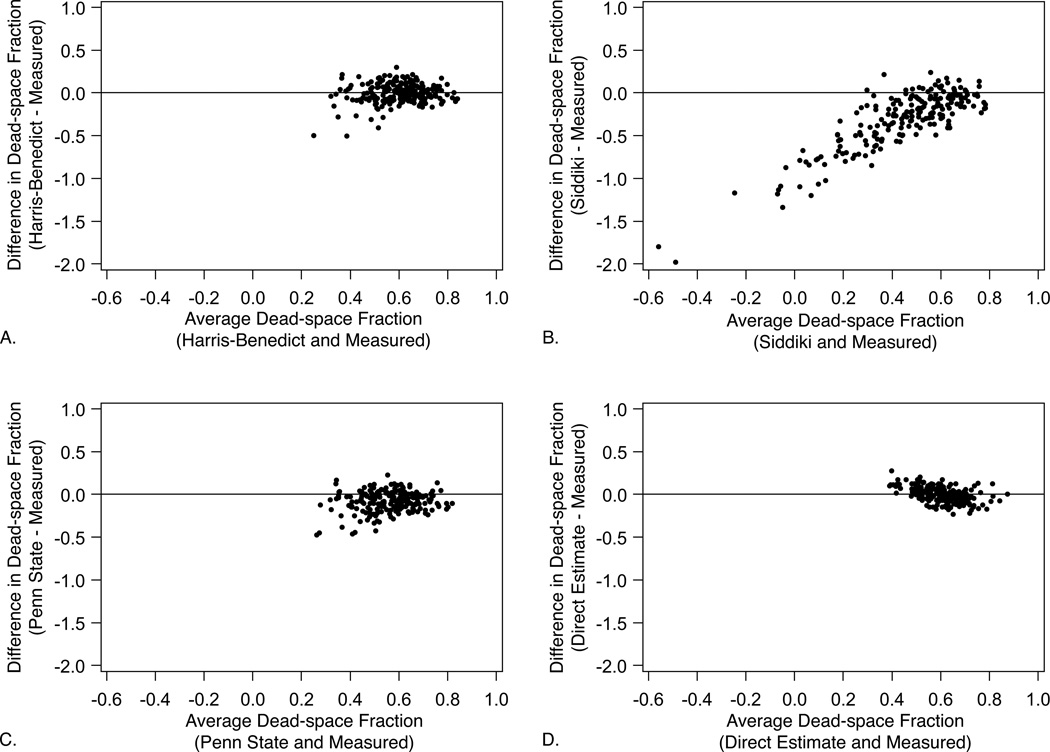
Bias was evaluated by comparing mean differences between estimated and measured dead-space fraction (Table 2). Both the Siddiki and Penn State estimates were significantly biased toward underestimation of measured dead-space fraction (mean difference −0.32 ± 0.35 and −0.08 ± 0.12, respectively; p < .01 for both comparisons). The unadjusted Harris-Benedict and direct estimates were unbiased (mean difference −0.01 ± 0.12 and 0 ± 0.09, respectively; p = .30 for unadjusted Harris-Benedict estimate; direct estimate unbiased by design).

Table 2.

Performance of estimating equations compared to measured dead-space fraction in V_D/V_T Cohort

	Method of Dead-space Estimation
	Harris-Benedict	Siddiki	Penn State	Direct
VD/VT mean ± SD, all patients	0.59 ± 0.13	0.28 ± 0.38	0.52 ± 0.14	0.60 ± 0.08
Survivors	0.58 ± 0.14	0.25 ± 0.39	0.50 ± 0.14	0.59 ± 0.07
Non-survivors	0.67 ± 0.11	0.47 ± 0.28	0.59 ± 0.11	0.66 ± 0.08
Bias: difference between measured and estimated VD/VT, mean ± SD	−0.01 ± 0.12	−0.32 ± 0.35*	−0.08 ± 0.12*	0 ± 0.09*†
Accuracy: 95th percentile of absolute difference between measured and estimated VD/VT	0.20	1.03	0.30	0.17
VD/VT accuracy threshold of ± 0.10
Accuracy (%)	70.1	26.5	52.5	73.0
Values overestimating (%)	15.7	3.4	4.9	13.7
Values underestimating (%)	14.2	70.1	42.6	13.2
VD/VT accuracy threshold of ± 0.20
Accuracy (%)	95.1	44.6	85.3	98.5
Values overestimating (%)	1.5	1.0	0.5	0.5
Values underestimating (%)	3.4	54.4	14.2	1.0
Correlation coefficient	0.58*	0.45*	0.56*	0.67*

Abbreviations: V_D/V_T = dead-space fraction

^*p< .01 between estimated and measured dead-space fraction

^†Direct estimate was unbiased by design.

Accuracy was evaluated first as the 95^th percentile of the absolute difference between measured and estimated dead-space fraction (Table 2). The unadjusted Harris-Benedict and direct estimates were the most accurate estimates of dead-space fraction (95^th percentile 0.20 and 0.17, respectively). The Penn State estimate displayed intermediate accuracy relative to the other formulations (95^th percentile 0.30). The Siddiki estimate was the least accurate (95^th percentile 1.03).

Accuracy was also evaluated as the proportion of dead-space fraction estimates within two pre-specified thresholds of measured dead-space fraction: ± 0.10 and ± 0.20 (Table 2). Again, the unadjusted Harris-Benedict and direct estimates displayed the best performance, with 70.1% and 73.0% of estimates within ± 0.10 of measured dead-space fraction, respectively, and > 95% of estimates within ± 0.20 for both formulations. By contrast, the Siddiki and Penn State estimates were considerably less accurate, predicting dead-space fraction to within ± 0.10 of the measured value only 26.5% and 52.5% of the time. The Siddiki estimate alone yielded negative values for dead-space fraction, while no estimate produced values ≥ 1.00. Graphical comparison of each estimate with measured dead-space fraction using Bland-Altman plots confirmed these findings (Fig. 1).

Figure 1.

Bland-Altman analyses comparing measured dead-space fraction with that determined by each estimating equation: (a) Harris-Benedict, (b) Siddiki, (c) Penn State, (d) direct estimate. Plots consist of the difference between estimated and measured dead-space fraction formulations (vertical axis) versus the average value of the two approaches (horizontal axis). Differences greater than zero indicate overestimation.

Prediction of Mortality

Measured dead-space fraction was significantly higher in non-survivors compared to survivors (0.67 ± 0.12 vs. 0.59 ± 0.12; p < .01). Estimated dead-space fraction also was significantly higher among non-survivors for all estimating equations (p < .01 for all comparisons) (Table 2).

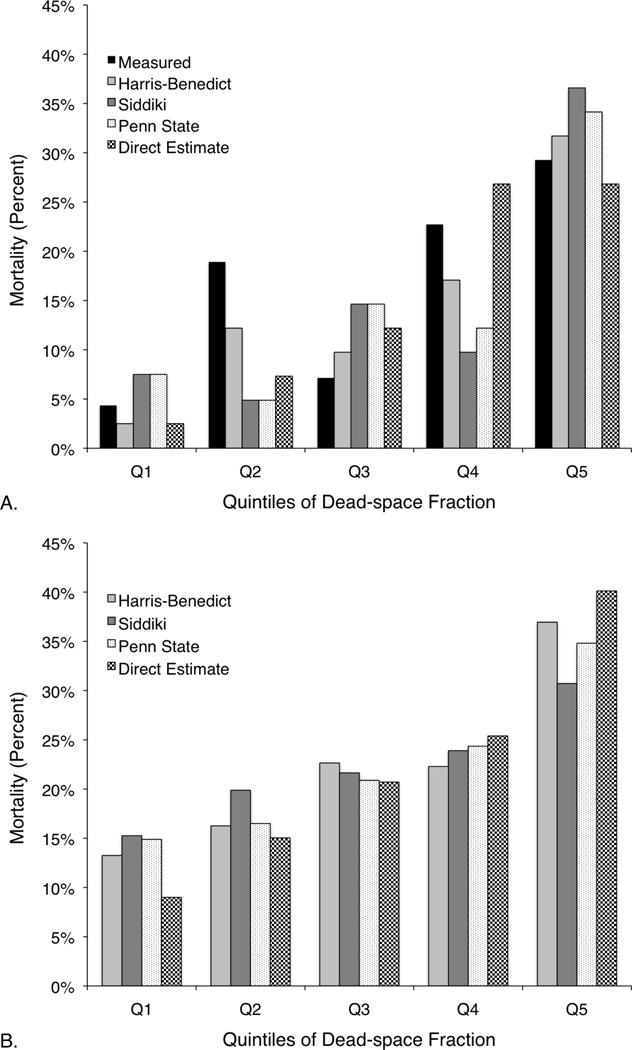
Mortality by quintile of measured and estimated dead-space fraction is reported in Figure 2. Quintiles were calculated separately for each formulation of dead-space fraction to account for potential differences in scaling. Mortality per unadjusted Harris-Benedict quintile was within ± 6.7% of that per measured dead-space fraction for all quintiles (Fig. 2A). No other estimating equation as closely approximated the measured dead-space fraction per-quintile mortality. In the ARDSNet cohort, mortality similarly increased with successive quintiles of each dead-space fraction estimate (Fig. 2B).

Figure 2.

Observed mortality by quintile of measured or estimated dead-space fraction: (a) among patients with measured dead-space fraction (V_D/V_T Cohort); (b) among patients without measured dead-space fraction (ARDSNet Cohort). Quintiles were calculated separately for each formulation of dead-space fraction.

In the unadjusted analysis, higher measured dead-space fraction was significantly associated with increased risk of death (Table 3). The multivariable model-building process identified measured dead-space fraction, APACHE II, and PEEP as statistically significant independent predictors of death, with clinical trial enrolled and Berlin ARDS severity forced into the model for face validity but not reaching statistical significance. In the multivariable analysis, for every 0.05 increase in measured dead-space fraction, odds of death increased by 36% (OR 1.36, 95% CI 1.10–1.68; p < .01).

Table 3.

Odds ratios (95% CIs) for death per 0.05 increase inmeasured or estimated dead-space fraction^*

	Measured	Harris-Benedict	Siddiki	Penn State	Direct
VD/VTCohort
Unadjustedanalysis	1.36 (1.14–1.62)	1.40 (1.14–1.71)	1.12 (1.04–1.22)	1.36 (1.13–1.63)	1.74 (1.34–2.27)
Multivariable analysis†	1.36 (1.10–1.68)	1.55 (1.21–1.98)	1.19 (1.07–1.31)	1.53 (1.21–1.95)	1.80 (1.26–2.56)
ARDSNet Cohort
Unadjustedanalysis	Not measured	1.16 (1.11–1.20)	1.04 (1.02–1.05)	1.14 (1.10–1.18)	1.47 (1.39–1.56)
Multivariable analysis†	Not measured	1.10(1.05–1.14)	1.03(1.02–1.05)	1.09(1.04–1.13)	1.41 (1.30–1.53)

^*Odds ratios for all formulations of dead-space fraction differ significantly from 1.0 with p< .01 for all analyses.

^†Multivariable model adjusted for APACHE, Berlin ARDS severity, PEEP, and clinical trial enrolled.

Each estimate of dead-space fraction also was significantly associated with mortality on unadjusted and multivariable analyses in both cohorts (p < .01 for all analyses). However, odds ratios for death varied considerably (Table 3) due to differences in scaling and accuracy of dead-space fraction estimates and variation in predicting the relationship between measured dead-space fraction and mortality. In the V_D/V_T cohort, the Harris-Benedict and Penn State odds ratios for death were most similar to that of measured dead-space fraction in both the unadjusted and multivariable analyses (multivariable model: OR_death per 0.05 increase in dead-space fraction, Harris-Benedict OR 1.55, 95% CI 1.21–1.98; Penn State OR 1.53, 95% CI 1.21–1.95). The Siddiki odds ratio was considerably lower (OR 1.19, 95% CI 1.07–1.31), while that of the direct estimate was higher (OR 1.80, 95% CI 1.26–2.56). In the ARDSNet cohort, the Harris-Benedict and Penn State odds ratios for death were similar to each other, while the Siddiki and direct estimate odds ratios differed considerably.

In the sensitivity analysis, only the direct estimate remained significantly associated with mortality after adding measured dead-space fraction to the model, indicating the direct estimate had an association with mortality that was independent of measured dead-space fraction.

Compared with modeling mortality using the Berlin definition alone, adding measured dead-space fraction significantly improved predictive validity in the V_D/V_T cohort, with an AUROC of 0.689 (95% CI 0.587–0.791) vs. 0.534 (95% CI 0.440–0.628; p = .02). Similarly, adding the unadjusted Harris-Benedict estimate to the Berlin definition significantly improved predictive validity for mortality in both the V_D/V_T cohort (AUROC 0.714, 95% CI 0.616–0.813 vs. 0.543; 95% CI 0.449–0.637; p < .01) and the ARDSNet cohort (AUROC 0.644, 95% CI 0.617–0.672 vs. 0.592, 95% CI 0.566–0.618; p < .01).

Prediction of Outlying Estimates

A post-hoc analysis was conducted to identify the subset of patients in whom the unadjusted Harris-Benedict estimate did not predict measured dead-space fraction accurately, to within ± 0.10. Among baseline characteristics, only PaCO₂ differed significantly between patients with inaccurate compared to accurate estimates (39 ± 9 vs. 41 ± 9, respectively; p = .04). Nearly half (43%) of patients with PaCO₂ < 30 mmHg had an inaccurate Harris-Benedict estimate, compared with just 28% of patients with PaCO₂ ≥ 30 mmHg (p = .17). Considering only underestimates, PaCO₂ was < 30 mmHg in 24% of patients; by contrast, only 8% of patients in whom the Harris-Benedict approach did not underestimate dead-space fraction had PaCO₂ < 30 mmHg (p < .01). Such marked hypocapnia occurred infrequently in our cohorts (in 10% and 9% of patients in the V_D/V_T and ARDSNet cohorts, respectively), as would be expected during lung-protective ventilation for ARDS. No comparable pattern was seen with overestimation.

DISCUSSION

The present study demonstrates that dead-space fraction is best estimated using the unadjusted Harris-Benedict equation for energy expenditure to predict measured dead-space fraction and its association with mortality. The Harris-Benedict and direct estimates predicted measured dead-space fraction most accurately. However, the direct estimate was associated with death independent of measured dead-space fraction, indicating a relationship with mortality beyond that explained by measured dead-space fraction. Still, even the Harris-Benedict approach, the best-performing estimate, predicted measured dead-space fraction to within ± 0.10 in only 70% of patients and ± 0.20 in 95% of patients – a considerable range given the scale of measure. Therefore, estimates of dead-space fraction should not replace prospective measurement in future clinical trials of ARDS. For secondary analyses of existing clinical trials data where dead-space fraction was not measured, the unadjusted Harris-Benedict estimate can be used to estimate the independent association between dead-space fraction and mortality.

Increased dead-space fraction is a clinical hallmark of ARDS that independently predicts patient outcomes (3, 4). For this reason, dead-space fraction was considered in formulating the 2012 Berlin definition of ARDS to lend further face validity to the definition (36). However, dead-space fraction was not included in the final Berlin definition because it is not routinely measured (36). The present study found that adjusting for measured dead-space fraction in the Berlin definition significantly improved predictive validity for mortality. Adjusting for estimated dead-space fraction using the Harris-Benedict approach similarly improved the Berlin definition’s predictive validity for mortality (3). These findings reinforce the need to adjust for dead-space fraction as a marker of ARDS severity that independently predicts mortality.

Secondary analyses of epidemiological and clinical trials data are a mainstay of ARDS research due to the expense and resources required to conduct clinical trials (37). Because such secondary analyses play a central role in shaping future directions of ARDS research and clinical practice, it is essential they incorporate known independent predictors of ARDS mortality. Oxygenation, respiratory system compliance, and dead-space fraction have been identified repeatedly as predictors of clinical outcomes from ARDS (2, 4, 7). While oxygenation and respiratory system mechanics are frequently considered, dead-space fraction is rarely measured in such studies and thus altogether ignored in secondary analyses.

Few prior reports have attempted to estimate dead-space fraction in ARDS. The Siddiki estimate (29) was shown previously in a study of just thirteen patients to substantially underestimate measured dead-space fraction (38), a finding confirmed here in a much larger cohort. In fact, the Siddiki estimate produced negative values for dead-space fraction in some patients because its use of hypermetabolic factors led to overestimating V̇CO₂ (39). Frankenfield et al. derived a predictive equation for dead-space fraction requiring measurement of end-tidal CO₂ in a heterogeneous population of critically ill patients (40). Their study excluded patients with FiO₂ > 0.60 due to equipment limitations, limiting generalizability to ARDS cohorts. Moreover, end-tidal CO₂ is not routinely captured in clinical trials or epidemiological data, limiting utility of this approach for the purpose of secondary analyses of existing data.

Alternative surrogates for dead-space fraction have been proposed. The ARDS Berlin Definition Task Force considered total minute ventilation standardized to a PaCO₂ of 40 mmHg (3, 41). Post-hoc analysis of the Berlin cohort found that stratifying patients with severe ARDS (PaO₂:FiO₂ ≤ 100) by standardized minute ventilation significantly improved mortality risk prediction (3). Sinha et al. proposed a similar formulation, the ventilatory ratio, which includes predicted minute ventilation and predicted PaCO₂ (42). Both approaches may be useful for bedside contemplation of minute ventilation requirements, but neither has been validated as a surrogate for measured dead-space fraction to support use in clinical research.

Important limitations to this study exist. First, estimated dead-space fraction is not intended for use in place of direct measurement in clinical practice or future prospective studies. Rather, this report highlights the need to incorporate measurement of dead-space fraction in future clinical trials and prospectively collected observational data. When measured dead-space fraction is unavailable, the unadjusted Harris-Benedict estimate may be considered for research purposes. The unadjusted Harris-Benedict estimate tends to underestimate dead-space fraction when PaCO₂ is < 30 mmHg. Thus, caution should be used when a large proportion of the study population has marked hypocapnia.

Second, the best-performing estimate here relies on the unadjusted Harris-Benedict equation for energy expenditure and assumes a respiratory quotient of 0.8 for all patients. Respiratory quotient fluctuates with feeding, nutritional status, and anaerobiosis (43, 44), factors not considered here. The unadjusted Harris-Benedict equation has been shown previously to be unreliable in predicting energy expenditure in critically ill patients (39), which in part may be due to variation in ventilator settings (15, 45, 46), metabolic stress (47, 48), and fasting status (44) in prior studies. By contrast, a singular focus on early ARDS and protocolized low tidal volume ventilation here likely improved its performance in estimating dead-space fraction. It is unclear how the unadjusted Harris-Benedict dead-space fraction estimate would perform in cohorts managed with different ventilator settings, prone positioning, or experimental interventions.

Finally, differences in mechanical ventilation practices directly affect measured dead-space fraction and may limit its utility as a marker of disease severity absent comparable settings. Tidal volume, PEEP titration, dynamic hyperinflation, and use of a brief end-inspiratory pause all have been shown to affect measured dead-space fraction irrespective of underlying disease severity (12–16). In this study, these effects likely were mitigated in part by use of protocolized lung-protective ventilation for all included patients, though between-patient variation still occurred (Table 1).

CONCLUSIONS

Dead-space fraction is one of few lung-specific independent predictors of mortality from ARDS. As such, dead-space fraction should be measured whenever possible in clinical trials and prospective epidemiological studies to permit adjustment for its effects in secondary analyses. For analyses of existing data where dead-space fraction was not measured, the unadjusted Harris-Benedict estimate should be considered to estimate the association between dead-space fraction and mortality.