Inclusion of vein traits improves predictive power for the leaf economic spectrum: a response to Sack et al. (2013)

Summary

A unified model for the leaf economics spectrum based on venation network geometry is shown to be valid, despite recent criticism in this journal.

Abstract

Our model for the worldwide leaf economics spectrum (LES) based on venation networks (Blonder et al., 2011, 2013) was strongly criticized by Sack et al. (2013) in this journal. Here, we show that the majority of criticisms by Sack et al. are based on mathematical and conceptual misunderstandings. Using empirical data from both our original study as well as others in the literature, we show support for our original hypothesis, that venation networks provide predictive power and conceptual unification for the LES. In an effort to reconcile differing viewpoints related to the role of leaf venation traits for the LES, we highlight several lines of further investigation.

Introduction

The worldwide leaf economics spectrum (LES) describes strong correlations between multiple leaf functional traits underlying resource allocation and fluxes in plants (Reich et al., 1997; Wright et al., 2004; Reich, 2014). These traits have broad ecological importance and include variables such as mass-normalized photosynthetic rate (A _m) and nitrogen content (N _m), leaf lifespan (LL), and leaf mass per area (LMA). Despite their importance, the origin of these patterns has remained obscure (Donovan et al., 2011).

Venation networks provide one hypothesis for the LES. The multiple functions of venation networks (e.g. mechanical support, water transport, sugar transport) and constrained planar geometry can result in functional and structural tradeoffs in leaves. In 2011, we proposed a mathematical model for the LES (Blonder et al., 2011) based on trade-offs associated with venation networks. This theory derives a series of equations that quantitatively predict various leaf functional traits and leaf functioning based on measurements of leaf vein traits. In 2013, we extended this model (Blonder et al., 2013) to include different types of covariation between vein traits and leaf morphology that would be selected for in different environments. The extended model also predicts how the global inter-specific LES should be modulated by differing selective pressures on different species or individuals (e.g. sun versus shade leaves within a species, or drought adaptation across species).

Recently in this journal, Sack et al. (2013) examined the theoretical basis and empirical evidence for the Blonder et al. (2011) venation model and found limited support. They instead proposed that venation networks are linked only to resource fluxes and not directly to structural investment or to leaf lifespan, because other variables are more important in driving these latter traits. While we agree that a critical examination of any model is indeed appropriate for scientific progress, the criticism by Sack et al. (2013) is based on incomplete understanding of our model. As we illustrate below, their conclusions are based on several mathematical and conceptual issues and also are based on an selective view of empirical data. Thus, despite the strong wording of Sack et al. (2013), we show that the Blonder et al. models remain an useful hypothesis that can provide conceptual clarity and falsifiable predictions for the LES.

Mathematical and conceptual misunderstandings

Sack et al. claim that our theory: (i) is circular; (ii) fails to constrain venation traits; (iii) has low sensitivity to venation traits; and (iv) has no empirical support (their Table 3). We show that each of these claims is not true.

Sack et al. claim that our theory is circular, although predictions are driven by variation in vein traits

Sack et al. state that our model is not driven by variation in vein traits, but rather by other LES traits. For example, we do derive an equation for area-normalized photosynthesis, then divide it by the equation for LMA to obtain an equation for mass-normalized photosynthesis (or similarly, for writing N _m as partially dependent on the volume of nonvein tissue, whose volume is assumed to be proportional to mass-normalized photosynthesis). However, their criticism of circularity also applies to any model for the LES that is based on mass- or area-normalized traits. Indeed, the generality of the LES and the validity of mass normalization has been a subject of recent controversy (Lloyd et al., 2013; Osnas et al., 2013). We instead believe that studying the mass basis of leaf traits accurately captures physiological and life history differences and is useful for understanding carbon balance in plants (Westoby et al., 2013).

We actually proposed that A _m, LL, LMA, and N _m are all functions of a small set of venation network traits: e.g. vein density (VD, mm^–1), inter-vein distance (IVD, mm), and vein loopiness (mm^–2). All of our equations are ultimately functions of only venation network traits, contrary to Sack et al.’s assertion. Fig. 1 is a causal flow diagram of our 2011 model’s equations 4–7. As we previously claimed, causality flows from vein traits to LES traits and not the other way around. Note, the diagram also shows several other traits, reflecting a subset of the parameters described in the original model and including several listed by Sack et al. in their Fig. 2. However, we treated all these additional leaf traits as constants, in order to explore the sole effect of VD (see also the following discussion on sensitivity analysis).

Fig. 1.

Structure of the Blonder et al. (2011) venation model for the leaf economics spectrum (LES). Light green boxes indicate venation traits; dark blue indicate LES traits; white boxes indicate other traits; arrows indicate causal relationships between variables; dashed lines indicate a subset of the other constant parameters in the model. The absence of arrows pointing to the venation traits demonstrates that the model is not circular. Here, we show vein density driving inter-vein distance and vein loopiness, which occurs when reticulate venation is assumed. A _m, mass-normalized photosynthetic rate; LL, leaf lifespan; LMA, leaf mass per area; N _m, nitrogen content.

Fig. 2.

Vein density (VD) and inter-vein distance (IVD) are closely related in our model, contrary to the claims of Sack et al. (2013). Our predictions are based on geometrical arguments that the product of VD and IVD (red points) is a dimensionless number taking a value between 1 (dotted line) and 2 (dashed line). Reanalysis of our published data (Blonder et al., 2011) shows that nearly all data fall within these analytic limits, with the outliers reflecting noise from finite-sized images being analysed (this figure is available in colour at JXB online).

Sack et al. claim that our 2011 model allows vein density and inter-vein distance to vary independently, when these variables must necessarily be negatively correlated

Sack et al. argue that veins that are spaced further apart (higher IVD) must also have a lower VD; therefore, VD and IVD cannot provide wholly independent parameters for the model. We completely agree with this statement, as it is one that we also made in Blonder et al. (2011; compare Box 1 ‘Geometrical constraints on leaf venation traits’ and text on page 93 with their Table 3.1). Indeed, we wrote that the product of vein density and inter-vein distance takes a positive constant value between 1 (no reticulation) and 2 (maximum reticulation). The implication is that our model predicts that VD and IVD will show a slope of –1 on log-log axes. Data replotted from our original paper support this prediction (Fig. 2). We have already relied on this strong relationship to parameterize all four of our central equations for A _m, LL, LMA, and N _m in terms of only vein density, by assuming reticulate venation.

Sack et al. also point out that our model assumes the product of inter-vein distance and leaf thickness are negatively correlated. This linkage is based on optimal flow considerations in a highly simplified leaf (Noblin et al., 2008). Sack et al. rightly note that hydraulic transport in the leaf is more complex than in our deliberately simplified model and that optimal flow is not always a valid assumption. We agree and we have published a revised model that highlights the causes and consequences of this variation for the LES (Blonder et al., 2013). Additionally, the proposed linkage between inter-vein distance and leaf thickness is found in five of the 10 datasets presented (their Table 3.3) and in other more recent publications (Brodribb et al., 2013; Zwieniecki and Boyce, 2014).

Sack et al. claim that the model is not sensitive to venation network traits, but their sensitivity analysis is mathematically incorrect

Sack et al. calculate the partial derivative of each of our equations with respect to the venation traits, evaluate this derivative at a mean trait value, and show that the resulting number is much smaller for vein traits than for other traits. The premise of their approach is flawed, as can be seen through a Taylor series expansion. Suppose that f is a function of two variables, x and y. To first order, the function can be approximated around a value (x ₀, y ₀) as:

$$f\left(x,y\right)\approx f\left(x_0,y_0\right)+\left(x-x_0\right){\frac{\partial f}{\partial x}|}_{x=x_0}+\left(y-y_0\right){\frac{\partial f}{\partial y}|}_{y=y_0}$$

Sack et al. claim that $\frac{\partial f}{\partial x}<<\frac{\partial f}{\partial y}$ implies that f is less sensitive to x than to y. However, this claim makes sense only if the two variables are on equivalent scales. If instead measurement units of x and y are on different scales or are simply incomparable (e.g. meters and seconds), then this comparison is erroneous.

Sack et al. incorrectly compare raw partial derivative values without consideration for the different units of each variable, making assessment of relative magnitudes impossible. For example, Sack et al. compare $\frac{\partial A_m}{\partial VD}$ to $\frac{\partial A_m}{\partial T}$, where T is leaf thickness, A _m is mass specific photosynthetic rate, and VD is vein density. In this example, the first derivative has units of photosynthesis×length while the latter has units of photosynthesis×length^–1, which are incomparable. Moreover, a change in f can be driven by variable x either by the partial derivative $\frac{\partial f}{\partial \xi }$ or by the change in the variable itself (x – x ₀). Sack et al. neglect to consider both the natural range of the variable and the units in which it is expressed. For example, Sack et al. state that $\frac{\partial LMA}{\partial VD}=8.8\times {10}^{-4}$ (without units, but they are g m^–1), which appears small compared to $\frac{\partial LMA}{\partial T}=3.0\times {10}^5$ (also without units, but they are g m^–3). Ignoring the previously discussed unit problem, the model appears more sensitive to T than to VD. But a realistic 10% change in VD is 1mm mm^–2, or 10³ m^–1, and a realistic 10% change in T 10 μm, or 10^–5 m. Then, the overall effect on LMA for each of these shifts is on the order of 8.8×10^–4×10³ ≈ 10⁰ g m^–2 for VD and 3.0×10⁵×10^–5 ≈ 10⁰ g m^–2 for T: i.e. nearly equivalent, contrary to the claims of Sack et al. Thus our model is sensitive to nonvenation traits, but it is also sensitive to venation traits, as originally intended.

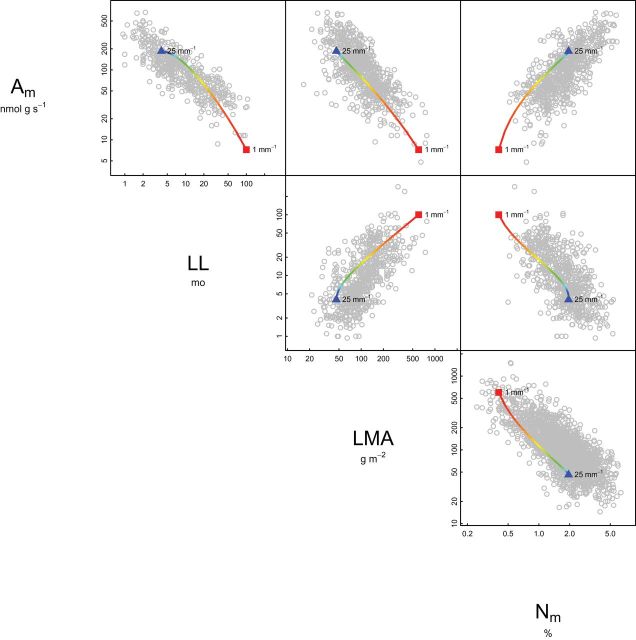
We instead suggest testing model sensitivity to venation traits by first holding all other model parameters constant, then varying VD across a reasonable range (e.g. 1–25mm^–1, the global range; Brodribb et al., 2007). We did this in Fig. 3 of our 2011 paper (redrawn here as Fig. 3) and found that variation in VD alone was sufficient to replicate the approximate slope and magnitude of all LES correlations between A _m, LL, LMA, and N _m. This published result has indicated that the model is sensitive to venation traits.

Fig. 3.

Predictions of our 2011 model are driven by variation in VD, contrary to the claims of Sack et al. (2013). This figure is redrawn from Fig. 3 of our original paper, assuming that VD×IVD=1, as for nonreticulate venation, and holding all but one model parameter (see Fig. 1) to constant values. VD was then varied across the global range. Circles indicate GLOPNET data for the worldwide leaf economics spectrum (LES) (Wright et al., 2004); rainbow lines beginning with red squares indicate predictions for VD=1mm^–1; blue triangles indicate predictions for VD=25mm^–1. Variation in VD, holding all other leaf traits constant, can account for the observed sign and slope of LES correlations. A _m, mass-normalized photosynthetic rate; LES, leaf economics spectrum; LL, leaf lifespan; LMA, leaf mass per area; N _m, nitrogen content; IVD, inter-vein distance; VD, vein density (this figure is available in colour at JXB online).

Sack et al., in their Table 3, say that empirical support for predicted correlations is weak, but we believe these conclusions are subjective

Sack et al. also challenge our model because they feel that empirical support for the proposed correlations is weak. However, the available data show some support our model. For example, our model proposes that VD should be correlated with each individual leaf trait (A _m, LL, LMA, and N _m). In the data cited by Sack et al. (their Table 3), one of one dataset supports the A _m–VD linkage (their Fig. 8), three of three datasets support the LMA–VD linkage (their Table 3.2), three of three datasets support the LL–VD linkage (their Table 3.4), and no data are presented for the N _m–VD linkage except our 2011 results, which support predictions. Moreover, our recent work in Arabidopsis thaliana showed that VD is causally associated with LES traits in the ways predicted by our original theory (B Blonder, F Vasseur, C Violle, B Shipley, B Enquist, D Vile, unpublished data). While we agree with Sack et al. that a clear assessment of our model with empirical data are needed, at this point, multiple lines of evidence at both the intra- and inter-specific scale are consistent with the main predictions of the Blonder et al. model.

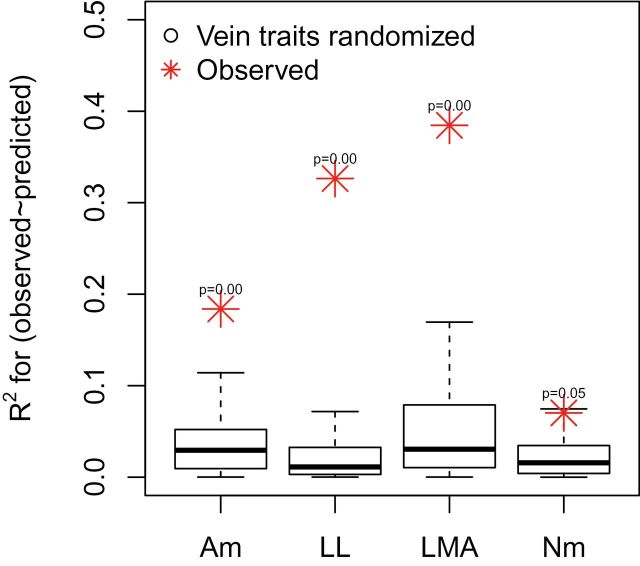
Moreover, Sack et al. further claim that model predictions are empirically not improved by the inclusion of vein traits (i.e. that other traits drive model predictions; their Fig. 6). We re-examined our original dataset, restricted to the more limited subset of observations considered not ‘erroneous’ by Sack et al. We preserved the structure of the analysis but chose uniformly random values for VD from 1 to 25mm^–1, then regressed observed and predicted values for the true dataset and the randomized dataset. Contrary to the analysis of Sack et al., we found that r ² values for this regression were significantly higher for all four LES traits, by an average of 20.4% across traits (Fig. 4) (R code available in Supplementary Appendix S1, available at JXB online). This result indicates that inclusion of vein traits improves predictive power for LES traits as described in our original model. It would be useful to further assess our theory by conducting this same analyses at both the within and between species scales using larger datasets where both LES and vein traits have been collected.

Fig. 4.

Inclusion of vein traits improves the correlation between observed and predicted values of leaf economics spectrum traits, contrary to the assertion of Sack et al. (2013). We reanalysed our published data and found that r ² values for a regression of predicted against observed values (not constrained to the origin) were significantly higher in all cases (red points) than for the same regressions when vein density was sampled uniformly randomly from its global range (black points) (n=100 random samples per trait). A _m, mass-normalized photosynthetic rate; LL, leaf lifespan; LMA, leaf mass per area; N _m, nitrogen content (this figure is available in colour at JXB online).

Moving forward

While the origin of the LES clearly remains controversial (Shipley et al., 2006; Donovan et al., 2011), our own empirical studies and the data compiled by Sack et al. (2013) indicate that venation networks do provide a useful basis for understanding the origin of the global LES. Below we outline four actions to move the field closer to a complete understanding of role of venation networks for the LES.

We agree that a sole focus on just one vein trait cannot explain all of the variation in the associated LES traits. Future work should work towards quantifying how other traits could also influence LES traits. As specified in our theory, several additional leaf structural and physiological traits can also influence the LES (Fig. 1). For example, variation in the mass density of vascular and nonvascular leaf tissue can provide a vein-independent source of LES trait variation. Inclusion of major veins in the model would also be useful. As Sack et al. rightly point out, these veins do make an important contribution to leaf volume and mass, although the volume contribution of minor veins does play an important role in high-VD leaves (Feild and Brodribb, 2013). Variation in other leaf anatomic structures (e.g. phloem architecture; Adams III et al., 2013) may also modulate the LES in ways that have not been adequately considered.

Our revised theory (Blonder et al., 2013) needs further constructive examination and testing by a wider group of investigators. We encourage the reader to examine our original papers and data to determine the merits and flaws of the approach, as well as collect data needed to further test it (e.g. paired measurements of LES traits, venation network traits, other anatomical traits such as leaf thickness and tissue density). Our revised theory also makes clear predictions for how venation traits mediate different economic strategies across differing environments. We are currently in the process of collecting detailed data within species, across species, and across environmental gradients to test many of these predictions.

We encourage the development of alternate theories for the origin of the LES that make predictions at both the intraspecific and inter-specific scales. Besides our theory, there is only one other general explanation for the LES, based on cell wall/volume partitioning (Shipley et al., 2006). Both theories depend on several variables but are focused on a single key variable. It is not clear if the ‘flux-trait-network’ framework presented by Sack et al. is an alternative to these two models or would lead to distinguishable predictions. Nonetheless, until a falsifiable alternative is developed, future work should assess support for each of these extant theories’ assumptions, and predictions in a comparative framework using identical data.

Genetic approaches can also be used to identify the causes of variation of LES traits. A recent search for QTLs and genes controlling the LES via analysis of a population of recombinant inbred lines of A. thaliana and mutants found several candidate genes, some of which are involved in vascular development (Vasseur et al., 2012). This highlights a LES-venation linkage that is in agreement with our theory. Further artificial selection or knockout experiments may provide further insight into this question (Donovan et al., 2011).

Conclusions

We maintain that a simple explanation for the LES has not been rejected and indeed seems achievable. For example, within the GLOPNET data, 82% of the variation in A _m, LMA, and N _m lies along a single axis (Wright et al., 2004). Additionally, structural equation modelling (Shipley et al., 2006) shows that all the correlations between A _m, LL, LMA, and N _m in the global GLOPNET dataset can be explained by a single latent (unmeasured and unidentified) variable that may be tied to leaf venation network geometry (B Blonder, F Vasseur, C Violle, B Shipley, B Enquist, D Vile, unpublished data). The generality of the global LES indicates the possibility of a general explanation. One general explanation was hypothesized and accurately presented in Blonder et al. (2011, 2013) and the potential role of one key venation trait in particular—minor venation density—appears to be central in driving coordinated shifts in multiple LES traits (Fig. 3).

Our theory is a deliberately simplified approach that emphasizes unifying concepts in order to link how selection on leaf venation geometry is a fundamental basis to understand the diversity of leaf form and function and the carbon balance of leaves. Our approach contrasts with the more complex ‘flux-trait-network’ perspective of Sack et al. because our theory: (i) provides clear mathematical derivations and predictions; (ii) deliberately starts with relatively few assumptions so as to generate a large number of predictions per free parameter; and (iii) provides a quantitative baseline for comparison and successive refinement in order to advance a more predictive understanding for how selection shapes integrated plant phenotypes.

Supplementary data

Supplementary data are available at JXB online.

Appendix S1. R code to duplicate analysis in Fig. 4.