Active Cell and ECM Movements During Development

Abstract

Dynamic imaging of the extracellular matrix (ECM) and cells can reveal how tissues are formed. Displacement differences between cells and the adjacent ECM scaffold can be used to establish active movements of mesenchymal cells. Cells can also generate large-scale tissue movements in which cell and ECM displacements are shared. We describe computational methods for analyzing multi-spectral time-lapse image sequences. The resulting data can distinguish between local “active” cellular motion versus largescale, tissue movements, both of which occur during organogenesis. The movement data also provide the basis for construction of realistic biomechanical models and computer simulations of in vivo tissue formation.

1 Introduction

Tissue engineering, the controlled construction of tissues—that is, cells and their extracellular matrix (ECM) environment—is a promising avenue of future biomedical applications. To realize this possibility, the dynamic and mutually interdependent relationship between cells and ECM has to be understood. Changes in local cell and ECM organization have a clear impact on cell differentiation, cell signaling, and further downstream effects with direct medical importance; for example, the durability of heart leaflet implants [9] or treatments to reduce malignant cell invasion [7]. The large-scale tissue movements, which characterize early embryonic development, are not replicated by typical culture techniques. Thus the ability of cells to translocate in conjunction with their microenvironment is generally underappreciated—so much so that it is often taken for granted that cells inevitably crawl along ECM fibers in response to repulsive or attractive biochemical cues. Yet, if investigators are interested in measuring modes of active cell locomotion, in situ, it is necessary to study cellular motion in the context of deformation of the surrounding ECM; i.e., as part of a composite tissue.

In the following sections we discuss experimental and computational techniques that we used to study ECM movements in live embryos, and the methods we used to compare cell and local ECM movement data to establish cell-autonomous motility relative to the ECM microenvironment.

2 Embryo Preparation

1. Fertilized wild-type or transgenic Tie1∷H2B-YFP quail eggs (Coturnix coturnix japonica) are incubated in the humidified atmosphere at 37 °C.

2. Embryos are removed from the eggs and mounted on Whatman 52 filter paper rings (Whatman International, Maidstone, England) as described in [2, 11, 12].

3. Embryos are staged according to the classification developed by Hamburger and Hamilton (HH) [8].

4. For further manipulations, embryos are placed onto culture dishes [3, 2], typically with their ventral surface facing away from the culture support.

3 In Vivo Labeling of ECM Antigens

Fluorophore conjugation is an efficient method to covalently label antibodies or other molecules of interest [10, 12]. To visualize ECM antigens in living quail embryos we use anti-fibrillin-2 antibody JB3 and anti-fibronectin antibody B3D6 (both from Developmental Studies Hybridoma Bank, Iowa City, IA).

1. Antibodies are conjugated to fluorophores using AlexaFluor 488, 555, and 647 Antibody Labeling kits (Molecular Probes, catalog numbers A-20181, A20187, and A-20186) as per manufacturer’s instructions. For microinjections, antibodies are solubilized in ePBS [11] at 1 μg/μL concentration.

2. For microinjection, embryos are oriented with their ventral (endodermal) surface up (away from the agar-albumen bed underlying the embryo in the culture dish).

3. The glass needle penetrates the endoderm at an acute angle (less than 45°).

4. Fluorophore-conjugated antibodies are delivered into the interstitial space by 6–20 pulses of 5–10 nl of antibody solution. Microinjections utilize a pneumatically driven Pico-Injector (Harvard Apparatus, Holliston, MA) associated with a hydraulic micromanipulator assembly (Narishige Scientific Instrument Laboratory, Tokyo). Each pulse lasts for 10 ms and the applied pressure is 3.5–5.0 psi.

Notes

Antibody microinjection at HH6-7 provides more extensive labeling of fibronectin and fibrillin-2 constituents of the developing heart compared to the antibody delivery at earlier stages. Proteins, other than immunoglobulins, such as human serum fibronectin (BD Biosciences, catalog number 354008) can similarly be labeled with AlexaFluor fluorophores and delivered into the living quail embryos by the same method [1].

4 Cell Transfection

Lipofectamine 2000(c)-mediated delivery of plasmid DNA into the embryo can be used for cell transfection, as an alternative method to electroporation techniques. For example, myocardial progenitors can be selectively labeled by chicken Cardiac Myosin Light Chain 2 (cmlc2) promoter-driven GFP or RFP reporter constructs. Endodermal cells can be visualized by local exposure of the pCAAGS-GFP plasmid (a gift from Dr. Olivier Pourquie, Institute of Genetics and Molecular and Cellular Biology, Strasbourg, France).

1. Ten micrograms of plasmid DNA is diluted in endotoxin-free water and mixed with OptiMEM I Reduced Serum Medium (Invitrogen, catalog number 31985-062) to yield the 40–50 μL volume, and incubated at room temperature for 5 min.

2. After incubation, 20 or 30 μL of Lipofectamine 2000 Transfection Reagent (Invitrogen, catalog number 11668-027) was added to the OptiMEM-DNA mixture (1:2 or 1:3 DNA:Lipofectamine 2000 ratio), and the resulting solution was incubated for 20 min at room temperature to allow the DNA-transfection reagent complex to form.

3. The transfection complex containing solution is microinjected into the subendodermal space of quail embryos in 10–15, 5–10 nl pulses.

4. For localized reagent diffusion (such as labeling cells from a small area) the viscosity of the transfection mixture is increased by adding equal volume of 20 % solution of Pluronic F-127 (Sigma) in PBS. Twenty to forty microliters of the resulting solution is applied directly onto the targeted cell layer using a standard plastic-tipped 100 μL micropipette.

5. Following the exposure to transfection reagents, embryos are incubated at 37 °C for 3–4 h, at which time the reporter fluorescence becomes detectable.

Note

We achieved the best efficiency for the myocardial progenitor transfection when the DNA-Lipo2000 mixture was delivered during the time interval between late HH5 and early HH7.

5 Epifluorescence Time-Lapse Image Acquisition

To visualize tissue-level movements we subjected quail embryos containing fluorescent markers to long-term (4–16 h) wide field time-lapse imaging. Our automated microscopy system consists of a computer-controlled epifluorescent microscope (Leica DMRXA2, DM6000B or DMIRE2), equipped with a motorized stage and connected to a cooled digital CCD camera (QImaging Retiga-SRV). The details regarding custom software developed to operate the equipment are described in detail elsewhere [4, 11]. The most recent version of the software (TiLa) is available as an open-source code from the authors on request.

In the majority of our experiments we use a 10× objective (0.25 NA). Images are acquired in both epifluorescence and differential interference contrast (DIC) modes. One time point of the image sequence typically includes 4–8 images taken at slightly overlapping xy locations of the embryo (“tiles”), with 7–9 focal (z) planes in each tile. The length of the time interval between consecutive time points depends on the number of focal planes, tiles, and optical modes and is usually within the range of 2–20 min. The duration of a typical time-lapse image acquisition is usually between 4 and 16 h. However, embryos within the imaging chamber remain viable for extended periods of time, allowing for up to 48 h-long imaging experiments if required. Up to 12 embryos can be imaged per recording.

The design of themulti-well glass bottomimaging chamber used and steps required for its construction are illustrated in [11]. Within the imaging chamber embryos reside on a layer of albumen/agar/glucose mixture [13] on their dorsal side. This supporting layer is created just prior tomounting the embryos by pipetting 0.8–1 ml of warm albumen/agar/glucose solution into each well of the 12-well chamber, and allowing it to solidify for 20–30 min at room temperature. We utilize a custom-made thick-walled cardboard incubator that encloses the entire microscope to maintain the temperature of the imaging chamber mounted on the microscope stage within the 37–38.5 °C range throughout image acquisition (see ref. [12]).

Following the image acquisition, embryos can be fixed with 4 % paraformaldehyde in PBS with 0.05 % azide (PBSa) at 4 °C, and subsequently subjected to whole-mount immunolabeling and/or histological sectioning as described in [12, 1].

6 Particle Tracking

Manual or automated tracking procedures yield the location x_k (t_n) of object k at time points t₁, t₂, t₃, …, t_n, corresponding to image frames I₁, I₂, …, I_n. The displacement of the object k between two frames, e.g., t₁ and t₂, is thus

$$\mathit{\Delta }{\mathbf{x}}_k(t_1,t_2)={\mathbf{x}}_k\left(t_1\right)-{\mathbf{x}}_k\left(t_2\right)$$ (1)

In practice, the time difference between t₁ and t₂ should be large enough so the displacements calculated in (1) are larger than the uncertainty of the positions x. For example, cell displacements smaller than the typical cell size are strongly affected by tracking details such as the definition of cell centroid.

7 Particle Image Velocimetry

Displacements of generic image features can be estimated by the analysis of the “optical flow.” We use the following particle image velocimetry (PIV) algorithm [15] implemented in MatLab (Mathworks, Inc.):

1. The similarity of two image tiles, T₁ and T₂, each of the same size, w × w, is characterized by their cross-correlation

   $$C(T_1,T_2)=\frac{1}{w^2}\sum _{i=1}^w\sum _{j=1}^w{h}_1(i,j)h_2(i,j)$$ (2)

   where h_n(i, j) denotes the normalized brightness of the pixel (i, j) in image tile T_n. If the raw brightness values are denoted as b_n(i, j), the normalization expresses these values relative to the average brightness

   $$m_n=\frac{1}{w^2}\sum _{i=1}^w\sum _{j=1}^w{b}_n(i,j)$$ (3)

   and scales the difference with the standard deviation

   $${\sigma }_n=\frac{1}{w}\sqrt{\sum _{i=1}^w\sum _{j=1}^w{\left(b_n(i,j)-m_n\right)}^2}$$ (4)

   as

   $$h_n(i,j)=\frac{b_n(i,j)-m_n}{{\sigma }_n}.$$ (5)
2. For an image pair, (I₁, I₂), typically taken from a sequence of images, the displacement of a certain image tile T₁ in image I₁ is determined by maximizing the cross correlation C(T₁, T₂) for all possible w × w subimage tiles T₂ within the image I₂:

   $$C(T_1,T_2^{\ast })\ge C(T_1,T_2)$$ (6)

   Thus, by this procedure we identify $T_2^{\ast }$ as the image tile in I₂ into which our original image tile T₁ moved and morphed.

3. To strike a balance between pattern specificity versus spatial resolution, the image tile $T_2^{\ast }$ is selected in two steps. First, to increase pattern specificity, T₁ is enclosed in a larger tile, $T_1^{\prime }$, of a size of 64 pixels in image I₁. Its best fit pattern $T_2^{\prime }$ is selected according to the maximal cross correlation requirement (6). In the second step, the smaller (typically w = 16 pixels wide) T₂* is selected by restricting its possible location within $T_2^{\prime }$, instead of the whole image I₂.

4. The procedure yields the estimated displacement of the tile T₁ as

   $$\mathit{\Delta }\mathbf{x}=C\left(T_2^{\ast }\right)-C\left(T_1\right)$$ (7)

   where C(T) denotes the coordinates of the center pixel of tile T.

5. Repeating the above steps for several tiles T₁, we obtain an array of estimated displacement vectors Δx(x) characterizing various image locations x (Fig. 1).

Fig. 1.

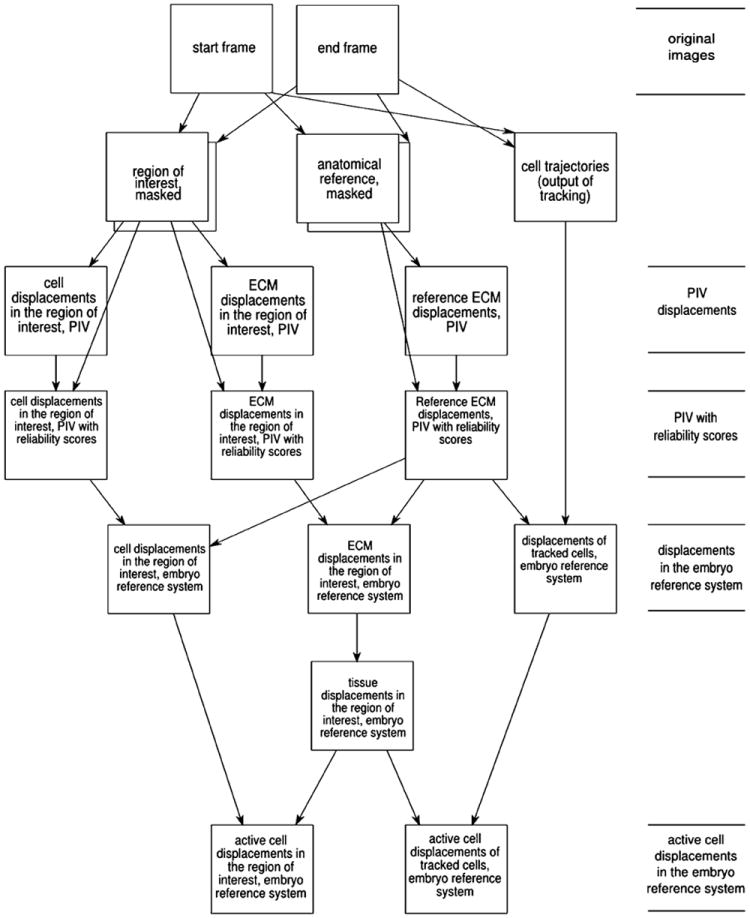
Image processing workflow to analyze cell and ECM displacements. Image pairs characteristic for a certain developmental stage are selected. The two sets of images were acquired in multiple focal (Z) planes and multiple microscopy modes. By a manual masking procedure, image regions are selected that contain either the region of interest or the anatomical reference used later. PIV analysis gives displacement estimation for the various optical modes, thus for the investigated cell population and ECM. The PIV data are weighted by the local standard deviation of the immunofluorescence intensity, which is used as a reliability score. Displacements obtained from a region of interest are registered to an anatomical frame of reference by subtracting displacement vectors characterizing an anatomical reference. Local tissue movements are established from ECM displacements by filtering techniques. Finally, the comparison of cell and local tissue movements yields cell-autonomous displacements

8 Image Registration

During time-lapse recordings living embryos shift position relative to the microscope objective; thus, an anatomical region of interest is often displaced by large-scale morphogenetic movements, an example being elongation of the vertebral axis. Thus, it is useful to relate the observed displacements to certain anatomical reference points. If the mean displacement of the reference points, Δx_ref, is established either by tracking or by PIV analysis, and rotational movements are negligible, we can easily express the displacements of our objects of interest within the frame of reference associated with the anatomical landmarks as

$$\mathit{\Delta }{\mathbf{X}}_k(t)=\mathit{\Delta }{\mathbf{x}}_k(t)-\mathit{\Delta }{\mathbf{x}}_{\mathrm{ref}}(t)$$ (8)

To reconstruct a trajectory within the anatomical frame of reference, these displacement values are accumulated as

$${\mathbf{X}}_k(t_n)=\sum _{i=1}^{n-1}\mathit{\Delta }{\mathbf{X}}_k(t_i)$$ (9)

9 Active Cell Motion Versus Tissue Motion

Using the same principle as in the previous section, we can define active cell displacements as displacements relative to the local ECM scaffold

$$\mathit{\Delta }{\mathbf{X}}_k^{\mathrm{active}}=\mathit{\Delta }{\mathbf{x}}_k-\mathit{\Delta }{\mathbf{x}}_{\mathrm{ECM}}.$$ (10)

This definition of active cell movement corresponds closely to the “conventional” in vitro scenarios where cellular motility occurs on a fixed two-dimensional surface or within (static) gels [6].

Fluorescent ECM tags can be used to map tissue movements in avian embryos [15, 16, 1]. This approach is motivated by the observation that, unlike cells, ECM filaments are passive tracers, incapable of active movements. This idea is backed by data showing that labeling of multiple distinct ECM glycoproteins, in a single specimen, yields similar motion patterns [17]; further, ECM filaments move similarly irrespective of their dorsal–ventral position [14]. Microinjected passive tracer particles, such as microbeads, are also convected similar to the ECM; thus for beads, or ECM, “independent” motion by these passive objects does not influence calculated active cellular displacements values [1].

The application of Eq. 10 requires that we have two displacement values from the same location: one for the cells of interest and one for the ECM scaffold. Thus it requires simultaneous imaging in multiple (at least two) optical modes, using two distinct fluorophores with no spectral overlap. In some experiments the traced cell population can be sparse and the ECM label highly nonuniform, Eq. 10. In such cases motion is evaluated only where both the cell and ECM signal are sufficiently strong. A practical way of characterizing fluorescence signal is the local standard deviation of brightness, σ, as defined in Eq. 4. Thus active cell movement data are available where the local σ is greater than a threshold value for both optical modes. While conceptually the ECM signal is better suited to act as a reference in Eq. 10, in practice we found that tissue movements are so dominant during early avian development that the optical flow derived from transmitted light DIC images yields highly similar displacement vectors [5]. This observation validates the concept that tissue flow can be quantified during early organ morphogenesis.

10 Subtracting Tissue Movements from Cell Locomotion

If a given object or pattern is located at the position x in image I₁, the corresponding location in image I₂ is x + Δx. From a number of such displacement vector data scattered within the field of view, a continuous displacement vector field can be calculated for each pixel location p = (i, j) by interpolation—for example, by fitting a thin plate spline for both the x and y components of the Δx displacement data. Of particular interest is the field v₁(p), which maps the location p₁ in the image I₁ forward in time to image I₂ as

$${\mathbf{p}}_2={\mathbf{p}}_1+{\mathbf{v}}_1({\mathbf{p}}_1).$$ (11)

This interpolation spline allows us to define a transformed image F₁ I₂ as

$${\mathbf{F}}_1{I}_2(\mathbf{p})=I_2(\mathbf{p}+{\mathbf{v}}_1(\mathbf{p})).$$ (12)

Thus, image F₁ I₂ is such a transform of image I₂ that each pixel is projected to the location it is moved from by the tissue flow v. Therefore, in image F₁ I₂ the tissue movements are eliminated by the transformation.

Similarly, the image I_n of the image sequence is transformed as

$${\mathbf{F}}_1{\mathbf{F}}_2\dots {\mathbf{F}}_{n-1}{I}_n=I_n(\mathbf{p}+{\mathbf{v}}_{n-1}(\mathbf{p})+{\mathbf{v}}_{n-2}(\mathbf{p}+{\mathbf{v}}_{n_1}(\mathbf{p}))+\cdots )$$ (13)

to obtain a movie showing cell activities without tissue movements.

11 Tissue Flow as Low-Pass Filtered ECM Movement

Cells can actively remodel, pull, and drag the ECM. Thus, our definition according to which cells move relative to a conveyorbelt like ECM (i.e., active cell motion is the difference between local cell and ECM movements) is obviously an approximation. Statistical analysis of high temporal resolution recordings of ECM movements [14] indicated that local cell activity results in fluctuations that change quickly, with a correlation time less than a minute. In contrast, tissue movements can be identified as ECM movements that are persistent in time (autocorrelation time being in hours). This observation allows a more precise extraction of tissue movements by low-pass temporal filtering of the ECM displacement data. A practical possibility is a linear (or low order polynomial) fit by minimizing the expression

$${\mathit{\Delta }}^2(\mathbf{x})=\sum _t{[\mathbf{v}(\mathbf{x},t)-\mathbf{A}(\mathbf{x})+\mathbf{B}(\mathbf{x})t]}^2$$ (14)

for each location x.