Context-Dependent Savings in Procedural Category Learning

Abstract

Environmental context can have a profound influence on the efficacy of intervention protocols designed to eliminate undesirable behaviors. This is clearly seen in drug rehabilitation clinics where patients often relapse soon after leaving the context of the treatment facility. A similar pattern is commonly observed in controlled laboratory studies of context-dependent savings in instrumental conditioning, where simply placing an animal back into the original conditioning chamber can renew an extinguished instrumental response. Surprisingly, context-dependent savings in human procedural learning has not been carefully examined in the laboratory. Here, we provide the first known empirical demonstration of context-dependent savings in a perceptual categorization task known to recruit procedural learning. We also present a computational account of these savings using a biologically detailed model in which a key role is played by cholinergic interneurons in the striatum.

Introduction

Environmental context plays an essential role in the efficacy of rehabilitation treatments for a variety of behavioral afflictions. For example, relapse of drug addiction is often triggered when the patient leaves the rehabilitation clinic and returns to the original context of their drug use (Higgins, Budney & Bichel, 1995). Thus, a clear understanding and ability to manipulate the mechanisms underlying context dependence in relapse is of paramount importance to the development of efficacious intervention protocols.

The propensity for relapse is often estimated experimentally by measuring savings in relearning following an intervention protocol that causes some trained behavior to disappear (e.g., a lever press in simple instrumental conditioning paradigms; Bouton, Winterbauer, & Todd, 2012; Marchant, Li, & Shaham, 2013). Savings of the original learning is often inferred by observing that relearning occurs more quickly than original learning (e.g., rapid reacquisition), or that return to the training environmental context can temporarily renew responding (e.g., renewal).

Ashby and Crossley (2011) proposed the first neurobiologically constrained model of savings in instrumental conditioning, and Crossley, Ashby and Maddox (2012) extended this model into the domain of human procedural learning. These models assumed that learning is instantiated via plasticity at cortical-striatal synapses and that this plasticity is gated by striatal cholinergic interneurons (called TANs for tonically active neurons). As their name implies, the TANs tonically fire in their default state, inhibiting striatal projection neurons (called MSNs for medium spiny neurons), and thereby preventing synaptic plasticity at cortico-striatal synapses. However, the TANs exhibit a pause in firing that is temporally aligned with the midbrain dopamine response (Morris et al., 2004), temporarily releasing MSNs from inhibition and facilitating cortical-striatal plasticity, when they receive strong input from the centremedian and parafascicular (CM-Pf) nuclei of the thalamus. Thus, the efficacy of the CM-Pf—TAN synapse controls whether or not the TANs pause, and whether learning at cortical-striatal synapses is possible.

These models successfully accounted for a broad array of savings-based phenomena, while simultaneously respecting a range of neurobiological constraints. Applied to savings-based paradigms, the models predict that extinction does not entail complete unlearning of the original behavior (presumably implemented at cortical-striatal synapses) because the TANs learn to quit pausing during the extinction treatment, which protects cortical-striatal synapses from alteration. They are also grounded in known basal ganglia anatomy, and they correctly account for single-cell recordings from striatal projection neurons as well as striatal interneurons (TANs) under a range of experimental conditions.

Neither of these previous models, however, was explicitly equipped to account for context-dependent savings. Nevertheless, there is preliminary evidence that the gating mechanism in the striatum (i.e., the TANs) could be sensitive to environmental context. Specifically, the input to the TANs (i.e., from the centremedian and parafascicular nuclei of the thalamus) are known to display context-specific firing (i.e., they fire only when specific features of the environment are present; Matsumoto et al., 2001). When endowed with this feature, the Crossley et al. (2013) model predicts context-dependent savings in human procedural learning. Surprisingly, to our knowledge, this prediction has never been previously tested. This article therefore makes two main contributions: we provide the first known empirical demonstration of context-dependent savings in human procedural learning, and we extend the Crossley et al. (2013) model to account for our behavioral results.

Materials and Methods

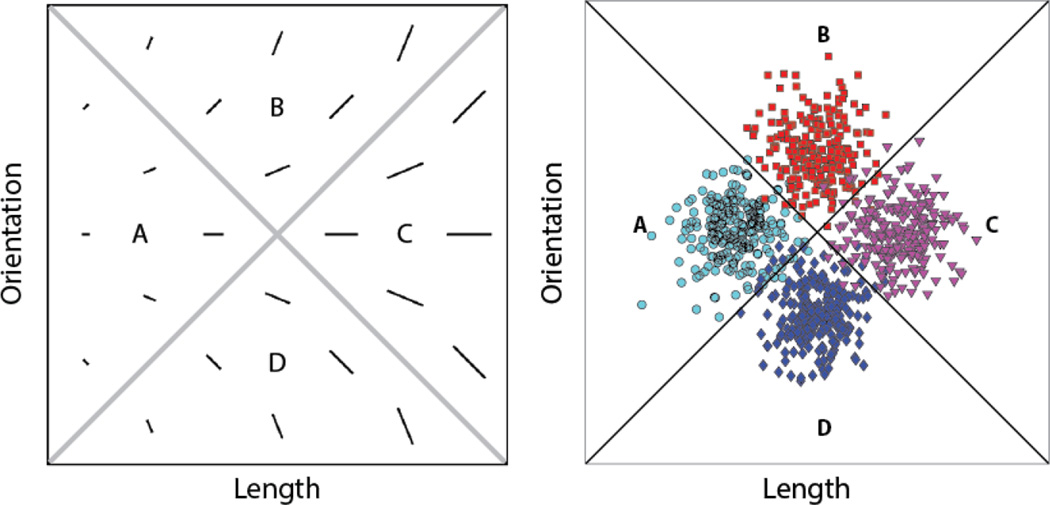
We examined savings in relearning in an information-integration (II) category-learning task. In II categorization tasks, stimuli are assigned to categories in such a way that accuracy is maximized only if information from two or more non-commensurable stimulus dimensions is integrated at some pre-decisional stage (Ashby & Gott, 1988). Typically, the optimal strategy in II tasks is difficult or impossible to describe verbally (which makes it difficult to discover via logical reasoning). An example of an II task is shown in Figure 1. In this case the four categories are each composed of single black lines that vary in length and orientation. The diagonal lines denote the category boundaries. Note that no simple verbal rule correctly separates the lines into the four categories. Nevertheless, many studies have shown that with enough practice, people reliably learn such categories, and the evidence is good that II category learning uses procedural memory and requires dopamine-dependent reinforcement learning in the striatum (e.g., Ashby & Maddox, 2005).

Figure 1.

Left) A few examples of stimuli that might be used in an information-integration (II) category-learning experiment. Right) The category distributions used here.

The II task used here included acquisition, intervention, and reacquisition phases of 300 trials each. These three phases were all identical except in the nature of the feedback provided after each response. During acquisition and reacquisition, feedback indicated whether each response was correct or incorrect. During the intervention phase, the feedback was random – that is, participants were informed that their response was correct with probability ¼ and incorrect with probability ¾, regardless of what response they actually made. The same protocol was used in Experiment 1 of Crossley et al. (2013).

The present experiment diverges from Crossley et al. (2013) in that the acquisition, intervention, and reacquisition phases could occur in different environmental contexts, where the context was defined by the background color displayed on the computer screen during presentation of the categorization stimulus. We examined savings in four different experimental conditions - AAA, ABA, AAB, and ABC. The three letters in each condition name indicate the context used during acquisition, intervention, and reacquisition, respectively. Context A always occurred with a green background, context B with a blue background, and context C with a red background.

Every stimulus in all three phases of Experiment 1 was a black line (as in Figure 1) that varied across trials in length and orientation. Identical II category structures were used in all three phases. These are represented abstractly in Figure 1. Also note that the categories overlap slightly such that the best possible accuracy with these categories is 95%.

The transition from the acquisition to the intervention phase occurred without the participant’s knowledge or any additional cue in the AAA and AAB conditions, but in the ABA and ABC conditions the transition coincided with a change in the background color. No participants in any condition were told that this transition indicated that feedback would be random. Similarly, the transition from the intervention phase to the reacquisition phase occurred without the participant’s knowledge in the AAA condition, but coincided with a background color change in the AAB, ABA, and ABC conditions.

Participants

There were 26 participants in the AAA condition, 18 participants in the ABA condition, 25 participants in the AAB condition, and 23 participants in the ABC condition. All participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. To ensure that only participants who performed well above chance were included in the post-acquisition phase, a learning criterion of 40% correct (25% is chance) during the final acquisition block of 100 trials was applied. Using this criterion, no participant in any condition was excluded.

Stimuli and Procedure

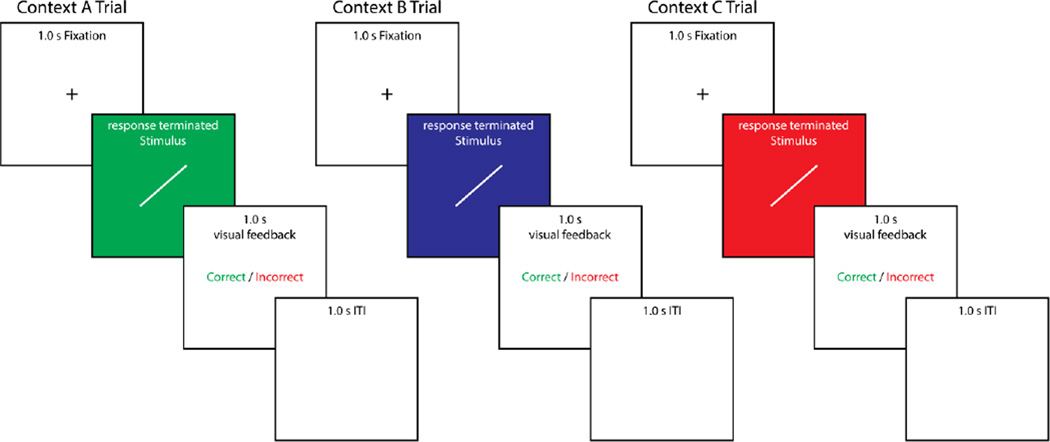
All stimuli and procedures were identical to those used in Crossley et al. (2013), with the exception of the different background colors in the different experimental phases. Example stimuli, as well as the complete category distributions are shown in Figure 1 and specified in Table 1. Example trials for each context are shown in Figure 2.

Table 1.

Category Distribution Parameters. Each random sample (x, y) from these distributions was converted to a stimulus by deriving the length (in pixels displayed at 1280 × 1024 resolution on 17-in. screens) as l = x and orientation (in degrees counterclockwise from horizontal) as o = y + 30.

	mu x	mu y	sig x	sig y	cov xy
A	72	100	100	100	0
B	100	128	100	100	0
C	100	72	100	100	0
D	128	100	100	100	0

Figure 2.

Example individual trials from each context.

Theoretical Modeling

We previously proposed a neurobiologically detailed computational model that describes a mechanism in the striatum that causes the extinction of observed procedural behavior but simultaneously protects the initial procedural learning from unlearning when rewards are no longer available or when rewards are no longer contingent on behavior (Crossley et al., 2013). The empirical results reported here imply that this mechanism is sensitive to environmental context. This section proposes an augmentation of our earlier model that specifies how this context sensitivity may be implemented.

The model proposed by Crossley et al. (2013) is characterized by a number of key features. First, it assumes that categories are learned by gradually associating regions of perceptual space represented in visual cortex with categorization responses represented in premotor cortex via synaptic plasticity at cortical-striatal synapses. This plasticity is derived from a DA-mediated reinforcement learning signal from the substantia nigra pars compacta. The striatum then drives response selection in motor regions of cortex via classic direct pathway network dynamics. Crossley et al. (2013) assumed that the key region of the striatum is the putamen and the key region of cortex is the premotor cortex (e.g., SMA and/or dorsal premotor cortex; Ashby et al., 2003; Maddox et al., 2004; Waldschmidt & Ashby, 2011). Second, the Crossley et al. (2013) model assumes that the TANs tonically inhibit cortical input to striatal projection neurons (as in Ashby & Crossley, 2011). The TANs are driven by neurons in the centremedian and parafascicular (CM-Pf) nuclei of the thalamus, which in turn are broadly tuned to features of the environment (). In rewarding environments the TANs learn to pause to stimuli that predict reward, which releases the cortical input to the striatum from inhibition. This allows striatal output neurons to respond to excitatory cortical input, thereby facilitating cortical-striatal plasticity. In this way, TAN pauses facilitate the learning and expression of striatal-dependent behaviors. When rewards are no longer available, the TANs cease to pause, which prevents striatal-dependent responding and protects striatal learning from decay. Thus, in effect, the TANs serve as a gate between cortex and the striatum. The default state of the gate is closed, but it opens when cues in the environment predict rewards. Third, DA-dependent reinforcement learning occurs at all cortical-striatal and CM-Pf –TAN synapses. Fourth, DA release is modeled discretely on a trial-by-trial basis and is a function of reward prediction error (RPE, which equals obtained reward minus predicted reward). In this capacity, the Crossley et al. (2013) model is qualitatively identical to our previous accounts of procedural categorization and instrumental conditioning (Ashby et al., 1998; Ashby & Waldron, 1999; Ashby & Crossley, 2011). However, Crossley et al. (2013) found that classic models of DA release that depend on RPE (Schultz, Dayan, & Montague, 1997; Tobler, Dickinson, & Schultz, 2003) were unable to account for fast reacquisition after random feedback. Thus, they proposed that the contingency between feedback and response confidence modulated DA release in two ways. First, it acts as a gain on the RPE signal, and second, low levels of contingency tend to reduce baseline DA levels (i.e., the amount of DA released to zero RPE). Using this more general DA model, Crossley et al. (2013) successfully accounted for fast reacquisition after random feedback as well as a number of other experimental manipulations.

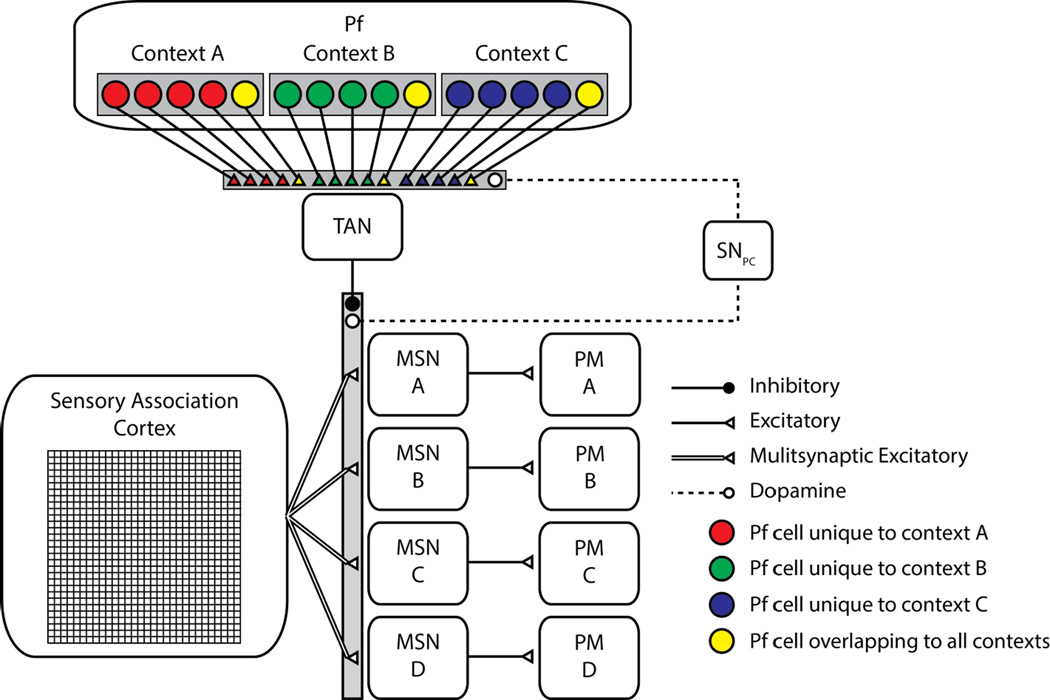
Here, we generalize the Crossley et al. (2013) model to make its behavior sensitive to environmental context. Specifically, we assumed that units in the CM-Pf layer are context-specific. This assumption is consistent with single-unit recordings showing that neurons in the CM-Pf are broadly tuned to features of the environment (e.g., Matsumoto et al., 2001). The model and simulation details are identical to those of Crossley et al. (2013) with two important exceptions. First, we simplified the basal ganglia network by removing relay nuclei in the direct pathway basal ganglia circuit (e.g., the globus pallidus and thalamus). This simplification was done simply to decrease simulation time, and does not change the qualitative properties of the model’s predictions in any way. Second, we added many context-specific units in the CM-Pf layer, giving the model the ability to display context-sensitive behavior. There were two types of context units: context-specific units that fire only when in their designated context (A, B, or C), and overlap units that fire in all contexts. There were 4 context-specific units per context for a total of 12, and a total of 3 overlap units. These numbers were chosen arbitrarily in an effort to capture intuitive notions about similarities between contexts with different colors. The architecture of the augmented model is shown in Figure 3.

Figure 3.

The model architecture used to simulate our experimental results. MSN – medium spiny neuron of the striatum. PM – premotor cortex. SN_pc – substantia nigra pars compacta. CM-Pf – centremedian and parafascicular nuclei of the thalamus.

All conditions were simulated with 300 acquisition trials, 300 intervention trials, and 300 reacquisition trials. The model was given valid feedback at the end of every acquisition- and reacquisition-phase trial, and random feedback at the end of every intervention-phase trial. Each simulation was replicated 100 times, the results were averaged, and the average results were then further split into blocks of 25 trials each. The within- and between-trial dynamics of the model were driven by the same simulation methods as described in Crossley et al. (2013). Full simulation details are provided in Appendix 2.

Results

Accuracy-based results

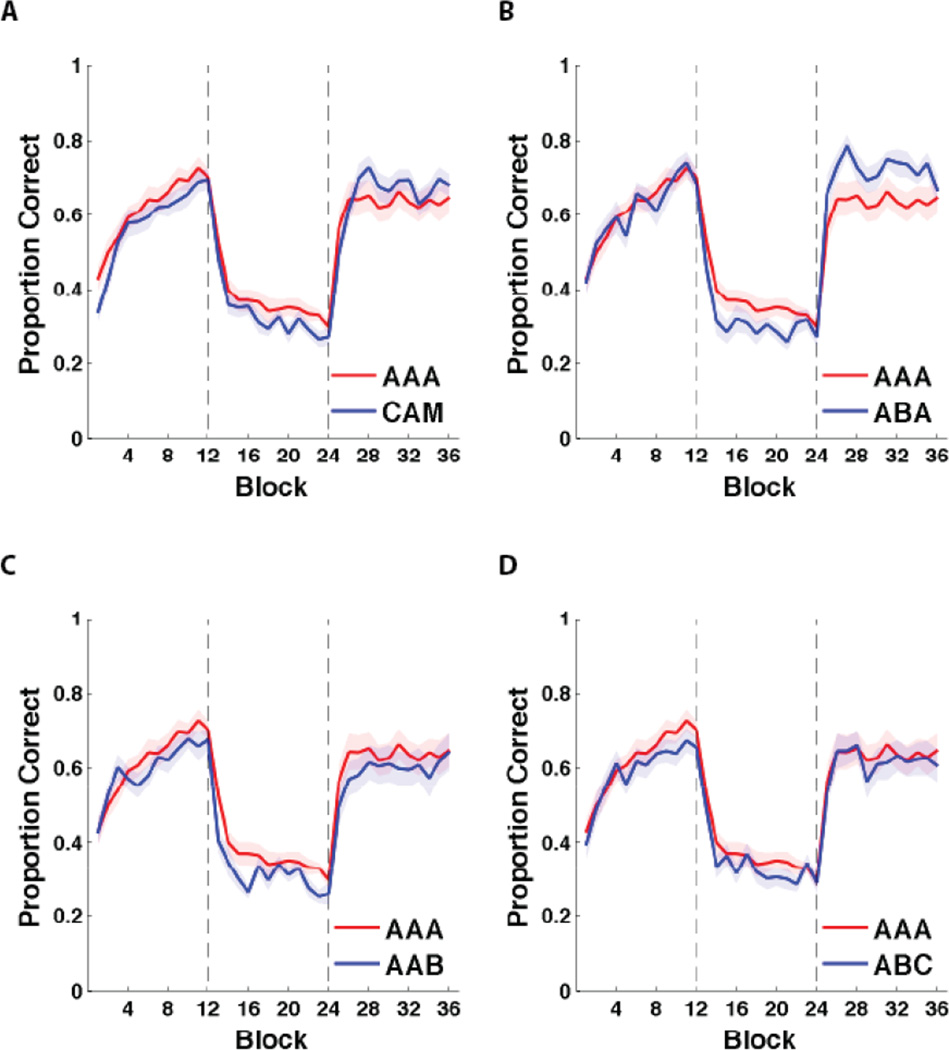
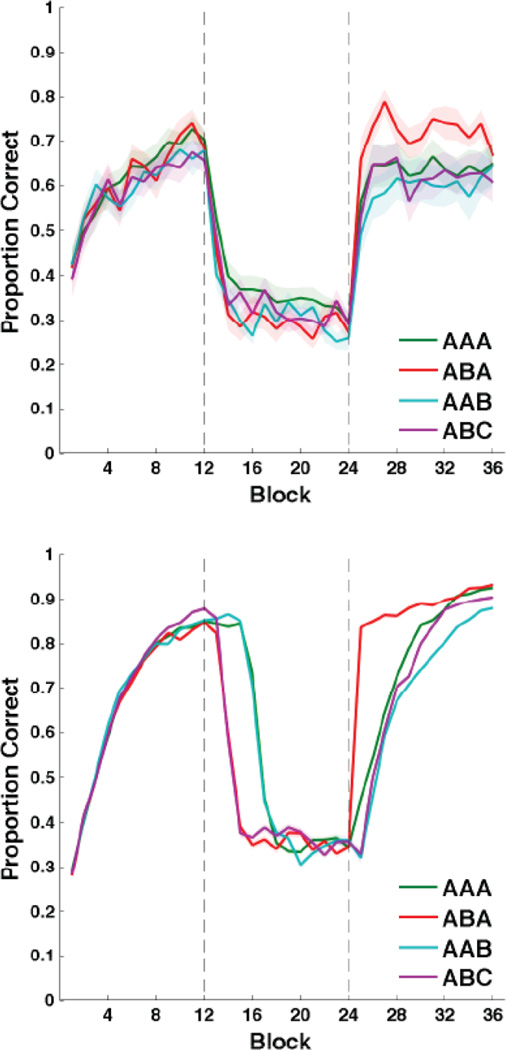
Figure 4 shows the mean accuracy for every 25-trial block of each condition including the original Crossley et al. (2013) data (henceforth called the CAM condition, for the last name initials of the authors). During intervention, a response was coded as correct if it agreed with the category membership shown in Figure 1 (feedback during intervention was fixed at 25%). Category structure and feedback contingencies were identical across all conditions. Participants from all conditions were able to learn the categories, and their accuracy fell nearly to chance during intervention. Note that all ANOVA results described below were done in R using the ‘lme4’ package with type 3 sums of squares and Satterthwaite approximation for degrees of freedom.

Figure 4.

Experiment 1 accuracy. A) AAA accuracy vs data from data from Crossley et al. (2013). B) AAA accuracy vs ABA accuracy. C) AAA accuracy vs AAB accuracy. D) AAA accuracy vs ABC accuracy. Accuracy during the intervention phase was computed relative to the true category labels, not the obtained feedback (which was fixed at 25%). Each block includes 25 trials, and bands represent SEM. Blocks 1–12 were in the acquisition phase, blocks 13–24 were in the intervention phase, and blocks 25–36 were in the reacquisition phase. Dashed vertical lines indicate transitions between phases.

To test these observations formally we performed a 5 conditions (CAM, AAA, ABA, AAB, ABC) × 3 phase (Acquisition, Intervention, Reacquisition) mixed design repeated measures ANOVA. All effects in the ANOVA (Condition, Phase, and Interaction) were significant [Condition: F(4,4350) = 8.55, P < .001; Phase: F(2,4347) = 1387.30, P < .001; Interaction: F(8,4347) = 8.85, P < .001]. We then tested for differences within each phase via three 5 conditions (CAM, AAA, ABA, AAB, ABC) × 12 block mixed design repeated measures ANOVA (one per phase). The acquisition ANOVA revealed a significant effects of block [F (4,1396) = 36.03, P < .001], but not of condition [F(11,1377) = 2.25, P = .06], or interaction interaction [F(44,1377) = .59, P = .99]. The intervention ANOVA revealed a significant effect of block [F(4,1395) = 9.69, P < .001] and condition [F(11,1375) = 16.94, P < .001], but not the interaction [F(44,1375) = .83, P = .78]. The reacquisition ANOVA revealed a significant effect of condition [F(4,1391) = 13.20, P < .001], and block [F(11,1375) = 3.69, P < .001] but the interaction was not significant [F(44,1375) = .50, P = .99]. Table 2 shows statistics for post-hoc pairwise comparisons underlying the above ANOVA results. The AAA condition displayed a significantly higher intervention accuracy than the CAM, ABA, and AAB conditions. ABA displayed significantly greater accuracy than any other condition. The CAM condition also displayed significantly greater accuracy during the reacquisition phase than the AAB and ABC conditions.

Table 2.

Statistics for pairwise comparisons. Degrees of freedom were adjusted using Satterthwaite's approximation, rounded down to the nearest integer. Shading indicates significance.

	Post-hoc Pairwise Comparisons
	Acquisition				Intervention				Reacquisition				Savings
	df	t	p	d	df	t	p	d	df	t	p	d	df	t	p	d
CAM-AAA	668	2.58	ns	0.20	647	3.49	< .05	0.27	633	−1.79	ns	0.14	320	−2.43	ns	0.27
CAM-ABA	498	2.02	ns	0.18	481	−1.40	ns	0.13	542	4.11	< .01	0.35	257	1.09	ns	0.14
CAM-AAB	656	1.17	ns	0.09	649	−1.43	ns	0.11	580	−3.98	< .01	0.33	316	−3.88	< .01	0.44
CAM-ABC	616	0.61	ns	0.05	595	0.81	ns	0.07	576	−2.85	< .05	0.24	288	−2.41	ns	0.28
AAA-ABA	475	−0.38	ns	0.04	496	−4.54	< .01	0.41	526	5.54	< .01	0.48	258	3.36	< .01	0.42
AAA-AAB	610	−1.46	ns	0.12	607	−4.80	< .01	0.39	600	−2.15	ns	0.18	304	−1.32	ns	0.15
AAA-ABC	578	−1.92	ns	0.16	584	−2.53	ns	0.21	583	−0.99	ns	0.08	289	−0.03	ns	0.00
ABA-AAB	462	−0.96	ns	0.09	467	0.08	ns	0.01	506	−7.49	< .01	0.67	251	−4.78	< .01	0.60
ABA-ABC	469	−1.41	ns	0.13	474	2.07	ns	0.19	487	−6.58	< .01	0.60	244	−3.33	< .05	0.43
AAB-ABC	566	−0.53	ns	0.04	564	2.15	ns	0.18	572	1.20	ns	0.10	282	1.26	ns	0.15

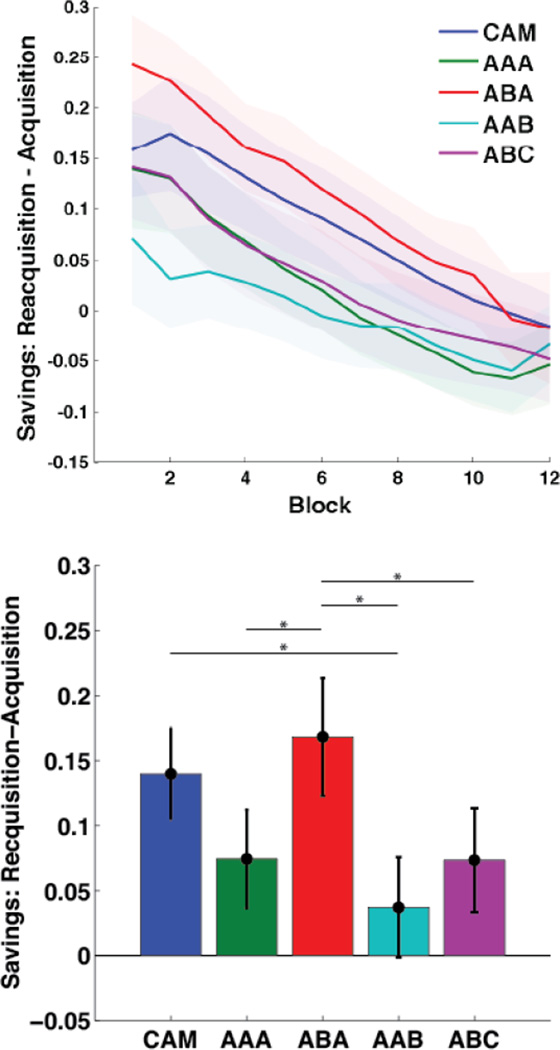
Finally, we estimated savings within each condition by subtracting mean accuracy during each block of Acquisition from mean accuracy during each block Reacquisition, and computing an repeated measures mixed design ANOVA on these difference scores. This ANOVA revealed a significant effect of condition [F(4,1396) = 10.64, P < .001] and block [F(11,1374) = 13.41, P < .001], but no significant interaction [F(44,1374) = .60, P = .98]. Post-hoc pairwise comparisons shown in Table 2 revealed that savings in the ABA condition was significantly greater than savings in every other condition except for the original Crossley et al. (2013) data (CAM). However, the savings in the CAM condition was only significantly greater than savings in the AAB condition. Savings in each condition is illustrated in Figure 5.

Figure 5.

Savings estimates. Top) Savings (Reacquisition - Acquisition) across blocks, smoothed with a 10 trial moving rectangular window. Each block includes 25 trials, and bands represent SEM. Bottom) Savings pooled across the first 6 blocks of acquisition and reacquisition. Error bars represent 95% confidence intervals.

Overall, we found the most savings in the ABA condition, the least savings in the AAB condition, and intermediate savings in the AAA and ABC condition. Even so, strong claims regarding the AAA condition are difficult since performance during the intervention phase in this condition was better than in all other conditions. Moreover, there were several differences between the AAA and CAM conditions, potentially reflecting the effect of background color on task performance.

Decision Bound Modeling

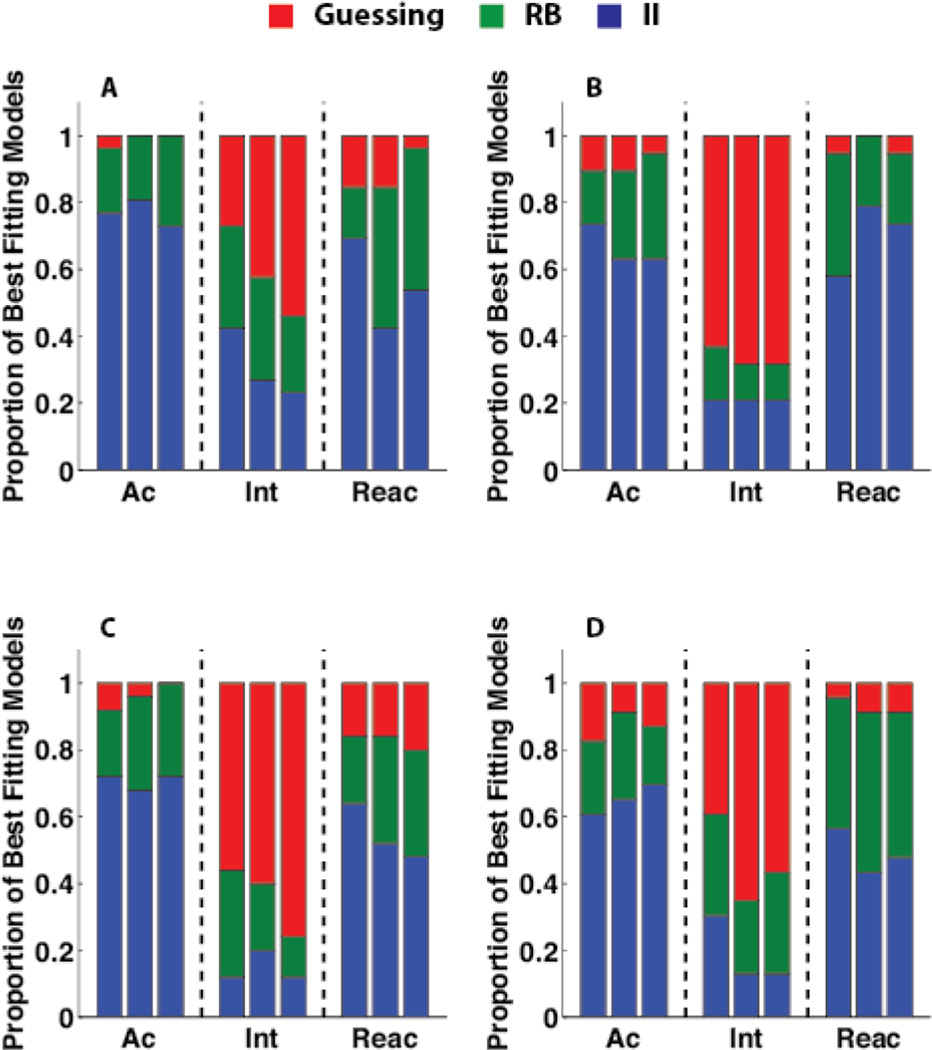
Human behavior is replete with explicit cognitive strategies, often defying explanations based in the simple stimulus-response associations thought to underlie procedural learning. Since our goal is to assess the context-dependence of savings in procedural category learning, we must be careful to control for the effect of rules or other explicit strategies in our observations. Our first line of defense is the use of II category structures, which require a procedural strategy to achieve optimal performance (95% for the categories used here). However, since participants do not perform optimally, it remains possible that their behavior was derived from rule use. Our second line of defense is to estimate participant's strategies by fitting decision bound models to the responses emitted by single participants (Maddox & Ashby, 1993; Ashby, Waldron, Lee, & Berkman, 2001). One type of decision bound model assumed a rule-based decision strategy, one type assumed an II (i.e., procedural) strategy, and one type assumed random guessing (See Appendix 1 for details). Figure 6 shows the number of best-fitting models of each type when applied to blocks of 100 trials, and Figure S2 shows the mean percent responses accounted for by each model per block. This figure shows that the vast majority of participants turn to random guessing when faced with random feedback in the intervention phase. It also shows that rule use during the reacquisition phase was slightly increased, relative to the acquisition phase, for all conditions except ABA. However, there were almost no significant changes between the last acquisition block and the first reacquisition block in any of the conditions except for significantly more participants best fit by a rule-based model during the first reacquisition block than during the last acquisition block in the ABC condition [t(44) = −2.10, p < 0.05].

Figure 6.

Decision-bound model fits. Number of participants in the four conditions of the Experiment whose responses were best accounted for by a model that assumed an information-integration (II) decision strategy, a rule-based strategy, or random guessing, A) condition AAA, B) condition ABA, C) condition AAB, D) condition ABC.

This raises an important question about how to estimate savings: If a participant shows savings (i.e., fast reacquisition relative to acquisition), but is best fit by an RB strategy during either of these phases, are their data reflective of procedural learning? To clarify this question we note that we can estimate different aspects of savings via two different dependent variables. The first is the classic accuracy difference between acquisition and reacquisition. The second is how many participants adopted a procedural strategy during these phases. With this in mind, we defined three exclusion criteria based on decision-bound model fits.

Exclusion 1 included all participants that met basic accuracy requirements by the end of acquisition (40% correct), and is therefore contaminated by explicit strategies. This makes this exclusion group a poor estimate of savings in procedural learning. However, remember that our main research question is not strictly about savings, but rather about context-dependence in savings (between condition comparisons of savings magnitude). Since once a rule has been learned, it can be abandoned and recalled quickly, rule-based strategies will tend to boost estimates of savings. Thus, including participants who adopted rule-based strategies, will tend to decrease differences in savings estimates between conditions. Therefore, exclusion 1 is the most conservative estimate of between-condition differences in savings. This is the exclusion we have focused on throughout the manuscript.

Exclusion 2 included only participants that were best fit by an II model during the last block of acquisition. Savings in procedural learning requires 1) procedural learning during acquisition, 2) protection of initial learning during intervention, and 3) fast access to this initial learning during reacquisition. This exclusion ensures that only participants that showed the best evidence for satisfying requirement 1 were included in the analysis. Some of these participant’s, however, switched to suboptimal rule-based strategies during reacquisition. Since rule-based strategies yield lower accuracy than procedural strategies, this exclusion criterion also yields conservative estimates of savings.

Exclusion 3 included only participants that were best fit by an II model during the last block of acquisition and the first block of reacquisition. This eliminates explicit strategies from our savings estimate, but suffers from somewhat circular reasoning. That is, savings is defined by differences between acquisition and reacquisition (either in accuracy or strategy), and this exclusion criteria excludes anybody who differed in strategy use between these phases, thereby presupposing the existence of savings.

Figure S1 summarizes our results across all three exclusion criteria. Differences between conditions are most pronounced by exclusion 1. The strongest trend in our data, appearing at all three exclusion criteria, is that ABA shows the most savings and AAB shows the least.

Theoretical Modeling

The bottom panel of Figure 7 shows the mean results from 100 simulations of the Figure 3 model applied to each of our experimental manipulations. Note that the model correctly captures the gross qualitative properties of our behavioral data. That is, the model correctly learns the categories, drops to near-chance performance during intervention, and then quickly recovers during reacquisition. Furthermore, the model exhibits the most savings in the ABA condition, the least savings in the AAB condition, and intermediate savings in the AAA, and ABC condition.

Figure 7.

Model compared to humans. Each block includes 25 trials, and bands represent SEM. Top) Accuracy in every condition throughout the entire experiment. Bottom) Simulated results obtained from the model shown in Figure 5. Accuracy during the intervention phase was computed relative to the true category labels, not the obtained feedback (which was fixed at 25%). Blocks 1–12 were in the acquisition phase, blocks 13–24 were in the intervention phase, and blocks 25–36 were in the reacquisition phase. Dashed vertical lines indicate transitions between phases.

There are two main discrepancies between the simulation results and the empirical data. First, the simulated ABA and ABC conditions extinguished considerably faster than the AAA and AAB conditions. The human data show only weak evidence for this qualitative pattern in that performance in the AAA condition was significantly better than in all other conditions during the Intervention phase. In the model, the primary factor that determines how quickly accuracy drops during the intervention phase is the rate at which the TANs stop pausing. This happens quickly in the ABA and ABC conditions because the context-B sensitive Pf units were not strengthened during the acquisition phase, and so simply switching to context B causes the TANs to immediately stop pausing, with accuracy following in lockstep. Thus, one possibility is that the neural representation of context in humans is considerably less distinct between contexts than in the current version of the model (e.g., humans might have more CM-Pf overlap units relative to the number of context-specific units). Another possibility is that humans are better at detecting random feedback than the model, and so extinguished too quickly – regardless of context – for us to observe a difference between the AAA and AAB conditions and the ABA and ABC conditions.

The second major discrepancy is that human accuracy asymptotes during the Reacquisition phase, but the model continues to improve. Crossley et al. (2013) suggested two possible reasons for this discrepancy. The first is general fatigue. Our human participants completed 700–800 total trials before their performance asymptote. The model, of course, never gets tired. The second is synaptic fatigue. For example, there is evidence that the threshold on post-synaptic activation that separates LTD from LTP increases after periods of high activity (Kirkwood, Rioult, & Bear, 1996; Bienenstock, Cooper, & Munro 1982). In our model, this threshold is determined by the parameter θ_NMDA. Since increasing this parameter decreases learning, it seems likely that allowing θ_NMDA to increase during the experimental session (e.g., as in the BCM model of Bienenstock et al., 1982) would improve the quality of the fits. However, adding this feature was not necessary to accomplish our principle goal: to test the qualitative sensitivity of savings in human procedural learning.

Discussion

Crossley et al. (2013) demonstrated savings in relearning (i.e., fast reacquisition) after accuracy was reduced to chance by an intervention phase composed of random feedback. The present article presents the first known empirical evidence of context-sensitive savings during human procedural learning. Our results further show that the degree of savings is modulated by environmental context in a theoretically predictable fashion. We observed the most savings in the ABA condition, the least savings in the AAB condition, and intermediate savings in the AAA and ABC condition. Savings in the AAA condition replicates the findings from Experiment 1 of Crossley et al. (2013). These results fall naturally out of our previous theoretical interpretation (Crossley et al., 2013) by adding the assumption that CM-Pf units fire in a context-specific fashion, as they seem to do in real CM-Pf neurons (Matsumoto, 2001).

Colors were not assigned to contexts in a randomized fashion, and we cannot rule out that this played some role in our results. The color red, for example, has been linked to avoidance motivation as well as physiological measures such as cortical activation (Elliot et al., 2007), and can also potentiate motor force and velocity output (Elliot & Aarts, 2011). We don’t know of any result more directly demonstrating the effect of color in a procedural learning task similar to the one used here, but the possibility remains viable. For instance, color may be responsible for the relative impairment in the AAA condition relative to the original Crossley et al. (2013) data.

Our experimental design was motivated by renewal experiments in appetitive instrumental conditioning, where the typical experiment includes three phases – acquisition, extinction, and renewal – which occur in different environmental contexts (e.g., cages with different flooring, lights, scents, etc.). During the acquisition phase, the animal learns to perform a simple instrumental response (e.g., a lever press) to obtain reward. Responding is severely reduced (i.e., extinguished) during the extinction phase by removing reward. Rewards remain unavailable during the renewal phase, yet instrumental responding can briefly but robustly return depending on the environmental context of the three phases. The amount of learning saved during the extinction phase is estimated by the magnitude of responding during the renewal phase. Robust savings are found in ABA designs and considerably smaller savings are observed in AAB and ABC designs¹ (Nakajima et al., 2000, 2002; Bouton et al., 2011). Therefore, the pattern of results obtained in our category-learning study is qualitatively identical to the results of the more traditional renewal studies within the appetitive instrumental conditioning literature.

The similarity of our results to those reported in instrumental conditioning paradigms comes despite significant differences in experimental methods. Instrumental conditioning is free response, with learning characterized by increases in response rate. Category learning, on the other hand, is forced choice, with learning characterized by increases in response accuracy. Thus, the definition of extinction in instrumental conditioning (i.e., a response rate of zero), cannot be applied to category learning. Nevertheless, we have previously proposed that similar neurobiological mechanisms mediate learning in each task (Ashby & Crossley, 2011; Crossley et al., 2013), and empirical and theoretical work on instrumental conditioning has made similar suggestions regarding psychological processes (Bouton et al., 2011). The similarity of the present results to those from instrumental conditioning supports this hypothesis, and our theoretical modeling suggests that a common neurobiological mechanism may drive context-dependent savings across species and behavioral paradigms.

Crossley et al. (2013) showed that savings in relearning after random feedback is problematic for all prior models of category learning and most straightforward adaptations of reinforcement learning models. However, a variety of cognitive models exist that could theoretically be modified to account for savings after random feedback. Included in this list are models that can quickly reallocate attention (Kruschke, 2011), models that depend on knowledge partitioning (Lewandowsky & Kirsner, 2000; Yang & Lewandowsky, 2004), generalizations of the rational model (Sanborn, Griffiths, & Navarro, 2010), and statistical inference models (Redish, Jensen, Johnson, & Kurth-Nelson, 2007; Gershman, Niv, & Blei, 2010) that allow different strategies to be employed in different contexts. The common thread among all of these models is that they postulate the existence of a gate that protects the learning acquired during training from being modified during the intervention phase. But in all of these models the gate is an abstract, hypothetical construct with unknown neurobiological origins. The model proposed here specifies a neurobiological gate (i.e., the TANs) and it is constrained by neurobiologically plausible learning mechanisms. In addition, our empirical results suggest that not only can this gate be closed during random feedback, but that its function may also be modulated by environmental context.

One obvious curiosity about our model is that we added context-sensitive units to the CM-Pf layer rather than adding additional cortical units or adding a layer corresponding to hippocampus and other medial temporal lobe structures. At first, both of these alternatives seem like natural options given that sensory cortex obviously has the ability to represent environmental cues and neurons in the hippocampus have been shown to display context-specific firing properties (Smith & Mizumori, 2006). Moreover, both send strong projections to the striatum. Even so, most afferents from cortex synapse primarily on MSNs. Since MSNs are narrowly tuned (i.e., they fire to a narrow set of cues) it is unlikely that the set of MSNs responsible for the categorization response will overlap with the set of MSNs that respond to environmental cues (Caan, Perrett, & Rolls, 1984; Nagy, Eördegh, Norita, & Benedek, 2003). The primary striatal projections from the hippocampus are to patch compartments, which are part of the limbic circuit and do not project via thalamus to cortex. These neuroanatomical details pose a serious challenge for the idea that context in our task is coded by either the cortex or the hippocampus. The TANs on the other hand receive their main input from the CM-Pf, which is broadly tuned to features of the environment, and therefore circumvents this potential difficulty.

In summary, we have demonstrated context-dependent savings in procedural category learning. We have also presented a computational account of these results using a biologically detailed model in which cholinergic interneurons in the striatum act as a context-sensitive gate on procedural learning and expression. However, since no single experiment is infallible, we are currently pursuing several future directions to further test our hypothesis. For instance, the same experiment could be repeated with rule-based categories to further control for explicit strategies in determining savings between groups, a concurrent explicit dual task could be included during various phases of the task to selectively impair explicit rule use, and the experiment could be done in non-human primates (which prior work shows learn II and RB categories in a fashion similar to humans; Smith et al., 2012) and pigeons (which prior work shows learn both RB and II categories procedurally; Smith et al., 2012).

Appendix 1: Decision Bound Models

Rule-Based Models

The General Conjunctive Classifier (GCC)

Three versions of the GCC (Ashby, 1992) were fit to the data. One version assumed that the rule used by participants is a conjunction of the type: “Respond A if the length is short and the orientation is shallow (e.g., less than 45 degrees), respond B if the length is short and the orientation is steep (e.g., greater than 45 degrees), respond C if the length is long and the orientation is shallow, or respond D if the length is long and the orientation is steep.” This version has 3 parameters: one for the single decision criterion placed along each stimulus dimension (one for orientation and one for bar width), and a perceptual noise variance. A second version assumed that the participant sets two criteria along the length dimension partitioning the lengths into short, medium, and long, and one criterion along the orientation dimension partitioning the orientations into shallow and steep. The following rule is then applied: “Respond A if the length is short, respond B if the length is short and the orientation is steep, respond C if the length is short and the orientation is shallow, or respond D if the length is long.” A third version assumed that the participant sets two criteria along the orientation dimension partitioning the orientations into shallow (e.g., less than 30 degrees), intermediate (e.g., between 30 and 60 degrees), and steep (e.g., greater than 60 degrees), and one criterion along the length dimension partitioning the lengths into long and short. The latter two models each have four parameters: three decision criteria, and a perceptual noise variance. The assignments of category labels to response regions were modified in the appropriate manner when being applied to the label switch condition.

Information-Integration Models

Striatal Pattern Classifier (SPC)

The SPC (Ashby & Waldron, 1999) has provided good fits to II categorization data in a variety of previous studies (e.g., Ashby et al., 2001; Maddox, Molis, & Diehl, 2002). The model assumes there are decision points that cover the perceptual space, each of which is associated with a response. In the present applications we assumed 4 decision points, one for each category. The SPC assumes that on each trial the participant gives the response associated with the decision point that is nearest to the percept. Because the location of one unit can be set arbitrarily, the model has 6 free response-unit parameters. One additional noise variance parameter is also included for a total of 7 parameters. The optimal model is a special case of the SPC in which the striatal units are placed in such a way that the optimal decision bounds are used. The optimal model contains only one parameter (i.e., noise variance).

Random Guessing Models

Fixed Random Responder Model

This model assumes that the participant guesses randomly and that all responses were equally likely. Thus, the predicted probability of responding “A”, “B”, “C”, or “D” is .25. This model has no free parameters.

General Random Responder Model

This model assumes random guessing, but that some responses are more likely than others. Thus, the predicted probabilities of responding “A”, “B”, “C”, and “D” are parameters that are constrained to sum to 1 (i.e., so this model has three free parameters).