Impact of positional difference on the measurement of breast density using MRI

Abstract

Purpose:

This study investigated the impact of arms/hands and body position on the measurement of breast density using MRI.

Methods:

Noncontrast-enhanced T1-weighted images were acquired from 32 healthy women. Each subject received four MR scans using different experimental settings, including a high resolution hands-up, a low resolution hands-up, a high resolution hands-down, and finally, another high resolution hands-up after repositioning. The breast segmentation was performed using a fully automatic chest template-based method. The breast volume (BV), fibroglandular tissue volume (FV), and percent density (PD) measured from the four MR scan settings were analyzed.

Results:

A high correlation of BV, FV, and PD between any pair of the four MR scans was noted (r > 0.98 for all). Using the generalized estimating equation method, a statistically significant difference in mean BV among four settings was noted (left breast, score test p = 0.0056; right breast, score test p = 0.0016), adjusted for age and body mass index. Despite differences in BV, there were no statistically significant differences in the mean PDs among the four settings (p > 0.10 for left and right breasts). Using Bland–Altman plots, the smallest mean difference/bias and standard deviations for BV, FV, and PD were noted when comparing hands-up high vs low resolution when the breast positions were exactly the same.

Conclusions:

The authors’ study showed that BV, FV, and PD measurements from MRI of different positions were highly correlated. BV may vary with positions but the measured PD did not differ significantly between positions. The study suggested that the percent density analyzed from MRI studies acquired using different arms/hands and body positions from multiple centers can be combined for analysis.

1. INTRODUCTION

Mammographic density is a proven risk factor for breast cancer.^1–5 Due to the inherent 2D nature of single projection mammography, it is difficult to obtain reliable quantitative measurement of density for risk assessment. Breast density analysis methods using other imaging modalities are being developed and tested.^6–12 Consistent and accurate quantification of breast density will provide very helpful information in clinical practice that can be used to inform women of their breast densities during screening,¹³ to improve risk assessment,¹⁴ and to evaluate longitudinal changes following therapeutic interventions to serve as response indicators.^15,16

Although other imaging modalities, such as optical imaging,⁷ ultrasound,^8–10 dual-energy mammography,¹¹ and breast CT,¹² have also been used for assessing volumetric breast density; MRI is the most studied alternative imaging modality.^6,17–23 MRI provides detailed 3D distribution of fibroglandular tissue not subject to the tissue-overlapping problem and thus is suitable for volumetric measurements. It has been shown that quantitative 3D MR-based analysis of breast density has the potential to provide an imaging biomarker for assessing cancer risk^22,24 or to predict therapeutic efficacy.^15,16,25 In order to serve as a reliable imaging biomarker, factors affecting the reproducibility in density measurement should be considered. Our group has devoted a substantial research effort to develop and refine a comprehensive 3D MR-based density method.^6,21,26 Potential sources of measurement variation that may arise from operators,⁶ imaging sequences,²⁷ scanners,²⁸ and physiology²⁹ have been investigated.

A previous study²⁸ found that the variation of fibroglandular tissue volume (FV) and percent density (PD) measured from four different MR scanners was approximately 5%, suggesting that the parameters measured using different scanners could be used for a combined analysis in a multicenter study. For the correlation of PD between each pair of MR scanners, however, the variation was higher when the Siemens scanner was compared with other scanners manufactured by different vendors. In that study, the arms/hands position for imaging using the Siemens scanner (hands-down, resting next to body) was different from the imaging done using GE and Philips scanners (hands-up, resting above the head); thus, it was postulated that the difference of arms/hands positions, hence the difference of breast positions, may partially account for the measurement variation.²⁸ Although in previous research⁶ we investigated the impact of breast/body positioning on the measured density, only two subjects were studied.

In the present research, we have performed a systematic study by enrolling 32 healthy subjects to receive repetitive MR scans. The purpose was to investigate the impact of different arm and body positions on the measured breast density. We also added one more imaging sequence using a lower spatial resolution to investigate the impact of imaging spatial resolution on the segmented density.

2. MATERIALS AND METHODS

2.A. Subjects

Thirty-two healthy Asian women (age 22–53, mean 41) were recruited for this study. The mean body height of these subjects was 159.4 cm (range 140–175 cm). The mean body weight was 56.6 kilograms (range 42–87 kilograms). Body mass index (BMI) ranged from 17.4 to 34.9 with mean ± standard deviation (STD) of 22.2 ± 3.5. None of the subjects had a history of any breast disease or breast surgery. At the time of MRI studies, none of the women reported use of hormonal medication or contraceptives. This study was approved by the institutional review board and was HIPAA compliant. Each subject gave written informed consent.

2.B. MR studies

MRI was acquired using a 1.5 T Siemens scanner (Somatom, Erlangen, Germany). The breast MR scans were performed bilaterally in axial sections. A four-channel breast coil was used. For each subject, only the 2D fast spin echo (FSE) nonfat-suppressed (or nonfat-sat) T1-weighted images were acquired and analyzed. The imaging parameters were TR/TE = 650/9.8 ms, parallel imaging with GRAPPA factor = 2, slice thickness = 2 mm, slicegap = 0, phase encoding R–L, bandwidth per pixel = 181 Hz, FOV = 330 mm, and number of signal average = 1. Each subject received four imaging sessions (four experimental settings), starting from a high spatial resolution (512 × 512) hands-up (i.e., both hands were held up above the head level) scan. After the first acquisition was completed, the subject was asked to remain still, and a low spatial resolution (256 × 256) scan was done using exactly the same hands-up position. Then, the subject was asked to move her hands down and to rest them along her waist areas. Another high resolution (512 × 512) MRI scan was acquired. Finally, the subject was asked to get off the examination bed and then to get on the bed again. The subject was then repositioned for another high resolution hands-up MRI scan. The total imaging acquisition time for these four scans was about 30 min. The acquired four sets of noncontrast-enhanced T1-weighted MR images were used for the analysis of breast density.

2.C. Breast segmentation

Currently, most of the reported 3D MR-based methods have been semiautomated, making operation of the methods time consuming and subject to the operator’s judgment. In this study, the segmentation was performed using a fully automatic chest template-based method.²⁶ This automatic breast MRI segmentation method has been shown to work very well and to generate accurate segmentation of the breast and fibroglandular tissue compared to the radiologist-established truth with only 1% error.²⁶ Unlike most model-based breast segmentation methods that use the breast region as the template,^30–32 the chest body region on a middle slice was used as the template in this study. Within the chest template, three body landmarks (thoracic spine and bilateral boundary of the pectoral muscle) were identified for performing the initial V-shape cut to determine the posterior lateral boundary of the breast. The chest template was mapped to each subject’s image space to obtain a subject-specific chest model. After removing the chest region, the chest wall muscle was identified and excluded to obtain a clean breast segmentation. The chest muscle boundary determined on the middle slice was then used as the reference for the segmentation of adjacent slices, and the process continued superiorly and inferiorly until all 3D slices were segmented.

After the breast region was completely segmented for all slices, the k-means clustering method was used to segment the fibroglandular tissue.²¹ In short, a bias field correction method combining the nonparametric nonuniformity normalization (N3)³³ algorithm and fuzzy-C-means (FCM)⁶ was applied to correct for the signal intensity inhomogeneity, and k-means clustering (k = 6) was used to separate the fibroglandular tissue (the lower three clusters) and the fatty tissue (the higher three clusters). The iterative N3 + FCM correction method has proven to be superior compared to using N3 or FCM alone.²¹ For segmentation of fibroglandular tissue, we have been using k = 6 to standardize the procedure for several years. The value of k was chosen based on our past experience analyzing many cases.^{6,15,16,21,23,25–29} For extremely fatty breasts, the number of clusters may need to be adjusted. However, for Asian women with relatively dense breasts, k = 6 (three for dense and three for fatty tissues) has worked very well.

After applying the automatic procedures, to ensure the accuracy of the fibroglandular tissue segmentation, the operator (Y. T. Tang) then checked the color-coded segmentation images slice by slice using the original T1-weighted images as the reference. In the case of inaccurate segmentation, which happened most often in the beginning and ending slices (upper and lower) of the breast, the operator made manual corrections using methods reported previously.²⁶ After the segmentation procedures were completed, the breast volume (BV), the FV, and the PD, defined as the ratio of FV/BV, were calculated.

2.D. Statistics

For each participant, age and BMI were recorded. Outcome measures included BV, FV, and PD as determined by MRI, for each breast and with the participant in each of the four different experimental settings. Descriptive statistics were obtained for continuous measures and categorical variables. Pearson’s correlation coefficient was used to assess the pairwise correlation of density measurements between the initial setting (high resolution hands-up position) and each of the other three experimental settings. A good correlation was defined as a correlation coefficient (r) with r > 0.7. A weak correlation was defined as 0.2 < r < 0.4. For each subject and each outcome measure, the coefficient of variation (CV) was calculated as the standard deviation divided by the mean value measured in four MR experimental settings, expressed as a percent, and was used to evaluate the measurement variation.

Further, a Bland–Altman plot (difference plot)³⁴ was used to analyze the agreement between two different MR studies using the initial setting (high resolution hands-up) as the reference. For example, for each subject and each breast, the breast volume and fibroglandular tissue volume were measured using the initial setting of high spatial resolution hands-up and again using the low resolution hands-up MR, and the percent density was calculated. The differences between BV, FV, and PD measurements at the two settings were computed and represent the variables that were analyzed. The coefficient of repeatability (CR) was calculated as two times the standard deviation of the differences. For each comparison, the 95% limits of agreement were computed as the average difference ±2 standard deviation of the difference.^34,35

To take into account the correlation among density results measured in four different experimental settings, the generalized estimating equation (GEE) method was applied with subjects as clusters, an exchangeable correlation structure, and a normal model with an identity link function. With this procedure, the mean response and the within-subject association among the repeated responses from the same individual are modeled separately.³⁶ GEE models were fit to data for the left and right breasts and the estimated mean difference in BV, FV, and PD was compared among the four experimental settings, adjusted for age and BMI. The Bonferroni–Holm multiple comparisons procedure was applied to maintaining an experiment-wise significance level of 0.05. Analyses were performed in SAS 9.2 (SAS Institute, Cary, NC).

3. RESULTS

3.A. Correlation of measurements from four MR settings

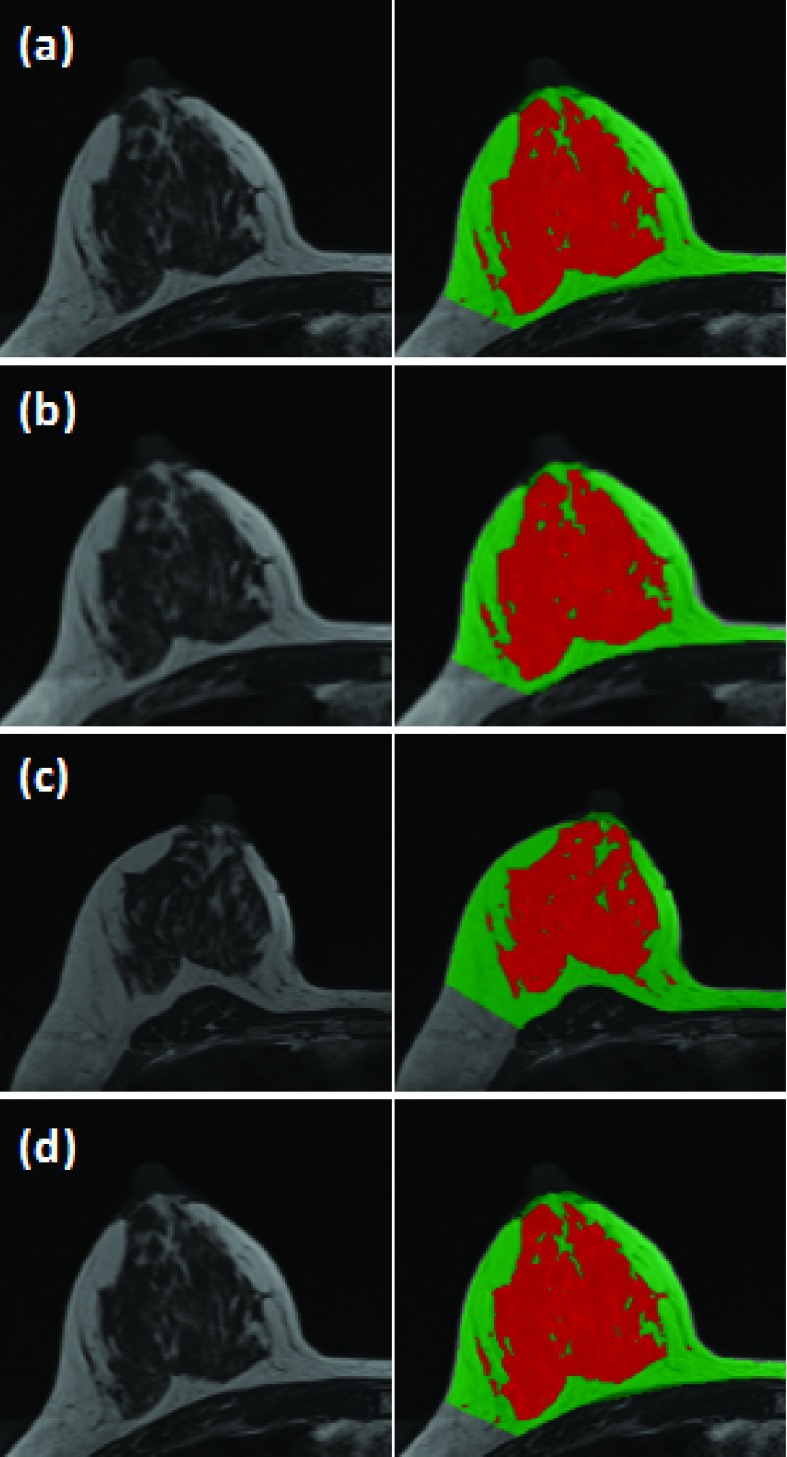
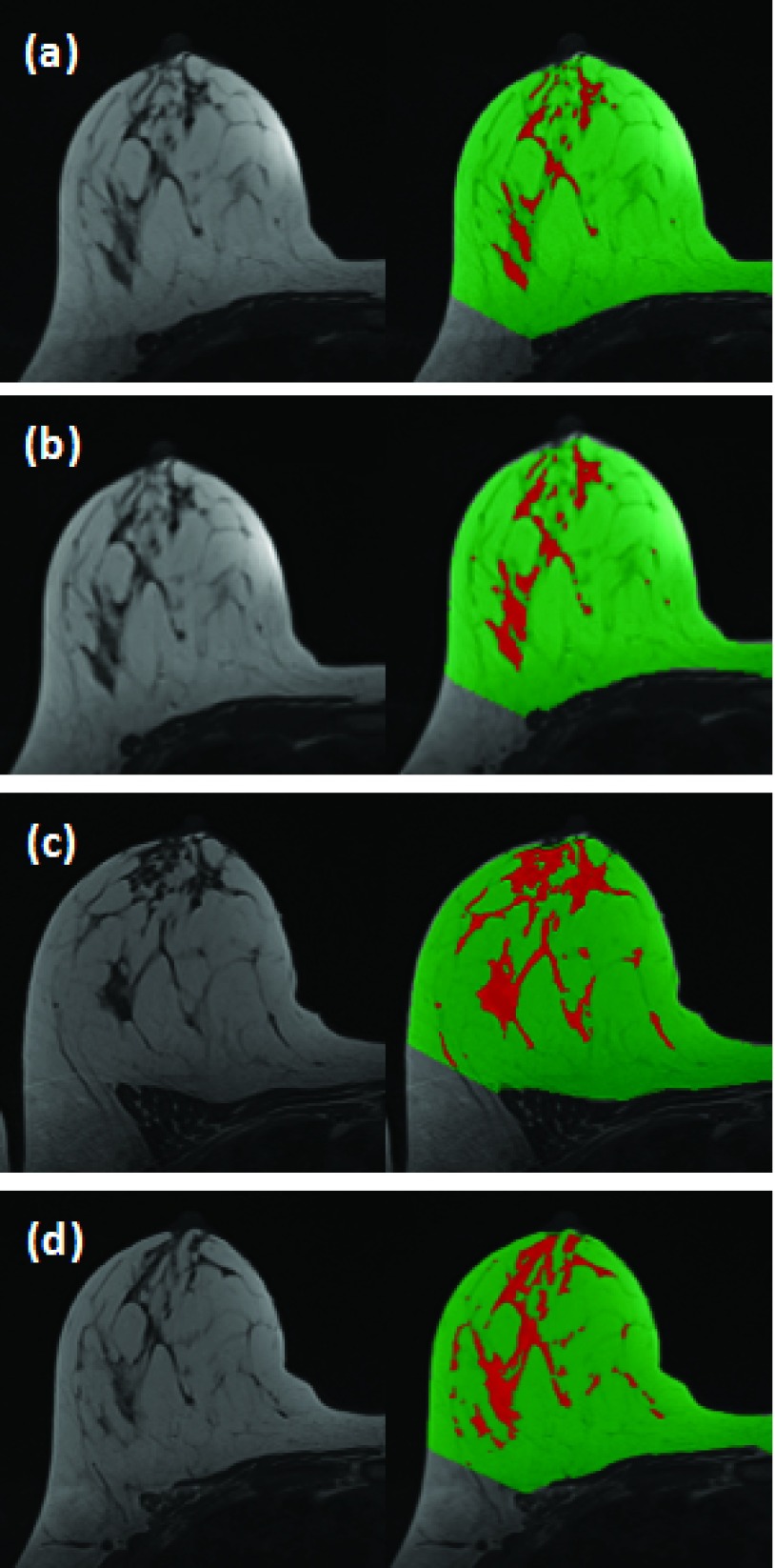
A total of 64 breasts were included in the analysis. We computed the coefficient of determination (R²) and correlation coefficient between measurements of BV, FV, and PD made at different settings. A high correlation was noted among all of the correlative studies. Figure 1 shows the R² values of the measured PD to investigate the impact of spatial resolution (high resolution hands-up vs low resolution hands-up), hands position (high resolution hands-up vs high resolution hands-down), and repositioning (high resolution hands-up vs another high resolution hands-up). The values for R² are >0.97 for each pair of positions and corresponding correlation coefficients are >0.98 (with p-values approaching 0). Figure 2 shows images acquired in four different experimental settings and the segmentation results from a subject with a high density. The measured FV is 95.48 (high resolution hands-up), 98.78 (low resolution hands-up), 98.76 (high resolution hands-down), and 96.74 cm³ (another high resolution hands-up). The values for PD are 19.03%, 20.45%, 19.07%, and 20.45%, respectively. The absolute differences are very small. The CV from four measurements is 1.7% for FV and 4.1% for PD. Figure 3 shows images from a subject with a low density. The measured FV is 20.88 (high resolution hands-up), 18.06 (low resolution hands-up), 28.39 (high resolution hands-down), and 23.95 cm³ (another high resolution hands-up). The values for PD are 2.84%, 2.34%, 3.39%, and 2.95%, respectively. Although the absolute differences are small, the CV from the four measurements is much larger compared to the case shown in Fig. 2, 19.4% for FV and 15.0% for PD.

FIG. 1.

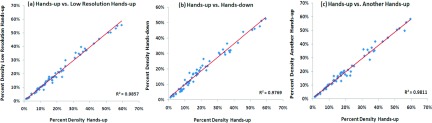
Correlation of PD in four MR experimental settings. (a) The low spatial resolution hands-up vs the initial setting of high spatial resolution hands-up; (b) high resolution hands-down vs the initial high resolution hands-up; (c) another high resolution hands-up after repositioning vs the initial high resolution hands-up. Note all R² > 0.97.

FIG. 2.

A 44 y/o healthy woman with BMI of 23.1. From top down: (a) the initial high resolution hands-up, (b) low-resolution hands-up, (c) high resolution hands-down, and (d) another high resolution hands-up after repositioning. The images acquired using the hands-down position appear different, and the other three with hands-up are similar.

FIG. 3.

A 34 y/o healthy woman with BMI of 31.1. From top down: (a) the initial high resolution hands-up, (b) low-resolution hands-up, (c) high resolution hands-down, and (d) another high resolution hands-up after repositioning. Similar to Fig. 2, the images acquired using the hands-down position appear different, and the other three with hands-up are similar.

3.B. Measurement variation among the four MR settings

The impact of age and BMI was evaluated using the GEE method, and it was found that changes in BMI were associated with BV, FV, and PD measurements among the four MR studies (all p < 0.036), whereas age did not have a significant influence on these measures (all p > 0.066). Women with lower BMI tended to have more consistent measures of FV and PD among the four MR experimental settings. There was a statistically significant difference in mean values of BV among four settings in the left breast and the right breast, respectively (left breast, score test p-value = 0.0056; right breast, score test p-value = 0.0016), adjusted for age and BMI. The difference in mean values of FV among four settings was much smaller. FV means differed significantly between settings for the right breast (score test p-value = 0.037) but not for the left breast (score test p-value = 0.093), adjusted for age and BMI. Despite the contrasting results for BV and FV, mean values for the ratio of FV to BV (PD) did not differ significantly among the four settings (score test p-value > 0.10 for left and right breasts). Table I displays the predicted means and standard deviations of volume and density for the left and the right breasts of 32 women measured in the four different MR experimental settings, adjusted for age and BMI.

TABLE I.

Breast volume, fibroglandular tissue volume, and percent density (predicted mean ± standard deviation) analyzed from MR images acquired in four experimental settings with different body/arm position and spatial resolution (N = 32), adjusted for age and BMI.

	Breast volume (cm3)		Fibroglandular tissue volume (cm3)		Percent density (%)
Setting	Left	Right	Left	Right	Left	Right
High resolution hands-up	418.4 ± 30.2	419.3 ± 30.8	72.9 ± 10.1	71.6 ± 9.2	20.7 ± 2.0	20.1 ± 1.8
Low resolution hands-up	419.1 ± 29.6	416.6 ± 30.4	73.2 ± 10.2	71.8 ± 9.3	20.5 ± 2.0	20.2 ± 1.9
High resolution hands-down	459.6 ± 28.5	465.4 ± 29.8	76.8 ± 10.1	74.6 ± 9.1	19.4 ± 1.8	18.9 ± 1.6
Another high resolution hands-up	425.5 ± 28.0	426.0 ± 28.7	74.7 ± 10.4	71.3 ± 8.8	20.6 ± 2.1	19.9 ± 1.8

3.C. Measurement results compared to the initial high resolution hands-up setting

Table II shows the mean difference and limits of agreements of BV, FV, and PD comparing different MR experimental settings and using the initial setting of high spatial resolution hands-up as the reference. The mean difference (or bias) between the high and low resolution hands-up MR studies was close to zero for BV, FV, and PD. In contrast, the hands-down MR study showed a mean difference for BV, FV, and PD that was the farthest away from zero among the three comparisons. It was also noted that the 95% limits of agreement for different comparisons tended to become larger as the mean difference increased. In particular, among the three comparisons, the hands-down MR study had the worst limits of agreement for BV, FV, and PD.

TABLE II.

Descriptive statistics on limit of agreements comparing volume and density measured in different experimental settings.

	Difference in measured volume and percent densitya
	Combined left and right breasts (N = 64)
Comparison	Mean	Standard deviation	Mean + 2STD	Mean − 2STD
Breast volume (cm3)
High resolution hands-up vs low resolution hands-up	0.98	19.80	40.58	−38.61
High resolution hands-up vs high resolution hands-down	−43.74	52.70	61.66	−149.14
High resolution hands-up vs another high resolution hands-up	−6.77	24.95	43.13	−56.67
Fibroglandular tissue volume (cm3)
High resolution hands-up vs low resolution hands-up	−0.26	5.83	11.41	−11.93
High resolution hands-up vs high resolution hands-down	−3.29	7.15	11.01	−17.59
High resolution hands-up vs another high resolution hands-up	−0.59	7.24	13.89	−15.08
Percent density (%)
High resolution hands-up vs low resolution hands-up	0.04	1.78	3.61	−3.52
High resolution hands-up vs high resolution hands-down	1.29	2.75	6.78	−4.21
High resolution hands-up vs another high resolution hands-up	0.22	2.12	4.45	−4.02

^aThe difference is calculated as (the value measured in the initial high resolution hands-up setting) – (values measured in the other three settings).

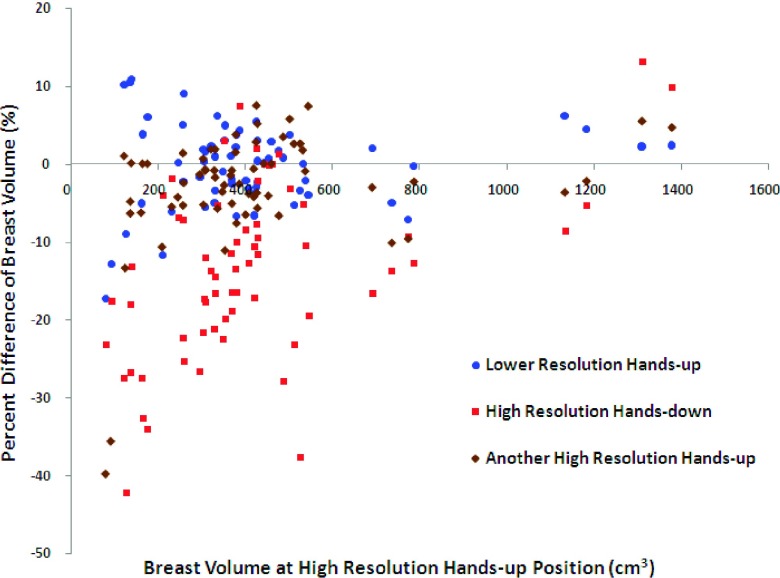
Figure 4 shows the Bland–Altman plots of BV measured in the other three settings compared with the BV measured in the initial high resolution hands-up study. As noted, the BV measured in the high resolution hands-down MR study tended to be larger compared to that measured in the high resolution hands-up MR study; thus, the differences in most cases showed negative values. Figure 5 shows the Bland–Altman plots of PD comparing the other three settings to the initial high resolution hands-up study as the reference. Figure 5(a) evaluates the resolution effect, and it shows that the data points on the Bland–Altman plot scattered evenly above and below zero with a mean difference of 0.04% and a standard deviation of 1.78%, suggesting that there was no consistent bias between high resolution and low resolution settings. Seven outliers falling out of two standard deviation lines (above and below the 95% limits of agreement) were noted. The mean BMI of these seven subjects (range 18.4–23.5, mean 20.5) was very close to the mean BMI of the whole cohort (range 17.4–34.9, mean 22.2). The mean age of these seven patients was similar to the entire cohort (40 vs 41 yr old). Thus, the outliers appeared to be random and not predictable. For comparison of hands-down to hands-up shown in Fig. 5(b), the range of differences is larger than that shown in Fig. 5(a), with a standard deviation of 2.75%. The mean difference of 1.29% is positive indicating a bias toward higher PD measured with the hands-up position than with the hands-down position. For the reposition effect shown in Fig. 5(c), the mean difference is also very close to zero (0.22%), but with a relatively high standard deviation of 2.12%. This is expected as some subjects may have been in a very different body position after getting off of the scan bed. It is not easy to reposition subjects to match that of the previous position.

FIG. 4.

Bland–Altman plots of BV between the initial high resolution hands-up and the other three MR settings. The percent difference on the vertical axis is calculated as the (BV measured at the initial setting − BV measured atanother setting)/(BV measured at the initial setting) × 100%.

FIG. 5.

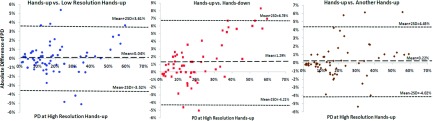
Bland–Altman plots of PD between the initial high resolution hands-up and the other three MR settings. Note x axis represents PD acquired at the initial high resolution hands-up MR scan, and y axis represents difference of PD calculated as [(PD measured at the initial setting) – (PD measured at another setting)]. The mean difference of percent density and 95% limits of agreement (mean difference ±2 standard deviation of the difference) are shown.

4. DISCUSSION

This study investigated the impact of positional difference on the measurement of 3D MR-based breast density. During breast MR studies, the shape of breast inside the coil may differ due to arms/hands and body positions of the subject. Although many MR-based breast density studies have been published,^17–22 this problem has not been systematically investigated and reported. In a previous study,⁶ two volunteers were asked to “twist” their bodies to change the position of breasts inside the coil. The results showed that the measurement variation averaged over five different breast positions was <5%. But that was not a real clinical scenario. Due to the design of the breast coil, and for the comfort of subjects, they may be asked to put their hands up above their heads or down around their waists. This may have affected the breasts’ position in the coil. Investigation of the impact of positional difference on the measurement of breast density is crucial when an accurate density measurement is required. For example, in some therapeutic interventions, such as chemotherapy^15,25 and hormonal therapy,¹⁶ a change of breast density following treatment compared to the baseline study (prior to the treatment) may be small. In these situations, knowledge of measurement variation due to positional difference is important for assessing true therapy-induced changes.

In this study, we used a fully automatic algorithm²⁶ to segment the breast and fibroglandular tissue. The previously developed semiautomatic methods^6,21,27 required operator interventions, which were time consuming, and subject to variations due to the operators’ personal judgment. The fully automatic method used in the present study was robust and accurate. In a study of 30 tested subjects,²⁶ the breast volumes measured by the automatic algorithm were very close to the radiologist-established truth, with a mean (±standard deviation) percent difference of 0.86% ± 0.72%. The mean percent difference of fibroglandular tissue segmentation was 1.03% ±  1.03%. For some cases analyzed in this study, the segmentation quality might not have been perfect, and operators would then have performed manual corrections. But as reported,²⁶ the corrections were very minor around 1%. Since the manual correction was the only operator-dependent procedure in the present study, the measurement variation from operator’s judgment was negligible. A highly accurate and reliable segmentation method was very important in our study as it allowed us to measure density precisely and to detect small changes resulting from positional differences. Without the availability of this fully automatic segmentation algorithm to minimize measurement variation, we would not able to investigate the impact of positional effect as done in this work.

The results obtained in this study showed high correlations (r > 0.98) for BV, FV, and PD in each pair of comparisons. Further analysis using the GEE model noted that BV and FV were significantly different (p < 0.05) or had a borderline significant difference among the four MR experimental settings. When the body/arm position was changed, the segmented breast volume result might change presumably due to the different coverage of breast tissues (mainly fat) in the imaging slab. For FV, since all fibroglandular tissues were already covered in the imaging slab, the coverage was not an issue; therefore, the difference in the measured FV most likely came from partial volume effects. Due to change of breast positions, the composition of breast tissue on each MR slice might differ and affect the segmentation results. The PD, ratio of FV/BV, was not significantly different among the studies. As PD is the most commonly used density parameter in most studies, our results indicated that PD acquired using different experimental settings in different centers might be combined for analysis. The GEE model analysis also found that women with lower BMI tended to have more consistent measures of FV and PD among the four MR experimental settings. A likely explanation was that women with lower BMI can have the entire breast placed into the coil and covered within the imaging slab regardless of positional changes.

The Bland–Altman plot was used to analyze the agreement between two different MR studies. The smallest magnitude of mean difference (bias) with the smallest standard deviation for BV, FV, and PD was noted when comparing the initial hands-up high vs low resolution studies, with exactly the same breast positions. The finding was comparable to a previous study showing that the spatial resolution of MR images did not significantly change the results of segmented FV and measured PD.²⁷ In all comparisons, the difference between hands-up and hands-down positions showed a mean difference that was the farthest away from zero and had the greatest 95% limit of agreement. It is possible that when the subject was in the hands-down position, more breast tissues (particularly the axillary fat pad) were covered in the imaging slab, which resulted in increased BV and decreased PD. Figure 4 clearly shows higher BV acquired at hands-down position compared to the initial hands-up position. However, when the outliers falling out of the two standard deviation lines were analyzed, there were no predictable features. As breast tissues are very soft, the way that the breasts are placed into the MR coil and the way that the subject moves arms/hands are the main reasons that lead to different results. This is unlikely to be predictable, so the best way to avoid the problem is to use a standardized way of positioning for a breast MR scan.

There were several limitations in this study. The subjects were Asian women with relatively small breasts and most of them were premenopausal. They had a narrow range of BV and BMI, not reflecting the real clinical scenario of women receiving breast MR studies. It is known that women of different ethnicities have different breasts, fibroglandular tissue volume, and percent density.²³ Thus, whether results found in Asian women in the present study can be generalized to other populations for women with different body figures and breast sizes needs to be further investigated. Fat-suppression sequences, which are commonly used in clinical studies for diagnosis of breast cancer, were not used in this study. Although we expected similar findings using fat-suppression sequences compared to nonfat-suppression, this should be investigated in the future.

5. CONCLUSIONS

We evaluated the measurements of BV, FV, and PD from MRI acquired using different arms/hands/body positions. Although in general, the results showed a high correlation between positions, different variations were seen in different experimental settings. BV and FV were significantly different among the four MR studies, but PD did not show a significant difference. The results from our study suggested the arms position, up or down, might lead to a substantial difference in the measured BV and FV, and in a multicenter study, the arm position should be standardized. The repositioning of subjects after each person left the scan bed and then got back onto the bed might have led to measurement variations as well, and a standardized positioning protocol with care may minimize the difference. The difference in the acquired imaging spatial resolution without changing the body positions had the smallest difference and variation. Understanding the factors that may lead to variations in quantitative breast density, data collected using different experimental settings from different institutions are critical for developing standardized protocols to facilitate combined data analysis in multicenter studies.