Technical Note: Measuring contrast- and noise-dependent spatial resolution of an iterative reconstruction method in CT using ensemble averaging

Abstract

Purpose:

The spatial resolution of iterative reconstruction (IR) in computed tomography (CT) is contrast- and noise-dependent because of the nonlinear regularization. Due to the severe noise contamination, it is challenging to perform precise spatial-resolution measurements at very low-contrast levels. The purpose of this study was to measure the spatial resolution of a commercially available IR method using ensemble-averaged images acquired from repeated scans.

Methods:

A low-contrast phantom containing three rods (7, 14, and 21 HU below background) was scanned on a 128-slice CT scanner at three dose levels (CTDI_vol = 16, 8, and 4 mGy). Images were reconstructed using two filtered-backprojection (FBP) kernels (B40 and B20) and a commercial IR method (sinogram affirmed iterative reconstruction, SAFIRE, Siemens Healthcare) with two strength settings (I40-3 and I40-5). The same scan was repeated 100 times at each dose level. The modulation transfer function (MTF) was calculated based on the edge profile measured on the ensemble-averaged images.

Results:

The spatial resolution of the two FBP kernels, B40 and B20, remained relatively constant across contrast and dose levels. However, the spatial resolution of the two IR kernels degraded relative to FBP as contrast or dose level decreased. For a given dose level at 16 mGy, the MTF_50% value normalized to the B40 kernel decreased from 98.4% at 21 HU to 88.5% at 7 HU for I40-3 and from 97.6% to 82.1% for I40-5. At 21 HU, the relative MTF_50% value decreased from 98.4% at 16 mGy to 90.7% at 4 mGy for I40-3 and from 97.6% to 85.6% for I40-5.

Conclusions:

A simple technique using ensemble averaging from repeated CT scans can be used to measure the spatial resolution of IR techniques in CT at very low contrast levels. The evaluated IR method degraded the spatial resolution at low contrast and high noise levels.

1. INTRODUCTION

Iterative reconstruction (IR) has become a popular choice for reducing image noise in computed tomography (CT), which can facilitate adoption of lower dose CT images while maintaining desired diagnostic image quality.^1–3 Different from conventional analytical reconstruction methods, represented here by filtered-backprojection (FBP), IR reconstructs images by iteratively optimizing an objective function, which typically involves a data fidelity term that is sometimes weighted by data-dependent statistics, and an edge-preserving regularization term that penalizes the roughness of the image while preserving edge structures.⁴ The data-dependent weighting and the regularization term, among other factors such as non-negative constraint and incomplete convergence of the optimization algorithm, result in nonlinear and nonstationary spatial resolution and noise properties in the reconstructed images. The spatial resolution in a local area of the image reconstructed from an IR method is typically dependent on the contrast and noise of the surrounding structures.⁵ This dependency is a primary reason why the amount of acceptable radiation dose reduction using IR is highly dependent on the diagnostic task, as the contrast of the anatomical structures of interest and the noise of the exams vary substantially in clinical practice.⁶ Therefore, in order to assess the spatial resolution of IR, it is necessary to perform measurements at various contrast and noise levels. The local modulation transfer function (MTF) measured using traditional approaches with high-contrast wires or beads is not complete descriptors of the spatial resolution with IR. Although the contrast- and noise-dependent spatial resolution has been demonstrated in theory or computer simulation,^5,7,8 direct experimental measurements became necessary only after IR methods become available on clinical CT scanners.

Previous studies have measured the spatial resolution of IR at medium to high-contrast levels.^9–11 One such study used the polyethylene (−90 HU) and acrylic (120 HU) test objects in the American College of Radiology (ACR) CT accreditation phantom.⁹ Another study used a customized contrast phantom, which consisted of objects with contrast in the range of 40–1000 HU, to establish conditions under which accurate measurement of noise power spectrum (NPS) and MTF could be achieved.¹¹ Considering that most subtle lesions have a relatively low contrast (<30 HU) and that low-contrast detectability is directly associated with the spatial resolution,¹² it is clinically more relevant to characterize the spatial resolution of IR for contrast levels of less than 30 HU. However, it is extremely challenging to perform precise spatial-resolution measurements at very low-contrast levels because of the noise contamination across low-contrast edges.

In this study, we propose a simple method that uses ensemble average of images from repeated scans to precisely measure the edge response function of low-contrast objects. We used this method to demonstrate the contrast- and noise-dependent spatial resolution of a commercially available IR method at very low-contrast levels (<30 HU).

2. METHODS AND MATERIALS

2.A. Experimental setup

A cylindrical phantom (Helical CT Phantom, CIRS, Inc., Norfolk, VA) was scanned on a dual-source 128-slice CT scanner (Definition Flash, Siemens Healthcare) operated in the single-source mode (only one of the two x-ray sources was used in the scan). The phantom had a diameter of 18 cm and a length of 4 cm and contained three groups of low-contrast objects at different contrast levels (7, 14, and, 21 HU below the liver equivalent background). Each contrast-level group included 8 objects: 6 spheres, 1 rod positioned parallel to the longitudinal axis of the phantom, and another rod positioned vertically to the longitudinal axis of the phantom. In a single axial image, these objects appear as 7 disks and 1 rectangular box, respectively. The diameters of the 7 disks were 10, 9.5, 6.3, 4.8, 4, 3.2, and 2.4 mm. The box dimension was 10 mm × 15 mm.

The experimental setup is shown in Fig. 1(a). Cylindrical phantoms having a length of 14 cm were abutted to each end of the low-contrast phantom to eliminate edge effects. A cross section of the low-contrast module is shown in Fig. 1(b). The scanning parameters were as follows: 120 kV, 64 × 0.6 mm detector collimation with the z-flying focal spot, 0.5 s rotation time, and helical pitch 0.8. Three mA settings were used: 240, 120, and 60 effective mAs (mAs/pitch), corresponding to a volume CT dose index (CTDIvol) of 16, 8, and 4 mGy, respectively. Automatic exposure control (CAREDose4D, Siemens Healthcare) was turned off.

FIG. 1.

Experimental setup (a) and cross section of the low-contrast phantom used (b).

The phantom was scanned 100 times at each dose level, and these reconstructed data sets were used to generate the ensemble averaged images. Images were reconstructed at 1 mm image thickness using four different reconstruction kernels: (1) B40, (2) B20, (3) I40-3, and (4) I40-5. The B40 and B20 are FBP kernels with B20 being smoother than B40. The I40 is one of the kernels with sinogram affirmed iterative reconstruction (SAFIRE, Siemens Healthcare). The I40-3 and I40-5 are two strength settings of I40, with stronger noise reduction in I40-5.

2.B. MTF measurement

Because of noise contamination, it is extremely challenging to obtain a precise measurement of the edge profile across a low-contrast boundary (Fig. 2).

FIG. 2.

Example images from one of the 100 repeated scans acquired at 16 mGy: (a) B40, (b) B20, (c) I40-3, (d) I40-5. Display window width/level = 40/50.

An ensemble average was performed on the central axial images containing the rectangular, in appearance, rods by calculating the mean of images from all 100 scans (Fig. 3). To avoid potential misalignment of the edges between slices, only the central slice in each scan was used. The ensemble-averaged image contained better-defined edge information for the three low-contrast objects than did measurements from a single image. For each image, 32 adjacent line profiles across the edge were averaged. After the mean edge profile for each boundary was extracted, a gradient operation was performed on each edge profile to obtain the line spread function (LSF). After zero padding, a fast Fourier transform (FFT) was applied to the LSF. The magnitude of the FFT was normalized to the zero frequency value, which yielded the MTF. The resultant MTF was an average of the MTF obtained from the left and right boundaries for each object [Fig. 3(a)]. For comparison, the MTF was also measured on a high-contrast (1050 HU) edge [Fig. 3(a)] using the same method.

FIG. 3.

Example images after ensemble average from the 100 repeated scans acquired at 16 mGy: (a) B40, (b) B20, (c) I40-3, and (d) I40-5. Display window width/level = 40/50.

A 10 cm FOV was used in the reconstruction of each image to ensure that the sampling density was sufficient to avoid aliasing in the spatial resolution measurements. The pixel size was 100 mm/512 ≈0.2 mm, which corresponds to a Nyquist frequency of 2.5 mm⁻¹. The limiting spatial resolution for a B40 kernel in the Flash scanner is ∼0.8 mm⁻¹, which is much lower than the Nyquist frequency.

2.C. Bias and standard deviation of MTF at different numbers of repeated scans

From the 100 repeated scans at each configuration, we performed an analysis to evaluate the effect when different numbers of repeated scans were used in the ensemble average and MTF measurement. A subset of scans was randomly selected from the original 100 scans, and the same ensemble average method was applied to the subset images to measure the MTF. The number of scans in the subset was set at 1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100, respectively, in order to evaluate the change of MTF as a function of the number of repeated scans. To obtain the mean and standard deviation of MTF, we used a resampling method similar to bootstrapping. For each number of repeated scans, we generated 200 subsets by randomly resampling from the original 100 repeated scans. The chance for selecting each scan was the same. The random resampling allowed replacement, i.e., repetitive selection of the same scan. For each subset, we measured the MTF using the ensemble average method. After obtaining the MTF results from all 200 randomly resampled subsets, the mean and standard deviation of MTF were calculated. This process was repeated for each number of repeated scans. The bias of the MTF was calculated as the difference between the mean at each number of repeated scans and that obtained from the original 100 repeated scans, which was considered the reference.

In this way, we obtained the bias and standard deviation of MTF as a function of the number of repeated scans, based on which one can determine how many repeated scans are necessary to reach a predetermined criteria of accuracy (represented by bias) and precision (represented by standard deviation).

3. RESULTS

Figures 4(a)–4(d) show the MTF for the four contrast levels (1050, 21, 14, and 7 HU), respectively, at the dose level of 16 mGy, for the four reconstruction kernels, including two FBP kernels (B40 and B20) and two IR kernels (I40-3 and I40-5).

FIG. 4.

MTF measured from the ensemble averaged images acquired at 16 mGy for four different contrast levels: (a) 1050 HU, (b) 21 HU, (c) 14 HU, and (d) 7 HU.

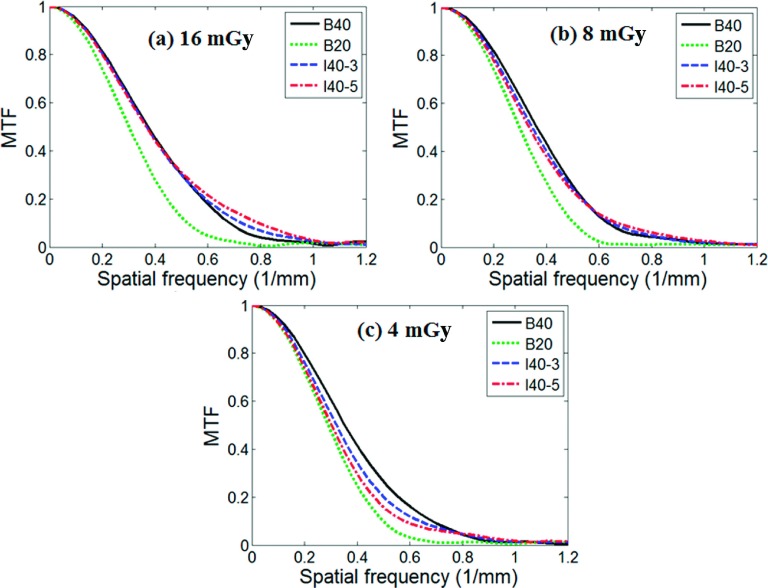
Figures 5(a)–5(c) compare the MTF of the four reconstruction kernels at the three dose levels, 16, 8, and 4 mGy, respectively, at a contrast level of 21 HU. A summary of all results is provided in Fig. 6, which compares the spatial resolution (quantified as the spatial frequency at 50% MTF, MTF_50%, normalized to the corresponding value of the B40 kernel) for B20, I40-3, and I40-5 as a function of contrast and dose levels.

FIG. 5.

MTF measured from the ensemble averaged images for three different dose levels: (a) 16 mGy, (b) 8 mGy, and (c) 4 mGy, at a contrast level of 21 HU. The corresponding noise standard deviations on the B40 images were 8.0, 11.9, and 16.7 HU, respectively.

FIG. 6.

Spatial resolution dependency on contrast and dose (noise) levels for (a) B20, (b) I40-3, and (c) I40-5. The spatial resolution is represented by the value of 50% MTF normalized to that in a B40 kernel.

As expected, the FBP kernel B20 was smoother than the B40 kernel at all contrast and dose levels, with the MTF_50% value being 80.1% of the B40 kernel. The variation was small with a standard deviation of 1.5% and a range of [77.3%, 81.9%], which was attributable to measurement errors. This ratio was consistent with the MTF measurements provided by the manufacturer, which predicted a ratio of MTF_50% at B20 and B40: 3.18/3.97 = 80.6% (personal communication).

The spatial resolution of the two IR kernels, I40-3 and I40-5, showed a strong dependency on both contrast and dose levels. At a high contrast of 1050 HU, both I40-3 and I40-5 had a MTF almost identical to that of B40, for all three dose levels, with a maximum difference of 2.8% in MTF_50%. This is expected according to the design of the studied IR method. With the decrease of the contrast level, the degradation of the MTF relative to B40 became more severe. At the dose level of 16 mGy, the MTF_50% value normalized to the B40 kernel decreased from 98.4% at 21 HU to 88.5% at 7 HU for I40-3 and from 97.6% to 82.1% for I40-5. With the increase of the noise level (as a result of the decrease of the dose level), the degradation of the MTF relative to B40 became more severe. At the contrast level of 21 HU, the MTF_50% value normalized to the B40 kernel decreased from 98.4% at 16 mGy to 90.7% at 4 mGy for I40-3 and from 97.6% to 85.6% for I40-5. The standard deviations of the CT numbers measured at the center of the FOV for the B40 kernel were 8.0, 11.9, and 16.7 HU, respectively, at each dose level.

Figure 7 shows the bias and standard deviation of MTF_50% when different numbers of repeated scans were used in the ensemble average. Only the results of the IR kernel, I40-3, were displayed. Results from other kernels had similar trend but different magnitudes. It can be seen that both bias and standard deviation decreased as the number of repeated scans increased. To reach a predetermined criteria of bias and standard deviation, the required number of scans increased when images became noisier and contrast level became lower. When the contrast was 1050 HU, one single scan was already sufficient to provide accurate and precise MTF measurement. When the contrast became lower, more and more scans were necessary to provide sufficiently low bias and standard deviation. At the highest noise at 4 mGy, for example, in order to reach a bias below 5% at 4 mGy, the required numbers of scans were 1, 20, 40, and 50 for contrasts 1050, 21, 14, and 7 HU, respectively. To reach a standard deviation below 15% at 4 mGy, the required numbers of scans were 1, 20, 50, and 80 for contrasts 1050, 21, 14, and 7 HU, respectively.

FIG. 7.

Bias (a)–(c) and standard deviation (d)–(f) of MTF_50% at the three dose levels (16, 8, and 4 mGy) as a function of the number of repeated scans that were used in the ensemble average and MTF measurement. Both bias and standard deviation at each number of repeated scans were shown as the percentage of the MTF_50% value measured when the original 100 repeated scans were used. The reconstruction kernel was I40-3.

4. DISCUSSIONS

We proposed an experimental method to measure the spatial resolution of IR for low-contrast levels in CT (<30 HU),¹³ which is clinically relevant for many diagnostic tasks involving subtle low contrast lesions such as liver metastases or pancreatic neoplasms. A recent publication after our original presentation also used ensemble averaging to measure the spatial resolution of another commercially available IR method (Veo, GE Healthcare).¹⁴ Circular objects were used in that study and the lowest two contrast levels measured were 13 and 33 HU. Both studies showed that the spatial resolution of IR was dependent on both the contrast and noise levels. It is interesting to note that their results demonstrated a much more dramatic change of spatial resolution across a wide range of contrast levels. For example, the width of the point spread function (PSF) for 1280 HU at full dose was only 37% of that for the 13 HU at quarter dose; there was a substantial increase of the PSF width (by ∼20%) when the contrast level decreased from 346 to 120 HU [Fig. 6(c) in Ref. 14].

In comparison, we observed less degradation of spatial resolution for the IR method studied: the relative MTF_50% for the 7 HU contrast at quarter dose was 79% of that in a FBP kernel and full dose. We did not observe much degradation of spatial resolution for 21 HU at full dose compared to 1050 HU. The reason for these differences is unclear but is likely to be partly attributable to the different design and performance of the two IR methods.

The dependency of spatial resolution on contrast and noise in IR is determined by the parameters used in the regularization term. In a published IR method,⁴ there were several parameters that controlled the trade-offs between spatial resolution and noise in the q-GGMRF prior, where the parameter c determined the approximate threshold of transition between low and high contrast regions. When c was set to 10 HU, for instance, the edge-preserving behavior of the algorithm had a transition at the contrast level at 10 HU. Therefore, when the contrast level was lower than 10 HU, it was essentially considered as noise fluctuation and received more smoothing during the reconstruction and the spatial resolution may be degraded; when the contrast level was higher than 10 HU, it was considered as a real edge and would receive less smoothing and the spatial resolution may be well maintained relative to high-contrast level. Therefore, the behavior of the contrast- and noise-dependent spatial resolution was expected to be closely related to the parameter setting of c. If a similar parameter was used in the evaluated IR technique, a theoretical relation among spatial resolution, noise, and contrast could be predicted and compared with our experimental results. This information, however, was not available to us.

In this study, 100 repeated scans were acquired and used in the ensemble average. This number was chosen empirically in our original experiment, mainly because it was practically feasible to acquire, and it is a relatively large number which we expected that it would yield sufficient accuracy and precision. Based on the analysis of bias and standard deviation of MTF, when different numbers of repeated scans were used in the ensemble average, it can be seen that the 100 repeated scans are more than enough for high-contrast and low-noise measurements but are reasonable choices for some of the high-noise and low-contrast measurements. One can predefine the accuracy and precision that need to be achieved and then select the number of scans based on the contrast of the object and the noise level. With the help from CT manufacturers, one can design a special quality control protocol that removes all pauses and waiting time in between scans. Using this special protocol, it is expected that a large number of repeated scans can be completed in a tolerable time frame.

In the ensemble average method, it is important to assume that the misalignment among repeated scans is negligible. This was verified by the MTF results measured on the high-contrast edge (1050 HU). Standard deviations of MTF, when different numbers of repeated scans were used, in the ensemble average were all approaching zero. The result obtained from one single scan is almost identical to the results from the average of the 100 scans, which showed that there was negligible geometrical misalignment among repeated scans.

Task-based image quality assessment using model observers has gained substantial attention in CT.^15–20 Image-based model observers require a large number of repeated scans to calculate the object template and covariance matrices, which do not directly involve the contrast- and noise-dependent MTF.^16,17,20 However, spatial frequency-domain model observers require a direct characterization of the CT system in terms of MTF and NPS, assuming locally linear shift-invariance of the system.^15,18,19 The key to the spatial frequency-domain based method is accurate measurement of MTF and NPS, which is very challenging for nonlinear reconstruction methods at very low contrast levels.¹¹ The experimental methods proposed in this report may be used to accurately characterize the MTF over a wide range of contrast and noise levels.

5. CONCLUSIONS

A simple method based on ensemble averaging from repeated scans was used to measure the spatial resolution of a commercially available IR method at very low-contrast levels. The contrast- and noise-dependent spatial resolution of the IR method was experimentally demonstrated. The method described can be implemented on any manufacturer’s system, allowing users to better understand the effects of IR on low-contrast spatial resolution, particularly as dose is decreased.