Distinguishing gramicidin D conformers through two-dimensional infrared spectroscopy of vibrational excitons

Abstract

Gramicidin D is a short peptide which dimerizes to form helical pores, adopting one of two conformations in the process. These conformations differ primarily in number of residues per turn and the hydrogen-bond registry between rungs of the helix. Using amide I 2D infrared (IR) and FTIR, we have demonstrated that it is possible to distinguish between the different conformers of gramicidin D in solution. We show that the spectra observed for this helical peptide bear no resemblance to the spectra of α- or 3₁₀-helices and that while the FTIR spectra appear similar to spectra of β-sheets, 2D IR reveals that the observed resonances arise from vibrational modes unlike those observed in β-sheets. We also present an idealized model which reproduces the experimental data with high fidelity. This model is able to explain the polarization-dependence of the experimental 2D IR data. Using this model, we show the coupling between the rungs of the helix dominates the spectra, and as a consequence of this, the number of residues per turn can greatly influence the amide I spectra of gramicidin D.

I. INTRODUCTION

Gramicidin D is a linear pentadecapeptide which can dimerize to form transmembrane pores, both in vivo and in vitro.^1,2 This rare combination of biological function and tractable system size has led to the widespread use of gramicidin D as a model system for studying ion conduction and protein-lipid interactions.^3–6 Despite the small size of the system, the history of gramicidin D is steeped in controversy; long after gramicidin D was crystallized in organic solvents, the structure of the ion conducting state in membranes remained contentious, despite a great number of solid-state Nuclear Magnetic Resonance (NMR) studies.^7–9 The primary reason for this is the existence of many subtly different conformers of gramicidin D, which are predominantly helical but differ in pitch and dimer contacts. These conformers are close enough in energy that the nature of the solubilizing lipid or detergent, or even the solvent the sample was initially prepared in, can determine the structure of the sample.^10–12

Gramicidin D is also rather unique in that the amino acids have alternating d-/l- stereochemistry.¹³ This results in an unusual hydrogen bonding pattern. Rather than all the amide groups pointing in the same direction along the helical axis, as with α- and 3₁₀-helices, the groups alternate direction, giving rise to a hydrogen-bonding pattern similar to β sheets. For this reason, these structures are usually referred to as β helices, though it is necessary to distinguish this usage from the parallel β helices commonly found in antifreeze proteins. Three variants of gramicidin D occur naturally and are labelled A, B, and C. They differ only in a single point mutation at residue 11, which is a tryptophan in gramicidin A, a phenylalanine in B, and a tyrosine in C. These mutations are known not to alter the structure or function of gramicidin.¹⁴

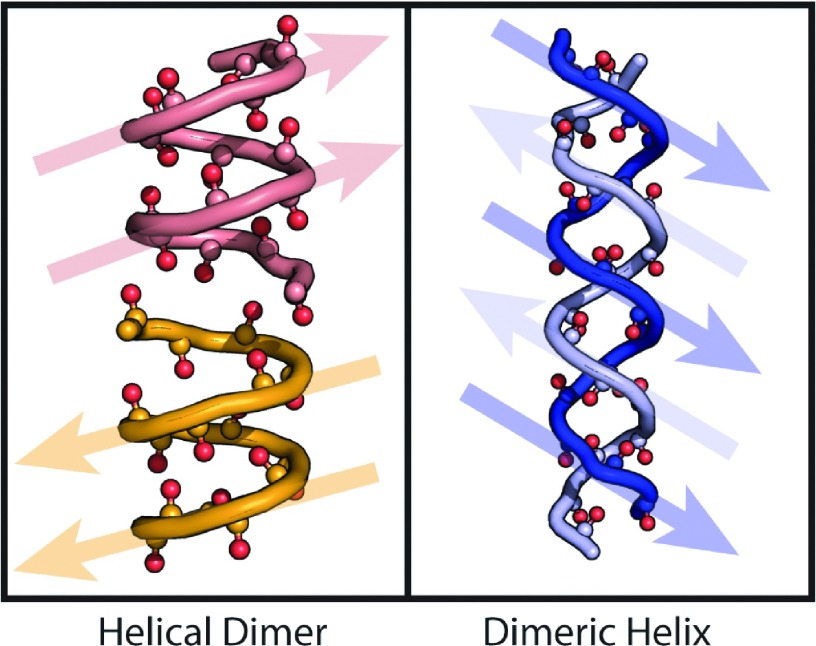
In this work, we focus on two distinct dimeric species known from x-ray crystallography and NMR to exist in lipid bilayers (Figure 1). They are the Helical Dimer (HD), a head-to-head dimer composed of two β helices which have parallel β-sheet contacts in the monomer unit¹⁴ and antiparallel β-sheet contacts at the interface, and the Dimeric Helix (DH), a double-stranded helix with antiparallel β-sheet hydrogen bonding contacts.¹⁵ Though these structures can be distinguished with Circular Dichroism (CD) spectroscopy,¹⁶ it has also been observed that differences in the amide I (carbonyl) stretch infrared (IR) spectra can distinguish between the different conformations.^12,17 This offers the possibility of studying gramicidin D in a diverse range of lipid structures, including those where artifacts arising from scattering in CD are known.¹⁸

FIG. 1.

Two structures of gramicidin D referred to in this work, showing the amide carbonyls along the main chain. The arrows show the N-to-C terminus direction to highlight the parallel sheet and antiparallel sheet regions.

Amide I IR spectroscopy has seen a surge in interest since the advent of ultrafast multidimensional experiments in the amide I region^19–21 and the development of structure-based spectroscopic models.^22–25 The delocalization of the amide I vibration across many peptide units offers the possibility for structural sensitivity at picosecond temporal resolution. This has been applied to study the hydration dynamics of proteins,²⁶ protein unfolding,²⁷ and energy transfer within a protein.²⁸ Though significant progress has been made in understanding the nature of the delocalized vibrations in proteins, this has largely been restricted to α helices and antiparallel β sheets. Here, we use 1D and 2D IR spectroscopy and excitonic modeling not only to determine the spectral signatures of the β-helix structure but also to demonstrate that IR can distinguish between two subtle variants of β helices. The extra dimension afforded by 2D IR spectroscopy allows us to elucidate the vibrational origins of the spectral differences between the HD and DH structures. Furthermore, we demonstrate that the spectra observed for the open-channel configuration are inconsistent with the dimeric helix structure, in support of the current literature consensus.

II. METHODS

A. Sample preparation

Gramicidin D (VGALAVVVWL X LWLW, where underscore refers to d-isomers and X = W, F, or Y for gramicidins A, B, and C, respectively) was purchased from Sigma-Aldrich as a natural product and used without further purification. Labile protons in gramicidin were exchanged for deuterons by heating gramicidin D in d1-ethanol (EtOD, Cambridge Isotopes) for 24 h. The solution was then lyophilized to provide the starting material for both helical dimer and dimeric helix sample preparations.

The structure of gramicidin D in micelles was controlled by choice of initial co-solvent and detergent. These preparations were adapted from literature preparations^14,16 to be compatible with IR spectroscopy, specifically, increasing the concentration of peptide and preparing the samples in deuterated solvents.

The HD form was prepared by dissolving exchanged gramicidin D in d3-trifluoroethanol (d-TFE, Cambridge Isotopes) to form a concentrated solution (50 mM). To 100 μl of the gramicidin D/d-TFE solution, 500 μl of 1 M Sodium Dodecyl Sulfate (SDS, Fisher Scientific) in D₂O (Cambridge Isotopes) was added dropwise while the solution was agitated. To this solution, a further 500 μl D₂O was added.

The DH form was prepared by dissolving the exchanged gramicidin D in EtOD at a concentration of 20 mM. To 300 μl of the gramicidin D/EtOD solution, 300 μl of exchanged Triton X-100 was added. After vortexing this solution, the sample was diluted with D₂O to a final volume of 2.5 ml and lyophilized. Triton X-100 was exchanged by heating a 10% v/v solution in D₂O for 24 h, followed by lyophilization. The excess of Triton X-100 was added to the gramicidin solution because some Triton X-100 is lost during the lyophilization process.

The samples were rehydrated in buffer (50 mM sodium phosphate, pD 7.5) to an approximate monomer concentration of 5 mM. Both the SDS and Triton X-100 solubilized samples were heated for 6 h at 50 °C. This is necessary for the Triton X-100 sample to ensure the DH form is entirely in the left-handed β helix with 5.5 residues per turn, as several conformations are initially formed.¹⁶ The sample should be completely in the left-handed 5.5 residues per turn conformer after 1 h. The SDS sample was heated only so both samples were treated consistently.

Circular dichroism spectroscopy was used to confirm the structure of gramicidin D in micelles from each preparation. Samples were diluted to give an A₂₈₀ of 0.5 in a 1 mm-pathlength, strain-free quartz cuvette (total gramicidin D concentration approximately 500 μM). Data were collected at 1 nm resolution on a Jasco J-1500 CD spectrometer and averaged over 5 data sets. The sign of the CD signal of the DH structure confirms our sample is the left-handed β-helix structure.

B. FTIR spectroscopy

Gramicidin-detergent solutions were briefly centrifuged to sediment any aggregates in solution. From the supernatant, approximately 30 μl of the solution was sandwiched between two CaF₂ windows separated by a 50 μm polytetrafluoroethylene (PTFE) spacer. This sample was also used for the nonlinear IR measurements.

FTIR spectra were collected on a Tensor 27 FTIR spectrometer (Bruker) for 256 averages each at a 2 cm⁻¹ resolution, against a background of dry air. Spectra of the buffer and buffer + detergent were also collected for background subtraction.

C. 2D IR spectroscopy

The spectrometer used to collect the 2D IR spectra has been described extensively elsewhere.²⁹ Briefly, 90 fs 800 nm pulses from a regenerative amplifier (Libra, Coherent, Inc.) were used to pump a commercial Optical Parametric Amplifier (Topas, Light Conversion), generating near-IR signal and idler pulses with wavelengths of 1.42 μm and 1.83 μm, respectively. These were combined in a AgGaS₂ crystal to generate signal at the difference frequency, 6.5 μm. The pulse length was determined to be 100 fs via a transient-grating frequency-resolved optical gating measurement.

A home-built 5-beam interferometer was used to generate 3 pulses in the boxcar geometry, generating the nonlinear signal in a phase-matched direction, which was then overlapped with a fourth pulse acting as a local oscillator for heterodyne detection. Delays between the pulses were controlled by motorized stages (Aerotech). Polarization was controlled by ZnSe wire-grid polarizers (Molectron, >100:1 extinction ratio) for each beam. The heterodyned signal was dispersed onto a liquid nitrogen cooled 2 × 64 pixel array mercury-cadmium-telluride detector (IR systems) to generate the ω₃ axis directly. The ω₁ axis was generated by stepping the delay between the first two pulses in 4 fs increments and Fourier-transforming the resulting free-induction decay.

For all data presented, the population time (time between the second and third pulse) was set to be 150 fs as a compromise between minimizing pulse-overlap effects (present at early waiting times) and energy transfer between modes (present at longer waiting times). Polarization was set to be either ZZZZ (referred to as parallel polarization, since all fields are parallel) or ZZYY (referred to as perpendicular, since the excitation fields are perpendicular to the detected signal).

III. RESULTS

A. FTIR spectra

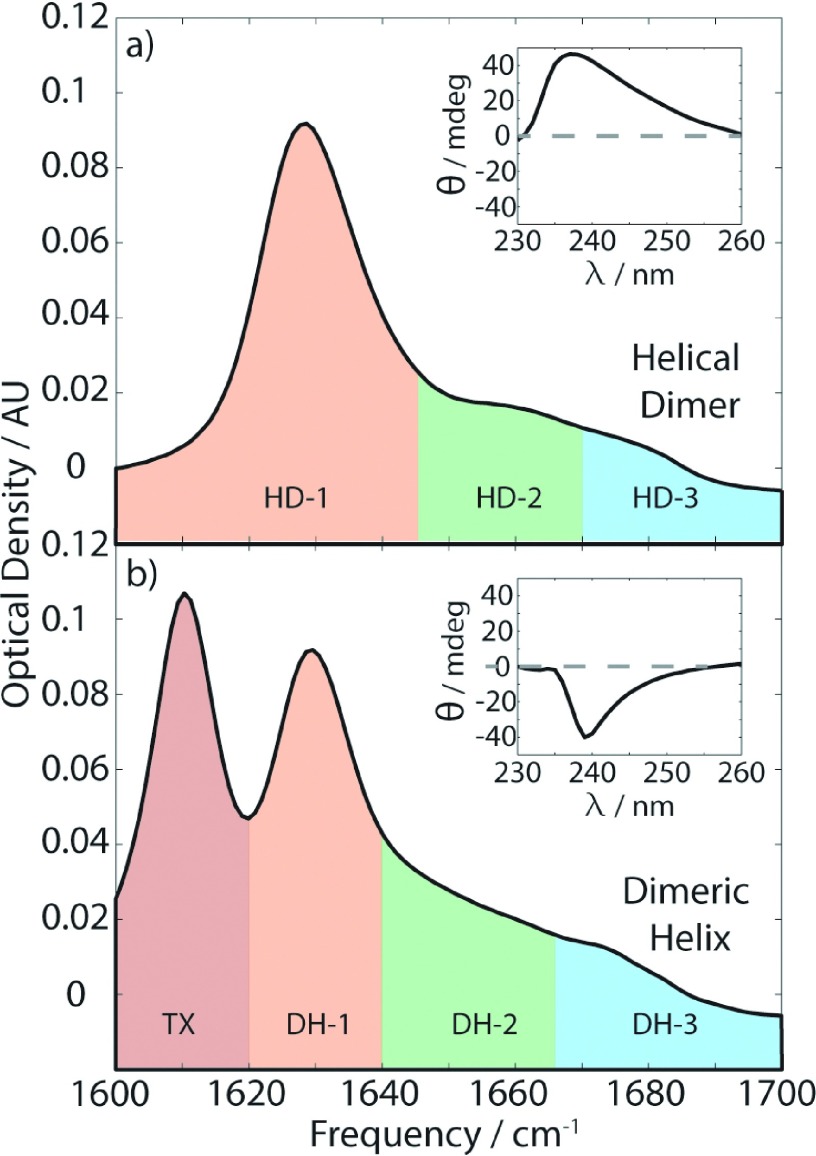
The buffer background subtracted FTIR spectra for DH and HD conformers of gramicidin D are shown in Figure 2. Notably, though both structures have helical backbones, their FTIR spectra bear no resemblance to the IR absorptions of α-helical proteins, resembling more spectra observed for antiparallel β-sheets.^30,31 Additionally, a peak is observed in the DH spectrum at 1610 cm⁻¹ corresponding to an aromatic in-plane stretching ring mode vibration from Triton X-100, so we limit our analysis to features at frequencies greater than 1615 cm⁻¹. The presence of DH and HD conformers was initially confirmed with CD spectroscopy. They are distinguished by opposite signs of the CD signal between 230 and 260 nm, as shown in the inset of Figure 2.

FIG. 2.

Experimental FTIR spectra for the helical dimer form of gramicidin, left, and dimeric helix form, right. Regions referred to in the text have been highlighted in color for clarity here. TX refers to an absorption due to Triton X-100. Insets show the CD spectra, demonstrating the difference in sign of the CD signals.

To assist with the discussion, we define three regions in each FTIR spectrum, labelled 1-3 and color-coded in Figure 2. The spectra for both structures show certain similarities, such as an intense sharp peak centered at ∼1630 cm⁻¹ in region 1 and a weaker feature at ∼1670-1680 cm⁻¹ in region 3. The largest differences between the spectra of the two structures are observed in region 2. The HD structure has a discernable peak in this region, which lies atop the tail from the intense peak in region I. The DH structure, however, shows a sloping continuum in this region. The DH spectrum is remarkably similar to the spectrum observed for poly-l-lysine at high pH, where it is thought that large β-sheets structures are formed.^32,33

B. 2D IR spectra

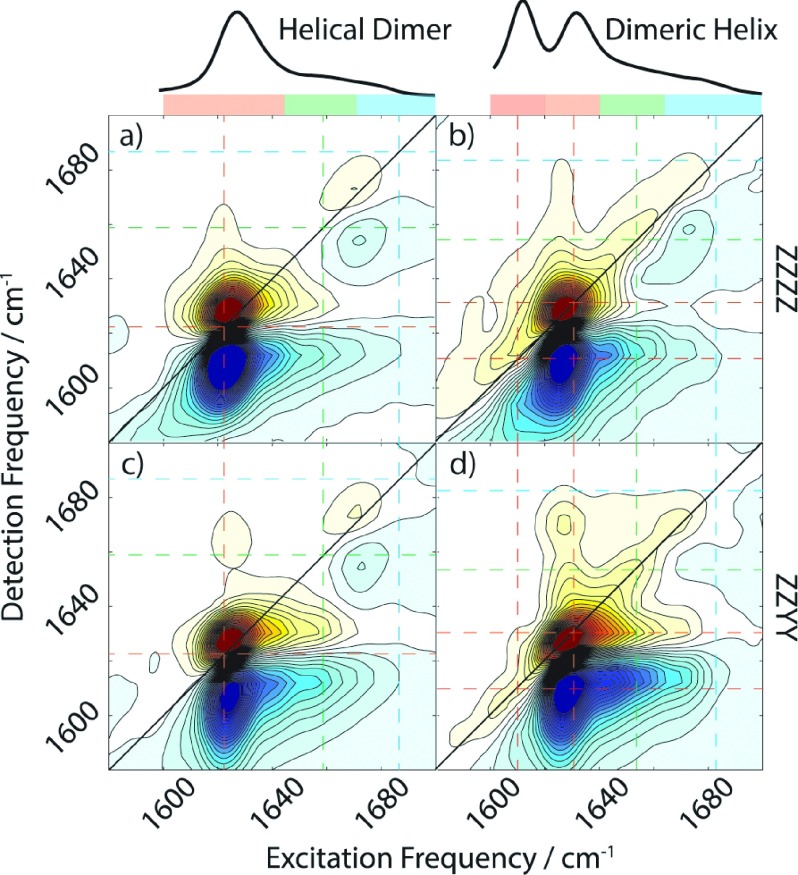
The features observed in Figure 2 become more pronounced in the 2D IR spectra, which are shown in Figure 3 for parallel and perpendicular polarization conditions. The HD and DH spectra show cross peaks between regions 1 and 3. A similar effect is observed in the 2D IR spectrum of a β-sheet, where the low frequency (1630 cm⁻¹) and high frequency (1680 cm⁻¹) peaks are connected with crosspeaks between them.²¹ Both conformers bear no similarity to 2D IR spectra observed for α- and 3₁₀-helices, where a single, rounded peak (actually two overlapping peaks) centered at 1650-1660 cm⁻¹ is found.^34,35 Also obvious is the difference along the diagonal in region 2. The HD spectra show two clearly separated peaks, while the DH spectra show a diagonally elongated ridge that tails off with increasing frequency. The 2D IR lineshape of the ridge in the DH conformation illustrates that it arises from a number of inhomogeneous states rather than a small number of homogeneously broadened peaks.

FIG. 3.

2D IR spectra of gramicidin D in SDS (HD, left) and TX-100 micelles (DH, right), for both ZZZZ (top) and ZZYY polarizations (bottom). Regions 1, 2, and 3 are highlighted with colored bars, and the center of these regions is shown with colored dashed lines.

Differences in peak amplitudes between FTIR and 2D IR can be attributed to the higher-order scaling of the transition dipoles in 2D IR with respect to linear absorption (∝μ⁴, rather than   ∝ μ²). This effect is responsible for the narrowing of peaks in 2D IR. The difference in dipole scaling is also responsible for the suppression of the aromatic C=C stretching resonance at 1610 cm⁻¹ from the Triton X-100 in the DH sample. In the linear spectrum, this peak is similar in intensity to the amide I peak since the difference in transition dipole is counterbalanced by the greater number of Triton X-100 molecules present in solution. In the 2D spectra, however, the peak is just barely visible.

C. Helical dimer spectra

The lowest and highest frequency peaks observed in the FTIR spectra are clearly resolvable in the 2D spectra, but the peak found in region 2 is not visible along the diagonal. However, the effect of this peak is seen in the 2D spectra in the form of an upper-left quadrant crosspeak between the region 2 peak and the intense region I peak (ω₁, ω₃ = 1625 cm⁻¹, 1660 cm⁻¹). The 2D spectrum collected with ZZYY polarization reveals a crosspeak to the high-frequency peak in region 3, evidenced by the vertical elongation of the regions 1 and 2 crosspeaks.

The effect of the crosspeaks may also be noted in the lower-right quadrant, but the effect is less pronounced due to spectral congestion, with cross-peaks appearing as tails rather than distinct features. The 2D IR spectrum shows only limited change in crosspeak shape and intensity with changing polarization conditions. The only discernable change is an increase in crosspeak intensity to the blue side of the intense peak (growth of intensity at ω₁, ω₃ = 1635 cm⁻¹, 1660 cm⁻¹ switching from ZZZZ to ZZYY). This suggests that the peaks highlighted previously have transition dipoles, which lie approximately parallel to each other.

D. Dimeric helix spectra

Similar to the helical dimer spectra, crosspeaks are observed between the peak in region 1 and the high frequency peak in region 3. Notable, however, is the crosspeak between the continuum of region 2 and the high frequency peak in region 3. This feature, though less distinct than the 1-3 crosspeaks, seems to be centered on 1645 cm⁻¹, suggesting the continuum feature is perhaps may not be simply a distribution of conformations, as has been suggested in the literature for poly-l-lysine, but rather a distribution of vibrational modes arising from a single conformation.³⁶

Unlike the HD spectra, the crosspeaks observed (ω₁, ω₃ = 1625 cm⁻¹, 1675 cm⁻¹) do show a significant dependence on the polarization scheme used. Significant enhancement in the relative intensity of the crosspeak is observed switching from ZZZZ to ZZYY, a feature shared by β-sheet spectra. Crosspeaks between perpendicular dipoles are expected to show this polarization dependence.

E. Transition dipole angles

One advantage of 2D IR is the ability to resolve angles between the transition dipoles of vibrational modes. The excitation of the sample creates an anisotropic distribution, even if the sample is initially isotropic (as is the case with micelles), so the signal will depend on the angle between transition dipoles contributing to a particular peak and the polarization of the pulses. Practically, this means that by comparing the relative amplitudes of the crosspeaks in parallel and perpendicular polarizations, it is possible to determine the angle between transition dipoles. If we define the depolarization ratio as the intensity ratio of a crosspeak between polarizations ρ = I_{ZZY Y}/I_ZZZZ, then the transition dipole projection angle is obtained from³⁷

$${\displaystyle {cos}^2\hspace{0.17em}\theta =\frac{7-6\rho }{1+12\rho }.}$$ (1)

This expression only constrains θ between 0° and 90°, since the cos² θ term precludes unambiguous determination of θ with respect to its supplement.

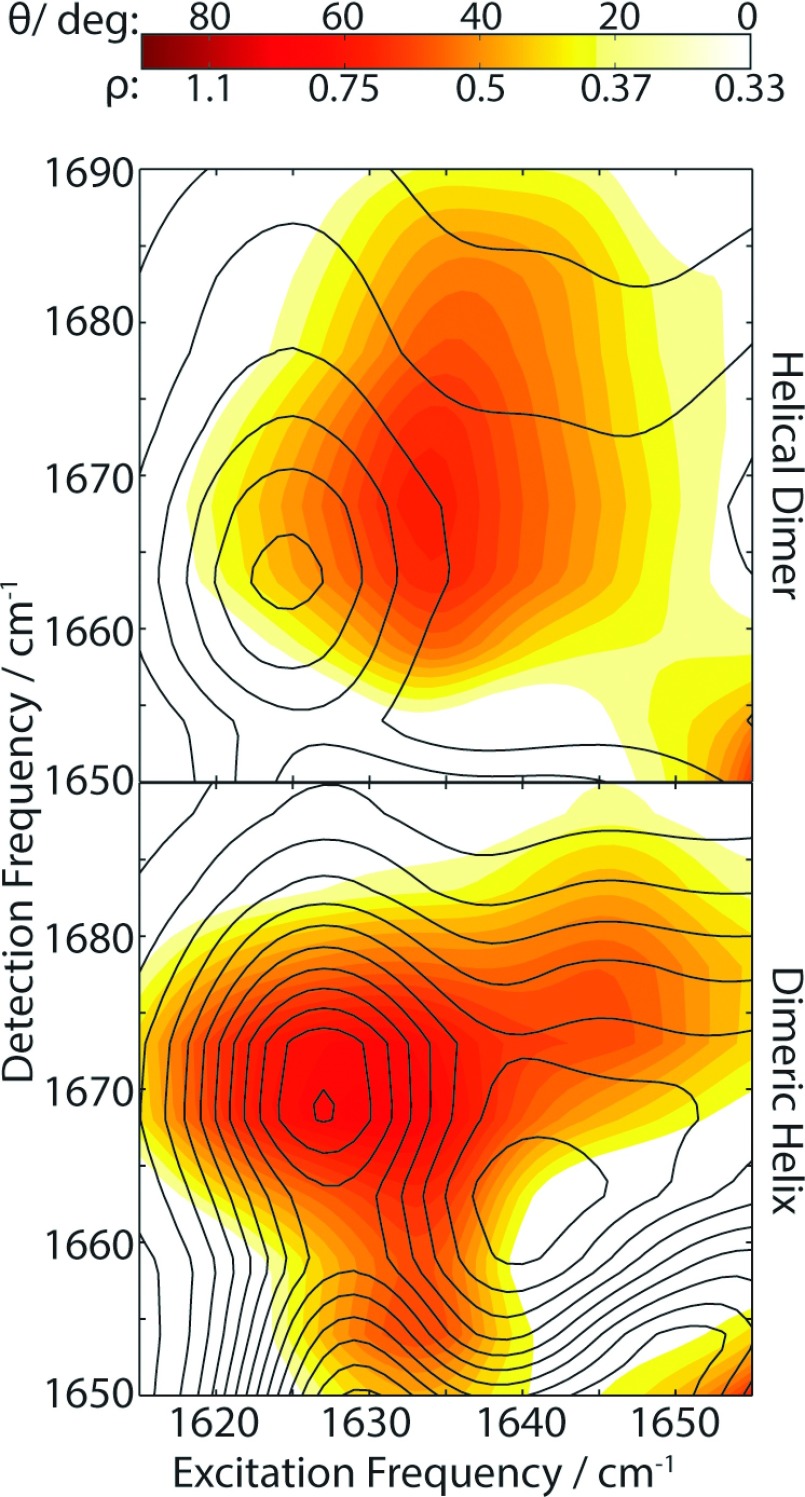
Figure 4 shows a 2D heatmap of the depolarization ratio and corresponding θ calculated with Eq. (1) for the upper left quadrant of the HD and DH 2D IR spectra. A comparison of the heatmap with the ZZYY crosspeak intensity contours shows a rather surprising result. The angle heatmap for the DH structure lines up closely with the crosspeak intensity and serves to highlight the underlying structure, such as the regions 2 and 3 crosspeaks discussed earlier. From the depolarization ratio, an angle θ ∼ 60° between the transition dipoles for the 1630 cm⁻¹ and 1670 cm⁻¹ modes is predicted. In the case of HD, the angle heatmap maximum does not correspond to the crosspeak intensity maximum but is shifted by approximately 10 cm⁻¹ along ω₁ to higher frequency. This observation indicates that there is substructure within region 1 for the HD spectrum, presumably as a result of overlapping transitions with a large dipole projection angle between them.

FIG. 4.

Heatmap of crosspeak intensity ratios of ZZYY to ZZZZ and the angles corresponding to those ratios.

IV. SPECTRAL MODELING

A. Bloch model

From the 2DIR spectra, it is clear that the helical dimer and dimeric helix conformations are distinguishable with IR spectroscopy, not simply from peak frequencies, but from the number, strength and coupling, and dipole angles between different absorptions. This is perhaps an unexpected result; both structures are dimeric, forming helical pore-like structures of similar lengths (∼20 Å for HD and ∼25 Å for DH) stabilized by β-sheet hydrogen-bonding patterns.

While IR spectroscopy tells us we can distinguish between the HD and DH conformations, it does not immediately reveal to us the origin of these differences. Extensive work has shown that protein CO groups do not vibrate in isolation, rather they couple to form delocalized excitonic modes. This delocalization can be described in a local amide Hamiltonian framework, where the diagonal elements of the Hamiltonian are the vibrational frequencies of each site and the off-diagonal elements are the couplings between sites. Diagonalizing this Hamiltonian generates the delocalized excitonic eigenstates and their corresponding energies. This Hamiltonian may be generated in many ways, the simplest and most generally applicable of which is the approach which takes a protein structure (from crystallography, NMR, or molecular dynamics (MD) simulation) and uses “spectral maps” to assign site energies and couplings.^22–24

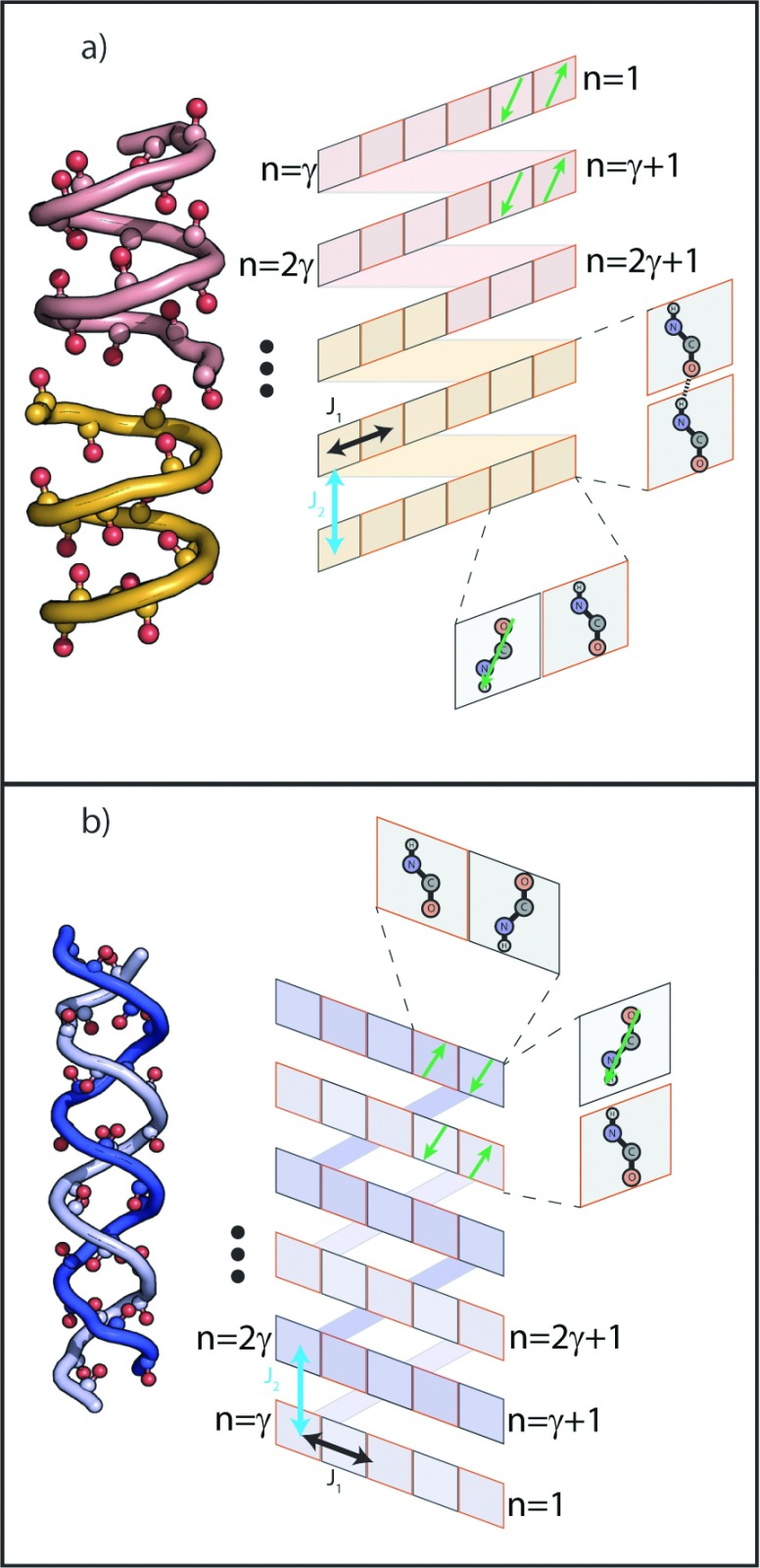
In the case of periodic structures, it is possible to develop analytical models based on a Bloch-wave approach. This has been used to a great effect with amide I spectroscopy of β-sheets to explain the observed peak frequencies and intensities in terms of their vibrational modes. To this end, we construct a Bloch-wave model of the HD and DH structures, using two idealized helices consisting of CO groups aligned along the helical axis (z). In this model, the helical structure does not represent the connectivity of the CO groups via the polypeptide backbone but rather the spatial arrangement of the individual amide I transition dipole moments for each peptide linkage. We define a screw operation (a rotation by ϕ, followed by a translation Δ) which connects adjacent sites, following the work of Loxsom on optical rotation by helices.³⁸ By virtue of the property ${\left\{C_z\left(\varphi \right)|\mathrm{\Delta }\right\}}^r=\left\{C_z\left(r\varphi \right)\right|r\mathrm{\Delta }\}$, any two sites in the helix may be related by this operation, allowing us to consider the helix as a pseudo-1D problem. Other useful variables to define are the number of residues per turn, γ, and the total number of sites N.

It is possible to take one of the two equivalent approaches to building our idealized model. In the standard approach, we can define a unit cell consisting of an adjacent pair of antiparallel CO groups which are replicated around the helix. Alternatively, we can replicate a single oscillator at each site and introduce the “Up-Down” alternating nature of the CO groups afterwards in the transition dipole when calculating intensities. The former case results in a helix exciton band split into sub-manifolds, corresponding to the replication of the symmetric and asymmetric modes of the unit cell. The other approach has the advantage of simplifying the interaction between different “rungs” of the helix, since we discuss coupling between individual CO groups. Because a simple interpretation of coupling between oscillators is important below, we choose to define our repeating unit as a single amide unit.

Next, we make some simplifying assumptions regarding the form of our Hamiltonian. Since the strongest couplings are between covalently and hydrogen-bonded residues, we account for only couplings between adjacent peptide units in the chain, and couplings between the nearest CO groups displaced vertically along the helical axis. The symmetry of our model indicates that we can use the same coupling constant for all adjacent oscillators (J₁) and for the interaction between two oscillators displaced vertically along the helical axis (J₂). Schematic summaries of our models are shown in Figure 5. Then, the matrix elements of our Hamiltonian are

$${\displaystyle H_{\mathit{ij}}={\omega }_0{\delta }_{n,n^{\prime }}+J_1{\delta }_{n,n^{\prime }\pm 1}+J_2{\delta }_{n,n^{\prime }\pm \gamma },}$$ (2)

where ω₀ is the zero-order (isolated) site energy, and n takes on values from 1 to N. For periodic systems, J_1,N = J₁, while for finite systems, J_1,N = 0. Armed with these variables and expressions, we may write down the following expressions for the exciton wavefunctions and energies when we apply periodic boundary conditions (PBC),^39,40

$${\displaystyle {\mathrm{\psi }}_m^p=\frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}exp\left(i{k}_{m}an\right)\left|n\right.〉,}$$ (3)

$${\displaystyle E_m={\omega }_0+2J_{1}cos\left(k_{m}a\right)+2J_{2}cos\left(\gamma k_{m}a\right),}$$ (4)

where $\left|n\right.〉$ refers to the nth replicated CO site, and a is the displacement unit of the screw operation between the nth and (n + 1)th site. Here, the exciton wavevector is

$${\displaystyle k_m=\frac{2\pi m}{Na},}$$ (5)

and the exciton states are indexed by m such that

$${\displaystyle -\frac{N-1}{2}<m\le \frac{N}{2}.}$$

FIG. 5.

(a) Helical dimer structure (PDB accession code 1JNO), left, and schematic representation of our model helix, right, and (b) dimeric helix structure (PDB accession code 1ALX). The model helix is unwound, and grey bars show the connections broken by the projection onto two dimensions. Couplings referred to in the main text are shown on the schematic.

These expressions have the familiar form of Frenkel exciton used to describe linear J- and H-aggregates;⁴¹ however, our systems differ in that the orientation of adjacent residues is flipped. The energies described by the first two terms in Eq. (3) show the typical exciton energy distribution for negative values of J₁, and this is further modulated by the periodicity of the helix by the third term.

Periodic boundary conditions are obviously unphysical, particularly, for a helix with only 5 or 6 complete rotations. A more realistic scenario is to consider a helix of finite length. For these open boundary conditions (OBC), it can be shown that the expressions for the wavefunction becomes⁴¹

$${\displaystyle {\mathrm{\psi }}_{m^{\prime }}^o=\sqrt{\frac{2}{N+1}}\sum _{n=1}^{N}sin\left(k_{m^{\prime }}an\right)\left|n\right.〉.}$$ (6)

The energies in this case are also given by Eq. (3), although now

$${\displaystyle k_{m^{\prime }}=\frac{\pi m^{\prime }}{\left(N+1\right)a}{m}^{\prime }=1,2,\dots ,N.}$$ (7)

The IR active modes of the system will be determined by the square of the exciton transition dipole moments, ${\tilde{\mu }}_{m0}$, which are expressed in terms of the site transition dipoles, μ_n0, as

$${\displaystyle {\tilde{\mu }}_{m0}=\sum _{n-1}^N〈{\psi }_m|n〉\hspace{0.17em}{\mu }_{n0}.}$$ (8)

Although the magnitude of μ_n0 does not vary by site, since CO groups alternate their direction along the helix, the z-projection of μ_n0 switches direction between adjacent sites, ${\mu }_{n0}^z={\mu }_z{\left(-1\right)}^n$. As a result, the IR active modes are observed at the top of the exciton band (high m values), where the wavefunction alternates sign site-to-site and the dipoles add constructively.

The modes parallel to the helical axis are of A symmetry, while those perpendicular to the helical axis are E symmetry, and the relative intensities of the two transitions will be tuned by the angle between the transition dipole and the helix. This is entirely consistent with the formalism developed by Higgs for the IR active modes of an arbitrary helix.⁴²

For the OBC case, the most intense peak is found at m′ = N, with a series of edge effect peaks that decrease in intensity for m′ = N − 2, N − 4, …. The effect of the OBC is to modulate the quickly varying component of the wavefunction with a slowly varying sinusoidal envelope. The number of half-waves in this envelope determines whether a particular m′ will be IR active or not, leading to only m′ = N − 2, N − 4, … having non-zero z dipole components. This is shown analytically in the supplementary material.⁴³

It is clear that the sign of J₂ will play a significant role in the structure of the exciton bands. In our ideal helices, the transition dipole alignment between rungs of the helix is either parallel (for the case that γ is even) or antiparallel (for the case that γ is odd). Thus, the registry between dipoles i and i + γ is expected to lead to positive J₂ for odd γ and negative J₂ for even γ. To determine average values for J₁ and J₂, we used coordinates from the Protein Data Bank (PDB) (accession codes 1JNO for HD and 1ALX for DH), positioned transition dipoles as described in Ref. 44, and calculated the transition dipole coupling using

$${\displaystyle J_{\mathit{ij}}=C\left(\frac{{\hat{\mu }}_i\cdot {\hat{\mu }}_j}{|{\mathit{r}}_{\mathit{ij}}{|}^3}-3\frac{({\hat{\mu }}_i\cdot {\mathit{r}}_{\mathit{ij}})({\hat{\mu }}_j\cdot {\mathit{r}}_{\mathit{ij}})}{|{\mathit{r}}_{\mathit{ij}}{|}^5}\right),}$$ (9)

where C = 580 cm⁻¹ Å.³ We arrived at values of J₁ = − 4 cm⁻¹ and J₂ = − 10 cm⁻¹, for the HD structure and of J₁ = − 4 cm⁻¹, J₂ = + 10 cm⁻¹ for DH. It should be noted that the results are qualitatively insensitive to variation of a few wavenumbers in these values. A value of 1655 cm⁻¹ was taken for ω₀, where this value was chosen to maximize agreement between the model spectra and experiment, and is similar to other values used in these calculations. A value of N = 30 was used, which is the total number of amide units in the gramicidin D dimer. We note here that the edge effects, perhaps unsurprisingly, show a significant dependence on the size of the system. This may have significant implications when comparing the spectroscopy of systems of varying sizes, but since this work focuses only on two conformers of gramicidin D which have the same number of amide units, we do not comment further on this. To calculate the intensity of each transition, we assume the same transition dipole position as Ref. 44, i.e., 20° from the C=O bond, towards the N in the N—C—O plane, centered on the CO bond. The calculated stick spectra were convolved with a Lorentzian function with a FWHM of 10 cm⁻¹.

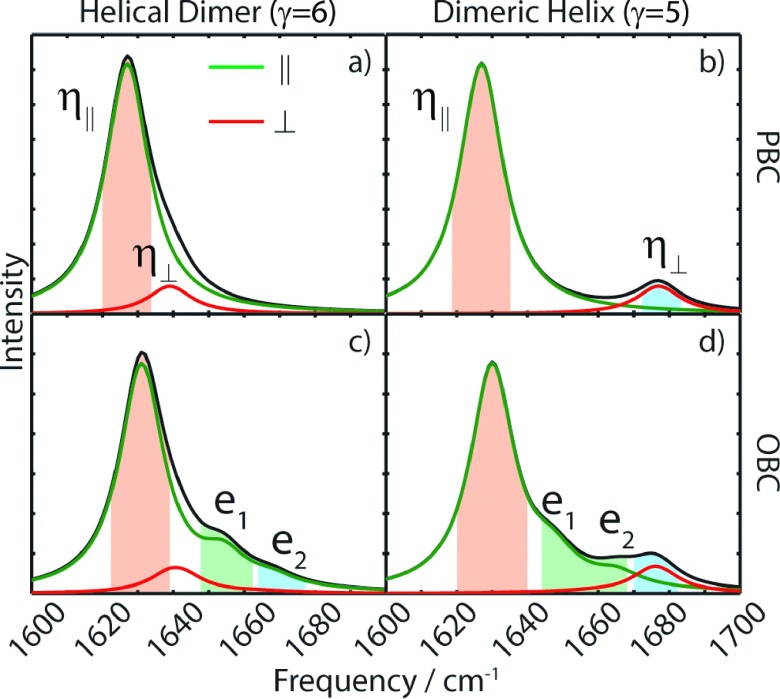
The resulting linear spectra from this model are shown in Figure 6 and decomposed into the contributions from the dipoles along the z axis and in the xy plane. Hereafter, we refer to transitions which lie along the z axis as parallel, and the components which lie in the xy plane as perpendicular. Overall, an excellent agreement is found between the open-boundary condition Bloch model spectra and the experimental data. The relative positions of the peaks are within a few wavenumbers of the experimental data, and all the qualitative features are captured.

FIG. 6.

Comparison of the calculated FTIR spectra with different boundary conditions for HD and DH forms for the Bloch model. Colored bars are used to highlight the regions discussed in the text. η and e labels refer to the modes discussed in the main text.

The differences between PBC and OBC calculations are most readily observed in region 2, which consists of peaks arising from finite-size effects (or edge effects). Unexpectedly, we find that the high frequency features in the HD structure (1660 cm⁻¹ and 1670 cm⁻¹) arise from edge-effects present only in the OBC calculations. This stands in contrast to β-sheet spectra, where calculations show a high frequency peak even for an infinite sheet.⁴⁵ Region 2 of the DH structure shows more structure in the model than in the experiment, which may be a reflection of the idealized geometry assumed. However, we note that this smoothly varying continuum structure is poorly reproduced by other calculations where idealized structure is not assumed.

The polarization of features is particularly revealing and is largely independent of boundary conditions. Both conformations have a strong band at 1630 cm⁻¹ that is polarized parallel to the helix axis, which we label η_∥. However, the frequencies of the weaker perpendicular absorptions, labelled η_⊥, vary with structure from 1640 cm⁻¹ for HD and 1676 cm⁻¹ for DH. These predicted η_⊥ resonance frequencies explain the projection angle measurement in Figure 4. The calculations suggest that the DH structure should have a maximum in θ corresponding to the crosspeak at ω₁, ω₃ = 1630, 1680 cm⁻¹. In the case of HD, the angle maxima should be observed for crosspeaks to the obscured component at 1640 cm⁻¹.

B. Empirical simulations

While the simplified Bloch model using idealized helices agrees well with experiment, NMR and X-ray crystallography structures show that the turns are irregular, and the CO groups have imperfect alignment relative to the helical axis. Furthermore, the CO groups in any protein may experience a heterogeneous electrostatic environment as the result of differences in hydrogen bonding, protein sidechains, and surrounding detergent and solvent. To assess what effect this disorder has on the spectra, we calculated spectra for the two structures by constructing a Hamiltonian incorporating pairwise couplings between all CO groups. The form of the Hamiltonian used was

$${\displaystyle H_{\mathit{ij}}={\omega }_0{\delta }_{\mathit{ij}}+J_{\mathit{ij}}\left(1-{\delta }_{\mathit{ij}}\right).}$$ (10)

The coupling, J_ij, was assumed to take the form of transition-dipole coupling (Eq. (8)), using the PDB coordinates 1JNO and 1ALX for the HD and DH conformations, respectively, and the dipole position and orientation as with the Bloch model. To incorporate energetic disorder, random Gaussian noise (FWHM 10 cm⁻¹) was added to the diagonal on a site-to-site basis, and the calculation was averaged over >5000 iterations. The value of ω₀ was chosen to maximize agreement between calculation and experiment, for the HD conformation, ω₀ = 1640 cm⁻¹ was used, while for the DH conformation, ω₀ = 1645 cm⁻¹ was used. The differences in ω₀ may be rationalized by noting the different electrostatic environments of the conformations—one is solvated by an anionic detergent, while the other is solvated by a neutral detergent. Indeed, it has been noted before that the IR spectrum of gramicidin D shows subtle changes with lipid or detergent identity.⁴⁶

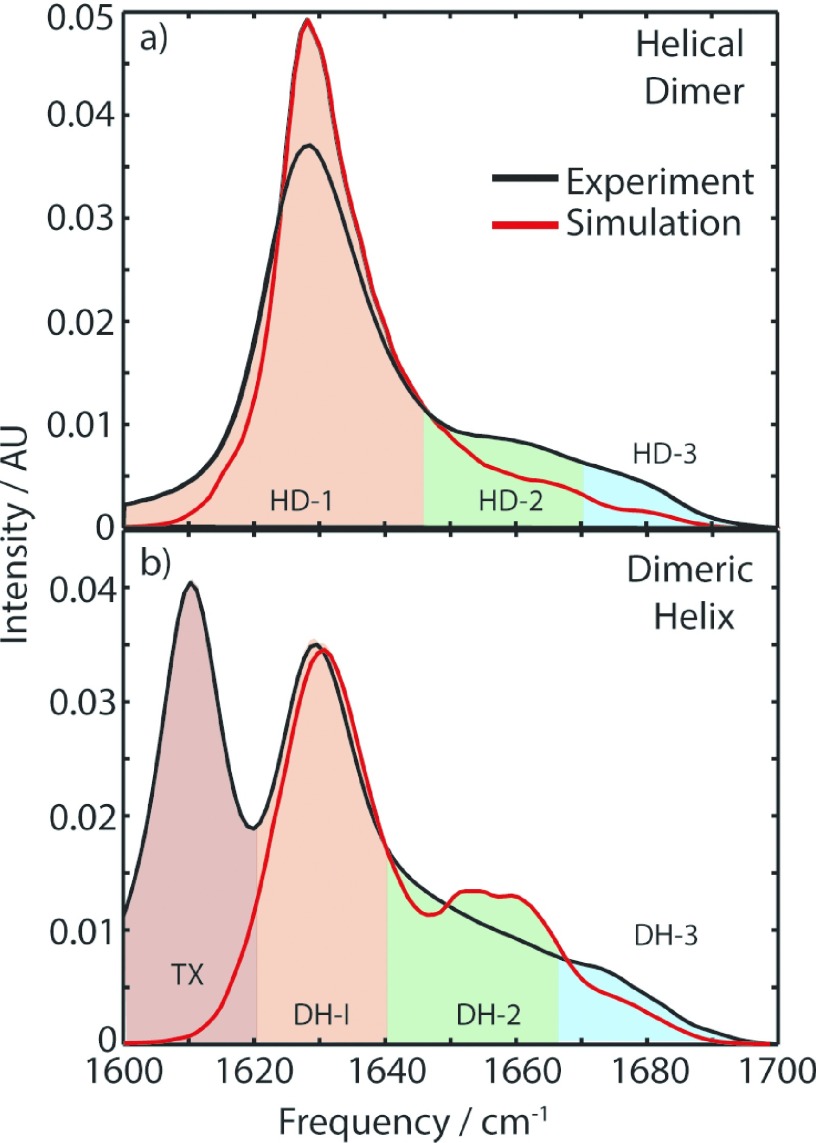
The comparison between calculated and experimental FTIR spectra is shown in Figure 7. The calculated spectrum for the HD conformation shows a strong peak in region 1 and weaker but distinct peaks in both regions 2 and 3. Remarkably for this simplified model, all calculated features are accurate to <5 cm⁻¹ for this structure and have a good agreement with spectra calculated with more sophisticated models.

FIG. 7.

Comparison between the experimental FTIR and the PDB structure-based calculated spectra. Spectra have been normalized to the integrated area within regions 1-3.

The simulated spectrum for the DH structure shows the greatest deviation from the experimental data. The peaks in regions 1 and 3 are well reproduced, but the smooth continuum of region 2 observed in experiment appears as a number of distinct peaks in the calculation. Since region 2 appears to be significantly influenced by edge effects in our Bloch calculation, it is reasonable to expect that an accurate calculation of this spectrum would have to average over the full conformational variation of protein and detergent. This approach was taken by Liang and Jansen in Ref. 47 where MD trajectories were used to incorporate conformational flexibility into the spectral calculations. These calculations are in good qualitative agreement with the results presented here. As expected, the main discrepancy between the two appears in the region 2, where edge effects are important. However, even this conformationally averaged, fluctuation-sensitive calculation does not capture the smoothly varying nature of region 2, instead showing discrete peaks.

The difference in region 2 aside, the 2D IR spectra calculated by Liang and Jansen are in good agreement with our experimental data—the homogeneous lineshape of the η_∥ peak is well captured, and the evidence of coupled modes, i.e., the crosspeaks, is also reproduced.

The structure observed in the PDB-based simulated spectrum of DH shows the same two-peak motif in region 2 as predicted by the Bloch model, suggesting the idealized model is indeed representative of the physical reality. This feature is also reproduced in the calculations of Liang and Jansen, which indicates these three distinct approaches are capturing the same physical picture of the vibrations.

As with the Bloch model, it is informative to compare the 2D polarization data to the calculations. A quantitative comparison of projection angles determined from the PDB structure calculations and from 2D IR experiments is given in Table I. From the eigenstates generated in our PDB structure-based calculations, we determined the angles between the modes which lie in regions 1, 2, and 3. To do this, we selected a center frequency (1635 cm⁻¹ for HD, to capture the η_⊥ mode, 1630 cm⁻¹ for DH) and took an intensity weighted average (±5 cm⁻¹ from the center frequency) of the angles between region 1 mode and region 2 or 3 modes. To extract a single number for the angle from the experimental data, we choose the maximum value from the heatmap in each of the regions listed.

TABLE I.

Comparison of angles between transition dipoles for the 1-2 and 1-3 crosspeak regions from experiment and PDB structure-based simulation.

	Experiment	Calculation
HD (regions 1 and 2)	60°	55°
HD (regions 1-3)	50°	42°
DH (regions 1 and 2)	50°	53°
DH (regions 2 and 3)	70°	69°

The results show remarkable agreement between experiment and our empirical simulations, though a note of caution should be sounded. In the case of overlapping resonances, the determination of angles from experimental spectra can vary considerably based on the methods used for determining the polarization ratio and is influenced by interference effects between resonances.³⁷ Nonetheless, the agreement between experiment and simulations is an important validation of the assumptions made in the construction of the simulation.

The angles determined from the 2D IR spectra and the PDB-structure calculation highlight an important point. Though we discuss the features of the spectra as though only one mode contributes to each peak, there are in fact many modes which contribute to each spectral feature. This is the reason for the discrepancy between the Bloch model, which predicts peaks to be either parallel or perpendicular to each other, and the experiment and simulations, which average over spectral regions and predict angles between the limiting values of 0° and 90°.

V. DISCUSSION

The distinct spectral patterns for the HD and DH conformers indicate that 2D IR spectroscopy is capable of revealing conformational differences through spectral variation and polarization differences in delocalized vibrational bands that differ subtly in the symmetry, placement, and orientation of oscillators within the helical structure. Further, the close correspondence of experimental 2D spectra and the predictions of our local mode model give us the confidence to discuss the underlying modes in some detail.

A. β-sheets

The similarity in hydrogen bonding pattern and spectra between the gramicidin D helices and β-sheets makes a review of the dominant modes in parallel and antiparallel β-sheets useful. The intense low frequency peak (∼1630 cm⁻¹) in β-sheets, usually designated ν_⊥, arises from CO groups oscillating in-phase in the direction perpendicular to the strands of the sheet and out-of-phase with each neighbor along the direction of the strand.^45,48 This results in a net transition dipole which lies in the plane of the sheet, perpendicular to the direction of the strands.

At this point, it is necessary to provide some clarification of the terms used in this section. The phase of a vibration refers to whether the CO bond is stretching or compressing, whereas the direction of the oscillator refers to the three-dimensional position of the static CO bond. Thus, two oscillators which are out-of-phase, but also lie antiparallel, will add constructively. This distinction is particularly important for the discussion later of phases of vibration of rung-displaced oscillators.

The second peak in a typical β-sheet spectrum is found at higher frequency (∼1680 cm⁻¹) and is much less intense. This peak originates from the mode where oscillators are in-phase along a strand, and out-of-phase between strands, and is designated ν_∥. These are shown schematically in Figure 8. As noted earlier, the amide I dipole does not lie perfectly along the CO bond coordinate but rather tilted slightly towards the nearby N atom. It is this tilt which is responsible for the transition intensity of the ν_∥ band—the off-axis component of the dipoles adds up constructively to give a readily observable, but much weaker band. Though the registry of the parallel and antiparallel β-sheets differs, their IR spectra are indistinguishable.⁴⁹ This serves to highlight an important difference between the two-dimensional sheet and the inherently three-dimensional helix—the HD and DH structures also differ primarily in hydrogen-bonding pattern but have distinct spectra.

FIG. 8.

Schematic comparison of the IR active modes in antiparallel and parallel β-sheets. (Top) Schematic illustrating the spatial arrangement of amide groups in the two structures. (Bottom) Schematic of the ν_⊥ and ν_∥ vibrational modes, color coding the CO vibrational phase for the individual amide sites (red/blue = + /−).

B. Helical dimer

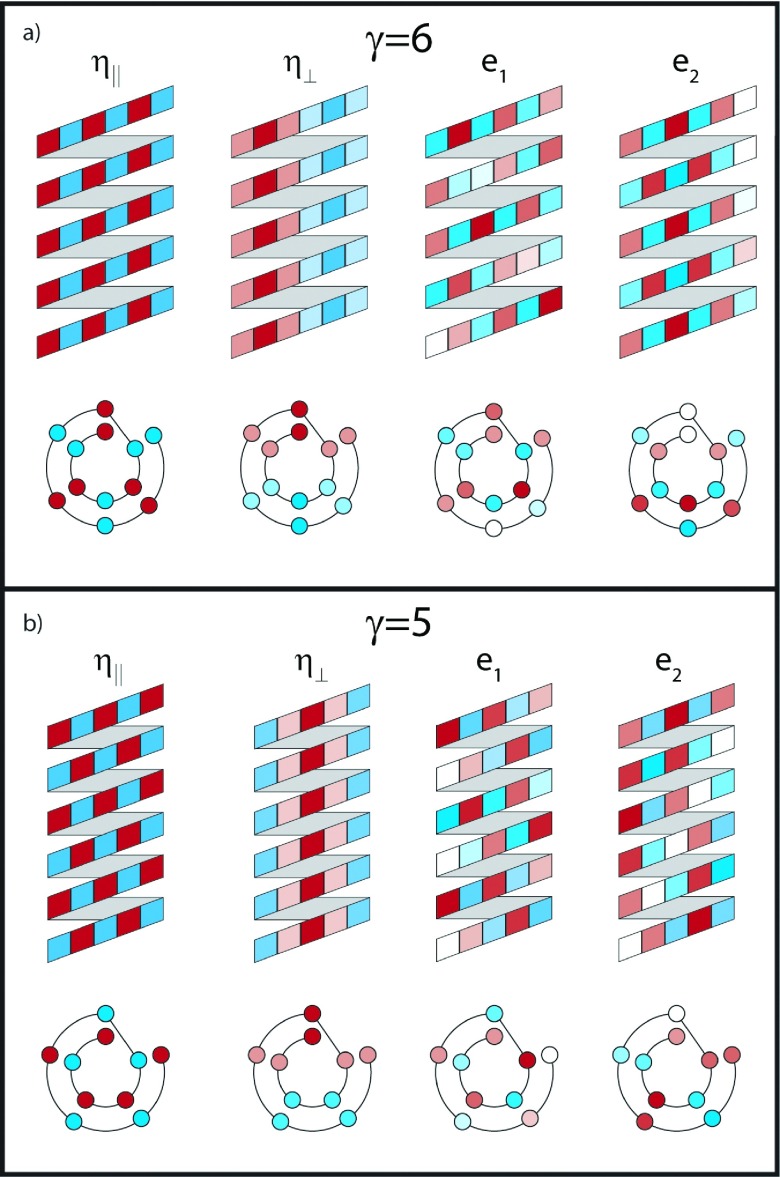
Returning to gramicidin dimer, we can analyze similar oscillator phase variations to describe the IR active modes of its two conformers. For the helical dimer, the dominant feature presented in experiments and in the Bloch model (for PBC or OBC) is the intense low-frequency mode near 1630 cm⁻¹, which we refer to as the HD η_∥ mode. The vibrational phases between nearest neighbors of the η_∥ mode (Figure 9) bear a striking resemblance to the ν_⊥ mode of β-sheets, although with strands wrapped around as a helix. The CO groups are in-phase between rungs, but out-of-phase with their immediate neighbors. The only difference between the result for the open and periodic boundary conditions is the relative contribution of the CO groups at the edges, which is reduced for OBC. The coefficients of the OBC modes are given in the supplementary material.⁴³

FIG. 9.

IR active modes from the γ = 6 and γ = 5 Bloch models. η_∥ and η_⊥ modes for both cases are calculated for periodic boundary conditions, while the edge modes, e₁ and e₂, are from the finite boundary conditions. The color represents the phase of oscillation (stretch, compress), while the color intensity represents the magnitude of the wavefunction coefficient for that mode.

Though the HD FTIR bears a striking similarity to the idealized β-sheet FTIR (as does the DH FTIR), the remaining peaks arise from significantly different modes. The perpendicular feature in Fig. 6(a) at ∼1640 cm⁻¹, which was identified by altering the polarization scheme in the 2D IR spectra, is the η_⊥ mode. The Bloch states using PBC or OBC show this mode is defined by a nodal plane which bisects the helix along the helical axis. Although there is no direct analogue to modes of infinite two-dimensional β-sheets, when the helix is unwrapped as in Figure 9, we see that it bears resemblance to the (k_x, k_y) = (2, 1) mode for a 2D particle-in-a-box. The η_⊥ frequency can be rationalized by the couplings between laterally displaced sites (J₁) and rung-displaced sites (J₂) in our model in Eq. (4). In-phase vibrations between rungs favor the negative couplings between rungs over the intermediate wavevector component along the strands. With this in mind, it becomes apparent why this mode appears at a frequency only slightly higher than the η_∥ peak, rather than at a significantly higher frequency as in the case for β-sheets. The features identified earlier in regions 2 and 3 arise solely from edge effects (labelled e₁ and e₂) and are only reproduced in the Bloch model with open boundary conditions. These modes are shown in Figure 9. Alternating phases between lateral neighbors, similar to the η_∥ and ν_⊥ modes, are observed, but e₁ and e₂ differ from these modes by the presence of a significant number of nodes. These nodes result in some rung-displaced oscillators being out-of-phase, the number of out-of-phase pairs determining which mode is higher in energy. This again is due to the larger value of J₂ relative to J₁. While the lateral interactions in these modes are generally similar to the low energy states, the inter-rung interactions dominate.

C. Dimeric helix

The intense η_∥ peak and η_⊥ peak in the DH experimental spectra are captured by the Bloch model. Like the β-sheet and HD η_∥ mode, the DH η_∥ mode has alternating phases on laterally displaced oscillators but differs by having alternating phases between the rung-displaced oscillators. Since the rung-to-rung orientation varies in the DH, all dipoles add constructively for this mode. This illustrates a key difference between the γ = 6 and γ = 5 models: the oscillators displaced by a rung in the even γ structures are parallel, while they are antiparallel for the odd γ case. As with the HD structure, the main effect of the boundary conditions is to slightly alter the amplitude of the mode on some oscillators, in the case of the η_∥ mode, curtailing the contribution from the oscillators at the ends of the helix.

The DH η_⊥ peak also bears a striking similarity to its HD counterpart, even though the two come at significantly different frequencies. This is another manifestation of the dominance of the inter-rung couplings in the spectroscopy of gramicidin D. Both modes are in-phase between rungs, but because the γ = 5 helix has antiparallel oscillators between rungs, this shifts this mode to much higher frequencies.

The edge modes show a similar relation to the η_∥ mode as the HD conformer, i.e., they are characterized by a number of node “defects” which give rise to non-uniform inter-rung phases. As noted earlier, the edge effect peaks are much sharper than in the experimentally observed spectrum. Even in the empirically calculated spectrum for DH, these peaks retain their structure. This suggests that the continuum structure does not arise solely from site energy disorder, as this is incorporated into our empirical model. One possibility is that there exists a large number of very subtly different conformations, all of which have edge modes at slightly different frequencies. However, as we noted earlier, if this is the case, then this conformational variation is not well captured by MD simulations, since this approach has been unable to reproduce the experimental data.

The agreement between the Bloch model spectra and both the empirical simulation and experimental spectra would seem to suggest that the DH helix has more of the γ = 5 model character than γ = 6, even though it formally has 5.6 residues per turn. In the crystal structure, any particular CO group has both a parallel (γ = 6 model) and an antiparallel (γ = 5 model) CO group above it. The origin of the dipole is not centered on the C atom, but rather offset along the C=O bond. Two CO groups pointing towards each other will be closer and couple more strongly than two parallel CO groups. This effect has been noted in β-sheet calculations, where it can result in the coupling between antiparallel oscillators being double that of the coupling between parallel groups,⁴⁴ so we would expect the DH spectra to be dominated by the coupling between antiparallel (γ = 5) groups.

D. Relation to existing literature

Our analysis of the spectral features of the HD and DH structures makes it clear that the coupling between rung-displaced oscillators is the dominating factor in the amide I spectra of gramicidin D. This, like many features of the gramicidin spectra, has an analog in the spectroscopy of β-sheets, since the strongest couplings between CO groups in both structures come from hydrogen-bonded oscillators on different strands.⁴⁴ This is consistent with observations that amide I spectra of gramicidin D are modified by the lipid or detergent environment. This is the case in Ref. 46 where spectra of the HD conformation show intensity and frequency shifts depending on whether they are acquired in a phosphatidylcholine bicelle or bilayer. This could be due to a compression or extension of the β-helix, which would change the magnitude of the coupling between rungs.

The paramount importance of the inter-rung couplings leads to interesting effects when the sign of the coupling constant changes between ideal γ = 5 and γ = 6 structures as a result of the opposite dipole orientation between adjacent sites. The sign of the coupling constant significantly alters the frequency of the mode perpendicular to the helical axis. Our simulations show that the spectra for the conducting form are only explained by and even value of γ, i.e., the DH structure is not compatible with the spectrum of the conducting form of gramicidin D, as has been suggested. Real structures are not restricted to integer numbers of residues per turn and so can have non-negligible coupling to parallel and antiparallel oscillators on the rungs above and below. To a first approximation, the number of residues per turn will determine whether a particular oscillator is closer to a parallel or antiparallel oscillator on the rung above. This would suggest that the amide I mode is sensitive to the registry of β-helices to differences, being influenced by even fractions of a residue per turn. This stands in contrast to the case for α- and 3₁₀-helices, which have extremely similar spectra despite a difference in registry comparable to the HD and DH structures. The key difference is the alignment of the oscillators along the helical axis—for α- and 3₁₀-helices, they all lie parallel.

The success of the Bloch model in reproducing the experimental data with only two coupling constants suggests that it is not necessary to include all, or even most, of the couplings between CO groups when simulating amide I spectra. Indeed, it has been shown that proteins may be decomposed into independent subunits in spectral simulations,⁵⁰ and that coupling between hydrogen-bond partners may dominate experimental spectra.⁵¹ This suggests that it may be possible to make optimized coupling maps, in the same manner as has already been done for optimization of the electrostatic site energy maps.^24,25

It is important to note that while the Bloch model is able to reproduce the dominant features of the spectrum, it represents an ideal case. One manifestation of this assumed ideality is an artificially large delocalization length. This can be illustrated by considering the inverse participation ratio for each eigenstate α,

$${\displaystyle L_{\alpha }={\left(\sum _n{\left|c_{n\alpha }\right|}^4\right)}^{-1}.}$$ (11)

For the most intense transition in the Bloch models, we find that the periodic boundary conditions give L_α = 30, which is the number of amide units in the model. The finite size model gives L_α = 21.3, because of the sinusoidal modulation of the wavefunction coefficients, as outlined in the supplementary material.⁴³ The empirical model outlined in Sec. IV gives values of 〈L_α〉 = 8.4 for the HD calculation and 〈L_α〉 = 7.4 for the DH calculation, where the angled brackets indicate the average value of L_α in the frequency range ±5 cm⁻¹ of the intense low frequency peak. This provides a more reasonable estimate of the delocalization length of the excitons in the helices, since site energy fluctuations are included in this model. In reality, couplings will also fluctuate, so we may consider these values of 〈L_α〉 as upper limits for what we might expect in reality. These numbers are similar to those obtained from similar calculations for α-helices⁵² (〈L_α〉 = 6.5).

Gramicidin D is not a stranger to the field of 2D IR. In addition to their calculations of the linear and 2D IR spectra of the HD and DH conformations, Liang et al. investigated the potential of isotope-labelled 2D IR for observing proton transport through the HD structure of gramicidin D.⁵³ One conclusion was that even with no protons in the channel, there should exist spectroscopically distinct sub-populations of residues (A3, A5, W9, and W11) with differing hydrogen-bond strength that might be observed through isotope labelling. This suggestion may not appear to be consistent with our work, which argues that identical site frequencies with some random disorder are adequate to describe the gramicidin D spectroscopy. However, in our case of quasi-degenerate oscillators, the spectroscopic features are dominated by strong inter-rung coupling, rather than the weaker site energy disorder. It remains possible that an amide I isotope label may be able to distinguish subtle shifts in site energy which are obscured by strong coupling effects in the absence of an isotope label, though the success of our quasi-degenerate oscillator approach suggests these shifts should be on the order of the coupling (∼10 cm⁻¹) or smaller, rather than the 25 cm⁻¹ splitting suggested by the calculations in Ref. 53.

Of more general interest is the application of this analysis to the study of biologically relevant phenomena observed in gramicidin D, such as internal gating or “Flicker Transitions.”^54,55 Many competing models have been proposed to explain these transient interruptions to ion conduction, such as subunit rotation or lateral diffusion. The prominent role of edge effect transition in the HD structure suggests that these may be useful marker bands for seeing monomer to dimer transition (as would be the case for a lateral diffusion gating mechanism). The strong dependence on the sign of the coupling constant between rungs offers the possibility of observing subunit rotations.

VI. CONCLUSIONS

In conclusion, we have demonstrated that amide I spectroscopy is able to distinguish between the helical dimer and dimeric helix forms of gramicidin D. We are able to observe clear spectral differences in the linear FTIR spectra, which arise from subtle structural differences in the peptide. However, 2D IR allows us to resolve issues of spectral congestion, and through polarization manipulation, reveal a peak in the helical dimer spectra which would otherwise remain hidden. We have demonstrated that the spectra of both structures are well-captured by a Bloch state model of ideal, highly symmetric helices. This model reveals that the amide I spectroscopy of gramicidin D is dominated by the coupling of oscillators between rungs of the helix and so is exquisitely sensitive to the number of residues per turn of the helices.