Skip to main content
PMC home page
Facts, Views & Vision in ObGyn logoLink to Facts, Views & Vision in ObGyn
. 2015;7(1):7–15.

Automated characterisation of ultrasound images of ovarian tumours: the diagnostic accuracy of a support vector machine and image processing with a local binary pattern operator

S Khazendar 1, A Sayasneh 2, H Al-Assam 1, H Du 1, J Kaijser 3, L Ferrara 4, D Timmerman 3, S Jassim 1, T Bourne 2,3,4
PMCID: PMC4402446  PMID: 25897367

Abstract

Introduction: Preoperative characterisation of ovarian masses into benign or malignant is of paramount importance to optimise patient management.

Objectives: In this study, we developed and validated a computerised model to characterise ovarian masses as benign or malignant.

Materials and methods: Transvaginal 2D B mode static ultrasound images of 187 ovarian masses with known histological diagnosis were included. Images were first pre-processed and enhanced, and Local Binary Pattern Histograms were then extracted from 2 × 2 blocks of each image. A Support Vector Machine (SVM) was trained using stratified cross validation with randomised sampling. The process was repeated 15 times and in each round 100 images were randomly selected.

Results: The SVM classified the original non-treated static images as benign or malignant masses with an average accuracy of 0.62 (95% CI: 0.59-0.65). This performance significantly improved to an average accuracy of 0.77 (95% CI: 0.75-0.79) when images were pre-processed, enhanced and treated with a Local Binary Pattern operator (mean difference 0.15: 95% 0.11-0.19, p < 0.0001, two-tailed t test).

Conclusion: We have shown that an SVM can classify static 2D B mode ultrasound images of ovarian masses into benign and malignant categories. The accuracy improves if texture related LBP features extracted from the images are considered.

Keywords: Decision support techniques, ovarian cancer, ovarian neoplasm, Support Vector Machines, ultrasonography

Introduction

Ovarian tumours are common and occur at all stages of life. Real-time ultrasonography is widely used to characterise ovarian tumours as benign or malignant. This may be achieved using the subjective impression of the examiner (Timmerman et al., 1999), applying ultrasound based simple rules and descriptors (Kaijser et al., 2013; Timmerman et al., 2010 a) or by using a variety of ultrasound based prediction models, such as the RMI (Risk of Malignancy Index) (Jacobs et al., 1990; Kaijser et al., 2013), and International Ovarian Tumour Analysis (IOTA) Group logistic regression models LR1 & LR2 (Kaijser et al., 2013; Sayasneh et al., 2013; Timmerman et al., 2010 b). These prediction models rely on the examiner identifying different ultrasound features in real time and using these to calculate the risk of a lesion being benign and malignant. Such an approach is dependent on the experience and skill of the examiner. The preoperative classification of ovarian masses using the subjective impression of ultrasound operators has been shown to be less precise when assessing static ultrasound images compared to those obtained during real-time examination (Van Holsbeke et al., 2008). In the latter study, the authors obtained an accuracy of 85% based on expert consensus opinion of static images compared to 89% for real-time ultrasonography (Van Holsbeke et al., 2008).

The texture of static images refers to the appearance, structure and arrangement of parts of an object within the image (Castellano et al., 2004). Studying texture features, which includes the visual patterns and properties of homogeneity can give important structural information about the surfaces in relation to the surrounding environment (Linares et al., 2004). Texture analysis is widely used in image processing, such as face images for classification and segmentation. Local Binary Pattern (LBP) is an effective technique that captures grey-scale invariant texture information (Ojala et al., 2002).

Different learning machines, such as Support Vector Machines (SVM), have been developed to classify data (Cristianini et al., 2000). An SVM is a computationally efficient classifier that learns the hyper-planes in a high dimensional feature space that separate examples (i.e. data points) of the positive class from the negative class (Cristianini et al., 2000). During the training stage, SVM builds a classification model based on training samples, which is a Hyperplane in the case of a linear SVM. To classify a new sample, the resulting Hyperplane will be used to assign a class. For example, an image will be predicted as a malignant case if it falls on the negative side of Hyperplane and as a benign case vice versa. Moreover, SVM performance is highly generalizable without the need to add a priori knowledge (Song et al., 2002; Sun et al., 2003).

The aim of this study was to develop a computerised system, capable of characterising images of ovarian masses as benign or malignant independent of an examiner being competent to identify the features required to make a diagnosis. For this study we used original or enhanced B mode static ultrasound images.

Materials and Methods

This is a retrospective cohort study carried out on static ultrasound images of ovarian masses from women recruited into the IOTA study (Timmerman et al., 2010 b). All women in this study underwent surgical removal of the mass between November 2005 and November 2013 with a known histological diagnosis. All women gave written informed consent to use and analyse the data (Timmerman et al., 2010 b). The 187 anonymous 2D ultrasound images were retrieved from the IOTA database (Astraia software gmbh, Germany) at the Department of Gynaecological Ultrasonography, Campus Gasthuisberg, KU Leuven, Belgium. This study was granted ethical approval by the University of Buckingham’s School of Science & Medicine Ethics Committee in May 2012. We have followed the STARD guidelines for diagnostic accuracy studies (Bossuyt et al., 2003).

Reference standard

The final outcome was the histological diagnosis of removed tissues as stipulated by the IOTA study protocol (Timmerman et al., 2010 b), and the classification of these as benign or malignant. Borderline tumours were classified as malignant. Tumours were classified using the criteria recommended by the World Health Organisation (WHO) (Tavassoéli et al., 2003).

Static images

Each image represented the 2D B mode ultrasound features of the surgically removed adnexal mass. The image used for each mass was selected by author JK that on subjective impression was most representative of the final histopathology. In total 187 images were used from 177 patients (112 images of Benign and 75 images of malignant tumours). In ten patients we used an additional 2D-image with another representative region of interest (ROI) that reflected the final histopathology. Histology results were available for all masses corresponding to the images used (Table I).

Table I. The histopathology of ovarian masses included in the study in the training and test groups.

Histopathology N (total N = 187)
Benign (n = 112) Mature teratoma 23
Endometrioma/endometriosis 15
Mucinous cystadenoma 23
Functional cyst 5
Ovarian fibroma 6
Serous cystadenoma 21
Serous cystadenofibroma 13
Other benign 6
(1 tubal abscess, 1 Brenner tumour, 1 Multilocular peritoneal inclusion cyst MPIC,
1 Mucinous cystadenofibroma, 1 subserous adenomyoma, 1 hydrosalpinx)
Malignant (n = 75) Borderline mucinous tumour 15
Borderline serous tumour 6
Serous cyst/adenocarcinoma 28
Mucinous cyst/adenocarcinoma 3
Endometrioid adenocarcinoma 6
Other ovarian cancer 17
(1 Lymphoma, 7 metastatic tumours (3 intestinal, 1 breast, 1 pancreatic,
1 gastric, and 1 lung cancers), 1 leiomyosarcoma,1 stromal tumour,
1 germ cell tumour, 2 clear cell carcinomas, 2 carcinosarcomas,
1 immature teratomas, 1 endometrial cancer)
Open in a new tab

Power or colour Doppler had been performed for ten images, but this did not affect the segmentation process of the grey scale features of the ROI, therefore they were accepted in the study. The analysis was confined to the grey scale information contained within the image. MATLAB (Matlab R2012a MathWorks, Natick, Massachusetts, USA) image processing software was used in this study.

Pre-processing

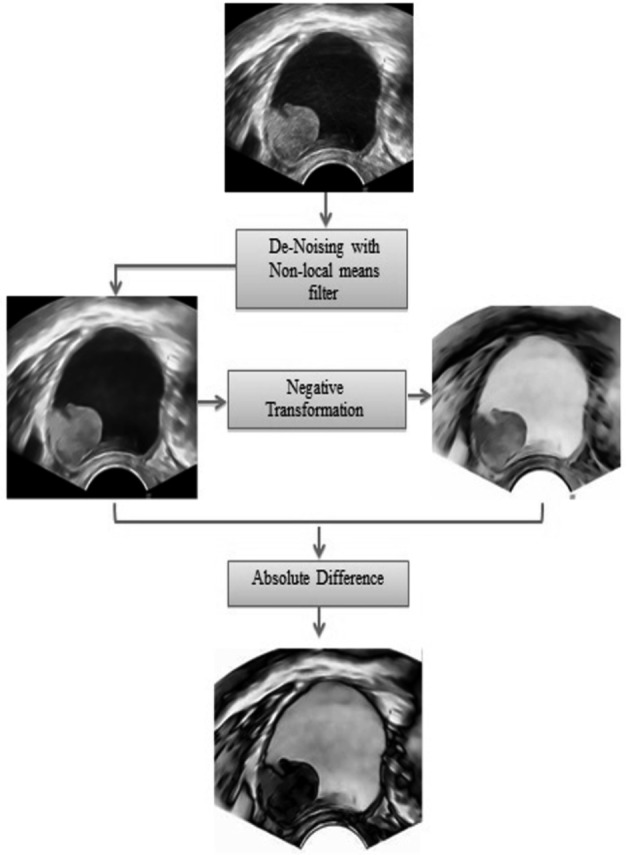
The original images were received in JPEG digitized format. Each image was pre-processed in three steps as illustrated in Figure 1. Firstly, we used a Non Local mean (NL-means) filter (Buades et al., 2005) to de-noise the image and reduce the negative impact of the Speckle noise (Fig. 2). Then, we conducted a negative transformation of each denoised image in preparation of the last enhancement step (Fig. 1). As a last step of the image pre-processing, we produced the enhanced copy of each image by obtaining the absolute difference between the de-noised image and its negative counterpart. As illustrated in Figure 1, the absolute difference has enhanced the edges in the original B mode image and produced a clearer texture of the cyst (the light grey shades in the resulting image).

Fig. 1. Pre-processing the image before segmentation.

Fig. 1

Open in a new tab

The Absolute Difference is a basic image processing operation that takes the absolute value of the difference between the values of the two corresponding pixels I1(i) and I2(i), from the two input images I1 (here is the filtered image) and I2 (here is the negative of the filtered image)

r(i) = ∣I1(i) - I2(i)∣

where r (i) represents the ith pixel in the result image. We apply the absolute difference operation on the de-noised image from the NL-means filtering step and its negative image. This means that

r(i) = ∣Intensitymax - 2×I(i)∣

Fig. 2. The NL-means de-noising method.

Fig. 2

Open in a new tab

Segmentation

Image segmentation refers to separating the ROI (which in our study is the ovarian tumour) from the background of the whole image. Automatic segmentation of the ROI is not a trivial problem and can be very difficult when the ROI shares the same greyscale colour as the background. In our work, we have manually segmented the ROIs by the first author SK and further confirmed the ROIs by an ultrasound examiner (author AS). Post segmentation, there are four types of output images: original whole image, original ROI, enhanced whole image, and enhanced ROI (Fig. 3).

Fig. 3. An example of the features transformation using pre-processing methods (left images column) and corresponding LBP processing (right images column). As a result 7 extra images were created from each original image.

Fig. 3

Open in a new tab

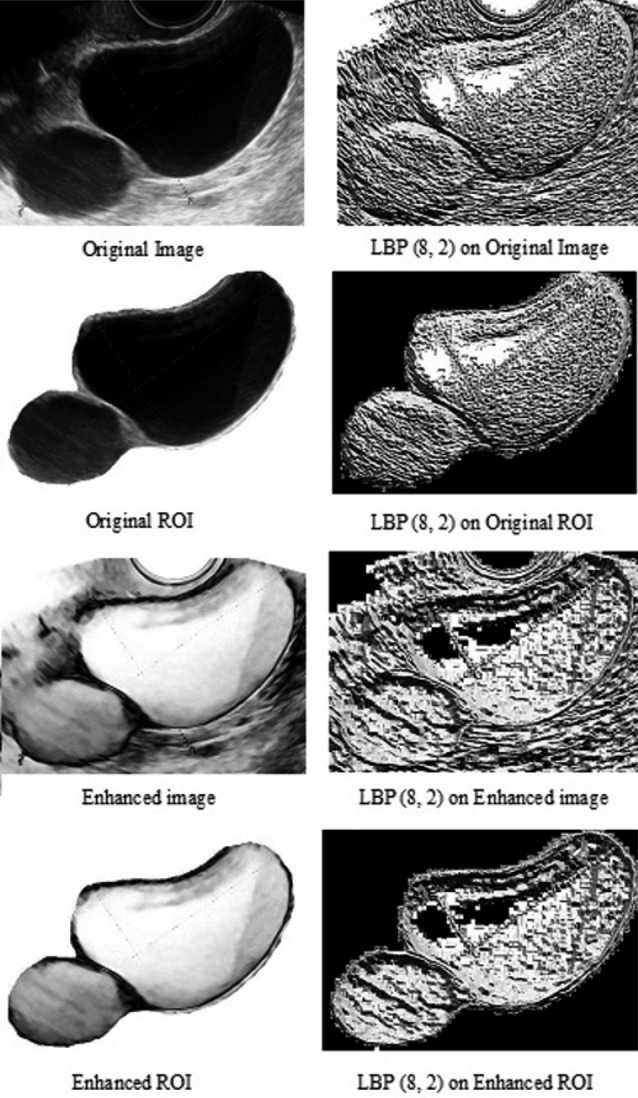
Image histogram of intensity

An image histogram shows the number of pixels in an image at each different intensity value. For an 8-bit greyscale image, there are 256 possible intensity values (0 is black and 255 is white), and the histogram of the image represents a frequency distribution of pixels amongst those values (Fig. 4).

Histogram of Local Binary Pattern (LBPH) for Texture

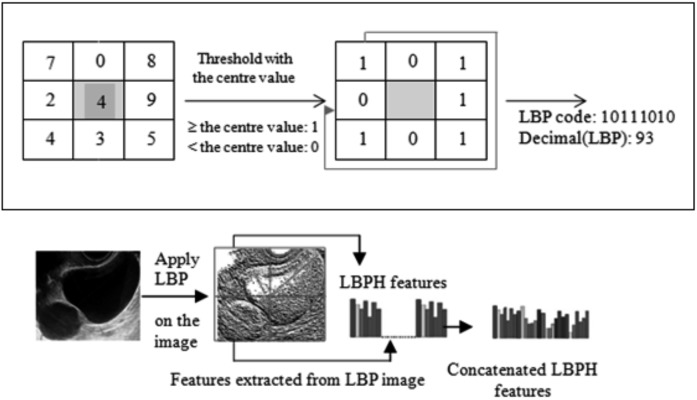
LBP normally refers to replacing image pixels with an 8-bit binary code that is derived from the pixel’s neighbourhood of pixels. It examines the eight neighbouring pixels ti (i = 0, 1, 2, ,,,, 7) of t in a clockwise order starting with the top left corner, and assigns 0 to the i-the bit if the pixel value of ti is less than that of t and 1 otherwise (Fig. 4) (Ojala et al., 2002). The corresponding LBP image is obtained by translating every 8-bit binary code into its decimal value in the range of 0 to 255. In this paper, we have used the LBP 256 bin obtained from window size of 5 × 5. We refer to this LBP form as the (8, 2) code.

Having obtained the LBP image we divided the image into 2 × 2 equal sized blocks, to capture localized texture information of ovarian tumours within the image. The 256-bin histogram was calculated for each block, and then the four histograms were concatenated and saved into a single feature vector for the whole image. That means we had 1024 feature components in one feature vector for each image (Fig. 4). The feature vector for the image was later used as a training instance for the SVM.

Fig. 4. Description of an ultrasound image of a functional cyst using a concatenated Local Binary Pattern histogram.

Fig. 4

Open in a new tab

Designing the test and training groups

For the 187 images used in this study, we created the LBP images from the original images (Fig. 4) using the (8, 2) form. The same procedure was repeated for the enhanced, original ROI and enhanced ROI images (Fig. 3). As a result we obtained 8 groups of 187 feature vectors in each group. These groups were: histograms of intensity for the original whole, LBP-transformed original whole, enhanced whole, LBP-transformed enhanced whole, original ROI, LBP-transformed original ROI, enhanced ROI and LBP-transformed enhanced ROI images.

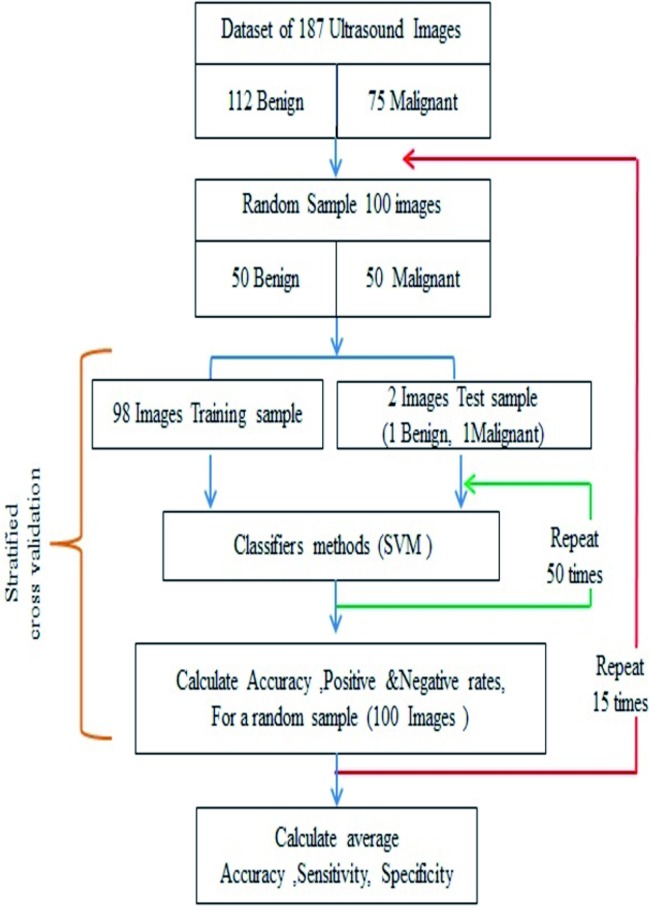
In order to address the class imbalance problem between benign (112 cases) and malignant (75 cases) in each data set and to develop a fair classification model for both cases, we randomly sampled 50 images of benign and 50 images of malignant tumours, totalling 100 images for training and testing the SVM. The sampling (without replacement) was performed using the Randsample function in Matlab (50 benign with Randsample (112, 50), and 50 malignant Randsample (75, 50)). For evaluation of performance, we employed a stratified 50-fold cross validation, which means applying the leave-one-out strategy to utilise the use of training examples. In an iterative process, one partition, i.e. two samples (one benign and one malignant), was taken as the test examples and the rest for training the SVM (Fig. 5). We repeated this process 15 times with a different random selection of 100 images (50 benign and 50 malignant) to reduce the random effect.

Fig. 5. A flow chart illustrating the randomised balanced cross validation process of selecting the training and test groups. This process was repeated 15 times to calculate the average diagnostic performance of the SVM in each one of the 8 main images’ groups.

Fig. 5

Open in a new tab

Statistical analysis

We calculated the average sensitivity, specificity and accuracy of the SVM for each of the 15 cycles. The same test was performed for each of the 8 main image groups. Medcalc software (MedCalc Software bvba, version 12, 2013, Belgium) was used to calculate the difference in accuracies between different groups. The two-tailed t test was used to compare means and p < = 0.05 was considered significant.

Results

The SVM learning machine was able to characterise static images of ovarian masses into benign or malignant with an average accuracy ranging between 0.62 and 0.78 (Table II).

Table II. Diagnostic performance of the Support Vector Machine on images processed using a Local Binary Pattern operator in the test group when using Radius R = 2.

Average diagnostics for SVM without LBP Average diagnostics for SVM & LBP (P = 8,R = 2) LBP/Histogram diff in Accuracy p
2 × 2 block image Sensitivity [95%CI) Specificity [95%CI) Accuracy [95%CI) Sensitivity [95%CI) Specificity [95%CI) Accuracy [95%CI)
Original image 0.63 [0.60-0.66] 0.61 [0.575-0.645] 0.62 [0.59-0.65] 0.69 [0.67-0.71] 0.66 [0.635-0.685] 0.67 [0.65-0.69] 0.05 [0.01-0.09] 0.01
Original ROI 0.68 [0.65-0.71] 0.645 [0.61-0.68] 0.66 [0.63-0.69] 0.75 [0.73-0.77] 0.72 [0.71-0.73] 0.74 [0.73-0.75] 0.08 [0.04-012] 0.0008
Enhanced image 0.59 [0.54-0.64] 0.64 [0.62-0.66] 0.62 [0.59-0.65] 0.80 [0.77-0.83] 0.77 [0.74-0.80] 0.78 [0.76-0.80] 0.16 [0.12-0.20] 0.0001
Enhanced ROI 0.66 [0.63-0.69] 0.65 [0.625-0.675] 0.65 [0.63-0.67] 0.77 [0.75-0.79] 0.77 [0.75-0.79 0.77 [0.75-0.79] 0.12 [0.09-0.15] 0.0001
Open in a new tab

SVM: Support vector machine. LBP: Linear binary processor. ROI: Region of interest.

We observed a general improvement in SVM average accuracy when images were processed by the LBP (8, 2) operator (Table II). This improvement in SVM diagnostic performance was statistically significant when LBP was applied to both original whole and ROI, as well as enhanced whole and ROI images (p value ranged between 0.0001 to 0.01) (Table II). Similarly, when the LBP was not applied (i.e. when the histogram of the spatial domain was used rather than the LBPH), the average accuracy of the SVM was improved when the learning machine was trained on ROI original images (0.66, 95%CI: 0.63-0.69) compared to whole area original images (0.62, 95%CI: 0.59-0.65) (difference of 0.04, 95%CI: -0.001 – 0.08, p = 0.06).

When the LBP was applied, the latter difference in SVM average accuracy between ROI and whole image characterization increased to 0.07 (95%CI: 0.04-0.08, p < 0.0001). Image enhancement alone, with no LBP did not improve the capability of the SVM to characterize the images, with an average accuracy of 0.62 (95% CI, 0.59-0.65) for both enhanced and non-enhanced whole images, and with no significant difference for enhanced and non-enhanced ROI images (average accuracy of 0.65 and 0.66 respectively (p = 0.6) (Table II). However, when the LBP was applied on enhanced images, there was a significant improvement in the average accuracy of the SVM to characterise whole images (from 0.67 to 0.78, p < 0.0001) and ROI images (from 0.74 to 0.77, p = 0.03).

In our data, we have tried the kNN (k-Nearest Neighbours) classifier, instead of SVM, using Euclidean distance metric when k = 1. However we found that the performance of the SVM was significantly better (Table III). We believe that this might be due to the better performance of an SVM with higher dimensionality.

Table III. Diagnostic performance of the kNN on images processed using a Local Binary Pattern operator. Euclidean distance metric when k = 1.

Average diagnostics for kNN & LBP (P = 8,R = 2) Average diagnostics for kNN without LBP
2 × 2 block image Sensitivity [95%CI] Specificity [95%CI] Accuracy [95%CI] Sensitivity [95%CI] Specificity [95%CI] Accuracy [95%CI]
Original image 0.55 0.56 0.55 0.65 0.59 0.62
Original ROI 0.62 0.53 0.58 0.71 0.49 0.63
Enhanced image 0.57 0.69 0.63 0.66 0.59 0.63
Enhanced ROI 0.69 0.56 0.63 0.73 0.46 0.60
Open in a new tab

kNN: k-Nearest Neighbours LBP: Linear binary processor. ROI: Region of interest.

Discussion

In this study we have shown that computer-based image processing technologies can automatically categorise static B mode ultrasound images as being derived from either benign or malignant ovarian cysts. This accuracy of this technique is not significantly different from the accuracy reported by ultrasound examiners using their subjective impression to read similar static ultrasound images (accuracy 0.85, difference of 0.08, 95% CI: -.0.006 to 0.16. p = 0.08) (Newcombe, 1998; Van Holsbeke et al., 2008). We have also shown that average diagnostic accuracy is better using an LBP coding operator on enhanced images. To the best of our knowledge this approach has not been previously described.

We believe our three-step enhancement method (non-local mean filter, negative transformation, absolute difference) together with the use of an LBP improved the ability of an SVM to correctly read images by highlighting the external and internal borders of the mass and improving the contrast in solid areas (Fig. 3). Others have described different automatic techniques for classifying ovarian masses images using static images (Zimmer et al., 2003) or by analysing the parameters data derived from these images (Biagiotti et al., 1999; Tailor et al., 1999). However, the novelty of our approach lies in using blocked non-uniform local binary pattern alone for the feature extraction stage on the enhanced images to achieve best result.

The IOTA group has previously developed prediction models for the classification of ovarian masses using Bayesian least squares SVM and relevance vector machines (Van Calster et al., 2007). These approaches were fundamentally different to the current approach as they relied on ultrasound examiners identifying and recording ultrasound-based variables in “real time” for model development (Van Calster et al., 2007). Thus however sophisticated the model, the limiting factor is the competence of the ultrasound examiner. They found an accurate performance of the model in the test set with a sensitivity and specificity above 90% and 80% respectively for all models (Van Calster et al., 2007). Other studies have also approached the problem using automated assessment of images. In one, an SVM was successfully used with an average classification accuracy of 86.90%, to classify ultrasound images representing three types of benign ovarian cysts: simple, endometriomas, and benign teratomas (Sohail et al., 2010). In this study, histogram moments with Grey Level Co-Occurrence Matrix (GLCM) based statistical texture descriptors were used for image processing (Sohail et al., 2010). Recently, an accuracy of 95% was reported for the characterisation of ovarian tumours using an adjunct Computer Aided Diagnostic (CAD) technique and data mining algorithms on 3D acquired ultrasound images of the ovary (Acharya et al., 2012). In this latter study, the authors used a Decision Tree (DT) classifier on the four most significant texture and high order spectra features. However in this study the images were taken from only 20 patients (10 benign and 10 malignant) (Acharya et al., 2012). Although the DT model had a higher accuracy than the approach we have reported, it was achieved using a large number of images (1000 images of benign and a further 1000 images from malignant tumours) derived from the same 20 patients (Acharya et al., 2012). Compared to the latter study, our SVM model was trained with fewer training images, from a larger number of women and included a wider range of pathologies. Despite the appeal of producing comprehensive rules, DT classifiers have known limitations such as being sensitive to small changes in the training set, rectilinear decision boundaries, and locating split points for continuous features. On the other hand SVM’s have known advantages for handling high dimensional data with non-linear decision boundaries (Tan et al., 2006). Taking a different approach, Acharya et al used advanced imaging and data mining technologies to classify benign and malignant ovarian masses with an accuracy of 99.8% (Acharya et al., 2014). This study used a probabilistic neural network (PNN) classifier, compared to the SVM used in our study. They also based the study on 20 patients, albeit examining 2600 images (50% benign and 50% malignant) derived from this cohort. Colour Doppler and 3D images were also used in this study whereas we used only B mode ultrasound information (Acharya et al., 2014). It is possible that the addition of 3D and Doppler information may improve our results further.

A strength of our study is the multidisciplinary cooperation between clinical experts in the IOTA group and the computing science team in the University of Buckingham. This cooperation was essential to understand the different features seen in static images of ovarian masses. Another strength is that we have access to a reasonable number of tumours with a diverse range of different benign and malignant pathological subtypes, with a prevalence of malignancy of 75/187(40%) in the study group. We also believe that the repeated randomized stratified cross validation of the SVM training and testing groups, is a robust methodology which has led to reliable results.

A weakness of our study is that we manually segmented the ultrasound images when obtaining the ROI, which may have caused selection bias. This is largely due to the fact that our primary focus was on the automatic feature extraction and image classification. Automatic segmentation of the ROI from ultrasound images is a known unsolved problem (Sohail et al., 2010) which may require extensive use of domain knowledge of the operator and need more future research. However, the results were still valid when the ROI was segmented and the LBP was applied on whole images (original and enhanced) (Table II). Indeed, the average accuracy was observed to be slightly higher when LBP was applied on enhanced whole images compared to enhanced ROI images (0.77) (Table II). Moreover, manual tracing is an available function in ultrasound machines; therefore this should not be a significant disadvantage when considering applying this technology in “real world” clinical practice. A further issue to consider is the selection bias of the ultrasound images themselves, as these have to contain the ROI if an accurate diagnosis is to be made and this in itself requires a level of competence from any ultrasound operator. Similarly, there was a selection bias caused by using different high specification machines, which is difficult to estimate. However this scenario is not unusual in imaging practice. Radiologists routinely review static images derived from different ultrasound machines that have been taken by a technician, this too can only be as accurate as the images provided. A reliance on the ROI being within an image supplied by a third party is therefore not unique to the use of computer processing technologies. Whilst we were careful to include a heterogeneous mix of pathology, once we have refined performance with more masses, it is critical that our approach is externally validated to see if the results are generalizable and have the potential to be transferred into every day clinical practice.

Conclusion

In this paper we have shown new evidence that computer learning machines using novel methodology have the potential to characterize static ultrasound images. There is good evidence to show subjective assessment by experts using TVS in real time is the optimal approach to the classification of ovarian pathology. However this level of expertise is not available in most clinical environments. By automating the recognition of ultrasound features that discriminate between the benign and malignant nature of an ovarian mass the need for expert review of images may be reduced. If test performance improves with training on more masses and is retained on external validation, the incorporation of such machine intelligence into the software of ultrasound equipment would become a possibility enabling ovarian mass characterisation to be effectively carried out even in clinical environments where access to highly specialist expertise is not available.

Acknowledgments

Tom Bourne and Ahmad Sayasneh are supported by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Imperial College Healthcare NHS Trust and Imperial College London. Dirk Timmerman is a Senior Clinical Investigator of the Research Foundation - Flanders (Belgium) (FWO). The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health. The author SK wishes to thank the Ministry of the Higher Education in Kurdistan for funding her PhD.

References

  1. Acharya UR, Mookiah MR, Vinitha Sree S, et al. Evolutionary algorithm-based classifier parameter tuning for automatic ovarian cancer tissue characterization and classification. Ultraschall Med. 2014;35:237–245. doi: 10.1055/s-0032-1330336. [DOI] [PubMed] [Google Scholar]
  2. Acharya U, Vinitha Sree S, Saba L, et al. Ovarian tumor characterization and classification: A class of GyneScanTM Systems. Conference proceedings. IEEE Eng Med Biol Soc (EMBC) 2012:4446–4449. doi: 10.1109/EMBC.2012.6346953. [DOI] [PubMed] [Google Scholar]
  3. Buades A, Coll B, Morel J. A non-local algorithm for image denoising. IEEE Comput Soc Conf Comput Vis Pattern Recognit. 2005;2:60–65. [Google Scholar]
  4. Biagiotti R, Desii C, Vanzi E, et al. Predicting ovarian malignancy: application of artificial neural networks to transvaginal and color Doppler flow US. Radiology. 1999;210:399–403. doi: 10.1148/radiology.210.2.r99fe18399. [DOI] [PubMed] [Google Scholar]
  5. Bossuyt PM, Reitsma JB, Bruns DE, et al. Towards complete and accurate reporting of studies of diagnostic accuracy: The STARD Initiative. Radiology. 2003;226:24–28. doi: 10.1148/radiol.2261021292. [DOI] [PubMed] [Google Scholar]
  6. Castellano G, Bonilha L, Li LM, et al. Texture analysis of medical images. Clin Radiol. 2004;59:1061–1069. doi: 10.1016/j.crad.2004.07.008. [DOI] [PubMed] [Google Scholar]
  7. Cristianini N, Shawe-Taylor J. An introduction to Support Vector Machines: and other kernel-based learning methods. Cambridge: Cambridge University Press; 2000. pp. 93–122. [Google Scholar]
  8. Jacobs I, Oram D, Fairbanks J, et al. A risk of malignancy index incorporating CA 125, ultrasound and menopausal status for the accurate preoperative diagnosis of ovarian cancer. Br J Obstet Gynaecol. 1990;97:922–929. doi: 10.1111/j.1471-0528.1990.tb02448.x. [DOI] [PubMed] [Google Scholar]
  9. Kaijser J, Bourne T, Valentin L, et al. Improving strategies for diagnosing ovarian cancer: a summary of the International Ovarian Tumor Analysis (IOTA) studies. Ultrasound Obstet Gynecol. 2013;41:9–20. doi: 10.1002/uog.12323. [DOI] [PubMed] [Google Scholar]
  10. Linares PA, McCullagh PJ, Black ND, et al. Feature selection for the characterization of ultrasonic images of the placenta using texture classification. IEEE Int Symp Biomed Imaging. 2004;2:1147–1150. [Google Scholar]
  11. Newcombe RG. Interval estimation for the difference between independent proportions: comparison of eleven methods. Stat Med. 1998;17:873–890. doi: 10.1002/(sici)1097-0258(19980430)17:8<873::aid-sim779>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
  12. Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans Pattern Anal Mach Intell. 2002;24:971–987. [Google Scholar]
  13. Sayasneh A, Wynants L, Preisler J, et al. Multicentre external validation of IOTA prediction models and RMI by operators with varied training. Br J Cancer. 2013;108:2448–2454. doi: 10.1038/bjc.2013.224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Sun YF, Fan XD, Li YD. Identifying splicing sites in eukaryotic RNA: support vector machine approach. Comput Biol Med. 2003;33:17–29. doi: 10.1016/s0010-4825(02)00057-4. [DOI] [PubMed] [Google Scholar]
  15. Sohail ASM, Rahman MM, Bhattacharya P, et al. Retrieval and classification of ultrasound images of ovarian cysts combining texture features and histogram moments. IEEE Int Symp Biomed Imaging. From Nano to Macro. 2010:288–291. [Google Scholar]
  16. Song Q, Wenjie H, Wenfang X. Robust support vector machine with bullet hole image classification. IEEE Trans Syst Man Cybern C Appl Rev. 2002;32:440–448. [Google Scholar]
  17. Tailor A, Jurkovic D, Bourne T, et al. Sonographic prediction of malignancy in adnexal masses using an artificial neural network. Br J Obstet Gynaeco. 1999;106:21–30. doi: 10.1111/j.1471-0528.1999.tb08080.x. [DOI] [PubMed] [Google Scholar]
  18. Tan P-N, Steinbach M, Kumar V. Introduction to data mining. Boston, Mass: Addison Wesley; 2006. pp. 256–276. [Google Scholar]
  19. Tavassoéli FA, Devilee P. Pathology and genetics of tumours of the breast and female genital organs. Third edition. Lyon: IRAC press; 2003. pp. 113–212. [Google Scholar]
  20. Timmerman D, Schwärzler P, Collins WP, et al. Subjective assessment of adnexal masses with the use of ultrasonography: an analysis of interobserver variability and experience. Ultrasound Obstet Gynecol. 1999;13:11–16. doi: 10.1046/j.1469-0705.1999.13010011.x. [DOI] [PubMed] [Google Scholar]
  21. Timmerman D, Ameye L, Fischerova D, et al. Simple ultrasound rules to distinguish between benign and malignant adnexal masses before surgery: prospective validation by IOTA group. BMJ. 2010;341:c6839. doi: 10.1136/bmj.c6839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Timmerman D, Van Calster B, Testa AC, et al. Ovarian cancer prediction in adnexal masses using ultrasound-based logistic regression models: a temporal and external validation study by the IOTA group. Ultrasound Obstet Gynecol. 2010;36:226–234. doi: 10.1002/uog.7636. [DOI] [PubMed] [Google Scholar]
  23. Van Calster , Timmerman D, Lu C, et al. Preoperative diagnosis of ovarian tumors using Bayesian kernel-based methods. Ultrasound Obstet Gynecol. 2007;29:496–504. doi: 10.1002/uog.3996. [DOI] [PubMed] [Google Scholar]
  24. Van Holsbeke C, Yazbek J, Holland TK, et al. Real-time ultrasound vs. evaluation of static images in the preoperative assessment of adnexal masses. Ultrasound Obstet Gynecol. 2008;32:828–831. doi: 10.1002/uog.6214. [DOI] [PubMed] [Google Scholar]
  25. Zimmer Y, Tepper R, Akselrod S. An automatic approach for morphological analysis and malignancy evaluation of ovarian masses using B-scans. Ultrasound Med Biol. 2003;29:1561–1570. doi: 10.1016/j.ultrasmedbio.2003.08.013. [DOI] [PubMed] [Google Scholar]

Articles from Facts, Views & Vision in ObGyn are provided here courtesy of The Walking Egg Foundation

RESOURCES