Assessing the quality of absolute hydration free energies among CHARMM-compatible ligand parameterization schemes

Abstract

MATCH, an Atom-Typing Toolset for Molecular Mechanics Force Fields, was recently developed in our lab. Here, we assess the ability of MATCH-generated parameters and partial atomic charges to reproduce experimental absolute hydration free energies for a series of 457 small neutral molecules in GBMV2, GBSW and FACTS implicit solvent models. The quality of hydration free energies associated with small molecule parameters obtained from ParamChem, SwissParam and Antechamber are compared. Given optimized surface tension coefficients for scaling the surface area term in the nonpolar contribution, these automated parameterization schemes with GBMV2 and GBSW demonstrate reasonable agreement with experimental hydration free energies (average unsigned errors of 0.9–1.5 kcal/mol and R² of 0.63–0.87). GBMV2 and GBSW consistently provide slightly more accurate estimates than FACTS while Antechamber parameters yield marginally more accurate estimates than the current generation of MATCH, ParamChem and SwissParam parameterization strategies. Modeling with MATCH libraries that are derived from different CHARMM topology and parameter files highlights the importance of having sufficient coverage of chemical space within the underlying databases of these automated schemes and the benefit of targeting specific functional groups for parameterization efforts in order to maximize both the breadth and depth of the parameterized space.

I. INTRODUCTION

In molecular mechanics simulations, ligand parameterization procedures are traditionally computationally intensive and can represent a bottleneck in structure-based drug design. Thus, it is imperative that information about well-parameterized compounds be leveraged to describe novel compounds under investigation and that rapid optimization strategies be developed that are transferable across a wide variety of functional groups. Several publically-available resources exist that generate topology and parameter files for a molecule of interest so that further molecular modeling may be performed in combination with established macromolecular force fields.

Automated ligand parameterization tools assume that the bonded parameters (i.e. force constants and equilibrium bond lengths, angles and torsions) and van der Waals parameters are relatively independent of the environment and so it is straightforward to assign these parameters for a novel compound given an extensive database of parameters for known compounds. To devise partial charges for each atom in a novel molecule there are two distinct strategies used. The first strategy, employed by the ligand parameterization program Antechamber, uses a restrained electrostatic potential to generate charges for the entire molecule concurrently, often based on ab initio calculations or parameterized methods that mimic these charge distributions. In contrast, tools such as MATCH, ParamChem and SwissParam use a fragment-based approach, where charge distributions of a molecule are built-up from charges that are assigned to the component fragments of the molecule. Halgren, in developing the MMFF94 force field, first proposed bond charge increment “rules” in which optimal charges are determined for fragments of molecules and these fragments are then pieced together to construct charge distributions for novel compounds¹.

All three fragment-based approaches mentioned above have become available recently for generating CHARMM-compatible ligand parameters and charge distributions. In our lab, the toolset of program libraries collectively titled Multipurpose Atom-Typer for CHARMM (MATCH) has been released.² The MATCH program itself was developed to learn atom-type definitions and bond charge increment rules from an arbitrary force field and MATCH libraries have been constructed by inferring atom-type definitions, parameters and bond charge increment rules from the CHARMM Generalized Force Field (CGENFF) topology and parameter files.³ MATCH parameters and a topology file for a given ligand can be obtained by uploading a small molecule PDB, mol, mol2 or sdf files via a web-interface (http://brooks.chem.lsa.umich.edu/software) or, alternatively, the MATCH source code and libraries can be downloaded and further customized for local use. In their on-going work to develop CGENFF, the Mackerell lab devised ParamChem, using a strategy similar to ours, which generates topology and parameter files for novel molecules given general rules based on CGENFF. These ParamChem topology and parameter files can be obtained by uploading a small molecule mol2 file to the ParamChem web-based facility (http://www.paramchem.org). The molecular modeling group at the Swiss Institute of Bioinformatics recently released SwissParam, a web interface (http://www.swissparam.ch) that generates CHARMM or GROMACS-compatible parameter and topology files in which the van der Waals parameters are assigned from the closest atom type in CHARMM22 and the remaining parameters and partial charges are derived from the Merck Molecular Force Field (MMFF).^1,4 While it is assumed that there may be some noise present by combining information from CHARMM22 and MMFF, this strategy takes advantage of the breadth of the chemical space covered by MMFF that is not explicitly represented in CGENFF.

Several studies have investigated the quality of automated parameterization tools by generating parameters for a diverse set of small organic molecules and computing their hydration free energies.⁵ Mobley et al. used Antechamber, the AMBER facility that generates ligand parameter and topology files using the General Amber Force Field (GAFF). Given the GAFF parameters and utilizing implicit solvent simulations, Mobley et al. computed the absolute hydration free energies for 499 small organic molecules and found that they agreed with those obtained from experiment to within ~2 kcal/mol.⁶ In a subsequent study, Mobley et al. found improved agreement between the calculated and experimental hydration free energies using the TIP3P water model in explicit solvent simulations for the same database of compounds, with RMS errors of 1.2 kcal/mol.⁷ In our recent study, where we optimized the surface tension coefficients for scaling the surface area term in the nonpolar contribution, most implicit solvent models demonstrated reasonable agreement with experimental hydration free energies with average unsigned errors=1.1–1.4 kcal/mol and R²=0.66–0.81.

Shivakumar et al. recently investigated a database of 239 small molecules; all but 18 of which were contained in the database that was studied by Mobley et al.^6,7 In their study, they evaluated the quality of hydration free energies that were computed for different force field parameters combined with implicit and explicit solvent.^8,9 Originally, calculated hydration free energy estimates for these 239 compounds were obtained using GAFF and CHARMm-MSI ligand parameters combined with charge assignments from ChelpG, RESP or AM1-BCC protocols. Overall, ligands modeled using the GAFF charge strategy in explicit TIP3P solvent environment provided the best agreement for the calculated hydration free energies compared with experimental values; specifically, GAFF parameters yielded an R² of 0.87 while the CHARMm-MSI/AM1-BCC parameters resulted in an R² of 0.76.⁸ In a more recent study, Shivakumar et al. computed hydration free energies from explicit solvent simulations using the OPLS-AA force field and charge parameterization scheme and achieved even better agreement with experiment (R²=0.94).⁹

In this work, we compare the ability of MATCH, ParamChem, SwissParam and GAFF, to generate parameters for a diverse set of small molecules and to reproduce their respective experimental absolute hydration free energies. Given MATCH's ability to learn atom-type definitions and bond charge increment rules, we also evaluate the quality of alternative MATCH libraries that are constructed from non-CGENFF CHARMM topology and parameter files. This analysis allows us to assess the value that is associated with enhancing the breadth and quality of the parameters that are already included in a given force field in terms of its ability to be used to extend to novel chemical contexts.

II. THEORY

Overview of implicit solvent models

The specifics of each implicit solvent model are already fully documented in the original papers and, in our recent study, we have highlighted the fundamental differences among the implicit solvent models that are investigated here.¹⁰ GBMV2 and GBSW models decompose the total hydration free energy into an electrostatic component and a nonpolar component and they employ variations of the Generalized Born model to approximate the electrostatic contribution to the solvation free energy. The GB formalism originally proposed by Still and coworkers is described by the equation¹¹:

$$\Delta G_{\mathit{elec}}^{GB}=-\frac{1}{2}\left(\frac{1}{{\epsilon }_m}-\frac{1}{{\epsilon }_{\mathit{solv}}}\right)\sum _{i=1}^N\sum _{j=1}^N\frac{q_i{q}_j}{\sqrt{r_{ij}^2+{\alpha }_i{\alpha }_j\text{exp}(r_{ij}^2∕\kappa {\alpha }_i{\alpha }_j)}}$$ (1)

where r_ij is the distance between the charges q_i and q_j, ε_m and) ε_solv are the dielectric constants assigned to the solute molecule and solvent respectively, N is the number of solute atoms, α_i is the effective Born radius for atom i and κ has a value of 4 in the work of Still et al.¹¹ and typically is set between 2 and 10.¹² The effective Born radius of each solute atom reflects the degree of its burial within the molecule and becomes the key parameter for the calculation of the electrostatic contribution to the solvation free energy. The effective Born radius for atom i can be calculated from the atomic electrostatic self-solvation energy in the Born equation¹³ (Eq 1):

$${\alpha }_i=-\frac{1}{2}\left(\frac{1}{{\epsilon }_m}-\frac{1}{{\epsilon }_{\mathit{solv}}}\right)\frac{q_i^2}{G_{\mathit{elec},i}^{GB}}$$ (2)

The primary advantage of GB models lies in their ability to estimate the Born radii by alternative, computationally-efficient means. Here, we focus primarily on volume-based GB models where the Coulomb Field Approximation (CFA), which approximates the electric displacement around an atom by the Coulomb field, is used to estimate the magnitude of the Born radius:

$$\frac{1}{{\alpha }_i}=\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{\mathit{solute}}\frac{1}{r^4}dV$$ (3)

where R_i is the intrinsic radius of atom i (the Born radius in the absence of all other atoms) which is often set equal to the van der Waals radius and where the second term is the Coulomb field integral which is computed over the volume of the solute excluding the sphere of radius R_i around atom i. Different flavors of GB models employ alternative approaches to calculating and scaling this integral and some include higher order correction terms to account for limitations in the CFA that arise from off-center charges and non-spherical volumes of many systems.

GBMV2^14,15 is a five-parameter analytical Generalized Born Molecular Volume model in which the molecular volume is constructed from a superposition of atomic functions. GBMV2 includes an empirical correction term, ΔG¹_elec, to the Coulomb field approximation, ΔG⁰elec, based on a measure for the deviation from the ideal spherical shape such that:

$$\Delta G_{\mathit{elec},i}=\Delta G_{\mathit{elec},i}^0+\Delta G_{\mathit{elec},i}^1$$ (4)

where the effective Born radii are estimated from:

$${\alpha }_i=\frac{S}{C_0{A}_4+C_1{A}_7}+D$$ (5)

In this formalism, A₄ is related to the Coulomb Field term in Eq. 3 and A₇ to the correction term, such that:

$$A_4=\left(\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{\mathit{solute}}\frac{1}{r^4}dV\right)$$ (6)

and

$$A_7={\left(\frac{1}{4R_i^4}-\frac{1}{4\pi }{\int }_{\mathit{solute}}\frac{1}{r^7}dV\right)}^{1∕4}$$ (7)

The fundamental advantage of this analytical approach over the grid representation is that forces are readily expressed.

Generalized Born with a smooth SWitching function model, or GBSW¹⁶, alleviates the numerical instability of solvent force calculations arising from discontinuities in the dielectric boundary by using a simple polynomial switching function to smooth the dielectric boundary. In the original GBSW formalism, a van der Waals surface representation replaces the more expensive molecular surface representation in GBMV. In GBSW, the two parameters C₀ and C₁ in Eq. 5 (with S=1 and D=0) are obtained for various smoothing lengths, 2w, to reproduce the exact self-solvation free energies from Poisson theory using a van der Waals definition of the dielectric boundary. With the smooth switching function, the Coulomb term is described by:

$$A_4=\left(\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{\mathit{solute}}\frac{V(r,\{r_{\alpha }\left\}\right)}{{\mid r-r_i\mid }^4}dV\right)$$ (8)

and the correction term is described by:

$$A_7={\left(\frac{1}{4R_i^4}-\frac{1}{4\pi }{\int }_{\mathit{solute}}\frac{V(r,\{r_{\alpha }\left\}\right)}{{\mid r-r_i\mid }^7}dV\right)}^{1∕4}$$ (9)

where V(r,{r_α}) is the solute interior volume and is defined by:

$$\left\{V\right(r,\left\{r_{\alpha }\right\})=1-\prod _{\alpha }\mathrm{H}(\mid r-r_{\alpha }\mid )$$ (10)

and where the atomic volume exclusion function, H_i(r), is given by:

$$\mathrm{H}\left(r\right)=\phantom{\{}\left\{\begin{array}{cc}0,\hfill & r\le R_i^{PB}-w\hfill \\ \frac{1}{2}+\frac{3}{4w}(r-R_i^{PB})-\frac{1}{4w^3}{(r-R_i^{PB})}^3,\hfill & R_i^{PB}-w<r<R_i^{PB}+w\hfill \\ 1,\hfill & r\ge R_i^{PB}+w\hfill \end{array}\phantom{\}}\right\}$$ (11)

where {R^PB} are the set of atomic radii that are used to define the dielectric boundary in the PB calculations.

The GBMV2 and GBSW implicit solvent models approximate nonpolar contributions to the total hydration free energy using a solvent-accessible surface area term. In traditional MM-PBSA and MM-GBSA methods, the total molecular solvent-accessible surface area, SASA, is used and the nonpolar contribution is described by:

$$\Delta G_{np}=\gamma \mathit{SASA}+\beta$$ (12)

where γ and β are the surface tension parameter and off-set values respectively.

In this study, we also consider the Fast Analytical Continuum Treatment of Solvation model, FACTS¹⁷, that was recently developed by Caflisch and coworkers.^17,18 This empirical strategy is significantly different from the above GB models in that it does not assume the Coulomb Field approximation and does not require the dielectric boundary between the solvent and solute to be defined. Instead FACTS is based on the analytical evaluation of the volume, A_i, and spatial symmetry, B_i, of the solvent that is displaced from around solute atom i. These two measures are combined in empirically parameterized equations to approximate the self-electrostatic energies:

$$\Delta G_{\mathit{elec},i}^{\mathit{FACTS}}={\alpha }_0+\frac{{\alpha }_1}{1+e^{-{\alpha }_2(A_i+b_1{B}_i+B_i+b_2{A}_i{B}_i-{\alpha }_3})}$$ (13)

where a_o and a₁ are determined by using the limiting cases of a fully buried and fully exposed atom respectively. The other parameters: b₁, b₂, a₂, a₃ and R^sphere (which defines the solute volume considered in calculating A_i and B_i) are optimized for each van der Waals radius. The self-electrostatic energies then provide the effective Born radii via Eq. 2. Similarly, the solvent-accessible surface area is approximated by:

$${\mathit{SASA}}_i^{\mathit{FACTS}}=c_0+\frac{c_1}{1+e^{-c_2(A_i+d_1{B}_i+B_i+d_2{A}_i{B}_i-c_3})}$$ (14)

and its corresponding parameters are optimized to reproduce exact SASA values. Since the FACTS model only requires the vectors between neighboring atom centers it is significantly faster than the corresponding families of GBMV and GBSW calculations and has been documented to be only four times slower than vacuum calculations.¹⁷

III. METHODS

Small molecule database

A large database of 499 small neutral organic compounds has been studied previously.¹⁰ The original database was made available from Mobley et al.⁷ which in turn was compiled from molecules from Rizzo et al.¹⁹, Guthrie²⁰ and their earlier studies.^21,22 Five duplicate compounds were identified in the original database of 504 compounds and were removed. This database contains a wide variety of chemical environments that are commonly encountered in drug design applications, including saturated and unsaturated hydrocarbons, aromatic and heterocyclic rings, halides and polar functional groups. Checkmol²³ was used to classify the functional groups that are represented in each molecule.

Small molecule parameterization

AMBER GAFF⁵/AM1-BCC^24,25 parameters and partial charges for all compounds in the database were obtained directly from the supplementary materials provided by Mobley et al.⁷ and the AMBER prmtop files were converted to the corresponding CHARMM topology and parameter files using the conversion tool AMBER2CHARMM as described previously.¹⁰ Sets of ParamChem and SwissParam parameters and partial charges were obtained by uploading the 499 mol2 files to the ParamChem (http://www.paramchem.org) and SwissParam (http://www.swissparam.ch) interactive websites, respectively. A MATCH library designated MATCH(cgenff_c36a) was constructed based on the CGENFF topology and parameter files in the c36a release of CHARMM (toppar/all36_cgenff.rtf and toppar/all36_cgenff.prm respectively). Another MATCH library designated MATCH(cgenff) was constructed from the CGENFF topology and parameter files in the c36b release which included updated parameters for several compounds. A third MATCH library designated MATCH(combined) was constructed from the union of five non-CGENFF CHARMM force field topology and parameter files, specifically, the force fields for proteins (toppar/all22_prot), nucleic acids (toppar/all27_na), carbohydrates (toppar/all35_carb), ethers (toppar/all35_ethers) and lipids (toppar/all36_lipid). To construct this MATCH(combined) library, a consistent atom type convention had to be developed in order to incorporate information from the individual CHARMM topology and parameter files. In most cases, individual force fields had the same parameter assignments for a given atom type definition. However, in the few cases in which two force fields assigned different parameters for a given atom type definition information from the more recently developed force field was incorporated into the MATCH(combined) library. Sets of MATCH parameters and partial charges for the ligands in the small molecule dataset were subsequently obtained based on these MATCH libraries.

Molecular dynamics simulations and analysis

Simulation trajectories were generated for each MATCH(cgenff_c36a) molecule in both vacuum and the GBMV2 implicit solvent environment. No cutoffs were used; covalent bonds involving hydrogen atoms were constrained using the SHAKE²⁶ algorithm and the time step was 1.5 fs. The temperature was maintained near 298 K by coupling all heavy atoms to a Langevin heat bath using a frictional coefficient of 10 ps⁻¹. Simulation trajectories were 10.5 ns in length. Snapshots were saved every 5 ps throughout the last 10 ns for subsequent free energy analysis with each combination of parameterization scheme and implicit solvent model. Simulation trajectories were generated and energy evaluations associated with the GBSW and FACTS implicit solvent models were obtained using the CHARMM molecular dynamics package c36b6.^27,28 Simulations were analyzed by the Bennett Acceptance Ratio method (BAR)²⁹ using a modified version of pyMBAR.³⁰ All simulations and calculations were performed on dual 2.66 GHz Intel Quad Core Xeon CPUs.

The GBMV2 model used a Lebedev angular integration grid with grid size of 38, geometric cross-term in the Still equation and κ=8 in Eq. 1; the multiplicative factor, S, and shift, D, of α_i in Eq. 5 were 0.9085 and −0.102 respectively. For the GBSW calculations, the half smoothing length, w, was 0.3 Å; the grid spacing in the lookup table was 1.5 Å and the optimized default values for the coefficients for the Coulomb Field approximation and correction terms were used (i.e. C_o and C₁ in Eq. 5). The GBMV2 and GBSW intrinsic radii were assigned from the van der Waals radii. Default FACTS parameters were employed with infinite nonbonded cutoffs. FACTS parameters were used that had been optimized for a solute dielectric constant of 1. van der Waals radii which had not been investigated in the original FACTS study had their FACTS parameters estimated by interpolation or extrapolation from the optimized FACTS parameters using the “tavw” option in CHARMM. To be consistent with the FACTS parameterization strategy, polar hydrogens were assigned van der Waals radii of 1.0 Å.

The nonpolar contribution was estimated from Eq. 12 in which the surface tension parameter, γ, was optimized with β=0. Nonpolar contributions were computed for each value of γ between 0.0 and 0.025 kcal/(mol·Å²) in increments of 0.0025 kcal/(mol·Å²) and the optimal surface tension coefficient was identified for each combination of parameterization scheme and implicit solvent model to be the value of γ that minimized the average unsigned error for the compounds that were included in the CHARMM CGENFF topology file. Thus, for a given parameterization scheme and implicit solvent model, a single optimized surface tension parameter was identified from the analysis of the CGENFF set of compounds and was used to compute the total hydration free energy for every compound.

IV. RESULTS & DISCUSSION

Coverage of automated parameter generation schemes

Of the 499 compounds in the full dataset for which GAFF parameters and AM1-BCC charges were already available, parameters and atomic charges were successfully generated for 491 and 468 compounds by MATCH(cgenff_c36a) and ParamChem, respectively. ParamChem successfully generated parameters for eight compounds for which MATCH(cgenff_c36a) failed while MATCH(cgenff_c36a) successfully generated parameter files for five compounds for which ParamChem failed. In total, 460 compounds were successfully processed by both parameterization schemes. SwissParam parameter and topology files were generated for all 460 compounds, except for ammonia and methane. GAFF parameter and topology files were available for all 460 compounds; however, N,N-dimethyl-p-nitrobenzamide was removed from the dataset because the energies that were calculated for this compound based on the trajectories that were generated from the MATCH parameters were extremely large. For ease of comparison across the parameterization schemes, this study focuses on the 457 compounds that were successfully processed by these four parameterization schemes. This dataset encompasses 82 compounds that are explicitly included in the CHARMM CGENFF topology file and 375 compounds for which parameters and atomic charges needed to be extrapolated and interpolated from known parameters. In essence, the 82 compounds were part of the training set for developing the MATCH libraries and ParamChem rules while the 375 compounds can be considered to be a test set. During this course of this analysis, an updated version of CGENFF was released (CHARMM version c36b), so results are reported for the MATCH libraries constructed from the latest version of CGENFF (MATCH(cgenff)).

For each parameterization scheme and implicit solvent model, the optimal nonpolar surface tension parameter, γ, was identified as the value that yielded the lowest average unsigned error (AUE) in the absolute hydration free energies among the 82 compounds that are included in the CHARMM CGENFF topology file. Given these optimal values for γ, the measures of model quality are summarized in Table 1.

Table 1.

Overall measures of model quality (in kcal/mol) for absolute hydration free energy predictions for trajectories analyzed using the GBMV2 and GBSW implicit solvent models and different parameterization schemes for the 82 CGENFF and 375 non-CGENFF compounds.

Param. scheme:	MATCH(cgenff)			ParamChem			GAFF			SwissParam
Implicit solvent model:	GBMV2	GBSW	FACTS	GBMV2	GBSW	FACTS	GBMV2	GBSW	FACTS	GBMV2	GBSW	FACTS
CGENFF
Opt γ	0.0075	0.01	0.0025	0.0075	0.01	0.0025	0.0075	0.02	0.0025	0.01	0.015	0.005
<|Error|>	0.97	0.94	1.22	0.99	0.96	1.25	0.88	0.95	1.20	1.12	0.99	1.20
<Error>	−0.10	−0.06	0.04	−0.11	−0.07	0.01	0.15	−0.04	0.30	0.32	0.10	0.17
R2	0.846	0.816	0.680	0.841	0.808	0.672	0.870	0.841	0.757	0.815	0.801	0.694
% |Error|:
<3 kcal/mol	100	99	96	100	99	96	99	98	94	93	96	94
<2 kcal/mol	90	93	85	90	93	85	90	90	82	77	84	77
<1 kcal/mol	60	62	49	57	60	49	65	61	55	55	61	62
non-CGENFF
<|Error|>	1.47	1.43	1.59	1.51	1.49	1.74	1.24	1.33	1.42	1.49	1.16	1.50
<Error>	0.31	0.23	0.29	0.03	0.01	0.08	0.35	0.07	0.52	0.24	0.05	0.00
2	0.688	0.669	0.566	0.634	0.633	0.482	0.758	0.701	0.628	0.721	0.744	0.508
% |Error|:
<3 kcal/mol	92	90	87	90	89	86	95	97	90	88	94	86
<2 kcal/mol	74	74	70	73	71	67	84	78	74	72	79	72
<1 kcal/mol	41	43	42	45	41	38	48	43	51	48	54	57

Recapitulating charge distributions for CGENFF compounds

The set of 82 molecules found in CGENFF were included in the training sets used by both MATCH(cgenff) and ParamChem to devise the underlying bond charge increment (BCI) rules in their respective parameterization strategies. Comparing the predicted partial charges that are based on these BCI rules with the original charges in the CGENFF topology file provides an estimate of the error that is specifically associated with the process of learning and re-applying the rules. Of the 1038 atoms in the 82 CGENFF molecules in this dataset, MATCH(cgenff) and ParamChem reproduce the CGENFF partial charge assignments within 0.005 e⁻ for 1022 and 997 atoms, respectively. For the remaining atoms, the partial charge differences are quite small and are less than 0.03 e⁻ and 0.06 e⁻ for MATCH(cgenff) and ParamChem, respectively. Deviations in the MATCH(cgenff) parameters are primarily due to the decision to keep the learned rules more general rather than permit highly specific definitions that while they would exactly reproduce the CGENFF charges they would likely be less transferable. In most cases, the local environment for atom type definitions was 1–2 bonds while the refinement rules for assigning bond-charge increments was 2–3 bonds from a given atom. The largest deviations between MATCH(cgenff) and the original CGENFF topology file arises from the inability of MATCH(cgenff) to reproduce partial charge distribution in CGENFF amines. For example, the H41 and H42 atoms in cytosine derivatives modeled in CGENFF have identical bond connectivity but different chemical environments due to the three-dimensional shape of the molecule. In this case, in CGENFF the H41 and H42 atoms are assigned partial charges of 0.37 e⁻ and 0.32 e⁻, respectively, whereas MATCH(cgenff), which is based on bond connectivity alone, assigns partial charges of 0.345 e⁻ to both hydrogen atoms, i.e., the average of 0.37 e⁻ and 0.32 e⁻.

However, while the changes in the partial charge assignments are relatively small, they do affect the estimated hydration energies. Figure 1 depicts the partial charge assignments and estimated hydration free energies for the three compounds that have deviations in molecular dipoles for ParamChem relative to the CGENFF compounds that are greater than 0.1 D. Note: there were no MATCH(cgenff) compounds whose dipoles differed from CGENFF by more than 0.1 D. The ParamChem partial charge distribution for chloroethane improves the quality of the estimated hydration free energy relative to the corresponding CGENFF estimate value while the partial charge distributions for pyrrole and fluorobenzene degrade the estimate.

Figure 1.

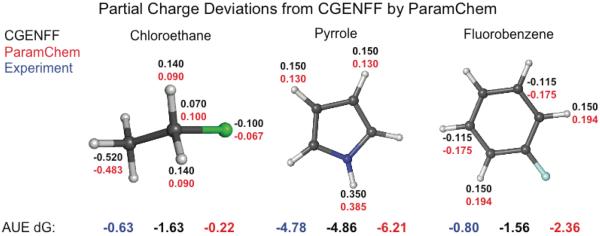
Schematic of the compounds whose partial charge distributions in ParamChem resulted in a molecular dipole difference of more than 0.01 Debye compared to the partial charge assignments in CGENFF. For clarity, only atoms whose ParamChem charges were more than 0.01 e⁻ from CGENFF are labeled. Note: MATCH(cgenff) charges essentially reproduce the CGENFF charges for these compounds so are not labeled.

Overall quality of absolute hydration free energy estimates for different parameterization schemes

The quality of the hydration free energies of the compounds in the small molecule dataset is summarized in Table 1 and provides a direct measure of the ability of the automated parameterization schemes to characterize the chemical space of a given compound as well as the quality of the parameters in the CGENFF topology file. MATCH(cgenff) and ParamChem parameters modeled with GBMV2 and GBSW implicit solvent models demonstrate good agreement with experimental hydration free energies across the 82 CGENFF compounds with AUEs of 0.94 to 0.99 kcal/mol and R² values between 0.81 and 0.85. Over half of the CGENFF compounds (57–62%) have hydration free energies that are correctly predicted within 1 kcal/mol of their experimental values. Most of the compounds (90–93%) have hydration free energies that are correctly predicted within 2 kcal/mol and almost all of the compounds (99–100%) have hydration free energies that are correctly predicted within 3 kcal/mol. Given that these compounds are the ones from which the libraries and databases of atom-typing definitions and bond-charge increment rules are derived, these results can be seen as the upper bound of the quality that can currently be expected from either MATCH(cgenff) or ParamChem automated parameterization strategies.

The overall quality of hydration free energy estimates using the MATCH and ParamChem parameterization schemes are comparable to those obtained when the small molecules are modeled with AMBER/GAFF parameters and AM1-BCC charges (AUEs of 0.88 to 0.95 kcal/mol and R² values of 0.84–0.87) and SwissParam (AUEs of 0.99–1.12 kcal/mol and R² values of 0.80–0.82). The percentage of compounds whose hydration free energies were correctly predicted within 1 kcal/mol of the experimental values by SwissParam is comparable to the other parameterization strategies. However, the results for correct predictions within 2 and 3 kcal/mol were slightly degraded to 77–84% and 93–96% respectively.

Extending parameterization schemes to novel contexts

For the remaining 375 compounds that are not included in the CHARMM CGENFF topology file, the quality of the hydration free energies of these compounds is a more direct measure of the ability of MATCH or ParamChem to extend their respective atom-typing and parameterization schemes to novel contexts. MATCH(cgenff) and ParamChem parameters modeled with GBMV2 and GBSW implicit solvent models demonstrate reasonable agreement with experimental hydration free energies across these 375 compounds with AUEs between 1.4 and 1.5 kcal/mol and R² values between 0.63 and 0.69. For this dataset, slightly less than half (41–45%) of the compounds have hydration free energies that are correctly predicted within 1 kcal/mol of their experimental values. About three-quarters of the compounds (71–74%) have hydration free energies that are correctly predicted within 2 kcal/mol and about ninety percent (89–92%) have hydration free energies that are correctly predicted within 3 kcal/mol.

Interestingly, just as the quality of the MATCH(cgenff) and ParamChem estimates of the hydration free energies of the compounds in the CGENFF training set was higher by ~0.5 kcal/mol compared with estimates for the non-CGENFF test set compounds, the quality of the estimates based on the GAFF/AM1-BCC parameterization scheme was ~0.4 kcal/mol higher for the CGENFF compounds than the non-CGENFF compounds. The AUEs for the 375 test compounds modeled by GAFF/AM1-BCC are 1.2–1.3 kcal/mol while the R² values are 0.70–0.76. Since AM1 charges are assigned de novo for each molecule and BCC corrections were parameterized with an extensive training set of 2775 compounds that spanned the functional space represented in the CGENFF and non-CGENFF sets, the CGENFF training set/test set designations should not be applicable for AM1-BCC parameterization scheme. Thus, the poorer estimates of the hydration free energies for the test compounds over the training set compounds suggest that the compounds in the test set are inherently more challenging to model than those in CGENFF. The SwissParam parameters also yielded a slight degradation (~0.2–0.4 kcal/mol) in the quality of the hydration free estimates for the test set relative to the training set of compounds. The AUEs for the 375 compounds modeled with SwissParam are 1.2–1.5 kcal/mol and had the largest R² values of any parameterization scheme of 0.72–0.74.

Targeting chemical classes for further parameter optimization

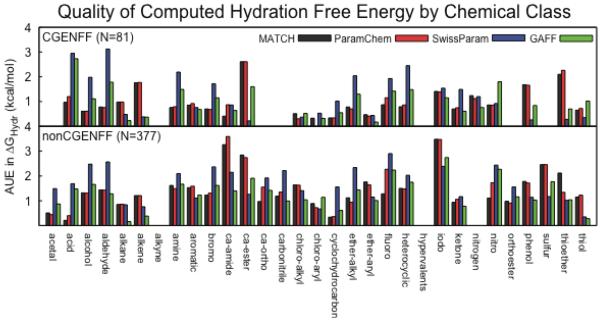
Across the 82 CGENFF compounds, a subset of the full CGENFF training set, as well as the test set of 375 compounds, the AUEs for the majority of the chemical classes are less than 1.5 kcal/mol. Figure 2 summarizes the AUEs of the compounds within each chemical class designation for each of the parameterization schemes with the GBMV2 implicit solvent model. Systematic deviations of computed hydration free energies relative to experiment are observed for several classes of compounds. Reliably reproducing experimental hydration free energies is challenging given the inherent limitations that exist in representing molecular charge distributions using a fixed-charge scheme rather than explicitly modeling the polarization. Furthermore, approximations that are made in the implicit solvent models and especially by representing the nonpolar contributions using a single optimized parameter, γ, for the surface tension coefficient may contribute to lower estimates of experimental hydration free energies. However, the differences in the quality of the hydration free energies that are observed across the chemical groups that are highlighted here are likely dominated by the challenges that arise in extending parameterization schemes to chemical space that is not well-represented in the training data, Figure 3 focuses on specific chemical classes that may be targeted for further parameterization efforts. These parameterization efforts can be viewed as increasing the breadth of compounds that are reliably covered by these automated rules or increasing the depth of the meaningful coverage of a particular region of chemical space.

Figure 2.

Average unsigned errors of hydration free energies by chemical class for four different parameterization schemes in the GBMV2 implicit solvent model for the A) 82 molecules that are in CGENFF and B) the 375 compounds that are not included in CGENFF.

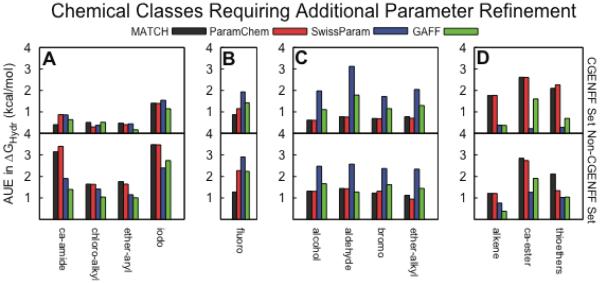
Figure 3.

Average unsigned errors of hydration free energies for specific chemical classes for (top panel) CGENFF molecules and (bottom panel) non-CGENFF compounds. Classes in which A) both MATCH(cgenff) and ParamChem have AUEs for the non-CGENFF set more than 1 kcal/mol worse than the CGENFF set; B) MATCH(cgenff) performs 1 kcal/mol better or worse than ParamChem; C) SwissParam performs more than 1 kcal/mol poorer than the other force fields; and D) both MATCH(cgenff) and ParamChem perform more than 1 kcal/mol poorer than either SwissParam or GAFF/AM1-BCC.

First, Figure 3A highlights the AUEs for the four chemical classes of compounds that have errors in their respective hydration free energy estimates that are more than 1 kcal/mol larger for the non-CGENFF compounds relative to the CGENFF compounds: iodo-, carboxylic acid amides (ca_amide), chloro-alkyl, ether-aryl compounds. The low AUEs in the context of CGENFF compounds and high AUEs in the context of non-CGENFF compounds for MATCH(cgenff) and ParamChem suggest that the learned rules in MATCH(cgenff) and ParamChem for these contexts are not sufficiently transferable to accurately model the chemical space associated with these groups. For example, the rules for iodine-containing compounds are severely limited in MATCH(cgenff) because the CGENFF topology file only contains iodobenzene. Thus, it is not surprising that the AUE for the iodo- compounds is so large when there are exclusively aliphatic iodo- compounds in the non-CGENFF test set. While there is extensive coverage of the carboxylic acid amide chemical class in CGENFF topology file with examples of primary, secondary and tertiary amides, the three compounds in the ca_amide group that perform particularly poorly are ones in which the amide is a substituent on a ring and there are no examples of this type in the CGENFF dataset.

The chloro_alkyl group in the CGENFF dataset is limited to three compounds: 111_trichloroethane, chloroethane and 11_dichloroethane. This coverage is insufficient to characterize the bond charge increments of the wide variety of aliphatic halide compounds in the nonCGENFF dataset. Unlike compounds in the iodo- and ca_amide groups in which both MATCH(cgenff) and ParamChem yield similar errors in their respective hydration free energies, several compounds in the chloro_alkyl group are modeled differently by MATCH(cgenff) compared with ParamChem. For example, MATCH(cgenff) yields poor hydration free energies for molecules that contain chloro groups on opposite sides of the molecule (e.g., 1,4-dichlorobutane, bis-2-chloroethylether and 1,1,2,2,-tetrachloroethane) whereas the high AUE for the chloro_alkyl group for ParamChem results from molecules that have three fluorine atoms bound to the same aliphatic carbon (e.g., isoflurane, halothane, 1_chloro_222_trifluoroethane). Thus, the degradation in hydration free energies for these latter molecules likely results from a less than ideal bond charge increment for fluoride rather than there inherently being a problem with modeling compounds containing chlorine. Finally, the degradation observed in the ether-aryl class of compounds is dominated by the error in modeling N,N-dimethyl-p-methoxybenzamide which suggests that the issue lies in the poor parameterization of the amide (as observed with the ca_amide group) rather than the ether functionality itself. Thus, while no specific parameterization efforts are required to improve the quality of the ether-aryl group, the larger errors for compounds in the iodo-, ca_amide and chloro_alkyl groups clearly suggest that subsequent generations of MATCH libraries and ParamChem rules would benefit from a broader template of well-parameterized training compounds for these chemical classes.

Second, examining the classes of compounds for which the AUEs differ significantly between force fields can be informative for identifying possible strategies for improving the parameterization of a particular functional group. Figure 3B highlights the AUEs in the chemical classes whose errors deviate by more than 1 kcal/mol between the MATCH(cgenff) and the ParamChem parameterization schemes. The AUE for the fluoro compounds in the CGENFF set are similar for MATCH(cgenff) and ParamChem. However, as depicted in Figure 1, the partial charge distribution for fluorobenzene modeled by ParamChem is significantly different from that modeled by MATCH(cgenff) and CGENFF itself. The underlying differences in the bond charge increment rules leads to larger differences when modeling the non-CGENFF compounds and the average error for ParamChem is about 1 kcal/mol larger than for MATCH(cgenff). In fact, ParamChem has the most difficulty producing accurate hydration free energies for molecules with multiple fluorine atoms bound to the same aliphatic carbon. Thus, it is likely that additional refinement rules within the ParamChem parameterization scheme could ameliorate the hydration free energies for this class.

Next, given the systematically poorer results for the alcohols, aldehydes, bromo- and ether alkyl groups modeled by SwissParam compared to the other force fields (see Figure 3C), further parameterization of these specific groups by the SwissParam developers would likely further strengthen SwissParam's performance. In fact, the aldehyde compounds yield the highest error for any group modeled by SwissParam with AUEs of 3.12 kcal/mol for CGENFF molecules and 2.56 kcal/mol for non-CGENFF molecules. In general, in these compounds, the partial charges assigned by SwissParam to the functional groups are systematically larger in magnitude than the corresponding charges modeled by MATCH(cgenff), ParamChem and GAFF. Schematics for compounds with the largest differences and the partial charge assignments across the force fields are presented in the Supplementary Materials.

Finally, the ca_ester, alkene and thioether classes of compounds are the only three classes that demonstrate a systematic degradation in the AUE for MATCH/ParamChem models compared to SwissParam and GAFF/AM1-BCC for the CGENFF molecules (see Figure 3D). These groups have AUEs of 2.6, 2.2 and 1.8 kcal/mol respectively in MATCH(cgenff) and ParamChem. The decrease in the quality of the esters (ca_ester) and alkenes for both MATCH(cgenff) and ParamChem is correlated with a systematic increase in the magnitude of the CGENFF partial charges of the respective functional groups compared with those assigned by SwissParam and GAFF parameterization schemes. For example, MATCH(cgenff) and ParamChem assign an average of 0.90 e⁻ to the carboxyl carbon of the esters which is ~50% larger than the corresponding partial charges assigned by SwissParam and GAFF. Similarly, the hydrogen atoms at the end of conjugated alkenes have partial charges of 0.21 e⁻ in MATCH(cgenff) and ParamChem compared with 0.10–0.15 e⁻ in SwissParam and GAFF. The thioether class in CGENFF only has one member: methylethylsulfide. In this case, the CGENFF assigned partial charge of the sulfur atom is −0.1 e⁻ while SwissParam and GAFF assign partial charges of −0.46 and −0.30 e⁻, respectively, which contributes to the increase in the molecular dipole from 0.24 to 0.43 D. Thus, the CGENFF parameters for these three chemical classes could be targeted for further improvement to more reliably reproduce experimental hydration free energies. Of course, given the differences in the parameterization philosophies across these force fields, simply adopting the GAFF or SwissParam partial charges for these compounds in order to reproduce hydration free energies estimated with an implicit solvent model cannot guarantee that these parameters will transfer appropriately to simulations in more realistic biomolecular contexts.

FACTS implicit solvent model

FACTS is a recently developed implicit solvent model in which the Born radii are parameterized so that the electrostatic component of the hydration free energy is estimated from pairwise interactions alone. Specifically, in the FACTS parameterization, the ΔG_elec is estimated from the density of neighboring atoms and their symmetrical arrangement around the atom in question. This parameterization scheme greatly increases the computational efficiency of the calculations; in fact, the original study reported that the computational expense was only four times that of the corresponding vacuum calculations. However, this strategy requires a higher degree of parameterization than other Generalized Born implicit solvent models.

Table 1 also summarizes the measures of model quality for the four parameterization schemes when the solvent environment is represented by FACTS. In this study, it is clear that regardless of the ligand parameterization scheme, the FACTS implicit solvent model exhibits a slight, but systematic, degradation in the quality of the hydration free energies relative to either GBMV2 or GBSW implicit solvent models. The AUEs tend to be about 0.2–0.3 kcal/mol higher for the FACTS models than either GBMV2 or GBSW models while the R² values tend to be lower by 0.1 to 0.15. Thus, these results suggest that modeling with FACTS, especially in contexts where computational resources are limited, is a viable alternative to the more costly, though more accurate, implicit solvent models. Furthermore, many atom types in this work rely on interpolations and extrapolations from the values for FACTS parameterized radii; thus, the quality of the FACTS model will also likely improve as more van der Waals radii are specifically parameterized and made available to the community. These results also suggest that the FACTS implicit solvent model is transferable across these CHARMM-compatible force fields.

Combining Force Fields in CHARMM

The development of CGENFF in CHARMM attempts to create general atom types and parameters for model compounds and fragments that may be important in biomolecular simulations. This philosophy stands in contrast to that for previous CHARMM force fields where atom types and parameters were optimized for very specific chemical space within the biomolecules that were being simulated, e.g., proteins, nucleic acids, lipids. Using the automated approach of MATCH, we explored the ability of the union of the non-CGENFF “context-specific” CHARMM force fields to extrapolate their parameters to model the chemical diversity in the small molecule dataset.

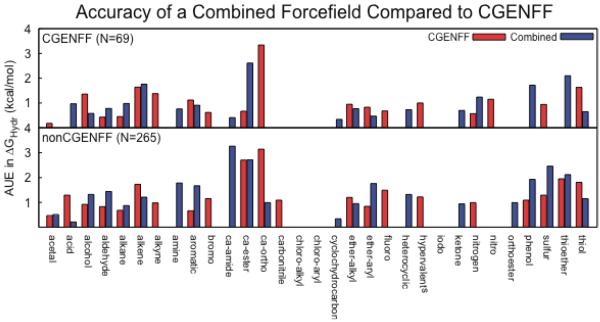
From the resulting MATCH(combined) libraries, topology and parameter files were successfully generated for 73 of the CGENFF compounds and 277 of the non-CGENFF compounds in the dataset. It was not clear, though, how meaningful subsequent hydration free energy calculations would be for this parameterization scheme. Since each of these CHARMM force fields was optimized individually, there was the potential that combining them might produce non-physical results, particularly for compounds that would encompass chemical space that overlapped with two or more CHARMM force fields, i.e., where rules were learned from different force fields. Table 2 summarizes the measures of model quality obtained for these compounds in each of the implicit solvent models and shows that, for the compounds that it could parameterize from the MATCH(combined) libraries, that the compounds are modeled at a comparable level of quality to that observed from the MATCH(cgenff) library. For the set of 73 CGENFF molecules the combined force field achieved virtually the same quality as MATCH(cgenff) and, interestingly, for the more challenging test set of 277 compounds, the MATCH(combined) parameters exhibited a slight but systematic improvement over the MATCH(cgenff) parameters with AUEs of 1.3–1.7 kcal/mol and R² values of 0.55 to 0.73. Thus, even though the non-CGENFF CHARMM force field parameters are optimized for specific chemical environments, the high quality of results is likely a product of the consistency of the overall philosophy governing the developing of CHARMM force fields and the coherence of the optimization procedures.

Table 2.

Overall measures of model quality (in kcal/mol) for absolute hydration free energy predictions for trajectories analyzed using the GBMV2, GBSW and FACTS implicit solvent models for the MATCH(cgenff) and MATCH(combined) libraries for the 73 CGENFF and 277 non-CGENFF compounds for which MATCH(combined) libraries successfully generated topology and parameter files.

Parameterization scheme:	MATCH(cgenff)			MATCH(combined)
Implicit solvent model:	GBMV2	GBSW	FACTS	GBMV2	GBSW	FACTS
CGENFF
Opt γ	0.0075	0.0075	0.0025	0.005	0.005	0.000
<|Error|>	1.00	0.94	1.24	1.00	1.00	1.24
<Error>	−0.06	−0.21	0.14	−0.25	−0.06	−0.11
R2	0.835	0.805	0.660	0.820	0.752	0.645
% |Error|:
<3 kcal/mol	100	99	96	95	97	90
<2 kcal/mol	89	89	85	90	88	85
<1 kcal/mol	56	62	49	59	60	47
non-CGENFF
<|Error|>	1.52	1.46	1.71	1.34	1.29	1.57
<Error>	0.17	−0.19	0.36	−0.39	−0.15	−0.16
R2	0.665	0.671	0.547	0.715	0.730	0.593
% |Error|:
<3 kcal/mol	92	90	86	91	95	91
<2 kcal/mol	73	74	67	81	82	72
<1 kcal/mol	40	35	38	49	43	37

Examining the differences in hydration free energy estimates by chemical class may again be useful to determine if there is any chemical space that could be optimized in CGENFF. The comparison between AUEs by chemical class for MATCH(cgenff) and MATCH(combined) is summarized in Figure 4. The three chemical groups with the largest improvement in hydration free energy estimates compared to those produced using the charges from MATCH(cgenff) are the amines, aldehydes and thiols with improvements on average of 1.1, 0.8 and 0.7 kcal/mol respectively. For the amines, increases in the partial charge on the nitrogen were responsible for the cases where the combined MATCH force field significantly outperformed the MATCH(cgenff) force field. For example, in triethylamine the partial charge on the amine nitrogen atom changes from −0.63 e⁻ in MATCH(cgenff) to −0.84 e⁻ in MATCH(combined) and is compensated by increases in the partial charges assigned to the adjacent carbon atoms from 0.03 e⁻ to 0.10 e⁻ and, thus, an increase in the N-C dipole. By contrast, the differences in the partial charge distributions of the thiol compounds results in a reduction in the S-C dipole and an improvement in the hydration free energy estimates. Similarly, the difference in the performance for the aldehyde group is dominated by three compounds, i.e., E-but-2-enal, E-hex-2-enal, and E-oct-2-enal in which the C=O dipole is systematically smaller in the MATCH(combined) parameterization. Thus, these three chemical classes that could be revisited in the CGENFF force field development and/or the MATCH(cgenff) libraries could be modified to incorporate the amine, aldehyde and thiol parameters and charge assignment rules.

Figure 4.

Average unsigned errors of hydration free energies by chemical class for the MATCH(cgenff) and MATCH(combined) parameterization schemes in the GBMV2 implicit solvent model for the A) 73 molecules that are in CGENFF and B) the 277 compounds that are not included in CGENFF.

V. CONCLUSION

We have recently developed MATCH, an Atom-Typing Toolset for Molecular Mechanics Force Fields, in our lab. This toolset is designed to construct force field-specific libraries containing parameters and bond charge increment rules that can be learned from the topology and parameter file for a given force field. Once constructed, the MATCH library can be used to assign parameters for an arbitrary compound provided that the chemical space represented in the compound was covered in the original force field.

We present a comparison of absolute hydration free energies that have been calculated for an extensive database of small neutral molecules using MATCH libraries constructed from CGENFF (MATCH(cgenff)) and a variety of CHARMM-compatible force fields in GBMV2, GBSW, and FACTS implicit solvent models. Of the 499 small molecules, topology and parameter files for 460 compounds were successfully generated from the ParamChem webserver and from the MATCH toolset libraries MATCH(cgenff), which were constructed from CGENFF. MATCH(cgenff) and ParamChem reproduce the partial charge distributions for most of the compounds in the dataset that were part of CGENFF.

Given optimized surface tension coefficients for scaling the surface area term in the nonpolar contribution, these automated parameterization schemes and GBMV2 and GBSW demonstrate reasonable agreement with experimental hydration free energies (average unsigned errors=0.9–1.5 kcal/mol and R²=0.63–0.87). The FACTS parameterization yielded hydration free energies that were slightly poorer than the GBMV2 and GBSW estimates, though at a fraction of the computational expense. Antechamber parameters (GAFF with AM1-BCC partial charges) resulted in marginally more accurate estimates than the current generation of MATCH, ParamChem and SwissParam parameterization strategies.

This study highlights the importance of having sufficient coverage of chemical space within the underlying databases of these automated schemes and the benefit of targeting specific functional groups for parameterization efforts in order to maximize both the breadth and depth of the parameterized space. By analyzing the quality of hydration free energies associated with different chemical classes, it was clear that (i) MATCH(cgenff) and ParamChem would benefit from further specificity in their learned rules associated with the iodo-, amides attached to rings, and chloro-alkyl groups; (ii) ParamChem accuracy would improve with additional refinement rules for modeling fluorine-containing compounds; (iii) SwissParam could leverage parameters from other force fields to improve how alcohols, aldehydes, bromo- and ether alkyls are modeled to better reproduce experimental hydration free energies; (iv) and parameters in CGENFF for esters, thioethers and alkenes would need to be revisited to reproduce the quality of hydration free energy estimates that are observed with GAFF/AM1-BCC and SwissParam. Finally, modeling with MATCH libraries that were derived from the non-CGENFF CHARMM topology and parameter files indicates that amine, aldehyde, and thiol parameters in MATCH(cgenff) could be improved by incorporating parameters from the context-specific force fields in CHARMM.

The overall success of these automated strategies for parameterizing arbitrary compounds indicates that a critical step forward has been taken towards making biomolecular simulations more readily accessible for a wide range of applications involving small molecules. The quality of the hydration free energies given these CHARMM-compatible force fields and implicit solvent models is promising and sets the stage for a systematic evaluation of the quality of protein-ligand binding affinities.