Significance
We provide the first experimental evidence (to our knowledge) that correlated population activity can serve as an extra channel to encode second-order features of sensory input in both the electrosensory and vestibular systems. Through further experiments and mathematical modeling, we show that such coding not only requires but is also optimally tuned to a nonzero level of variability. Finally, we demonstrate that only physiologically realistic decoding circuits that explicitly include the contributions of pairwise neural activity can reliably be used to reconstruct the envelope. Our results reveal new functional roles for correlated activity and neural variability that are generally applicable across systems and species.
Keywords: correlation, envelope, electrosensory, vestibular, neural coding
Abstract
Understanding how the brain processes sensory information is often complicated by the fact that neurons exhibit trial-to-trial variability in their responses to stimuli. Indeed, the role of variability in sensory coding is still highly debated. Here, we examined how variability influences neural responses to naturalistic stimuli consisting of a fast time-varying waveform (i.e., carrier or first order) whose amplitude (i.e., envelope or second order) varies more slowly. Recordings were made from fish electrosensory and monkey vestibular sensory neurons. In both systems, we show that correlated but not single-neuron activity can provide detailed information about second-order stimulus features. Using a simple mathematical model, we made the strong prediction that such correlation-based coding of envelopes requires neural variability. Strikingly, the performance of correlated activity at predicting the envelope was similarly optimally tuned to a nonzero level of variability in both systems, thereby confirming this prediction. Finally, we show that second-order sensory information can only be decoded if one takes into account joint statistics when combining neural activities. Our results thus show that correlated but not single-neural activity can transmit information about the envelope, that such transmission requires neural variability, and that this information can be decoded. We suggest that envelope coding by correlated activity is a general feature of sensory processing that will be found across species and systems.
Although correlated activity and neural variability are both observed ubiquitously in the brain, their functional roles have been the focus of much debate (1, 2). Indeed, the conventional wisdom that both are detrimental to coding by introducing redundancy and noise, respectively, has been recently challenged (3, 4). Here, we investigated the effects of variability on the coding by correlated activity of naturalistic sensory stimuli that often have rich spatiotemporal structure characterized by first- and second-order attributes. Specifically, we considered how neural populations within the electrosensory system of weakly electric fish and the vestibular system of monkeys respond to stimuli consisting of a fast time-varying carrier waveform (i.e., first-order attribute) whose amplitude or envelope (i.e., second-order attribute) varies independently on a longer timescale. Envelopes are critical for perception (5, 6), yet their neural encoding continues to pose a challenge to investigators because they are nonlinearly related to the stimulus waveform (7). Previous studies have shown that single neurons can transmit envelope information through changes in firing rate (8, 9) when the relationship between the stimulus input and the output firing rate is nonlinear. In contrast, here, we focused on neuronal responses that were linearly related to the stimulus waveform.
Weakly electric fish generate an electric field around their body through the electric organ discharge (EOD) (for review, see ref. 10). Peripheral electroreceptor afferents scattered over the animal’s skin respond to the low-intensity changes in EOD amplitude frequently encountered under natural conditions (11) through linearly related changes in firing rate (12). Although previous studies have shown that envelope information under these conditions reaches higher brain regions, thus giving rise to perception and behavior (13), the processing of low-intensity envelopes by the afferent population is not well understood.
The vestibular system provides information about head motion relative to space that is necessary for maintaining posture, computing spatial orientation, and perceiving self-motion (14). This essential system is well characterized anatomically and displays important differences with the electrosensory system. Peripheral afferents respond to head velocity through changes in firing rate that are linearly related to the stimulus (15, 16) but exhibit a much wider range of resting discharge variability than electroreceptor afferents (12). Although low-intensity envelopes are a prominent feature of vestibular signals encountered during natural self-motion (17), the neural mechanisms underlying their processing by vestibular neurons are not well understood.
Here, we show that correlated but not single-neuron activity encodes envelopes in both the electrosensory and vestibular systems. Through a combination of mathematical modeling and computational analyses, we further show that such coding is found for wide ranges of parameter values and is optimal for a nonzero level of neural variability. We suggest that correlation coding provides a general neural strategy to encode the commonly observed second-order features of sensory input across sensory systems.
Results
Correlations Between Spike Trains Encode Second-Order Stimulus Attributes.
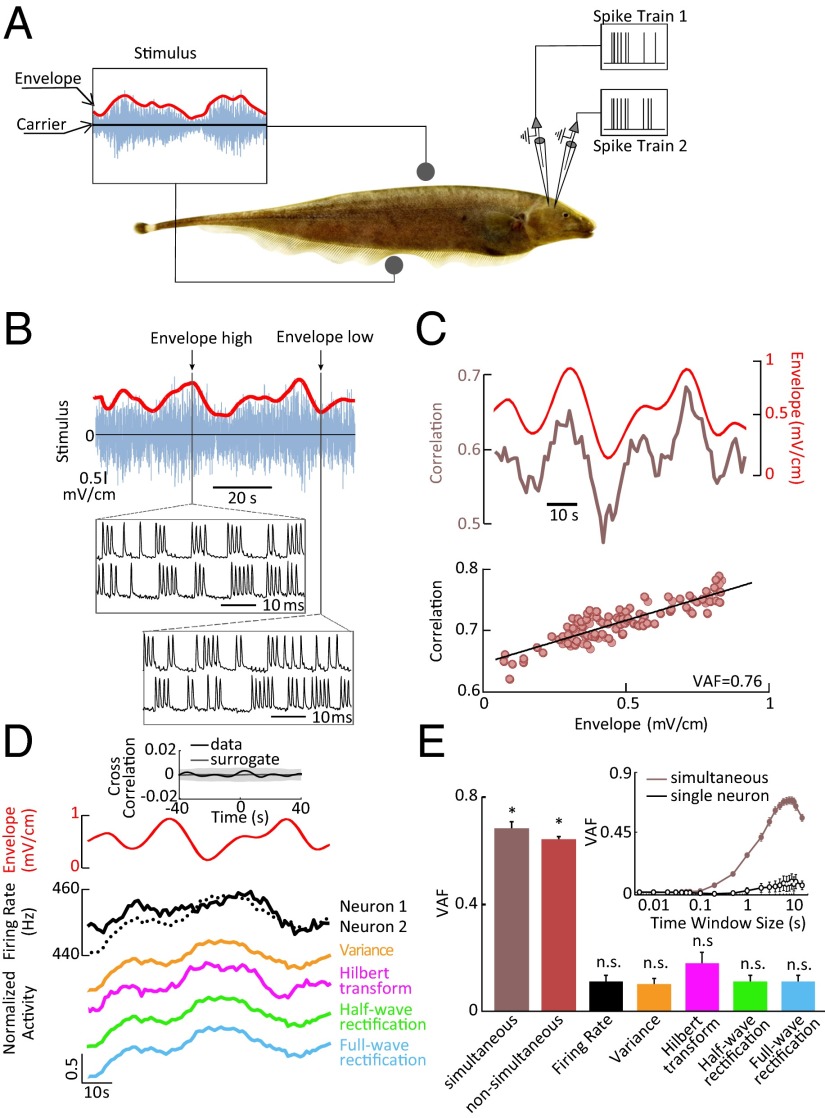
We studied neural responses to stimuli consisting of a noisy waveform (Fig. 1A, blue) whose envelope (Fig. 1A, red) varied independently and more slowly in time. We initially focused on the electrosensory system of weakly electric fish because (i) its neural circuitry is well characterized (10); (ii) it is feasible to perform pairwise recordings from electroreceptor afferents in awake behaving animals (18); and (iii) noise stimuli closely mimic natural sensory signals encountered by these fish (11) as they routinely evoke behavioral responses (19). When we examined simultaneous recordings from afferent pairs, we found that spike trains were more similar when the envelope was high (Fig. 1B). We quantified this similarity using the correlation coefficient (SI Materials and Methods) and found strong covariation with the envelope (Fig. 1C, Top). We quantified the degree to which the envelope could be predicted from the correlation coefficient by computing the variance-accounted-for (VAF) (SI Materials and Methods and Materials and Methods), which ranges between 0 (no predictability) and 1 (optimal predictability). The high VAF value (0.76) obtained indicates that the correlation coefficient is a reliable predictor of the envelope (Fig. 1C, Bottom).
Fig. 1.
Correlated but not single-neuron activity encodes the stimulus envelope in weakly electric fish electroreceptor afferents. (A) Electroreceptor afferents were stimulated with a noisy waveform (20-Hz cutoff frequency) (blue) whose amplitude (i.e., envelope, red) varied independently and consisted of low-pass–filtered white noise (0.05-Hz cutoff frequency). (B) Time-varying stimulus (blue) with zero mean (horizontal black line) and its envelope (red). (Insets) Spiking responses from an example afferent pair to stimulus segments characterized by high and low envelopes. Note that, although the total numbers of spikes were similar in both conditions (21 for high envelope vs. 23 for low envelope), coincident spikes were more frequent when the envelope was high (15 for high envelope vs. 8 for low envelope). (C, Top) Time-varying envelope (red), and correlation coefficient (brown) from the same pair. (Bottom) Correlation coefficient as a function of envelope showing a strong linear relationship as characterized by a high variance-accounted-for (VAF). (D, Top) Time-varying envelope (red), and corresponding firing rates of both neurons (black). (Bottom) Signals obtained after applying nonlinear transformations to the single-neuron activity. (Inset) Cross-correlation function between the envelope and an example single electroreceptor neuron’s spiking activity (solid black) as well as uncorrelated surrogate data (solid gray). The band shows the 95% confidence interval of the surrogate dataset. (E) Population-averaged VAF values for the correlation coefficient computed from simultaneous recordings (brown; n = 16 pairs), nonsimultaneous recordings (red; n = 153), as well as for single-neural activity after applying either no transformation or the same nonlinear transformations as in D (black and colored bars; n = 32). No significant difference in coding performance as quantified by VAF was observed (P = 0.12, rank sum test, df = 168). The asterisk (*) indicates statistical significance at the P = 0.01 level using a Wilcoxon rank sum test. n.s., not statistically significant. (Inset) VAF computed from correlated activity of pairs of afferents recorded simultaneously and from single-neuron activity as a function of the time window used to calculate the correlation coefficient. The filled circles indicate statistically significant values from zero at the P = 0.05 level using a t test. The open circles indicate that the values were not significantly different from zero.
Importantly, the activity of individual single neurons did not provide detailed information about the envelope (Fig. 1D, Top). Indeed, the cross-correlation function between the single electroreceptor’s spiking activity and the envelope was not significantly different from that obtained from surrogate data that was, by construction, uncorrelated with the envelope (P > 0.3, Kolmogorov–Smirnov test; n = 32) (Fig. 1D, Top, Inset). We further found that standard nonlinear transformations that are typically used to extract the envelope from a signal also did not provide detailed information about the envelope when applied to the single electroreceptor neurons (Fig. 1D, Bottom). Overall, the pairwise correlation coefficient reliably predicted the envelope as quantified by a high VAF observed across our dataset (Fig. 1E). Similar results were obtained when randomly pairing nonsimultaneous recordings (Fig. 1E), indicating that such coding is robust. This is discussed further below. In contrast, waveforms obtained by applying either linear or nonlinear transformations to the single-neuron activity did not reliably predict the envelope as quantified by negligible VAF values (Fig. 1E).
We next investigated whether the value of the time window over which both the time-dependent correlation coefficient and firing rate are computed influences envelope-coding performance. This is because correlations reflecting common activity can be measured at different timescales, ranging from a few milliseconds (i.e., synchrony) to seconds (i.e., slow covariation of firing rates) (20). We found that the correlation coefficient provided detailed information about the envelope for integration time windows >1 s (Fig. 1E, Inset). However, for all time windows, single-neuron activity did not reliably predict the envelope, as quantified by negligible VAF values (Fig. 1E, Inset). Importantly, the time windows considered are comparable with neuronal integration time constants observed experimentally (21, 22).
Envelope Coding by Correlated Activity in Leaky Integrate-and-Fire Neuron Models.
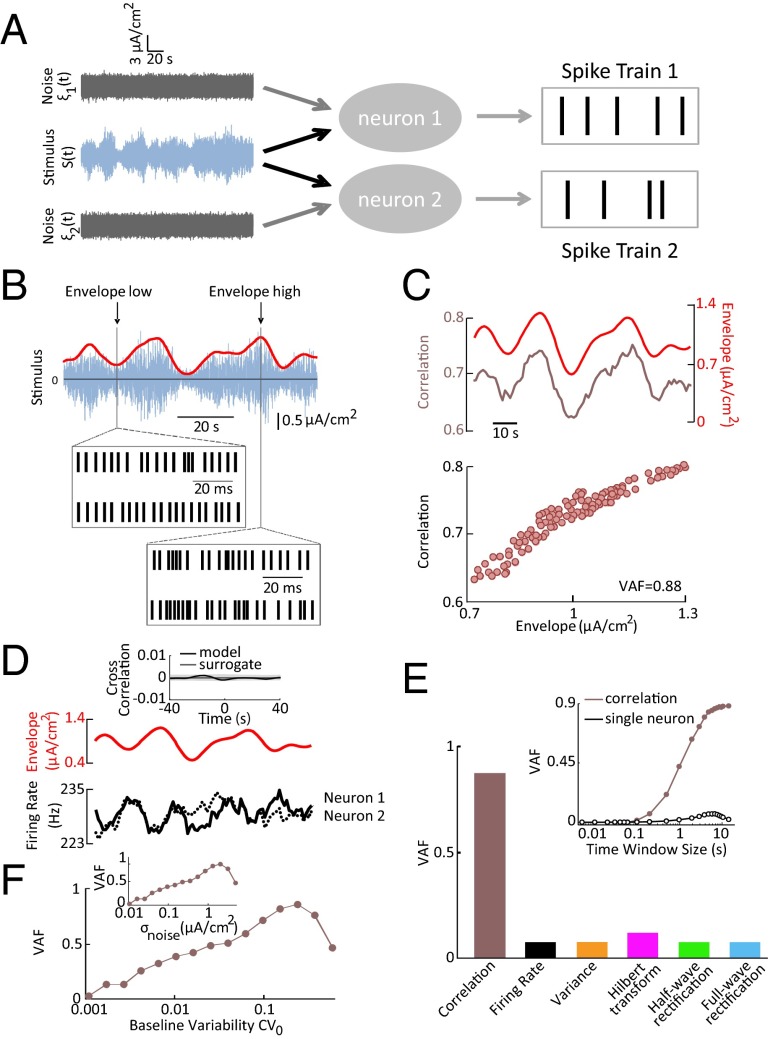
Our results thus far lead to the interesting question: how does correlated activity encode the envelope? To answer this question, we simulated a pair of spiking neuron models using the leaky integrate-and-fire formalism. The inputs to both model neurons consisted of a constant bias current Ibias, a common stimulus S(t) with zero mean and SD σstim, and normally distributed noise sources ξ1(t), ξ2(t) with zero mean and SD σnoise (Fig. 2A, SI Materials and Methods). The output spike trains of our model neurons were analyzed in the same manner as the experimental data. We assumed that the noises received by each of the model neurons [i.e., ξ1(t), ξ2(t)] were independent and identically distributed [<ξi(t)ξj(t′)> ∝ δ(t − t′) if i = j and <ξi(t)ξj(t′)> = 0 otherwise]. Despite its relative simplicity and the fact that the patterns of the simulated neuron spike trains were different from those of electroreceptors (compare Figs. 1B and 2B), our model was able to accurately reproduce our experimental results (Fig. 2B). Specifically, the degree of similarity between both model neurons’ spiking responses increased as a function of the envelope (Fig. 2B, compare Middle and Bottom). This can be understood intuitively because, although the noise intensity is independent of the envelope, the stimulus intensity and thus the signal-to-noise ratio is larger when the envelope is higher. Consistent with our experimental findings (Fig. 1C), the pairwise correlation coefficient reliably predicted the envelope as quantified by a high VAF (Fig. 2C). In contrast, individual single-model neuron activity did not provide detailed information about the envelope (Fig. 2D). Indeed, the cross-correlation function between the single model neuron’s spiking activity and the envelope was not significantly different from zero (P > 0.3, Kolmogorov–Smirnov test) (Fig. 2D, Top, Inset). The signals obtained by applying nonlinear transformations to the single-model neuron activity also could not reliably predict the envelope as quantified by negligible VAF values (Fig. 2E). Furthermore, as was the case experimentally, the correlation coefficient most reliably predicted the envelope when computed for time windows > 1 s (compare Insets of Figs. 1E and 2E).
Fig. 2.
An integrate-and-fire type neuron model predicts that correlated-based coding of envelopes is optimal for a nonzero level of neural variability. (A) Two leaky integrate-and-fire neurons received a common stimulus S(t) (blue) as well as two independent noise sources ξ1(t), ξ2(t) (gray). (B) Time-varying stimulus (blue) with zero mean (horizontal black line) and its envelope (red). (Insets) Spiking responses to a stimulus segment characterized by a high and low envelope. (C, Top) Time-varying envelope (red), and correlation coefficient (brown) from our pair of model neurons. (Bottom) Correlation coefficient as a function of envelope showing a strong linear relationship as characterized by a high variance-accounted-for (VAF). (D, Top) Time-varying envelope (red), and corresponding firing rates of the single model neurons (Bottom; black). (Inset) Cross-correlation function between the envelope and our single model neuron’s spiking activity (solid black) as well as uncorrelated surrogate data (solid gray). The band shows the 95% confidence interval of the surrogate dataset. (E) VAF values for correlation coefficient as well as for single neural activity after applying either no transformation or the same nonlinear transformations as in D. (Inset) VAF computed from correlated activity of pairs of model neurons and from single-neuron activity as a function of the time window used to calculate the correlation coefficient. Abbreviations are the same as in Fig. 1. (F) VAF computed from the correlation coefficient as a function of variability as quantified by the coefficient of variation from the baseline activity CV0. Different values of CV0 were obtained by varying the noise intensity σnoise in our model between 0.1 and 20 μA/cm2. (Inset) VAF as a function of noise intensity σnoise.
To test whether envelope coding by correlated but not single-neuron activity is robust in our model, we next systematically varied parameters such as the bias current Ibias, the stimulus intensity σstim, and the noise intensity σnoise. We found that correlated population activity encoded the envelope independently of single-neuron activity over a wide range of parameter values. Specifically, this was the case for higher values of Ibias as well as intermediate values of σstim and σnoise (Figs. S1A and S2A). Furthermore, we found that the stimulus input–firing-rate output relationship was approximately linear in this regime (Figs. S1B and S2B). In contrast, single-neuron activity could only predict the envelope for regions in parameter space (Figs. S1A and S2B) that were characterized by a nonlinear stimulus input–firing-rate output relationship (Figs. S1B and S2B) (SI Materials and Methods, Model Simulations).
Our model also makes the unexpected prediction that envelope coding by correlated neural activity requires neural variability as quantified by either the noise intensity σnoise or the coefficient of variation of the baseline (i.e., in the absence of stimulation) activity CV0. Both quantities are strongly correlated with trial-to-trial variability in the neural response to repeated presentations of the stimulus (18, 23, 24). We found that the VAF between correlation coefficient and envelope was maximal for a nonzero value of CV0 (Fig. 2F) and σnoise (Fig. 2F, Inset). Intuitively this makes sense because both infinitesimally small and infinitely large values of CV0 or σnoise give rise to regimes where the correlation coefficient is always equal to zero and unity, respectively, and thus independent of the envelope.
Envelope Coding by Correlated Vestibular Afferent Activities.
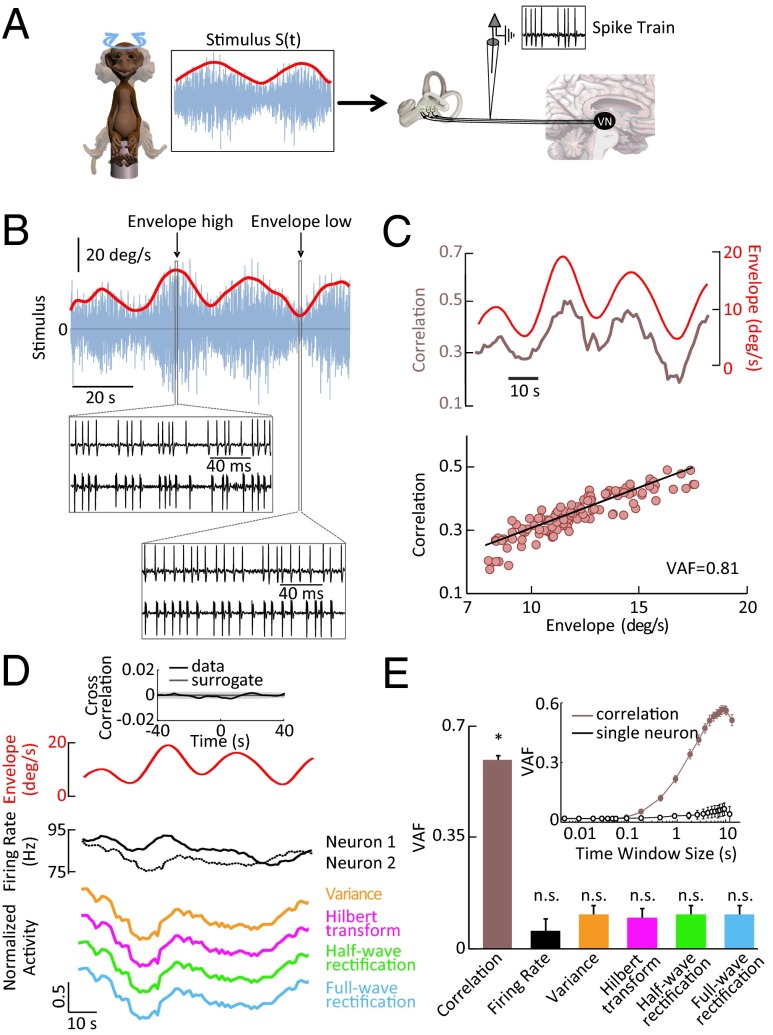
Our modeling and associated analyses have made the important prediction that envelope coding by correlated activity is optimal for a nonzero level of neuronal variability. To test this prediction experimentally, we recorded from afferents in the primate vestibular system (Fig. 3A; SI Materials and Methods). These afferents are particularly well suited because they display a much wider range of variability than that observed for electroreceptor afferents (12, 15), which is due in part to distinct ionic conductances and morphological features at their peripheral terminations (25).
Fig. 3.
Correlated but not single-neuron activity encodes the stimulus envelope in primate vestibular afferents. (A) The spiking activity of individual vestibular afferents were recorded from macaque monkeys during rotational stimuli whose angular velocity consisted of a noisy waveform (20-Hz cutoff frequency) (blue) whose amplitude (i.e., envelope, red) varied independently and consisted of low-pass–filtered white noise (0.05-Hz cutoff frequency). (B) Time-varying stimulus (blue) with zero mean (horizontal black line) and its envelope (red). (Insets) Spiking responses from an example vestibular afferent pair to a stimulus segment characterized by a high and low envelope. Note that, although the total numbers of spikes were similar (∼21), coincident spikes were more frequent when the envelope was high (16 vs. 9). (C, Top) Time-varying envelope (red), and correlation coefficient (brown) from the same pair. (Bottom) Correlation coefficient as a function of envelope showing a strong linear relationship as characterized by a high variance-accounted-for (VAF). (D, Top) Time-varying envelope (red), and corresponding firing rates of both neurons (black). (Bottom) Single-neural activity after applying nonlinear operations as in Fig. 1. (Inset) Cross-correlation function between the envelope and an example single vestibular afferent’s spiking activity (solid black) as well as uncorrelated surrogate data (solid gray). The band shows the 95% confidence interval of the surrogate dataset. (E) Population-averaged VAF values for correlation coefficient (red; n = 121 pairs), as well as for firing rate and for single-neural activity after applying nonlinear operations (black and colored bars; n = 18). The asterisk (*) indicates statistical significance at the P = 0.01 level using a Wilcoxon rank sum test. (Inset) VAF computed from correlated activity of reconstituted pairs of afferents and from single-neuron activity as a function of the time window used to calculate the correlation coefficient. Filled circles indicate statistically significant values from zero at the P = 0.05 level using a t test. Open circles indicate that the values were not significantly different from zero.
We first investigated whether vestibular afferents display envelope coding by correlated activity. The waveform and envelope of motion stimuli (Fig. 3A; SI Materials and Methods) resembled vestibular signals encountered in a naturalistic setting (17). We obtained results that were qualitatively similar to those described above for the electrosensory system: spiking responses from pairs of single vestibular afferents were more similar when the envelope was high (Fig. 3B, compare Middle and Bottom) and the correlation coefficient between pairs of vestibular afferents strongly covaried with the envelope waveform as quantified by a large VAF (Fig. 3C). Furthermore, as seen in Fig. 3D, neither linear nor nonlinear transformations applied to the single-afferent activity gave detailed information about the envelope signal as quantified by negligible VAFs (Fig. 3E). Moreover, the cross-correlation function between the single afferent’s spiking activity and the envelope was not significantly different from zero (P > 0.3, Kolmogorov–Smirnov test; n = 18) (Fig. 3D, Top, Inset). Finally, we found that the correlation coefficient most reliably predicted the envelope for relatively large (>1 s) time windows (Fig. 3E, Inset). Thus, correlated but not single vestibular afferent activity encodes the envelope in a manner similar to that observed for electroreceptor afferents and our model.
Envelope Coding by Correlated Activity Is Optimal for a Nonzero Level of Neural Variability.
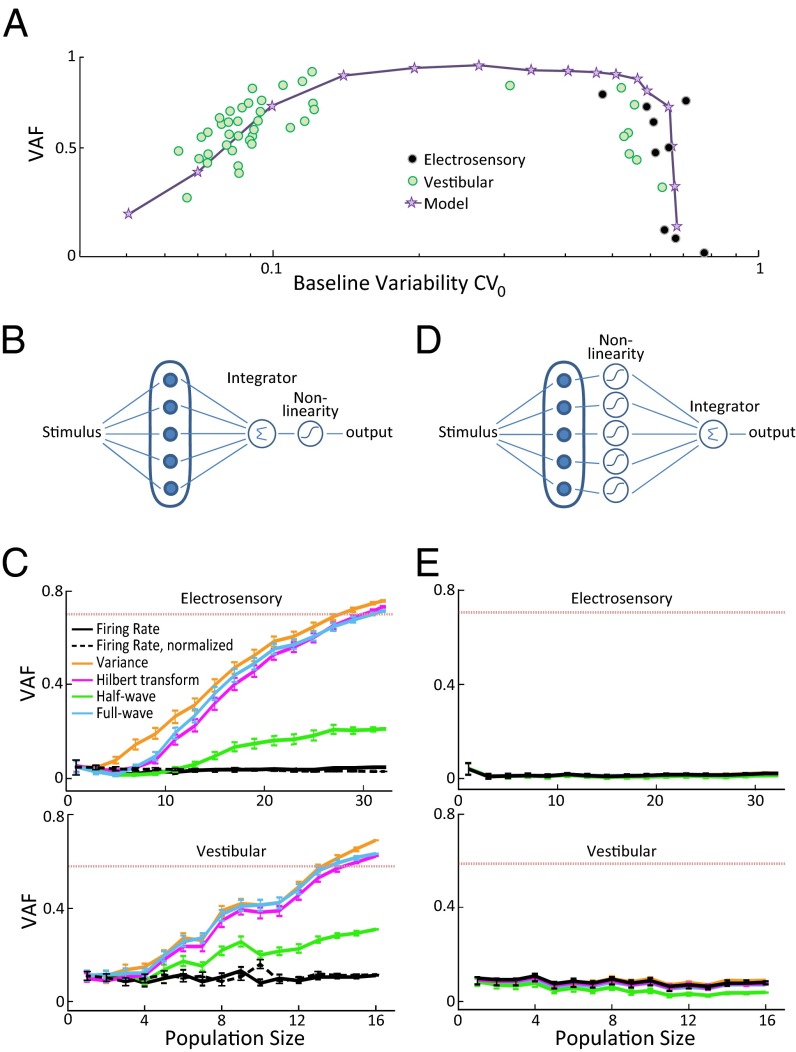
Next, to test our model’s prediction that envelope coding by correlated activity is optimally tuned to a nonzero level of neural variability, we plotted the coding efficiency as a function of variability quantified from baseline activity (i.e., in the absence of stimulation) for pairs of vestibular afferents. Confirming our modeling prediction, the largest VAF values were seen for vestibular afferent pairs with intermediate levels of variability (Fig. 4A, green circles). Even more strikingly, superimposing data obtained from electroreceptor afferent pairs revealed that vestibular and electroreceptor afferent pairs with similar levels of variability also display similar VAFs (Fig. 4A, compare black and green circles). This marked overlap between the datasets from both sensory systems given important differences (12, 15). Furthermore, we found that our model could reproduce the experimentally observed relationship between coding efficiency and neural variability seen in both datasets (Fig. 4A, compare stars with black and green circles). Thus, our results suggest that the same relationship between the efficiency of envelope coding by correlated activity and neural variability is shared across sensory systems and species.
Fig. 4.
Can the brain decode information carried by correlated neural activity? (A, Top) VAF obtained from the correlation coefficient as a function of baseline variability defined as the geometric mean of the coefficient of variations for pairs of electroreceptor afferents (black circles), vestibular afferents (green circles), and variability defined as CV0 from our model (purple stars) when we covaried both noise intensity and bias current (SI Materials and Methods). We note that there are few data points in the intermediate variability range: this is most likely because the probability of finding vestibular afferents in this range is relatively low (15, 42). (B) Schematic of a physiologically realistic decoder for which the individual afferent neuron’s activities are first averaged before applying a nonlinear transformation. (C) Performance of the decoder described in B quantified by VAF as a function of population size for the electrosensory (Top) and the vestibular (Bottom) dataset. The population-averaged value obtained from the correlation coefficient from neuron pairs is also shown (dashed red line) for comparison. (D) Schematic of a decoder based on applying a nonlinear transformation on each individual neuron’s spiking before averaging. (E) Performance of the decoder described in D quantified by VAF as a function of the number of afferents for the electrosensory (Top) and the vestibular (Bottom) dataset. The population-averaged value obtained from the correlation coefficient obtained from neuron pairs is also shown (dashed red line) for comparison.
Decoding Information About Second-Order Stimulus Attributes Carried by Neural Correlations.
The results above demonstrate that correlated neural activity reliably encodes second-order sensory information. However, information carried by neural activity is only useful to an organism if it is actually decoded by higher-order brain areas. To test whether information about the envelope can actually be decoded, we considered a neural circuit for which the output is a nonlinear function of the summed activities of single neurons (Fig. 4B). Because downstream neurons nonlinearly integrate input from convergent afferent axons in both the electrosensory and vestibular systems (16, 26), this circuit effectively functions as a physiologically realistic decoding algorithm. Indeed, we found that this circuit’s decoding performance improved with increasing population size using several standard nonlinear functions (Fig. 4C, Top and Bottom, colored traces). In contrast, linear summation of the single-neuron activities alone led to poor performance that did not improve with increasing population size (Fig. 4C, solid black). Similar results were obtained when linearly summing the normalized (i.e., subtracting the mean value and dividing by the maximum value) single-neuron activities (Fig. 4C, dashed black). Thus, nonlinear integration is necessary to observe improved decoding performance with increasing population size.
The neural circuit considered above (Fig. 4B) explicitly includes the contributions of pairwise interactions between neurons (i.e., “cross-terms”) toward decoding information about the envelope because the nonlinear transformation is applied after summation (SI Materials and Methods). However, the observed improvement in performance in this circuit could have been due to simple averaging the variability over a neural population. To address this possibility, we considered an alternate neural circuit in which a nonlinear operation is first performed on each individual neuron’s spiking activity followed by summing (Fig. 4D). Unlike the neural circuit considered in Fig. 4B, this circuit does not take into account joint statistics because the nonlinear transformation is applied before summation (SI Materials and Methods). Thus, if the improvement in performance observed in Fig. 4C was due to simple averaging, then we should observe an improvement in performance with increasing population size similar to that seen in Fig. 4C. If, on the other hand, the improvement in performance was instead due to taking into account joint statistics, then we should observe poor performance that does not improve with increasing population size. We found that the performance of this latter decoding algorithm was poor and did not significantly improve with increasing population size (Fig. 4E), thereby showing that taking into account pairwise joint statistics between neural spike trains is necessary to recover information about second-order stimulus attributes.
Discussion
We investigated the responses of both fish electrosensory and primate vestibular afferents to naturalistic stimuli. In both systems, we found that pairwise correlated but not single-neuron activity provided detailed information about the second-order attributes of the stimulus (i.e., the envelope). Through a combination of modeling and theoretical analyses, we predicted that this coding is optimal for a nonzero level of neural variability. We validated this prediction experimentally and found that both electrosensory and vestibular neurons were described by the same tuning function relating coding efficiency to neural variability. Finally, we found that the envelope information contained in correlated neural activity can only be decoded when joint statistics are taken into account. Taken together, our results suggest that envelope coding by correlated activity is a general strategy used across sensory systems and species to transmit information about behaviorally relevant stimulus attributes.
Correlated neural activities have been observed ubiquitously in the central nervous system (2), and it is now well accepted that their structure is dynamically regulated by several factors (27–31). This has led to the interesting hypothesis that correlated activity carries information not found in single-neuron activity (31, 32). Indeed, our results provide an experimental demonstration of this phenomenon by showing that correlated but not single-neuron activity transmits information about a behaviorally relevant stimulus feature. Traditionally, neural correlations have been separated into signal (i.e., correlations between the average neural responses) and noise (i.e., correlations between neural variabilities) components. Here, we showed that correlation coding by correlated activity was similar when using either simultaneous or nonsimultaneous recordings. Our findings thus demonstrate that signal correlations carry envelope information. Importantly, the structure of noise correlations can strongly depend on the stimulus’ spatiotemporal frequency content (28, 33). These results suggest that noise correlations carry information that may not be found in single-neuron activity, but further studies in other brain areas are needed to test this interesting hypothesis.
Across sensory systems, natural stimuli tend to display prominent first- and second-order attributes that are critical for perception (5, 7, 34, 35). In the electrosensory system, second-order attributes carry important information about the relative distance between conspecifics (11). It is likely that higher brain areas decode information about second-order attributes carried by correlated electroreceptor activity because weakly electric fish display strong and reliable behavioral responses to these attributes (13). Indeed, pyramidal cells within the electrosensory lateral line lobe strongly respond to envelopes at the single-neuron level (36) presumably through nonlinear integration of afferent synaptic input (26). In the vestibular system, neurons within the vestibular nuclei also nonlinearly integrate convergent vestibular afferent input (16) and are thus expected to strongly respond to the envelopes found in natural vestibular stimuli (17). However, further studies are needed to test these important predictions.
Our results have shown that neural variability is necessary to observe envelope coding by correlated neural activity. The role of neural variability in sensory coding has been the focus of much debate (1). On the one hand, the common wisdom is that variability is an unavoidable consequence of having neurons interconnected and should then be minimized (e.g., by pooling neural activities) to mitigate detrimental effects on neural coding. The vestibular system is uniquely well suited to study the role of variability in coding because afferents display a wide range of resting discharge variability. Interestingly, hair cells giving rise to vestibular afferents with high resting discharge variability can only be found in amniotes. It is, furthermore, thought that their recent evolution was triggered by changes in vestibular stimulus statistics resulting from transitioning from an aquatic to a terrestrial environment (37), which is incompatible with the above point of view that variability is detrimental to neural coding. Alternatively, it has been more recently postulated that neural variability instead forms a key element of the neural code by promoting increased information transmission (1). Indeed, theoretical studies posit that trial-to-trial variability in the neural response can effectively increase information transmission (38). Our results showing that correlated activity can optimally transmit information about the envelope for a nonzero level of variability provide a novel beneficial role for neural variability in sensory coding.
We note that, when the relationship between the stimulus waveform input and the firing-rate output is nonlinear, single-neuron activity can provide detailed information about the envelope as previously observed (8, 9, 39). Response nonlinearities (e.g., rectification, phase-locking) are more likely to be elicited by stimuli with relatively large intensities (40–42). However, natural stimuli are usually characterized by relatively low intensities yet can give rise to robust behavioral responses (13, 17, 43, 44). In these conditions, our results show that single-neuron activity instead does not provide detailed information about the envelope.
Thus, we propose that the coding of low-amplitude envelopes by correlated but not single-neuron activity is a general feature of sensory processing. Our results show that, in this regime, correlated but not single-neuron activity can provide detailed information about the envelope that can be recovered by pooling neural activities before performing a nonlinear transformation. We speculate that envelope coding by correlated activity will be preferentially found in neurons that display relatively high levels of spontaneous activity because these neurons tend to respond to low-intensity slowly time-varying stimuli through linearly related changes in activity around the spontaneous level. Such neurons can be found throughout the brain including cortex (15, 45–47). It is thus very likely that, across species, other sensory systems use similar decoding strategies that take advantage of the fact that correlated activity carries information about distinct stimulus attributes such as the envelope to ensure accurate perception and behavioral responses.
Materials and Methods
A detailed description of the methods is provided in SI Materials and Methods. All procedures were approved by the McGill University's Animal Care Committee and were in compliance with the guidelines of the Canadian Council on Animal Care. In brief, recordings from electrosensory and vestibular afferents were obtained using standard techniques. Spike trains were recorded in response to stimuli S(t) lasting 120 s and consisting of a 0- to 20-Hz noise carrier whose amplitude (i.e., envelope) was modulated independently (0–0.05 Hz). Correlations were quantified using the correlation coefficient. Variability was quantified by computing the coefficient of variation of the baseline activity (i.e., in the absence of stimulation), CV0, which is strongly correlated with trial-to-trial variability in the neural response to repeated stimulus presentations (18, 23, 24). VAF was used to assess the ability of a given time-varying signal to predict the envelope. Unless otherwise indicated, all error bars indicate SEs, and all statistical tests were Wilcoxon rank sum tests, except where stated otherwise. Our model consisted of two neurons receiving a common stimulus S(t) with intensity σstim as well as independent and identically distributed Gaussian white-noise sources with intensity σnoise. Simulations shown in Fig. 2 were obtained using σnoise > σstim, and model spike trains were analyzed in the same way as the experimental data.
Supplementary Material
Acknowledgments
We thank L. Maler for critical reading of the manuscript. This research was supported by the Canadian Institutes of Health Research (M.J.C. and K.E.C.) and the National Institutes of Health (K.E.C.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1418224112/-/DCSupplemental.
References
- 1.Stein RB, Gossen ER, Jones KE. Neuronal variability: Noise or part of the signal? Nat Rev Neurosci. 2005;6(5):389–397. doi: 10.1038/nrn1668. [DOI] [PubMed] [Google Scholar]
- 2.Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7(5):358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- 3.Hong S, Ratté S, Prescott SA, De Schutter E. Single neuron firing properties impact correlation-based population coding. J Neurosci. 2012;32(4):1413–1428. doi: 10.1523/JNEUROSCI.3735-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008;9(4):292–303. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shannon RV, Zeng FG, Wygonski J. Speech recognition with altered spectral distribution of envelope cues. J Acoust Soc Am. 1998;104(4):2467–2476. doi: 10.1121/1.423774. [DOI] [PubMed] [Google Scholar]
- 6.Bertoncini J, Serniclaes W, Lorenzi C. Discrimination of speech sounds based upon temporal envelope versus fine structure cues in 5- to 7-year-old children. J Speech Lang Hear Res. 2009;52(3):682–695. doi: 10.1044/1092-4388(2008/07-0273). [DOI] [PubMed] [Google Scholar]
- 7.Stamper SA, Fortune ES, Chacron MJ. Perception and coding of envelopes in weakly electric fishes. J Exp Biol. 2013;216(Pt 13):2393–2402. doi: 10.1242/jeb.082321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fairhall AL, Lewen GD, Bialek W, de Ruyter Van Steveninck RR. Efficiency and ambiguity in an adaptive neural code. Nature. 2001;412(6849):787–792. doi: 10.1038/35090500. [DOI] [PubMed] [Google Scholar]
- 9.Lundstrom BN, Fairhall AL, Maravall M. Multiple timescale encoding of slowly varying whisker stimulus envelope in cortical and thalamic neurons in vivo. J Neurosci. 2010;30(14):5071–5077. doi: 10.1523/JNEUROSCI.2193-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chacron MJ, Longtin A, Maler L. Efficient computation via sparse coding in electrosensory neural networks. Curr Opin Neurobiol. 2011;21(5):752–760. doi: 10.1016/j.conb.2011.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fotowat H, Harrison RR, Krahe R. Statistics of the electrosensory input in the freely swimming weakly electric fish Apteronotus leptorhynchus. J Neurosci. 2013;33(34):13758–13772. doi: 10.1523/JNEUROSCI.0998-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gussin D, Benda J, Maler L. Limits of linear rate coding of dynamic stimuli by electroreceptor afferents. J Neurophysiol. 2007;97(4):2917–2929. doi: 10.1152/jn.01243.2006. [DOI] [PubMed] [Google Scholar]
- 13.Metzen MG, Chacron MJ. Weakly electric fish display behavioral responses to envelopes naturally occurring during movement: Implications for neural processing. J Exp Biol. 2014;217(Pt 8):1381–1391. doi: 10.1242/jeb.098574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cullen KE. The neural encoding of self-motion. Curr Opin Neurobiol. 2011;21(4):587–595. doi: 10.1016/j.conb.2011.05.022. [DOI] [PubMed] [Google Scholar]
- 15.Goldberg JM. Afferent diversity and the organization of central vestibular pathways. Exp Brain Res. 2000;130(3):277–297. doi: 10.1007/s002210050033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Massot C, Schneider AD, Chacron MJ, Cullen KE. The vestibular system implements a linear-nonlinear transformation in order to encode self-motion. PLoS Biol. 2012;10(7):e1001365. doi: 10.1371/journal.pbio.1001365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Carriot J, Jamali M, Chacron MJ, Cullen KE. Statistics of the vestibular input experienced during natural self-motion: Implications for neural processing. J Neurosci. 2014;34(24):8347–8357. doi: 10.1523/JNEUROSCI.0692-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chacron MJ, Maler L, Bastian J. Electroreceptor neuron dynamics shape information transmission. Nat Neurosci. 2005;8(5):673–678. doi: 10.1038/nn1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chacron MJ, Doiron B, Maler L, Longtin A, Bastian J. Non-classical receptive field mediates switch in a sensory neuron’s frequency tuning. Nature. 2003;423(6935):77–81. doi: 10.1038/nature01590. [DOI] [PubMed] [Google Scholar]
- 20.Litwin-Kumar A, Oswald AMM, Urban NN, Doiron B. Balanced synaptic input shapes the correlation between neural spike trains. PLoS Comput Biol. 2011;7(12):e1002305. doi: 10.1371/journal.pcbi.1002305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cannon SC, Robinson DA. Loss of the neural integrator of the oculomotor system from brain stem lesions in monkey. J Neurophysiol. 1987;57(5):1383–1409. doi: 10.1152/jn.1987.57.5.1383. [DOI] [PubMed] [Google Scholar]
- 22.Prescott SA, De Koninck Y. Integration time in a subset of spinal lamina I neurons is lengthened by sodium and calcium currents acting synergistically to prolong subthreshold depolarization. J Neurosci. 2005;25(19):4743–4754. doi: 10.1523/JNEUROSCI.0356-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chacron MJ, Longtin A, Maler L. The effects of spontaneous activity, background noise, and the stimulus ensemble on information transfer in neurons. Network. 2003;14(4):803–824. [PubMed] [Google Scholar]
- 24.Yu XJ, Thomassen JS, Dickman JD, Newlands SD, Angelaki DE. Long-term deficits in motion detection thresholds and spike count variability after unilateral vestibular lesion. J Neurophysiol. 2014;112(4):870–889. doi: 10.1152/jn.00280.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eatock RA, Hurley KM. Functional development of hair cells. Curr Top Dev Biol. 2003;57:389–448. doi: 10.1016/s0070-2153(03)57013-2. [DOI] [PubMed] [Google Scholar]
- 26.Berman NJ, Maler L. Neural architecture of the electrosensory lateral line lobe: Adaptations for coincidence detection, a sensory searchlight and frequency-dependent adaptive filtering. J Exp Biol. 1999;202(Pt 10):1243–1253. doi: 10.1242/jeb.202.10.1243. [DOI] [PubMed] [Google Scholar]
- 27.Cohen MR, Maunsell JH. Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci. 2009;12(12):1594–1600. doi: 10.1038/nn.2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chacron MJ, Bastian J. Population coding by electrosensory neurons. J Neurophysiol. 2008;99(4):1825–1835. doi: 10.1152/jn.01266.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vaadia E, et al. Dynamics of neuronal interactions in monkey cortex in relation to behavioural events. Nature. 1995;373(6514):515–518. doi: 10.1038/373515a0. [DOI] [PubMed] [Google Scholar]
- 30.Litwin-Kumar A, Chacron MJ, Doiron B. The spatial structure of stimuli shapes the timescale of correlations in population spiking activity. PLoS Comput Biol. 2012;8(9):e1002667. doi: 10.1371/journal.pcbi.1002667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.deCharms RC, Merzenich MM. Primary cortical representation of sounds by the coordination of action-potential timing. Nature. 1996;381(6583):610–613. doi: 10.1038/381610a0. [DOI] [PubMed] [Google Scholar]
- 32.Ishikane H, Gangi M, Honda S, Tachibana M. Synchronized retinal oscillations encode essential information for escape behavior in frogs. Nat Neurosci. 2005;8(8):1087–1095. doi: 10.1038/nn1497. [DOI] [PubMed] [Google Scholar]
- 33.Ponce-Alvarez A, Thiele A, Albright TD, Stoner GR, Deco G. Stimulus-dependent variability and noise correlations in cortical MT neurons. Proc Natl Acad Sci USA. 2013;110(32):13162–13167. doi: 10.1073/pnas.1300098110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev. 2004;84(2):541–577. doi: 10.1152/physrev.00029.2003. [DOI] [PubMed] [Google Scholar]
- 35.Baker CL., Jr Central neural mechanisms for detecting second-order motion. Curr Opin Neurobiol. 1999;9(4):461–466. doi: 10.1016/S0959-4388(99)80069-5. [DOI] [PubMed] [Google Scholar]
- 36.McGillivray P, Vonderschen K, Fortune ES, Chacron MJ. Parallel coding of first- and second-order stimulus attributes by midbrain electrosensory neurons. J Neurosci. 2012;32(16):5510–5524. doi: 10.1523/JNEUROSCI.0478-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Eatock RA, Songer JE. Vestibular hair cells and afferents: Two channels for head motion signals. Annu Rev Neurosci. 2011;34:501–534. doi: 10.1146/annurev-neuro-061010-113710. [DOI] [PubMed] [Google Scholar]
- 38.McDonnell MD, Ward LM. The benefits of noise in neural systems: Bridging theory and experiment. Nat Rev Neurosci. 2011;12(7):415–426. doi: 10.1038/nrn3061. [DOI] [PubMed] [Google Scholar]
- 39.Rosenberg A, Issa NP. The Y cell visual pathway implements a demodulating nonlinearity. Neuron. 2011;71(2):348–361. doi: 10.1016/j.neuron.2011.05.044. [DOI] [PubMed] [Google Scholar]
- 40.Savard M, Krahe R, Chacron MJ. Neural heterogeneities influence envelope and temporal coding at the sensory periphery. Neuroscience. 2011;172:270–284. doi: 10.1016/j.neuroscience.2010.10.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Metzen MG, Chacron MJ. Neural heterogeneities determine response characteristics to second-, but not first-order stimulus features. J Neurosci. 2015;35(7):3124–3138. doi: 10.1523/JNEUROSCI.3946-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sadeghi SG, Minor LB, Cullen KE. Response of vestibular-nerve afferents to active and passive rotations under normal conditions and after unilateral labyrinthectomy. J Neurophysiol. 2007;97(2):1503–1514. doi: 10.1152/jn.00829.2006. [DOI] [PubMed] [Google Scholar]
- 43.Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu Rev Neurosci. 2001;24:1193–1216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- 44.Deemyad T, Metzen MG, Pan Y, Chacron MJ. Serotonin selectively enhances perception and sensory neural responses to stimuli generated by same-sex conspecifics. Proc Natl Acad Sci USA. 2013;110(48):19609–19614. doi: 10.1073/pnas.1314008110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kuffler SW. Discharge patterns and functional organization of mammalian retina. J Neurophysiol. 1953;16(1):37–68. doi: 10.1152/jn.1953.16.1.37. [DOI] [PubMed] [Google Scholar]
- 46.Luczak A, Barthó P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62(3):413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: Explanation of the large variability in evoked cortical responses. Science. 1996;273(5283):1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.