Loose coupling in the bacterial flagellar motor

Significance

Many species of bacteria swim using rotating helical propellers called flagella. Flagellar rotary motors obtain energy from the transmembrane gradient of ions (either H⁺ or Na⁺). Physiological properties of the motor have been studied for more than 40 y and have led to the longstanding view that the motor is tightly coupled, meaning that each revolution is associated with the movement of a fixed number of ions across the membrane. Simulations described here indicate that this may not be the case: A loosely coupled mechanism can explain all of the observations that have been taken to indicate tight coupling, as well as some measurements that are more difficult to account for within the tight-coupling framework.

Abstract

Physiological properties of the flagellar rotary motor have been taken to indicate a tightly coupled mechanism in which each revolution is driven by a fixed number of energizing ions. Measurements that would directly test the tight-coupling hypothesis have not been made. Energizing ions flow through membrane-bound complexes formed from the proteins MotA and MotB, which are anchored to the cell wall and constitute the stator. Genetic and biochemical evidence points to a “power stroke” mechanism in which the ions interact with an aspartate residue of MotB to drive conformational changes in MotA that are transmitted to the rotor protein FliG. Each stator complex contains two separate ion-binding sites, raising the question of whether the power stroke is driven by one, two, or either number of ions. Here, we describe simulations of a model in which the conformational change can be driven by either one or two ions. This loosely coupled model can account for the observed physiological properties of the motor, including those that have been taken to indicate tight coupling; it also accords with recent measurements of motor torque at high load that are harder to explain in tight-coupling models. Under loads relevant to a swimming cell, the loosely coupled motor would perform about as well as a two-proton motor and significantly better than a one-proton motor. The loosely coupled motor is predicted to be especially advantageous under conditions of diminished energy supply, or of reduced temperature, turning faster than an obligatorily two-proton motor while using fewer ions.

The rotary motor of bacterial flagella obtains energy from the transmembrane gradient of protons or sodium ions (1, 2). Although molecular details remain unclear, a general outline of its mechanism has emerged from a combination of genetic, biochemical, and physiological studies. The energizing ions flow through a set of membrane-embedded protein complexes formed from MotA and MotB (or their homologs PomA and PomB in Na⁺-powered motors), each with subunit composition MotA₄MotB₂ (3−7). The complexes are held in place by binding to peptidoglycan and thus function as the stator (the part that is nonrotating with respect to the cell body) (8, 9). Each motor contains several stator complexes (10) that function independently (11–13) to produce torque and that are in exchange with membrane pools (14). An invariant aspartate in MotB (Asp32 in Escherichia coli) is the only evolutionarily conserved proton-binding residue essential for rotation. On the basis of this and other evidence, Asp32 has been proposed to form a binding site for the energizing ions (15, 16). Mutations of Asp32 in MotB induce conformational changes in MotA, in a region in MotA that has been shown to interact with the rotor protein FliG (17). Together, these findings point to a mechanism based on conformational changes in the stator, initiated by ion binding/dissociation at Asp32 and acting at the MotA/FliG interface to drive movement of the rotor.

The structure of the MotA₄MotB₂ complex is not known at high resolution, but biochemical and mutational studies have established certain important features of its architecture. MotB has a single transmembrane (TM) segment (8) and a carboxyl-terminal domain in the periplasm that functions to bind peptidoglycan (9). MotA has four TM segments, two relatively short segments in the periplasm and two larger segments in the cytoplasm (18). The segment of MotA between TM2 and TM3 contains well-conserved charged residues that engage in electrostatic interactions with charged residues of FliG (19–21). The Asp-32 regulated conformational change has been shown to affect this rotor-interacting region of MotA (17). In a model for membrane segment arrangement deduced from cross-linking, each MotA₄MotB₂ complex is predicted to contain two distinct proton channels, leading to two well-separated Asp32 sites (22−24). This raises the question of whether the power stroke can be initiated by the binding of a single ion or requires ion binding at both Asp32 sites.

A model of the motor mechanism must account for the following physiological properties. (i) When the viscous load is large and the rotation rate consequently slow (as in experiments with tethered cells where the rotation rate is about 10 Hz), the motor torque is proportional to protonmotive force (Δp) (25). (ii) The torque at high load is approximately the same in D₂O as in H₂O and changes little with temperature over the range 4–38 °C (26). (iii) When the load is light, the speed is much greater (27, 28), is at least approximately proportional to Δp (29), and, in this case, depends on both temperature and solvent isotope (30). (iv) As motor speed increases as a consequence of decreasing viscous load, the torque falls gradually at first, then drops more steeply once a characteristic “knee” speed is reached (28).

The observations at high load can be explained by assuming that the motor uses a fixed number of ions to drive each revolution and that the rates of the elementary chemical events within the motor (ion binding and dissociation, conformational changes, and associated forward and backward rotor steps) are fast relative to the net rate of rotation. Under these assumptions, the heavily loaded, slow-turning motor will function as a reversible engine to convert the energy of the protons used (n ⋅ q ⋅ Δp per revolution, with n the number of ions and q the elementary charge) into the work of rotation (2π ⋅ N, with N being the torque). This tight-coupling model was proposed more than 30 years ago to account for the linear torque-vs.-Δp relationship and the absence of thermal and isotope effects (26) and has since remained the favored interpretation (e.g., ref. 31). Observation iii indicates that as the external load is decreased, the finite rates of internal processes become important, with proton movement(s) being rate limiting to at least some extent. Observation iv, the shape of the torque−speed characteristic, is indicative of a power stroke mechanism in which the rotor is actively driven as opposed to a “Brownian ratchet” mechanism based on the rectification of thermal motions (32).

If the tight-coupling model holds and the ion-motive force is known, measurements of torque in the low-speed limit can be used to estimate the number of ions used per revolution. On the basis of extensive measurements with a Na⁺-fueled motor, Berry and coworkers recently estimated this coupling ratio at 37 ions per revolution (31). Measurements of motor stepping indicate 26 rotor steps per revolution (33, 34), and electron microscopic reconstructions (35) and other observations concerning rotor architecture (36–38) also appear consistent with a FliG copy number of 26 [varying somewhat between specimens (35, 39)]. The value of 37 ions per revolution deduced from torque measurements would then correspond to a noninteger coupling ratio (∼1.42 ions per step). This can be explained in terms of tight coupling but requires an alternative model for rotor organization in which the number of FliG subunits is about 37 rather than 26 (40, 41), and an alternative interpretation of the steps as being due to passive rotor−stator interactions with 26-fold symmetry rather than the actual torque-generating events (42). Here, we describe a simple model for the motor mechanism that is based on the twin-channel architecture of the stator and that can account for presently available physiological, structural, mutational, and biochemical data. The key feature of the model is loose coupling, specifically, the ability of the stator complex to execute power strokes driven by either one or two energizing ion(s). Simulations show that a motor operating on this loose-coupling principle can reproduce the observed physiological properties of the motor, including those that have been considered hallmarks of tight coupling. Under the relatively light loads pertinent to a swimming cell, the loosely coupled motor performs as well as or slightly better than a two-proton, tightly coupled motor. Under conditions of decreased ion-motive force or decreased temperature, the loosely coupled motor appears advantageous, rotating substantially faster than a two-proton motor while using fewer ions.

Results

Model.

A model of the motor mechanism was constructed around the following assumptions. (i) The stator exists in two conformations. The Asp32 ion-binding sites are accessible from the outside of the membrane (the periplasm) in conformation I and from the inside (the cytoplasm) in conformation II. (ii) In the ion-free state, the two conformations are equally stable. Ion binding to the Asp32 site(s) stabilizes conformation II relative to conformation I. Binding of ions to both sites has twice the stabilizing effect (in terms of state energies) as binding of a single ion. (iii) In the ion-bound states (whether with one or two ions), the conformational transition is coupled to rotor movement. In the ion-free state, the II → I transition serves to reset the conformation of the stator but is not coupled to rotor movement. Details of the rotor−stator interaction are not specified in the present model but must be such as to ensure a very high duty cycle; i.e., to prevent back-slippage of the rotor at practically all times (43). Specific proposals for the conformational change and for the forces involved in rotor−stator engagement have been described elsewhere (24, 38).

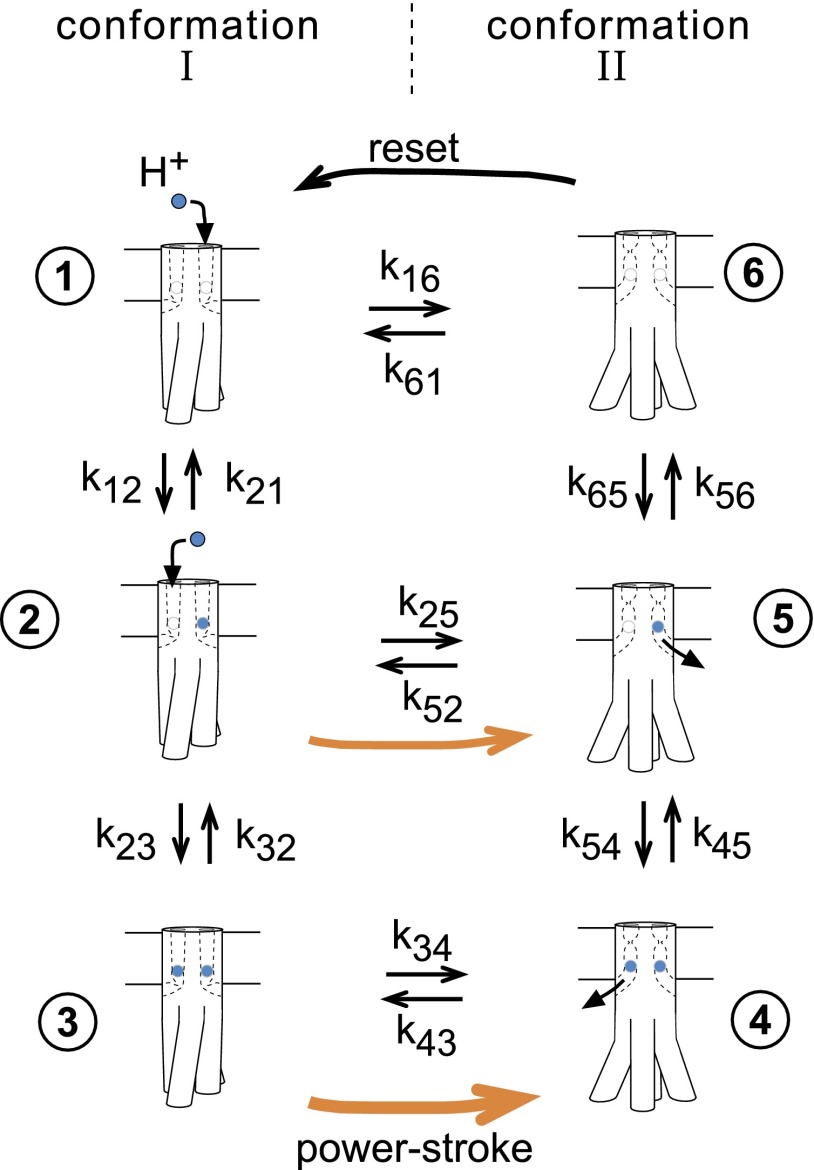
The model thus has six states, consisting of two conformations each capable of binding zero, one, or two protons. The corresponding reaction network is shown in Fig. 1. Transitions between states are assumed governed by simple mass action rate laws. The model is parameterized in terms of (i) k_step, an intrinsic rate of conformational change, given as the geometric mean of rate constants for the forward and backward conformational transitions; (ii) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$, the bimolecular rate constant for proton binding to an Asp32 site; and (iii) pK_I and pK_II, the pK values of the Asp32 site in the two conformations. The two Asp32 sites are assumed independent; i.e., proton binding is noncooperative. The following discussion is in terms of protons but would apply to sodium ions as well. Additional variables include the proton gradient, expressed in terms of the effective pH values on the input (periplasmically exposed) and output (cytoplasmically exposed) sides of the Asp32 site, and the load, given in terms of the work associated with a forward rotor step.

Fig. 1.

Flexible stoichiometry model. The stator is assumed to have two ion-binding sites, each formed mainly from the Asp32 of a MotB subunit. Binding of an ion (H⁺ or Na⁺; colored blue) stabilizes conformation II relative to conformation I; binding of two ions has twice the stabilizing effect. Protons have access to Asp32 from the periplasm in conformation I, and can exit to the cytoplasm in conformation II. When the stator is in an ion-associated state (whether with one ion or two), the conformational change is coupled to movement of the rotor by 1/26th of a revolution. Orange arrows indicate the steps involving rotor movement, the thicker one signifying the power stroke driven by the energy of two ions and the thinner one the less forceful power stroke driven by just a single ion. In transition 6 →1, which involves the states not bound to any ions, the stator conformation is reset, but without any accompanying movement of the rotor. Parameters are defined in Table S1, and expressions for the rate constants are given in Table S2. The structure of the stator is not known; the shape of the stator and the conformational change pictured are diagrammatic only, intended to indicate that the power stroke will entail fairly large movements in the cytoplasmic domain of MotA.

Rate constants for the transitions in the reaction network (Fig. 1) were expressed in terms of these parameters (Table S2). In general, proton binding will affect the relative energies of the two conformations, and was assumed here to change the forward (I → II) and backward (II → I) conformational transitions symmetrically (i.e., accelerating one and slowing the other by the same factor to maintain constancy of the “intrinsic” rate, k_step). Load was likewise assumed to act symmetrically on rates of forward and backward stepping transitions. The model does not assume kinetic barriers to any particular conformational transition(s) such as that between the singly protonated states. Loose coupling arises from this allowance of movement in either the singly or doubly protonated state (as opposed to an explicit “leakage” process introduced in parallel with the transducer). To allow comparison with tightly coupled models, reduced reaction networks corresponding to one-proton and two-proton mechanisms were also analyzed, using the same parameter sets.

Torque−Speed Characteristics.

Properties of the three models (one proton, two proton, flexible) were explored by solving the relevant steady-state rate equations either analytically or numerically (with equivalent results), for loads ranging between zero and stall, various rates of conformational change and proton association/dissociation, and a range of values for pK_I and pK_II. Initial simulations used a proton gradient (ΔpH) of 2.5 units. The concave-down shape of the torque−speed relation has been shown to be indicative of a power stroke mechanism (32). In the present model(s), a power stroke means an exergonic I → II transition and implies an increased pK in conformation II (examples in Fig. S1). Further requirements for concave-down shape are that the pKs not be too low and that rates of conformational change be rate limiting to at least some extent (Fig. S1).

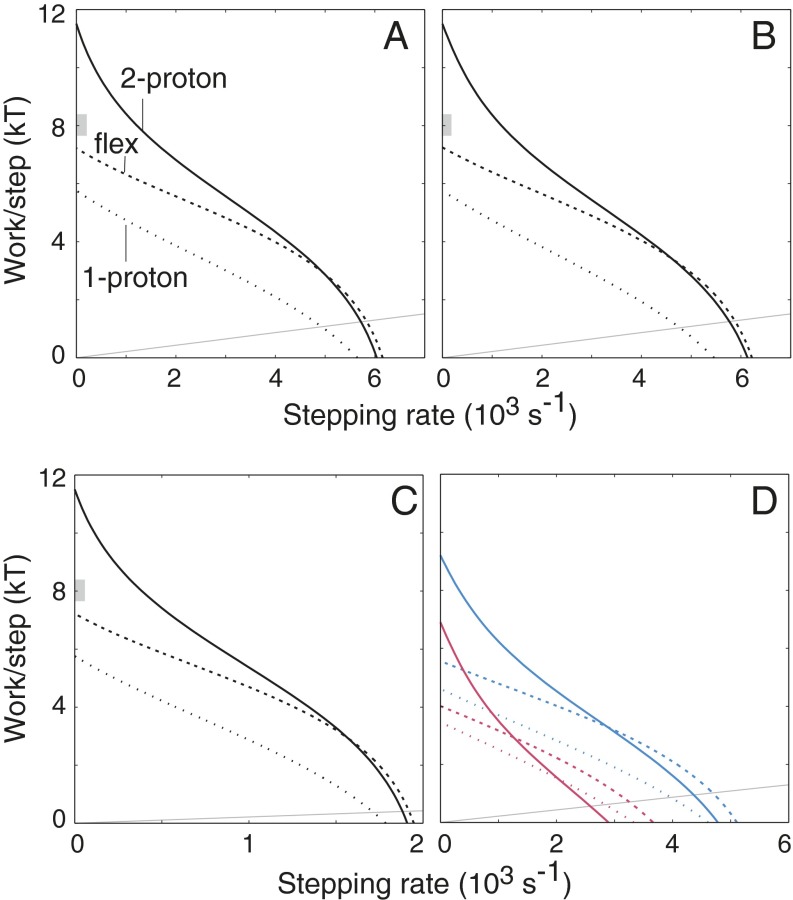
Representative torque−speed characteristics for the three models are shown in Fig. 2. In the measured curves (28), torque decreases gradually at first as speed increases from zero. This shallow slope in the low-speed range is more readily obtained with the flexible stoichiometry motor than with either tightly coupled motor; the two-proton motor in particular displays more steeply decreasing torque. As follows from an assumption of tight coupling, the stall torque of the two-proton motor is exactly twice that of the one-proton motor. The flexible motor produces an intermediate torque that, under the assumption of 26 steps per revolution (33, 34), is close to the recent measurements of Lo et al. (31) (range indicated by gray bars in Fig. 2 A−C). In the low-load range, the flexible stoichiometry and two-proton motors give similarly shaped curves, but with the flexible motor turning slightly faster in most cases (Fig. 2; additional examples in Fig. S2). The one-proton motor is significantly more sensitive to load and is also slower for most parameterizations. Exceptions are when stepping is very fast or proton transfer is very slow, in which case the use of just a single proton is advantageous (Fig. S2).

Fig. 2.

Torque−speed characteristics for the two-proton, one-proton, and flexible stoichiometry motors. In all panels, relative torque is represented on the vertical axis in terms of the work done per rotational step, in units of kT. (A) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹² M⁻¹⋅s⁻¹, k_step = 10⁴ s⁻¹, pK_I = 5.4, pK_II = 7.1, pH_ext = 5.4, pH_int = 7.9 (ΔpH = 2.5). (B) Proton movements 10-fold faster than in A (${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹³ M⁻¹⋅s⁻¹), k_step decreased to 9 × 10³ s⁻¹ (to give maximum speed similar to A). (C) Both proton transfer and stepping rates decreased (as might occur at lower temperature): ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10^11.5 M⁻¹⋅s⁻¹, k_step = 10^3.5 s⁻¹. (D) As in A, except with ΔpH decreased to 2.0 (blue curves) or 1.5 (red curves). At the operating point relevant to a swimming cell, proton use by the flexible motor is 1.92 H⁺/step for ΔpH = 2 and 1.67 H⁺/step for ΔpH = 1.5. In each panel, the thin gray line is the estimated load line for a flagellar filament working in a bundle of four filaments (44), driven by a motor that contains 11 stator complexes (13) each executing 26 steps per revolution (33, 34). In A−C, the gray block on the y axis indicates the range of torque measured by Lo et al. (31) in the high-load limit, again assuming 26 steps per revolution.

The operating point of the motor will occur where its torque−speed characteristic intersects the line describing the viscous load. The load line will be relatively shallow for a flagellar filament in a bundle and steeper for individual filaments, for tethered cells, or in situations of increased viscosity. The estimated load line for a flagellar filament working in a bundle of four filaments (44) (thus, rotating CCW) in water is shown in each of the panels of Fig. 2. With full energization of 2.5 pH units (Fig. 2 A−C), the flexible motor is slightly faster than the tightly coupled two-proton motor at a relevant load. When the proton gradient is decreased, the flexible motor acquires a greater advantage, turning significantly faster than the obligatorily two-proton motor while at the same time using fewer protons (Fig. 2D; additional examples below). The favorable attributes of the flexible stoichiometry motor are seen over a wide range of parameterizations (Fig. S2). Exceptions are when conformational change is very fast (in which case the tightly coupled two-proton transducer is fastest; Fig. S2F) or when proton transfer steps are slow (in which case the one-proton transducer is fastest; Fig. S2 A and D).

Deuterium Isotope Effect.

When the load is light, the motors of E. coli rotate about 1.5 times faster in H₂O than in D₂O (4, 30, 45). The magnitude of this effect implies that proton transfer is rate limiting to a certain, although not very great, extent (30). To simulate the deuterium isotope effect, both pK values were increased by 0.4 units (46). Rate ratios (H₂O/D₂O) were computed for various parameter sets, and ratios in the range 1.3–1.7 were taken as consistent with experiment. By this analysis, pK_II was found to be restricted to a maximum value of about 7.4 (Fig. S3), for a range of values of the other parameters. This ceiling on pK_II reflects the requirement that proton dissociation from conformation II not be too rate limiting. The simulations predict that the stall torque of the flexible stoichiometry motor will be slightly (∼10%) increased in D₂O, because increased proton affinity will favor the two-proton pathway. Torque has been reported to be the same in D₂O as in H₂O in some studies (26, 30) but was increased by about 20% in D₂O in another study (45).

Dependence on Protonmotive Force.

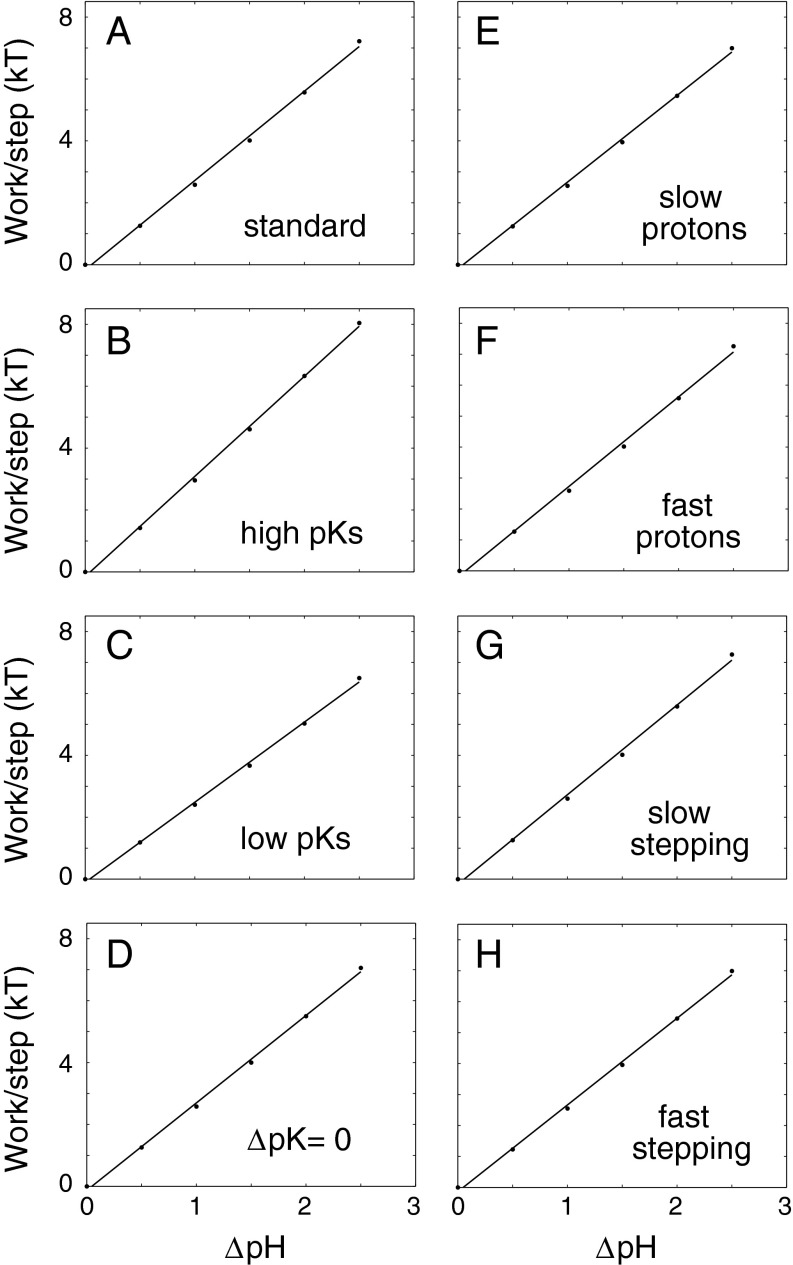
The proton electrochemical potential was treated as consisting entirely of a pH gradient, under the assumption that the electrical component will be converted into a pH difference by the proton channels leading to the Asp32 site. A calculation of the effective pH at Asp32 thus requires specifying the position of Asp32 in the electric potential gradient. Asp32 is fairly near the inner end of the MotB TM segment, and studies in a motile Streptococcus indicate a fractional electrical distance between three fourths and all of the way toward the cytoplasm (47). Accordingly, an 80:20 partitioning of the Δψ component (with Asp32 situated 20% from the inside) was assumed. A 70:30 partitioning gave similar results. Stall torque and maximum speed were computed for ΔpH values ranging from 0 to 2.5. Tightly coupled models such as the one- and two-proton motors here display linear relations between stall torque and ΔpH, as a consequence of energy conservation. More notably, a very nearly linear torque−ΔpH relationship is observed for the variable stoichiometry motor (Fig. 3). The closely linear relation between torque and ΔpH is a robust property of this loosely coupled motor, persisting over a wide range of stepping rates (Fig. 3 G and H), protonation rates (Fig. 3 E and F), and pK values (Fig. 3 B–D).

Fig. 3.

Dependence of stall torque on the proton gradient, for the flexible stoichiometry motor operating under various parameterizations. (A) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹² M⁻¹⋅s⁻¹, k_step = 10⁴ s⁻¹, pK_I = 5.4, pK_II = 7.1 (basic parameter set; others differ as indicated). (B) High pKs: pK_I = 5.9, pK_II = 7.6. (C) Low pKs: pK_I = 4.9, pK_II = 6.6. (D) ΔpK = 0: pK_I = pK_II = 6.25. (E) Slow protons: ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹¹ M⁻¹⋅s⁻¹. (F) Fast protons: ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹³ M⁻¹⋅s⁻¹. (G) Slow stepping: k_step = 10³ s⁻¹. (H) Fast stepping: k_step = 10⁵ s⁻¹. Under the assumptions of tight coupling and efficient energy conversion, slopes of the fitted lines in A–H would correspond, respectively, to apparent coupling ratios of 1.25, 1.41, 1.12, 1.23, 1.22, 1.26, 1.26, and 1.22 protons per step. At a rotation rate of 10 Hz typical of a tethered-cell experiment, and with a proton gradient of 2.5 pH units, actual coupling ratios of these motors would be 11, 17, 4, 2.7, 10, 12, 2.6, and 60 protons per step.

Measurements of motor speed under light load also display an approximately linear dependence on Δp (29). Gabel and Berg suggest that this linearity might be due to a proton channel with ohmic resistance acting in series with the force-generating transducer (29). The finite conductance of the channel(s) leading to Asp32 might be a factor limiting motor speed, but here we sought to determine whether the flexible stoichiometry transducer is sufficient to give a linear speed-vs.-Δp relation. Speed at a fairly small load (corresponding to the 0.4 μm beads used in ref. 29), and torque at high load, were computed for various values of the proton gradient, and are plotted against each other in Fig. 4. This treatment of the data reflects the approach used in the experiments, which measured the rotation speeds of lightly loaded and heavily loaded motors on the same cell, then used the torque of the heavily loaded motors as a proxy for relative Δp (29). For certain parameterizations (which prove to be the ones that also satisfy the constraints on curve shape and isotope effect), a nearly linear relation is seen between speed and relative Δp (Fig. 4). Low pKs make the curve flatter at low values of Δp (Fig. 4C), whereas slow proton transfer or the absence of a power stroke (ΔpK = 0) causes flattening at high Δp (Fig. S4). An approximately linear relation is also seen for the tightly coupled one-proton motor (Fig. S4). The two-proton motor shows larger deviations from linearity, with its speed dropping more sharply as Δp is decreased from the maximum (Fig. 4; additional examples in Fig. S4). Calculations of proton flux indicate that the variable stoichiometry motor responds to a decrease in Δp by using significantly fewer protons per step (Fig. 4 A−C, Lower, and Fig. S4).

Fig. 4.

Relationship between speed at light load and relative protonmotive force (Δp, as inferred from torque at high load). (A−C) (Upper) Curves for the flexible stoichiometry motor, using the parameters of Fig. 3 A−C. The speed at fairly light viscous load [that of 0.4-μm-diameter beads in water (29)]. is plotted against the torque at high load [used here as a proxy for relative protonmotive force (29)]. (Lower) The proton coupling ratio. As Δp decreases, the flexible motor uses fewer protons per step. (D−F) Speed vs. Δp curves for the tightly coupled two-proton motor, using the same parameters. (A and D) Standard, (B and E) high pK, and (C and F) low pK. (The coupling ratio of this motor is exactly two by construction.)

Temperature.

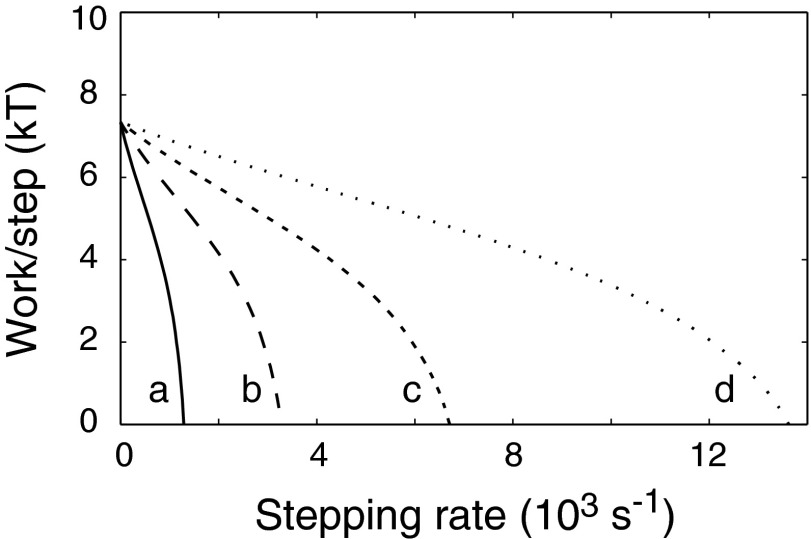
The near constancy of stall torque with temperature is a distinctive feature of flagellar motor physiology that has been taken to indicate an essentially reversible, and thus tightly coupled, mechanism (26). Temperature would be expected to affect rates of both proton transfer and conformational change. To model the effects of temperature, rate constants for conformational change and proton transfer were varied over ca. 10-fold ranges, and stall torques and zero-load speeds were computed. Although the zero-load speeds varied by more than a factor of 10 (mainly tracking stepping rates), stall torques remained the same within 3% (Fig. 5 and Table S3). The near invariance of torque belies large differences in the underlying action: When rotating at 10 Hz (a speed typical of tethered cells), the motors described by these parameter sets would be using between 3.5 and 21 protons per step (Table S3).

Fig. 5.

Insensitivity of torque at high load to rates of proton transfer and stepping. ΔpH = 2.5, pK_I = 7.1, pK_II = 5.4 for all simulations. Other parameters: (a) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10^11.5 M⁻¹⋅s⁻¹, k_step = 2 × 10³ s⁻¹; (b) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹² M⁻¹⋅s⁻¹, k_step = 5 × 10³ s⁻¹; (c) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10^12.5 M⁻¹⋅s⁻¹, k_step = 10⁴ s⁻¹; and (d) ${\mathrm{k}}_{{\mathrm{H}}^{+}}$= 10¹³ M⁻¹⋅s⁻¹, k_step = 2 × 10⁴ s⁻¹. At a rotation rate of 10 Hz (typical of a tethered-cell experiment), motors a−d would use 3.6, 6.4, 11, and 21 protons per step, respectively. Values of stall torque and zero-load speed for these and additional parameter sets are listed in Table S3.

Discussion

The present model was developed to explore the mechanistic implications of the dual-channel architecture of the stator, a feature that was proposed several years ago (22) but whose implications have remained largely unexplored. Loose coupling was not introduced as a prerequisite of the model but arises as a consequence of making the simplest assumption about the behavior of the stator: In the absence of specific ad hoc restrictions on which conformational changes are permissible, a dual-ion energy transducer will be loosely coupled because it can undergo a power stroke when bound to either one or two ions. Simulations show that such a loosely coupled model, described with just four parameters (five if the Δψ partitioning is included), can give a satisfactory account of the physiological properties of the motor. Specifically, it predicts (i) a very nearly linear relation between stall torque and protonmotive force (Fig. 3); (ii) a nearly linear relation between low-load speed and high-load torque (a proxy for Δp) (Fig. 4); (iii) the observed temperature and isotope effects (Fig. 5 and Fig. S3); (iv) the general shape of the torque-vs.-speed curve (Fig. 2 and Fig. S2); and (v) the magnitude of the torque at high load, which would correspond to a stoichiometry of about 1.42 protons per step in a tightly coupled model based on 26 steps/revolution (Fig. 2) (31). Thus, properties that have been taken to indicate tight coupling can be accounted for as readily in a loosely coupled mechanism. Importantly, the mechanism does not involve any additional complexity beyond what is already implicit in the dual-channel architecture of the stator, and its important properties (e.g., linear dependences on Δp) are preserved over a wide range of parameterizations.

In pioneering modeling studies, Oosawa and coworkers suggested that loose coupling might be necessary to account for the smooth rotation of the motor at small values of Δp where the energy per proton is less than the thermal energy kT (48). Tightly coupled models were subsequently shown to be capable of reproducing this smoothness, however, and thus remained in favor. Loose coupling has the potential disadvantage of allowing purely energy-dissipating processes (in Fig. 1, a cycle through states 2-3-4-5-2 that allows proton translocation uncoupled to any net rotation). At the loads relevant to a swimming cell, however, the single-ion pathway is predicted to act mainly in the forward direction to augment the speed of the motor, rather than allowing substantial backward slippage (Fig. 2). Further, the ability of the motor to sense increased load and to respond by incorporating additional stator complexes (49) would tend to maintain the operating point in the relatively high-speed region where back-slippage is minimized. Under suboptimal conditions such as diminished energy supply, lowered temperature, or more shallow load lines (appropriate to partially grown or broken filaments), the flexible stoichiometry transducer is predicted to be especially advantagous, stepping even faster relative to the two-proton transducer while also, especially in the case of decreased Δp, using fewer ions.

Natural selection has presumably operated to maximize swimming speed under the most pertinent conditions of load and energy supply. A stator with two ion-binding sites appears clearly better than one with just a single site; the single-proton transducer is predicted to be competitive only when loads are very light and intrinsic stepping rates are relatively fast (Fig. 2 and Fig. S2). We suggest that the optimal solution is the two-site, flexible transducer, because evolution could operate on its relevant properties (mainly the pKs) to balance the benefits of single-ion operation (fuel economy, speed at low Δp or low temperature) against the costs of slippage (some wasted ions under certain circumstances). A corollary is that stators of various species may exhibit differing pK values, reflecting their evolution under different circumstances and selective pressures. This might allow experimental test of the flexible stoichiometry hypothesis. Stators with different pK values, obtained either from different species or by mutation, may be found to produce different torques even when present in the same motor (in a resurrection experiment with tethered cells, for example).

Direct measurements of ion flux through the motor have not been made. In one study, motor-dependent flux was inferred from changes in proton flow that occurred on stalling the motors of a motile Streptococcus species with antiflagellin antibody. Results indicated an approximately constant proportionality between proton flow and motor rotation rate, as the rate varied with changing temperature, solvent isotope, or Δp (45). Simulations indicate that the flexible stoichiometry motor can depart somewhat from this proportionality when speed is varied by changes in Δp (Fig. 4 and Fig. S4); nevertheless, given the range of Δp that was examined and the uncertainty in the measurements, the results in Streptococcus appear consistent with the loosely coupled model here.

The present treatment of proton movements, as taking place directly to and from bulk solution, is likely an oversimplification. Most arriving protons will be carried on buffer molecules, and their entry into the channel is likely to be facilitated by proton-binding groups around the channel mouth. Proton dissociation from Asp32 is also likely to be accelerated by transfer to specific neighboring groups, to enable the observed high rates of rotation [which would correspond, in some cases (30), to proton flux in excess of 300,000 s⁻¹ per motor). This very rapid, localized drainage of protons from the periplasm must be compensated by the action of electron-transport-driven proton pumps, some nearby (50) but the majority clustered in large patches that have been termed “respirazones” (51). Diffusional transport from the respirazones to the motor would entail some resistive free-energy loss and an accompanying reduction in the Δp actually applied at the transducer. In this case, the performance advantage of the flexible transducer at submaximal Δp (Fig. 2C) might be important even when the nominal (bulk) Δp is near its maximum.

In summary, the present analysis indicates that a motor mechanism formulated around a loose-coupling principle can account for the known properties of the flagellar motor and that loose coupling, rather than being detrimental, could enhance motor performance under a number of physiologically relevant conditions. Comparative studies of stators from different species or mutational analyses designed to manipulate stator pKs might provide experimental tests of the proposal.

Materials and Methods

Linear differential equations describing the reaction network in Fig. 1 were solved for steady state by Guassian elimination, and the resulting formulas were entered directly in the data-plotting program Kaleidograph. Relative probabilities of each intermediate at steady state were used to compute rates of stepping and of proton transfer. Alternatively, differential equations describing the reaction network were programmed in R and run numerically until steady state was reached. Simulations in R shared a core set of instructions using the deSolve package. Steady-state concentration distributions were again used to compute rates of stepping and proton transfer. In both cases (analytical or numerical solution), the analysis was done for the full reaction network with all transitions allowed (the flexible transducer) and also for tightly coupled one- or two-proton versions. In the one-proton transducer, association of a second proton was disallowed; in the two-proton transducer, the conformational change of the singly protonated state was disallowed.

The protonmotive force was treated as a ΔpH imposed at the Asp32 site. External and internal pH values at full energization (ΔpH = 2.5 units) were 7.9 and 5.4, based on the assumption that there is an actual bulk pH gradient of 0.5 units (pH_ext 7.0, pH_int 7.5) and a Δψ [magnitude (2.303)(2)(RT/F, with R the gas constant, T temperature, and F the Faraday constant)] partitioned 80:20 between the exterior and interior. The fully deenergized state was assumed to have pH_ext = pH_int = 7, and pH_ext and pH_int at intermediate states of energization (ΔpH = 0.5, 1.0, 1.5, 2.0) were obtained by linear interpolation.