Microstructural Parameter-Based Modeling for Transport Properties of Collagen Matrices

Short abstract

Recent advances in modulating collagen building blocks enable the design and control of the microstructure and functional properties of collagen matrices for tissue engineering and regenerative medicine. However, this is typically achieved by iterative experimentations and that process can be substantially shortened by computational predictions. Computational efforts to correlate the microstructure of fibrous and/or nonfibrous scaffolds to their functionality such as mechanical or transport properties have been reported, but the predictability is still significantly limited due to the intrinsic complexity of fibrous/nonfibrous networks. In this study, a new computational method is developed to predict two transport properties, permeability and diffusivity, based on a microstructural parameter, the specific number of interfibril branching points (or branching points). This method consists of the reconstruction of a three-dimensional (3D) fibrous matrix structure based on branching points and the computation of fluid velocity and solute displacement to predict permeability and diffusivity. The computational results are compared with experimental measurements of collagen gels. The computed permeability was slightly lower than the measured experimental values, but diffusivity agreed well. The results are further discussed by comparing them with empirical correlations in the literature for the implication for predictive engineering of collagen matrices for tissue engineering applications.

Introduction

Type I collagen, as a natural polymer, is the major structural and mechanical component of the extracellular matrix (ECM) of tissues and organs. As such it is an ideal starting material for next generation tissue-engineered medical products and regenerative medicine strategies. Since many tissue properties are related to the hierarchical design and collagen fibril microstructure of the ECM, research efforts have been focused on how to modulate collagen building blocks to engineer collagen matrices with desired functional properties [1–5]. Relevant functional properties generally include: mechanical properties (e.g., elastic modulus and ultimate strength) and transport properties (e.g., hydraulic permeability and solute diffusivity). However, most of these studies have been performed via iterative experimentations. A computational model capable of predicting functional properties from the structural characteristics of the collagen matrices can significantly accelerate this procedure and ultimately realize the successful design of functional collagen matrices for tissue engineering and regenerative medicine.

So far the majority of structure–function relationships as they relate to engineered tissue constructs have been developed through empirical measurements and subsequent phenomenological curve-fittings. The main structural parameters used to modulate mechanical or transport properties typically include polymer concentration or fibril density, porosity, pore size, pore shape, pore interconnectivity, and compressive strain. It has been widely known that low collagen concentration results in increased transport properties such as permeability [6,7] and diffusivity [6,8–10]. However, at the same time, it decreases mechanical properties such as compressive modulus [2,7]. Other studies showed that the pore size or porosity of the collagen matrix was also correlated to permeability [11,12] and mechanical properties [13,14].

Recently, computational efforts to correlate the microstructure of fibrous and/or nonfibrous scaffolds to mechanical properties have been reported [9,15–19]. Computational modeling of these scaffolds offers a competitive advantage over using empirical studies alone by incorporating additional adjustable parameters (e.g., fibril diameter and fibril arrangement) that specify specific microstructural elements that contribute to macrolevel physical properties. However, most of these studies have used simplified shape, arrangement, or isotropic orientation as the basis for their models without any additional characterization of the 3D collagen network. Recently, Stylianopoulos et al. developed the random growth algorithm [20,21] to create a model of collagen networks for permeability calculations [22]. In these studies, they characterized anisotropic random networks using the second-order orientation tensor. Another study also employed the same algorithm to develop a mathematical model of diffusion with varying fiber structures in collagen gels and tumors [23].

In spite of recent efforts to establish quantitative structure–function relationships for 3D engineered biomaterials, the predictability of functional properties from microstructural parameters is still significantly limited. This is mainly due to the emerging of various novel biomaterials for tissue engineering and to the difficulty of identifying and quantifying their microstructural characteristics. These parameters include fiber/fibril structure, arrangement, and intermolecular crosslinks [24,25].

So far, it has been known that transport properties are determined by the compounding effects of various factors such as porosity, pore size/shape, fibril density, fibril size/shape, matrix composition, matrix orientation, and fibril interconnectivity [22,26–28]. For example, even though the matrix porosity is similar, the permeability can be different according to the fiber orientation [26]. Recently, studies showed that the branching point, one of the characteristics that distinguish monomer from oligomer, is another parameter affecting transport and mechanical properties [24,25]. It was observed that even though the porosity was similar by modulation of different fibril diameters and branching points, the resulting values differed with the different numbers of the branching points. Thus for experimental or computational design, the contributions between matrix porosity and branching points need to be dealt with separately.

In this study, a new computational model was developed capable of predicting functional properties of 3D collagen matrices based on their microstructural characteristics. We employed branching points, as a measure of collagen microstructure [25], since the branching points can be independently controlled while keeping the porosity and fibril diameters constant. As reported previously [24,25], mechanical properties, i.e., storage modulus, could be changed by varying the ratio of monomer to oligomer, and ultimately stem cell differentiation can be guided. In addition, an increase in oligomer content results in a higher number of branching points per total fibril length but it also results in lower segment length. The present computational framework incorporates quantifiable microstructural characteristics of self-assembled 3D collagen matrices to predict and estimate matrix transport properties. To validate the computational model, collagen gels with varying microstructure were constructed and fibril microstructures were analyzed by confocal microscopy. Then, the 3D collagen matrices were constructed by either: (i) 3D reconstruction of the confocal microscopy images, named as the image-based method or (ii) prediction from the specific number of branching points, which is named the parameter-based method. After construction of the matrices, finite element analysis (FEA) was performed to calculate hydraulic permeability and diffusivity. The predicted results were compared with experimental measurements and also with available structure–functionality relations in the literature.

Computational Method

Figure 1(a) shows a flow chart of the 3D image-based reconstruction modeling process from image acquisition to computational analysis of permeability and diffusivity. First, fibril microstructures were visualized and quantified from collecting confocal image stacks as reported in the previous studies [24,25]. Geometric information from confocal microscopy and Imaris was exported to a 3D cad program (PTC Creo parametric 2.0) for reconstruction of a collagen matrix model as shown in Fig. 1(b). Then, unstructured-tetrahedral fine meshes smaller than the size of fibril diameter were employed as shown in Fig. 1(c). Finally, permeability and diffusivity were estimated using the FEA (ansys 14.0)

Fig. 1.

Schematic illustrations of the image-based reconstruction. (a) Flow chart for model reconstruction, permeability, and diffusivity calculations: confocal image acquisition (confocal reflectance/fluorescence microscopy), data acquisition (Imaris Filament Tracer), 3D reconstruction (PTC Creo parametric 2.0), mesh generation (icem-cfd, ansys 14.0), and FEA to determine permeability and diffusivity values. (b) Image-based reconstruction of monomer matrix. (c) Representative mesh generation of monomer matrix.

Figure 2(a) shows a concept for the “microstructural parameter-based reconstruction” portion of the computational model based on branching points as the key input parameter. First, branching points, obtained from experimental measurements for matrices prepared with oligomer:monomer ratios of 100:0, 50:50, and 0:100, were randomly generated in a domain. Each point was then connected to its two closest neighboring points to form a fibril using a two neighboring point connection (TNPC) algorithm. The main characteristic of the TNPC algorithm is that one point has at least two connections with other points in the vicinity as shown in Fig. 2(b). The resulting fibril network structures representing oligomer:monomer ratios of 0:100, 50:50, and 100:0, generated by the microstructure parameter-based reconstruction, were distinct from one other as shown in Fig. 3. The resulting geometric information then was exported to ansys-icem cfd to construct cylindrical fibrils with a diameter size of 400 nm which was measured on a confocal microscopy image [25]. Recently, it was found that confocal microscopy tends to overestimate the size of an object compared to scanning electron microscopy (SEM) [29]. Thus, we also utilized 100 nm-sized diameter measured by SEM for monomer matrix (type I rat tail collagen) as reported in the other studies [30]. Figure 2(c) shows a close-up image of 3D fibril network with 100 nm diameter obtained from the parameter-based model. Since fibrils are connected via branching points, the model yields connections that appear to be in a bent configuration (Fig. 2(d)) [30]. Thus, the parameter-based model mimics the tortuous collagen fibrils as shown in many SEM images.

Fig. 2.

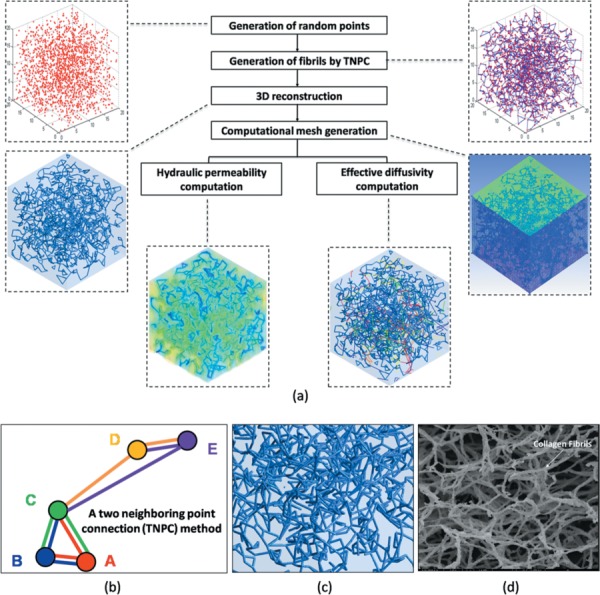
Schematic illustrations of the parameter-based reconstruction. (a) Flow chart for model reconstruction, permeability, and diffusivity calculations: generation of random points (experimental data), generation of fibrils and 3D reconstruction (TNPC algorithm), computational mesh generation, and FEA to determine permeability and diffusivity values. (b) TNPC method which connects each point with its two closest neighboring points to form a fibril. (c) Close-up image of 3D fibril network with 100 nm diameter fibril. (d) SEM image of rat tail collagen [30].

Fig. 3.

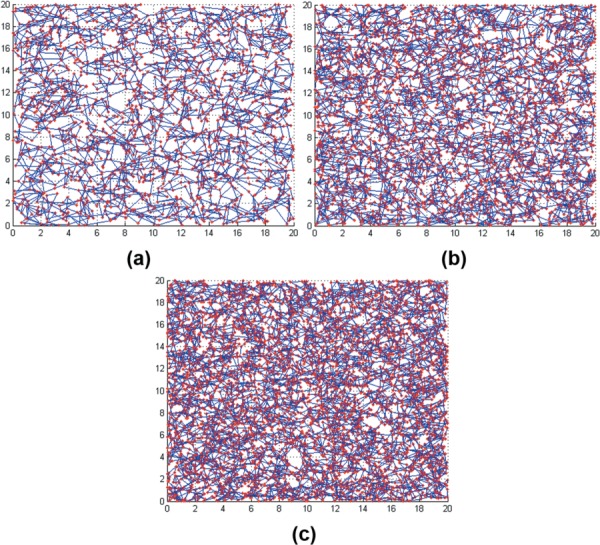
Collagen networks generated by the parameter-based method (top-view). There is a clear difference in microstructure among 0:100, 50:50, and 100:0 ratios.

Calculations of permeability (fluid flow) and diffusivity (particle transport) were carried out separately. First, to characterize the creeping flow within porous media (e.g., biological tissue), Darcy's law was used to determine hydraulic permeability [22,31]

$$k=\frac{U\mu L}{\Delta p}$$ (1)

where U, k, μ, Δp, and L are the average velocity in the fluid domain, hydraulic permeability, dynamic viscosity, pressure difference, and thickness of the collagen matrix, respectively. The two equations were used to describe fluid motion, mass and momentum conservation with assumptions of an incompressible fluid, no body force, and steady state. The governing equations are as follows:

$$\nabla ·\mathbf{u}=0$$ (2)

$$\mathbf{u}·\nabla \mathbf{u}=-\nabla p+\mu {\nabla }^2\mathbf{u}$$ (3)

where u, p, and μ are the fluid velocity field with components (u, v, w), pressure, and dynamic viscosity, respectively.

Diffusivity can be calculated using the following relation [32]:

$$〈\Delta r^2〉=2d·D·\Delta t$$ (4)

where $〈\Delta r^2〉$ is mean square displacement (MSD), d is dimension (here d = 3), D is the effective diffusivity, and Δt is the time step. Here, the MSD of particles can be estimated by simulating the random motion of particles within the matrices. To mimic particle random motion, a particle transport equation was solved by taking two forces into consideration: drag force and Brownian force. The particle transport equation used in this study is given by [33]

$$m_{\mathrm{p}}\frac{d{\mathbf{V}}_{\mathbf{p}}}{\mathit{dt}}=\frac{1}{8}\pi {\rho }_{\mathrm{f}}{d}_{\mathrm{p}}^2{C}_D|{\mathbf{V}}_{\mathbf{f}}-{\mathbf{V}}_{\mathbf{p}}|({\mathbf{V}}_{\mathbf{f}}-{\mathbf{V}}_{\mathbf{p}})+\mathbf{G}\sqrt{\frac{6\pi d_{\mathrm{p}}\mu k_{\mathrm{B}}T}{\Delta t}}$$ (5)

where m _p, d _p, V_p, ρ _f, C_D, V_f, G, μ, k _B, T, and Δt are the particle mass, particle diameter, particle velocity, fluid density, particle drag coefficient, fluid velocity, Gaussian random number with zero mean and unit variance, dynamic viscosity, Boltzmann constant, absolute temperature, and time step, respectively. Table 1 shows the values of several significant parameters used. The first and second terms on the right—hand side show the drag force and the Brownian force. The drag force term in Eq. (5) can be reduced to the Stokes drag force for the behavior of a spherical particle in creeping flow. Brownian force was added by using a fortran code. C_D was obtained using the Schiller–Naumann correlation for a spherical particle as follows:

Table 1.

Parameters used for diffusivity calculation of 0:100, 50:50, and 100:0 ratios in this study

Parameter	Dimension
Particle mass (m p)	5.56 × 10−22 (kg)
Particle diameter (d p)	10.2 (nm)
Fluid density (ρ f)	1000 (kg/m3)
Fluid dynamic viscosity (μ)	1.002 × 10−3 (Pa s)
Boltzmann constant (k B)	1.38 × 10−23 (m2 kg·s−2 K−1)
Temperature (T)	293 (K)

$$C_D=\frac{24}{{\mathrm{Re}}_{\mathrm{p}}}(1+0.15{\mathrm{Re}}_{\mathrm{p}}^{0.687})$$ (6)

where Re_p, the particle Reynolds number, is defined as

$${\mathrm{Re}}_{\mathrm{p}}=\frac{|{\mathbf{V}}_{\mathbf{f}}-{\mathbf{V}}_{\mathbf{p}}|d_{\mathrm{p}}}{\nu }$$ (7)

where ν is the kinematic viscosity, which is given by the dynamic viscosity, μ, divided by the fluid density, ρ.

For numerical accuracy, the grid dependency test was performed with three different meshes using the grid convergence index method based on Richardson extrapolation [34]. The relative error among the permeability values was within 3 ± 1.5% and a discretization error related to the extrapolated value was within 2.4 ± 1.4%. In addition, sensitivity tests were performed to determine the effects of random seeding on the permeability values by seeding the same number of random points in the domain three times. The variation in the permeability was found to be less than 4% of the averaged values. Besides, the sensitivity to other parameters was tested; these tests included effects of domain size, domain shape, and boundary conditions at the side surfaces (i.e., free-slip and periodic) on the permeability. The maximum relative error was within 5%.

The high resolution discretization scheme with second-order accuracy was used for the convective terms based on the boundedness principles used by Barth and Jesperson [35]. Total central processing unit time per model was dependent on the models and equations ranging from 1 to 7 h. Root mean square residuals indicating local discrepancy of conservation equation per control volume were employed for the convergence with the criteria set to 10⁻⁴–10⁻⁶.

Materials and Methods

All type I collagens were derived from the dermis of market weight pigs. The preparation procedure of monomeric and oligomeric collagens was described previously [3,25,36]. Briefly, purified oligomer and monomer collagens were lyophilized from 0.1 M acetic acid solutions then dissolved in 0.01 N hydrochloric acid (HCl). Collagen concentration was determined using a Sirius Red (Direct Red 80) assay as previously described [36] and all collagen formulations were standardized based upon purity and polymerization potential. Finally, by mixing these purified monomers and oligomers properly, matrices with different oligomer:monomer ratios are generated (e.g., 50:50 is generated by mixing monomers and oligomers in a 1:1 ratio).

All collagen formulations were polymerized under identical reaction conditions to produce 3D matrices as described previously [3]. Neutralized collagen solutions were kept on ice prior to the induction of polymerization by warming to 37 °C. All collagen matrices were polymerized at the desired collagen concentration (1.5 mg/ml) and oligomer to monomer ratios (0:100, 50:50, and 100:0) in Lab-Tek chambered coverglass slides (Nunc, Thermo Fisher Scientific, Rochester, NY) and prepared for immunostaining as described previously [25].

In order to obtain the diffusivity within the collagen scaffolds with 1.5 mg/ml, an integrative optical imaging (IOI) experiment was performed using four different types of FITC-labeled dextrans, 4 kDa (hydrodynamic radius = 1.3 nm), 10 kDa (2.1 nm), 40 kDa (5.1 nm), and 500 kDa (12.6 nm). The details for IOI have already been reported in the other studies [37,38]. Each experimental group was repeated at least three times (n ≥ 3). One-way ANOVA was performed for statistical analysis, and the differences were considered statistically significant when p < 0.05. Results are presented in a range of the mean ± one standard deviation.

Results

Confocal microscopy images of monomer (oligomer:monomer = 0:100) and oligomer (100:0) matrices, which demonstrate clear differences in collagen fibril microstructure, were obtained in the previous study [24]. These images show monomer matrices with long, entangled fibrils, whereas oligomer matrices show more branched-fibril networks. Moreover, the images suggest that monomer matrices have larger pore sizes than the oligomer matrix through image visualization. These visual observations are supported by estimations of porosity through image-based models and mean pore size through theoretical prediction. The average porosity of monomer matrices, 0.923 (which ranges 0.9–0.95), is higher than the average porosity of oligomer matrices, which measured at 0.845 (within a range of 0.79–0.9) (p < 0.05). This difference in porosity between matrices was also corroborated by previous studies which showed that oligomer matrices have higher fibril volume fractions (inverse of porosity) than monomer matrices [3,25].

Figure 1(b) shows a representative reconstructed monomer matrix using the image-based method. After computation, all velocity values in the domain were averaged, the average value was substituted into Eq. (1) for the permeability calculation. Average permeability for monomer matrices (7.67 × 10⁻¹³ m²) is significantly higher than oligomer (2.10 × 10⁻¹³ m²) (p < 0.05). Permeability for monomer matrices ranges from 7.0 × 10⁻¹³ m² to 9.5 × 10⁻¹³ m², whereas that for oligomer matrices ranges from 2.0 × 10⁻¹³ m² to 2.5 × 10⁻¹³ m². All permeability values obtained from the computational model are smaller than those measured experimentally; the experimental study yielded 3.1 × 10⁻¹² m² for monomer and 1.0 × 10⁻¹³ m² for oligomer [24]. However, regardless of whether permeability is determined experimentally or calculated through simulation, the permeability value for monomer matrices is consistently larger than that for oligomer matrices.

Figure 4 shows representative (a) velocity vectors and (b) a contour for permeability calculations. Computational analysis began with the assumption of a nonslip boundary condition of the fibril surface. The velocity magnitude on the fibril surface is zero (Fig. 4), and all velocity values were averaged for permeability calculations. Parameters that were used to describe matrices prepared at oligomer to monomer ratios of 0:100, 50:50, and 100:0 are summarized in Table 2. The critical parameter used to distinguish these three formulations is the interfibril branching point. 100:0 matrices exhibited the highest branching point density due to the high number of branching points within the matrix, followed by 50:50 and 0:100. In contrast, porosity and mean branch length decreased with increasing oligomer content.

Fig. 4.

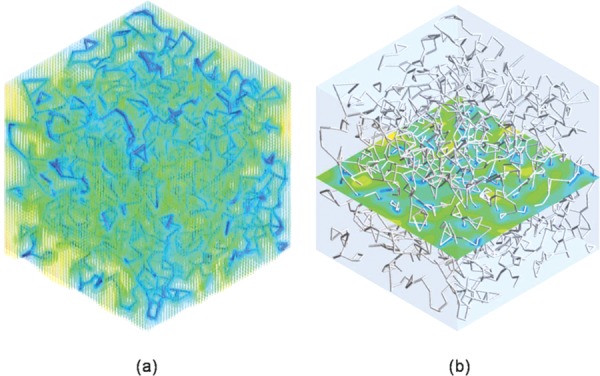
Representative computational results for permeability calculation (oligomer:monomer 0:100). (a) Velocity vectors. (b) Velocity contour. The fibril surface was assumed as having the nonslip boundary condition, and the velocity magnitude on the fibril surface is held at zero. All computed velocity values were averaged for permeability calculation.

Table 2.

Parameters used from the parameter-based models for matrices prepared with oligomer:monomer ratios of 100:0, 50:50, and 0:100

	Oligomer:monomer ratio
Parameter-based-model	100:0	50:50	0:100
Interfibril branching point	5120	3520	1920
Representative element volume (μm3)	20 × 20 × 20	20 × 20 × 20	20 × 20 × 20
Mean branching length (μm)	0.77	0.88	1.09
Porosity (D f = 400 nm)	0.786	0.823	0.873
Porosity (D f = 100 nm)	0.984	0.987	0.993
Image-based-model	100:0		0:100
Fluid domain volume (μm3)	50 × 50 × 5		50 × 50 × 5
Porosity	0.845		0.923

Figure 5 shows the permeability values obtained from parameter-based models, image-based models, other predictive models, and experiments. In order to be consistent with previously calculated microstructural property results, 400 nm diameter fibrils with a nonslip boundary condition were employed [25]. The permeability value for 0:100 is the highest at 2.06 × 10⁻¹³ m² followed by 50:50 at 9.44 × 10⁻¹⁴ m² and 0:100 at 7.00 × 10⁻¹⁴ m². The magnitude of difference between 0:100 and 100:0 is similar to that of the image-based models and experiment; with 0:100 permeability being ∼3 times higher than 100:0. However, as in the image-based model, the overall computed values were lower than the experimental data. Furthermore, the discrepancy between experiments and parameter-based models with 400 nm diameter fibril is larger than the difference observed between empirical data and image-based model predictions.

Fig. 5.

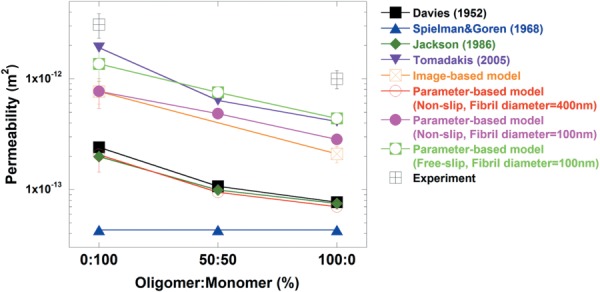
Comparison of permeability values generated from computational methods with different diameters (d = 100 nm and d = 400 nm), and predictive models for 0:100, 50:50, and 100:0, and previously conducted experiments for 0:100 and 100:0 [24]. Computational and predicted values are lower than experimental values. The developed models (image- and parameter-based) generated values closer to the experimental data than other predictive models.

One potential explanation for lower permeability values calculated from the parameter-based models is the possibility of an overestimated fibril diameter (400 nm) and the corresponding lower porosity, compared to the true fibril conditions. During the quantification of microstructural parameters from the confocal reflectance microscopy images, a specific threshold value was used to extract fluorescent and reflectance intensity of collagen fibrils. During this process, the chosen threshold may have been at a level that yielded overestimations for fibril diameters. Recently, it has been found that a feature size measured by a laser scanning confocal microscopy tends to be relatively high [29]. In addition, this study showed that other imaging techniques, such as the SEM, produce more accurate feature size or diameter. Along those lines, we recently measured the fibril diameter of rat tail collagen (monomer-based collagen) as 101.6 nm using SEM [30]. Based on those results, an additional group with 100 nm-sized diameters was included to the parameter-based model to examine the effect of fibril diameter on permeability. The smaller diameter measurement resulted in porosity values for 0:100, 50:50, and 100:0 increased to 0.993, 0.987, and 0.984, respectively (Table 2). These values are more similar to the porosity (∼0.98–0.99) obtained from direct calculation of 1.5 mg/ml collagen matrices or reported in other studies [7,39]. Permeability values also increased for each matrix (7.72 × 10⁻¹³ m² for 0:100, 4.84 × 10⁻¹³ m² for 50:50, and 2.83 × 10⁻¹³ m² for 100:0) at 100 nm fibril diameter compared to 400 nm (p < 0.05). However, these values remain approximately four times lower than the experimental data.

Lower computational results could also be attributed to inaccurate assumptions made concerning the fibril surface. In reality, fluid might slip on the surface of the fibril due to fibril diameter values that fall on the nanoscale. Therefore, a free-slip boundary condition was also tested. Under free-slip conditions, permeability values for each model increase to 1.36 × 10⁻¹² m² for 0:100, 7.51 × 10⁻¹³ m² for 50:50, and 4.39 × 10⁻¹³ m² for 100:0 (Fig. 5). This change to a free-slip surface condition resulted in model-predicted permeability values that were only twofold lower than experimental results, compared to a fourfold difference observed under the nonslip condition.

The effective diffusivity of four different-sized FITC-labeled dextrans (4, 10, 40, and 500 kDa) was measured within each collagen matrix. An effect of molecular size on the diffusivity was observed for monomer and oligomer matrices as shown in Fig. 6. However, there is no significant difference between the observed diffusivity of the two formulations (p > 0.05), except at 500 kDa (p < 0.05 but the difference is very small). This observation supports the previous work that suggested that matrix diffusivity is not affected by microstructural contents, particularly at low collagen concentration (∼1 mg/ml) [24].

Fig. 6.

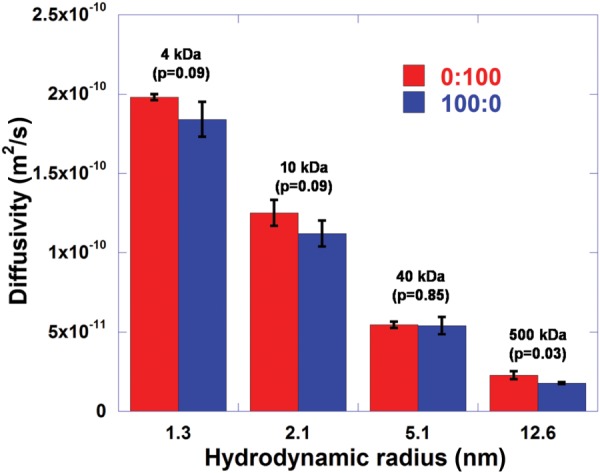
Diffusivity values of FITC-labeled dextran with four different sizes (4 kDa, 10 kDa, 40 kDa, and 500 kDa) for 0:100 and 100:0. The effect of molecular size on the diffusivity is clearly observed for both 0:100 and 100:0. However, there is no significance difference between the two formulations (p > 0.05), except for 500 kDa (p < 0.05).

Figure 7(a) shows a representative image of Brownian motion of 40 kDa particles in the parameter-based monomer collagen network. Particles move randomly within the void space within the matrix and occasionally collide with the fibril surface. For diffusivity calculations, particle displacement was first extracted as shown in Fig. 7(b). This graph shows a typical Gaussian distribution for all models, but there seems to be no notable difference in displacement frequency among 0:100, 50:50, and 100:0. This trend was reflected in the diffusivity values obtained from each model. As in the experimental results, the average diffusivity values determined from the model for 0:100, 50:50, and 100:0 were similar to one another as shown in Fig. 8. Results from the image-based model were also similar.

Fig. 7.

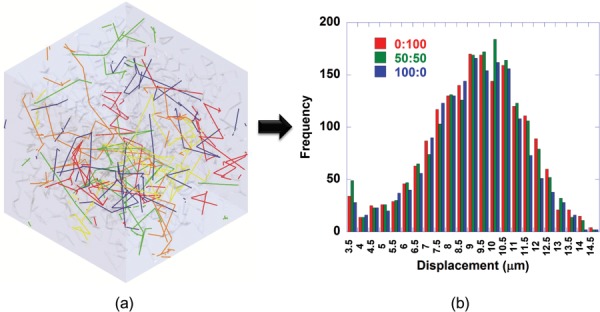
Representative results for diffusivity calculation of 40 kDa dextran using the parameter-based model. (a) Particle random motion (0:100). (b) Particle displacement distribution (0:100, 50:50, and 100:0). All matrices show a typical Gaussian distribution of particle displacements with no notable difference in displacement frequency among 0:100, 50:50, and 100:0.

Fig. 8.

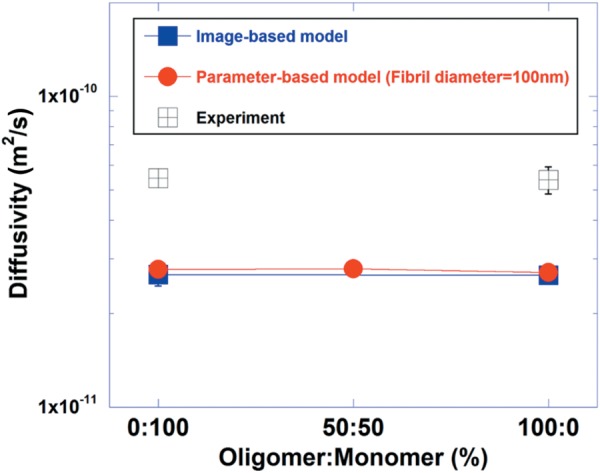
Diffusivity values obtained by computational methods (image-based model and parameter-based models) and IOI experiments. No significant differences were noted between the diffusivity values among 0:100, 50:50, and 100:0. Experimental values are approximately twice higher than computational values.

Similar to what was observed from permeability measurements, there is a slight discrepancy in diffusivities determined from experimental and computational methods. The diffusivity values determined from IOI experiment are approximately twofold higher than what was obtained from parameter- and image-based models formulations (0:100, 50:50, and 100:0). This result could be attributed to the assumption about the rigidity of particles. In this study, particles were assumed to be rigid bodies that do not transform, even though they collide with fibrils or other particles. In reality, the dextran particles, a kind of polymer, might be flexible enough to move more quickly when encountering a barrier such as fibrils or other particles. Studies have shown that a flexible object tends to diffuse more rapidly than a rigid one. For example, the flexible polyethylene glycol (PEG) probe diffused more rapidly compared to the rigid dendrimer probe with a corresponding hydrodynamic radius [40]. In addition, uncertainty or gap between real particle movement and the exact solution from the particle transport equation might contribute to the difference.

Discussion

Capability of designing biomaterials and scaffolds with desired functional properties can significantly advance tissue engineering. Various computational models and empirical correlations have been proposed, but most of the available computational and empirical models predict the functional properties based on fibers or fibrils with specific shapes, where these are mostly a bundle of cylinders and do not consider the microstructural characteristics of realistic collagen networks [22,26]. However, collagen matrices have extremely complex microstructures with high degrees of entanglements and branching. The complexities of these matrices can lead to difficulties when attempting to approximate the microstructure with simple array configurations, thus limiting the ability to precisely design biomaterials with desired transport properties of fluid and solutes including proteins, soluble factors, and drugs.

The present computational models address these limitations by incorporating key design parameters of collagen matrices—collagen content and branching points, to accurately reconstruct 3D fibrous microstructures and predict subsequent transport properties. These design parameters can be easily quantified as described previously [24,25], so that a library of relevant parameters can be created for different types of fibrous scaffold materials. These parameters, then, are readily available to be used to design new engineered matrices with desired transport properties without the need for further empirical characterization of their microstructural and bulk physical properties.

Although the computed properties in the present study were closer to the measured values than previous studies, the computed permeability generally underestimates the measured data. One possible reason is the assumption of a nonslip boundary condition on the fibril surface. Since the fibril diameter is on the nanometer scale (∼100 nm), it is similar in magnitude to the mean free path of the molecules (65 nm for air and <65 nm for water), and fluid might slip on the fibril surface [41]. To validate this hypothesis, a free-slip boundary condition was applied to the fibril surface. As a result, all permeability values for 0:100 (1.36 × 10⁻¹² m²), 50:50 (7.51 × 10⁻¹³ m²), and 100:0 (4.39 × 10⁻¹³ m²) increased by a factor of two compared to the nonslip condition but remained two times lower than experimental data (Fig. 5). Another possible reason for this occurrence is the assumption that the collagen fibril is an impermeable solid, which neglects the details of molecular level structure, particularly molecular level porosity. In general, collagen is a complex protein with a hierarchical structure consisting of several subunits. Its basic unit consists of three polypeptide chains (two α1 and one α2) that assemble in a helical configuration to a procollagen molecule within the cell during collagen biosynthesis. Upon extrusion to the extracellular space and after undergoing enzymatic modifications, the now tropocollagen molecules interact to form microfibrils and then in sequence to form higher order fibrils. Ultimately, bundles of fibrils give rise to the formation of fiber or fiber bundles that are considered to be the maximum unit of collagen [5,42,43]. Due to the hierarchical structure of collagen, several experiments have been carried out to measure the porosity of fibrils or fibers. Sanjeevi et al. confirmed through moisture adsorption methods that collagen fibers have pores with radii ranging from 5.5 nm to 7.5 nm [44]. Boki et al. showed that maximum radius of micropores in raw collagen fibers is less than 2 nm using the nitrogen adsorption method [45]. Other groups have sought to perform molecular level analyses of collagen. Buehler et al. performed mechanical analysis of collagen fibers in order to relate molecular level mechanical properties to those of the entire material system [5,46]. This suggests that additional aspects must be taken into account when performing mechanical analyses at a smaller scale compared to larger scale analysis. For example, they found that splitting a fiber into fibrils or molecules increases surface area which in turn leads to increased chain mobility or diffusion.

Recently, several studies developed a computational model of the single mineralized collagen microfibril as a porous structure, composed of tropocollagen, mineral, and noncollagenous components, to investigate the relationship between the structure and the mechanical behavior using the finite element method [47–49]. Results showed that some mechanical properties (e.g., elastic modulus) significantly differed between single fibrils with and without extra-collagenous components. In contrast, the fibril used in this study for the numerical analysis was assumed to be a solid body which is not permeable to the fluid. We expect that the porosity of the collagen structure is a significant factor contributing to those higher transport values we observed experimentally. To the best of our knowledge, there has been no analysis or direct measurement of any transport property such as permeability at the molecular level. However, if the relationship trend observed by Buehler and other studies holds for transport, then we may expect transport properties of collagen on the molecular level to differ compared to the macro level, thus providing insight into the source of the discrepancy in permeability values observed between the simulation and the experiment.

Table 3 summarizes several permeability predictions for 3D collagen networks that take into account parameters such as porosity, fibril radius, and/or diameter. Furthermore, Fig. 5 shows permeability values generated by various researchers, including the values generated by model simulations and experiments in the present study. Overall, computational and predicted results are lower than experimental results. Our image-based and parameter-based models yielded values that were closer to experiment data than other prediction models, and within the same order of magnitude. In particular, the values, generated from parameter-based model with a free-slip condition and Tomadakis's prediction, are closest to the experiment values. From these observations, we can conclude with reasonable certainty that the parameter-based model developed in the current study is a reliable method to predict permeability values within 3D collagen matrices.

Table 3.

Predictive models for permeability calculation in 3D fibril networks

Author	Correlation	Comment
Davies [50]	$k/r_{\mathrm{f}}^2={[16(1-\phi ){}^{1.5}(1+56(1-\phi ){}^3)]}^{-1}$	$r_{\mathrm{f}}$: Fibril radius $\phi$: Porosity
Spielman and Goren [51]	$1/3+5/6[\sqrt{k}{K}_1(r_{\mathrm{f}}/\sqrt{k})/r_{\mathrm{f}}{K}_0(r_{\mathrm{f}}/\sqrt{k})]=1/4(1-\phi )$	$r_{\mathrm{f}}$: Fibril radius $\phi$: Porosity $K_{\mathrm{p}}$: Modified Bessel function of the second kind with order p
Jackson and James [52]	$k/r_{\mathrm{f}}^2=(3/20(1-\phi ))(-\ln (1-\phi )-0.931)$	$r_{\mathrm{f}}$: Fibril radius $\phi$: Porosity
Tomadakis and Robertson [18]	$k/r_{\mathrm{f}}^2=(\phi /8\ln {}^2\phi )((\phi -{\phi }_{\mathrm{p}}){}^{\alpha +2}/(1-{\phi }_{\mathrm{p}}){}^{\alpha }{[(\alpha +1)\phi -{\phi }_{\mathrm{p}}]}^2)$	$r_{\mathrm{f}}$: Fibril radius $\phi$: Porosity ${\phi }_{\mathrm{p}}$: Percolation threshold (0.037 for 3D) $\alpha$: Constant (0.661 for 3D)

Measured diffusivity values show almost no difference between 0:100 and 100:0. One possible theory to explain the similarity between the two matrices is that the pore sizes of the matrices are much larger than the particle sizes used. For the measurement, although the maximum hydrodynamic diameter used was 25.2 nm (500 kDa) (Fig. 6), the particle diameter was much smaller than the predicted pore size of oligomer and monomer matrices. Mean pore sizes for both formulations can be predicted using the Carman–Kozeny equation [53], which is a function of permeability and porosity

$$D_h=\sqrt{k\frac{{\psi }_{\mathrm{CK}}}{\phi }}$$ (8)

where D_h is mean pore size, ψ _CK is the Carman–Kozeny factor (32 for cylinder), $\phi$ is the porosity, and k is the matrix permeability. The mean pore size of 0:100 is approximately 2.57 μm, and mean pore size of 100:0 is smaller at around 1.5 μm. Although these values are lower than what has been measured experimentally, they are still much higher than the 25.2 nm (500 kDa) used in the study (i.e., 102 times and 60 times higher for monomer and oligomer, respectively). The result suggests that under the current experimental and computational conditions, the microstructures of both matrices provide a sufficient space for particle movement. As was the case for the permeability values, experimental diffusivity results are higher than computational results. However, the degree of difference between the two is lower at approximately twofold, which means that the computed values are on the same order of magnitude as the experimental results. Nevertheless, it is possible that the difference is due to the assumptions made concerning the particle body, which was assumed to be rigid in the computation as described above.