Abstract
Accurate insertion of needles to targets in 3D anatomy is required for numerous medical procedures. To reduce patient trauma, a “fireworks” needle insertion approach can be used in which multiple needles are inserted from a single small region on the patient’s skin to multiple targets in the tissue. In this paper, we explore motion planning for “fireworks” needle insertion in 3D environments by developing an algorithm based on Rapidly-exploring Random Trees (RRTs). Given a set of targets, we propose an algorithm to quickly explore the configuration space by building a forest of RRTs and to find feasible plans for multiple steerable needles from a single entry region. We present two path selection algorithms with different optimality considerations to optimize the final plan among all feasible outputs. Finally, we demonstrate the performance of the proposed algorithm with a simulation based on a prostate cancer treatment environment.
I. Introduction
Accurately inserting a needle to a specific target in a patient’s anatomy is difficult due to lack of maneuverability, limited visibility, and possible obstructions between the needle entry point and the target. A new class of steerable needles, composed of a highly flexible material and with a bevel-tip, are capable of following controlled, curved trajectories, enabling them to reach previously inaccessible targets while avoiding anatomical obstacles [17], [2], [1]. Because the needle bends in the direction of the bevel, the feasible paths of these needles can be approximated by concatenating constant-curvature arcs. By enabling avoidance of sensitive structures, steerable needles have the potential to reduce patient trauma that can result from the needle puncturing or cutting sensitive, healthy tissues.
In this paper, we explore a new approach to further reduce patient trauma for cases in which the physician must reach multiple targets during the same procedure. We use a “fireworks” trajectory [6] in which needle paths are computed to multiple targets from a single entry region or port in the patient’s skin. Planning motions for steerable needles in this context requires that the needle paths reach multiple targets from the same entry region while avoiding obstacles and satisfying the kinematic constraints of the needles’ motion.
We explore motion planning of “fireworks” insertion of steerable needles by extending a previously developed sampling-based motion planning method [18]. The steerable needle planner considers 3D environments with obstacles, enabling modeling of patient-specific anatomical obstacles extracted from medical images. The approach is inspired by Rapidly-exploring Random Trees (RRTs); our algorithm quickly grows a forest of RRTs to explore the configuration space and find feasible paths for all targets. Computing paths to all targets simultaneously can accelerate motion planning compared to executing a separate planner for each target, e.g. by reusing samples and reducing collision detections computed. Our approach also leverages the fact that the entry location is defined as a region rather than a point; due to the kinematic constraints of steerable needles, it may not be possible to reach all targets from a single entry point. Our method considers a surface corresponding to an entry port on the patient’s skin, and minimizes the size of this surface while still reaching all targets.
We present two path selection algorithms to optimize the final plan among feasible outputs. We evaluate the algorithm using a 3D environment inspired by prostate cancer brachytherapy treatment, a type of radiation treatment in which physicians use needles to implant radioactive sources inside the prostate.
II. Related Work
The use of a bevel tip for a medical needle significantly affects the bending forces acting on the needle during insertion [13]. Based on this observation, Webster et al. [16] developed and experimentally verified a nonholonomic model of the needle’s motion in stiff tissues based on a generalized bicycle model. This model can be approximated by arcs of constant curvature in the direction of the bevel-tip. The radius of that curvature is not significantly affected by the insertion velocity [17].
There has been much work on motion planning for steerable bevel-tip needles in a 2D workspace that incorporates the effects of tissue deformations and motion uncertainties. Alterovitz et al. [2] addressed the challenge of accurately steering a needle around obstacles to a target in deformable tissue. They formulate the motion planning problem as a nonlinear optimization problem that uses a simulation of tissue deformation during needle insertion as a function in an optimization that minimizes needle placement error. To consider motion uncertainties due to needle/tissue interaction, Alterovitz et al. efficiently discretized the state space of the needle and formulated the motion planning problem as a Markov Decision Process (MDP) to maximize the probability of successfully reaching the target [3], [1]. Alterovitz et al. also generalized this approach into the Stochastic Motion Roadmap (SMR), a sampling-based framework for planning under motion uncertainty [4].
Recent methods have considered more complex 3D environments. Park et al. developed a diffusion-based motion planning algorithm to numerically compute a path [14]. By representing the bevel-tip needle’s 3D motion as a screw motion, Duindam et al. [7] formulated the 3D motion planning problem for steerable needles as an optimization problem with a discretized control space and incorporated obstacle avoidance. Duindam et al. also developed a fast motion planner using a geometric approach that is not guaranteed to find a solution when one exists [8]. Inspired by the Rapidly-exploring Random Tree (RRTs) algorithms, Xu et al. [18] developed a 3D sampling-based motion planner that efficiently builds a global tree to quickly and probabilistically explore the entire workspace and search for a feasible plan.
The method of Rapidly-exploring Random Trees (RRTs), which was first introduced by LaValle [10], is a successful roadmap-based motion planning method that has shown its potential in dealing with motion planning problems for nonholonomc systems [11]. It incrementally grows a tree toward the target configuration by searching feasible paths in the configuration space, and provides an efficient and quick search in complex environments of high dimensions with different constraints [11]. Based on the original RRTs structure, many variants have been developed to improve the efficiency of searching [9], extend RRTs to more complex configuration space (𝒞-space) [5], and enhance the ability to explore difficult regions in searching the environment [15]. In this paper, we extend our RRT-inspired algorithms developed in [18] and propose an RRT-forest exploration strategy together with a plan selection algorithm to efficiently solve the motion planning problem for the “fireworks” insertion.
III. Problem Statement
The problem we address is to compute motion plans for multiple steerable needles from a single entry region to multiple targets. We assume that all needles satisfy the properties of bevel-tip steerable needles: each needle is sufficiently flexible such that rotating the needle at the base will not change its position in the workspace and each needle’s motion through the tissue is fully determined by its tip, meaning that the needle shaft follows the path cut by the needle tip. We also assume that all needles used in a procedure have identical properties (i.e. follow paths with the same curvatures). In our current implementation, we define the feasible workspace is a stiff 3D cuboid and all spatial obstacles are approximated using 3D spheres with various radii to simplify computational expense for collision detection. (Multiple needle insertion planning in a deformable environment and with more geometrically complex obstacles will be considered in future work.)
Given an entry region and a set of target configurations, the problem is to determine a set of feasible paths and the corresponding sequences of controls (insertion depths and rotations for each steerable needle) so that each target can be reached by a needle tip inserted from the entry region while avoiding obstacles and staying inside the workspace. Formally, the inputs and outputs are:
Input: Boundaries of the workspace, parameters of all steerable needles, obstacles locations, an entry region in the entry surface to insert all needles, and a set of target coordinates to reach.
Output: For each target coordinate, a needle path defined by its entry point and a sequence of controls, or a report that no path was found.
IV. Kinematics of Bevel-Tip Flexible Needles
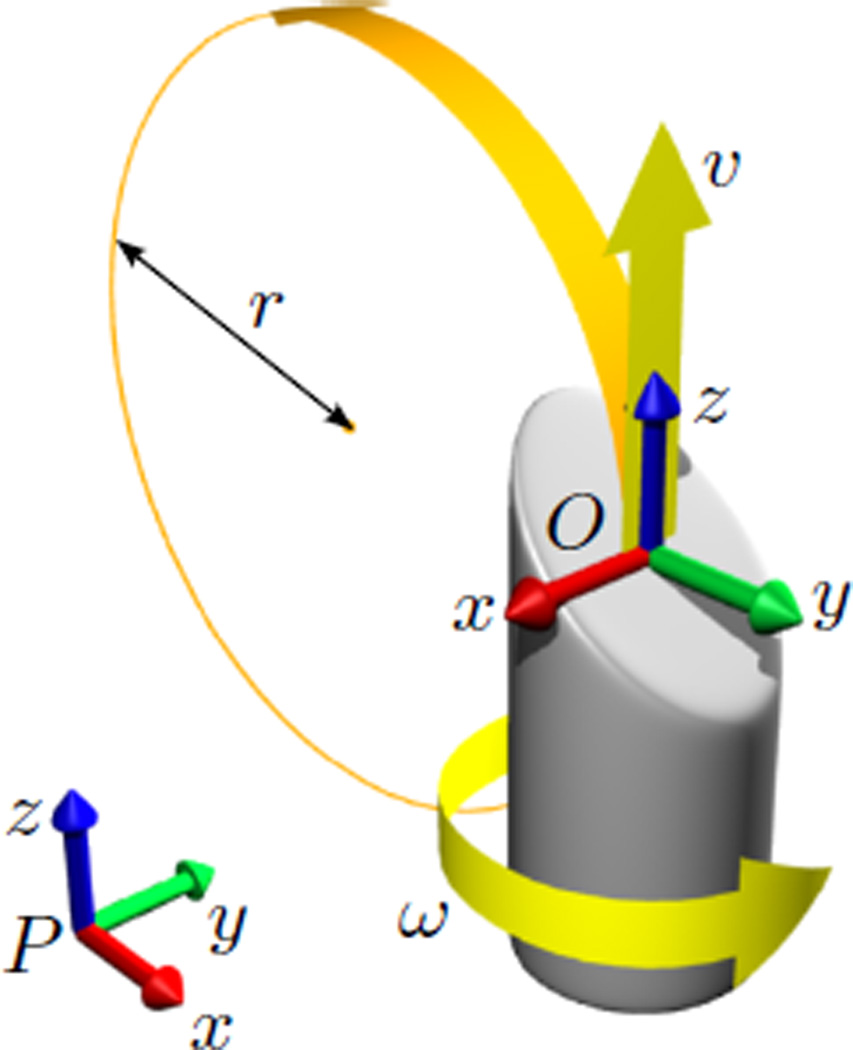
We summarize the kinematics of bevel-tip steerable needles; for more details see [17], [7]. Consider the bevel-tip needle shown in Fig. 2. Referring to the notation in [12], attach a spatial frame P to the base of the needle and a body frame O to the geometric center of the needle’s bevel tip, respectively. The configuration of the needle tip can be represented by the 4-by-4 transformation matrix of the object frame relative to the spatial frame,
where RPO ∈ SO(3) is the rotation matrix and pPO ∈ T(3) is the position of frame O relative to frame P.
Fig. 2.
Model of the bevel-tip needle.
The motion of the needle is fully determined by two motions of the bevel tip: insertion with velocity υ(t) in the z direction and rotation with velocity ω(t) about the z axis of the body frame O [16], [7]. It has been experimentally shown [17] that the bevel-tip needle will approximately follow a curved path with constant curvature while pushed with zero bevel rotation velocity, i.e. ω = 0. The instantaneous velocity of the needle tip can be represented in the body frame O as
| (1) |
When is constant, i.e., υ(t) and ω(t) are constant, the configuration of the needle tip relative to the spatial frame after being pushed for a time interval t is
| (2) |
where gPO(0) is the initial configuration of the needle frame relative to the spatial frame, and
| (3) |
According to the kinematics analysis in [7], the trajectory of the needle only depends on the ratio ω/υ but not on the values of the two individual terms. Therefore, we discretize the entire insertion into N steps with N time segments {I1, ⋯, IN} and assume that the velocity in each single step, , is constant. The final needle tip configuration can be computed as a product of exponentials [12], [7]
| (4) |
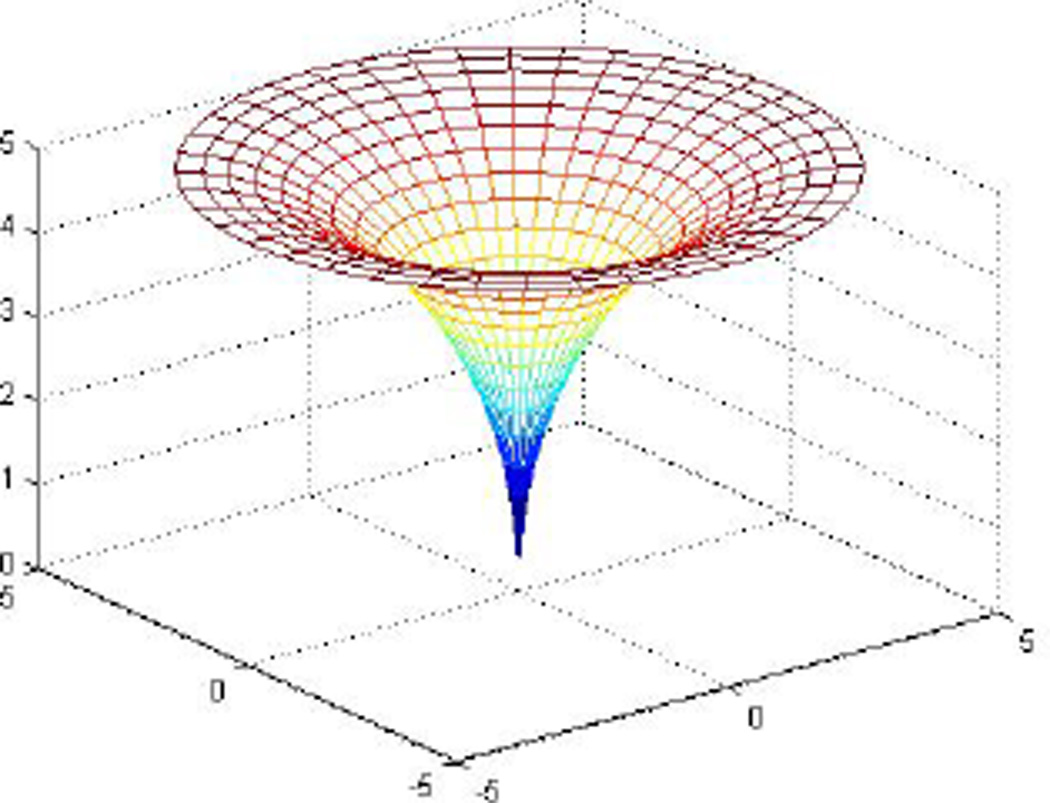
Note that the bevel-tip needle can only follow curved paths with a curvature κ = 1/r, as shown in Fig. 2. For this reason, reachable configurations of the needle are locally constrained inside the volume of a region (see Fig. 3) defined by
| (5) |
where (px, py, pz) are coordinates of a point in the body frame O.
Fig. 3.
The reachable region of local needle motion.
V. Motion Planning for Multiple Steerable Needles
A. “Fireworks” needle insertion planning
The configuration of the needle tip is determined by its position (x, y, z) together with its three Euler angles (φ, θ, ψ). However, the insertion task only requires the needle to reach a specific position in the 3 dimensional workspace, equivalent to ℝ3. Following its kinematics (2), the needle’s trajectory to reach a target at gPO(t) can be computed backwardly from its target as
| (6) |
Given the workspace’s boundaries, ([xmin, xmax], [ymin, ymax], and [zmin, zmax]), the obstacles information, the target locations sgoal and the specified entry zone Sentry, a motion planning algorithm based on RRTs with backchaining has been developed to quickly explore the configuration space from the target to find feasible soultions for insertion tasks with single needle and single target (SNST) [18].
For “fireworks” needle insertions, one can separatively execute the algorithm for SNST for each individual target. However, repeated sampling procedures for each needle unnecessarily increases the computational cost. Moreover, separated collision detection for a needle in an environment with previous solutions of other needles also requires extensive computational cost. By extending that algorithm, we propose a new algorithm to quickly grow a forest of RRTs to search feasible paths for all targets simultaneously.
Algorithm 1 (Forest of RRTs with backchaining): For all , initialize the forest ℱ by initializing all trees 𝒯i rooting at . Randomly sample a state srand in the collision free configuration space 𝒞𝒮free. For all trees in the forest, the reachable neighbor test is executed for all nodes si ∈ 𝒯i to find a reachable set , which contains all nodes reachable from srand. The nearest neighbor search is executed inside to find the nearest neighbor of srand, denoted by , which has the shortest distance to srand. The distance used in the nearest neighbor search can be defined in different ways by defining different metrics on the configuration space. Then we uniformly sample the negative control space −𝒰, and apply all sampled control inputs to for a small time increment δt > 0 to generate a set of possible new states from any 𝒯i. Again, the nearest neighbor of srand, , is added to each 𝒯i. This approach is repeated until the number of iterations reaches a predefined limit. Finally, a path selection process is executed to find a set of “optimal” feasible paths based on specific optimization criteria, or a failure report is output with no feasible plan found.
One concern of RRT-based motion planning algorithm with backchaining is the efficient growth of the reversed RRTs toward the entry region. In order to grow the forest quickly toward the entry region, we apply a biased sampling strategy in 𝒞𝒮free, in which the state srand is sampled with a higher density in Sgoal than elsewhere in the configuration space. If srand collides with any obstacle, it is discarded and new states are sampled until one in 𝒞𝒮free is found.
The control inputs are sampled uniformly in the control space, using CONTROL_SAMPLING(), within a predefined range [υmin, υmax] × [ωmin, ωmax]. The full Algorithm 1 is shown in Table I and Table II.
TABLE I.
The scenario of Algorithm 1.
| BUILD_FOREST(Sinit, Sgoal) |
| 1. for all |
| 2. |
| 3. ℱadd_tree(𝒯i) |
| 4. while No_of_Iteration < Max_Iteration |
| 5. srand ← RANDOM_STATE() |
| 6. ℱ ← EXTEND_FOREST(ℱ, srand) |
| 7. p*=SELECT_PATHS(ℱ) |
| 8. RETURN p* |
TABLE II.
Detailed procedure of Algorithm 1.
| RANDOM_STATE() |
| 1. p = rand(0, 1) |
| 2. if p < p1 |
| 3. srand =UNIFORM_SAMPLE(Sinit) |
| 4. if p1 < p < p2 |
| 5. srand =UNIFORM_SAMPLE(Sgoal) |
| 6. else |
| 7. srand =UNIFORM_SAMPLE(CSfree/(Sinit ∪ Sgoal)) |
| 8. RETURN srand |
| EXTEND_FOREST(ℱ, srand) |
| 1. for all 𝒯i ∈ ℱ |
| 2. EXTEND_TREE(𝒯i, srand) |
| 3. RETURN ℱ |
| EXTEND_TREE(𝒯, srand) |
| 1. |
| 2. |
| 3. (snew, unew) ← NEW_STATE(snear, srand, 𝒰) |
| 4. 𝒯 .add_vertex(snew) |
| 5. 𝒯 .add_edge(snear, snew, unew) |
| 6. RETURN 𝒯 |
| REACHABLE_NEIGHBORS(𝒯, srand) |
| 1. For all si ∈ 𝒯 |
| 2. if si is reachable from srand |
| 3. add si to Sreach |
| 4. RETURN Sreach. |
| NEW_STATE(snear, srand, 𝒰) |
| 1. 𝒰rand ← CONTROL_SAMPLING(𝒰) |
| 2. FOR all ui ∈ 𝒰rand |
| 3. snew(i) = snear + Fqnear (s, −ui)δt |
| 4. Snew = ∪isnew(i) |
| 5. snew ← NEAREST_NEIGHBOR(Snew, srand) |
| 6. unew = −ui such that si = snew |
| 7. RETURN snew, unew |
B. Paths Selection
If a target is reachable from the entry region, Algorithm 1 will output a set of feasible paths for this target, denoted by Pi. SELECT_PATHS() will select and output the “best” plan, , for the given target set Sgoal, where is the “best” path for . With consideration of different optimization criteria, different path selection strategies can be applied.
1) Plan with minimal twists
While inserting a needle into the patient’s body, rotating the needle base may cause damages to the tissue. Because of the discretization of the needle’s kinematics, the more segments a feasible path contains, the more damage it will cause on the tissue because each segment includes a twist. In addition, uncertainties in needles’ motions will greatly affect the performance and accuracy of the insertion. Since the control of the needles is open loop, the more control inputs a feasible path has, the more uncertainties this path will involve. Let nk be the number of control inputs corresponding to the kth path in Pi, the for each can be selected using the following minimal twists strategy,
This minimizes the lengths of paths, which is equivalent in our formulation to minimizing the number of twists.
2) Plan with minimal insertion region
Inserting multiple needles to reach multiple targets may require an entry region with a larger surface area. This will increase the complexity of the treatment as well as the trauma on the patient. As described above, Algorithm 1 considers this issue by exploring the connectivity between different targets so that possible plan may be found to reach multiple targets with only one needle. Besides that, the entry region can be further minimized based on the output path sets, Pis. Let be the corresponding entry point of the k’th path, , for target si. The optimal plan P* can be selected by using the following minimal entry region strategy,
where is the Euclidean distance between . This strategy minimizes the maximal distance between possible entry points of any two needles.
The proposed path selection strategies above optimize across the paths that were computed by the RRT approach. Due to the probabilistic nature of RRTs and the termination of the algorithm based on iteration count, the paths generated by the RRT represent only a subset of the feasible paths. Hence, the paths computed by the selection strategies are not guaranteed to be optimal.
VI. Simulation and Discussion
A. Simulation setup
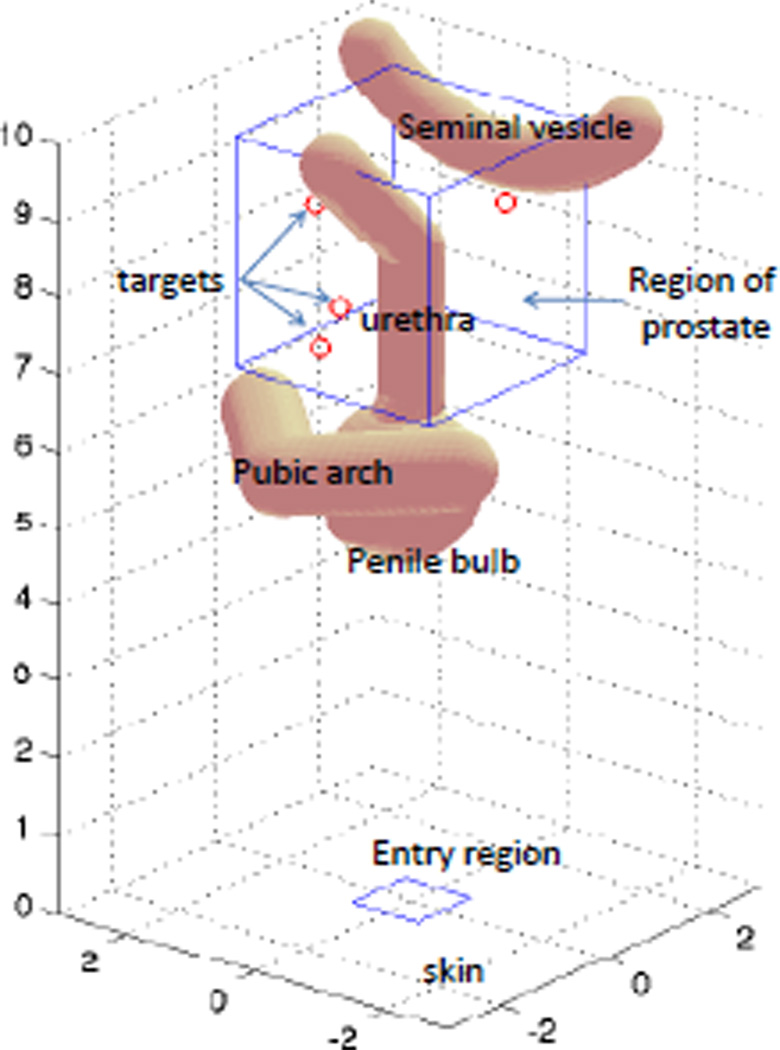
We implement the proposed RRT-Forest-based motion planning algorithm for multiple steerable needles insertion using an approximated 3D prostate environment. For our preliminary experiments, we use a set of spherical obstacles with different radii to approximate the real environment as shown in Fig. 4. The entire workspace is defined as a cubiod with coordinates (−3, 3) × (−3, 3) × (0, 10). The region of interest around the prostate is defined as a cube of 3×3×3 located at the top of the workspace. The feasible entry region is defined as a 2×2 square in the skin plane (X-Y plane). The assumption of spherical obstacles allows for fast collision detection. Interference of different needles is not considered until selecting the final optimal insertion plan. Simulations are run on a laptop with an AMD® TurionTM64 2.1 GHz CPU, 4 GB memory, and the Microsoft® Windows Vista™ operating system.
Fig. 4.
The simulation setup: An approximated environment for multiple needle insertion.
B. Simulation Results
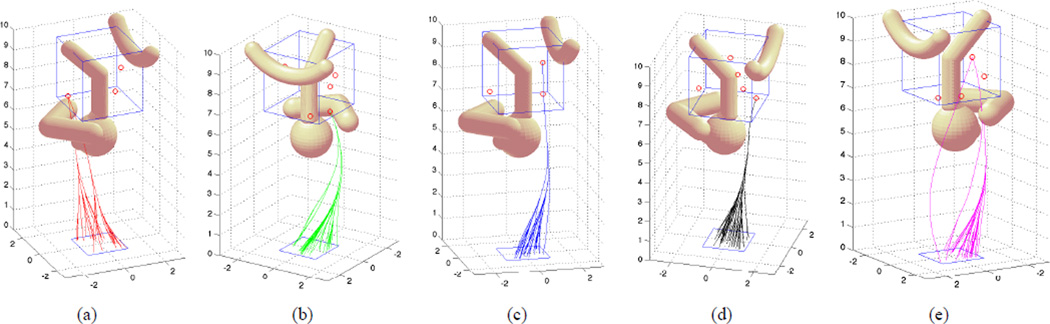
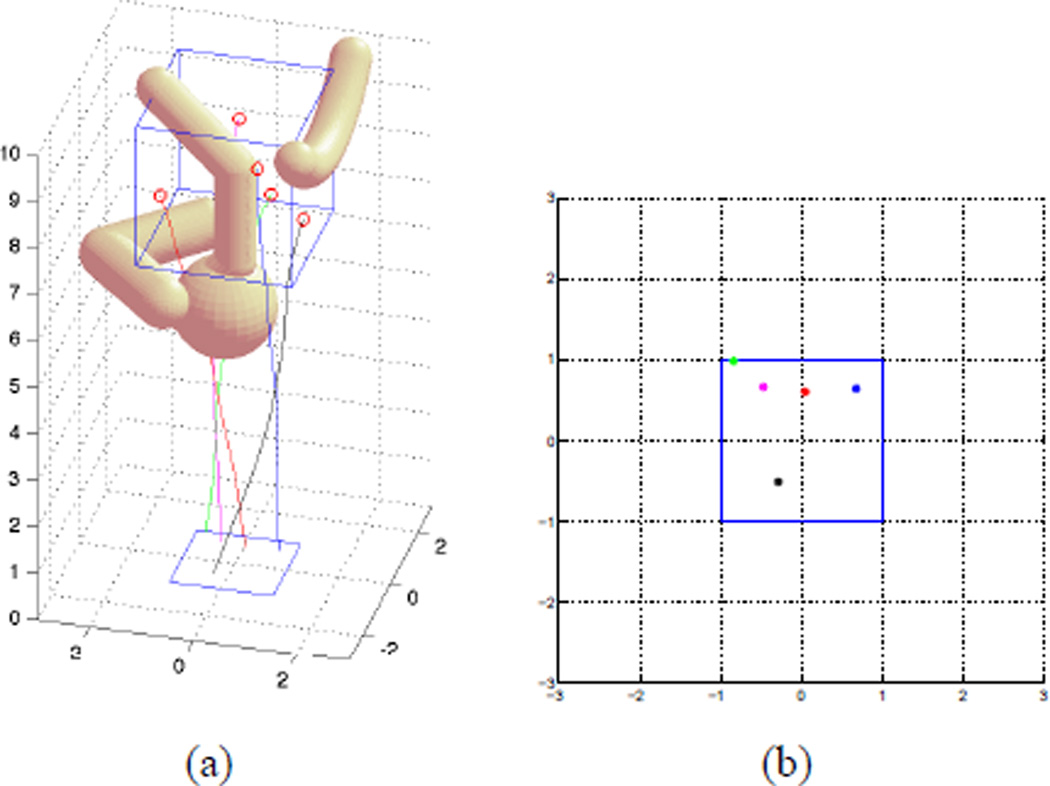
The insertion task is to insert multiple needles from the 2×2 rectangular entry region centered at (0, 0, 0) in the skin plane to reach 5 targets, which are randomly generated in the region of interest. The range of the uniformly sampled control inputs are defined by insertion depth in the range of [0.1, 0.5] and rotation angle in the range of [0, 2π]. We ran 5 trials, all of which successfully found feasible plans within 10000 iterations with an average computational time of 57573 seconds. Figure 7 shows the feasible plans found for all 5 targets in one trial.
Fig. 7.
Feasible paths found for one trial: For each of the 5 targets, a set of feasible paths is found. With any path in the path set, a steerable needle can be inserted from the single entry region to reach the target.
We also compared Algorithm 1 to separately executing the SNST algorithm for each target. Using the SNST algorithm, feasible paths for each target were successfully found in 10000 iterations with a computational time of 87755 seconds. Algorithm 1 was 34% faster than executing the SNST algorithm multiple times. This is because it used every random sample to explore all 5 random trees, which is more efficient that separately applying the SNST algorithm.
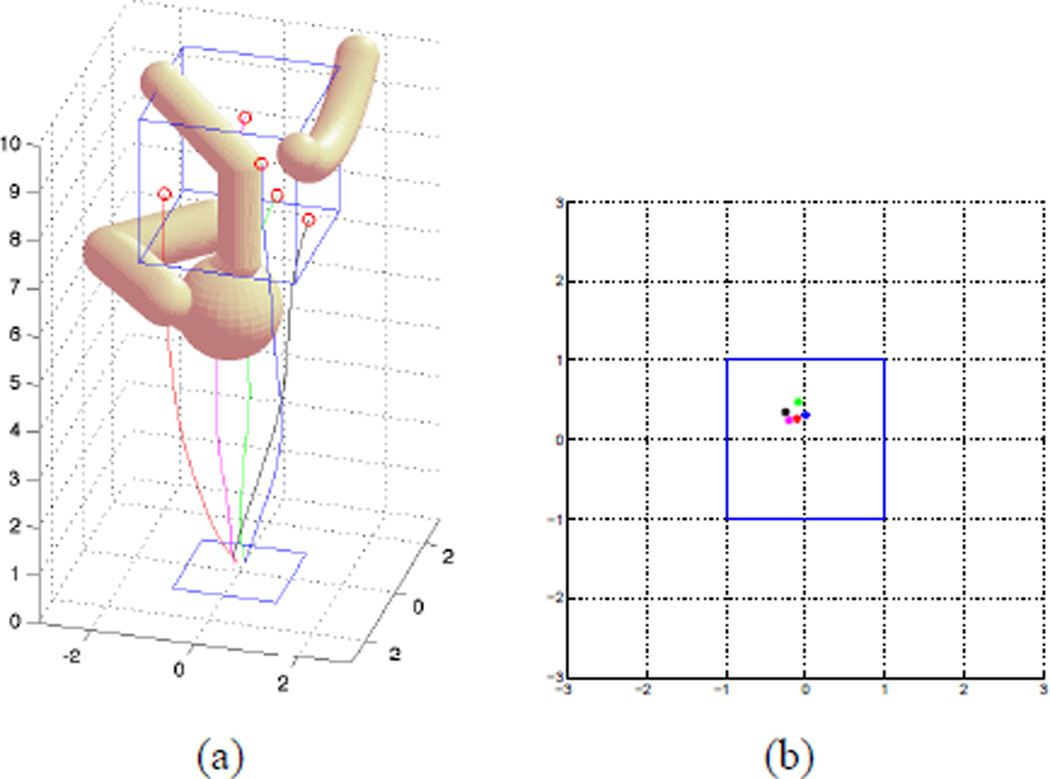
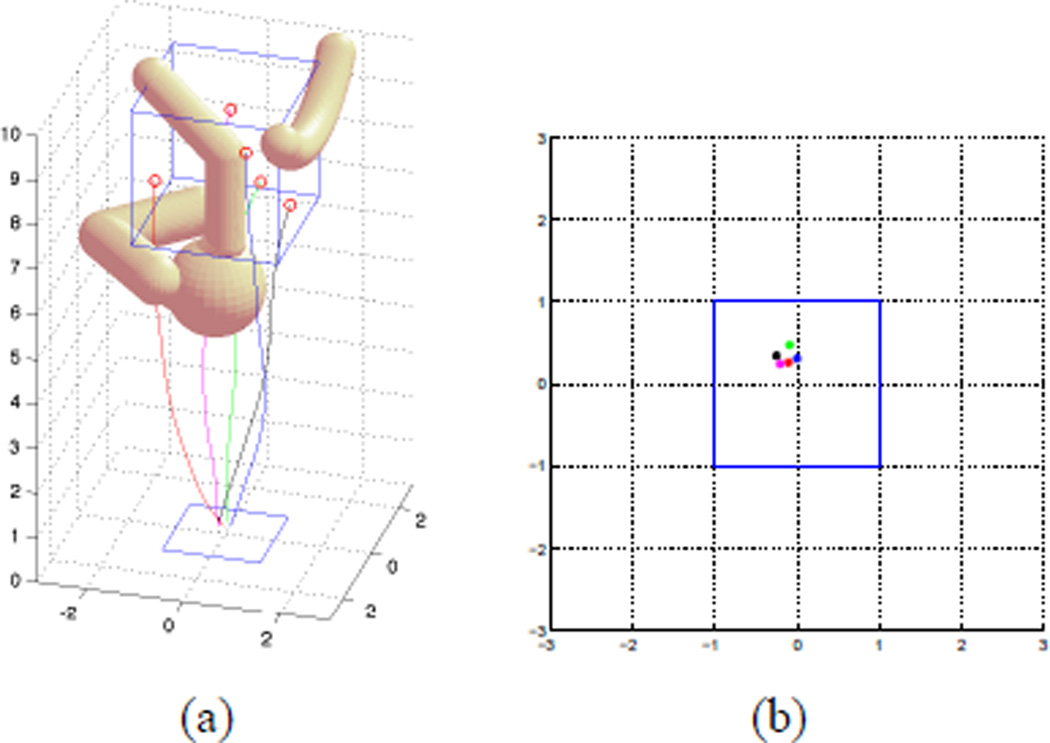
Figure 5(a) shows the “optimal” plan selected using minimal twist strategy, and Figure 5(b) shows the corresponding entry points. Figure 6(a) shows the “optimal” plan selected using the minimal entry region strategy, and Figure 6(b) shows the corresponding entry points.
Fig. 5.
A set of paths for simulation task 1: For all the 5 targets, only one path from each path set is selected with plan selection algorithm 1 to minimize twists of the path.
Fig. 6.
A set of paths for simulation task 1: For all the 5 targets, only one path from each path set is selected with plan selection algorithm 2 to minimize region for insertion.
C. Discussion
The RRT-Forest-based algorithm efficiently explores the collision-free configuration space and its connectivity. With the minimal twist strategy, the entry points for all targets are selected in a way to minimize the path length to the corresponding target. However, this leads to a relatively larger entry region. With the minimal entry region strategy, the entry region is further minimized among all possible plans. As shown in Figure 6(b), the “optimal” plan for this trial can be reduced into a circular region of radius less than 0.3. This can significantly reduce the complexity of the treatment as well as the patient’s trauma.
VII. Conclusions and Future Work
In this paper, we presented an algorithm for motion planning of multiple bevel-tip steerable needles to reach multiple targets in 3D environments with obstacles. This algorithm is inspired by the RRT-based motion planning algorithm with backchaining for solving the feasible entry point planning problem for a single needle [18]. The proposed algorithm builds an RRT forest data structure and provides a quick and more efficient exploration from all targets toward a single entry region to find feasible plans. We considered two path selection strategies: minimizing the number of needle twists and minimizing the size of the entry region. We conducted preliminary experiments in a 3D environment that approximates the prostate and surrounding obstacles.
In this paper, we only considered stiff environments with non-deformable spherical obstacles. In future work, we will explore motion planning for multiple steerable needles in deformable environments with more complex obstacles.
Fig. 1.
An example of ”fireworks” steerable needle insertion: 5 needles are inserted from very small entry region to reach 5 targets in the workspace while avoiding collision with the obstacles.
Acknowledgement
The authors would like to thank Allison Okamura, Greg Chirikjian, Noah Cowan, and Kyle Reed at the Johns Hopkins University, and Vinutha Kallem at University of Pennsylvania for their valuable assistance to this work.
This work was supported by NIH grant R01 EB006435 and the Netherlands Organization for Scientific Research.
Contributor Information
Jijie Xu, B. Thomas Golisano College of Computing and Information Science, Rochester Institute of Technology, USA. (jijie.xu@rit.edu).
Vincent Duindam, Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, USA.
Ron Alterovitz, Department of Computer Science, University of North Carolina at Chapel Hill, USA. (ron@cs.unc.edu).
Jean Pouliot, Helen Diller Family Comprehensive Cancer Center, University of California, San Francisco, USA.
J. Adam M. Cunha, Helen Diller Family Comprehensive Cancer Center, University of California, San Francisco, USA
I-Chow Hsu, Helen Diller Family Comprehensive Cancer Center, University of California, San Francisco, USA.
Ken Goldberg, Department of Industrial Engineering and Operations Research and the Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, USA. (goldberg@berkeley.edu).
References
- 1.Alterovitz R, Branicky M, Goldberg K. Motion planning under uncertainty for image-guided medical needle steering. Int. J. Robotics Research. 2008 Nov.27(no. 11–12):1361–1374. doi: 10.1177/0278364908097661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alterovitz R, Goldberg K, Okamura AM. Planning for steerable bevel-tip needle insertion through 2D soft tissue with obstacles; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2005. Apr. pp. 1652–1657. [Google Scholar]
- 3.Alterovitz R, Lim A, Goldberg K, Chirikjian GS, Okamura AM. Steering flexible needles under Markov motion uncertainty. Proc. IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS) 2005 Aug.:120–125. [Google Scholar]
- 4.Alterovitz R, Siméon T, Goldberg K. The Stochastic Motion Roadmap: A sampling framework for planning with Markov motion uncertainty. In: Burgard W, Brock O, Stachniss C, editors. Robotics: Science and Systems III (Proc. RSS 2007) Cambridge, MA: MIT Press; 2008. pp. 246–253. [Google Scholar]
- 5.Branicky MS, Curtiss MM, Levine J, Morgan S. RRTs for nonlinear, discrete, and hybrid planning and control; Proceedings IEEE Conference Decision & Control; 2003. [Google Scholar]
- 6.Cunha A, Pouliot J. Dosimetric equivalence of non-standard brachytherapy needle patterns. Medical Physics. 2008;(no. 6):2737–2737. [Google Scholar]
- 7.Duindam V, Alterovitz R, Sastry S, Goldberg K. Screw-based motion planning for bevel-tip flexible needles in 3d environments with obstacles; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2008. May, pp. 2483–2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Duindam V, Xu J, Alterovitz R, Sastry S, Goldberg K. 3d motion planning algorithms for steerable needles using inverse kinematics. Proc. Workshop on the Algorithmic Foundations of Robotics. 2008 doi: 10.1007/978-3-642-00312-7_33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kuffner J, LaValle S. RRT-connect: An efficient approach to single-query path planning; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2000. [Google Scholar]
- 10.LaValle SM. Rapidly-exploring random trees: a new tool for path planning. Department of Computer Science, Iowa State University; 1998. TR 98-11. [Google Scholar]
- 11.LaValle SM. Planning Algorithms. Cambridge, U.K.: Cambridge University Press; 2006. available at http://planning.cs.uiuc.edu/. [Google Scholar]
- 12.Murray R, Li Z, Sastry S. A Mathematical Introduction to Robotic Manipulation. CRC Press; 1994. [Google Scholar]
- 13.O’Leary MD, Simone C, Washio T, Yoshinaka K, Okamura AM. Robotic needle insertion: Effects of friction and needle geometry; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2003. [Google Scholar]
- 14.Park W, Kim JS, Zhou Y, Cowan NJ, Okamura AM, Chirikjian GS. Diffusion-based motion planning for a nonholonomic flexible needle model; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2005. pp. 4611–4616. [Google Scholar]
- 15.Rodriguez S, Tang X, Lien J, Amato N. An obstacle-based rapidly-exploring random tree; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2006. pp. 895–900. [Google Scholar]
- 16.Webster RJ, III, Memisevic J, Okamura AM. Design consideration for robotic needle steering; Proc. IEEE Int. Conf. Robotics and Automation (ICRA); 2005. [Google Scholar]
- 17.Webster RJ, III, Kim JS, Cowan NJ, Chirikjian GS, Okamura AM. Nonholonomic modeling of needle steering. Int. J. Robotics Research. 2006 May;25:509–525. [Google Scholar]
- 18.Xu J, Duindam V, Alterovitz R, Goldberg K. Motion planning for steerable needles in 3d environments with obstacles using rapidly-exploring random trees and backchaining; Proc. IEEE Int. Conf. Automation Science and Engineering (CASE); 2008. Aug. pp. 41–46. [Google Scholar]