Abstract
Recent experiments monitoring the healing process of wounded epithelial monolayers have demonstrated the necessity of MAPK activation for coordinated cell movement after damage. This MAPK activity is characterized by two wave-like phenomena. One MAPK “wave” that originates immediately after injury, propagates deep into the cell sheet, away from the edge, and then rebounds back to the wound interface. After this initial MAPK activity has largely disappeared, a second MAPK front propagates slowly from the wound interface and also continues into the cell sheet, maintaining a sustained level of MAPK activity throughout the cell sheet. It has been suggested that the first wave is initiated by Reactive Oxygen Species (ROS) generated at the time of injury. In this work, we develop a minimal mathematical model that reproduces the observed behavior. The main ingredients of our model are a competition between ligand (e.g., Epithelial Growth Factor) and ROS for the activation of Epithelial Growth Factor Receptor, and a feedback loop between receptor occupancy and MAPK activation. We explore the mathematical properties of the model and look for traveling wave solutions consistent with the experimentally observed MAPK activity patterns.
Keywords: MAPK, ROS, EGF, ligand, traveling wave
Introduction
Coordinated cell movement is an essential feature of many biological processes, such as wound healing, embryonic morphogenesis, and tumor growth [15]. In wound healing, cell migration and cell contraction are the two main mechanisms responsible for wound closure. Cell contraction is the dominant mechanism in the closing of small wounds through the so called “purse-string” process [13]. For larger wounds, cell contraction is not sufficient, and surrounding cells must migrate to close larger wounds. While the two mechanisms are not mutually exclusive, there are cases where cell migration is the only healing process [34], such as when a strip of cells from an epithelial layer is removed [23]. Despite the existence of experimental assays targeting cell migration during wound healing, there are still many open questions. For example, what mechanical and biochemical phenomena regulate the switch from resting cells before injury to motile cells after injury? Is it the availability of free space that leads cells to move toward wound closure? What determines the speed of cell migration? To be able to answer these questions, we need to understand both the mechanical and biochemical aspects of cell migration, and how they might regulate each other. While some of the physical mechanisms of cell movement have been studied [4, 34, 19, 14], the complex regulation of the wound healing process by biochemical signals and feedback pathways remains poorly understood. Matsubayashi et al. monitored cell migration of monolayers of epithelial cells after wounding and observed two “waves” of phosphorylation of Mitogen Activated Protein Kinase (MAPK)[16]. Within this context, a MAPK activation wave consists of a sequential increase of MAPK activity from cells at the wound edge to cells farther away from it (see Fig. 1). In more recent experiments, Nikolić et al. observed the same MAPK activation patterns under various wounding protocols, and identified Reactive Oxygen Species (ROS) as regulatory factors of MAPK activity during healing [20]. A schematic of these experiments is shown in Fig. 1. Our goal is to build a mathematical representation of the intercellular signaling mechanisms observed in these two set of experiments [16, 20].
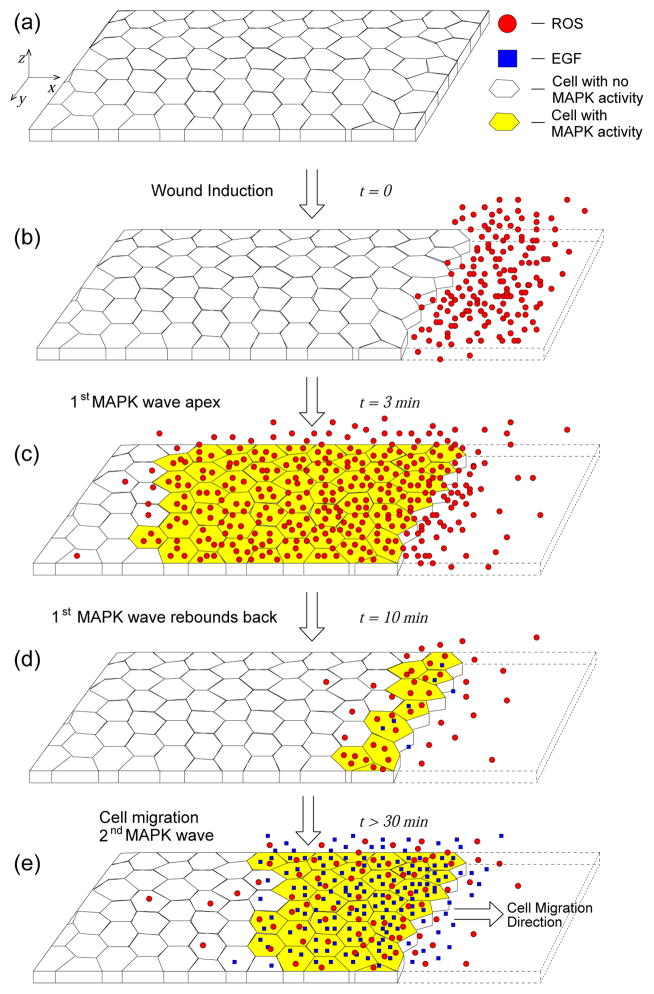
Figure 1.
Schematic of MAPK activation during epithelial wound healing [16, 20]. The system extends ~ 3mm in the z-direction normal to the cell monolayer. (a) The main elements of the experiments: a monolayer of epithelial cells; the cells have either MAPK activity (yellow) or not (no color filling). There are two diffusible signals responsible for MAPK activation, ROS (red circles) and EGF (blue squares). (b) At time t = 0 a strip of cells is removed from the epithelial layer creating a wound. As a result of the injury, ROS molecules are released at wound edge [20]. (c) ROS diffuses and promotes MAPK activation. This is the first MAPK wave observed in [16, 20], it reaches its farthest point from the wound edge after 3 minutes. (d) The first wave “rebounds” back to wound edge as ROS generated by the wound is either consumed or diffuses away. At the same time the feedback loop between MAPK/EGFR/EGF promotes EGF release by MAPK-active epithelial cells (blue dots near wound edge). The “rebound” wave returns to the cells around the wound edge after 10 minutes from injury. (e) About 30 minutes after injury, the cells begin to move into the empty space left by the wound. Cell movement promotes ROS release. The combination of ROS production by migrating cells and EGF release by MAPK-active cells ignites the second sustained MAPK wave.
In general, MAPK activation is achieved through a cascade characterized by the sequential activation of three protein kinases [5]. Because of its relevance and ubiquity, MAPK and its activation pathway remain the subject of many computational and mathematical modeling studies [21]. Huang and Ferrell [8] proposed a system of 18 differential equations representing the 10 reactions that compose the three-kinases MAPK cascade. A mathematical and computational analysis of the system showed that the cascade has the effect of amplifying an input signal (e.g., receptor phosphorylation) in such a way that its overall behavior can be compared to that of a cooperative enzyme [10]. These first computational studies sparked additional modeling efforts that, coupled with ongoing discoveries by experimentalists, have led to many more advanced models that exhibit characteristics (e.g., bistability, ultrasensitivity, oscillations, etc.) of the MAPK signaling pathway [26, 7, 32, 31].
Here, we are not interested in the intracellular dynamics of MAPK, but rather on its role within the wound healing signaling network. For this reason, we will treat the MAPK cascade as a black box, using the results in [5, 6] to essentially represent the whole cascade as a switch for signal transmission. In this approach, MAPK is the output of the “signaling switch”. ROS are one input that can activate the switch, but are unlikely to be the only one because of the different properties of the two activation waves. As suggested in [20] and in other wound healing experiments [39, 2], other candidate inputs are diffusible ligands and their cell receptors. Epidermal Growth Factor (EGF) and EGF Receptor (EGFR) also play essential roles in promoting cell migration, proliferation and wound closure [38, 9]. Moreover, positive and negative feedbacks between EGFR signaling and the MAPK cascade have been demonstrated experimentally and verified computationally [30, 11, 12]. Although Nikolić et al. suggest EGF, as well as other molecules, as possible signals, they did not pursue the topic in their work. However, they did identify ROS as direct regulators of MAPK activity in their wound healing experiments. Since ROS have been shown to induce EGFR activation in the absence of EGF [27], this finding is in agreement with other studies that showed the regulatory role of ROS in wound healing [29, 33] and MAPK signaling [36, 17].
Because of the documented connection between diffusible signals, wound healing, and MAPK activation, we propose a mechanistic model based on ligand-mediated intercellular signaling. We use a continuum approach that is justified by the facts that the observed MAPK patterning spans many epithelial cells, and that the concentrations of the species relevant to MAPK activation are high [25, 18]. Because we are focusing on the signaling dynamics of the system, we do not model directly cell migration. Accordingly, we represent the positive feedback loop between MAPK signaling and cell migration through ROS production due to the mechanical stresses induced by migrating cells [33]. As a result, the model reproduces the observed MAPK activation pattern, and is consistent with the qualitative experimental features observed in [16, 20].
MAPK dynamics during wound healing
Before introducing the mathematical model, we present the experimental observations on which our model is based. In 2004, Matsubayashi et al. studied wound healing in epithelial monolayers of Madin-Darby canine kidney (MDCK) cells [16]. They wounded the monolayers by removing a strip of cells from them, and then monitored cellular responses to the wound itself. The authors observed that, after injury, both the cells at wound margin and the submarginal cells migrate to close the wound. The number of cells remained essentially constant, an indication that cell proliferation did not play a role in this system. To investigate the cellular response after wounding, the authors stained the cells with ERK1/2 antibodies. ERK1/2 is a MAPK that had been shown to contribute to wound healing. The images showed a peculiar pattern of MAPK activation consisting of two “waves”: a fast transient one and a slow sustained one. Within this context, a MAPK activation wave consists of a sequential increase of MAPK activity from cells at the wound edge to cells farther away from it (see Fig. 1). The rapid transient wave is generated at wound onset and spreads from marginal to submarginal cells. This wave reaches its peak (i.e., the furthest distance from the wound margin) after 3 minutes and quickly recedes back to the wound edge after about 10 minutes. During the retreat of the wave, MAPK activity disappears sequentially from cells farther away from the wound to cells at the wound edge. After the first wave, MAPK activation is confined to the wound margin until the onset of a second “wave”. The second MAPK activation wave starts 30 minutes after wounding and propagates from the marginal cells to the submarginal ones at a constant speed that is much slower (about two orders of magnitude) than the first wave. The authors observed that the second wave kept propagating for the duration of the experiments (4 to 6 hours), and also that MAPK was inactive once the opposing edges of the wound confronted one another.
Matsubayashi et al. concluded that the observed MAPK activity is necessary for wound healing, but could not identify a specific mechanism or signal that contributes to MAPK activation. They did propose the existence of a feedback loop between cell movement and MAPK activation that promotes coordinated cell migration.
Nikolić et al. extended Matsubayashi et al.’s experiments by probing the epithelial wound healing assay with different wounding protocols to further elucidate the properties of MAPK activation [20]. They observed that the two wave motifs are always present after mechanical injury. The kinematic description of the MAPK waves matches the one given by Matsubayashi et al., with the first wave reaching a maximum distance from the wound edge of about 480 μm after 3 minutes, then receding back to the wound edge until the onset of the second wave, 30 minutes after wounding, as depicted in Fig. 1. The authors were also able to detect ROS production at the wound site immediately following injury and investigated the role of ROS with respect to MAPK activation. They discovered that ROS is necessary for MAPK activation since both MAPK waves were absent during experiments in which ROS were inhibited. Nikolić et al. concluded that both MAPK waves are necessary for wound healing, and proposed a sequence of events to explain MAPK dynamics. This sequence starts with ROS production at the wound edge after mechanical wounding, ROS then ignites the first, fast, MAPK activation wave that promotes coordinated cell migration. The second MAPK wave and cell migration seem to be linked through a feedback loop, since they have the same kinematic properties, as also suggested by Matsubayashi et al.
Mathematical Model
The experimental results from [16, 20] provide evidence of precise spatio-temporal MAPK signaling for the regulation of cell migration during wound healing, without determining the exact biochemical events that govern it. Nikolić et al. identified ROS as signaling molecules responsible for the initial wave of MAPK, but they also stated that more diffusible signals are needed to explain the MAPK dynamics [20]. As stated in the Introduction, we propose that two diffusible signals, ROS and EGF, are sufficient to explain the observed spatio-temporal MAPK pattern. In fact, ROS and EGF molecules are both able to diffuse in the extracellular space (ROS can also move across the cell membrane) and to phosphorylate the EGF membrane receptor (EGFR), that activates the MAPK cascade. EGF induces phosphorylation of the cytoplasmic tail of EGFR by binding to it. Reynolds et al. (2003) showed that ROS can also induce EGFR phosphorylation even in the absence of EGF by binding to intracellular phosphatases in the domain of the EGFR molecules. Also well documented is the positive feedback between EGF and the MAPK cascade, and its ability to produce long range signaling through autocrine relays [25]. Finally, ROS can be generated by mechanical stresses like the ones generated by the migrating cells in the wounded epithelium [36], thus providing a feedback loop between MAPK activation, cell motility, and further ROS production. These four signaling mechanisms are summarized in Fig. 2 and constitute the main ingredients of our mathematical model.
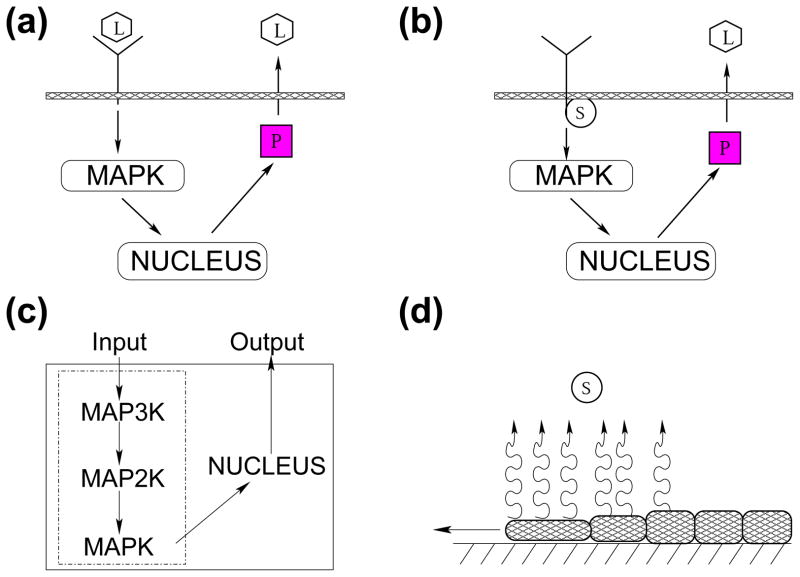
Figure 2.
Schematic of biophysical events during wound healing. (a) diffusible ligands (L) phosphorylate membrane receptors by binding to them, activating the MAPK cascade that leads to the production of intracellular protease (P). Protease induces ligand release. (b) ROS (S) can also interact with membrane receptors by inducing phosphorylation of their cytoplasmic tail, which also activates the MAPK cascade and promotes release of ligands into the extracellular matrix. Diffusible ligand and ROS represent two independent triggers of the MAPK cascade. (c) Schematic of the three-kinase cascade that characterize MAPK signaling. Note that in our model we do not represent the cascade in details, but we replace it with a Hill function. (d) The stresses caused by cell movement toward wound closure lead to ROS release [28, 36, 1].
The wound healing system is a three-dimensional one, and the migration of individual cells toward wound closure is not always normal to the wound edge as shown by cell tracking experiments [20]. Here, we simplify the analysis by considering the cell layer in cross section as a semi-infinite straight line, with the wound initially positioned at the origin (cf. Fig. 2(d)). The resulting two-dimensional system consists of a semi-infinite cell layer that is immersed in medium of infinite height (the medium in [20] is 3mm thick which is much larger than any other length scale in the problem). We model four species: ROS, one diffusible ligand (e.g., EGF), one ligand receptor (e.g., EGFR), and playing the role of the output of the MAPK cascade “black box”, a protease that is the intracellular precursor of the ligand (e.g., the piece completing the feedback loop between EGF and the MAPK cascade in Figs. 2-(a) and 2-(b)). We denote the local concentrations of ROS, EGF, EGFR, and protease by L, S, R, and P respectively. As depicted in Fig. 2, the signal can be transmitted to the cell in two different ways: through a ligand-receptor complex (CL ≡ R · L) and a ROS-receptor complex1 (CS ≡ R · S). We will assume that the number of available cell membrane receptors is in excess, implying that R is approximately constant and that ROS-ligand-receptor complexes are negligible [25, 18].
A schematic representation of the system is given in Fig. 3. The governing equations and boundary conditions of our model are
Figure 3.
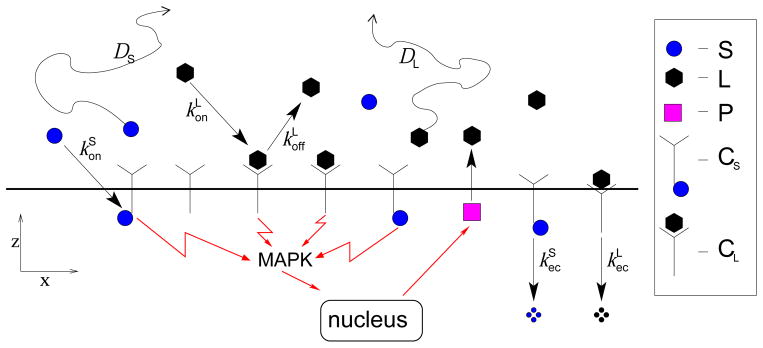
Schematic of simplified signaling pathway during wound healing: ligands (L) and ROS (S) are free to diffuse and bind to cell surface receptors. This binding forms complexes (CS and CL) that activate MAPK signaling. Complexes are lost due to endocytosis or, in the case of ligand-receptor complexes, through ligand unbinding and endocytosis. Intracellular proteases (P) release extracellular ligands (L). Note that receptor are assumed to be in excess. Conversely, ligand-ROS-receptor complexes are negligible.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Equations (1) and (4) describe the diffusion of ligands and ROS in the extracellular medium with diffusion constants DL and DS, respectively. Eqn. (2) accounts for the flux of ligand across the surface of the cellular layer consisting of ligand-receptor complex formation with rate constant , ligand-receptor complex dissociation with rate constant , and extracellular ligand release by intracellular protease with rate gL. Eqn. (3) governs the kinetics of ligand-receptor complexes, with new complexes forming at rate and dissociating with rate . The rate of receptor-mediated endocytosis of the ligand-bound receptor complexes is represented by . Eqn. (5) describes the difusive flux of ROS due to formation of ROS-receptor complexes with rate and to ROS production by the functional ΠS(CL, X, T). The kinetics of ROS-receptor complexes is represented by Eqn. (6) and its terms are analogous to the ones in Eqn. (3), except that there is no ROS release from ROS-receptor complexes in accordance with the experimental results by Reynolds et al. [27]. The last equation describes the cellular response to extracellular signaling through the activity of intracellular proteases. Within the wound healing framework, protease activity is directly related to ERK1/2 activity measured in [20]. In particular, the protease dynamics is characterized by a degradation term with rate constant kP and a source term ΠP(CL, CS) with maximum production rate gP. To complete the description of the mathematical model, we need to impose reasonable functional forms for ΠP and ΠS.
The role of the functional ΠP(CL, CS) is to represent the intermediate biochemical steps that lead to protease production. These steps include the MAPK cascade and any other reaction in the feedback loop between ligand binding and ligand release (e.g., the solid box in Fig. 2-(c)). In the literature, ΠP is usually represented as a sigmoidal function of cell surface complexes such as the Hill function [5, 6, 35]. If the level of receptor signaling is given by the total concentration of complexes (CL + CS), we propose the following functional form:
| (8) |
where n is an effective Hill coefficient, and CA represents the activation threshold of the signaling pathway.
Defining the ROS source ΠS is more problematic since the experimental evidence suggests an interplay between cellular signaling and cell migration, thus involving mechanical forces whose description goes beyond the scope of this study. Conversely, the production of ROS due to wound induction is embedded in the initial conditions of the system and it is not described in ΠS. Generally, ROS production increases with cell metabolism [36]. In our case, metabolic increase may be related to cells becoming motile [1, 36] and/or to ligand signaling [28]. We use a Hill function multiplied by a decaying exponential to represent the spatially-dependent ΠS:
| (9) |
The Hill functional represents ROS production from motile cells after MAPK activation. The delay TD represents the delay between MAPK activation and cell migration. The exponential factor in Eqn. (9) describes reduction in ROS production due to the decrease in cell motility further from the wound edge at X = 0. This choice of ΠS represents the feedback loop between MAPK signalling and cell deformation through its signaling pathways. We assume that cell motility is initiated by MAPK signaling through ligand and ROS binding. Then, motile cells release ROS as a byproduct of the mechanical stresses arising from cell motion.
Dimensionless model
Upon introducing the following dimensionless quantities
we express the system of equations in dimensionless form:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where the dimensionless parameters are
| (17) |
The parameters α and ν characterize the relative rates of diffusion and binding, while β represents the strength of complex degradation relative to ligand dissociation. The parameters ε and δ describe the speed of binding and endocytosis relative to ligand release mediated by intracellular species, and η is the ratio of diffusivity between ROS and EGF ligand.
The dimensionless protease and ROS production functions become
| (18) |
| (19) |
where , τ = TDkP, λ = kxL, and sA = (SAkP)/gP.
Fast-Binding Approximation
Before we proceed to the analysis of the model, we make an assumption that significantly simplifies the model and that is also justifiable biophysically [25, 18]. The range of values of kP, , and given in Table 1 shows that kP is approximately one order of magnitude smaller than the other parameters (there is no value for in Table 1, but from the literature about ROS it is safe to assume that [36]). In our analysis we assume that ligand dissociation and complex degradation is fast compared to protease degradation, e.g., . In this limit, ε and δ are small and Eqns. (12) and (13) can be treated as a singular perturbation. On time scales of protease degradation the concentration of ligand-receptor and ROS-receptor complexes are approximately that of the surface concentration of free ligand and ROS, respectively. If we consider only the “outer” solutions of Eqns. (12) and (13), our full model reduces to the three equations:
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where all functions now represent “outer” solutions valid at times beyond initial transients in complex formation. In the Supplemental Information (SI), we show that the fast-binding approximation is accurate for the parameters used in our analysis. Explicit numerical solutions of the full set of dimensionless Eqs. 10–16 are compared with those derived from the fast-binding approximation (Eqs. 20–24), leading to Table 1 in the SI.
Table 1.
Typical values of model parameters.
Analysis & Results
The spatio-temporal MAPK activation patterns can arise from different mechanisms. For example, one (or more) activation patterns could consist of a traveling front connecting two stable steady states, corresponding to high and low MAPK concentrations. In this section we describe the steady states of the system of Eqns. (20)–(24) and present an overview of the qualitative behavior of the solutions of the model. After establishing the dynamics of the mathematical model, we use the known model parameters to determine the nature of the MAPK patterns and some of their properties. Our analysis focuses on the model behavior at the cell layer level and neglects what happens to ROS and ligand concentrations in the bulk where molecules are simply diffusing.
Numerical solver
The complexity of our model requires analysis through numerical simulations. For this purpose we implemented a numerical solver in Fortran consisting of a centered finite difference scheme applied to a uniform discretization along the direction of the cell layer (e.g., x), and a staggered three-point finite difference scheme applied to an optimal geometrical grid discretization (see [22]) along the direction normal to the cell layer (e.g., z). The equations are time-integrated using an explicit Euler discretization. This type of solver has been shown to maximize accuracy and minimize run-time when applied to problems that require an accurate resolution of the boundary data (e.g., species concentrations at cell layer level), but not of the data in the bulk (e.g., ROS and EGF concentrations in the extracellular matrix) [22]. The boundary conditions of the problem consist of an homogeneous Dirichlet boundary condition at z = ∞, and homogeneous Neumann boundary conditions at x = 0, ∞. The instant of wound induction is taken as the zero of time, at which the ligand and protease concentrations are assumed to be zero throughout the domain. ROS concentration is also zero everywhere except around x = 0, where s(x = 0, z = 0, t = 0) = δ(0), with the Dirac delta-function approximated by a tall, thin Gaussian centered at x = 0. The solver and its implementation are described in more detail in the SI.
Steady States & Traveling Fronts
Multistability is a common feature of reaction-diffusion systems similar to ours. For our model, all the steady states of the system, except the trivial one, will be spatially inhomogeneous because of the non-local nature of the problem. Therefore, by equilibrium solution of the system we mean solutions that are constant in space across the epithelial layer, but not along the normal direction. Within this context, the steady states of the model described by Eqs. (20)–(24) satisfy:
| (25) |
where the overbar indicates that the value of ligand or ROS concentration is taken at z = 0 (e.g., l̄ = l(x, z = 0, t)). In particular, the following condition needs to hold:
| (26) |
This equation is always satisfied by the trivial solution (l̄ = 0, s̄ = 0), but under certain conditions it can have two more solutions, as highlighted in Fig. 4-(a). In this case the three roots are two stable steady states, l̄0 and l̄2, and an unstable one, l̄1. The two stable steady states represent a state of no ligand signaling, l̄0 = 0, and a state of active ligand signaling, l̄2 > 0, respectively. From Fig. 4, we can also infer how ROS concentration s̄ and the activation threshold cA control the steady states of the system. If we fix the activation threshold at a sufficiently high value, the system attains only the trivial steady state, l̄ = l̄0 = 0, unless there is enough ROS to sustain the signaling pathway, as shown in Fig. 4-(b). Conversely, if we fix s̄, the system will be bistable only if the activation threshold cA is sufficiently small (Fig. 4-(c)).
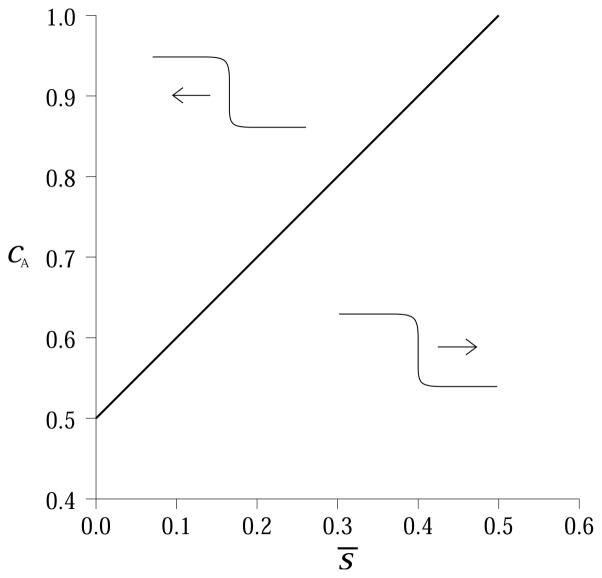
Figure 4.
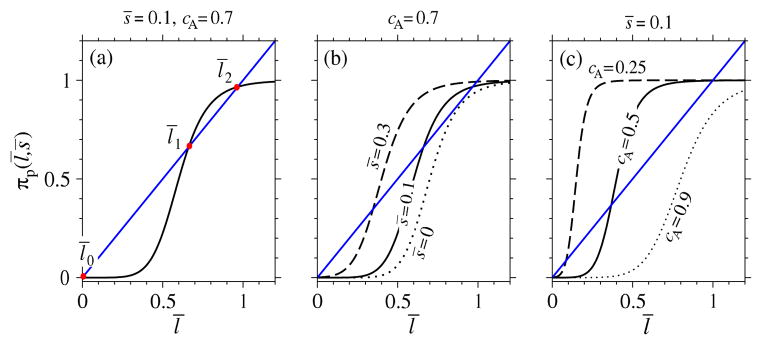
Steady state configurations. (a) graphical solution of Eqn. (26) for s̄ = 0.1, and cA = 0.7. There are three solutions representing two stable steady states (l̄0 and l̄2) and one unstable equilibrium (l̄1). (b) if we fix the activation threshold (cA = 0.7), different values of ROS concentration lead to different steady state configurations. Bistability is possible if there is enough ROS, otherwise the only stable steady state is the one with no MAPK activity. (c) we fix ROS concentration to s̄ = 0.1 and graphically solve Eqn. (26) for different values of cA. Bi-stability can arise only if the activation threshold is sufficiently small. The Hill coefficient n = 8 was used in all plots.
Now that we have established the conditions for bistability, we wish to determine the existence of traveling waves connecting the two stable equilibria. Unfortunately, the model is too complicated to prove the existence of traveling waves unless we simplify it. We can prove the existence of traveling waves for a simpler scenario in which the concentration of ROS at cell layer level, s̄, is constant and in the limit n → ∞ for the Hill coefficient of πp. In this limit, the sigmoidal protease production function πp approaches a Heaviside function centered at cA – s̄:
| (27) |
Under these conditions, the system is bistable for 0 < cA – s̄ < 1, and the roots of Eqn. 26 are l̄0 = 0, l̄1 = cA – s̄, and l̄2 = 1. The existence of traveling fronts in the presence of bistability follows from the work of Cabre et al. [3]. In addition, we can determine the velocity and direction of the traveling fronts by proceeding as in [18], obtaining:
| (28) |
which gives an implicit relation for v, the velocity of the traveling wave for a fixed concentration of ROS. The integration variable q in the above integral arises from the Fourier transform used to derive Eqn. 28. From Eqn. 28, we find that the front velocity is a monotonically increasing function of the parameter α (see Eqn. 17). This result is expected since an increase in α corresponds to either an increase in ligand diffusivity or a decrease in ligand binding, and both changes result in the front reaching farther distances in a shorter amount of time. The direction of the front is determined by the threshold cA – s̄. If cA – s̄ < 1/2, the front of active MAPK will move away from the wound, and deep into the cell layer. If cA – s̄ > 1/2, MAPK activity will recede toward the wound. Regimes that delineate forward and backward traveling MAPK waves are indicated in Fig. 5. These results provide useful insight for the general case of n < ∞ and diffusing ROS. Numerical simulations show that for Hill coefficient as low as n = 6, the instantaneous front velocity is within 10% of that obtained from Eqn. 28. To summarize, we showed that the system can have two stable steady states and that traveling wave solutions connecting them are possible. In particular, ROS concentration can determine the existence, velocity and direction of the fronts by effectively regulating the activation threshold of the MAPK cascade.
Figure 5.
Traveling waves connecting the state of MAPK activation and the state of MAPK inactivity can move toward or away from the wound depending on ROS concentration at cell layer level (s̄) and activation threshold (cA) when n → ∞. The thick black line indicates conditions under which the front is not moving. Regimes above the line lead to traveling waves moving toward the wound, while those below the line lead to fronts moving away from the wound.
ROS/EGF regulation of MAPK activation
In this section we explore the parameter space of the wound healing assay to determine the nature of the MAPK fronts observed in [16, 20]. To avoid ambiguity, we divide the MAPK dynamics during wound healing into three wave-like events. The first event corresponds to the fast activation of MAPK initiated by the wound. It lasts until the activation front reaches its maximum depth in the cell layer. The second event is characterized by decrease of MAPK activity. It moves from deep into the epithelial monolayer toward the wound. These first two events qualitatively correspond to the first “rebounding wave” observed in the experiments [16, 20]. The last event consists of a slow activation front that starts near the wound edge and moves away from the wound. This last “wave” is initiated when the cells in the layer start moving to close the wound itself, and is sustained when the wound is large, preventing closure in finite time [20].
To reproduce the observed MAPK dynamics, we numerically integrated Eqns. (20)–(24) using the ligand related parameters given in Table 1. Although we could not find analogous references for physical parameters of ROS, we estimated parameter values from various sources. We used the self-diffusivity of water together with the Einstein relation to bound the value of η between 10 and 100. From the results in [27], it seems reasonable to assume . We assume that the initial concentration of ligand and protease is zero, while the concentration of ROS is represented by a narrow Gaussian with width equal to the size of a single cell; it represents the ROS initially released by cell rupture. Our numerical results are summarized in Figs. 6 and 7.
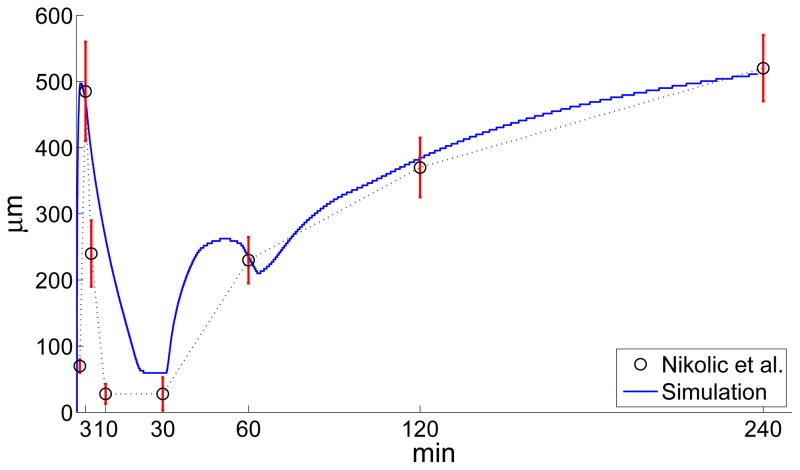
Figure 6.
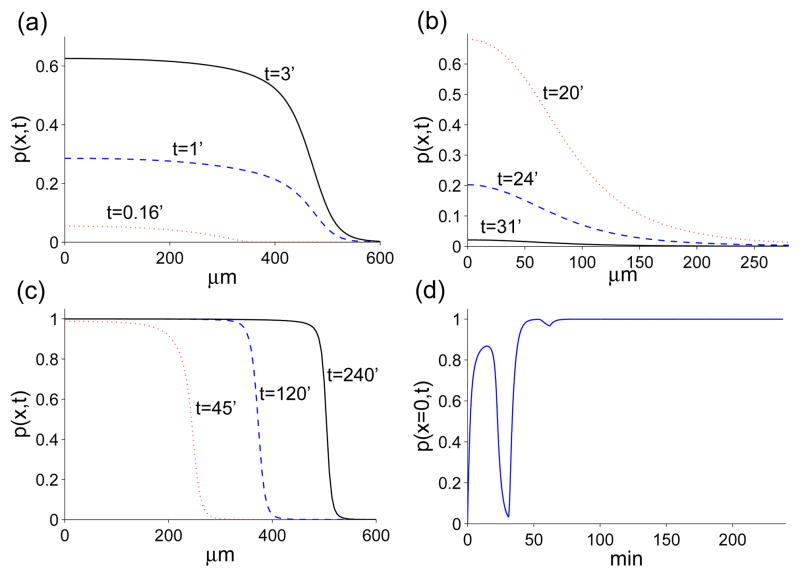
Time evolution of the distance from the wound edge of the MAPK front. The circles and the intersecting vertical bars represent the average front position and one standard deviation error bars, respectively. Their values have been obtained from the experimental data in [20]. The solid trace has been obtained through a computer simulation of Eqns. (20)–(24) with dimensionless parameters: α = 0.35, η = 16, ν = 5, cA = 0.625, n = 6, γ = 2, pA = 0.975, m = 9, λ = 0.55, τ = 2.56. These parameters are based on kP = 5.6 × 10−3s−1, DL = 5.6 × 10−7cm2s−1, , gL = 0.54 × 10−2s−1, gP = 0.17 × 108cm−2s−1, R = 3.2 × 1011cm−2, , CA = 109cm−2, TD = 420s.
Figure 7.
Time evolution of protease. (a) after injury the fast diffusion of ROS drives MAPK activation. (b) as ROS diffuses away, the positive feedback loop between MAPK and ligand is not strong enough to sustain signaling and the depth of the front decreases. (c) once the cells start moving, ROS production and the ligand-protease feedback loop fuel the activation front. (d) time evolution of protease concentration at x = 0. The parameters used to obtain these plots are the same as the ones used to generate Fig. 6.
Fig. 6 compares the time evolution of the distance of the front from the wound as predicted by Eqns. (20)–(24) with the experimental values observed in [20] for scratch wounds. The position of the front is determined by evaluating the inflection point of protease concentration after each time step. From Fig. 6, we notice that the model does a good job to match the experimental data during increasing MAPK activity, but the model does not represent the decrease in MAPK activity as well. This result is due to the fact that the driving element of MAPK activation is the sharp functional πp, and during MAPK activation the profile of p(x, t) is also sharp (see Fig. 7-(a) and (c)). Conversely, the decrease of MAPK activity corresponds to πp ~ 0, and a dissipating concentration profile p(x, t). For nearly flat density profiles (cf. the profile corresponding to 31min in Fig. 7(b)), the inflection point is experimentally difficult to resolve and may appear to retract extremely fast even though the inflection point of p(x, t) stays stationary as the gradients in p(x, t) disappear. This effect may sugest a faster retraction in the wave front position than is predicted by the model (the ~ 5–20 minte regime in Fig. 6).
Another interesting feature of the MAPK front is the hump at ~ 40–50 minutes. This feature is due to the time delay, τ, in Eqn. 19 which retains a memory of the initial, fast wave (~ 0 – 5 minutes). The experimental data is too sparse to reliable resolve this hump, if it actually occurs. More likely in reality, the delay in ROS generation, Eqn. 19, should not be a sharp time translation, but rather a smoothed memory function described by an integral kernel.
Nonetheless, our overall model is able to qualitatively replicate the observed MAPK behavior. Fig. 7 shows the time evolution of the profiles of the three MAPK “waves”. The first wave (Fig. 7-(a)) is driven by ROS production at the onset of wound and its fast diffusion. However, there is not enough ROS for either ligand or protease concentration to reach the signaling steady state. As a result, the first “wave” can only propagate as far as ~ 480μm before receding. As ROS diffuses away, protease concentrations decrease (Fig. 7-(b)) until the cells start to move (after about 30 minutes from injury). At that time, ROS is produced by the moving cells and fuels the positive feedback loop between ligand and protease. This feedback is strong enough to increase protease levels until they reach a signaling steady-state. At this point, the front moves like a traveling wave (Fig. 7-(c)), with its speed and distance traveled regulated by the ROS source function πs. We can also track the time-evolution of the variables in the model. Fig. 7-(d) shows how protease concentration at the wound edge, x = 0, changes in time. From this graph we observe that during the first MAPK event the protease concentration never reaches the “signaling” steady-state and eventually decreases. During the third wave, protease concentration reaches the “signaling” steady-state and remains there as shown by the flat part of the graph in Fig. 7-(d). Note the dip around T = 60 min due to the time delay in ΠS.
To summarize, only the third MAPK front behaves as a traveling wave, while the initial two events (corresponding to the first “rebounding wave” observed in experiments) are actually transient, diffusion-driven patterns.
Conclusions
We have formulated a mathematical model for the dynamics of intercellular signaling observed during wound healing experiments. From this model, we were able to replicate the signaling patterns observed in [16, 20], and to provide mechanistic insight regarding their nature. From our results, the cooperative behavior between ROS and a diffusible ligand is necessary to explain the observed MAPK activation patterns during epithelial wound healing. Our choice of EGF as the signaling ligand is based upon our literature review, but lacks experimental evidence within the epithelial wound healing assay. However, we showed that the properties of EGF (and EGFR) fit the profile for the unidentified diffusible signals mentioned in [20]. Our model can be expanded to incorporate other diffusible signaling molecules. Although it may be possible to find physiologically realistic sets of parameters that lead to signaling patterns consisting of three separate traveling waves, the parameters associated with the EGF/ROS/MAPK system lead to only one final traveling wave. The first two notable events (initial MAPK wave and its “rebound”) being described by purely diffusive and decaying dynamics, respectively.
An aspect of our current model that needs improvement and further analysis is the determination of the ROS source function ΠS. From the experiments in [20], this term seems to be negligible since extracellular ROS was detected only up to ~ 10min after wounding. However, there is substantial evidence indicating that cell motility and EGFR-driven MAPK activation can induce ROS production. A plausible explanation for these conflicting results could be that ROS produced after wounding is fully recaptured by intracellular processes (including EGFR phosphorylation) and never crosses the cell membrane. Nonetheless, we performed many numerical tests and found that if ΠS = 0 (data not shown), then all three MAPK events are diffusion driven and the signaling pattern is due to the different diffusion properties of ROS and ligand (EGF).
Currently, we represent the positive feedback between MAPK signaling and cell deformation through the molecular species responsible for MAPK activation. A more physically realistic approach would involve the modeling of the forces transmitted by adjoining cells that are contracting and extending while moving toward wound closure, then couple these forces with a biochemical signal (e.g., ROS) that can activate MAPK. There are many obstacles in implementing such model. Some of the cells at the wound edge develop lamellipodia and lead the migration, while the majority of the remaining cells seem to move through a tug-of-war mechanism [37]. It is also very difficult to experimentally quantify the mechanical forces responsible for cell migration. Recently, Trepat et al [37] were able to obtain direct measurements of cell traction and stress in a spreading, uninjured, epithelial layer. Additional complications arise from the multi-scale and three-dimensional nature of the problem, as well as stochastic effects due to the tug-of-war mechanism [37]. Nonetheless, our simple model could be extended by replacing πS with a more realistic mechano-chemical functional.
Supplementary Material
Acknowledgments
We thank M. Gibbons, S. Shvartsman, and C. Muratov for useful discussion. This work was supported by NSF grant DMS-0349195 and NIH grant K25AI058672.
Footnotes
ROS are known to activate EGFR by associating with its cytoplasmic tail, and inactivating its phosphatase activity. Kinetically, modeling this process is equivalent to irreversible ROS-EGFR (CS ≡ R · S) complex formation.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Ali MH, Mungai PT, Schmacker PT. Stretch-induced phosphorylation of focal adhesion kinase in endothelial cells: role of mitochondrial oxidants. Am J Physiol Lung Cell Mol Physiol. 2006;291:38–45. doi: 10.1152/ajplung.00287.2004. [DOI] [PubMed] [Google Scholar]
- 2.Block ER, Matella AR, SundarRaj N, Iszkula ER, Klarlund JK. Wounding induces motility in sheets of corneal epithelial cells through loss of spatial constraints. J Biol Chem. 2004;279:24307–24312. doi: 10.1074/jbc.M401058200. [DOI] [PubMed] [Google Scholar]
- 3.Cabre X, Sola-Morales J. Layer solutions on a half-space for boundary reactions. Comm Pure Appl Math. 2005;I.VIII:1678–1732. [Google Scholar]
- 4.DiMilla PA, Barbee K, Lauffenburger DA. Mathematical model for the effects of adhesion and mechanics on cell migration speed. Biophys J. 1991;84:2907–2918. doi: 10.1016/S0006-3495(91)82027-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ferrell JE. Tripping the switch fantastic: how a protein kinase cascade can convert graded inputs into switch-like outputs. Trends Biochem Sci. 1996;12:460–466. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
- 6.Ferrell JE. How responses get more switch-like as you move down a protein kinase cascade. Trends Biochem Sci. 1997;8:288–289. doi: 10.1016/s0968-0004(97)82217-7. [DOI] [PubMed] [Google Scholar]
- 7.Hornberg JJ, Binder B, Bruggeman FJ, Schoeberl B, Heinrich R, Westerhoff HV. Control of MAPK signalling: from complexity to what really matters. Oncogene. 2005;24:5533–5542. doi: 10.1038/sj.onc.1208817. [DOI] [PubMed] [Google Scholar]
- 8.Huang CF, Ferrell JE. Ultrasensitivity in the mitogen-activated protein kinase cascade. PNAS. 1996;93:10078–10083. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Joslin EJ, Opresko LK, Wells A, Wiley HS, Lauffenburger DA. EGF-receptor-mediated mammary epithelial cell migration is driven by sustained ERK signaling from autocrine stimulation. J Cell Sci. 2007;120:3688–3699. doi: 10.1242/jcs.010488. [DOI] [PubMed] [Google Scholar]
- 10.Keener J, Sneyd J. Mathematical Physiology. Springer; Berlin: 1998. [Google Scholar]
- 11.Kholodenko BN. Cell signalling dynamics in time and space. Nat Rev Mol Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kholodenko BN. Untangling the signalling wires. Nature Cell Biol. 2007;9:247–249. doi: 10.1038/ncb0307-247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kiehart DP. Wound healing: The power of the purse string. Curr Biol. 1999;9:R602–R605. doi: 10.1016/s0960-9822(99)80384-4. [DOI] [PubMed] [Google Scholar]
- 14.Maini PK, McElwain DLS, Leavesley D. Travelling waves in a wound healing assay. Appl Math Lett. 2004;17:575–580. [Google Scholar]
- 15.Martin P, Parkhurst SM. Parallels between tissue repair and embryo morphogenesis. Development. 2004;131:3021–3034. doi: 10.1242/dev.01253. [DOI] [PubMed] [Google Scholar]
- 16.Matsubayashi Y, Ebisuya M, Honjoh S, Nishida E. ERK activation propagates in epithelial cell sheets and regulates their migration during wound healing. Curr Biol. 2004;14:731–735. doi: 10.1016/j.cub.2004.03.060. [DOI] [PubMed] [Google Scholar]
- 17.McCubrey JA, LaHair MM, Franklin RA. Reactive oxygen species-induced activation of the MAP kinase signaling pathways. Antiox Redox Sign. 2006;8:1775–1793. doi: 10.1089/ars.2006.8.1775. [DOI] [PubMed] [Google Scholar]
- 18.Muratov CB, Posta F, Shvartsman SY. Autocrine signal transmission with extracellular ligand degradation. Phys Biol. 2009;6:13. doi: 10.1088/1478-3975/6/1/016006. [DOI] [PubMed] [Google Scholar]
- 19.Murray JD. Mathematical Biology II: Spatial Models and Biomedical Applications. Springer; Berlin: 2003. [Google Scholar]
- 20.Nikolić DL, Boettiger AN, Barbeckans JD, Shvartsman SY. The role of boundary conditions in an experimental model of epithelial wound healing. AJP-Cell Physiology. 2006;291(1):C68–C75. doi: 10.1152/ajpcell.00411.2005. [DOI] [PubMed] [Google Scholar]
- 21.Orton RJ, Sturm OE, Vyshemirky V, Calder M, Gilbert DR, Kolch W. Computational modelling of the receptor-tyrosine-kinase-activated MAPK pathway. Biochem J. 2005;392:249–261. doi: 10.1042/BJ20050908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Posta F, Shvartsman SY, Muratov CB. Compensated optimal grids for elliptic boundary-value problems. J Comput Phys. 2008;227:8622–8635. doi: 10.1016/j.jcp.2008.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Poujade M, Grasland-Mongrain E, Hertzog A, Jouanneau J, Chavrier P, Ladoux B, Buguin A, Silberzan P. Collective migration of an epithelial monolayer in response to a model wound. PNAS. 2007;104:15988–15993. doi: 10.1073/pnas.0705062104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pribyl M, Muratov CB, Shvartsman SY. Discrete models of autocrine cell communication in epithelial layers. Biophys J. 2003;84:3624–3635. doi: 10.1016/S0006-3495(03)75093-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pribyl M, Muratov CB, Shvartsman SY. Long-range signal transmission in autocrine relays. Biophys J. 2003;84:883–896. doi: 10.1016/S0006-3495(03)74906-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Qiao L, Nachbar RB, Kevrekidis IG, Shvartsman SY. Bistability and oscillations in the huang-ferrell model of MAPK signaling. PLoS Comp Biol. 2007;3:1819–1826. doi: 10.1371/journal.pcbi.0030184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reynolds AR, Tishcer C, Verveer PJ, Rocks O, Bastiaens PIH. EGFR activation coupled to inhibition of tyrosine phosphatases causes lateral signal propagation. Nature Cell Biol. 2003;5:447–453. doi: 10.1038/ncb981. [DOI] [PubMed] [Google Scholar]
- 28.Rhee S, Bae Y, Lee S, Kwon J. Hydrogen peroxide: A key messenger that modulates protein phosphorylation through cysteine oxidation. Sci STKE. 2000;53:pe1–pe4. doi: 10.1126/stke.2000.53.pe1. [DOI] [PubMed] [Google Scholar]
- 29.Roy S, Khanna S, Nallu K, Hunt TK, Sen CK. Dermal wound healing is subject to redox control. Mol Ther. 2006;13:211–220. doi: 10.1016/j.ymthe.2005.07.684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Santos SDM, Verveer PJ, Bastiaens PIH. Growth factor-induced MAPK network topology shapes erk response determining PC-12 cell fate. Nature Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
- 31.Sasagawa S, Ozaki Y, Fujita K, Kuroda S. Prediction and validation of the distinct dynamics of transient and sustained ERK activation. Nat Cell Bio. 2005;7:365–373. doi: 10.1038/ncb1233. [DOI] [PubMed] [Google Scholar]
- 32.Schoeberl B, Eichler-Jonsson C, Gilles ED, Muller G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nature Biotech. 2002;20:370–375. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- 33.Sen CK, Roy S. Redox signals in wound healing. Biochim Biophys Acta. 2008;1780:1348–1361. doi: 10.1016/j.bbagen.2008.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sherratt JA, Murray JD. Models of epidermal wound healing. Proc Roy Soc Lond. 1990;241:29–36. doi: 10.1098/rspb.1990.0061. [DOI] [PubMed] [Google Scholar]
- 35.Shvartsman SY, Muratov CB, Lauffenburger DA. Modeling and computational analysis of EGF receptor-mediated cell communication in Drosophila oogenesis. Development. 2002;129:2577–2589. doi: 10.1242/dev.129.11.2577. [DOI] [PubMed] [Google Scholar]
- 36.Torres M. Mitogen-Activated Protein Kinase pathways in redox signaling. Front Biosc. 2003;8:369–391. doi: 10.2741/999. [DOI] [PubMed] [Google Scholar]
- 37.Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA. Physical forces during collective cell migration. Nat Phys. 2009;5:426–430. [Google Scholar]
- 38.Wiley HS, Shvartsman SY, Lauffenburger DA. Computational modeling of the EGF-receptor system: a paradigm for systems biology. TRENDS Cell Biol. 2003;13:43–50. doi: 10.1016/s0962-8924(02)00009-0. [DOI] [PubMed] [Google Scholar]
- 39.Xu K, Ding Y, Ling J, Dong Z, Yu FX. Wound-induced HB-EGF ectodomain shedding and EGFR activation in corneal epithelial cells. Inv Ophthalmol Vis Sci. 2004;45:813–820. doi: 10.1167/iovs.03-0851. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.