WHAT IS A MOMENT ARM? CALCULATING MUSCLE EFFECTIVENESS IN BIOMECHANICAL MODELS USING GENERALIZED COORDINATES

Abstract

Biomechanics researchers often use multibody models to represent biological systems. However, the mapping from biology to mechanics and back can be problematic. OpenSim is a popular open source tool used for this purpose, mapping between biological specifications and an underlying generalized coordinate multibody system called Simbody. One quantity of interest to biomechanical researchers and clinicians is “muscle moment arm,” a measure of the effectiveness of a muscle at contributing to a particular motion over a range of configurations. OpenSim can automatically calculate these quantities for any muscle once a model has been built. For simple cases, this calculation is the same as the conventional moment arm calculation in mechanical engineering. But a muscle may span several joints (e.g., wrist, neck, back) and may follow a convoluted path over various curved surfaces. A biological joint may require several bodies or even a mechanism to accurately represent in the multibody model (e.g., knee, shoulder). In these situations we need a careful definition of muscle moment arm that is analogous to the mechanical engineering concept, yet generalized to be of use to biomedical researchers. Here we present some biomechanical modeling challenges and how they are resolved in OpenSim and Simbody to yield biologically meaningful muscle moment arms.

INTRODUCTION

Biological systems are much more complex than engineered systems at similar scales. To reduce this complexity when investigating biomechanical aspects of vertebrates (e.g., gait disorders in humans [1–3], the mechanics of human running [4, 5], or the maximum speed of a Tyrannosaurus [6, 7]), a practical and widely used approach is to model them as multibody systems, with rigid bodies for bones and physiologically-relevant generalized coordinates assigned to represent joint mobility. Biomechanical researchers then study the multibody system, using well-understood principles of mechanics to obtain a deeper understanding of the biological system—for example, determining which muscles contribute most to mass center acceleration during running [5]. Unfortunately, neither the mapping from biology to a useful multibody model nor the extraction of clinically relevant results from a multibody simulation is straightforward. For example, biologists have a well-developed concept of “joint” that does not map neatly to the body-to-body interconnections in a multibody system. In practice we encounter problems of definition, modeling, implementation, and interpretation.

In this paper we illustrate these issues by closely examining a single aspect of biomechanical modeling: how to determine a meaningful “moment arm” for muscles. Biomechanical researchers and clinicians are keenly interested in this quantity, by which they mean roughly the “effectiveness” of a particular muscle at generating a particular motion of interest (for example, knee flexion during gait [8]), with application to surgical and rehabilitation planning [9]. But transferring the mechanical concept of moment arm—the distance from force line of action to center of rotation—to biology is deceptively difficult. What is the “line of action” for a muscle that follows a curved, evolving path over the skeleton and connective tissue [10]? Where is the “center of rotation” when a muscle spans several joints, or when a single biological joint like a knee or shoulder requires a mechanism to represent accurately [11, 12]? How is the moment arm usefully defined when the joints a muscle spans exhibit coupled rotational and translational motion, as biological joints commonly do [13]?

We have developed two open source software packages that together resolve these issues: OpenSim [14], an application biomechanical researchers and clinicians use to model and study actively controlled, muscle-actuated biological systems in motion, and Simbody [15], a high-performance generalized coordinate multibody library built specifically to support the unique features of biologically-derived multibody models.

This paper is organized as follows. First, we present issues that arise in biomechanical multibody models that complicate muscle moment arm calculation. Then we discuss how we map from the biologist’s viewpoint to the rigorous problem definition needed for multibody treatment. Given the definition, we then compare several methods for calculating moment arm using available multibody operators, and present the precise definition and calculation used in OpenSim. Finally, we argue that the chosen method satisfies both the rigorous definition and the expectations of biomechanical researchers and clinicians.

BIOMECHANICAL MODELING ISSUES

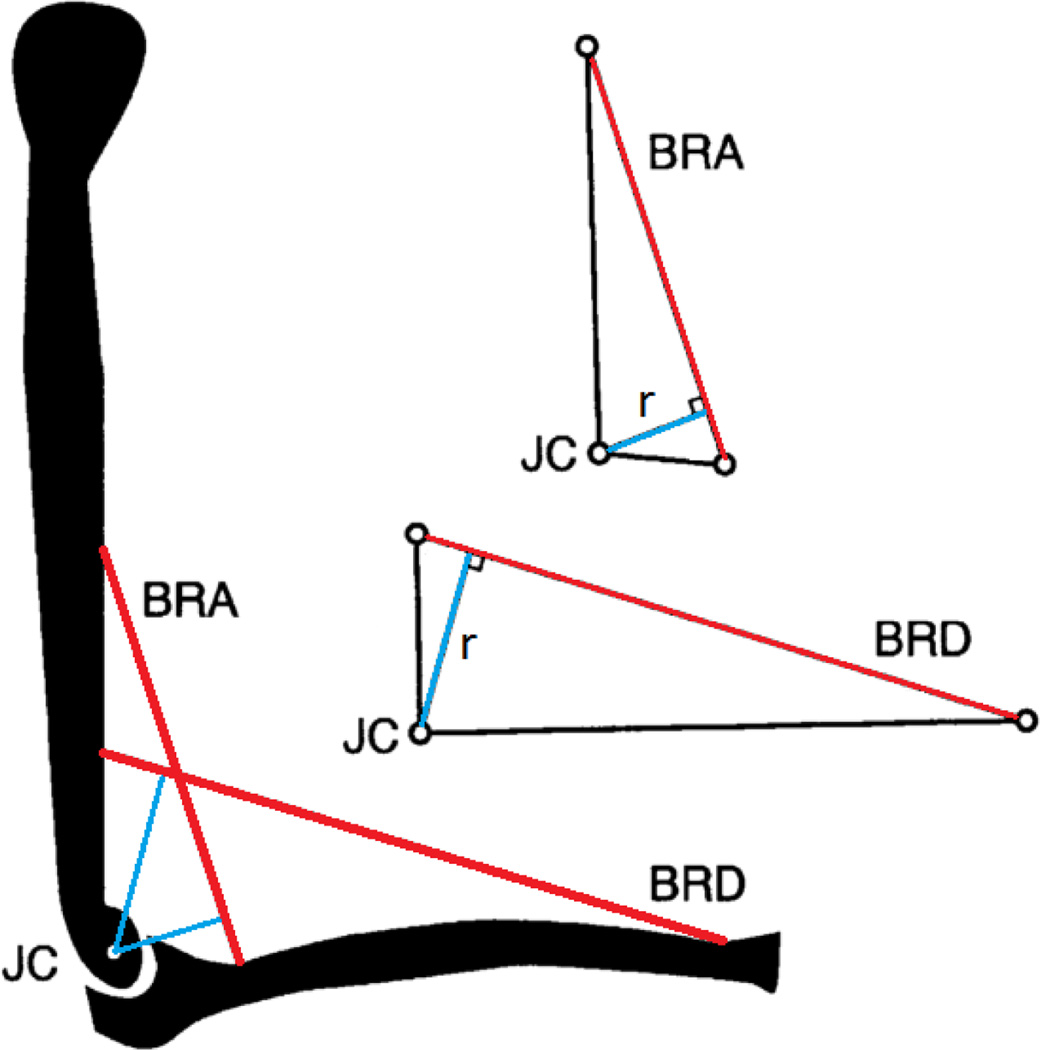
Moment arm is such a simple concept in mechanics that it is easy to assume it should be simple in biomechanics as well. Figure 1 (adapted from Ref. [17]) shows a straightforward case. The brachialis (BRA) and brachioradialis (BRD) muscles are modeled here as straight-line musculotendon actuators; the elbow, by a revolute joint with a well-defined joint center (JC). The moment arm r is determined using the conventional mechanics definition given in the introduction.

Figure 1.

AN EASY CASE: MOMENT ARM IS DISTANCE FROM LINE OF ACTION TO JOINT CENTER.

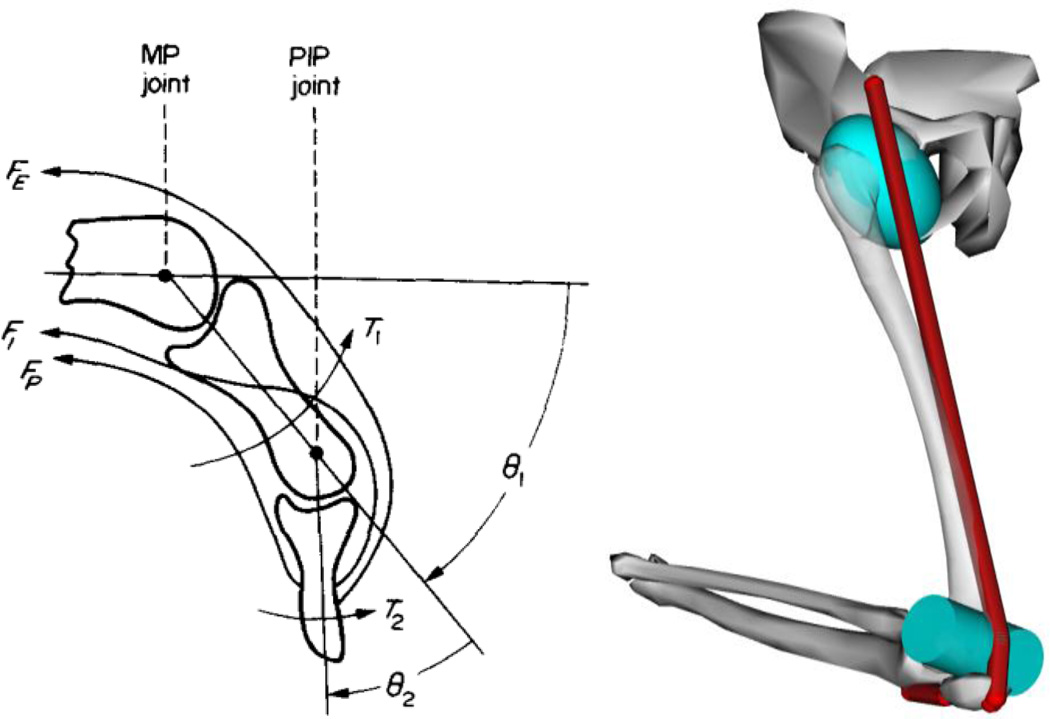
However, a simple mechanism-like approximation of a biological system, such as that of Figure 1, is often inadequate for drawing clinically meaningful conclusions. Figure 2 (left) is an anatomical drawing from Ref. [18] of a finger model showing the curved paths of three tendons, each crossing two joints. Figure 2 (right) shows an OpenSim model from Ref. [19] of the lower limb including path points and geometric obstacles used to approximate a multiarticular musculotendon path, and including a moving patella constrained to track knee rotation. These are representative of the more general situations for which “muscle moment arm” must be defined and calculated. In each case, a muscle generates a scalar tension force s along its path; the moment arm r (with units of length) of that muscle about a “joint of interest” should characterize its effectiveness at generating a torque τ about that joint, such that τ=rs. Defining these quantities is made difficult by the fact that the “joint of interest” may not be any of the individual connections between bones, but can be a measurable quantity that is internally a composition of several joints. For example, Gonzalez et al. [20] modeled wrist flexion-extension kinematics as two coupled revolute joints with the total flexion angle divided evenly between the two. Then the moment arm measures the effectiveness of the muscle at producing total wrist flexion.

Figure 2.

HARDER CASES: TENDONS CROSS MULTIPLE JOINTS, SLIDE OVER OBSTACLES.

As a further implementation difficulty, consider that the desirable use of generalized (relative) coordinates in biomechanics may require coordinate choices that reflect the coupled rotations and translations generated by the complex geometry of joints [13]. This can lead to generalized coordinates and generalized forces that cannot be interpreted directly in any familiar units, such as angles, lengths, forces, or moments. For example, a model may define a generalized coordinate that ranges from 0 to 1 as the joint it controls performs a coordinated rotation and translation in three dimensions.

Muscle modeling

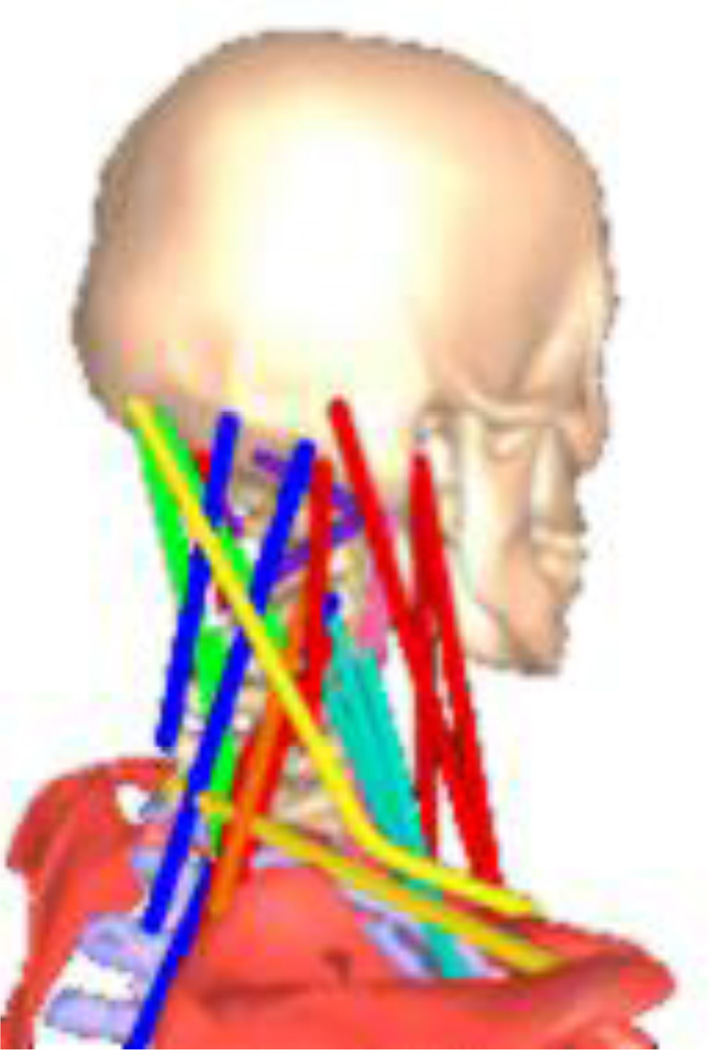
While real muscles are distributed over a volume, biomechanists commonly model them as one or more thin, curved musculotendon (MT) actuators following the centroid of the muscle volume, comprising an active muscle fiber and passive tendon in series [21]. An MT actuator is considered to connect an “origin” point fixed on one body to an “insertion” point fixed on a distal body, via a minimum-length curved path possibly passing (frictionlessly) through “via points” and over “wrapping surfaces” fixed to these or other bodies. Such bodies may be located arbitrarily within the multibody connectivity graph; they do not necessarily lie along a common branch. For example, the model described in Ref. [11] has a patella with multiple MT attachments connected to the tibia but constrained to be coordinated with the knee angle. A neck “joint” may provide just a few degrees of freedom, but involve the coordinated motion of a half dozen vertebrae with muscles that cross all of them and slide over geometric obstacles. Figure 3 shows a neck model [22] reproduced with permission from Ref. [23].

Figure 3.

VASAVADA NECK MODEL.

Moving muscle points

One OpenSim modeling feature, “moving muscle points” (MMPs) has implications for moment arm calculation. These are path via points whose locations are specified functions of the configuration, typically using spline curves keyed to generalized coordinate values and fit through empirically-obtained data, such as the MRI images of the spine used in Ref. [24]. These can produce excellent kinematic models, but because no physical mechanism is provided to drive the motion of these points (which are under load from the muscle), unaccounted work would be done at those points in kinetic and dynamic studies. However, MMPs can be used as a modeling step to determine the shapes of workless wrapping surfaces to be used in those studies.

While OpenSim can calculate moment arms for models with MMPs, results will differ from empirical measurements made on physical systems so must be used cautiously. This is discussed further below.

Reference model

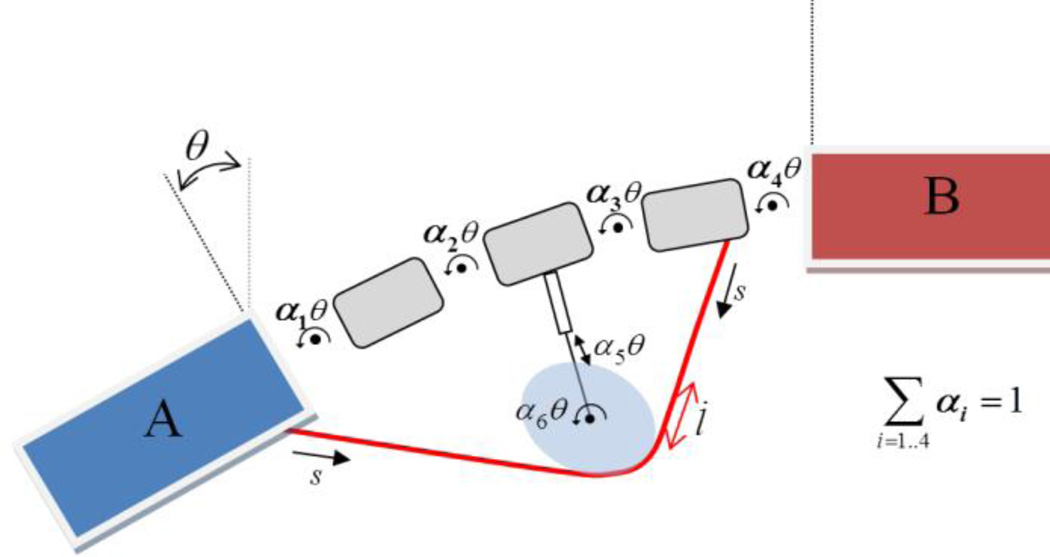
For the remainder of this paper, we will use the multibody model shown in Figure 4 to clarify the calculation of moment arms. This simplified model captures all the issues of relevance to moment arm calculation that arise in multibody models produced by OpenSim users. There is a well-defined angle of interest θ that relates the orientation of body B to that of body A, and there is a particular MT actuator of path length l with origin point on A and insertion point on one of the intermediate bodies. We would like to know the moment arm r_θ of this MT actuator with respect to θ, over a range of values for θ.

Figure 4.

IDEALIZED BIOMECHANICAL MULTIBODY MODEL.

As shown, the angle of interest θ is the sum of four coupled angles: θ_i = α_iθ, i=1‥4. Other coupled coordinates θ_5,6 are present and affect l via a frictionless wrap surface, but are not part of the definition of θ (a patella is modeled similarly, with θ the knee angle). Note that the angles θ_i are not necessarily the same as the generalized coordinates q, which can have any units. However, there are six coupler constraints (discussed below) in this model so that there is just a single remaining degree of freedom between A and B for purposes of moment arm calculation. Any other unconstrained mobilities are locked if necessary so that l=l(θ).

Although only one wrap surface is shown, there can be many more and the muscle path is expected to follow a smoothly-evolving trajectory over them, which requires the solution of a nonlinear computational geometry problem for each configuration. This calculation is generally solved approximately, leading to numerical variability in the calculated path length l, which is problematic for estimation of the path length time derivative $\dot{l}$. Consequently, we will be interested in moment arm calculations that can be performed without explicit calculation of $\dot{l}$.

DEFINITION OF MUSCLE MOMENT ARM

We would like a clinically-useful definition of muscle moment arm that can be used for biomechanical models such as the ones described above. Biomechanists view muscle moment arm r as an instantaneous measure of the effectiveness with which the contraction force of a given muscle can generate a torque at a “joint of interest,” while in a given configuration q. The result is expected to be a scalar quantity with units of length, and to depend only on geometry (not material or mass properties). That means the definition must involve only kinematic relationships so that r=r(q). To be useful, calculation of r must also be fast since biomechanists expect to obtain plots of moment arms versus configuration for numerous muscles as an incidental output of simulations involving extensive motion.

Given the requirement that a moment arm depends only on some joint-associated kinematic quantity θ, we can designate the muscle’s moment arm with respect to that quantity as r_θ, and define it as follows:

$$r_{\theta }\triangleq \frac{{\tau }_{\theta }}{s}$$ (1)

where τ_θ is a scalar representing the “effective torque” acting about θ that is due to the scalar tension force s>0 generated by muscle activation. Following Lieber [9], we take Eqn. (1) as the fundamental definition of muscle moment arm. Determination of effective torque will be discussed below.

In general, the joint of interest may reflect the complex combined effect of several internal components; we require that there is a well-defined angular quantity θ determined kinematically as θ=θ(q) associated with the joint, as illustrated in Figure 4. Therefore, a muscle’s moment arm is defined only for angles θ that determine muscle path length l kinematically. That is, we expect a small displacement dθ to produce a small length change dl that depends only on q, not on velocities, forces, or masses. All generalized coordinates q that can affect θ are thus assumed to be coupled; any that are not coupled explicitly by a constraint will be held constant during the moment arm calculation (they are “coupled” with a coupling factor α=0).

When calculating moment arm, we expect that all constraints affecting the relevant kinematics are workless. This implies that wrapping surfaces and via points are frictionless, and that all motions that can affect the muscle or joint are enforced using physically-valid, time-independent constraint elements. Provided that any motion of our model satisfies these constraints, work equivalence [25] allows us to conclude that

$$sdl={\tau }_{\theta }d\theta$$ (2)

where l=l(q) is the musculotendon path length along which tension s is acting. Combining (2) with the moment arm definition (1) we have

$$r_{\theta }=\frac{dl}{d\theta }$$ (3)

Equation (3) provides a convenient method for calculating moment arm, especially in a laboratory setting [18, 26] where it is referred to as the “tendon excursion method,” but it must be emphasized that this is not a definition but a consequence of the assumption that all constraints are workless. Definition (1) is more general; however, in this paper we will primarily address moment arm calculations for which the assumption behind Eqn. (3) holds. As noted above, models containing MMPs violate this assumption. For those models, calculations based directly on Eqn. (1) can still be performed, but we caution that they cannot be expected to match empirical results measured with methods based on Eqn. (3).

Note that all the quantities we used in the definition above are ordinary physical quantities: angles, lengths, forces, and torques. In practice, biomechanists build multibody models using generalized coordinates and corresponding generalized forces. It is worth emphasizing again that such quantities may truly be generalized—they do not necessarily have physical units. Therefore, careful conversion to physical units is essential to use generalized coordinates to calculate physically-meaningful quantities like moment arm. We will address this conversion below.

Specification of a “joint of interest”

An OpenSim user requesting a moment arm calculation specifies a muscle, and chooses one of the available angular quantities that may be affected by that muscle. OpenSim 3.0 offers only a generalized coordinate subset for this purpose, so θ is always one of the q’s; however, that is not a necessary restriction for the methods to be presented. Currently, when the angle of interest is the sum of several coupled rotations as in Figure 4, the coordinate associated with one of them (called the independent coordinate) is scaled so that it reads as the total angle rather than just the angle it controls directly. Muscles crossing wrist, ankle, neck, and back may be modeled with a single independent coordinate measuring the total angle, while several dependent coordinates are coupled to it. Coupler constraints are added separately to enforce the desired cooperative motion of the dependent coordinates. The algorithm below does not require this approach, but there must be some way to calculate θ from the q’s and $\dot{\theta }$ from the $\dot{q}’s$.

Note that a muscle path may cross several independent coordinates, such as a hip and knee angle as in Figure 2. When moment arm is calculated for one of those coordinates, the others are held rigid (meaning again that it is seen as coupled temporarily, with a coupling factor of 0).

Modeling assumptions

To calculate muscle moment arms as defined above, using the methods to be described below, certain assumptions about properties of the biomechanical models must hold. These are implied by the discussion above but are made explicit here.

Assumption 1

kinematically-determined path geometry. Although an MT path includes both muscle fiber and tendon segments whose relative lengths vary dynamically, we assume that the total length l for a given MT path is just a kinematic quantity l (q) (typically representing the shortest path from origin to insertion) that can be calculated once the poses of all the bodies are known via specification of the generalized coordinates q. So for any given MT path we have

$$l=l(q)$$ (4)

This implies that the path is massless and frictionless.

Assumption 2

uniform tension and linear tension-to-force transmission. Force generation by an MT actuator is completely characterized by a scalar tension s ≥ 0 acting uniformly along the path, such that the matrix of spatial forces F applied by the muscle in a given configuration is just a linear function of s:

$$F(q;s)=T(q)s$$ (5)

where T is the muscle’s instantaneous “force transmission matrix,” a stacked vector of per-body spatial vectors. We expect that, assuming a particular configuration q, a muscle element can efficiently compute F given s; T is not necessarily calculated explicitly.

Assumption 3

physical modeling of MT path kinetics. Any motion of the points at which an MT path applies forces must be modeled in a physically realizable manner by workless constraints or contact with frictionless geometric obstacles. Widely used “coupler constraints” (which constrain the relative motion of a set of generalized coordinates using gear-like transmission elements) are workless and enable moment arm calculations involving composite joints. This assumption can be relaxed to permit moment arm calculation for models containing MMPs, although there are some important caveats we will discuss.

THE MULTIBODY SYSTEM

A few properties of Simbody’s generalized coordinate multibody systems are necessary for the derivation below and are summarized here.

Generalized speeds u are not always the same as time derivatives $\dot{q}$ of the generalized coordinates q, although they are closely related. This distinction will be important below because generalized forces f are dual to generalized speeds, but not to generalized coordinate derivatives. In Simbody, the relationship between generalized speeds and generalized coordinate derivatives is given by a block diagonal matrix N(q):

$$\dot{q}\triangleq \frac{dq}{dt}=Nu$$ (6)

There is a dual relationship between forces and velocities when measured in the same basis. The contribution of generalized speed u_i to body B’s spatial velocity V^B (at B’s origin) is:

$$V_i^{\mathrm{B}}=J_i^{\mathrm{B}}{u}_i$$ (7)

where Jacobian $J_i^{\mathrm{B}}=J_i^{\mathrm{B}}(q)$, and $V^{\mathrm{B}}=\sum V_i^{\mathrm{B}}$. (This holds in Simbody’s formulation even with prescribed motion, which always enters through prescribed generalized coordinates and speeds.) The dual of this relationship relates a spatial force F^B applied at body B’s origin to its contribution to the generalized force f_i acting at mobility u_i:

$$f_i={(J_i^{\mathrm{B}})}^T{F}^{\mathrm{B}}$$ (8)

The equations of motion for the multibody model representing our system at the acceleration level are

$$M\dot{u}+G^T\lambda =f_{\text{applied}}-f_{\text{inertial}}$$ (9)

$$G\dot{u}=b$$ (10)

Here f_applied is the generalized force equivalent of all applied forces including gravity, and f_inertial is the generalized force equivalent of the gyroscopic and Coriolis forces. λ is the vector of Lagrange multipliers needed to enforce the acceleration-level constraints in Eqn. (10), which arise from differentiation of the position (holonomic) and velocity (nonholonomic) constraints. G=G(q) is the constraint Jacobian and b contains time and velocity dependence, if any. M is the generalized mass matrix (not actually formed in an O(n) multibody code). Simbody can efficiently calculate $\dot{u}$ and λ given the state (q and u) and the applied forces. Alternatively, given the state, $\dot{u}$, and λ, Simbody can efficiently determine the applied generalized forces using inverse dynamics.

“Coupler constraints” are holonomic constraints c(q)=0 that constrain a subset of generalized coordinates directly, such as q₅ = q₈ / 2 or even $q_1+2q_2+3q_3^2=0$. Sets of these constraints are commonly used in biomechanical models to introduce empirically-observed coordination across composite joints without modeling the complex biological components that are responsible for that coordination. This modeling strategy removes unwanted degrees of freedom, one per coupler constraint. Twice differentiating couplers gives constraints as in Eqn. (10), enforced by joint torques generated by workless transmission elements acting among the related coordinates.

METHODS TO CALCULATE MOMENT ARM

Starting with the definition in Eqn. (1), there are a variety of ways to calculate moment arm differing in precision, implementation difficulty, and conceptual difficulty.

Perturbation method

We can calculate r_θ = dl/dθ directly by finite differencing. That is, we can make a small perturbation Δθ, satisfy all position constraints, update geometric calculations including recalculation of the MT path over obstacles, and measure the resulting change Δl. The advantage of this method is that it directly implements Eqn. (3), and it is conceptually very simple. It is also the method of choice for measuring moment arm in the laboratory, because angular perturbations of cadavers are practical to perform [27, 28]. However, it has several drawbacks for computation: it produces an approximate answer, and it involves linearization difficulties due to the complex path geometry and the need to ensure satisfaction of the nonlinear holonomic constraints. Also, because this calculation is done at the position level, it includes only holonomic constraints and cannot account for nonholonomic constraints such as rolling (if those are present in the model).

As noted above, a model containing MMPs does not satisfy the workless constraint assumption behind Eqn. (3), so the perturbation method cannot produce correct moment arms for these models.

Path velocity method

An easier and exact computation is available using velocities, since we have

$$r_{\theta }=\frac{dl}{d\theta }=\frac{dl/dt}{d\theta /dt}\equiv \frac{\dot{l}}{\dot{\theta }}$$ (11)

That is, if we can calculate $\dot{l}(\dot{\theta })$ then we need only enforce $\dot{\theta }=1$ (for example), satisfy all velocity constraints, then obtain $r_{\theta }\dot{l}(1)$. This is probably the best way to calculate moment arm for systems that satisfy the assumptions of Eqn. (3), provided the operator $\dot{l}(\dot{\theta })$ is available. Unfortunately, as we have discussed it can be difficult to calculate $\dot{l}$; consequently, we would like to find an alternative method that does not depend on that calculation.

Partial velocity method

By Assumption 1 above, we have l=l(q) so

$$\dot{l}\triangleq \frac{dl}{dt}=\sum _i\frac{\partial l}{\partial q_i}\frac{\partial q_i}{\partial t}=P\dot{q}=PNu$$ (12)

with the last equality due to Eqn. (6). P(q) is a 1×n_q “partial velocity matrix” [29] whose i^th entry is the scalar p_i = ∂l/∂q_i. Because we assumed kinematic coupling between the generalized coordinates and θ, $\dot{\theta }$ determines the corresponding generalized speeds. So we can write

$$u=C_{\theta }\dot{\theta }$$ (13)

for some coupling matrix C_θ(q) (an n×1 column matrix with entries c_i), where q, u and C_θ are understood to involve just the path of a given MT. Then from Eqn. (12) we have

$$\dot{l}=PN{C}_{\theta }\dot{\theta }$$ (14)

Next, comparing (14) with (11), we find that

$$r_{\theta }=PN{C}_{\theta }$$ (15)

If we had an explicit representation of P, this would be a good way to calculate r_θ. However, this would imply that we could easily calculate $\dot{l}=P\dot{q}$, contradicting our earlier assumption that $\dot{l}$ is not easily obtained. In models where P can be obtained, this is a practical method for computing moment arm; for example, see Ref. [30].

Since generalized forces are dual to generalized speeds, we will now look at how to use forces instead of velocities to calculate r_θ.

Generalized force method

Simbody can map body spatial forces F to generalized forces f via an operator that calculates

$$f=J^{T}F$$ (16)

in O(n) time, where J=J(q) is the system Jacobian that maps generalized speeds to the body spatial velocities they produce. J is logically assembled from the body Jacobians in Eqn. (7), although it is not formed explicitly by Simbody. Eqn. (5) tells us how to calculate F from a given muscle tension scalar s, using the muscle’s force transmission matrix T. Substituting Eqn. (5) into (16) gives

$$f(s)=J^{T}Ts$$ (17)

The n×1 column matrix J^T T maps muscle tension to generalized force. Because of the necessary power equivalence $f^{T}u=s\dot{l}$, the dual to (17) that maps generalized speeds to $\dot{l}$ is

$$\dot{l}(u)=T^{T}Ju$$ (18)

(compare with Eqns. (7) and (8)). Combining Eqns. (11), (13), (17), and (18) gives

$$r_{\theta }=\frac{\dot{l}}{\dot{\theta }}=\frac{f^{T}u}{s\dot{\theta }}=\frac{f^T{C}_{\theta }}{s}$$ (19)

This provides the algorithm we need for calculating moment arm without calculating $\dot{l}$ directly:

1. Determine the coupling matrix C_θ for the angular quantity of interest θ (see below).

2. Apply unit tension s=s₀ to the muscle of interest and map to body spatial forces F(s) using the muscle’s force transmission Eqn. (5).

3. Use the Simbody operator defined by Eqn. (16) to map body spatial forces F to generalized forces f.

4. Use Eqn. (19) to compute r_θ = f^T C_θ / s₀.

The above algorithm is the method that is used in OpenSim 3.0 to calculate muscle moment arm.

Calculating the coupling matrix C_θ

To calculate C_θ, we prescribe the rate of change for the angular quantity of interest to any non-zero value: $\dot{\theta }={\dot{\theta }}_0$. We then use Simbody’s velocity solver to find the compatible set of generalized speeds u such that all velocity-level constraints are satisfied and $\dot{\theta }(u)={\dot{\theta }}_0$. Now each $u_i=c_i{\dot{\theta }}_0$, so $c_i=u_i/{\dot{\theta }}_0$ and we have determined $C_{\theta }=u/{\dot{\theta }}_0$.

Calculating effective torque

We want to show that our moment arm calculation is consistent with the definition in Eqn. (1) and thus provides a biologically-relevant result. This requires a method to map from generalized forces f(s) provided by the multibody system via Eqn. (17) to the physical torque τ_θ used in the definition.

Since all constraints are presumed to be non-working, the total power p from our reference system in Figure 4 should be the sum of power contributions at the θ_k angles that are coupled to θ. That is,

$$p=\sum {\tau }_k{\dot{\theta }}_k=\sum {\tau }_k{\alpha }_k\dot{\theta }={\tau }_{\theta }\dot{\theta }$$ (20)

$$\Rightarrow {\tau }_{\theta }=\sum {\alpha }_k{\tau }_k$$ (21)

Equation (21) provides the algorithm we need to compute the effective torque τ_θ from the individual joint torques τ_k. There remains one unresolved issue: in a multibody model using generalized coordinates, we will calculate generalized forces, which are not necessarily torques. Also, the angles θ_k and angular rates ${\dot{\theta }}_k$ are not necessarily the same as the corresponding generalized coordinates q_k and speeds u_k, since OpenSim permits, and biomechanists commonly exploit, arbitrary scaling of generalized coordinates.

Denote the scaling of the k^th generalized speed w_k such that ${\dot{\theta }}_k=w_k{u}_k$. Then we must have τ_k = f_k / w_k because f_ku_k and ${\tau }_k{\dot{\theta }}_k$ measure the same physically-meaningful power. So now we can use Eqn. (17) to find f(s) and calculate τ_θ = ∑α_kf_k/w_k and compare it with r_θs.

However, from the definition of C_θ in Eqn. (13) and the definitions of w_k and ${\dot{\theta }}_k$ above, we see that $u_k=c_k\dot{\theta }={\dot{\theta }}_k/w_k={\alpha }_k\dot{\theta }/w_k\Rightarrow c_k={\alpha }_k/w_k$. That permits simplification of our calculation of τ_θ to

$${\tau }_{\theta }=\sum c_k{f}_k=f^T{C}_{\theta }$$ (22)

The generalized coordinate weights w_k drop out of the calculation so do not affect the result. Now substitute Eqn. (22) into (19) to see that the generalized force method for calculating moment arm directly satisfies the definition in Eqn. (1). Since the definition does not rely on the workless constraint assumption, this method can be used even in the presence of MMPs in the model but results will be inconsistent with the tendon excursion method, which does not measure effective torque directly.

OpenSim 3.0 uses this method of calculating effective torques to confirm that its reported muscle moment arms have the meaning that biomechanical researchers seek: they characterize the effectiveness with which MT actuators can generate torques of interest.

CONCLUSION

We have presented challenges in mapping between biomechanical systems and multibody models in order to rigorously define a muscle moment arm that has a clear and unambiguous biomechanical meaning and can be correctly implemented and tested. Resolution of these issues required close communication between researchers and dynamicists, and patience in overcoming differences in terminology and expertise. This led to the generalized force method presented above which is fast, uses easily-obtained quantities, and delivers useful results.

We have embodied this work in our open source OpenSim and Simbody codes, which are widely used in biomechanics research. We encourage other dynamicists and biomechanists to engage in this ongoing collaboration, and to explore and enhance these community resources located at https://simtk.org/home/opensim and https://simtk.org/home/simbody.

NOMENCLATURE

Our terminology here follows Ref. [13] to avoid ambiguity due to conflicting uses of the same terms in biology and multibody dynamics. Spatial vectors following Jain [16] are used to simplify notation.

joint

biologically-relevant locus of skeletal articulation; may involve several bones and connective material

generalized (coordinate, speed, force)

arbitrary basis for compact representation of positions, velocities, and forces in a multibody system

spatial (position, velocity, force)

quantities that combine rotational and translational elements to simplify notation; spatial position is also called “pose”

mobilizer

topological connection between two bodies that provides mobility (1–6 generalized degrees of freedom) for the child body relative to its parent in the multibody tree, parameterized with generalized coordinates, speeds, and forces; some authors use “hinge”

mobilities

mobilizer-provided degrees of freedom whose rate of change is directly represented by particular generalized speeds and at which the corresponding generalized forces act

Symbols

A,B

labels for bodies of the multibody system

n

number of mobilities

u

vector of n generalized speeds

f

vector of n generalized forces

q

vector of n_q ≥ n generalized coordinates

l

length of musculotendon path

s

scalar tension along musculotendon path

r

moment arm (units of length)

F^B

spatial force on body B (a wrench; that is, combined torque and force vectors)

V^B

spatial velocity of body B (angular, linear velocity)

F

set of spatial forces, one per body of interest, arranged as a stacked vector of spatial forces

J

Jacobian matrix that maps between spatial and generalized speeds and forces

T

a muscle’s force transmission matrix mapping tension to spatial forces applied to bodies

θ

an angular quantity of interest

r_θ

moment arm about a particular angle of interest

τ_θ

effective torque about a particular angle of interest

C_θ

coupling matrix relating generalized speeds to $\dot{\theta }$

For muscle moment arm calculations, we always work with one muscle at a time. To avoid unnecessarily complicated notation, it is to be understood here that the symbols refer to the subset of the multibody model (bodies and mobilities) that affects the muscle of interest.

Symbols used only once are introduced where they appear.