Substrate Tunnels in Enzymes: Structure-Function Relationships and Computational Methodology

Abstract

In enzymes, the active site is the location where incoming substrates are chemically converted to products. In some enzymes, this site is deeply buried within the core of the protein and in order to access the active site, substrates must pass through the body of the protein via a tunnel. In many systems, these tunnels act as filters and have been found to influence both substrate specificity and catalytic mechanism. Identifying and understanding how these tunnels exert such control has been of growing interest over the past several years due to implications in fields such as protein engineering and drug design. This growing interest has spurred the development of several computational methods to identify and analyze tunnels and how ligands migrate through these tunnels. The goal of this review is to outline how tunnels influence substrate specificity and catalytic efficiency in enzymes with tunnels and to provide a brief summary of the computational tools used to identify and evaluate these tunnels.

INTRODUCTION

Nature has produced a diverse array of enzymes all of which have the same overall goal, to catalyze a particular reaction. While, in a general sense, function is conserved, enzymes have developed a myriad of structural intricacies to accomplish this task, often referred to as structure-function relationships[1]. Understanding these relationships involves a comprehensive knowledge of both the catalytic mechanism and the structural features that make that reaction possible. While catalysis often relies on a small subset of residues found within the active site of the enzyme[2], other features such as substrate specificity, proper orientation, and catalytic efficiency may involve non-active site residues or features[3,4,5]. The extent to which the body of the protein is involved in the mechanistic process is partially determined by the location of the active site within the protein.

In some enzymes such as chymotrypsin, the active site is relatively surface exposed while in others, such as the Cytochrome P450 family it is buried deeply within the core of the protein. In enzymes with buried active sites, there is an additional step required in the ligand binding process because potential substrates must pass through the body of the protein in order to access the active site. Compared to proteins with surface exposed active sites, this architecture allows for more potential protein-ligand interactions to occur as the substrate must navigate through a series of tunnels prior to binding to the active site.

To date, enzymes spanning all six enzyme classes have been found to contain buried active sites which are connected to the surrounding environment by tunnels[6]. While in many of these enzymes, the active site residues and mechanism of catalysis have been well studied, the number and functional significance of the tunnels that connect the active sites to the protein surface have not been extensively characterized[6]. The investigation of enzyme tunnels is a relatively new field of research; however, recent studies have elucidated various mechanisms through which protein tunnels contribute to enzyme function.

In this review we will summarize key theoretical developments and provide supporting examples illustrating the role of tunnels in determining substrate specificity and catalytic efficiency in enzymes with buried active sites. In the final section, we will summarize the computational approaches and algorithms that have been developed and applied to better understand protein tunnels.

I. The Influence of Protein Tunnels on Substrate Specificity

Keyhole-Lock-Key Model

Over the years, several theories have been developed to describe how enzymes select and bind various substrates. Starting with Fischer's “lock and key” model over a century ago[7], our understanding of enzymes has evolved to include the induced fit model [8,9] and models based on conformational selection[10]. Structurally, a buried active site accessed by one or more tunnels adds another layer of complexity to the ligand binding process. Recently, the “keyhole-lock-key” model has been proposed which specifically addresses how tunnels or “keyholes” in proteins influence enzyme activity, specificity, and stereoselectivity[6].

The crux of this model is that, in proteins with buried active sites, ligand binding occurs in two distinct processes (i) migration of the ligand through the body of the protein and subsequently (ii) the ligand binding in the active site[6]. By decomposing the process in this way, the theory suggests that in addition to complementarity between the ligand and the active site, there must also be complementarity between the ligand and the binding tunnel. In other words, the tunnel itself is, in part, responsible for determining ligand specificity and theoretically it is possible to alter ligand binding by modifying the ligand binding tunnel[6]. In the following section, four factors implicated in substrate specificity within tunnels will be discussed; tunnel geometry, physico-chemical properties, gating mechanisms and protein dynamics.

Tunnel Geometry

The importance of shape complementarity in both protein-ligand binding [11] and protein-protein interactions[12] is one of the most fundamental determinants of molecular interactions. Although often overlooked, the shape and size of binding tunnels may contribute significantly to ligand binding in proteins with buried active sites. Tunnels come in a wide assortment of shapes and sizes including U-shaped tunnels[13], L-shaped tunnels[14], tunnels with adjacent pockets[15] and many forms in-between[6]. In most cases tunnels function as extensions of the binding site of an enzyme and are involved in ligand entry and egress as well as in the stabilization of the ligand in its natural binding mode. The physical shape and size of a tunnel may not only dictate the maximum size of a corresponding ligand but can also establish the number of potential interactions or barriers that a ligand may encounter as it migrates toward the active site.

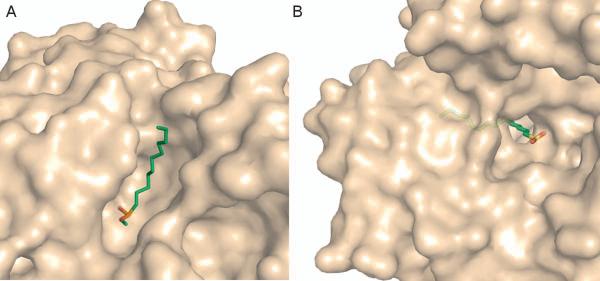
Lipases are a diverse family of enzymes that catalyze the hydrolysis of fatty acids and also provide an interesting example of how tunnel geometry influences substrate specificity. All members of this enzyme family display a conserved quaternary structure[16], catalytic triad, and reaction mechanism[17,18]. However, the size and geometry of the actual binding site differs significantly between various lipase isozymes as does the size of the associated substrate(s)[19]. For instance, the binding site of human pancreatic lipase (HPL) is a wide, shallow depression on the enzyme surface (Figure 1A)[17]. Structurally, this pocket can accommodate a fatty acid with a chain length around eight carbon atoms[17]. Contrarily, the binding site of Candida rugosa lipase (CRL) is a 22Å long tunnel (Figure 1B) capable of accommodating fatty acids with chain lengths around 17 carbon atoms[20]. It is thought that differences in the size of these extended binding sites are related to substrate specificity, specifically the chain lengths of the fatty acids they hydrolyze[17].

Figure 1.

Comparison of HPL and CRL binding sites. A) In HPL (PDB-code: 1LBP) the binding site is a surface exposed trough and the inhibitor, undecane phosphonate methyl ester (green sticks), binds along the face of the protein. B) Binding tunnel of CRL (1LPO). The inhibitor hexadecane sulfonate is shown in green sticks and binds into a tunnel in the CRL enzyme. Only a small portion of the ligand remains at the surface of the enzyme. It is thought that the different sized binding pockets play a role in substrate selectivity, especially in terms of the length of the chain that each lipase can accommodate.

Furthermore, various studies of lipase binding pockets have shown that altering tunnel lining residues can change the chain length specificity of the enzyme[21,22]. In CRL, molecular modeling was used in combination with experimental directed mutagenesis to produce several CRL variants with mutated fatty acid binding tunnels[23]. Schmitt et. al. found that mutations near the tunnel opening resulted in complete inability to hydrolyze C4 and C6 chains while increasing the specificity toward C8 chains[23]. Alternatively, mutations within the tunnel alter the chain length specificity more mechanistically, wherein the location of the mutation influences the chain length specificity[23]. In summary, hydrolysis of shorter fatty acids that did not reach the mutation site was unaffected, but the hydrolysis of longer fatty acids capable of reaching the mutation site, was reduced or even prevented[23].

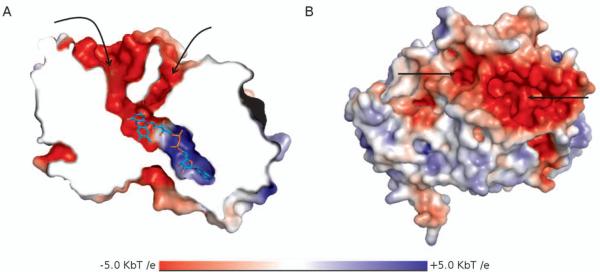
In addition to tunnel length, the shape of the tunnel can provide insight into substrate specificity. The active site of polyamine oxidase (POA) is at the bottom of a 30Å long, rigid U-shaped tunnel (Figure 2) [13]. It has been proposed that the shape of this tunnel allows for recognition of the terminal ends of substrates[13]. The shape and depth of the tunnel allow for the entire substrate to enter and remain completely solvent inaccessible, while the “walls” of the tunnel allow for substrate/inhibitor discrimination via van der Waals contacts and unique (CH^...O-H), weak hydrogen bonds[13,24].

Figure 2.

U-shaped binding tunnel of polyamine oxidase (1B37) colored by electrostatic potential, A) A cutaway of the protein is shown to expose the binding tunnel and the adjacent pocket where the catalytic flavin moiety sits (shown in cyan sticks). B) A surface representation of POA shows the tunnel openings at the surface of the protein.

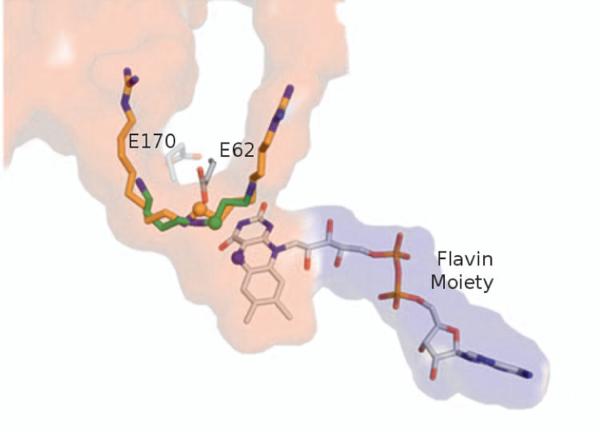
It has been suggested that many POA inhibitors work by binding in an “out of register” mode in comparison to the natural substrate, spermidine[24,25]. Studies have suggested that when the natural substrate binds, an extensive hydrogen bonding network combined with direct interactions with two glutamate residues (E62 and E170) that lie on either side of the tunnel align the C9-N10 bond within a reactive distance of the flavin moiety in the binding site (Figure 3)[24]. Inhibitors like guazatine which contain extended chains or inhibitors lacking terminal primary amines like MDL72527 interact with several of the same residues. However, an alternative hydrogen bonding pattern and different atoms interacting with the two glutamate residues pulls the targeted C-N bond of the inhibitor too far from the reactive flavin to be oxidized, hence the “out of register” binding mode (Figure 3)[24]. The overall cause of the “out of register” binding mode is likely due to a combination of both tunnel shape and the physico-chemical properties of the tunnel.

Figure 3.

Out-of-register binding mode in POA. Binding of the inhibitor guazatine (orange sticks, 1H82) in comparison to the natural substrate spermidine (green sticks, 3L1R). The C-N (C shown with a green sphere) bond of spermidine comes into close contact with the reactive nitrogen of the flavin moiety, shown in a blue sphere. However, guazatine binds in a slightly different mode placing the reactive carbon bond (indicated with an orange sphere) slightly shifted away from the reactive flavin. Residues E62 and E170 located on either side of the binding tunnel are thought to play a critical role in substrate differentiation.

Physico-Chemical Properties

While the overall shape of the tunnel provides a general framework for determining substrate specificity, the physico-chemical properties of this framework provide an additional level of selective power. As with shape complementarity, physico-chemical complementarity in the binding site is well established [26,27] and forms the basis for all structure-based computational methods, such as docking [28]. These methods assume that properties of the active site must be complimentary to those of the ligand. For instance, a hydrogen bond donor in the active site is paired with a hydrogen bond acceptor on the ligand. According to the key-keyhole-lock theory, a similar principle applies to tunnels, making the physico-chemical properties of a tunnel a crucial determinant of substrate specificity. For instance, under this theory it would be unlikely that a positively charged substrate will traverse down a positively charged tunnel to reach the active site even if the active site was complimentary to the ligand.

The oxidase enzyme Fms1 provides an illustration of the importance of physico-chemical properties in tunnels. Fms1 has a similar U-shaped tunnel topology to POA and has the same natural substrate, spermidine, as well as a similar catalytic mechanism[29]. However, in Fms1, substitution of approximately 10 tunnel lining residues results in a more hydrophobic tunnel and gives rise to an alternative hydrogen bond network between the tunnel and the ligand[29]. It has been proposed that the different tunnel composition causes spermidine to bind more shallowly in the tunnel exposing a different bond in the ligand to the catalytic flavin moiety ultimately leading to different oxidation products from the two enzymes[25,29].

Electrostatic interactions within tunnels can also influence substrate recognition. This is a phenomenon that is widely used in receptors and ion channels, where the passage channel often assumes the opposite charge of the substrate or ion that it binds/transports[30,31]. Yet, electrostatic steering and ionic tethering have also been shown to be important in determining substrate specificity and influencing catalysis in various enzymes [32,33]. Studies of enzymes like aldehyde dehydrogenase (ALDH) suggest that a similar phenomenon may also be important in ligand movement through tunnels.

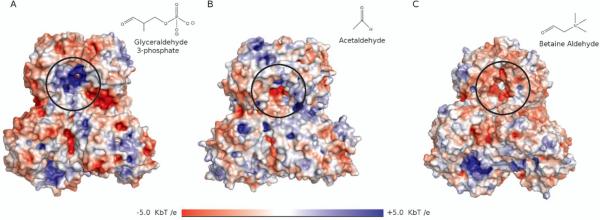
A systematic comparison of a dozen ALDH enzymes revealed significant differences in the electrostatic potential between different subfamilies depending on the charge of the natural substrate [34]. Several members of the ALDH family, including ALDH4, ALDH5, ALDH6, ALDH7, and ALDH11, bind negatively charged or neutral substrates and these isoforms were found to have a positive electrostatic potential at the tunnel surface and entrance (Figure 4A)[34]. On the other hand, ALDHs such as ALDH9, ALDH10, ALDH25, ALDH26 and ALDH27 demonstrate specificity towards positively charged substrates and were found to have negatively charged residues at the tunnel entrance and throughout the tunnel (Figure 4C)[34]. Similar features have also been observed in acetylcholinesterase[35] and in polyamine oxidase (Figure 2B)[13].

Figure 4.

Electrostatic potentials in the binding tunnels of ALDH enzymes; the entrances to each tunnel have been circled in black and the substrates have been shown in the upper right corner of each panel. A) ALDH11 (1EUH) has a positive potential and binds a negative substrate, glyceraldehyde-3-phosphate. B) ALDH2 (4KWF) has a relatively neutral binding tunnel and binds the neutral substrate, acetaldehyde. C) ALDH9 (2WME) has a negatively charged binding tunnel and binds the substrate, betaine aldehyde, which is positively charged.

Gating Elements

Just as binding sites have been known to structurally adapt to substrates, tunnels have also been found to adapt to accommodate certain substrates. Tunnel gating is broadly defined as a reversible conformational change in the protein structure that controls passage of substrates into and out of proteins [36]. Gating can occur on several levels ranging from a single side chain motion, as is often seen with phenylalanine residues[37], up to entire domain movements, such as a lid opening and closing[38]. Gating elements have been found to be important for determining substrate specificity in a multitude of systems as well as controlling solvent accessibility and synchronization of reactions [36]. Recently, Gora et.al. have published an excellent review discussing several aspects of gating mechanisms and outlining many systems where gates are present[36], therefore, only a few examples of how gating influence substrate specificity in tunnels will be presented here.

Several single-residue gates have been identified and characterized in the toluene monooxygenase family [39,40,41]. In toluene-4-monooxygenease (T4MO), one of the main substrate entrance tunnels is gated by an aspartate residue (D285). It was initially thought that this residue sterically prevents entrance of bulky hydrophilic substrates like 2-phenylethanol (PEA) because mutating this gating residue into a series of smaller, non-charged residues led to a general increase in activity of T4MO toward PEA[42]. However, the most active mutant was found to be an aspartate to glutamine mutation and it was proposed that the functionality of this gate is based primarily on charge as opposed to size[42].

In a related enzyme, toluene-ortho-xylene monooxygenase (ToMO), the size of the residue at position 314 was found to be inversely proportional to enzyme activity[43]. In the wildtype enzyme, the glutamine residue at this position forms a gate approximately 25Å from the active site. Mutating this glutamine into a series of smaller residues revealed a proportional increase in enzyme activity[43]. It was then proposed that replacement of glutamine with smaller residues resulted in a permanently opened gate which was thought to be responsible for the observed increase in the rate of substrate (p-nitrophenol) oxidation[43].

In addition to gates formed by individual or small clusters of residues, some gates are formed by coordinated loop or domain movements. Thioesterase Rv0098 of Mycobacterium tuberculosis (thioesterase) has a long L-shaped binding tunnel leading to the active site[14]. The crystal structure suggests that the binding pocket tightly accommodates the co-crystalized ligand, dodecenoate, which contains 13 carbon atoms, and suggested that the enzyme did not have space for larger ligands. Puzzlingly, biochemical studies suggested that the enzyme showed a general preference for long-chain fatty acids containing between 16 and 18 carbon atoms [14]. Subsequent computational studies revealed that the bottom of the active site tunnel is composed of a highly flexible loop region that changes conformation expanding the active site tunnel to accommodate the larger substrates[44].

Tunnel Dynamics

The influence of gates on substrate specificity can be ascribed to a localized feature or set of features, but the overall dynamics of the enzyme can also play a role in determining substrate specificity. This is apparent in the Cytochrome P450 (CYP) enzyme family. This class of enzymes is responsible for the metabolism of xenobiotics, drugs, and many naturally occurring compounds[45]. CYP enzymes have evolved with a deeply buried active site that is accessible by several, often conserved, tunnels[46]. Despite metabolizing a multitude of compounds, each CYP isozyme has a distinct, albeit sometimes overlapping substrate metabolism profile[47,48]; while some CYPs metabolize a large array of compounds, others are restricted to a more modest number. Although differences in the size of the binding site itself between isozymes has long been known to contribute to substrate specificity[49], more recently it has been proposed that this diversity may be achieved through differences in structural flexibility across the various isozymes[46,50,51,52,53].

Skopalík et.al. used MD simulations to evaluate the flexibility of three CYP enzymes; CYP2A6, which has a narrow substrate specificity, CYP2C9, which is known to be moderately substrate specific, and CYP3A4 which is the most promiscuous of the CYP enzymes[54]. The authors identified 10 flexible regions (FRs) that showed significant variation between the three isozymes that correlate with substrate diversity [54]. In other words, the FRs were most rigid in CYP2A6 and most flexible in CYP3A4[54], which directly correlates with their substrate specificity. It was theorized that the increased flexibility was required in order to adequately accommodate a wider variety of substrates in CYP3A4, and vice versa for CYP2A6.

Along with the inherent dynamics of the enzyme itself, it has been suggested that the enzyme's environment may also play a role in determining substrate binding by stabilizing certain tunnels[55]. Sgrignani et. al. compared substrate egress in two models of human aromatase, one in which the enzyme was free in water and another in its natural environment, anchored to a membrane [55]. It was found that when anchored to the membrane aromatase exhibits alternative dynamics, especially at the membrane interface, resulting in a noticeable difference in the frequency of ligand egress through tunnels that interact with the membrane as compared to the non-membrane bound simulation[55]. The authors propose that the local membrane environment stabilizes certain tunnels in the aromatase enzyme and therefore alters substrate binding [55,56,57].

In this section, we have provided several illustrations of how tunnels or “keyholes” in the key-keyhole-lock model, influence substrate specificity. Tunnel shape, physico-chemical profile, gating mechanisms, and protein dynamics can all affect how a ligand transitions from bulk solvent into the buried binding site. Oftentimes, a single tunnel can employ several of these strategies, as is the case in PAO, CYP enzymes, and Fms1, to name a few.

II. Tunnel Influence on Enzyme Catalysis

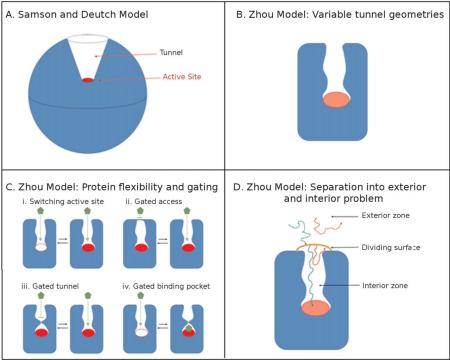
The implications of tunnels are not limited to substrate specificity. Tunnels have also been found to directly influence enzyme kinetics. Smoluchowski's theory on particle aggregation in the early 1900s[58], formed the basis for several expanded kinetic models of enzymatic reactions [59,60] . In 1977, Samson and Deutch proposed a model to explain diffusion-controlled binding to a buried active site[61]. The authors developed a steady-state model based on substrate binding to a spherical enzyme wherein the active site is represented as a cap at the base of a conical indent (Box 1, Panel A) [61].

Box 1

The evolution of kinetic models to explain ligand binding to enzymes with buried active sites.

Later, Zhou generalized the formalism to any other tunnel geometries (Box 1, Panel B) and proposed a model that included the potential for tunnel gating [62]. In the most recent version of this model (Box 1, Panel C), tunnel flexibility is accounted for in terms of (i) the active site switching between active and inactive conformations, (ii) a gate or (iii) bottleneck that opens or closes the tunnel, and (iv) a binding-site rearrangement due to ligand binding that induces a lid or bottleneck closure[63,64]. Within this formalism the binding process is broken into an exterior and interior process, the process of diffusive ligand binding to the tunnel entrance and ligand reaction with binding site or release from interior region, respectively (Box 1, Panel D). This separation allows for the efficient computation of ligand-enzyme association and reaction in the framework of Brownian Dynamics simulations.

As suggested by the continuous development of kinetic models to better describe ligands binding to buried active sites, tunnels can play a critical role in enzyme kinetics. In this section, several examples of tunnel structural elements that influence catalytic rate will be discussed. More specifically, focus will be on structural properties that influence (i) the rate of substrate binding, (ii) the rate of cofactor binding, and (iii) the catalytic implications of product egress.

Influence of Tunnels on Substrate Binding Rates

A recent study of Cytochrome P450 1A2 (CYP 1A2) provides a clear example of the potential for tunnel lining residues to directly influence the rate of enzyme catalysis. A naturally occurring mutation in a phenylalanine residue (F186) in the D-E loop of CYP 1A2, nearly 30Å from the active site, was found to cause a significant reduction in the enzyme's V_max [65,66]. Using computational modeling, it was shown that this mutation altered the structural dynamics of the enzyme, specifically in the C, D, and E-helices and connecting loop regions. This, in turn, caused the main substrate access channel to preferentially adopt a closed conformation, as compared to the wildtype enzyme[66]. By enforcing a preferentially closed state of the access tunnel, the rate of substrate binding was slowed, ultimately leading to a reduction in V_max[66].

A similar phenomenon has been observed in acetylcholine esterase (AchE). The biological role of this enzyme, breaking down the neurotransmitter acetylcholine, requires a very rapid turnover rate and yet the active site of AchE is buried at the bottom of a ~20Å “active site gorge”. This gorge is lined with 14 aromatic residues and electrostatic calculations have shown that the gorge has an overall negative electrostatic potential [67]. It was proposed that, in order to achieve near diffusion limited turnover, electrostatic steering of the acetylcholine moiety is likely occurring [35,67]. The current theory is that the rapid rate of substrate binding is facilitated by electrostatic interactions between the positively charged acetylcholine moiety and the partially negatively charged π-electron clouds of the aromatic residues lining the tunnel[35]. Mutational studies have corroborated this theory, as the alteration of several of these aromatic residues results in a slower k_cat in comparison to the wildtype enzyme[68].

Influence of Cofactor Transport on Enzyme Catalysis

Oftentimes, enzymes require auxiliary molecules or cofactors in addition to the substrate to carry out a given reaction. Water, for instance, is a key mediator of many catalytic mechanisms[69,70] and several enzymes have tunnels that appear to be dedicated to water transport[46,71]. The transport of cofactor molecules like water can play a critical role in enzyme catalysis.

One of the most well characterized examples of the importance of tunnels in co-factor transport is Dha haloalkane dehalogenase from Rhodoccoccus rhodochrous (Dha). Using a combination of computational and mutational studies, Pavlova et.al. produced a Dha mutant with a 32-fold increase in activity towards trichloropropane (TCP) [71]. A series of five mutations in the enzyme's main water access channel were found to significantly reduce in the ability of water to access the active site. The authors propose that closing off the water tunnel effectively reduces competition by water for the active site nucleophile and ultimately increases TCP degradation, as evidenced by an increase in k_cat as compared to the wildtype enzyme[71]. Interestingly, the restriction of this access tunnel also resulted in the rate limiting step of catalysis switching from the chemical reaction, in the wildtype, to product release, in the mutant[71].

Tunnels can also affect the catalytic rate via substrate channeling[72] wherein a tunnel connects two distant active sites[72,73]. In carbamoyl phosphatase synthase (CPS) for instance, a four-step reaction is necessary to produce carbamoyl phosphate from bicarbonate, glutamine, and ATP[74]. This reaction occurs across three different active sites in the CPS complex that are connected by a tunnel nearly 100Å long[75]. It has been theorized that this tunnel serves to increase catalytic efficiency by 1) facilitating direct transit of intermediates and co-factors between successive active sites and 2) preventing premature or unintended side-reactions involving the intermediates[75].

The physical properties of these tunnels support these findings. For instance, the tunnel that transports the charged carbamate moiety is primarily lined with backbone atoms preventing spurious hydrolysis of the labile carbamate intermediate[75]. In addition, mutations which block or constrict the ammonia tunnel decouple the removal of ammonia from glutamine from the ATPase activity, resulting in a significant reduction in carbamoyl phosphate synthesis and an increase in K_m of approximately 40-fold[76].

Influence of Tunnels on Product Egress Rates

As alluded to in the previous example of Dha haloalkane dehalogenase, catalysis in enzymes with buried active sites is also influenced by the tunnels that allow product release. Although much less well studied compared to substrate entrance, there have been a few studies explicitly covering product egress. Recently, Klvana et.al. studied product release in eight Dha mutants[77] and furthermore, a putative egress pathway and mechanism of ammonia leaving the nitrogenase binding site has recently been proposed [78].

In one notable example, glutathione transferase, a detailed product egress pathway and egress kinetics have been studied. In this enzyme, the rate limiting step is known to be product release[79]. Using mutational studies combined with crystal structure analysis, it has been suggested that the tunnel lining residue, tyrosine 115, plays a central role in the release of the glutathione bound product[79]. Mutating this residue to phenylalanine resulted in a 3.6-fold increase in the k_cat of the enzyme[79]. It was suggested that the tyrosine to phenylalanine mutation destroyed a critical hydrogen bond between residue 115 and serine 209 of the C-terminus, resulting in increased local flexibility and more rapid product egress[79].

The examples presented above indicate that tunnel architecture and dynamics can have a direct impact on substrate specificity as well as enzyme catalysis and suggest that enzyme function can be affected by altering the residues or inherent dynamics of these tunnels. A better understanding of the relationship between enzyme function and tunnel dynamics is crucial to exploiting such findings.

III. Computational Identification and Evaluation of Protein Tunnels

In all of the examples presented above, computational methods were instrumental to develop and/or rationalize experimental findings. As the field of tunnel identification and functional characterization grows, we believe computational methods will continue to play a key role in exploring and explaining structure-function relationships in tunnels. Therefore, we have opted to include a short section in this review dedicated to summarizing the main components of computational tunnel identification methods.

Much like small molecule docking which is comprised of (i) pose searching and (ii) pose scoring[80], tunnel prediction can generally be broken down into two parts; tunnel identification and tunnel evaluation. Various different algorithms have been developed and implemented for those two tasks with significant variations in the required computational resources.

Tunnel Identification

Tunnel algorithms are generally split into two categories; those which calculate tunnels based on the protein structure alone, and those which incorporate the ligand or a probe molecule into the tunnel identification process. In the former, geometric algorithms such as Voronoi diagrams are used to identify tunnels leading from the active site to the surface of the protein, and thus are often referred to as “geometric methods” [81,82]. In the latter, a ligand or ligand-like molecule is used to probe the protein structure of interest for possible entrance/exit pathways using techniques like molecular dynamics (MD) simulations[83]. We will refer to such methods as “explicit-ligand” methods. The key difference between these two approaches is that geometric methods identify all tunnels in a given protein without consideration of the ligand, where explicit-ligand methods directly evaluate a single tunnel or multiple tunnels relevant to a specific ligand.

Geometric Methods

Geometric methods simplify the task of tunnel identification by converting the protein structure into a geometrically tractable problem. Early methods used grid based approaches wherein the protein is placed on a grid and any points that overlap with atoms of the protein are removed revealing the accessible space in the protein [84,87]. More recent geometric methods are based on the use of Voronoi diagrams [82,85,86]. In these methods, the protein atoms serve as guide to produce a series of edges that describe the accessible space in the protein, which represent tunnels (Figure 5). Voronoi based methods are currently the most popular choice for the identification of protein tunnels.

Figure 5.

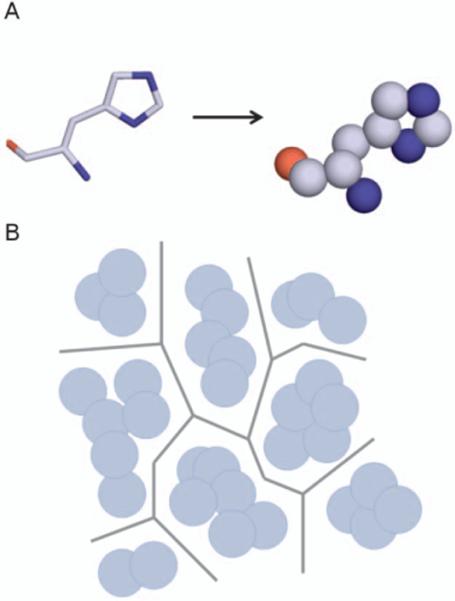
Implementation of Voronoi diagrams in tunnel prediction. A) First atoms of protein residues are converted into spheres based on the van der Walls radii of the atoms. B) Voronoi edges are plotted as to maximize the distance between adjacent spheres. Series of edges represent potential tunnels in the structure. Methods such as Dijkstra's algorithm can then be used to identify connected edges that result in the shortest paths from binding site to bulk solvent.

Geometric methods are advantageous in that calculation time and computational expense are usually minimal. In addition, many of these methods are capable of generating a detailed report of the tunnel dimensions and surrounding atoms. However, the underlying principles of geometric tunnel prediction prevent the direct inclusion of protein flexibility in the calculation. As the importance of protein flexibility has become widely recognized by the computational community[88], this is seen as a main disadvantage of these methods. To account for some degree of protein flexibility, the use of protein ensembles is becoming increasingly common in geometric tunnel prediction algorithms[86].

However, the use of Voronoi diagrams on multiple structures often produces several closely related tunnels, for instance, as many as 30 tunnels can be found in as few as five conformations of the same protein structure using Caver. This necessitates the use of clustering for efficient analysis. The ambiguity in deciphering between two closely related tunnels makes clustering highly subject to interpretation and clustering approaches vary widely from program to program. To date, there is not yet an explicitly defined set of criteria to define clusters, and few studies have explicitly investigated the influence of clustering on the quality of tunnel prediction[89].

While ensemble methods aim to include some elements of flexibility that are inherent to the protein, the influence of the ligand is not considered. In other words, the impact of ligand migration on protein dynamics is not explicitly accounted for. Ligand induced protein flexibility, however, has been shown to be critical in many systems containing tunnels[90].

Explicit Ligand Methods

To address this issue, methods that explicitly include the ligand and protein flexibility have recently been developed. For the most part, these methods are based on the use of MD simulations and incorporate both ligand migration and protein flexibility. The main issue in these methods is that the timescale of ligand (un)binding is much longer than is currently accessible by unbiased simulations. In some cases the ligand may be small enough that rather minor modifications, such as changing the ligand temperature in relation to the protein may be enough to encourage ligand exit and subsequent tunnel identification [91]. In addition, Monte Carlo based methods such as GCMC/BD (Grand Canonical Monte Carlo/ Brownian Dynamics) and GCMC/MD (Grand Canonical Monte Carlo/ Molecular Dynamics) have also been used to explore movement of small ions through channels [92,93,94]. These methods have been used to simulate small ligands (ions and water) passing through channels, but have not yet been applied to larger ligands.

To date, the majority of simulations of larger ligands migrating through tunnels employ methods that coerce the ligand from the active site using an external force. For instance in Random Expulsion Molecular Dynamics(REMD) [83], which is one of the most widely implemented methods [95,96,97], a randomly oriented force is applied to the ligand until it exits the protein. If the ligand encounters a barrier, the direction of the force is changed. In this way, the ligand can “feel” along the protein to identify egress tunnels. Each successful run identifies one possible pathway for ligand egress, thus multiple runs are often needed to explore proteins that may have multiple tunnels. In a related method, IterTunnel, the ligand is pulled rather than pushed along pathways. In this method, steered molecular dynamics is used to pull the ligand along pre-calculated tunnels that are updated periodically as the ligand moves through the protein and opens (or closes) new tunnels [98].

The main disadvantage of explicit-ligand methods, is that they require extensive MD simulations, which necessitates significant computational resources. In both programs, only a single tunnel is identified per run and therefore, in order to fully investigate potential entrance/egress tunnels of a substrate/product in an enzyme with more than one tunnel, several MD simulations are necessary. In addition, these simulations do not always result in successful ligand egress (REMD) or if used haphazardly could result in non-realistic tunnels (IterTunnel). While these methods of tunnel identification often provide very detailed description of protein and ligand dynamics as the ligand moves through the protein, performing and analyzing the necessary simulations may prove challenging for casual users.

Tunnel Evaluation

Establishing which tunnels are likely to be more favorable for certain biological processes, e.g. which tunnel is preferred for entry/exit of a specific ligand, is currently the greatest challenge in tunnel prediction. A variety of methods based on various tunnel properties have been used to make such predictions.

Tunnel length and width are two metrics which are commonly used to evaluate tunnels in geometric-based tunnel identification programs[82,84,86]. In these methods, the ligand itself is not accounted for and the underlying assumption is that tunnels that are shorter and wider are more likely to be favorable for ligand passage than tunnels that are narrower and longer. Recently, methods have been developed that provide a topographically detailed description of the physico-chemical properties of the tunnel, such as hydrophobicity and electrostatics, based on the tunnel lining residues[85].While such features are not yet explicitly included into the ranking scheme of any geometric method, this type of extensive reporting is a novel development and may provide a basis for more detailed evaluation methods. One critical consideration in these scoring schemes is that the interaction or potential interaction between the ligand and the tunnel are not explicitly accounted for or evaluated.

Explicit-ligand methods, on the other hand, do specifically evaluate ligand passage through a given tunnel. In some programs, including REMD, this evaluation is done based on the observed frequency of ligand passage through a specific tunnel over the course of multiple simulations. In general multiple simulation runs wherein the ligand explores one path per run are combined and the number of times the ligand progresses through each path with respect to the total number of runs completed is calculated[83]. Alternatively, in IterTunnel the potential of mean force (PMF) of a ligand passing through a tunnel is calculated using umbrella sampling combined with the weighted histogram analysis method (WHAM) and this value is used to energetically evaluate tunnels[98]. While both methods require extensive simulations, the output of each is slightly different. In the case of REMD, the use of multiple simulations through a single channel provides a more comprehensive picture of the different events that may occur in that tunnel during ligand transit, but this method does not explicitly provide energetic information. On the other hand, the bulk of the IterTunnel simulations are performed at various points along the tunnel (umbrella sampling) as opposed to repeatedly sampling the transit though the entire tunnel, which is performed only once in IterTunnel[98]. The output of the IterTunnel is a detailed free-energy profile of that specific transit event, but cannot readily account for potential alternative events along the same ligand migration pathway.

To date, there have been no systematic studies comparing different tunnel evaluation methods and there is no consensus yet on the “best” way to evaluate tunnels computationally. Some have reported that frequency approaches, such as used in REMD, are in agreement with the work estimated using steered molecular dynamics calculations[55] and cost-based functions, such as those used in Caver[86].However, alternative and more accurate methods of identifying conformational changes and quantifying the energetic cost of ligand migration are needed to more fully understand ligand migration through tunnels.

From the multitude of examples where computational predictions of tunnels have been used to inform and explain experimental findings suggests that these methods are capable of providing useful and relevant data on tunnel dynamics and behavior. As the demand grows for a more holistic understanding of enzymatic processes it is likely that computational methods of tunnel prediction and evaluation will become increasingly instrumental to gain new insight into structure-function relationships in proteins with buried active sites.

CONCLUSION

The ubiquity of tunnels across the protein classes indicates that they have evolved to meet various requirements in terms of substrate recognition and catalysis and there is a growing interest in trying to understand the underlying structure-function relationships in tunnel-containing enzymes. In this review we have outlined several features of tunnels including tunnel architecture, dynamics and physico-chemical properties and have also provided several examples of how these features influence substrate specificity and enzymatic function. In addition, we have summarized several of the computational methods that have been critical in furthering our understanding of tunnel location, composition, function and dynamics.

Understanding tunnels and how they function provides a more complete picture of enzymatic processes and opens the door to novel methods of interfering with or altering enzyme function. Prokop et. al. recently published a comprehensive review of how protein tunnels are being exploited to alter substrate specificity or catalytic rate in protein engineering and design. Furthermore, tunnels are of growing interest in the drug design community and some the first attempts to use tunnel data to design novel drug compounds are now underway [99]. Despite a growing interest in the field, many factors of ligand migration through tunnels remain poorly understood, such as the propensity for multiple molecules to enter through the same or different tunnels, the resonance time of a given substrate/product within a tunnel, and how the energetic properties of the tunnels change after catalysis. Improving our understanding of structure-function relationships in tunnel containing enzymes will likely lead to the increasing exploitation of tunnels in various fields that aim to understand and modify protein function.