Abstract
A joint analysis of FEV1 (Forced Expiratory Volume after one second) and height is reported using novel methodology, as well as a single-trait analysis of smoking status. A first goal of the study was to incorporate dense genetic marker information in a random regression (Bayesian) model to quantify the relative contributions of genomic and environmental factors to the relationship between FEV1 and height. Smoking status was analysed using a probit random regression model and a second goal of the study was to estimate the genomic heritability of smoking status. Estimates of genomic heritabilities for height and FEV1 are equal to 0.47 and to 0.30, respectively. The estimates of the genomic and environmental correlations between height and FEV1 are 0.78 and 0.34, respectively. The posterior mean of the genomic heritability of smoking status is equal to 0.14 and provides evidence for the presence of genetic factors associated with the trait. Under the data augmentation strategy introduced, the joint posterior distribution of FEV1 and height factorises into two independent posterior distributions. This simplifies programming and results in excellent numerical behaviour. The approach can be readily extended for the joint analysis of an arbitrary number of traits. Details are shown in an Appendix.
Introduction
Lung function is a predictor of health, and a low lung function is a strong risk factor for mortality (Lange et al., 1990; Chinn et al., 2007; MacNee et al., 2008). Forced expiratory volume after one second (FEV1 hereinafter) is the most widely used and quoted lung function test in clinical practice as well as in patient based research and epidemiological studies (Kerstjens et al., 1997).
It is well established that FEV1 is phenotypically related to height (or alternatively, to body mass index), sex and smoking status. The purpose of this work is to have a closer look at these phenotypic relationships, and to incorporate dense genetic marker information to quantify the relative contributions of genomic and of environmental factors. More specifically, we present a joint (two-trait) Bayesian analysis of height and FEV1, conditional on smoking status, modelled as two Gaussian traits. The joint analysis informs about the degree of genomic and environmental associations between FEV1 and height and provides an estimate of the proportion of the variance of each trait captured by genetic marker information (genomic heritability). We also carry out a whole-genome Bayesian single-trait analysis of smoking status, recorded as a binary variable and invoking a liability threshold model (Wright, 1934). The use of whole-genome information allows the investigation of possible genetic factors associated with smoking status and retrieves an estimate of the genomic heritability on the scale of liability.
In a classical genome wide associations study (GWAS) the focus is to detect significant SNP effects using extremely low p-values derived from single-marker regressions. Testing SNPs for association one at a time can be a sensible option when traits show simple Mendelian inheritance with one or few loci involved. However, there is increasing evidence that a number of important traits and diseases are affected by a very large number of genes (McClellan and King, 2010), as well as environmental factors. In this situation, a better false positive and false negative performance is achieved analysing all SNPs jointly (Hoggart et al., 2008) using whole genome random regression (WGRR) models, as in Yang et al. (2010) and de los Campos et al. (2013). For a recent review of different linear models and their implementation in the context of WGGR see de los Campos et al. (2013).
These methods, largely developed in the field of animal breeding (e.g. Meuwissen et al., 2001), were proposed as a way of confronting the so-called missing heritability problem and have been used for estimation of the proportion of variance accounted for by regression on common SNPs (Yang et al., 2010; Lee et al., 2011), for prediction of genetic values of complex traits (Meuwissen et al., 2001) and for prediction of genetic risk to diseases (Wray et al., 2007; Daetwyler et al., 2008). The WGRR models have been implemented using either single trait or two-trait restricted maximum likelihood (as in Yang et al., 2010, and Lee et al., 2012) or using Bayesian, Markov chain Monte Carlo methods (McMC), for example, as in Meuwissen et al. (2001), and more recently, Janss et al. (2012) and Zou et al. (2013)) who include methods for the analysis of binary traits.
In the present work, the fitting of the highly parameterised genomic models for the joint analysis of FEV1 and height is made possible using a novel strategy that greatly alleviates the computational complexity and improves the numerical behaviour of the algorithm. Using this strategy the joint posterior distribution of the two-traits factorises into two independent posterior distributions. The extension to an arbitrary number of traits is straightforward. In the case of the binary analysis, the McMC algorithm updates the genomic variance and the genomic values in one step.
The article is organised as follows. The heading Material and Methods includes subsections with descriptions of the data, of the models for the single trait analysis of FEV1, conditional on SMOKING status and HEIGHT, and of the model for the joint analysis of FEV1 and HEIGHT. There is also a section that explains methods used for comparing versions of the models with and without marker covariates, and for studying how inferences are affected by prior assumptions and by putative population substructure. Details of the McMC implementation are also briefly mentioned. The section Results reports on the single trait analysis of FEV1, on the joint analysis of HEIGHT and FEV1 and on the single-trait analysis of SMOKING status. In the last section of the article we discuss some of the implications of our findings. Important technical details are relegated to appendices. In Appendix 1 we present the singular value decomposition which plays a central part of the Bayesian implementation. Appendix 2 describes the data augmentation strategy for the two-trait analysis of FEV1 and HEIGHT, and details of the prior and posterior distributions. Appendix 3 provides a detailed description of the model for SMOKING status, including the prior and posterior distributions, and details of the McMC algorithm. Appendix 4 presents the form of the induced prior distribution of the genomic heritability of FEV1, given the assumed prior distributions of the environmental and genomic variances, based on results in Sorensen and Gianola (2002). Finally Appendix 5 indicates the form of the induced prior distribution of the genomic heritability for SMOKING status, given the prior distribution of the genomic variance. The results in Appendices 4 and 5 are used to study the influence of prior assumptions, on posterior inferences of genomic heritability.
Material and Methods
The data
The British 1958-cohort data consist of longitudinal records from individuals born during a single week in 1958 in England, Scotland and Wales. A detailed description and sources of access to the data can be found in Power and Elliott (2006). The present study uses a subset of the original data consisting of records from approximately 3, 000 individuals that have been genotyped for 1 million SNPs using the 1M Affymetrix chip. After standard editing, the final number of markers amounted to 696, 823. From the 3, 000 individuals, records on FEV1, HEIGHT and SMOKING STATUS were also extracted, together with information on social status and sex which were included as environmental covariates. The latter were chosen on the basis of their effect on the dependent variables determined from preliminary analyses. SMOKING STATUS is registered as a binary trait: Never smoked/currently a smoker or have smoked. After editing the data to ensure that FEV1 measurements complied with the guidelines from the task force on Standardisation of Lung Function Testing (Miller et al., 2005), 2, 260 individuals remained for analysis. The size of the data set places a limit to the strength of our inferences. However the statistical methods implemented in this study are free from asymptotic assumptions and large sample approximations and provide a complete and fair picture of the degree of posterior uncertainty (conditional on the model posed).
Phenotype and genotype data from the British 1958 Birth Cohort are freely available to research scientists worldwide on application to the Access Committee for CLS cohorts. Information on the application procedure can be found on the website: http://www2.le.ac.uk/projects/birthcohort. The software to fit the models will be freely available from the authors and we are currently working on making it suitable for distribution.
The single trait model for FEV1, conditional on HEIGHT and SMOKING status
Before embarking on the two-trait analysis of FEV1 and HEIGHT we fitted a single trait model to FEV1, conditional on SMOKING STATUS and on HEIGHT. The objective is to confirm and illustrate, in the case of our data, how FEV1 is affected by a number of factors, including HEIGHT and SMOKING STATUS (these are treated as covariates in the single trait analyses).
Two single trait models are fitted. The first one is a standard fixed effects model with an overall mean, an effect of sex and linear regressions of FEV1 on HEIGHT and on SMOKING status. The prior distributions of the parameters associated with the mean, sex effects and linear regression coefficients are assumed to be normal, with zero mean and variance equal to 105. The second single trait analysis was based on a mixed effects model with the same covariates as the former and additionally, genomic values , as defined in (7) and (8). Variance components are assumed to have scaled inverse chi square a priori distributions with degrees of freedom equal to 4.5. The scale parameter of the residual variance was set equal to 0.32 and in order to investigate the sensitivity of the results to prior assumptions, three models with three different scale parameters of the genomic variance were investigated. This results in different induced prior distributions of the genomic heritability of FEV1, conditional on HEIGHT and SMOKING status, with respective modal values equal to 0.01, 0.06 and 0.13. Technical details can be found in Appendix 4.
The two-trait model for FEV1 and HEIGHT and the model for SMOKING status
The joint analysis of FEV1 and HEIGHT conditional on dispersion parameters, is based on assigning normal structures to both traits. The linear models for FEV1 (f) and HEIGHT (h) are
| (1a) |
| (1b) |
where yi, ei and μi, i = f, h are column vectors of length n, equal to the number of individuals, and Xi are observed incidence matrices. The n×m matrix W contains elements which are labels for the m observed marker genotypes (defined below). The vector of systematic effects μi contains the effect of sex and social status, and also smoking status as covariate in the case of FEV1. The choice of these covariates was based on preliminary analyses.
The m × 1 column vectors of unobserved marker effects (bf, bh) are assumed to be realisations from
| (2) |
where are variances of marker effects, σbfbh are covariances of marker effects and I is the m × m identity matrix. The vectors W b in (1) represent genomic values, which are proxies for the unobserved (true) genetic values.
The residual terms (ef, eh) are assumed to be realisations from
| (3) |
where are residual variances and σef eh are residual covariances. The residual terms capture departures of the genomic values from the true genetic values (for example, due to unaccounted interactions or imperfect linkage disequilibrium between markers and genotypes at causal loci), and unspecified environmental effects. The I matrices in (3) are of dimension n×n. The linear structures (1), together with (2) and (3), give rise to the joint model for (yf, yh), conditional on (μf, μh) and on dispersion parameters, equal to
| (4) |
The model is implemented using a strategy described in Appendix 2, which also includes details of prior assumptions.
SMOKING STATUS is analysed as a single binary trait (yi = 1 if individual i is a smoker or has smoked; yi = 0 if never smoked) with a liability threshold model, used by Wright (1934) in studies of the number of digits in guinea pigs, and by Bliss (1935) in toxicology experiments. In the threshold model, it is postulated that there exists a latent or underlying unobserved variable (liability) which has a continuous distribution. The unobserved liability is described by the linear model
| (5) |
where μs contains the effect of social status only (in these data data, the proportion of smokers is the same (0.56) in both sexes), and bs is an m × 1 vector of marker effects affecting the liability of smoking status. This vector of marker effects is assumed to have the normal distribution
where is the variance of the marker effect, the same for all markers. The vector of residual terms in (5) is assumed to have the normal distribution
The standard parameterisation in the case of binary responses is to assume that the observed response yi = 1 if the liability exceeds the threshold (set equal to zero), and if it is smaller than the threshold, the observed value is yi = 0. Then for the ith individual,
where and are the ith row of matrices Xs and W, and is the value of the liability for individual i. The parameters of the model for smoking status are including the residual variance component of the liability that is set arbitrarily equal to 1. Further details of the model and its McMC implementation can be found in Appendix 3.
The genomic heritability and genomic correlation
The elements of the n × m matrix W = {Wij} are normalised marker labels
| (6) |
where Xij can take values 0, 1 or 2 according to the number of copies of the allele coded as 1 of SNP j in individual i, with frequency estimated with . All the models are parameterised using n × 1 vector of genomic values g, defined as
| (7) |
The conditional variance of g given W is
| (8) |
The term is the n×n matrix of average (over SNPs) realised genomic relationships among the n individuals (genomic relationship matrix) and is the genomic variance (Hayes et al., 2009). With standardised marker labels, a genomic heritability or proportion of variance accounted for by the SNPs can be defined as
| (9) |
Likewise, a genomic covariance between trait f and h is
and the genomic correlation is
| (10) |
When the markers are the causal loci (the case of perfect linkage disequilibrium between markers and causal loci) then , the heritability of the trait, and the genomic correlation is equal to the genetic correlation between traits. In general the markers are in imperfect linkage disequilibrium with the causal loci and therefore and the absolute value of rG represent lower bounds for the heritability of the trait and for the absolute value of the genetic correlation between traits (Yang et al., 2010).
Model comparison and influence of prior assumptions
The quality of fit of versions of the various models including and excluding marker information was studied using the pseudo log-marginal probability of the data. This is a standard measure of model comparison (Gelfand, 1996) and is defined and computed as follows. Consider data vector , where yi is the ith datum, and y−i is the vector of data with the ith datum deleted. In the case of the bivariate analysis of HEIGHT and FEV1, yi has two elements, one for each trait, and y−i is the vector of data corresponding to both traits, with yi deleted. The conditional predictive distribution has probability density
| (11) |
where θ is the vector of parameters of the model. This density can be interpreted as the probability of each data point given the remainder of the data; a low value indicates that the datum is poorly fit by the model. The actual value of p (yi|y−i) is known as the conditional predictive ordinate (CPO) for the ith observation. Thepseudo log-marginal probability of the data or pseudo marginal likelihood is given by
| (12) |
The collection of conditional predictive densities is equivalent to the marginal probability of the data, when the latter exists (Besag, 1974). The associated pseudo Bayes factor for comparing two models M1 and M2 (Gelfand et al., 1992; Gelfand, 1996) is
| (13) |
A Monte Carlo approximation of the CPO (11) for observation i is given by (Gelfand, 1996)
| (14) |
where N is the number of McMC draws, Mk is a label for model k, and θ(j) is the jth draw from the posterior of θ under model Mk. The so-called LogCPO’s reported below are based on
Larger values indicate a relative better fit.
We also performed a limited study to investigate the influence of some of the prior assumptions on inferences of genomic heritability. Technical details are shown in Appendices 4 and 5.
Model implementation
The implementation of the Bayesian models uses Markov chain Monte Carlo (McMC). A description of the salient features of the McMC algorithm can be found in Appendix 2. One of these is a data augmentation strategy which in the case of the bivariate analyses renders the likelihoods of the two traits conditionally independent, given a vector of augmented parameters. This simplifies computation and can be generalised in an obvious manner to an arbitrary number of traits. A second important detail concerning the threshold model is the joint updating of the genomic variance and of the complete vector of genomic values, which leads to excellent mixing behaviour of the McMC chain. In both the bivariate Gaussian model and the threshold model, a singular value decomposition of the genomic relationship matrix allows joint updating of the complete vector of genomic values (Janss et al., 2012). Details of this decomposition are in Appendix 1.
The McMC algorithm was implemented using single long chains. Convergence was studied by running the algorithm using different starting values and by visual inspection of traceplots of Monte Carlo draws of posterior distributions of chosen parameters. A little experimentation indicated that a chain length of 110, 000 resulted in Monte Carlo coefficients of variation of genomic heritabilities and genomic correlations smaller than 3%. The single trait analyses of FEV1 and of SMOKING status took approximately 2 hours to execute. The two-trait analysis took a little more than 3 hours.
Quantifying the effect of population structure on inferences of genomic heritabilities
The effect of putative population substructure on inferences of genomic heritability was investigated using the approach described in Janss et al. (2012). Janss et al. (2012) show that the mixed model with marker effects as implemented in this work is equivalent to a random regression on all marker-derived principal components. The influence of a particular eigenvector on inferences depends on the magnitude of the regression coefficient of the phenotype on the eigenvector. This is governed by the size of the eigenvalue of the associated eigenvector. Eigenvalues of small size lead to small regression coefficients and the effect of the associated eigenvectors on inferences is minimal.
When individuals cluster due to population substructure, the within cluster genomic heritability is
| (15) |
where αj is the regression coefficient of the phenotype on the jth eigenvector and n is the number of individuals (phenotypes). When the eigenvectors are sorted according to the decreasing size of their eigenvalues, expression (15) is the genomic heritability remaining after the largest d eigenvectors have been excluded. Below we provide estimates of genomic heritability for HEIGHT, FEV1 and SMOKING STATUS after removing the d = 20 largest eigenvectors.
Results
Raw means (standard deviations in brackets) for FEV1 are 3.79 l (0.68 l) in males and 2.80 l (0.66 l) in females; for height 175.9 cm (6.8 cm) in males and 162.5 cm (6.2 cm) in females and the proportion of smokers in the data (currently a smoker or have smoked) is 56% in both sexes.
Single-trait analysis of FEV1
The results of the single trait analyses are displayed in Table 1 in the form of estimated posterior means and posterior standard deviations. The estimates of sex effects, and the regressions on height and on smoking status are virtually identical in both models. The range in height is more than 40 cm in both sexes. The estimate of the regression of FEV1 on height is 0.043, implying that height can explain differences in FEV1 ranging approximately 1.7 l (i.e. 0.043 l/cm × 40 cm = 1.72 l). An alternative interpretation is that height accounts for approximately 30% of the total variation in FEV1 (i.e. 0.0432 × 6.32/0.25 ≈ 0.542 ≈ 0.30, where 0.54 is the (phenotypic) correlation between FEV1 and height, and 6.32 and 0.25 are the (phenotypic) variances of height and FEV1, respectively).
Table 1.
Single-trait analysis of FEV1 excluding (SNP EXCLUDED) and including (SNP INCLUDED) whole-genome marker information. The figures represent estimated posterior means (estimated posterior standard deviations in brackets).
| PARAMETER | SNP EXCLUDED | SNP INCLUDED |
|---|---|---|
| Sex (effect of female, l) | −0.404 (0.031) | −0.407 (0.031) |
| Regression on height (l/cm) | 0.043 (0.002) | 0.043 (0.002) |
| Regression on smoking status (l) | −0.126 (0.021) | −0.125 (0.021) |
| Residual variance | 0.252 (0.008) | 0.221 (0.024) |
| Genomic variance | 0.032 (0.023) |
It is interesting to observe that differences in FEV1 between males and females are not only explained by size, since there is an important sex effect (−0.404 l) after correcting for height.
The effect of smoking is not strikingly large, but this may reflect the way it is measured in the present study, where ex- and current smokers belong together in the same category.
The mixed effect model extracts a genomic component of variance from the residual variance of the fixed effects model, that comprises a little less than 13% of the total variance of FEV1 (corrected for effects of sex, height and smoking status). This figure, based on a posterior mean, can be interpreted as an estimate of the (conditional) genomic heritability of FEV1 (holding height and smoking status constant). Further analyses reported below indicate that statistical support for genomic variability of FEV1 in these data, after correction for HEIGHT and SMOKING status, is rather weak.
A fixed effects model with an overall mean, an effect of sex and linear regressions of FEV1 on height and height-squared and on smoking status was also fitted. The estimate of the residual variance was again 0.252 (see the second column of Table 1) and the estimate of the regression coefficient of FEV1 on height-squared was 1.27 × 10−4l/cm2. The remaining estimates were indistinguishable with those in the second column of Table 1, and the adjusted coefficient of determination R2 of the model with height as covariate and that with height-squared as covariate were both 0.566.
Model fit and influence of the prior distribution
The LogCPO for the model that includes marker information (genomic model) is −1, 653.14; for the model without marker information, the figure is −1, 654, 11. This corresponds to a ratio of the pseudo Bayes factor (13) equal to 2.64 in favour of the genomic model. This constitutes weak evidence for a genetic component a ecting FEV1, after adjusting for SMOKING status and HEIGHT. This conclusion is further supported by studying the effects of prior information on posterior inferences. Table 2 displays the consequences of using different values of the scale parameter of the prior distribution of the genomic variance, on both, the induced prior distribution of the genomic heritability and on its posterior distribution. Derivation of the induced prior density of the genomic heritability can be found in Appendix 4. Values of the scale parameter associated with the genomic variance equal to 0.01, 0.04 and 0.10 translate into modal values of the induced prior distribution of the genomic heritability equal to 0.01, 0.06 and 0.13, respectively. The changes at the level of the prior distribution of genomic heritability, by factors 6 and 2, respectively (from 0.01 to 0.06 and to 0.13), translate into changes at the level of posterior modes by factors 4 and 1.6, respectively (0.03 to 0.11 and to 0.18). The table also provides figures for the prior and posterior mean and the 95% highest posterior density intervals. The results show that prior information is very influential on posterior inferences and confirm the weakness of the genomic signal associated with FEV1, after it has been adjusted for HEIGHT and SMOKING. The bivariate analysis reported below casts further light on the nature of the relationship between FEV1 and HEIGHT.
Table 2.
Effects of different values of the scale parameter of the prior distributions of genomic variance () on the modal and mean value of the induced prior distribution andon posterior inferences of genomic heritability () for FEV1. The degrees of freedom parameter is set equal to 4:5, and the scale parameter of the environmental variance is set equal to 0:32, in all cases. The last row shows the 95% highest posterior density (HPD) intervals.
| 0.01 | 0.04 | 0.10 | |
|---|---|---|---|
| Mode prior | 0.01 | 0.06 | 0.13 |
| Mean prior | 0.05 | 0.16 | 0.27 |
| Mode posterior | 0.03 | 0.11 | 0.18 |
| Mean posterior | 0.06 | 0.13 | 0.21 |
| 95% HPD | (0.005; 0.131) | (0.044; 0.276) | (0.090;0.353) |
FEV1, conditional on HEIGHT and SMOKING status, was also analysed using restricted maximum likelihood (REML) using the software developed by Madsen and Jensen (2011). The REML estimate of genomic heritability was 0.07 with an asymptotic standard error equal to 0.13. This measure of uncertainty of the REML estimate includes values outside the allowed parameter space.
Joint analysis of FEV1 and height and single trait analysis of smoking status
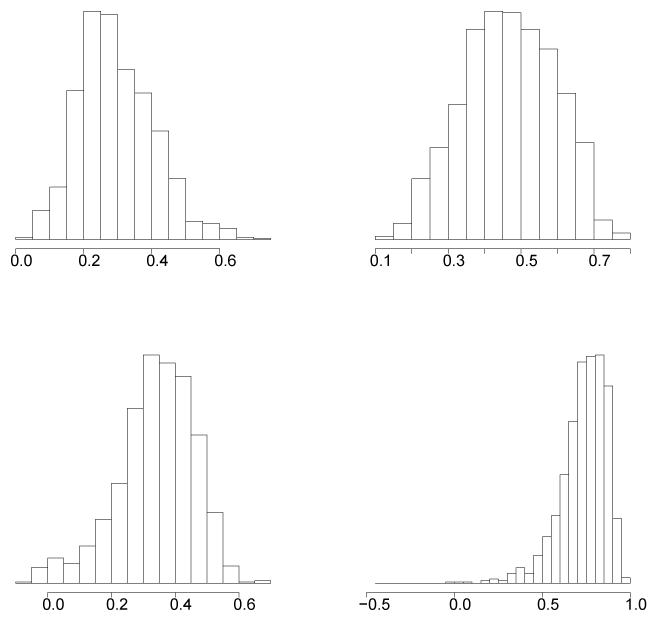
The results of the joint analysis of FEV1 and height are displayed in Table 3. The marginal genomic heritabilities of FEV1 and of height (based on estimated posterior means) are 30% and 47%, respectively, indicating that an important proportion of the total variance for these traits is explained by genetic marker information. The estimated posterior mean of the genomic heritability for height is very similar to estimates reported in other studies (Yang et al., 2010; Janss et al., 2012). The genomic correlation between these traits is positive, as expected, and large (estimated posterior mean equal to 0.73; estimated posterior mode equal to 0.78), almost three times larger than the environmental correlation. The environmental correlation is moderate, and 99% of the probability mass includes positive values of the environmental correlation. This indicates that environmental factors that affect one trait in one direction have also a partial effect on the other trait in the same direction. Histograms of Monte Carlo estimates of the genomic heritability for FEV1 and height, and of the genomic and environmental correlations are displayed in Figure 1, that provides a complete picture of the degree of posterior uncertainty.
Table 3.
Joint analysis of FEV1 and HEIGHT and single-trait analysis of SMOKING STATUS. The figures represent estimated posterior means and 95% highest posterior intervals in brackets, below). Diagonals: genomic heritabilities; upper off-diagonal: genomic correlation; lower off-diagonal: environmental correlation.
| TRAIT | FEV1 | HEIGHT | SMOKING |
|---|---|---|---|
| FEV1 | 0.30 (0.08; 0.51) |
0.73 (0.47; 0.95) |
- |
| HEIGHT | 0.34 (0.04; 0.54) |
0.47 (0.22; 0.70) |
- |
| SMOKING | - | - | 0.14 (0.04; 0.24) |
Figure 1.
Histograms of Monte Carlo estimates of posterior distributions. TOP: genomic heritabilities of FEV1 (left) and height (right). BOTTOM: environmental (left) and genomic (right) correlations between FEV1 and HEIGHT.
The single trait analysis indicated that the phenotypic correlation between FEV1 and height is approximately 0.5 (0.043 × 6.3/0.55, where 6.3 and 0.55 are the standard deviations of height and FEV1, respectively). This is confirmed by the joint analysis which additionally, provides insight into the nature of this correlation. Another observation from the joint analysis is that the phenotypic regression of FEV1 on height, equal to 0.043 l/cm, can be partitioned into a genomic component, 0.024 l/cm, and a residual component, 0.019 l/cm (these are obtained from knowledge of the genomic covariance, equal to 1.019, and the residual covariance, equal to 0.806, and dividing each by the phenotypic variance of height, equal to 42.3).
The results of the joint analysis can be used to draw conditional inferences. A little manipulation of the output indicates that the conditional genomic heritability of FEV1 (holding height constant) is of the order of 13% (using the posterior mode of 0.78 as point estimate of the genomic correlation), in good agreement with the output from the single trait mixed model. Taken at face value, this indicates that a large proportion of the genomic variability in FEV1 is explained by genomic variability in height.
To investigate whether smoking status accounts for part of the genomic variation for FEV1, the joint analysis was repeated fitting a model without smoking status as covariate. The estimate of genomic variance of FEV1 did not differ from that obtained fitting the full model. This provides indirect evidence for lack of genomic covariability between FEV1 and smoking status.
The bivariate analysis was also carried out using REML. The estimates of genomic heritability of FEV1 and HEIGHT (asymptotic standard errors in brackets) were 0.25 (0.11) and 0.41 (0.12), respectively. The REML estimate of the genetic and environmental correlations were 0.84 (0.15) and 0.29 (0.12), respectively. The overall picture provided by the REML analysis is similar to that from the Bayesian analysis. However, particularly in small samples, inferences based on a joint maximiser of a 6-dimensional hypersurface (2 genomic variances, 2 environmental variances and 2 covariances), as provided by the REML estimates, are expected to differ from those based on marginal distributions, as provided by the Bayesian approach.
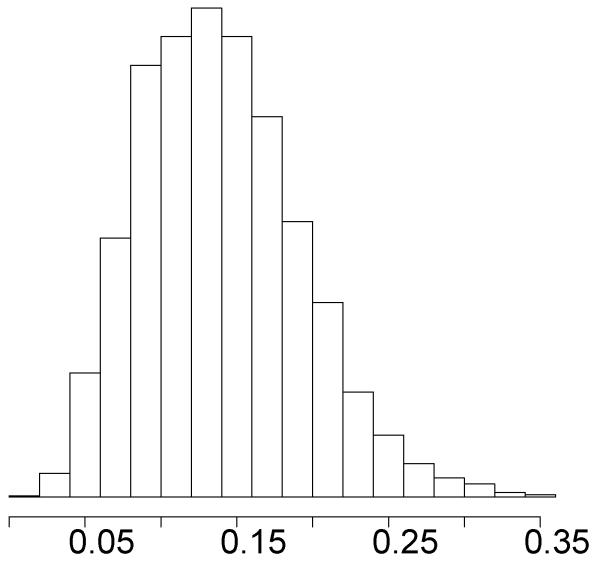
The single trait analysis of smoking status retrieves an estimated posterior mean of genomic heritability equal to 0.14 and a posterior mode of 0.13. A histogram of the Monte Carlo estimate of the genomic heritability is shown in Figure 2. Notice that the posterior distribution is a little asymmetrical but reasonably sharp, notwithstanding the rather coarse measure of smoking in the present data.
Figure 2.
Histogram of Monte Carlo estimate of the posterior distribution of the genomic heritability of smoking status.
There have been early studies documenting the presence of genetic variation on smoking consumption (Swan et al., 1990) and on smoking initiation and nicotine dependence (Vink et al., 2005). Both studies used twins. More recently, a variant associated with nicotine dependence was detected in a genome-wide association study (Thorgeirsson et al., 2008). However, a quantification of variation explained by genetic factors using whole genome marker regression models, as far as we know, has not been previously reported.
In general, the results from these analyses must be interpreted with the necessary caution in view of the limited amount of data.
Model fit and influence of the prior distribution
The LogCPO’s for the joint analysis of HEIGHT and FEV1 were computed for two versions of the model. In the first one, marker information was not included and the correlation between traits was only of environmental origin. The second version included marker information as reported in Table 3, and the correlation structure between the traits has a genomic and an environmental component. The LogCPO’s for these two models were −8, 357.99 and −7861.21, respectively, indicating a substantially larger quality of fit in favour of the model with genetic marker information. This result is in marked contrast with that presented in the univariate analysis of FEV1, conditional on SMOKING STATUS and HEIGHT. Clearly, genetic factors are important when FEV1 and HEIGHT are analysed jointly. However in the case of FEV1, a large proportion of the genomic variance is explained by HEIGHT. Therefore when marker information is added in the analysis of FEV1, corrected for HEIGHT and SMOKING STATUS, only a modest improvement of fit is observed.
The LogCPO’s for the analysis of SMOKING status with and without marker information were −1530.51 and −1, 532.51, respectively. This corresponds to a ratio of the pseudo Bayes factor (13) equal to 7.4 in favour of the genomic model.
The effect of varying the scale parameter of the scaled inverse chi square prior distribution of the genomic variance, on both, the modal value of the induced prior distribution of the genomic heritability, and on posterior inferences of heritability for SMOKING STATUS, is summarised in Table 4. Details of the derivation of the induced prior distribution of genomic heritability, based on the prior distribution of genomic variance, are shown in Appendix 5. The degrees of freedom parameter was kept unchanged at a value of 4.5. Values of the scale parameter of the scaled inverse chi square prior distribution of the genomic variance, equal to 0.11, 0.23 and 0.46, induce modal values for the prior distribution of heritability equal to 0.07, 0.15 and 0.28, respectively. This translates in posterior modes of genomic heritability equal to 0.11, 0.13 and 0.15, respectively. The figures indicate that prior information is mildly influential, but that there is substantial Bayesian learning from the data. A change of effectively 100% in the prior modal values results in corresponding changes at the level of posterior modes of between 15% and 18%. This result is perhaps a little unexpected, in view of the limited amount of data and the rather coarse measure used to analyse SMOKING.
Table 4.
Effects of different values of the scale parameter (Sg) of the scaled inverse chisquare prior distribution of the genomic variance on the modal value of the induced prior and posterior distribution of genomic heritability (), for SMOKING STATUS. The degrees of freedom parameter is set equal to 4:5. The last row shows the 95% highest posterior density (HPD) intervals.
| Sg | 0.11 | 0.23 | 0.46 |
|---|---|---|---|
| Mode prior | 0.07 | 0.15 | 0.28 |
| Mode posterior | 0.11 | 0.13 | 0.16 |
| Mean posterior | 0.12 | 0.14 | 0.16 |
| 95% HPD | (0.042; 0.210) | (0.057; 0.233) | (0.082;0.257) |
Quantifying the effect of population structure on inferences of genomic heritabilities
The posterior means of the genomic heritabilities for FEV1, HEIGHT and SMOKING STATUS were 0.296, 0.465 and 0.140, respectively. After removal of the 20 largest eigenvectors, the posterior means were 0.292, 0.460 and 0.138, respectively. Clearly, unaccounted substructure in these data do not affect inferences of genomic parameters. Not surprisingly, these results agree with those reported by Janss et al. (2012), where a similar data set was used and where further details can be found.
Discussion
The present work reports the results of a genomic analysis of FEV1, height and smoking, where the first two traits are analysed jointly and smoking is analysed as a single binary trait. The data consist of a little more than 2, 200 nominally unrelated individuals. The incorporation of rich genetic marker data in the form of almost 700, 000 SNP genotypes and the use of a whole-genome random regression approach whereby all markers were fitted simultaneously, made possible the extraction of a considerable amount of information from a relatively small number of unrelated individuals. With this data structure, this could not have been achieved using traditional quantitative genetic methods that rely on pedigree information.
The Bayesian method used in this work has a number of attractive features. One of these is the ability to incorporate prior information, and importantly, to quantify how this a ects inferences. In contrast with traditional likelihood-based methods, the Bayesian approach implemented using McMC is free from asymptotic assumptions and does not incur in measures of uncertainty that span invalid values of the parameters (the 95% asymptotic confidence interval of the REML estimator of genomic heritability of FEV1, conditional on smoking status and height is (−0.19; 0.33)). This is particularly important in scenarios with limited data or with highly parameterised models, as is the case here. The posterior distributions displayed in figures 1 and 2 illustrate this point. If data had been very informative the histograms would tend to be symmetric. The limited amount of information in the data is well captured by the Bayesian machinery and avoids understating uncertainty. Further, in our experience with highly parameterised hierarchical models, Bayesian McMC methods show more stable numerical behaviour than likelihood-based alternatives. The McMC implementations provides a very flexible environment and allows to study the consequences on inferences of not only using different prior distributions but also of using different likelihoods. This flexibility extends to the possibility of constructing measures of global model fit with little extra programming effort, that, in contrast to traditional likelihood, allow comparisons involving non-nested models. Often the Bayesian McMC models take longer time than those based on traditional likelihoods. However, given the huge efforts and costs often involved in collection of data, this may not always be the correct criterion to guide the choice of the method of analysis.
The single trait analysis of smoking status revealed a genomic component of variability at the level of the liability. The posterior mean of this genomic heritability is 0.14. An implication of the existence of genomic variation is that one can quantify the probability that an individual turns out to be a smoker, given the smoking status of its parents. Specifically, if neither father nor mother smoke, the answer is obtained computing
where yo = 1 is the smoking status of an offspring (smoker or have smoked), and yf = 0, ym = 0 represent the smoking status of the father and mother respectively (never smoked). A little mathematics involving numerical integration of multivariate normal distributions reveals that the answer is 51%. If both parents smoke or have smoked we obtain Pr (yo = 1|yf = 1, ym = 1) = 0.60. These figures must be compared with the (marginal) probability of drawing an individual that smokes from the data, which is 56%. These calculations assume that the regression of the offspring on its father is the same as that on its mother and equal to one half the genomic heritability. This is admittedly a rather simple model to describe a complex behavioural trait (knowledge of the genomic correlation could be supplemented with knowledge of the fraction that quantifies effect of parental environment, for example the smoking status of the parents) but is used here as an illustration. A more refined analysis would retrieve the probability that the individual smokes, given its genetic marker information (and information of other determining factors), which involves isolating genetic markers that are associated with the trait. This is the kind of promise held by personalised medicine, that still remains a task for the future, with the exception of simple Mendelian diseases with known mechanisms of inheritance.
The main conclusions from this study are that HEIGHT and FEV1 are genetically and environmentally correlated, and that approximately 60% (0.782 × 100) of the total genomic variation in FEV1 is explained by its genomic association with HEIGHT. After accounting for HEIGHT and SMOKING status, genomic variability explains 13% of the total variance of FEV1. However, judging by the measures of global fit and by the influence of prior information on posterior inferences, statistical support in favour of genomic variation for FEV1, after adjusting for HEIGHT and SMOKING status, is weak. The study also provides evidence for the presence of genetic factors associated with SMOKING STATUS. Indeed, approximately 14% of the total variation on the liability scale is explained by genetic markers. This figure must be interpreted as a lower bound of the heritability of the trait.
The Bayesian McMC methods use here can in principle be extended quite easily to partitioning the total genomic variation into components due to chromosomes or chromosome segments in a single analysis and to localising regions with strong genomic signals (Janss et al., 2012). Such information, combined with knowledge already available of metabolic pathways and gene networks could lead to a deeper understanding of the mechanisms involved. However, inferences of this kind would require a larger amount of genotyped individuals than those available here.
In a recent study Klimentidis et al. (2013) presented pedigree-based estimates of heritability of FEV1 (and other pulmonary function traits) based on whole-genome marker data (genomic heritability). In contrast with our study, theirs used family data, did not correct for HEIGHT, and report estimates of approximately 50% based on both the marker and the pedigree data. In the present study the estimate of the genomic heritability from the marginal posterior distribution of FEV1 is 30% (see Table 3), 60% of that reported by Klimentidis et al. (2013). This discrepancy is in good agreement with evidence from the literature: the unaccounted 40% in our case, is often interpreted as missing heritability observed in analyses involving nominally unrelated individuals. One explanation is imperfect linkage disequilibrium between markers and QTL, exacerbated by the fact that marker and causal loci may have different distributions of allele frequency (Yang et al., 2010). In this situation, the realized proportions of allele sharing at markers and at causal loci can be very different. This is exacerbated with unrelated individuals (de los Campos et al., 2013). A number of approaches have been suggested to adjust the marker-based relationship matrix in order to obtain estimates of genomic heritabilities that are more in line with the trait heritability (Speed et al., 2012; Lee et al., 2013; Speed et al., 2013). However it is doubtful whether these alternatives can mitigate the fact that the likelihood function of the marker-based model may misrepresent the underlying data generating process. This can lead to inferential problems that can further contribute to the discrepancy between genomic and trait heritabilities (de los Campos and Sorensen, 2013). More research is needed to fully understand the properties of inferences based on WGRR models.
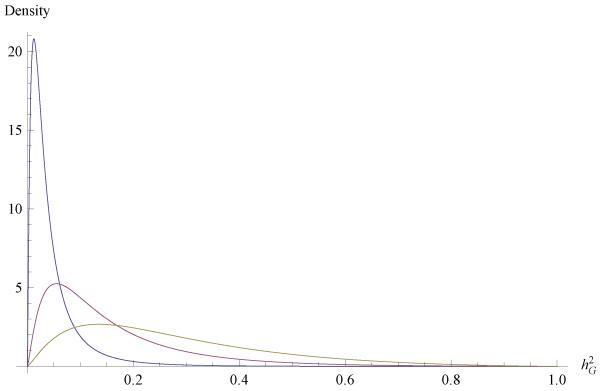
Figure 3.
Induced prior distribution of genomic heritability for FEV1, with vi = 4.5, (i = e, f), , and (from left to right) , 0.04 and 0.10.
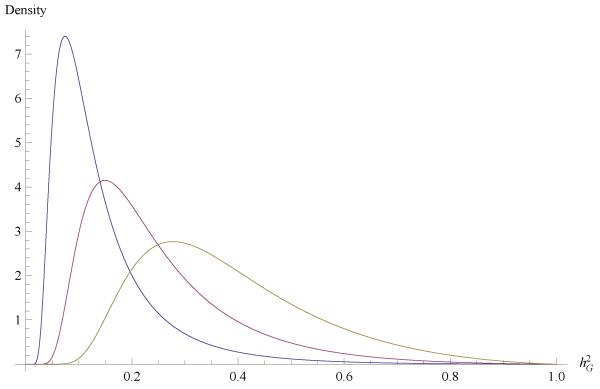
Figure 4.
Induced prior distribution of genomic heritability for SMOKING STATUS, with v = 4.5 and (from left to right) S2 = 0.11, 0.23 and 0.46.
Acknowledgements
DS acknowledges financial support from NIH grant R01GM099992.
Appendix 1: the singular value decomposition of the genomic relationship matrix
For the three traits, the matrix W is decomposed as
and therefore
where U = [U1, U2, …, Un], of order n × n is the matrix of eigenvectors of WW’, Uj is the jth column (dimension n × 1), and D is a diagonal matrix with elements equal to the eigenvalues λ1, λ2, …, λn associated to the n eigenvectors. Since WW’ is non-negative definite the eigenvalues are λi ≥ 0, i = 1, 2, …, n (due to the centering of W, its rank is equal to n-1, and the last eigenvalue is equal to zero. Therefore the last diagonal element of D is equal to zero). The eigenvectors satisfy U’U = UU’ = I. The n × 1 vector of principal components α are assumed to originate from the distribution
| (16) |
This decomposition results in important computational advantages because the fully conditional posterior distribution of the vector α (for the three traits) is Gaussian with diagonal covariance matrix (de los Campos et al., 2010; Janss et al., 2012). Notice that
where is the genomic relationship matrix and is the genomic variance. Since Uα and Wb are both Gaussian, with the same mean and variance, they represent two parameterisations of the same probability model. The vector of genomic values can be expressed as .
Appendix 2: An augmented hierarchical model for FEV1 and HEIGHT, and prior and posterior distributions of the augmented model
Here we present a data augmentation strategy of the two-trait analysis of FEV1 and height that leads to conditional independence of the conditional posterior distributions of each trait.
In a first step, the n × 1 vectors of genomic values gi = Wbi are replaced by . The new expressions are
| (17a) |
| (17b) |
The observed n × n matrix is defined as
where WW’ = UDU’. The column vectors of length n, αi, are assigned the linear structures
| (18a) |
| (18b) |
Prior distributions
The n × 1 vectors δi are , i = f, h. The scalars, vf, vh are N(0, 105) iid random variables, and the n × 1 vector s1 is a N (0, I) iid random variable. The column vectors ei in (17) are expressed as
| (19a) |
| (19b) |
In (19), , are n × 1 independently distributed vectors, z1 is a N (0, I) n×1 independently distributed vector, and the q’s are iid N (0, 105) random variables.
The conditional augmented model, given vf , vh, qf , qh, , , , , generates the following covariance structures:
| (20) |
| (21) |
The relationship between the random variables defined in (2) and (3) and those in (20) and (21) is:
The posterior distribution
Let
be the vector of parameters of the augmented model. Let
The posterior distribution is
| (22) |
In the augmented model, the posterior distribution of the complete data factorises into two conditionally independent terms.
The prior distribution of the parameters of the model admits the factorisation
| (23) |
The McMC algorithm
The fully conditional posterior distributions are standard, and therefore the McMC updating strategy consists of a Gibbs sampler with either scaled inverse chi square distributions for the variance parameters, or normal distributions for the remaining parameters.
Appendix 3: The model for SMOKING STATUS
SMOKING STATUS is analysed as a single binary trait (yi = 1 if individual i is a smoker or has smoked; yi = 0 if never smoked) with a liability threshold model, used by Wright (1934) in studies of the number of digits in guinea pigs, and by Bliss (1935) in toxicology experiments. An McMC implementation of the threshold model was described by Albert and Chib (1993) and a quantitative genetic application was presented by Sorensen et al. (1995).
In the threshold model, it is postulated that there exists a latent or underlying variable (liability) which has a continuous distribution. The standard parameterisation in the case of binary responses is to assume that the response yi = 1 is observed, if the liability exceeds the threshold (set equal to zero), and if it is smaller than the threshold, yi = 0.
The vector of liabilities of dimension n × 1 is modelled as
with
| (24) |
The residual variance component of the liability is set equal to 1. Define
Then the liability of individual i is assumed to be a draw from
| (25) |
where is the ith row of matrix Z. For individual i
| (26a) |
| (26b) |
| (26c) |
where Φ is the cdf of N (0, 1). One can therefore write
| (27) |
where I is the indicator function, equal to 1 if the argument is satisfied, and equal to 0 otherwise. Expression (26a) implies that
and therefore in general, the term can be written as
| (28) |
Prior distributions
The vector of parameters of the model, augmented with the vector of liabilities (Albert and Chib, 1993), is
and assuming that p (μ) ∝ constant, the prior distribution admits the factorisation
The prior distribution of is specified in (16). The prior of is a scaled inverted chi square distribution and of is shown in (25).
The posterior distribution
The posterior distribution is
| (29) |
where the last line is obtained using (28).
The McMC algorithm
The McMC algorithm samples
where D includes the remaining parameters (that is, all parameters except the one to be updated) and the observed data. Assuming an improper uniform prior distribution for μi, the update based on the single-site Gibbs sampler consists of drawing from
| (30) |
where .
The fully conditional posterior distribution of the liability is proportional to . Using (29)
The term in square brackets has the effect of truncating the . The density of the fully conditional posterior distribution for the ith observation becomes
| (31) |
This implies that if and the fully conditional posterior density is proportional to , which is truncated normal with support (−∞, 0). If yi = 1, and the fully conditional posterior density is proportional to , which is truncated normal with support (0, ∞).
Joint updating of α and
We write the fully conditional posterior distribution of α and as
where
and the density of the marginal distribution is
| (32) |
where .
The joint updating strategy consists of updating first α from and secondly from .
Updating α from The fully conditional posterior distribution of α is
which leads to
| (33) |
where
| (34) |
Updating from Expression (32) is of the form
| (35) |
Let . Then (35) can be written
| (36) |
Regarded as a function of this does not reduce to a standard density and a Metropolis Hastings update is necessary. The strategy implemented is based on a Gaussian random walk kernel on . Specifically, let represent the current value and let be the proposed value, drawn from . This is a normal distribution with mean and variance k. The variance k is a user-tuned input parameter. If is normally distributed then the density q of is log-normally distributed and the Metropolis-Hastings ratio takes the form
| (37) |
where q is the log-normal density
Notice that
To arrive at (35) we use
Appendix 4. Single trait analysis of FEV1: Influence of the prior distributions of the genomic and environmental variances on the induced prior distribution of the genomic heritability
The prior distributions of the genomic and environmental variances for FEV1 are a scaled inverse chi square distributions with scale parameters , and degrees of freedom vg, ve, respectively. The densities are
As shown in Sorensen and Gianola, 2002, page 109, the density of the induced prior distribution of the genomic heritability is given by
| (38) |
where ai = vi/2, , i = e, f. Using vi = 4.5, (i = e, f), and , the modal values of (38) for , 0.100 and 0.200, are 0.055, 0.134 and 0.306, respectively. These three prior distributions of FEV1 are shown in Figure 3.
Appendix 5. SMOKING STATUS: Influence of the prior distribution of the genomic variance on the induced prior distribution of the genomic heritability
The prior distribution of the genomic variance is a scaled inverse chi square distribution with scale parameter S2 and degrees of freedom v. This density takes the form
| (39) |
The genomic heritability is
and the inverse function is . The Jacobian is given by and the induced prior density of is given by
| (40) |
The modal values of the three distributions, using v = 4.5 and (from left to right) S2 = 0.11, 0.23, 0.46, are equal to 0.07, 0.15 and 0.28, respectively. These three prior distributions of FEV1 are shown in Figure 4.
References
- Albert JH, Chib S. Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association. 1993;88:669–679. [Google Scholar]
- Besag J. Spatial interaction and the statistical analysis of lattice systems (with discussion) Journal of the Royal Statistical Society Series B. 1974;36:192–326. [Google Scholar]
- Bliss CI. The calculation of the dosage-mortality curve. Annals of Applied Biology. 1935;22:134–167. [Google Scholar]
- Chinn S, Gislason T, Aspelund T, Gudnason V. Optimum expression of adult lung function based on all-cause mortality: Resutls from the Reykjavik study. Respiratory Medicine. 2007;101:601–609. doi: 10.1016/j.rmed.2006.06.009. [DOI] [PubMed] [Google Scholar]
- Daetwyler HD, Villanueva B, Woolliams JA. Accuracy of predicting the genetic risk of disease using a genome-wide approach. PloS One. 2008;3(10):e3395. doi: 10.1371/journal.pone.0003395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Gianola D, Rosa GJM, Weigel KA, Crossa J. Semiparametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genetics Research. 2010;92:295–308. doi: 10.1017/S0016672310000285. [DOI] [PubMed] [Google Scholar]
- de los Campos G, Hickey J, Pong-Wong R, Daetwyler HD, Calus MPL. Whole genome regression and prediction methods applied to plant and animal breeding. Genetics. 2013;193:327–345. doi: 10.1534/genetics.112.143313. doi:10.1534/genetics.112.143313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Sorensen D. Comments on pitfalls of predicting complex traits from SNP’s. Nature Reviews Genetics. 2013;894 doi: 10.1038/nrg3457-c1. doi:10.1038/nrg3457-c1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Vazquez AI, Fernando R, Klimentidis YC, Sorensen D. Prediction of complex human traits using the genomic best linear unbiased predictor. PLOS Genetics. 2013;9(3):e1003608. doi: 10.1371/journal.pgen.1003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand AE. Model determination using sampling-based methods. In: Gilks WR, Richardson S, Spiegelhalter DJ, editors. Markov Chain Monte Carlo in Practice. Chapman and Hall; 1996. pp. 145–161. [Google Scholar]
- Gelfand AE, Dey DK, Chang H. Model determination using predictive distributions with implementation via sampling-based methods. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian Statistics. Vol. 4. Oxford University Press; 1992. pp. 147–167. [Google Scholar]
- Hayes B, Visscher PM, Goddard ME. Increased accuracy of artificial selection by using the realized relationship matrix. Genetics Research. 2009;91:47–60. doi: 10.1017/S0016672308009981. [DOI] [PubMed] [Google Scholar]
- Hoggart CJ, Whittaker JC, De Lorio M, Balding DJ. Simultaneous analysis of all SNPs in genome-wide and re-sequencing association studies. PLOS Genetics. 2008;4(7):e1000130. doi: 10.1371/journal.pgen.1000130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janss LLG, de los Campos G, Sheehan N, Sorensen D. Inferences from genomic models in stratified populations. Genetics. 2012;192:693–704. doi: 10.1534/genetics.112.141143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerstjens HAM, Rijcken B, Schouten JP, Postma DS. Decline of FEV1 by age and smoking status: facts, figures, and fallacies. Thorax. 1997;52:820–827. doi: 10.1136/thx.52.9.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klimentidis YC, Vazquez AI, de los Campos G, Allison D, Dransfield MT, Thannickal VJ. Heritability of pulmonary function estimated from pedigree and whole-genome markers. Frontiers in Genetics. 2013;4 doi: 10.3389/fgene.2013.00174. doi:10.3389/fgene.2013.00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange P, Nyboe J, Appleyard M, Jensen G, Schnohr P. Spirometric findings and mortality in never-smokers. Journal of Clinical Epidemiology. 1990;43:867–873. doi: 10.1016/0895-4356(90)90070-6. [DOI] [PubMed] [Google Scholar]
- Lee SH, Wray NR, Goddard ME, Visscher PM. Estimating missing heritability for disease from genome-wide association studies. The American Journal of Human Genetics. 2011;88:294–305. doi: 10.1016/j.ajhg.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Wray NR, Goddard ME, Visscher PM. Estimation of SNP heritability from dense genotype data. The American Journal of Human Genetics. 2013;93:1151–1157. doi: 10.1016/j.ajhg.2013.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Yang J, Goddard ME, Visscher PM, Wray N. Estimation of pleiotropy between complex diseases using single-nucleotide polymorphism-derived genomic relationships and restricted maximum likelihood. Bioinformatics. 2012;28:2540–2542. doi: 10.1093/bioinformatics/bts474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacNee W, Maclay J, McAllister D. Cardiovascular injury and repair in chronic obstructive pulmonary disease. Proceedings of the American Thoracic Society. 2008;5:824–833. doi: 10.1513/pats.200807-071TH. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen P, Jensen J. A User’s Guide to DMU, version 6, release 5.0; A Package for Analysing Multivariate Mixed Models. Aarhus University; Denmark: 2011. http://dmu.agrsci.dk/dmuv6guide.5.0.pdf [Google Scholar]
- McClellan J, King MC. Genetic heterogeneity in human disease. Cell. 2010;16:210–217. doi: 10.1016/j.cell.2010.03.032. [DOI] [PubMed] [Google Scholar]
- Meuwissen THE, Hayes BJ, Goddard ME. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157:1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MR, Hankinson J, Brusasco V, Burgos F, Casaburi R, Coates A, Crapo R, Enright, van der Grinten P, Gustafsson P, Jensen R, Johnson DC, Macintyre N, McKay R, Navajas D, Pedersen OF, Pellegrino R, Viegi G, Wanger J. Standardisation of spirometry. European Respiratory Journal. 2005;26:319–338. doi: 10.1183/09031936.05.00034805. [DOI] [PubMed] [Google Scholar]
- Power C, Elliott J. Cohort profile: 1958 British birth cohort (National Child Development Study) International Journal of Epidemiology. 2006;35:34–41. doi: 10.1093/ije/dyi183. [DOI] [PubMed] [Google Scholar]
- Sorensen D, Andersen S, Gianola D, Korsgaard IR. Bayesian inference in threshold models using Gibbs sampling. Genetics, Selection, Evolution. 1995;27:229–249. [Google Scholar]
- Sorensen D, Gianola D. Likelihood, Bayesian, and MCMC Methods in Quantitative Genetics. Springer-Verlag; 2002. p. 740. Reprinted with corrections, 2006. [Google Scholar]
- Speed D, Hermani G, Johnson MR, Balding DJ. Improved heritability estimation from genome-wide SNPs. The American Journal of Human Genetics. 2012;91:1011–1021. doi: 10.1016/j.ajhg.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D, Hermani G, Johnson MR, Balding DJ. Response to Lee et al.: SNP-based heritability analysis with dense data. The American Journal of Human Genetics. 2013;93:1155–1157. doi: 10.1016/j.ajhg.2013.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swan GE, Carmelli D, Rosenman RH, Fabitz RR, Christian JC. Smoking and alcohol consumption in adult male twins: Genetic heritability and shared environmental influences. Journal of Substance Abuse. 1990;2:39–50. doi: 10.1016/s0899-3289(05)80044-6. [DOI] [PubMed] [Google Scholar]
- Thorgeirsson TE, Geller F, Sulem P, Rafnar T, et al. A variant associated with nicotine dependence, lung cancer and peripheral arterial disease. Nature. 2008;452:638–642. doi: 10.1038/nature06846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vink JM, Willemsen G, Boomsma DI. Heritability of smoking initiation and nicotine dependence. Behavior Genetics. 2005;35:397–406. doi: 10.1007/s10519-004-1327-8. [DOI] [PubMed] [Google Scholar]
- Wray NR, Goddard ME, Visscher PM. Prediction of individual genetic risk to disease from genome-wide association studies. Genome Research. 2007;17:1520–1528. doi: 10.1101/gr.6665407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. An analysis of variability in number of digits in an inbred strain of guinea pigs. Genetics. 1934;19:506–536. doi: 10.1093/genetics/19.6.506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, Goddard ME, Visscher PM. Common SNP’s explain a large proportion of the heritability for human height. Nature Genetics. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou X, Carbonetto P, Stephens M. Polygenic modeling with Bayesian sparse linear mixed models. PLOS Genetics. 2013;9 doi: 10.1371/journal.pgen.1003264. doi:10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]