Development, growth and maintenance of β-cell mass: Models are also part of the story

Abstract

Pancreatic β-cells in the islets of Langerhans play a crucial role in regulating glucose homeostasis in the circulation. Loss of β-cell mass or function due to environmental, genetic and immunological factors leads to the manifestation of diabetes mellitus. The mechanisms regulating the dynamics of pancreatic β-cell mass during normal development and diabetes progression are complex. To fully unravel such complexity, experimental and clinical approaches need to be combined with mathematical and computational models. In the natural sciences, mathematical and computational models have aided the identification of key mechanisms underlying the behavior of systems comprising multiple interacting components. A number of mathematical and computational models have been proposed to explain the development, growth and death of pancreatic β-cells. In this review, we discuss some of these models and how their predictions provide novel insight into the mechanisms controlling β-cell mass during normal development and diabetes progression. Lastly, we discuss a handful of the major open questions in the field.

1. Introduction

Fluctuations in the level of glucose concentration caused by food intake or physical activity occur continuously in the body. Glucose homeostatic regulation by insulin maintains a stable and normal level of glucose in the blood and is considered a fundamental aspect of a healthy metabolic condition. In the islets of Langerhans, pancreatic β-cells are at the core of this regulatory mechanism by secreting insulin upon metabolic demand to keep glucose concentration within a narrow range (Bonner-Weir, 1994), which makes insulin and glucose dynamics largely correlated with β-cell mass (Larsen et al., 2003). Besides insulin and glucose, other factors and hormones are also involved in controlling the activity of pancreatic β-cells, such as glucagon, somatostatin and ghrelin. These hormones are secreted by α-, δ- and ε-cells, which are also located in the islets of Langerhans (Kim et al., 2009). The islets also have the pancreatic polypeptide-secreting PP cells and other non-endocrine cell types (e.g. endothelial cells), which are important for pancreatic β-cell activity. All of these factors generate a very complex network of negative and positive feedbacks that govern β-cell activities.

The β-cell mass regulation is a highly complex developmental and physiological system. Its development and homeostasis is regulated by numerous variables and parameters in different hierarchical layers of spatial and temporal organization. Excellent reviews of the molecular regulation of early pancreatic development and β-cell differentiation, proliferation and apoptosis are available in the literature (Ackermann and Gannon, 2007; Bonner-Weir et al., 2012; Elghazi and Bernal-Mizrachi, 2009; Kulkarni et al., 2012; Weir et al., 2013; Yesil and Lammert, 2008). These reviews are primarily focused on the experimental and clinical work on β-cell mass development and homeostasis.

The complexity of the β-cell mass regulation can be unraveled by combining experimental and theoretical tools, which have the potential to analyze a complex web of interactions and feedback loops. A combination of experimental, mathematical and computational analyses has been very successful in providing novel insights to understand the mechanisms regulating stimulus-secretion coupling in pancreatic β-cells (Bertram and Sherman, 2000; Bertram et al., 2007; Sherman, 1996). The mathematical and computational modeling of glucose homeostasis, diabetes and its associated complications is rapidly growing. Currently, a few models exist that are used to design treatment protocols for diabetic patients, some of which have been recently reviewed in the literature (Ajmera et al., 2013; Nyman et al., 2012). In this review, we provide an overview of the complex hierarchical organization of the β-cell mass and its development, and describe some of the contributions made by mathematical and computational models to understand the mechanisms controlling the development and homeostasis of β-cell mass.

2. The total pancreatic β-cell mass is the result of a balance between neogenesis, proliferation and apoptosis during normal development

Like any other cell population, the net growth rate of β-cells is determined by the three developmental factors: β-cell neogenesis, β-cell replication and β-cell death (Bonner-Weir, 2001; Bonner-Weir and Sharma, 2002; Lee and Nielsen, 2009) (Figure 1). β-cell neogenesis can occur from stem or progenitor cells during embryonic or postnatal growth. Stem or progenitor cells can arise from diverse locations such as pancreatic ducts, islets and bone marrow. There are other mechanisms of neogenesis, which include trans-differentiation of pancreatic acinar and liver cells, differentiation of intra-islet precursors or splenocytes, epithelial-mesenchymal transition (Gershengorn et al., 2004; Lipsett and Finegood, 2002; Sapir et al., 2005), and induced genetic reprogramming of adult exocrine cells to functional β-cells (Zhou et al., 2011). During normal development, progenitors of β-cells receive multiple simultaneous signals: some are mitogenic and others induce differentiation (Dhawan et al., 2007). External signals need to be interpreted through cellular signaling pathways to commit the progenitor cell either to the mitotic cell cycle or to abrogate it for differentiation. Understanding the regulation of these signals and the external modulation of transcription factors involved in these processes is essential for determining the outcome of cellular (re)programming of β-cells progenitors in healthy and pathological conditions.

Figure 1.

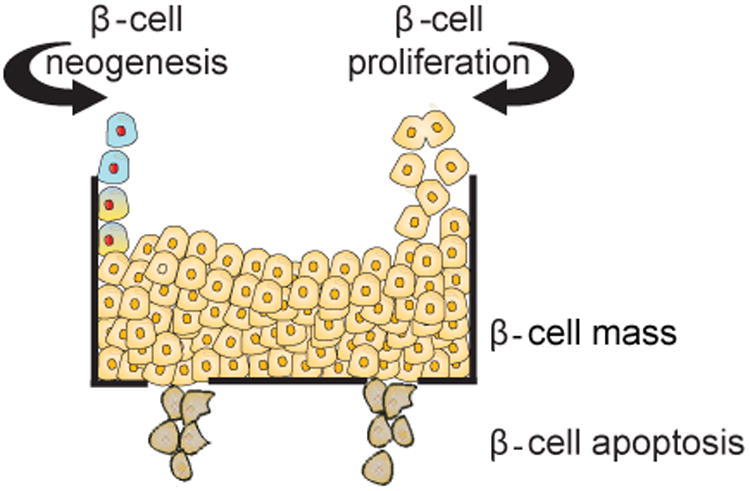
The β-cell mass is regulated by a balance of β-cell formation either by neogenesis of β-cells from stem cell/progenitor β-cells or replication from existing β-cells, and β-cell death through β-cell apoptosis. Mathematical and computational models of the net growth of β-cell are governed by the sum of the rates of β-cell neogenesis, replication and death.

Finegood et al. (Finegood et al., 1995) described the dynamics of beta-cell mass growth in wild type rats with a mathematical expression governing β-cell neogenesis, β-cell replication and apoptosis. By quantifying the difference in net growth and apoptosis in β-cells, it was discovered in this study that these cells exhibit a wave of β-cell apoptosis in neonates. During the fetal period, it is generally accepted that β-cells are formed by neogenesis (Finegood et al., 1995), although quantifying the differentiation of β-cell precursors is difficult (Wang et al., 1994; Xu et al., 1999). After birth, pancreatic β-cells are formed via replication of mature beta-cells rather than neogenesis (Dor et al., 2004; Finegood et al., 1995; Montanya et al., 2000; Teta et al., 2007), though replication is generally very slow in adults (Teta et al., 2005). The mathematical model by Finegood et al. adopts β-cell proliferation terms declining with age, which is supported by developmental or regeneration studies in mice, rats, pigs and humans (Bock et al., 2003; Hanley et al., 2010; Rankin and Kushner, 2009; Tschen et al., 2009). Interestingly, the model proposed by Finegood et al. predicts β-cell apoptosis to peak around 10–17 (postnatal) days in the rat, significantly affecting the net growth rate of the β-cell population during normal development.

Manesso et al. (Manesso et al., 2009) developed a model with three elements: β-cell replication of existing β-cells, β-cell production from other sources and β-cells lost through β-cell apoptosis. This model is similar to the one proposed by Finegood et al. (Finegood et al., 1995), and it was used to investigate whether β-cell formation is derived exclusively from β-cell replication or significantly affected by other sources of β-cells during the adult phases of rat development. They showed that the formation and maintenance of adult β-cells depends largely (∼80%) on sources of β-cells independent from β-cell duplication. It is plausible that β-cells arise from either a single source, such as differentiation from a pancreatic stem cell pool (Bernard et al., 1999; Noguchi et al., 2006; Zulewski et al., 2001), or from several sources.

2.1. Modeling the complex gene regulatory network modulating β-cell and other pancreatic cell neogenesis

The neogenesis of pancreatic cells from stem cells or other differentiated cells occurs via differentiation or trans-differentiation controlled by the modulation of key transcription factors via a gene regulatory network with multiple interacting feedback loops (Dhawan et al., 2007). To understand the complex feedback mechanisms underlying control of cell fate in this network, Zhou et al. (Zhou et al., 2011) developed a large scale mathematical model of ordinary differential equations, which captures gene expression patterns to produce β-, δ-, α-cells and exocrine pancreatic cells (see, Figure 2). The model predicts gene perturbation resulting in lineage reprogramming of pancreatic cells, such as the generation of β-cells. For example, the model shows that a paired box gene 4 (Pax4) knockout suppresses β- or δ-cells programming, whereas the prevalent expression of the transcription factor Brain 4 (Brn4) suppresses α-cells but leaves β- or δ-cell development unaffected.

Figure 2.

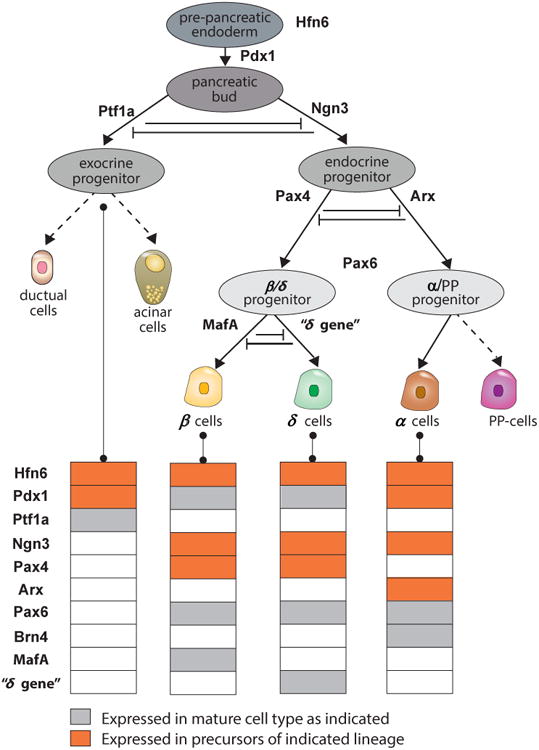
Cell lineages of mouse pancreatic cells and their gene expression patterns start from Pdx1+ cells. These cells gradually differentiate into exocrine, α, β and δ cells. Genes patterns colored in gray are permanently expressed in mature cell lines, while genes colored in yellow are transiently expressed. In the model of Zhou et al. (Zhou et al., 2011) cells commit through three binary cell fate decisions into various lineages. In the first branch, exocrine and endocrine lineages are committed from PdK1+ cells. Ngn3+ cells are the endocrine progenitor cell line for β/δ or the α (glucagon producing) lineages. The β/δ precursors commit to produce either β cells or δ cells in the third binary decision line. Figure redrawn with modifications from Zhou et al. (Zhou et al., 2011).

The discovery of Notch signaling in the cell fate decision of multi-potent pancreatic progenitor cells between the exocrine and endocrine lineages (Apelqvist et al., 1999) led to the development of simple gene regulation network and cell-cell interaction models by de Back et al. (de Back et al., 2013a; de Back et al., 2013b). They proposed mathematical models that combine gene regulation with two contact-mediated signaling mechanisms: lateral inhibition and lateral stabilization. In the models, de Back et al. (de Back et al., 2013a; de Back et al., 2013b) assume that pro-endocrine cells laterally inhibit via Notch signaling endocrine specification of their neighboring cells, forcing them into an exocrine fate. They also assume that exocrine pancreas cells laterally stabilize cell fate of neighboring exocrine pancreas cells via cell-cell contact. Notch lateral inhibition induces regular patterns of cells in a tissue (Collier et al., 1996). As a consequence, de Back et al.'s model (de Back et al., 2013b) predicts several potential patterns of scattered endocrine cells. In this model, the strength of lateral stabilization modulates endocrine-to-exocrine cell-type ratio. de Back et al. (de Back et al., 2013a) also suggest that a loss of lateral inhibition induces the direct transdifferentiation from acinar to islet cells and affects cell density as well as the size and structure of cellular aggregates in the pancreas. These models suggest a potential role for lateral stabilization in the modulation of lineage specification, as well as a role for cellular spatial patterning during pancreas development. However, these predictions need experimental validation..

2.2. β-cells longevity, β-cell turnover and the development of type 2 diabetes

β-cell longevity affects β-cell turnover and could play a role in the development and progression of type 2 diabetes (Manesso et al., 2011; Manesso et al., 2009). Although mathematical models of β-cell mass have provided novel insights into the role of β-cell neogenesis, replication and apoptosis, it remains unclear how the molecular, biochemical and cellular mechanisms controlling β-cell longevity cause the decline in β-cell proliferation or net growth. In mathematical biology, the time-dependent decline in the net growth of a cellular population or organism is generally described with density-dependent population growth models. In those models, the net growth rate is a phenomenological monotonic decreasing function driven by the number of cells or organisms in the population. The decrease in the net growth could be the result of multiple factors in cellular populations, such as cell-cell contact proliferation inhibition, or depletion of food, oxygen or space. These and other density-dependent mechanisms of β-cell growth could be further investigated with mathematical models and provide novel insights into the factors fueling β-cell proliferation to restore glucose homeostatic regulation in diabetes patients.

It is known that β-cell functionality changes with age, and these changes could be responsible for the progression of type 2 diabetes. For example, insulin secretion in healthy humans decreases with age (Basu et al., 2003). This decrease in functionality could be controlled by different factors, such as insulin/IGF-I signaling (Gems and Partridge, 2008), free radicals (Schulz et al., 2007) and decrease in mitochondrial function (Bonawitz and Shadel, 2007). Interestingly, Cnop et al. (Cnop et al., 2010) found that there is no difference in the lifespan of β-cells from healthy, type 2 diabetic and obese subjects by quantifying lipofuscin accumulation and building a three-dimensional computational model of lipofuscin-containing β-cells. In contrast, Manesso et al. (Manesso et al., 2011) reported that the lifespan of β-cells in 10-month old human islet-amyloid-polypeptide transgenic rats was 5 months shorter than that of nondiabetic controls, with the former possessing an average lifespan of 1 month. Manesso et al. (Manesso et al., 2011) calculated the mean β-cell age and lifespan using the classical McKendrick-von Foester equation (Caswell, 2001) that describes the age-based heterogeneity of β-cells in terms of the time-varying β-cell net growth model previously developed by the same group (Manesso et al., 2009). The shorter lifespan of β-cells could be one of the causes of the decrease in β-cell mass observed animal models and patients with type 2 diabetes.

2.3. Changing in β-cell mass during the progression of type 1 diabetes

Pechhold et al. (Pechhold et al., 2009) systematically studied β-cell mass during the progression of type 1 diabetes using flow cytometry and quantitative techniques in pancreatic islet single cell suspensions from NOD mice and experimental autoantigen-specific diabetes EAD mice. They found that β-cell proliferation rapidly increases at diabetes onset in NOD and EAD mice, and that this proliferation is closely correlated with their elevated blood glucose level. Interestingly, treating these animal models with exogenous insulin or islet transplantation to restore normoglycemia was shown to bring the β-cell proliferation rate back to its original value observed in control animals.

The situation is different, however, for adult non-human primates (vervet monkeys) administered with type 1 diabetes-inducing streptozotocin, an agent that is toxic to β-cells. Using the β-cell mass model in Manesso et al. (Manesso et al., 2009), Saisho et al. (Saisho et al., 2009) showed that while ∼80% of new β-cells in non-streptozotocin treated monkeys are primarily formed from neogenesis rather than replication, the streptozotocin-treated monkeys display no increase in β-cell turnover (neogenesis and apoptosis). In other words, β-cell formation is minimal in streptozotocin-induced diabetes, despite marked hyperglycemia.

These contradictory results could be due to the specific nature of the animal models. Additional research needs to be carried out to clarify the observed differences between the above animal models.

3. Pancreatic β-cell replication and mass is regulated by a compensatory response to signals and metabolism

Multiple sources of experimental evidence from rodents suggest that pancreatic β-cells replicate in response to metabolic changes. In both the adult rat and mouse, β-cell replication can be induced with a high-fat diet (Tschen et al., 2009) or multiple-day glucose infusion (Alonso et al., 2007; Bonner-Weir et al., 1989). Pancreatic β-cells also replicate more quickly in certain physiological conditions, as this has been observed during the progression of pregnancy (Parsons et al., 1992) and obesity (Butler et al., 2003; Pick et al., 1998). This experimental data suggests that β-cells have a compensatory response to increased insulin requirements in mice (Alonso et al., 2007; Tschen et al., 2009) and rats (Lee et al., 1989). In fact, data collected from the MIN6 insulin secreting cell-line reveal that insulin secretion, in response to elevated glucose, may exert autocrine effects via the PI-3K pathway to protect against apoptosis and stimulate proliferation (Muller et al., 2006). These results have motivated the development of mathematical models to evaluate and quantify the interaction(s) of β-cell mass with glucose and insulin.

3.1. Modeling the relationship between β-cell mass, insulin and glucose

Extensive studies have been carried out to examine and quantify the effects of glucose and insulin on the dynamics of β-cell number and mass using mathematical models (Szabat et al., 2012). Lipsett and Finegood (Lipsett and Finegood, 2002) showed that neogenesis is crucial for β-cell expansion during prolonged hyperglycemia using a mathematical model coupling β-cell mass, replication, and size (each quantified either indirectly, using surrogate measures, or directly, using markers for apoptosis and replication, in animal models). More complex mathematical models coupling β-cell mass, insulin and glucose (known as βIG models) have been proposed to investigate how β-cell mass is affected by insulin and glucose levels (Topp et al., 2000; Topp et al., 2004; Topp et al., 2007; Wang et al., 2012). In these models, β-cell mass can attain two steady-states: a healthy and functional level of β-cell mass, and a pathological one in which the mass is below a critical threshold (Topp et al., 2000). The models also predict that the β-cell mass depends not only on the overall glycemic load (Topp et al., 2000), but also on the glycemic load dynamics (Wang et al., 2012): β-cell mass is negatively affected by largely fluctuating glycemic loads, while β-cell mass is not affected by “constant glycemic infusion”. In the case of prolonged glycemic load, Topp et al. (Topp et al., 2000) showed that moderate hyperglycemia induces growth in β-cell mass by shifting the mass towards the healthy steady state, whereas extreme hyperglycemia leads to a reduction in β-cell mass towards the pathological steady state or by progressively elevating glucose at a rate that the β-cell mass cannot handle efficiently.

Some of these results have been confirmed experimentally by analyzing cross-sectional images of pancreata of male Sprague Dawley rats infused with either saline or 50% glucose (2 ml/h) for 0-6 days (Lipsett and Finegood, 2002). Rat pancreata infused with glucose show an increase in the density of β-cell neogenic focal areas (peaking at day 3) and a reduction in the replication of duct-cells in comparison to rat pancreata infused with saline solution. This result suggests that there is an increase in acinar-cell transdifferentiation and dedifferentiation to increase β-cell mass. Interestingly, although the duct associated β-cell mass was shown to be roughly the same in both groups, a 70%-increase in the number of acinar-associated single β-cells was observed after 3-4 days of glucose infusion.

The direct effect of glucose on the dynamics of β-cell mass was also analyzed quantitatively by developing a compartmental model coupling insulin storage and glucose regulation with the slow dynamics of β-cell cycle (Gallenberger et al., 2012). In this model, glucose is assumed to stimulate the transition from the G₁ to the S phase of the cell cycle, which is an important checkpoint in β-cell replication (Cozar-Castellano et al., 2006; Cozar-Castellano et al., 2008). Given that insulin metabolizes glucose, we would expect insulin to affect β-cell cycle indirectly in this model. Gallenberger et al.'s (Gallenberger et al., 2012) model reconfirms the observed β-cell mass adaptability to metabolic demand, but it cannot explain how insulin induces anti-apoptotic signal in β-cells (Johnson et al., 2006). The balance between cell cycle replication and β-cell mass, and how it is affected by moderate and prolonged hyperglycemia, remains an open question that can be investigated quantitatively.

3.2. Modeling cellular signals regulating β-cell mass

In mice, β-cell replication has been induced by intracellular factors, such as Akt (Fatrai et al., 2006), or extracellular growth factors like incretin (Drucker, 2006), lactogen (Vasavada et al., 2000), glucagon-like peptide 1 (Buteau et al., 2003) and growth hormone (Liu et al., 2004). Recently a new hormone, betatrophin, has been discovered to play an important role in β-cell replication in mice. The transient expression of betatrophin in mouse liver and fat tissue specifically promotes pancreatic β-cell proliferation and expands functional β-cell mass (Yi et al., 2013).

Cyclin-dependent kinases activation, particularly Cdk4, could be one of the potential molecular mechanisms regulating β-cell growth by cellular and metabolic signals, such as betatrophin or glucose (see, Figure 3). Cdk4 promotes the S-phase of the cell cycle and mitosis in β-cells by phosphorylating and inhibiting retinoblastoma protein, which sequesters E2F transcription factors and chromatin modifiers critical for G1/S transition (Lee et al., 2010). The lack of Cdk4 in mice has been shown to cause β-cell hypoplasia and diabetes (Cozar-Castellano et al., 2006). By using DNA analog-based lineage-tracing methods and developing a β-cell growth mathematical model that takes into account dormant (quiescent) and active (proliferative) cells, Lee et al. (Lee et al., 2010) showed that Cdk4 promotes β-cell replication by activating the cell cycle in dormant cells and facilitates the activation of β-cell progenitors in the ductal epithelium, with a larger contribution from the latter in the total increase of insulin-positive cells. Lee's mathematical model shows that the proliferation of islet β- and ductal epithelial cells is considerably induced one week after partial pancreatectomy in Cdk4^R24C/R24C mutant mice, and the expression level of pancreatic and duodenal homeobox 1, a transcription factor necessary for pancreatic development and β-cell maturation, is increased 1 to 2 days post–partial pancreatectomy.

Figure 3.

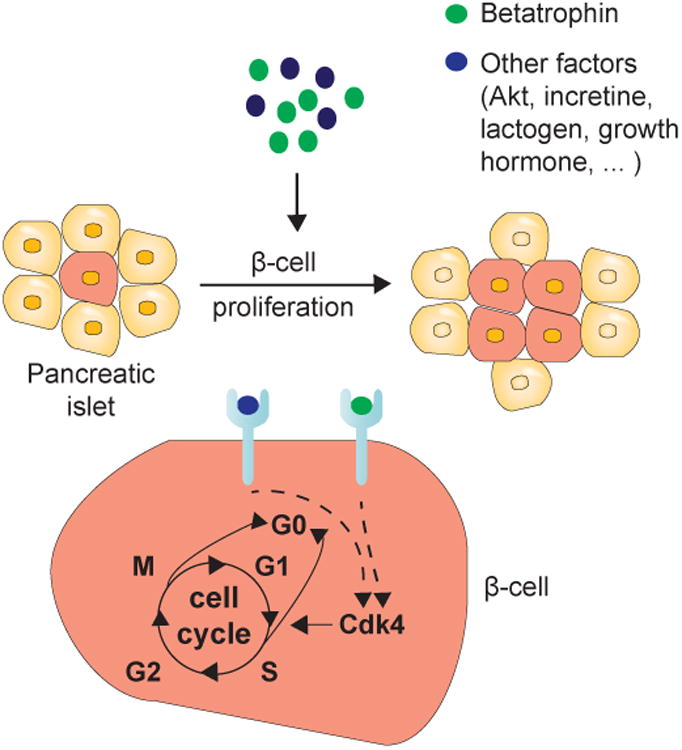
β-cell proliferation can be induced by betatrophin, glucose and other signals. For example, betatrophin is a hormone upregulated in liver and fat tissue, which could either act alone or in combination with other factors to increase β cell proliferation. The mechanism activating β-cell proliferation by betatrophin or other signals remains unknown. There is evidence that it leads to cell cycle re-entry through the regulation of cell cycle activators or inhibitors. Figure redrawn with modifications from Lickert (Lickert, 2013).

Lee's model is one of the first attempts to understand how cellular signals induce β-cell proliferation. As we begin to understand the role of other cellular and metabolic signals, the models discussed in this section can be extended to investigate the role of complex signaling networks in the regulation of β-cell mass.

3.3. Models of β-cell mass reduction in type 1 and type 2 diabetes

Ribbing et al. (Ribbing et al., 2010) proposed a semi-mechanistic population pharmacokinetic model incorporating fasting plasma glucose, fasting insulin, insulin sensitivity, and β-cell mass to investigate the mechanisms of β-cell mass reduction in type 2 diabetes patients. The model was developed using data from 3 clinical trials (phase II/III) with tesaglitazar, a peroxisome proliferator-activated receptor agonist. The β-cell mass, insulin and glucose dynamics is governed with an extended version of the βIG model previously developed by Topp et al. (Topp et al., 2000), which we discussed in Section 3.1. Ribbing et al.'s (Ribbing et al., 2010) model predicts 40% to 60% lower β-cell mass in type 2 diabetes patients (suggesting a significant decrease or insufficiency in insulin secretion), and realistic improvements of β-cell mass and insulin sensitivity with treatment.

Similar results have also been reported in animal models of type 2 diabetes, such as the male leptin-receptor deficient fa/fa zucker diabetic fatty rats and the human islet-amyloid-polypeptide transgenic rats (Finegood et al., 2001; Manesso et al., 2009). Obese fa/fa rats display a disruption in islet architecture, β-cell degranulation and 51% loss in β-cell mass by postnatal 8-12 week. These effects are reversible with an early thiazolidinediones intervention or rosiglitazone treatment (both of which are medications for treating type 2 diabetes) starting at postnatal week 6. Finegood et al. (Finegood et al., 2001) discovered that β-cell replication rate in obese fa/fa rats is ∼47-68% below the wild-type rat baseline by postnatal week 12 using their model of β-cell mass net growth, which we presented in Section 2. Treating obese fa/fa rats for 10 weeks with rosiglitazone increases the β-cell replication rate. The model also shows that the net β-cell loss in obese fa/fa rats is 5-fold higher than that of rats treated with rosiglitazone for 6 weeks.

In an attempt to unravel the mechanisms governing the adaptations to obesity in the normoglycemic animals, and the failure of adaptation in the animals that develop diabetes, Topp et al. (Topp et al., 2007) used quantitative morphometry analysis combined with their βIG model (Topp et al., 2000). They compared two groups: (1) male zucker fatty and lower-fat-fed female zucker diabetic fatty rats, which are obese but normoglycemic, and (2) male zucker diabetic fatty and high-fat-fed female zucker diabetic fatty rats, which are also obese but develop diabetes between 7 and 10 weeks of age. Rats in group (1) exhibit an increase in β-cell mass and a constant level of β-cell secretory capacity in response to a falling insulin sensitivity, whereas rats in group (2) exhibit a greater reduction in insulin sensitivity and a slower expansion in β-cell mass with constant β-cell secretory capacity. Taken together, these results suggest that a net increase in β-cell death (Finegood et al., 2001), excessive insulin resistance and insufficient β-cell mass adaptation play a significant role in the pathogenesis of type 2 diabetes (Topp et al., 2000).

The role of blood-glucose in the regulation of β-cell proliferation remains largely unexplored during the progression of type 1 diabetes, because most of the biomedical efforts are considered futile in the face of continued autoimmune-mediated destruction. The inflammatory infiltrate within the pancreatic islets and the scarcity of residual β-cells at disease onset are two technical problems that severely compromise the microscope-based analysis of β-cell numbers and phenotype, and limit the scope of such studies. Therefore, it is unclear at this point whether residual β-cells at disease onset are capable of responding to signals known to stimulate their expansion and regeneration under various conditions.

Other intracellular processes involved in β-cell loss during type 1 and type 2 diabetes, such as proinsulin misfolding, islet amyloid polypeptide misfolding and aggregation in β-cells, as well as endoplasmic reticulum stress (Atkinson et al., 2011; Donath et al., 2005; O'Sullivan-Murphy and Urano, 2012; Sun et al., 2015; Westermark et al., 2011), have also been analyzed and quantified mathematically (Sandefur and Schnell, 2011; Schnell, 2009). For example, Bailey et al. (Bailey et al., 2011) used a mass-action kinetic model of aggregation pathway to show that the reaction scheme for the formation of insoluble cytotoxic amyloid plaques from misfolded islet amyloid polypeptide must follow a specific nucleation and elongation pattern to generate outcomes consistent with experimental data. They also suggest interventional therapies, involving changes in the rates of fibril elongation or nucleation, to affect the accumulation of this cytotoxic oligomer species. Schnell (Schnell, 2009) proposed a model of the unfolded protein response to investigate the influence of the endoplasmic reticulum associated folding and degradation fluxes during the activation of endoplasmic reticulum stress in β-cells. Jaberi-Douraki et al. (Jaberi-Douraki et al., 2014) expanded this model to study the role of endoplasmic reticulum stress in type 1 diabetes. They tested the hypothesis that autoimmune destruction of β-cells causes an increase in endoplasmic reticulum stress in surviving β-cells (by forcing them to synthesize and secrete defective insulin), which in turn induces the unfolded protein response in these cells to restore protein homeostasis and normal insulin synthesis (Atkinson et al., 2011). Specifically, a differential equation model that combines macroscopically the autoimmune destruction of β-cells (β-cell homicide) with endoplasmic reticulum stress induced apoptosis (β-cell suicide) (Bottazzo, 1986) was used to achieve this. The study showed that the unfolded protein response may not be a successful therapeutic target to treat type 1 diabetes because of the dominance of β-cell “homicide”.

4. Islets have an optimal functional size and architecture

The islets exhibit a unique architecture governed by insulin-secreting β-cells, glucagon-secreting α-cells, somatostatin-secreting δ-cells, ghrelin-secreting ε-cells, pancreatic polypeptide-secreting PP cells and other non-endocrine cell types, such as endothelial cells (Kim et al., 2009). Immune cells, particularly macrophages, are also involved in the morphogenesis of the pancreas (Homo-Delarche and Drexhage, 2004). Islets range in size from small clusters of approximately 10 cells to large clusters comprised of several thousand endocrine cells (Jo et al., 2011b). While β-cell mass in healthy mammals is proportional to body weight, the large range of islet sizes appears similar between species and independent of body size, suggesting the existence of an optimal functional size (Jo et al., 2012). At this point, it is not fully understood how islets reach particular sizes during development. In addition, it is unclear how the islet size changes under distinct physiological (pregnancy and aging) and pathological (obesity and diabetes) conditions.

Islet size determines islet-architecture, especially in humans (Kilimnik et al., 2012). There are differences in cytoarchitectural composition of islets between species (Brissova et al., 2005; Cabrera et al., 2006). For example, rodent islets possess organized structure: β-cells localized predominately in the center and α- and δ-cells in the periphery (Kim et al., 2009; Sujatha et al., 2004). In primates, α-cells are scattered throughout the islets and intertwined with β-cells (Brissova et al., 2005; Cabrera et al., 2006), while in other species (such as dogs and pigs) islet structures are intermediates between those of rodents and primates (Wieczorek et al., 1998). Cabrera et al. (Cabrera et al., 2006) suggest that these differences in islet architecture have implications on β-cell function, which can make them responsive to a low concentration of glucose (1 mM) in primates and non-responsive to such concentration in rodents.

In humans, on the other hand, no differences are observed in islet distribution/density between the head and body regions of the pancreas, but the islet distribution/density is 2-fold higher in the tail (Wang et al., 2013). In contrast to rodents, human islet cellular composition and architecture are similar throughout the pancreas, making glucose-stimulated insulin secretion from isolated islets in different regions of the pancreas roughly the same (Wang et al., 2013).

Cross-sectional, large-scale imaging and unbiased quantitative studies of islet size distributions have been conducted to determine the underlying mechanisms regulating the development and formation of these islets in mice and rats (Jo et al., 2012; Miller et al., 2009). As it is difficult to capture the islet architecture developmental dynamics in situ with experiments alone, mathematical and computational modeling has become an attractive tool to investigate islet growth and its pattern formation mechanisms.

4.1. A branching cell proliferation model can explain the size distribution of islets

Jo et al. (Jo et al., 2007) provided the theoretical foundations to investigate islet cell proliferation by implementing a branching cell division model with coherent proliferation. Cells replicate with a probability λ, and do not replicate with the complementary probability (1- λ) (Figure 4A). In the model, λ corresponds to the net growth probability, which takes into account the average proliferation and apoptosis rates. The model assumes that islet neogenesis is negligible after certain developmental stage, and islet growth is a random process in which cells within the same islet proliferate with identical rate regardless of islet size.

Figure 4.

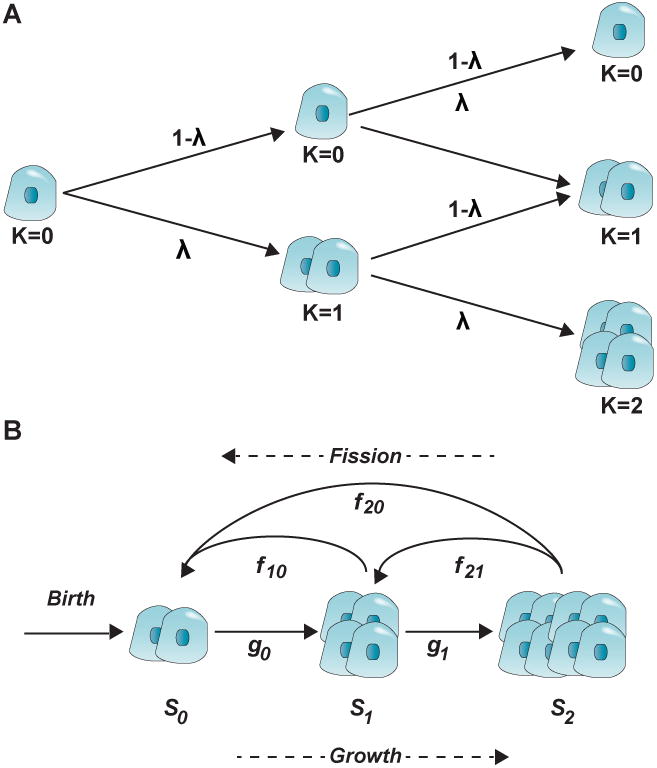
(A) Branching cell proliferation model with coherent division in an islet. Cells replicate with a rate equal to λ, and do not replicate with a rate equal to (1- λ). The figure illustrates up to two rounds of replication. The rounds of replication are denoted with k. Figure redrawn with modifications from Jo et al. (Jo et al., 2007). (B) Islet development model governed by birth, growth, and fission. In this model by Jo et al. (Jo et al., 2011b), new islets appear with a birth rate, then growth (by proliferative or neogenesis expansion) with rates g_i and break (by fission) with rates f_ij depending on the islet size. Figure redrawn with modifications from Jo et al. (Jo et al., 2011b).

The model by Jo et al. (Jo et al., 2007) and its successors (Jo et al., 2011a; Kang et al., 2008) reveals that islet development follows a lognormal or Weibull distribution of the islet sizes with the peak size of ∼100 cells, depending on whether cells in an islet proliferate cohesively or independently. This result was confirmed experimentally by tagging β-cells in transgenic mice with a fluorescent protein to monitor and quantify islet growth and development (Miller et al., 2009). In addition, Miller et al. (Miller et al., 2009) discovered that long stretches of interconnected islets are located along large blood vessels in the neonatal pancreas. They hypothesize that the elongated islet structures spanned by α-cells are sites of (random) fission that facilitates the eventual formation of new islets. Miller et al. (Miller et al., 2009) also propose that the proliferation of endocrine cells (including β-cells) is contiguous, forming branched cordlike and nonspherical structures in both embryos and neonates within which β-cell differentiation occurs (Hara et al., 2006). They further suggest that subsequent β-cell expansion within these islets may still occur, resulting in an increased islet volume and the formation of spherically shaped islets. Interestingly, Miller et al. (Miller et al., 2009) predicted that the lognormal probability density function deviates leftward at postnatal day 10, indicating a regression in the number of elongated structures by fission events.

4.2. Islet size development is a balance of small islets expansion and larger islets fission

A coherent proliferation model of islet cells cannot explain the deviations in size distribution of islets observed during mice postnatal development. Following the islet fission prediction made by Miller et al. (Miller et al., 2009), Jo et al. (Jo et al., 2011b) proposed a mathematical model for islet development, which incorporates three variables: islet birth, growth and fission. In the model new islets appear with a birth rate, then grow (by proliferative or neogenesis expansion) and break (by fission) with rates depending on the islet size (see, Figure 4B). The model was tested with imaging data from an intact mouse pancreas from birth to eight months (Jo et al., 2011b). It predicts that smaller islets are more prone to growth than larger islets. Large interconnected islet-like structures divide by fission actively at approximately three weeks of age, resulting in a tight range of islet sizes with a lognormal distribution as reported previously (Jo et al., 2007; Miller et al., 2009). After 4 weeks of postnatal development, islet formation becomes dormant and adult β-cell proliferation is low in all islets.

The predictions made by the islet birth, growth and fission model are not in full agreement with another quantitative-stereological study of postnatal islet and β-cell expansion in mice (Herbach et al., 2011). This study reported that the absolute number and total volume of both islets and β-cells increase significantly in mice after birth, reaching a steady state at postnatal day 90. There is a pronounced increase in the mean islet volume between postnatal days 10 and 45 that is accompanied by a decline in the number of proliferating β-cells from postnatal day 10. The study also showed that the diabetic dominant negative glucose-dependent insulinotropic polypeptide receptor transgenic mice exhibit a reduction in the numbers of islets and β-cells starting from postnatal day 10, as well as a decrease in islet neogenesis. No differences in early islet-cell proliferation and apoptosis were observed between the control and transgenic mice. Interestingly, Jo et al. (Jo et al., 2007) found that most islets at steady-state are bigger than the expected minimal size of ∼10 cells necessary for stable synchronization of bursting β-cells through electrical gap-junction coupling (Meda et al., 1986), which plateaus beyond the critical size of ∼100 cells.

4.3. The cytoarchitecture of islets coordinates β-cell function

Nittala et al. (Nittala et al., 2007) compared the functional role of the islet cytoarchitecture electrophysiologically by implementing mathematical models, which look at the functional characteristics of β-cell clusters, such as the fraction of cells able to burst, the synchronization of bursting β cells, the bursting period, the plateau fraction, and the amplitude of intracellular calcium oscillation. They found that the hexagonal closest packing cluster is the only cellular arrangement able to correctly model intercellular coupling and burst synchronization of β cells in each islet. The hexagonal closest packing cluster is a close approximation of the β-cell arrangement in islets (Hellman et al., 2009). It also captures the degree of intercellular coupling composed of three parameters: β-cell cluster size, the number of intercellular couplings each β cell has, and the inter-β cell gap junctional coupling strength. The hexagonal closest packing cluster is implemented with a computational algorithm, which models the structure of an islet in three dimensions (see Figure 5).

Figure 5.

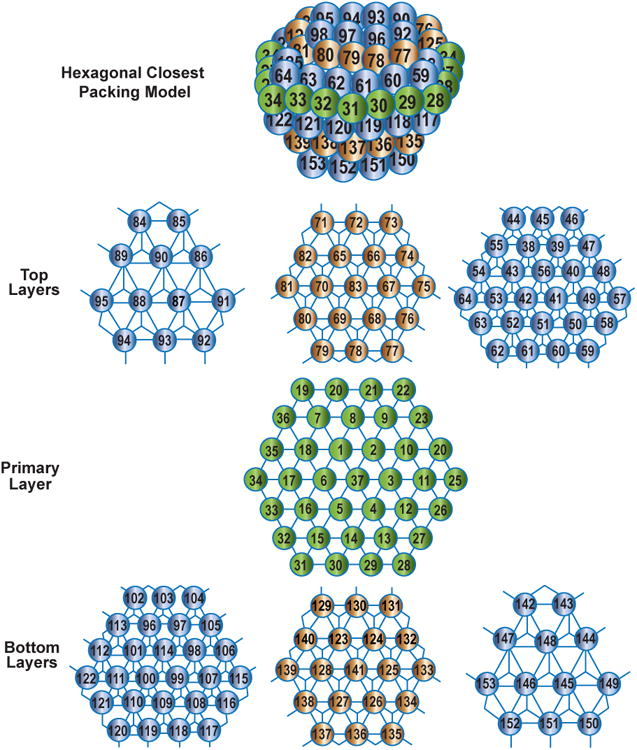
Hexagonal closest packing cell cluster model of the islet provides a close approximation to the β-cell arrangement in islets. It is based on a computer algorithm that captures the degree of intercellular coupling composed of three parameters: β-cell cluster size, the number of intercellular couplings each β-cell has, and the inter-β cell gap junctional coupling strength. In the illustration, we show the three layers of cells, which form the spherical islets. Figure redrawn with modifications from Nittala et al. (Nittala et al., 2007).

The study also confirmed that most of the islets at steady-state are bigger than the expected minimal size of ∼10 cells necessary for stable synchronization of bursting β-cells through electrical gap-junction coupling by using a hexagonal closest packing cell cluster model for the islets cytoarchitecture (Nittala et al., 2007). They reported that the ideal plateauing fraction occurs when the number of β-cells in the cluster is ∼100, the number of inter-β-cell couplings of each β-cell is 6 and the coupling strength is ∼200 pS. According to their model, a 70%-loss in β-cells does not affect synchronized bursting behavior, which reflects the non-linear hyperbolic nature of the islet cytoarchitecture (Nittala and Wang, 2008).

4.3.1. The cytoarchitecture of islets in type 1 and type 2 diabetes

During the progression of type 1 diabetes, the β-cell attrition disrupts pancreatic islet anatomy, leading to the impairment of the integrity of β-cell connectivity and synchrony achieved by gap-junctional coupling (Meda et al., 1986). Stamper et al. (Stamper et al., 2014) analyze the islet cytoarchitecture during the progression of type 1 diabetes using a hexagonal closest packing cluster model. In their model, they assume that β-cells occupy 50-70% of the human islets, whereas α- and δ-cells that lack the electrical connectivity to β-cells occupy the rest. The increase of α- and δ-cells in the islets reduces the number of cells available for gap-junctional coupling, leading to a reduction in the site open probability for coupling within this type 1 diabetes hexagonal closest packing cluster model. They found that a 70% loss in β-cells during the progression of type 1 diabetes is sufficient to drop the site open probability below the critical threshold essential to maintain synchrony between bursting β-cells. They also found that there is a transient phase of islet functional recovery after type 1 diabetes onset and insulin-treatment, which could explain the honeymoon phenomenon during treatment.

Stamper et al.'s (Stamper et al., 2014) findings are in agreement with earlier quantitative stochastic simulations using a Hodgkin-Huxley type model of a three-dimensional cellular cluster of mouse β-cells coupled by gap-junctions (Sherman and Rinzel, 1991). Sherman and Rinzel's (Sherman and Rinzel, 1991) model incorporates the progressive damage of β-cells following a pattern similar to that found during type 1 diabetes progression (Portuesi et al., 2013). They found that the cluster model can maintain robust dynamics with regular calcium oscillations (an essential ingredient for effective insulin release), even after 69% loss in β-cells. In contrast, at higher percentages of β-cell loss, calcium oscillations are completely abolished in the model, which supports de Vries and Sherman's (De Vries and Sherman, 2000) observation that bursting in β-cells scales up with cluster size.

In type 2 diabetes patients, there are changes in endocrine cell mass (including β-cells) occurring in large islets of (cadaveric) pancreatic sections (Kilimnik et al., 2011), especially in the head regions of the pancreas (Wang et al., 2013). In fact, large islets (>60 mm in diameter) are preferentially lost in type 2 patients when compared to non-diabetic subjects. Jo et al. (Jo et al., 2013) found that the β-cell fraction in large islets decreases whereas α-cell fraction increases in type 2 diabetes patients. Interestingly, the individual total cell area of both types of cells is decreased for these patients. Jo et al. (Jo et al., 2013) obtained these results by combining immunohistochemical and imaging methods with semi-automated mathematical analysis based on constructing (random and regular) network models of α- and β-cells to quantify cellular arrangement in islets and calculate the probabilities of contact between both cell types.

4.4. The cytoarchitecture of islets coordinates interactions between β-, α- and δ-cells

The regulation of glucose homeostasis depends on the secretion of three islet secreted hormones: insulin (secreted by β-cells), glucagon (secreted by α-cells) and somatostatin (secreted by δ-cells). The secretion of these hormones is tightly regulated by islet structure. However, the mechanisms regulating their controlled secretion remain to be deciphered, particularly how insulin, glucagon and somatostatin play a role maintaining glucose homeostasis in circulation. According to the standard physiology textbooks, insulin decreases the glucose level in circulation, in contrast to glucagon that increases it. To this date, it is unclear how somatostatin affects glucose homeostasis. Glucagon paradoxically enhances insulin secretion (Brereton et al., 2007), insulin inhibits glucagon secretion (Ravier and Rutter, 2005), whereas somatostatin appears to inhibit the secretion of both of these hormones (Daunt et al., 2006).

To unravel the mechanism of interaction between insulin, glucagon and somatostatin, Jo et al. (Jo et al., 2009) proposed a compartmental mathematical model of α-, β-, and δ-cells. In the model, each compartment can take one of two states: active and silent. Jo et al. (Jo et al., 2009) model paracrine signals of neighboring cells, cell-to-cell variations in response to external glucose concentrations as well as insulin- and glucagon-sensitive glucose dynamics. The model proposes that asymmetric interactions between α- and β-cells contribute to the dynamic stability observed during the perturbed glucose levels. The model shows that the suppressive effects of somatostatin on glucagon and insulin secretion prevent the “wasteful” co-secretion of these two hormones at normal glucose level. The mutual suppressive effects of somatostatin on glucagon and insulin secretion also make the glucose dose-responses of insulin secretion more pronounced at high glucose levels.

Hong et al. (Hong et al., 2013) investigated the interaction between β- to δ-cells using a coupled phase oscillator model to described the out-of-phase synchrony in the release of glucagon and insulin and the in-phase synchrony in the release of insulin and somatostatin (Hellman et al., 2009). They showed that β-cells need to exert a positive feedback onto δ-cells to guarantee an in-phase synchrony.

From a technical standpoint, it is currently very difficult to measure the small amount of somatostatin secreted from δ-cells (∼femtomole). As a consequence, the analysis of Jo et al.'s (Jo et al., 2009) and Hong et al.'s (Hong et al., 2013) models is of great importance to understand how the intracellular communication of islet cells can provide an effective control system for glucose homeostasis.

5. Conclusions

The islets' development, structure and homeostasis play an essential role in the functionality of the β-cell mass, which is responsible for the insulin secretion and glucose homeostasis in circulation. Differentiation of β-cells changes as they develop from a multipotent precursor cell line to full maturity. The maintenance of the mature β-cell population is controlled by β-cell proliferation, differentiation from other cell lines, and cellular and metabolic signals. Dysregulation in the homeostasis of the β-cell population can lead to β-cell death, altered β-cell function, and diabetes.

Experimental scientists are paying a lot of attention to animal models of diabetes, and how these models can realistically represent the human disease. The behavior of isolated β-cells and islet β-cells from animal models appears to have a great deal of heterogeneity at times. Adding to the complexity of the animal models, the pancreatic islets and β-cells have very rich and complex developmental dynamics, composed of multiple variables and parameters– some of which we cannot measure experimentally due to the physical limitations of laboratory instrumentation and techniques. For these reasons, mathematical and computational modelers are now paying a great deal of attention to the pancreatic islets and the β-cell population.

In this review, we have seen that models can provide novel insights into the mechanisms of islet and β-cell development. Many of the predictions made by these models have been validated experimentally or have informed new experiments to unravel the mechanisms underlying the regulation of the β-cell population. When it is not easy to test or observe a molecular or cellular mechanism with the present experimental techniques, models have discovered interactions, which most likely would have gone unnoticed for numerous years. We hope that the models presented here illustrate how the fruitful collaboration between basic scientists, clinicians and modelers may help to clarify complex problems in the field of diabetes. This review also serves to emphasize that unaided intuition and experiments alone often cannot explain the behavior of complex biomedical systems with feedback across different levels of biological organization. We need the support of mathematical and computational models.