Comparing hyperbolic, delay-amount sensitivity and present-bias models of delay discounting

Abstract

Delay discounting is a widely studied phenomenon due to its ubiquity in psychopathological disorders. Several methods are well established to quantify the extent to which a delayed commodity is devalued as a function of the delay to its receipt. The most frequently used method is to fit a hyperbolic function and use an index of the gradient of the function, k, or to calculate the area under the discounting curve. The manuscript examines the behavior of these quantification indices for three different datasets, as well as provides information about potential limitations in their use. The primary limitation examined is the lack of mechanistic specificity provided by either method. Alternative formulations that are thought to provide some mechanistic information are examined for the three separate datasets: two variants of a hyperboloid model (Rachlin 1989 Judgment, decision and choice. New York: W. H. Freeman) and the quasi-hyperbolic model (Laibson 1997 Q J Econ 112 443-477). Examination of the parameters of each formulation suggests that the parameters derived from the quasi-hyperbolic model allows groups and conditions within the three datasets to be reliably distinguished more readily than the hyperboloid models. However use of the quasi-hyperbolic model is complex and its limitations might offset its ability to discriminate within the datasets.

1. Introduction

Delay or temporal discounting is a process by which individuals derive the subjective value of a commodity, which is available following a delay, by creating a composite of the commodity’s magnitude and the delay to its receipt (e.g., Peters & Buchel, 2011). Researchers are interested in this process for several reasons. First, from a basic science perspective, calculations of this type are common in everyday life and understanding the neural and psychological bases for these calculations provides information about critical processes driving decision-making. Second, the value of delayed commodities is lower in individuals exhibiting a wide variety of psychopathologies, including substance dependence, pathological gambling, attention deficit hyperactivity disorder and conduct disorder (e.g., Bickel, et al., 2012; Perry & Carroll, 2008; Robbins, et al., 2012, see Weafer, et al., 2014 for a recent review); implying that the delay discounting process is quantitatively, or possibly qualitatively, different in diagnosed individuals compared to undiagnosed individuals.

Studies examining delay discounting in human participants examine choices between smaller, sooner and larger, later rewards. Obtaining preferences between the two types of reward permits researchers to identify the value of the smaller, sooner reward that is equivalent to the larger, later reward over a series of specific delay values (“indifference points” at the specific delays). There are numerous tasks to do this, many of which are described and critically evaluated by Madden and Johnson (2010). When indifference points have been identified for a series of delays, researchers quantify the subjective value for the larger reward as a function of the delay in two main ways.

One way is to fit mathematical models to the data. The most widely-used model is based on a hyperbolic function:

$$V=\frac{A}{1+kD}$$ Equ. 1

Where V represents the subjective value of the larger, later reinforcer (indifference point), A represents the magnitude/amount of the larger, later reward, k is a fitted parameter that measures steepness of the discounting curve with larger values indicating greater/steeper discounting, and D represents the delay to the delivery of the larger, later reward (Mazur, 1987; see Killeen 2009 for a discussion of whether subjective utility provides a better metric than subjective value). While this model has been used extensively, as with any fitting procedure, there are questions relating to what is the appropriate metric to quantify goodness of fit for this nonlinear model, the threshold level of the different metrics to determine whether a fit is “acceptable”, and what should be done when there are systematic residuals to the fit, which suggest that the function does not capture the underlying discounting process adequately (Johnston & Bickel, 2008).

A second way to quantify delay discounting that has been widely adopted is to assess the area under the “curve” (AUC) created by plotting the indifference points at each delay. That is, the AUC is calculated by summing the areas of the normalized trapezoids formed by consecutive indifference points at each delay value (Myerson, et al., 2001). Due to normalization, an AUC of 1.0 is associated with indifference points that are both equal to the objective value of the larger, later reward and invariant as a function of delay. As the AUC decreases towards a minimum of 0.0, the effect of delay on the indifference points at each delay, which represent the subjective values, is expected to be more pronounced. The AUC method does not assume any specific mathematical form and so goodness-of-fit issues are not a concern. However, like any AUC function, very different patterns of indifference points may produce identical summary AUC values, making it difficult to draw conclusions about the effects of delay on subjective value based solely on AUC information.

Both of these quantification methods enable researchers to describe the effects of the delay discounting process under various conditions and as a result of various manipulations (e.g., Green & Myerson, 2004, 2013; Odum, 2011). However, neither provides information about the mechanisms by which variables, such as the characteristics of the participants or size of the larger,later reward, affect the degree of discounting (Bickel, et al., 2014; Mackillop, 2013). In this manuscript we use three datasets to explore the behavior of k, the slope of the hyperbolic function, and AUC between groups and across conditions. These datasets are then used to look at other commonly used quantification procedures that have been proposed to provide additional information about factors underlying the delay discounting process.

2. Description of datasets used

Two datasets focus on comparisons between different groups of individuals (the ADHD and the SMOKING datasets) and one dataset focuses on comparisons between two delayed reward amount conditions collected using a within subject design (AMOUNT dataset). The delay discounting task used in all datasets was based on that described in Mitchell (1999), though delays and amounts differed between datasets (Table 1).

Table 1.

Comparison of the parameters of the delay discounting tasks used in the three datasets.

Dataset	Outcome type	SS delay (days)	SS amount	LL delay	LL amount
ADHD	Hypothetical	0	$0-$10.50	0, 7, 30, 90, 180 days	$10
SMOKING	Potentially real; Hypotheticala	0	$0-$50	2, 4, 8, 14, 22 weeks	$50
AMOUNT	Hypothetical	0	$0-$10.50b	0, 7, 30, 90, 180, 365 days	$10
			$0-$105		$100

Note.

SS: smaller, sooner reward alternative

LL: larger later reward alternative

^aANOVAs revealed no differences between the indifference points collected for each of the five delays for the hypothetical reward delivery conditions and conditions in which rewards were potentially real, i.e., one question was selected at random and payment delivered according to the participant's preferences for that question; this lack of difference is consistent with data reported in Madden, Begotka, Raiff & Kastrern, 2003; Madden, Raiff, Lagorio, Begotka, Mueller, Hehli & Wegener 2004.

^bThe order in which the $10 and $100 tasks were administered was counterbalanced between participants.

All discounting data were assessed for systematicity (Johnson & Bickel, 2008: Criterion 1); that is, beginning with the second shortest delay, an indifference point was judged to be nonsystematic if it was larger than the indifference point for the preceding delay by more than 20% of the larger, later reward. Participants with one or more nonsystematic indifference points were excluded from all analyses that we reported. In the ADHD dataset, 39 participants were excluded (22 ADHD-diagnosed and 17 undiagnosed) from a total of 240 initial participants. In the SMOKING dataset, all data was systematic. In the AMOUNT dataset, 2 participants generated nonsystematic data on $10 task and 1 was nonsystematic on the $100 task; data from these three individuals were consequently excluded from all $10 and $100 task data analyses. All equation fits were performed using the Excel 2010 Solver add-in (Microsoft, Redmond WA).

The ADHD dataset examined here includes 105 ADHD-diagnosed and 96 undiagnosed children, aged 9.28 and 8.70 years (SD = 1.28 and 1.07). Some of the data were previously published in Wilson, et al., (2011), but additional data have been added from individuals recruited as part of the continued research efforts. All participants were recruited in the same way as described in Wilson, et al. (2011), that is, a two-stage process was used to generate information that could be presented to a clinical diagnostic team. Each team member arrived at a ‘best estimate’ diagnosis for ADHD independently using DSM-IV TR criteria (American Psychiatric Association [APA], 2000). If consensus was not readily achieved, the child was excluded from the study. To be assigned a diagnosis of ADHD, the following conditions had to be met: (1) the child’s symptoms could not be better accounted for by another disorder, (2) evidence of impairment had to be apparent, e.g., high impairment ratings on the Strengths and Difficulties Questionnaire (Goodman, 2001), in the parent/teacher comments, or in the school record, and (3) a cross-situational presentation was required, i.e., some elevation in both parent and teacher reports. Exclusion criteria included current major depression or learning disability, or history of mania, psychosis, or autism spectrum disorder. ADHD-diagnosed children who were prescribed non-stimulant medication were excluded and those children prescribed stimulant medication underwent a 24–48-hour washout prior to testing, dependent on the specific medication prescribed. ADHD-diagnosed and undiagnosed children were followed for three years and a complete diagnostic and neurocognitive assessment was completed at each annual assessment. Only data drawn from the first year for children whose diagnosis was consistent across the three annual assessments were included in the dataset.

The SMOKING dataset includes delay discounting data from 120 individuals (60 regular smokers and 60 never smokers, aged 31.25 and 30.45 years with SD = 9.42 and 9.36). The majority of data were drawn from Mitchell & Wilson (2012), Experiments 1 and 2, with additional data collected during another study (in preparation). Regular smokers reported that they had smoked an average of at least 15 cigarettes each day for the past year or longer, while never smokers reported that they had smoked fewer than 20 cigarettes in their lifetime. As described in Mitchell & Wilson (2012), all participants were screened to ensure that they were a regular smoker or never smoker, were age 18 or older, had a high school diploma or equivalent, were not pregnant, were not taking any prescription drugs (except birth control), and were fluent English speakers. Exclusion criteria were a history of substance use disorder except nicotine dependence (DSM-IV TR criteria: APA, 2000), current physical or psychiatric problems, and a history of serious psychiatric disorder (DSM-IV, Axis 1 disorders). Participants abstained from alcohol and drug use for 12 hours prior to testing sessions, though smokers were asked to smoke as normal.

The AMOUNT dataset contains delay discounting task data from 29 individuals, whose data were included in Mitchell & Wilson (2010; Group 1). Participants were 16 males and 13 females, aged 30.59 years (SD 8.89). As noted in Mitchell & Wilson (2010), and similarly to the SMOKING dataset participants, participants were age 18 or older, had a high school diploma or equivalent, were not pregnant, were not taking any prescription drugs (except birth control), and were fluent English speakers. Exclusion criteria were the same as in the SMOKING dataset: a history of substance use disorder except nicotine dependence (DSM-IV criteria: APA, 1994), current physical or psychiatric problems, and a history of serious psychiatric disorder (DSM-IV, Axis 1 disorders). Participants provided breath and urine samples to verify abstinence from alcohol and illicit drugs that might impact cognition. As noted earlier, only data from participants that generated systematic discounting data in both the delayed $10 and $100 gain conditions were used in the current manuscript.

3. Comparing the k-values and AUCs for the three datasets

For each individual, k-values were derived from fitting the hyperbolic function (Equ. 1) using Excel Solver with a seed values of k = 0. The k-values generated differed widely between datasets. Comparing the k-value histograms for the different studies makes this immediately clear (Figure 1: top panels). The ADHD dataset has k-values ranging from 0.000 - 21.941, the SMOKING dataset contains values ranging from 0.001 - 14.343 and the AMOUNT dataset contains values ranging from 0.000 - 0.289 (all values rounded to 3 decimal places). These differences cannot be accounted for by differences in the units of k between the datasets: 1/days for the ADHD and AMOUNT datasets and 1/weeks for the SMOKING dataset. Notice that it is a simple matter to convert the k-values in the SMOKING dataset from 1/weeks to 1/days by dividing k by 7, and if that were done, the differences between the ranges of k-values between datasets would remain. There are many factors that could influence these differences in k between the datasets, beyond the obvious differences in the characteristics of participants, including differences in amount of the larger, later reward (e.g., Green, et al., 1997; Kirby & Marakovic, 1995) and the range of delays examined (e.g., Read & Roelofsma, 2003); consequently this dataset-based difference in k-values was viewed as indicating any issues associated with the validity of the delay discounting performance across the datasets.

Figure 1.

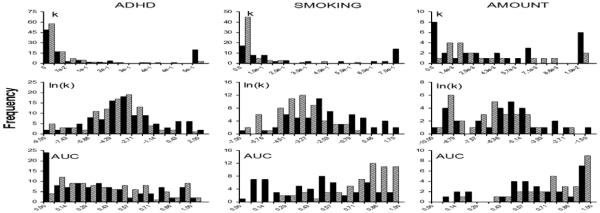
Top panels: Histograms for k-values found using the hyperbolic function (Equ. 1) for the ADHD, SMOKING and AMOUNT datasets. Middle panels: Histograms for the natural logarithm-transformed values of k for the three datasets. Bottom panels: Histograms for the normalized area under the curve (AUC) created by the indifference points for each dataset. Black bars represent frequencies for groups/conditions expected to be associated with steeper discounting: ADHD-diagnosed children, regular smokers, $10 delayed reward amount condition. Gray bars represent frequencies for groups/conditions expected to be associated with shallower discounting: undiagnosed children, never smokers, $100 delayed reward amount condition. Note that the bars associated with the highest k, ln(k) and AUC value for each histogram includes all individuals with values larger than the maximum x-axis value.

As can been seen from Figure 1 (top panels) and Table 2, for all three datasets, the distributions of k-values for groups (ADHD-diagnosed, undiagnosed, regular smokers and never smokers) and for conditions ($10 or $100 delayed reward) were highly positively skewed and more peaked than the normal distribution, making parametric analyses of k inadvisable due to deviations from normality. This observation is common in the literature, though histograms with skewness and kurtosis statistics are not commonly provided. Although the distributions appear similar in Figure 1 (top panels) within the ADHD dataset groups, the SMOKING dataset groups and the AMOUNT conditions, nonparametric tests revealed significant differences between groups and conditions (ADHD: Mann-Whitney U = 4055.00, z = −2.39, p = 0.017; SMOKING: Mann-Whitney U = 781.00, z = −5.35, p = 0.000; AMOUNT: Wilcoxon Signed Ranks z = −3.56, p = 0.000). These group and condition differences within datasets are somewhat more graphically apparent when k is logarithmically-transformed (Figure 1, middle panels); a transform that substantially normalized the distributions (Table 2), as has been reported in previous research. For each dataset, the sample with the steeper discounting functions (ADHD-diagnosed children, regular smokers, $10 delay reward amount) exhibits a more rightward-centered distribution, indicative of less negative logarithm values. The heightened power associated with parametric tests, when the normality assumption is met, is reflected in the smaller p-values when t-tests are used to compare the groups and conditions differences (ADHD: t[189.346] = −3.240, p = 0.001; SMOKING: t[108.050] = −6.201, p = 0.000; AMOUNT: t[28] = 3.982, p = 0.000; notice Levene’s test was significant, indicating that use of the degrees of freedom associated with unequal variances was appropriate). These results replicate data from several other groups (for ADHD-diagnosed and undiagnosed individuals: e.g., Scheres et al., 2006; but also see Rubia,et al., 2009; for regular smokers and never smokers: e.g., Bickel, et al., 1999; Mitchell, 1999; for different reward amounts: e.g., Kirby & Marakovic, 1995; Green et al., 1997).

Table 2.

Parameter values obtained by fitting the hyperbolic function (Equ. 1) for the groups and conditions within each dataset. Akaike Information Criterion (AlC) measure for the fit of the hyperbolic function is provided and the Area Under the Curve (AUC) created by the indifference points is also shown.

Dataset	Median k	Mean ln(k)	Median AICa	Mean AUC
ADHD
Diagnosed	0.041*	−2.942*	−0.760	0.393
Undiagnosed	0.024	−4.010	1.262	0.463
SMOKING
Smokers	0.128*	−1.842*	17.022	0.485*
Never smokers	0.021	−3.831	18.175	0.753
AMOUNT
$10	0.003*	−6.020*	−3.274	0.649*
$100	0.001	−6.950	20.384	0.777

^aCalculated using the formula $AIC=2p+n\left(\text{ln}(SSe∕n)\right)$, where p represents the number of parameters (p = 1 for the hyperbolic function [Equ. 1]), n represents the number of data points (n = 5 or 6 delays), and SSe is the sum of squares for the error term of the regression. Smaller numbers are interpreted as indicating superior fits.

^*p < 0.05 comparing k, In(k) and AUC parameters between groups or conditions within a dataset (see text).

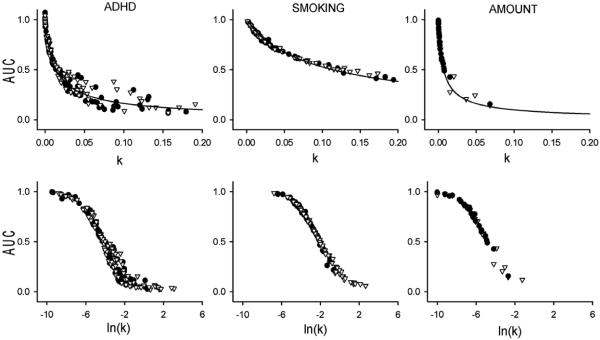
While the AUC index provides a less normal distribution than the logarithmically-transformed k-vales for the datasets (Figure 1, bottom panel; Table 2), the values were within ranges appropriate for use of parametric statistics. It was somewhat unexpected that t-tests indicated no significant difference between the AUC-values for the ADHD-diagnosed and undiagnosed children (t[199] = 1.650, p = 0.101), although this lack of difference replicated the smaller-sample findings reported in Wilson et al. (2011) and, as noted earlier, others have also reported a lack of difference between ADHD-diagnosed and undiagnosed individuals. In contrast, in the SMOKING dataset, regular smokers exhibited significantly smaller AUC values than never smokers (t[107.270] = 6.144, p = 0.000) and in the AMOUNT dataset, a $10 delayed reward was associated with a smaller AUC than a $100 delayed reward (t[28] = −4.158, p = 0.000). Examining Figure 1 (bottom panel) it is apparent that the AUC values for groups within the ADHD dataset exhibited more overlap than did the groups in the SMOKING dataset and the conditions in the AMOUNT dataset. But to understand the dissociation between k-values and the AUC index illustrated by these datasets comparisons, the relationship between AUC and k was examined using scatterplots (Figure 2). This figure clearly illustrates the nonlinear relationship between AUC and both the k-values (top panel) and logarithmically-transformed k-values (bottom panel). In the case of the AUC versus the k-values, there is a monotonically decreasing relationship for all datasets. To better illustrate that the gradient of this monotonic decreasing function varies across datasets, only k-values less than 0.20 are shown in the top panels. These differences in gradient presumably are caused by differences in the intervals between delays in each of the datasets on the areas of the trapezoids used to calculate the AUC. Such nonlinearities presumably contribute to the differential ability of the k-values and AUCs to distinguish between groups and conditions, and these observations should remind researchers that a difference in one measure does not imply a difference in the other. Also, this graphical demonstration of different AUC-k relationships underscores the recommendation that, even with normalization, AUC values should only be compared between studies if the delay range and intervals between examined delays are the same.

Figure 2.

Top panels: Scatterplots showing the relationship between the areas under the curve (AUC) created by the indifference points for the discount functions for each individual and the k-values for that individual, obtained using the hyperbolic function (Equ. 1) for the ADHD, SMOKING and AMOUNT datasets. The unbroken line represents the AUC values that would be obtained if the area was calculated from the hyperbolic curve at each specific value of k. Notice that, although only participants with systematic discounting functions were included (Johnson & Bickel 2008), there were a few individuals with AUC values greater than 1.0 indicative of a one or more indifference points being larger than the amount of the delayed reward. These larger indifference points are made possible because of the task parameters used (Table 1), which include smaller, sooner amounts that are larger than the larger, later amount. For individuals with these larger indifference points, k was 0.0 or slightly negative, resulting in no value being calculated for ln(k). Also notice that the k-values in the top panels are truncated at 0.20 for each dataset to better show how the relationship varied between datasets. Bottom panels: Scatterplots for the AUC indices as a function of the full range of natural logarithm-transformed values of k for the three datasets. Open triangles represent values for individuals in groups/conditions expected to be associated with steeper discounting: ADHD-diagnosed children, regular smokers, $10 delayed reward amount condition. Filled circles represent values for individuals in groups/conditions expected to be associated with shallower discounting: undiagnosed children, never smokers, $100 delayed reward amount condition.

Comparison within each dataset reveals that, for the SMOKING dataset, there is a high level of correspondence between the k and AUC values for individuals, independent of group. This is less apparent in the ADHD or AMOUNT datasets. For the ADHD dataset, at k-values of 0.03 – 0.20, the relationship between k and AUC was relatively variable, with a tendency for ADHD diagnosed individuals to exhibit higher AUC values. For the AMOUNT dataset, at k-values of 0.01 – 0.08, variability in the relationship was observed. Such variability reflects deviations from the hyperbolic discount function that result in disproportionately large or small-area trapezoids, which in turn causes AUC values to be larger or smaller than those predicted if the hyperbolic function (Equ. 1) fit the observed data perfectly (unbroken line on Figure 2: top panels). Another method of examining deviations from hyperbolic discounting is to measure the residuals from fitting Equ. 1. These tend to be negative at the shorter delays and positive at the longer delays. This was clearly the case for the SMOKING and AMOUNT datasets (Figure 3), but to a much lesser degree for the ADHD dataset. Systematic variation in the residuals is one factor that has motivated researchers to identify other ways to describe delay discounting performance. Another is the lack of information provided by the hyperbolic function or AUC about the neural or psychological processes underlying delay discounting, or about the variables affecting it. Mathematical descriptions of delay discounting performance that attempt to provide such information are the topics of the following section.

Figure 3.

The mean residuals for participants in the three datasets obtained by subtracting the indifference points for individuals in each group or condition from the best fitting hyperbolic discounting function for the individual (Equ. 1). Notice that mean residuals for individuals may not result in symmetrical positive and negative residuals if indifference points are not normally distributed. Black bars represent frequencies for groups/conditions expected to be associated with steeper discounting: ADHD-diagnosed children, regular smokers, $10 delayed reward amount condition. Gray bars represent frequencies for groups/conditions expected to be associated with shallower discounting: undiagnosed children, never smokers, $100 delayed reward amount condition.

4. Description of other quantification procedures

As noted above, use of the hyperbolic function and the AUC index provides a popular quantitative description of the underlying delay discounting process but provides no information about the incorporation of environmental variables that influence discounting nor the mechanisms driving performance. Examining what is known about the neural mechanisms is beyond the scope of this manuscript but a growing literature using functional magnetic resonance imaging (fMRI) seeks to identify these mechanisms and there has been much debate about where delay discounting performance reflects the action of a single neural process (e.g., Kable & Glimcher, 2010; Monterrosso & Luo, 2010) or dual/multiple processes (e.g., McClure, et al., 2004). Paralleling the discussions about the number of processes associated with the neural correlates of delay discounting, several categories of theoretical model have been suggested over the last 30 years that propose that delay discounting reflects the operation of multiple psychological/neural/decision-making processes and propensities (see Doyle 2013 for a recent summary of the mathematical models associated with these).

4.1 Models focused on sensitivity to delay and amount

One category of models has focused on the empirical fact that delay discounting is measured in situations when the delay and amounts (sizes) of rewards vary between alternatives. That is, several mathematical models have been proposed in which the delay discounting function is viewed as interplay between an individual’s sensitivity to reward delay and to reward amount. One of the earliest forms using sensitivity to delay and sensitivity amount was derived from the generalized matching law (Baum, 1974) and characterized by exponents that moderate the value of the alternatives. This formulation was used extensively by Alexandra Logue and her colleagues (e.g., Forzano & Logue 1995; Logue, 1988; Rachlin, et al., 1986) as well as by James Mazur (e.g., Mazur 1984, 1986). More recent formulations of this idea of delay and amount sensitivity have included the multiplicative model proposed by Ho, et al. (1999), in which delay and reward “quality”, which the authors relate to reward amount, are evaluated separately using different terms to extend the basic hyperbolic function provided in Equ.1:

$$V=A\cdot \frac{1}{1+q∕Q}\cdot \frac{1}{1+k.D}$$ Equ. 2

V, A, k and D represent the same parameters as in the hyperbolic function (Equ. 1), and q is a fitted parameter that moderates the effects of Q, reward quality, which contributes to the incentive value of the reward. A slightly different approach is taken by Locey & Dallery (2009), in which a sensitivity exponent (z) is added to A to modulate an individual’s response to both reward amount and delay in combination:

$$V=A^z\cdot \frac{1}{1+k\cdot D}$$ Equ. 3

The models in Equ. 2 and 3 have elicited some studies to explore the behavior of the various parameters. However, their use has been circumscribed partly because the formulations cannot easily accommodate the effects of reward amount in probability discounting. Probability discounting can be described well using a hyperbolic function in which “odds again reward delivery” is substituted for “delay” (Rachlin et al., 1991). However, In probability discounting, larger, more probabilistic rewards are discounted more steeply than smaller, “for sure” rewards (e.g., Green et al., 1999; Mitchell & Wilson, 2010; Myerson,et al., 2003). This is the opposite relationship to that observed for reward amount and the gradient of the delay discounting function. Because the q and z variables in Equ. 2 and 3 are exclusively associated with reward quality/amount and there is no mathematical way that their effects can differ according to whether the choice is between delayed or probabilistic alternatives, removing the ability of these models to account for both delay and probability discounting parsimoniously.

This generalization restriction is not a problem for a related pair of models that have been proposed by Howard Rachlin (e.g., Rachlin 1989) and by Len Green and Joel Myerson (e.g., Myerson & Green 1995, Green & Myerson 2004), as described by Myerson et al. (2011). In both models an exponential s parameter is added to the denominator of the hyperbolic function (Equ. 1), which represents the nonlinear scaling of amount and/or delay and is derived from the psychophysical power law (Stevens, 1957). Thus, according to the Rachlin formulation:

$$V=\frac{A}{1+b{D}^a}$$ Equ. 4

And in the Myerson & Green (1995) “hyperboloid” model:

$$V=\frac{A}{{(1+bD)}^s}$$ Equ. 5

b is used in the above equations to emphasize that this multiplier is not interpreted identically to the k parameter found in the hyperbolic function (Equ. 1), because of the role of s. Notice that if s = 1, both equations are equivalent to the hyperbolic function, and b will be equivalent to k. Further, if the larger, later reward is immediate, such the D = 0, then V = A if s > 0 for Equ. 4 and s ≥ 0 for Equ. 5. Thus, the constraint that the subjective value and the objective value of the reward are equivalent when the larger, later reward is immediate, also constrains s to not take negative values.

From a theoretical standpoint it is unclear whether the one model is superior to the other (McKerchar, et al., 2009; Rachlin 2006). As noted by McKerchar et al. (2009), the position of the s exponent in Rachlin’s formulation (Equ. 4) indicates that it moderates the effects of delay only, while its position in the hyperboloid (Equ. 5) indicates that it could moderate the effects of amount and/or delay. While this dual function potentially increases the flexibility and utility of the hyperboloid function, an important limitation is that there is no inherent means to distinguish the proportion of the exponent’s value related to sensitivity to amount and that related to sensitivity to delay.

Some prior work has examined how parameters vary between probability and delay discounting (e.g., McKerchar, et al., 2010). In the current analysis we examine the behavior of the b and s parameters when both equations were fitted individuals’ data from the ADHD, SMOKING and AMOUNT datasets (seed values for fits: b = 0, s = 1). Notice that values of s had to be explicitly constrained to values > 0.0001 for Rachlin’s formulation (Equ. 4), as indicated earlier, because using no constraint resulted in s-values of zero being identified, which produces an undeterminable number when D = 0 (0⁰) and halted the fitting algorithm. Also, in the SMOKING dataset, data from 5 individuals (2 regular smokers and 3 never smokers) could not be fit because no single solution converged for the hyperboloid (Equ. 5).

Given the difficulty of distinguishing between Rachlin’s formulation and the hyperboloid on a theoretical basis, one strategy to distinguish them has been to determine which provides the better fits to the data (McKerchar et al. 2009). However, first, comparisons to the hyperbolic function (Equ. 1) were made. As shown in Tables 2 and 4, for all three datasets, the median values of the Akaike Information Criterion (AIC), which assesses model fit adjusting for the number of fitted parameters, were lower for Rachlin’s formulation than for the hyperbolic function (Equ. 1). This indicates that the Rachlin formulation fit the data better, even after adjusting for the larger number of fitted parameters. Nonparametric tests examining the participants in the ADHD and SMOKING datasets for each group indicated that these differences were actually statistically significant (all ps < .000); although the AIC did not differ significantly for either condition in the AMOUNT dataset, perhaps due to the substantially smaller number of participants in that study. A somewhat similar pattern of differences emerged when comparisons of the AIC values for the hyperboloid (Equ. 5) to the hyperbolic were made, except that the hyperboloid AIC was not different from the hyperbolic for ADHD-diagnosed children, but was significantly smaller for the $100 AMOUNT condition (p = 0.004). Perhaps of more interest, comparisons between Rachlin’s formulation and the hyperboloid indicated mixed results. Nonparametric tests indicated that fits were significantly better for Rachlin’s formulation for the ADHD-diagnosed and undiagnosed children (p < 0.000), and for the never smokers in the SMOKING dataset (p = 0.012) but did not differ significantly for the regular smokers in that dataset, nor for either condition in the AMOUNT dataset. Thus, it appears that, while both Rachlin’s formulation and the hyperboloid generated better data fits than the hyperbolic function, Rachlin’s formulation generated slightly superior fits in some, though not all, instances when the two were compared. This is in slight contrast to McKerchar et al. (2009), which reported fits for both models greater than 0.95 using an R-squared measure of fit, with no significant differences in fit between the two models.

Table 4.

Median b and s values of models incorporating amount and delay sensitivity (Rachlin's formulation [Equ. 4] and the hyperboloid [Equ. 5]) for the groups and conditions within each dataset. Percentage of s values > 1 and the median Akaike Information Criterion (AlC) are also shown.

	Equ. 4: A/1+bD5				Equ. 5:A/(l+bD)5
Dataset	b	s	%s > 1a	AIC	b	s	%s > 1a	AIC
ADHD
Diagnosed	0.054	1.000	15.2	−5.513	0.034	1.000	31.4	−1.731
Undiagnosed	0.012	1.000	10.5	−3.956	0.004	1.000	36.5	−1.883
SMOKING
Smokers	0.364*	0.397	3.3	8.224	4.075	0.386	5.0	8.829
Never smokers	0.136	0.260	3.3	7.190	0.344	0.201	5.0	7.558
AMOUNT
$10	0.017*	1.000	3.4	−7.661	0.003*	1.000	6.9	−3.412
$100	0.001	1.000	0	18.631	0.001	1.000	3.4	20.919

^aIt is expected that s values will not be significantly greater than 1 for Equ. 4 (e.g., Green & Myerson 2004; McKerchar et al. 2009). To determine the extent to which this occurred, s values were used in their untransformed state (Equ. 4), or were transformed to natural logarithms (Equ. 5) to reduce skewness and/or kurtosis. A confidence interval upper bound was created using the formula $[\stackrel{‒}{X}+1.96(\sigma ∕\sqrt{n})]$. This was used to calculate a boundary beyond which s was viewed as “significantly” greater than 1.

^*p < 0.05 comparing parameters between groups or conditions within a dataset; ADHD and SMOKING datasets used Mann-Whitney U test and the AMOUNT dataset used Wilcoxon signed ranks.

Similarly to the k-values derived from fitting the hyperbolic function (Equ. 1), values for b and for s derived from fitting Equ. 4 and 5 were not normally distributed (Table 3). These deviations from normality were substantially more pronounced for parameters derived from the hyperboloid (Equ. 5), and were similar to levels of skewness and kurtosis observed when the hyperbolic function was fit. Deviations from normality were lower for the parameters derived from Rachlin’s formulation (Equ. 4). Transformation to natural logarithms for b and s parameters improved skewness and kurtosis values in all datasets for parameters derived from fitting the hyperboloid but did not increase normality for parameters derived from Rachlin’s formulation appreciably. Because transforms could not be applied uniformly to both types of model, all parameter comparisons between groups and conditions were performed using nonparametric statistics.

Table 3.

Skewness (and kurtosis) values for b and s for models incorporating amount and delay sensitivity (Rachlin's formulation [Equ. 4] and the hyperboloid [Equ. 5]) for the groups and conditions within each dataset.

	Equ. 4: A/1+bD5		Equ. 5:A/(1+bD)5
Dataset	b	s	b	s
ADHD
Diagnosed	4.65 (23.68)	0.85 (−0.11)	10.23 (104.83)	2.54 (6.83)
Undiagnosed	3.77 (16.68)	0.05 (−0.89)	6.82 (45.41)	2.44 (6.62)
SMOKING
Smokers	4.09 (17.52)	0.29 (1.88)	7.62 (58.00)	6.45 (43.56)
Never smokers	1.72 (3.10)	1.47 (2.36)	6.23 (41.37)	5.90 (36.21)
AMOUNT
$10	3.23 (10.07)	1.81 (5.07)	5.39 (29.00)	5.37 (28.88)
$100	2.79 (7.05)	−0.04 (1.78)	5.39 (29.00)	2.22 (27.86)

As shown in Table 4, in the ADHD dataset, neither the b nor s parameters derived from Rachlin’s formulation (Equ. 4) or the hyperboloid (Equ. 5) differentiated the ADHD-diagnosed and undiagnosed children (Mann-Whitney U: all z-scores < |1.71|, all ps > 0.08). This was unexpected, given that the gradient of the hyperbolic function (k: Equ. 1) clearly differentiated between these groups, and there were significant correlations between this gradient and both b-values derived from Rachlin’s formulation and the hyperboloid (rho = 0.53 and 0.53 respectively, N = 201, ps < 0.000), though not for s-values of either model. For the SMOKING dataset, only Rachlin’s b differentiated between regular smokers and never smokers (Mann-Whitney U = 889.00, z = −4.78, p < 0.000; all other z-scores < |1.62|, all p > 0.10). Like the ADHD dataset, this was unexpected because gradients differed according to the hyperbolic function (Equ. 1) and again there were significant correlations between this measure and the b-values from Rachlin’s formulation and the hyperboloid (rho = 0.82, N = 120, p < 0.000 and rho = 0.27, N = 115, p = 0.004, respectively). In contrast to the results for the between group datasets, in the AMOUNT dataset b-values derived both Rachlin’s formulation (Equ. 4) and the hyperboloid (Equ. 5) differentiated between the $10 and $100 conditions (Wilcoxon Signed ranks z = −2.50, N = 29, p = 0.013 and z = −2.63, N = 29, p = 0.006 respectively). s-values did not (z < |1.20|, all ps > 0.23). Again, both Rachlin’s formulation and the hyperboloid b-values were significantly correlated to the gradients of the $10 and $100 derived using Equ. 1 (all rho > 0.72, N = 29 ps < 0.000). Thus, in the three different datasets, the b-parameter from Rachlin’s formulation was more reliably associated with group or condition differences, the b-parameter for the hyperboloid only differentiated between within subject conditions rather than between groups. The s-parameters derived from both equations did not distinguished between groups or conditions for any dataset.

In discussions of both equations in the literature, and during their development, the focus has primarily been on interpreting the s-parameter. The b-parameter is viewed as determining the rate of discounting when s is constant. Given the lack of statistical differences in s for group or condition comparisons within the three datasets examined, the importance of the values of b seems undeniable. Although it is seemingly less sensitive to group differences than statistics based on the gradient of a hyperbolic function (Equ. 1), presumably because variance contributing to the hyperbolic gradient is being divided between the b and s parameters. It has been argued that sensitivity to amount and delay should be invariant regardless of differences in amount (McKechar et al. 2010), so the lack of difference might be anticipated for the AMOUNT dataset. However, this argument does not apply to the ADHD or SMOKING datasets, where it might be anticipated that sensitivity to reward amount and delay might drive differences in delay discounting between the groups. However, several facets of the data complicate interpretation of the parameters. First, b and s within each equation were significantly negatively correlated in just over half of the groups and conditions; for Rachlin’s formulation (Equ. 4), ADHD rho = −0.80 p < 0.000; SMOKING rho = −0.17 ns; AMOUNT $10 rho = −0.77 p < 0.000; AMOUNT $100 rho = −0.30 ns; for the hyperboloid (Equ. 5), ADHD rho = −0.73 p < 0.000; SMOKING rho = −0.65 p < 0.000; AMOUNT $10 rho = −0.63 p < 0.000; AMOUNT $100 rho = −0.02 ns. These correlations indicate that the b and s parameters are not independent, which complicates their interpretation and the mechanistic inferences that can be drawn about the processes associated with them. Second, for each dataset there is a small percentage of individuals for whom the s parameter was greater than 1, where greater than 1 is defined as greater than a threshold generated by calculating the 95% confidence interval above 1 (see Table 4). For the Rachlin formulation, the expectation is that s will be less than or equal to 1 because of the psychophysical constant for prospective temporal judgments, which is inherent in delay discounting (e.g., Ho, et al., 2002; Han & Takahashi 2012; Kirkpatrick 2013). Indeed a psychophysical constant of less than 1 as has been demonstrated in several duration timing paradigms (e.g., Cui 2011; Kane & Lown 1986;). The percentage of participants with s-values of 1 or less was lower for values derived from Rachlin’s formulation than from the hyperboloid (Table 4), but in the case of the ADHD dataset, over 10% of study participants had fitted s parameters >1, suggesting a significant violation of the theoretical basis of Rachlin’s formulation (Equ. 4) in the ADHD dataset. The reasons for the violation in this dataset rather than the others may be attributable to developmental effects on timing (e.g., Droit-Volet, et al., 2001), given that the larger s-values are observed in both ADHD-diagnosed and undiagnosed children. As noted earlier, the s parameter from the hyperboloid (Equ. 5) is not similarly constrained because it is the ratio of two sensitivity parameters. Thus, simple mathematics indicate that such a ratio will be larger than 1 under several circumstances, for example, if the value of numerator sensitivity parameter is greater than 0.5 and the denominator parameter is lower than 0.5. However, it is unclear that the contribution of each separate sensitivity factor can be determined within this experimental framework. Still it is troubling that groups for which sensitivity to amount and/or delay might be anticipated to differ based on research indicating differences in reward sensitivity (ADHD-diagnosed children and regular smokers) exhibited no differences in the s parameter derived from either equation. Understanding the interaction between b and s, what is truly represented by each and the neural and psychological factors underlying each, is critical if we are to understand the separate and interacting roles of amount and delay in delay discounting. Currently neither Equ. 4 nor 5, provides information allowing us to move towards such an understanding, and future research needs to address this knowledge gap.

4.2 Models focused on present bias and delay sensitivity

A somewhat different perspective on delay discounting is apparent in the quasi-hyperbolic models (also known as the β-δ models). Like the models focused on sensitivity to delay and amount, these models also incorporate two factors. One factor represents bias towards commodities available right now (the β term). Some authors have viewed this as analogous to the “hot”, impulsive processes discussed by Walter Mischel (Metcalfe & Mischel 1999; also see Bickel et al. 2012; McClure et al. 2004), because a high level of present bias might be expected to be accompanied by an inability to delay gratification. Somewhat counterintuitively, high levels of present bias are represented by lower values of β. The other is a factor associated with the devaluation of the delayed commodity (the δ term) as a function of its delay due to systematic amalgamation of factors that have not been fully determined such as time horizon (e.g., Petry, et al., 1998; Teucsher & Mitchell 2011; Yi, et al., 2012), uncertainty about receipt (e.g., Takahashi, et al., 2007), instability of future self (e.g., Ersner-Hershfield, et al., 2009; Joshi & Fast 2013). This factor has been viewed as analogous to the “cool”, executive functions also discussed by Walter Mischel and others. Again, higher levels of δ are associated with steeper devaluation of the delayed reward (see https://decisionsciences.shinyapps.io/Shiny/pt_qtd_shiny.Rmd for an interactive graphical depiction). Simply put, mathematically this model states:

$$V=A\left(\beta {\delta }^{\tau }\right)$$ Equ. 6

Where V represents the subjective value of the larger, later reinforcer (indifference point), A represents the amount of larger, later reward, β and δ are fitted parameters as described above, and τ is the length of the delay (Laibson 1997). Notice that there is a discontinuity in the function such that, if τ = 0, it is stated that V = A. Further, both β and δ are constrained so that 0 ≤ β ≤ 1 and 0 ≤ δ ≤ 1. As can be seen from Equ. 6, the foundation of this model is an exponential discounting model (Samuelson, 1937): δ^τ; a model that predicts that there is a constant rate of discounting over time for a specific commodity. Empirical work has demonstrated that the consistent preferences for specific commodities predicted by an exponential discounting model do not hold (e.g., Kirby 1997; Kirby & Santiesteban 2003; Richards et al., 1999), but the addition of the β term permits an individual’s preferences to alter and exhibit limited time inconsistencies, but only if β < 1. That is, the value of the commodity is A when τ = 0, but its value begins to decline as soon as τ > 0 at a rate δ^τ. If β < 1, there is a more precipitous drop in V as soon as τ > 0, because V is reduced not only by δ^τ but by also by β, which makes the multiplier of A even smaller, e.g., (0.5 × 0.9^τ) < (0.9 × 0.9^τ).

It should be noted that discounting rates once τ > 0 are consistent and exponential, which, as noted earlier, does not appear to be supported by the empirical data. However, comparisons between the hyperbolic function (Equ. 1) and exponential functions have not incorporated a β-parameter and so this form of the β-δ models is essentially untested (but see the recent article by Haushofer, et al., 2013). Given the lack of comparisons in the literature and the popularity of these models in the economic literature it seems reasonable to examine how there parameters behave when assessed for the three datasets examined previously. As in those analyses, the data from individuals in each of the three datasets was fitted using Microsoft Excel 2010 Solver on the indifference points for delays (τ) > 0 (seed values β = 0 and δ = 1). The fitting algorithms in Excel Solver are less sophisticated than using a maximum likelihood approach which using all choices not only the indifference points (e.g., Myung 2003). Consequently, there is the risk of identifying a local maximum when minimizing the SS_error. Identifying such an issue is simple and merely requires examining different seed values and assessing whether the solutions are the same. This strategy has rarely resulted in changes in parameters derived by fitting Equ. 4 or 5, but that was not the case when fitting the β-δ model (Equ. 6). Comparing the parameters and AIC between seed values of 0, 1 with seed values of 1, 1 revealed that either the β or δ parameter changed by at least 0.01 between seed values for 19 ADHD-diagnosed and 8 undiagnosed children from the ADHD dataset, 5 regular smokers from the SMOKING dataset and 9 from the AMOUNT dataset (7 in the $10 condition and 2 in the $100 condition). These alterations highlight the importance for researchers of providing information associated with fitting techniques, if maximum likelihood approaches are not used.

Despite the issue of local minima, Eq. 6 fits were good and an examination of the AIC values using nonparametric statistics indicated that the AIC for the β-δ model were significantly lower, indicating a better fit, than the hyperbolic function (Equ. 1) for the ADHD-diagnosed and undiagnosed children, and for regular smokers and never smokers (all ps < 0.000) but did not differ significantly for the $10 or $100 delayed reward amount condition (ps > 0.440). A fairly consistent picture emerged when the AICs for the β-δ model were compared with AICs for Rachlin’s formulation and the hyperboloid. Rachlin formulation AIC were significantly lower than those of the β-δ model, indicating a better fit for Rachlin’s formulation, for the ADHD-diagnosed and undiagnosed children (ps < 0.025), and for the regular smokers and never smokers (ps < 0.007), while Rachlin’s formulation provide better fits in the $10 condition but the two did not differ for $100. A more mixed picture was apparent when the AIC values for the hyperboloid and β-δ models were compared. In the ADHD dataset, the β-δ model AICs were significantly lower, signifying better fits, for both ADHD-diagnosed and undiagnosed children (ps < 0.000) than those of the hyperboloid, but the pattern was reversed for regular smokers and never smokers (hyperboloid AIC < β-δ model: ps < 0.000). In the AMOUNT dataset, the two models did not differ significantly in AIC values.

Unlike the b and s parameters derived from Rachlin’s formulation (Equ. 4) and the hyperboloid (Equ. 5), nonparametric tests to compare β and δ-values between groups and conditions, revealed consistent differences in β (Figure 4) such that values were lower in ADHD-diagnosed children, regular smokers and the $10 delayed reward condition. These results match our intuitions about these groups and conditions, in that we would anticipate these groups to exhibit the highest levels of present bias and therefore lowest values of β. This result is somewhat at variance with data reported by Mitchell & Wilson (2012) using a subset of the SMOKING data set in which no difference between β-values were observed. However, there are several important differences that might account for this difference. Mitchell & Wilson (2012) used a more sophisticated version of the simple β-δ model (see Equ. 7 below) coupled with a maximum likelihood fitting approach, and perhaps most critically, used data that included choices between alternatives for which both alternatives were delayed, negating the influence of present bias. Arguable, a more complete understanding of the β-value will be derived when researchers compare cases in which choices between alternatives for which present bias can play a role a role and alternatives in which it cannot. In contrast to the consistent differences in β between datasets, only the SMOKING dataset exhibited a group difference in δ such that regular smokers has a significantly lower δ value, indicating heightened devaluation of delayed rewards. This finding was similar to that reported by Mitchell and Wilson (2012). Initial analyses were conducted to examine the degree to which the parameters were correlated. However, the preponderance of parameter values of 1.0 resulted in scatterplots with a strongly defined “corner” that made even nonparametric analyses inappropriate, even in samples as large as the ADHD dataset. However the mere form of these scatterplots argues against a high degree of correlation.

Figure 4.

The median β and δ values for participants in the three datasets. Black bars represent frequencies for groups/conditions expected to be associated with steeper discounting: ADHD-diagnosed children, regular smokers, $10 delayed reward amount condition. Gray bars represent frequencies for groups/conditions expected to be associated with shallower discounting: undiagnosed children, never smokers, $100 delayed reward amount condition. * p < 0.05, ** p < 0.01 comparing parameters between groups or conditions within a dataset; ADHD and SMOKING datasets used Mann-Whitney U test and the AMOUNT dataset used Wilcoxon signed ranks.

In a similar way to the amount and delay sensitivity, unfortunately none of the three datasets contained any data that would permit present bias or discounting rate to be assessed independently. If the mathematical descriptions of delay discounting, such as Equ. 4, 5 and 6, are to move understanding of the processes responsible for delay discounting forward, the variables represented in the equations must be assessed, and if possible manipulated, and the effects on equation parameters measured.

5. Conclusions and recommendations

The hyperbolic model (Equ. 1) provides a good description for empirically collected delay discounting data (e.g., Madden & Johnson, 2010). It identifies relationships between groups and conditions that often conform well to our intuitions when it is viewed as an index of impulsivity and self-control; that is, groups viewed as more impulsive/less self-controlled exhibit the steeper discounting inherent in heightened preference for the smaller, sooner rewards relative to the larger, later rewards. Examination of the behavior of the gradient of the function (k) for our three datasets revealed that normality assumptions were violated in all datasets, but could be met if data were transformed using logarithms, as has been done previously (e.g., Mitchell, 2004). Based on these analyses, and those of other researchers, it is recommended that normality assumptions should always be examined prior to analyzing hyperbolic function k-values. Further, parametric statistics should only be used following appropriate data transformations, assuming that these transformations have normalized the distributions.

The area under the curve measure (AUC) was nonlinearly related to the gradient of the hyperbolic discounting function for all three datasets. Consequently, AUC analyses may yield the same relationships between groups and conditions as analyses of k-values but not always, especially if the data includes extremely steep or shallow discounting curves. This point was made in our analyses. While analyses of the SMOKING and AMOUNT datasets revealed the same group or condition differences using k and using AUC, the AUC indices were less sensitive to group differences in the ADHD dataset, presumably due to the presence of these extreme values. Analyses of datasets by other research groups are needed to quantify the frequency with which discordant results are produced, but until that time, it is recommended that the hyperbolic function k-values should be reported instead of or in conjunction with AUC indices if there are a high proportion of steep or shallow discounting curves amongst the individuals being examined.

To move beyond descriptive models, to those models that incorporate factors hypothesized to play a causal role in the observed gradient of the delay discounting curve, several formulations have been proposed. In our comparison of the Rachlin formulation (Equ. 4) and the hyperboloid (Equ.5), it because clear that the models were difficult to differentiate at an empirical or theoretical level. Based on AIC measures, these models fit the data better than the hyperbolic function, and the Rachlin formulation fit somewhat better than the hyperboloid. Further, Rachlin’s formulation differentiated between the difference groups and conditions in more instances than the hyperboloid, although neither model differentiated between the groups and conditions as well as the hyperbolic function. However, it was apparent that the theoretical assumptions associated with Rachlin’s formulation were violated during the fitting process, and the implications of such violations should be weighed when determining whether either model was in fact superior. To different degrees, both models suggest that sensitivity to delay and/or delayed reward amount play a critical role. This idea is highly appealing but neither model permits the amount and delay sensitivities to be disentangled, reducing the explanatory power of the proposals. In addition, independent verification of the parameters is unavailable making it difficult to test the validity of these two very similar models. It is recommended that future research move towards developing methods to quantify reward amount and delay sensitivities and create formulations that permit the influence of each to be examined separately.

An alternative set of models suggest delay discounting can be broken down into factors that include bias towards an immediate item and a longer-term discounting factor. These models have been examined less than the amount-delay sensitivity models and so we recommend that future research efforts strive to better understand these models and their adequacy to account for differences in delay discounting. It is not clear what factors drive present bias, e.g., amount possibly, and it is recommended that future work attempts to examine and identify such factors. There is an appeal in the idea of incorporating a present bias factor as other research has suggested that framing of time, including dates, can have profound effects on delay discounting functions (e.g., Kable & Glimcher, 2010; Mitchell & Wilson, 2012; Scholten & Read, 2010). It may the case that a similar argument could be made with other forms of discounting, that rewards available “for sure” and rewards available with no effort required are subject to a certainty bias and an effortless bias, but research on this is lacking. It is recommended similar models of these decision-making paradigms should be created and their explanatory power evaluated.

While no single explanatory model fitted data in the three datasets more closely than another model, the β-δ model did consistently differentiate between groups and conditions in a similar way to the descriptive hyperbolic function, though the AIC levels were not consistently higher than those of the Rachlin or hyperboloid models. Additional comparisons between models are recommended. However, conclusions based on the ability to differentiate between groups should be tempered with caution because of uncertainties inherent in the use of a fitting technique in which the critical measure of present bias is derived without including data in which both reward alternatives are delayed. It is recommended that future work should include such conditions so that the influence on preference of smaller, immediate rewards can be differentiated from the influence of smaller, sooner rewards. In connection with this refinement, it should be noted that more sophisticated models of the β-δ model (Equ. 6) have been proposed to both address concerns about the unlikeliness that there is a consistent discounting rate when τ > 0 and to map more closely only the burgeoning neuroimaging literature on intertemporal choice. One such model, proposed by van den Bos & McClure (2013), separates the present value component from the discounting rate and uses an additional factor (ω) to moderate the extent to which each factor influences the valuation of a commodity:

$$V=A[\left(\omega \right)\left({\beta }^{\tau }\right)+(1-\omega )\left({\delta }^{\tau }\right)]$$ Equ. 7

While this model does have some intuitive appeal, and neuroscientists are attempting to link neural activity to specific parameters, it remains unclear how environmental factors contribute to β or, for that matter, δ. It is recommended that future research should include manipulations anticipated to affect single parameters so that researchers can evaluate the adequacy of these formulae to quantify the action of discounting mechanisms. In addition, research should include conditions in which both reward alternatives are delayed should be included so that present bias can be assessed, and variables that might influence present bias, so that β-δ models can be more effectively compared with other more traditional models, and any differences between participant populations on present bias can be identified.

Highlights.

• Mathematical indices of delay discounting were compared for 3 datasets

• The hyperbolic function slope (k) consistently differentiated groups and conditions

• Area under the discounting function curve did not consistently differentiate

• Models including amount and delay sensitivity also did not differentiate

• Present value bias did differentiate though interpretational caveats are suggested