Quantification and simulation of layer-specific mitral valve interstitial cells deformation under physiological loading

Abstract

Within each of the four layers of mitral valve (MV) leaflet tissues there resides a heterogeneous population of interstitial cells that maintain the structural integrity of the MV tissue via protein biosynthesis and enzymatic degradation. There is increasing evidence that tissue stress-induced MV interstitial cell (MVIC) deformations can have deleterious effects on their biosynthetic states that are potentially related to the reduction of tissue-level maintenance and to subsequent organ-level failure. To better understand the interrelationships between tissue-level loading and cellular responses, we developed the following integrated experimental-computational approach. Since in-vivo cellular deformations are not directly measurable, we quantified the in-situ layer-specific MVIC deformations for each of the four layers under a controlled biaxial tension loading device coupled to multi-photon microscopy. Next, we explored the interrelationship between the MVIC stiffness and deformation to layer-specific tissue mechanical and structural properties using a macro-micro finite element computational model. Experimental results indicated that the MVICs in the fibrosa and ventricularis layers deformed significantly more than those in the atrialis and spongiosa layers, reaching a nucleus aspect ratio of 3.3 under an estimated maximum physiological tension of 150 N/m. The simulated MVIC moduli for the four layers were found to be all within a narrow range of 4.71–5.35 kPa, suggesting that MVIC deformation is primarily controlled by each tissue layer’s respective structure and mechanical behavior rather than the intrinsic MVIC stiffness. This novel result further suggests that while the MVICs may be phenotypically and biomechanically similar throughout the leaflet, they experience layer-specific mechanical stimulatory inputs due to distinct extracellular matrix architecture and mechanical behaviors of the four MV leaflet tissue layers. This also suggests that MVICs may behave in a layer-specific manner in response to mechanical stimuli in both normal and surgically modified MVs.

1. Introduction

Once largely considered as simple, passive fluidic functional components of the heart, heart valves are now deemed dynamic structures that actively remodel and have their own vasculature and innervation D’Amore et al., 2009; Sacks and Yoganathan, 2008). Mitral valve (MV) mechanical loading results from the combination of blood flow-induced fluid shear stresses, changes in annular and papillary dimensions, and cyclic pressure: all integrating to produce net tissue stresses. Within the four layers of the MV leaflet tissue, there resides a heterogeneous population of interstitial cells (Filip et al., 1986; Messier et al., 1994; Mulholland and Gotlieb, 1996; Taylor et al., 2003). Among all valve interstitial cells (VICs), mitral valve interstitial cells (MVICs) have characteristics of both fibroblasts and smooth muscle cells. Studies of VICs in both human and porcine valve tissues have revealed that the cells are not localized to any particular region or layer of the leaflet, but are present throughout the valve leaflet tissues (Bairati and DeBiasi, 1981; Merryman et al., 2006b).

Interest in VICs has grown in recent years as they are believed to be critically important in valve tissue homeostasis and pathophysiology. Primarily, VICs serve to maintain the structural integrity of the leaflet tissue via protein synthesis and enzymatic degradation. Their phenotype, which ranges from fibroblast-like to myofibroblast-like, is plastic and reversible. VICs in normal healthy valves are quiescent, whereas they become activated and contractile in pathological valves (Rabkin-Aikawa et al., 2004; Rabkin et al., 2002). While their dualistic nature is not fully understood, the multi-functionality of VICs may involve cell-to-cell communication, tissue remodeling, wound healing, and contraction (Mulholland and Gotlieb, 1996). When the phenotype of the resident VICs is myofibroblast-like, the cells are actively remodeling the extracellular matrix (ECM), indicating that VIC phenotypic state at a given time is related to the current remodeling demands of the tissue (Rabkin et al., 2002). Recent work by Grande-Allen demonstrated the interrelationship between substrate stiffness, VIC phenotype and synthetic properties (Grande-Allen and Liao, 2011; Stephens et al., 2010a; Stephens et al., 2011). Simmons used micropipette aspiration techniques to quantify the elastic properties of VICs. Their results indicated that the VIC elastic modulus increases with pathological differentiation (Wyss et al., 2012), and that VIC phenotypic plasticity and mechanical adaptability are regulated both biomechanically and biochemically, which, in turn, affect the progression of diseases and pathologies.

Our group has demonstrated that VICs from the aortic and mitral valves are significantly stiffer than those from the pulmonary and tricuspid valves (Merryman et al., 2007; Merryman et al., 2006c). By quantifying collagen biosynthesis and cytoskeletal composition using alpha-smooth muscle actin (α-SMA) and the molecular chaperone heat-shock protein 47 (HSP47) as bio-indicators, we found that the mitral and the aortic VICs contain significantly more α-SMA and HSP47 (Merryman et al., 2006a). Moreover, we found that the aortic VICs have a greater ability to contract free-floating collagen gels compared to the pulmonary VICs under identical experimental conditions (Merryman et al., 2007), indicating a greater ability to remodel collagenous soft tissues. This can be linked to the regulatory function of the endothelium on the mechanical properties of the aortic valve leaflets (El-Hamamsy et al., 2009). These studies revealed the unique properties of VICs to form cellular networks within collagen gels and spontaneously interact with the extracellular matrix to induce contractile forces. MVICs seeded in three-dimensional collagen gels could generate 50% of the total force significantly faster than the VICs of the aortic and tricuspid valves, suggesting that the distinct functional properties of VICs reflect the mechanical function of the heart valves (Smith et al., 2007).

In biomechanics, the presence of normal tissue stresses has long been considered to be closely related to tissue homeostasis (Chuong and Fung, 1986; Fung, 1991; Lanir, 2009; Ogden, 2003; Taber and Humphrey, 2001). Moreover, it has been shown that pathophysiological alterations in mechanical loading can lead to stress changes and subsequent tissue adaptation (Fung and Liu, 1991; Liu and Fung, 1989). In the MV, numerous pathological factors, such as tachycardia-induced cardiomyopathy (Stephens et al., 2009) and mitral regurgitation (Stephens et al., 2008), have been shown to affect MV tissue structure and extra-cellular matrix composition. Collectively, disease- and repair-induced alternations in MV geometry result in altered tissue stresses—these changes in tissue-level stresses and deformations could subsequently lead to tissue remodeling that would ultimately affect the long-term durability of MV surgical repair.

Advances in MV computational modeling and simulation research have been significantly made in the past two decades, including development of constitutive models for the MV tissues (May-Newman and Yin, 1998; Prot and Skallerud, 2009; Prot et al., 2007; Skallerud et al., 2011; Weinberg and Kaazempur Mofrad, 2007), image-based patient-specific computational modeling (Mansi et al., 2012; Stevanella et al., 2011; Votta et al., 2008; Wang and Sun, 2013), fluid-structure interaction modeling (Einstein et al., 2004; Kunzelman et al., 2007), inverse approaches for assessing the in-vivo biomechanical properties of the MV (Lee et al., 2014; Rausch et al., 2012), and coupled left ventricle-mitral valve modeling for investigating ischemic mitral regurgitation (Wenk et al., 2010). These efforts represent important steps towards the development of physiologically realistic models of functioning heart valves.

Yet, no existing models make the connection between organ- and tissue-scale simulations to cellular mechanotransduction and mechanobiological responses. Moreover, there is still a lack of quantitative data in the heart valve literature relating the regional tissue stress and homeostasis to the underlying cellular function. In particular, there is growing evidence that cyclic tissue strains can profoundly influence the biosynthetic responses of VICs, both in vitro (Balachandran et al., 2009b; Balachandran et al., 2006b; Carruthers et al., 2012b; Gupta et al., 2007; Gupta et al., 2009; Konduri et al., 2005) and in vivo (Quick et al., 1997; Stephens et al., 2009). Ideal phenomenological models should be able to simulate VIC behavior in response to mechanical inputs such as tissue-level and cellular strains and the induced cellular biosynthetic responses. Such a model would enable predictions of the phenotypic and biosynthetic responses of VICs due to altered valvular tissue stresses in various heart valve repair scenarios. Clearly, a necessary first step is the ability to predict layer-specific MVIC deformations from the macroscopic tissue deformations as presented in this work.

As in-vivo MVIC deformations cannot be measured directly with existing experimental techniques, we developed an integrated computational, in-situ experimental approach to explore the interrelationship between tissue stress, MVIC deformation and mechanical properties in the MV anterior leaflet (MVAL) tissue. First, we utilized a newly-developed in-vitro assessment technique to quantify the in-situ layer-specific MVIC deformations within each of the four layers of the MVAL tissues under controlled biaxial stretch over a range of physiological tension loading. This method allows us to acquire sufficient information to construct layer-specific computational models of the MV leaflet. Next, we incorporated available histological and microstructural information of the MVAL tissues into a macro-micro finite element (FE) computational framework for modeling both MVAL tissues and MVIC microenvironment. This integrated approach enabled the quantification of layer-specific MVIC deformations in the MVAL tissue under controlled biaxial tension loading, the estimation of the MVIC modulus, and the investigation of the interrelationship between MVIC stiffness and deformation to layer-specific mechanical and microstructural properties.

2. Methods

2.1 Valve tissue preparation and real-time deformation measurement

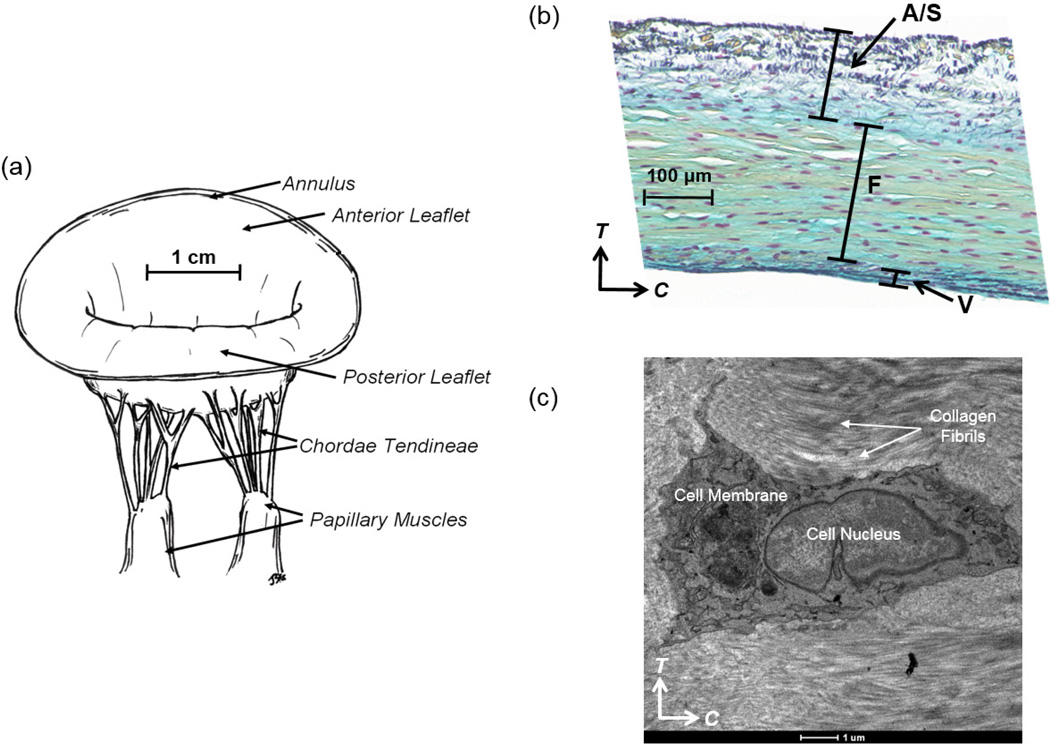
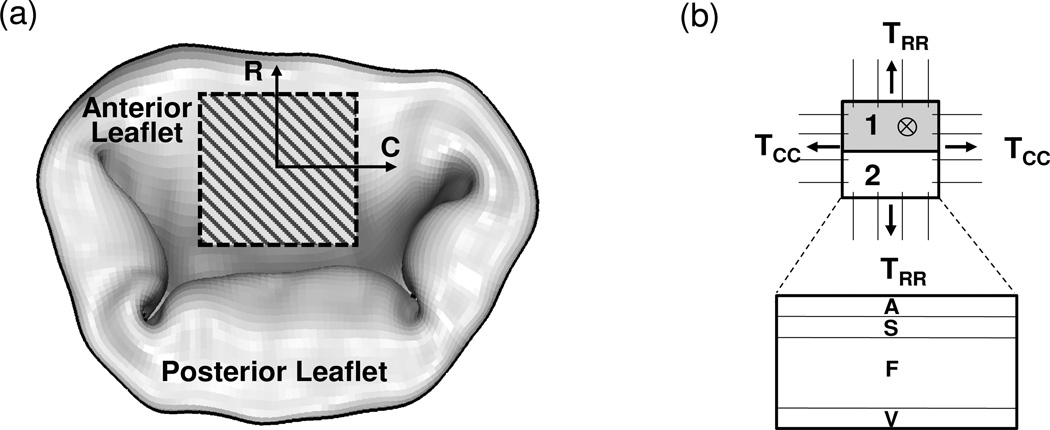
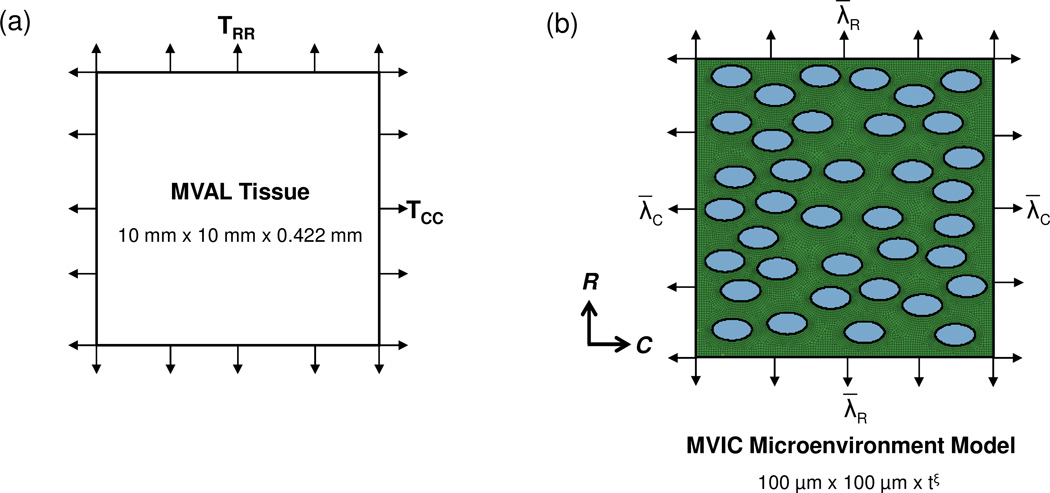
We begin by presenting the experimental methods to quantitatively characterize layer-dependent MVIC deformations under controlled physiological loading. First, fresh ovine hearts from 40 kg sheep were acquired from a local USDA approved abattoir. MV leaflets were dissected and the surrounding myocardium was carefully trimmed from the leaflets (Fig. 1-a). Tissue samples of 10 mm×10 mm were then taken from the center region of the MVAL, below the annulus and above the first chordae tendineae attachment site (Fig. 1-a, Fig. 2-a). The samples were loaded into a miniature biaxial testing system, in which the specimen’s circumferential and radial directions were aligned with the device axes. Four graphite fiducial markers were placed in the center of each tissue sample and their positions were tracked optically in real time. The real-time tissue-level deformation gradient tensor F was computed by using standard surface strain calculation techniques (Sacks et al., 2006) based on the measured marker displacements using a single four-node bilinear finite element. The MV leaflets were loaded to 5, 10, 20, 50, 100, and 150 N/m, and ${\overline{\mathrm{\lambda }}}_{\mathrm{C}}$, ${\overline{\mathrm{\lambda }}}_{\mathrm{R}}$, and ${\overline{\mathrm{\lambda }}}_{\mathrm{T}}=\mathrm{1/}{\overline{\mathrm{\lambda }}}_{\mathrm{C}}{\overline{\mathrm{\lambda }}}_{\mathrm{R}}$, the tissue-level stretches in the circumferential, radial and transmural directions, respectively, were determined from F under the assumption of an incompressible material (Sacks, 2000).

Figure 1.

(a) Illustrative diagram of the native ovine mitral valve, demonstrating key anatomical components: two main leaflets (anterior leaflet and posterior leaflet), annulus, chordae tendineae and papillary muscles, (b) stained histologic image showing four-layered structure of the MV tissue (A: atrialis, S: spongiosa, F: fibrosa, V: ventricularis), and (c) transmission electron microscopy (TEM) image of the intact MVIC residing in the fibrosa layer of the MVAL, showing the MVIC microenvironment and its alignment with the collagen fibrils in the circumferential direction (scale bar=1 µm, C: circumferential direction, and T: transmural direction).

Figure 2.

Schematic diagrams of (a) ovine MV anterior and posterior leaflets and the region of interest for the 10mmx10mm MVAL specimen (C: circumferential direction and R: radial direction), and (b) experimental setup for the mini-biaxial testing, followed by histologic & thickness analyses (the first 7 µm section) and measurements of the MVIC NAR (the second 30 µm section) using MPM imaging.

2.2 Valve tissue fixation and imaging

Three tissue specimens (n=3) from the MVAL center region were measured at the unloaded state (0 N/m tension) and at each tension level, resulting in a total of 21 samples. Each sample was fixed in 2% aqueous paraformaldehyde (PFA) solution for 2 hours in the loaded configuration, and then split into two sections for the following analyses (Fig. 2-b). The first 7 µm section was stained with Movat’s Pentachrome to distinguish the histologic four layers of the MV leaflet: atrialis, spongiosa, fibrosa, and ventricularis layers (Kunzelman et al., 1993; Sacks and Yoganathan, 2008), and to quantitatively measure the thickness changes and the microstructural compositions among different layers under biaxial tension loading. The second 30 µm section was paraffin-embedded and cryosectioned along the circumferential-transmural surface. The sample slides were then deparaffinized, permeabilized with Triton-X for 20 minutes, and stained with Sytox Green (Invitrogen Corp., CA, USA) at a 1:250 concentration for another 30 minutes. After being gelvatol-mounted and cover-slipped, each sample slide was taken for imaging under the multi-photon microscopy (MPM) system (Watkins, 2001) at an excitation wavelength of 830 nm with an incremental z-step of 1 µm. Here, the MPM was used to image the MVIC Cytox green nuclei via two-photon excited fluorescence (TPEF) with a TPEF-filter set up at 525±50 nm.

2.3 In-situ determination of MVIC nuclear orientation and deformation

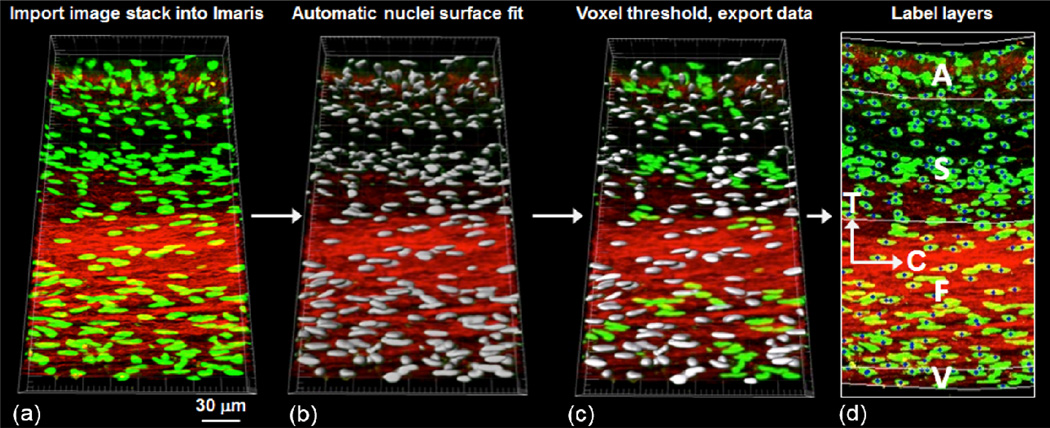
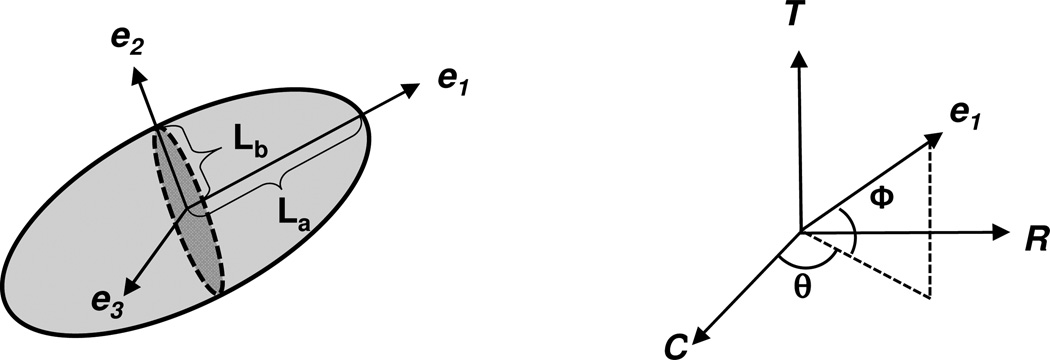
MVIC nuclear orientation and deformation for each tissue layer and tension level were measured and analyzed as follows. The TPEF-MPM image stacks were first imported into Imaris software (Bitplane AG, Zurich, Switzerland) for 3D nuclear deformation visualization and quantitative analysis (Fig. 3-a). Individual surface was then fitted to each nuclear point cloud (Fig. 3-b), and erroneous detections were eliminated using an automated maximum voxel threshold and a minimum voxel threshold of 250 (Fig. 3-c). The eigenvectors associated with each 3D nuclear surface were determined based on an assumed MVIC ellipsoidal geometry (Fig. 4) using an in-house MATLAB program (The Mathworks Inc., Natick, MA, USA), and the corresponding major and minor axes of each MVIC ellipsoid were converted into the nuclear aspect ratio (NAR=L_a/L_c). Note that we utilized the NAR as a dimensionless indicator of MVIC deformation (Sacks et al., 2009). In addition, the eigenvectors for each cell were converted into the spherical coordinates to define the 3D orientation of each MVIC with orientation angles θ and ϕ. Moreover, the four layers of the MV tissue were identified from a maximum intensity z-projection of collagen networks on the MPM images, and the quantitative data of each MVIC nucleus was automatically associated with its respective layer (Fig. 3-d). Note that for each specimen, the nuclear aspect ratio and orientation angles of MVICs associated with each layer were determined and averaged over all the MVICs residing in each of the four different layers, and the mean (n= 3 samples) was then calculated and reported.

Figure 3.

Schematic of the MVIC deformation analysis procedure: (a) stack of images obtained from TPEF-MPM imported into Imaris for 3D visualization of Cytox Green stained MV interstitial cell nuclei, (b) automatic 3D surface fit to all cell nuclei using built-in analysis functions in Imaris, (c) exported voxel data with a specified threshold for gathering quantitative information, and (d) MV cell nuclei information associated with the four layers of the MVAL tissue using a MATLAB algorithm (C: circumferential direction, T: transmural direction).

Figure 4.

(Left): schematic of the local coordinate system (e₁, e₂, e₃) defining the three principal axes of a MVIC nucleus based on the ellipsoidal geometry; (right): its orientation with respect to the global coordinate system (C: circumferential, R: radial direction, T: transmural direction).

2.4 Morphological analysis of layer-specific compositions and microstructures of the MVAL tissues

Layer-specific mass fractions of matrix and fibers (${\mathrm{\omega }}_{\mathrm{m}}^{\mathrm{\xi }},{\mathrm{\omega }}_{\mathrm{c}}^{\mathrm{\xi }}$, and ${\mathrm{\omega }}_{\mathrm{e}}^{\mathrm{\xi }}$) were determined by quantitatively assessing the Movat-stained and circumferentially-oriented MVAL sections using ImageJ (National Institute of Health, Bethesda, MD) in accordance with the methods previously described (Flanagan et al., 2006). Here, we adopted the subscripts m, c, e to denote matrix, collagen fiber and elastin fiber components, respectively, and the superscript ξ to denote the layer identifier, which refers to ξ=1-atrialis, 2-spongiosa, 3-fibrosa, and 4-ventricularis layers of the MVAL. The color deconvolution method (Ruifrok and Johnston, 2001) was adopted to separate the red/green/blue (RGB) image into collagen (yellow), elastin (black), and ground substance (blue) components. Background corrections were further applied by subtracting the integrated optical density (IOD), which is the sum of pixel values, from the white pixel intensity. For all three components, each layer was represented as a region of interest (ROI) and layer-specific mass fractions were calculated by ${\mathrm{\omega }}_{\mathrm{i}}^{\mathrm{\xi }}=\mathrm{I}\mathrm{O}{\mathrm{D}}_{\mathrm{i}}^{\mathrm{\xi }}/(\mathrm{I}\mathrm{O}{\mathrm{D}}_{\mathrm{m}}^{\mathrm{\xi }}+\mathrm{I}\mathrm{O}{\mathrm{D}}_{\mathrm{c}}^{\mathrm{\xi }}+\mathrm{I}\mathrm{O}{\mathrm{D}}_{\mathrm{e}}^{\mathrm{\xi }})$, i=m,c,e. In order to compensate for the layer-specific thicknesses, the above quantified layer-specific mass fractions were used to determine the volume fractions of matrix and collagen and elastin fibers: ${\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}={\mathrm{\omega }}_{\mathrm{m}}^{\mathrm{\xi }}\times {\mathrm{t}}^{\mathrm{\xi }}/{\mathrm{t}}_{\text{leaflet}},{\mathrm{\varphi }}_{\mathrm{c}}^{\mathrm{\xi }}={\mathrm{\omega }}_{\mathrm{c}}^{\mathrm{\xi }}\times {\mathrm{t}}^{\mathrm{\xi }}/{\mathrm{t}}_{\text{leaflet}}$ and ${\mathrm{\varphi }}_{\mathrm{e}}^{\mathrm{\xi }}={\mathrm{\omega }}_{\mathrm{e}}^{\mathrm{\xi }}\times {\mathrm{t}}^{\mathrm{\xi }}/{\mathrm{t}}_{\text{leaflet}}$ as will be employed in the finite element modeling introduced in the subsequent sections, where t^ξ is the thickness of each layer and t_leaflet is the total thickness of the MVAL tissue (Table 1).

Table 1.

MVAL Layer-specific structural and mechanical parameters

	MVAL Tissue Layers
	Atrialis	Spongiosa	Fibrosa	Ventricularis
ECM Preferred Fiber Direction	Radial	Radial	Circumferential	Circumferential
Effective Fiber Orientation Index, OIξ (deg.)	21.86	81.97	30.25	30.25
Fiber Splay Standard Deviation, σξ (deg.)	16.21	86.65	22.49	22.49
Thickness (µm)	43.2	41.5	319.6	17.3
MVIC Dimension in the Major Axis e1, La (µm)	5.84	6.13	6.68	6.18
MVIC Dimension in the Minor Axis e2, Lb (µm)	3.49	3.71	3.64	3.41
MVIC Nuclei Aspect Ratio at 0 N/m Tension, NAR0	2.42	2.41	2.49	2.51
Collagen Mass Fraction, ${\mathrm{\omega }}_{\mathrm{c}}^{\mathrm{\xi }}$	0.231	0.203	0.671	0.309
Elastin Mass Fraction, ${\mathrm{\omega }}_{\mathrm{e}}^{\mathrm{\xi }}$	0.601	0.198	0.088	0.555
Matrix Mass Fraction, ${\mathrm{\omega }}_{\mathrm{m}}^{\mathrm{\xi }}$	0.168	0.599	0.241	0.136
Volume Fraction of Matrix, ${\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}$	0.017	0.059	0.182	0.006
Volume Fraction of Effective Fibers, ${\mathrm{\varphi }}_{\mathrm{f}}^{\mathrm{\xi }}={\mathrm{\varphi }}_{\mathrm{e}}^{\mathrm{\xi }}+{\mathrm{\varphi }}_{\mathrm{c}}^{\mathrm{\xi }}$	0.085	0.039	0.576	0.036

Next, we employed the measured fiber splay structural data for each of the four layers using second harmonic generation (SHG) methods (Fata et al., 2013) and reported in (Carruthers et al., 2012b) to define the layer-specific material axial direction μ^ξ and the fiber splay standard deviation σ^ξ (Table 1). It should be noted that in our studies of MV fiber structure in (Carruthers et al., 2012b) the collagen and elastin fibers always coincided and had very similar orientation distributions, so we combined their collective effects into a single homogenized or effective fiber response. In addition, to be consistent with the experimental data, we utilized a Gaussian distribution function for representing the fiber angular orientation distribution of the measured fiber splay. The fiber splay was directly derived from the measured orientation index (OI) used in (Carruthers et al., 2012b) to denote the strength of fiber splay alignment. In that study, the OI was defined as the angular width in which 50% of the total number of fibers occurs. The fiber splay standard deviation σ^ξ associated with each of the four layers can be derived directly from the OI value using $\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{\mathrm{O}{\mathrm{I}}^{\mathrm{\xi }}}{2\sqrt{2}{\mathrm{\sigma }}^{\mathrm{\xi }}}\right)-\frac{1}{2}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{180°}{2\sqrt{2}{\mathrm{\sigma }}^{\mathrm{\xi }}}\right)=0$ (Sacks et al., 1997).

2.5 Finite element model development

Next, we developed a multi-level computational framework at both macroscopic and microscopic scales to investigate the interrelationship between layer-specific mechanical behaviors and the measured MVIC deformations obtained in Section 2.3, which incorporated tissue-level deformations from the planar equi-biaxial tension loading of the MVAL tissue (Fig. 5-a) with the modeling of the MVIC microenvironment (Fig. 5-b) considering the layer respective microstructure and composition (Fig. 1-b). The details of the proposed computational modeling were described in the subsequent subsections.

Figure 5.

The macro-micro finite element (FE) model utilized in our investigations of MVIC deformations: (a) schematic diagram of tissue-level modeling of the region of interest of the MVAL tissue under equi-biaxial tension loading, and (b) schematic diagram of MVIC microenvironment modeling with tissue-level deformations as prescribed boundary displacements considering 37 uniformly distributed MV interstitial cells embedded in the layer-specific representative volume element (RVE). (t^ξ denotes layer-specific thickness)

2.5.1 FE modeling of the MVAL tissue under planar equi-biaxial tension loading

For FE modeling of the MVAL tissue under planar equi-biaxial tension loading, a specimen of the central region (10 mm × 10 mm) of the MVAL tissue was discretized into 400 (20×20) four-node membrane (M3D4) elements with a thickness of 0.422 mm, and uniform tractions were gradually applied on the four edges of the MVAL tissue from 0 to 150 N/m in order to simulate the experimental loading protocol. Adequate clamped boundary conditions were prescribed to avoid rigid-body motions in the FE numerical simulation. The mechanical behavior of the MVAL tissue was simulated by the following incompressible simplified structural model with an exponential form of the effective fiber ensemble stress, developed in our recent study (Fan and Sacks, 2014). This constitutive model was implemented in a user material subroutine in commercial finite element software ABAQUS 6.13 (SIMULIA, Dassault Systemes, Providence, RI, USA)

$${\mathbf{S}}_{\text{leaflet}}=\sum _{\mathrm{\xi }=1}^4\left\{{\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}{\mathrm{\mu }}_{\mathrm{m}}\right(\mathbf{I}-{\mathrm{C}}_{33}{\mathbf{C}}^{-1})+{\int }_{-\mathrm{\pi }/2}^{\mathrm{\pi }/2}{\mathrm{\Gamma }}^{\mathrm{\xi }}(\mathrm{\theta }){\mathrm{S}}_{\text{ens}}^{\mathrm{\xi }}[{\mathrm{E}}_{\text{ens}}(\mathrm{\theta }),{\mathrm{c}}_0,{\mathrm{c}}_1]\mathbf{N}(\mathrm{\theta })\otimes \mathbf{N}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }\},$$ (1)

Where

$${\mathrm{S}}_{\text{ens}}^{\mathrm{\xi }}[{\mathrm{E}}_{\text{ens}}(\mathrm{\theta }),{\mathrm{c}}_0,{\mathrm{c}}_1]={\mathrm{\varphi }}_{\mathrm{f}}^{\mathrm{\xi }}{\mathrm{c}}_0\left\{\text{exp}\right[{\mathrm{c}}_1{\mathrm{E}}_{\text{ens}}(\mathrm{\theta })]-1\}.$$ (2)

Here, S_leaflet is the total tissue second Piola-Kirchhoff stress tensor, c₀, c₁, and μ_m are material constants (Table 2). Physically, μ_m represents the non-fibrous tissue components or “matrix” effective shear modulus. Γ^ξ(θ) and ${\mathrm{S}}_{\text{ens}}^{\mathrm{\xi }}$ are the fiber angular orientation distribution function and the effective fiber ensemble stress, respectively, associated with each layer ξ. E_ens(θ)=N^T(θ)EN(θ) is the effective fiber ensemble strain, N(θ)=[cos(θ),sin(θ)]^T is the unit vector defining the common preferred fiber direction of the fiber ensemble at the reference configuration, E=(C−I)/2 is the Green-Lagrange strain tensor, C=F^TF is the right Cauchy-Green deformation tensor, F is the deformation gradient, I is the second-rank identity tensor, ${\mathrm{C}}_{33}=1/({\mathrm{C}}_{11}{\mathrm{C}}_{22}-{\mathrm{C}}_{12}^2)$ is determined as the consequence of the incompressibility condition, and ⊗ denotes dyadic tensor product. In addition, ${\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}$ and ${\mathrm{\varphi }}_{\mathrm{f}}^{\mathrm{\xi }}={\mathrm{\varphi }}_{\text{collagen}}^{\mathrm{\xi }}+{\mathrm{\varphi }}_{\text{elastin}}^{\mathrm{\xi }}$ are the layer-specific volume fractions of the matrix and effective fibers, respectively, determined from histological analysis data of the MVAL tissue as described in Section 2.4.

Table 2.

Material parameters of the simplified structural constitutive model for the ovine MVAL tissue

	ϕm	ϕf	μm (kPa)	c1 (kPa)	c2	σa (deg.)
MVAL Tissue	0.264	0.736	28.41	0.917	22.13	36.85

^aThe standard deviation of the fiber angular orientation distribution function was the direct measurement from the small angle light scattering (SALS) test from the previous study of the excised ovine MVAL tissues (Lee et al., 2014).

We assumed here that the matrix includes both non-fibrous substances and water, which is responsible for the low-tension (toe-region) response and the incompressibility of the planar tissue. It was also assumed that each layer has the same proportional mechanical response as those for the bulk MVAL tissue but varies in the microstructures, such as the material axial direction and fiber splay, and the layer-specific effective volume fractions of effective fibers and matrix ${\mathrm{\varphi }}_{\mathrm{f}}^{\mathrm{\xi }}$ and ${\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}$. As mentioned previously in Section 2.4, we employed a Gaussian distribution function with mean μ^ξ and standard deviation σ^ξ for the fiber angular orientation distribution function for each MVAL tissue layer

$${\mathrm{\Gamma }}^{\mathrm{\xi }}(\mathrm{\theta })=\frac{\text{exp}[-\frac{{(\mathrm{\theta }-{\mathrm{\mu }}^{\mathrm{\xi }})}^2}{2{\left({\mathrm{\sigma }}^{\mathrm{\xi }}\right)}^2}]}{\text{erf}\left(\frac{\mathrm{\pi }}{2\sqrt{2}{\mathrm{\sigma }}^{\mathrm{\xi }}}\right)\sqrt{2\mathrm{\pi }}{\mathrm{\sigma }}^{\mathrm{\xi }}}\text{with}{\int }_{-\mathrm{\pi }/2}^{\mathrm{\pi }/2}{\mathrm{\Gamma }}^{\mathrm{\xi }}(\mathrm{\theta })\mathrm{d}\mathrm{\theta }=1.$$ (3)

Nodal displacements and elemental stress and strain fields were the primary output data from this level of the FE simulations. Tissue-level stretches along the circumferential and radial directions (${\overline{\mathrm{\lambda }}}_{\mathrm{C}}$, ${\overline{\mathrm{\lambda }}}_{\mathrm{R}}$) were computed based on the in-plane strain tensor associated with the equi-biaxial stretching protocol described in Section 2.1. Tissue-level stretch in the transmural direction was then determined based on the incompressibility condition, i.e., ${\overline{\mathrm{\lambda }}}_{\mathrm{T}}=\mathrm{1/}{\overline{\mathrm{\lambda }}}_{\mathrm{C}}{\overline{\mathrm{\lambda }}}_{\mathrm{R}}$. Numerically predictions were compared with experimental measurements to characterize material parameters c₀, c₁, and μ_m associated with the constitutive model in Eq. (1) for the bulk MVAL tissues by iteratively minimizing the error of the stretch-tension relationship between the FE simulation results and the experimental data. This procedure was automatically performed using an in-house MATLAB program that generates ABAQUS input file with updated parameters, executes FE simulations, extracts data from ABAQUS output database file, analyzes the stretch-tension responses, and performs parameter estimation with general-purpose nonlinear optimization technique.

2.5.2 FE modeling of the MVIC microenvironment

To explore the relative role of layer-specific ECM mechanical properties and microstructural composition on the layer-specific MVIC deformations, we developed the following finite element model of the MVIC microenvironment (Fig. 5-b). The MVIC microenvironment for each of the four layers was idealized as a representative area element (RAE) of 100 µm × 100 µm embedded with 37 uniformly distributed, horizontally aligned ellipsoidal inclusions. Here, we assumed that the size of the chosen RAE is relatively small, yet representative, on the circumferential-radial plane compared to the characteristic dimensions of the MVAL tissues, and the selected number of ellipsoidal inclusions was justified by the spatial distribution of MVICs in the leaflet based on our experimental observations. The MVIC geometry was simulated by an ellipsoidal inclusion with layer-specific dimensions based on the measurements from Section 2.3 (Table 1). The following considerations were made in this level of the FE simulations:

1. Layer-specific ECM mechanical responses were modeled by a structural constitutive model similar to the one used for FE simulations of the MVAL tissue under equi-biaxial tension in Section 2.5.1 (c.f. Eq. (1)) with considerations of layer-specific volume fractions of non-fibrous matrix and collagenous fibers (${\mathrm{\varphi }}_{\mathrm{m}}^{\mathrm{\xi }}$ and ${\mathrm{\varphi }}_{\mathrm{f}}^{\mathrm{\xi }}$) and layer-specific preferred fiber direction as well as fiber splay (Γ^ξ(θ)).

2. The MVIC mechanical responses were modeled by a Saint-Venant Kirchhoff material, which is an extension of the linear elastic model to the nonlinear, large-deformation regime:

   $${\mathbf{S}}_{\mathrm{M}\mathrm{V}\mathrm{I}\mathrm{C}}^{\mathrm{\xi }}={\mathrm{\lambda }}^{\mathrm{\xi }}\mathrm{t}\mathrm{r}(\mathbf{E})\mathbf{I}+2{\mathrm{\mu }}^{\mathrm{\xi }}\mathbf{E}$$ (4)

   where λ^ξ and μ^ξ are the material constants associated with each individual layer that can be related to the infinitesimal strain theory material constants E^ξ and ν^ξ ~0.5 using E^ξ = μ^ξ (3λ^ξ + 2μ^ξ)/(λ^ξ + μ^ξ) and ν^ξ = λ^ξ/2(λ^ξ + μ^ξ) (Simo and Hughes, 1998).

3. The interfaces between the MVICs and MVAL ECM were assumed to be perfectly bonded with no interfacial debonding nor slipping (Huang et al., 2007), as illustrated in the transmission electron microscopy (TEM) image of the MVIC microenvironment in the fibrosa layer (Fig. 1-c).

4. Consistent with related work on valvular tissues (Buchanan and Sacks, 2013), the MV leaflet tissue was considered as four perfectly bonded layers so that the layers were deformed homogeneously according to the tissue-level deformations. One plane-stress finite element RAE model was built for each layer, in which the thickness of the MVIC region for each layer was specified as the dimension of the third ellipsoidal axis based on the initial nuclear aspect ratio (L_c=L_a*NAR₀) and twice of this thickness was adopted for the MVAL ECM region. The typical RAE finite element model for the MVIC microenvironment has about 26,500 nodes and 26,600 elements.

5. Tissue-level stretches in the circumferential and radial directions (${\overline{\mathrm{\lambda }}}_{\mathrm{C}}$, ${\overline{\mathrm{\lambda }}}_{\mathrm{R}}$), determined at the previous tissue-level FE simulation stage (Section 2.5.1), were applied as incremental nodal displacements on the four edges of the RAE model to mimic the tissue forces acting on the MVIC microenvironment.

Displacement and strain fields were the primary output from this level of FE modeling for the MVIC microenvironment. The parameter estimation described in Section 2.5.1 was employed to characterize the material constant of the MVIC for each of the four layers. In brief, the effective layer-specific MVIC NAR as a function of applied tension was computed based on the three principal stretches (λ_C, λ_R and λ_T=1/ λ_Cλ_R) averaging over the elements within each of the 37 ellipsoidal inclusions. The numerically predicted NAR-tension response was then compared to the experimental measurements, and layer-specific MVIC modulus E^ξ was determined by iteratively minimizing the difference between the numerical and experimental NAR-tension relationships.

3. Results

3.1 MVIC deformation analysis

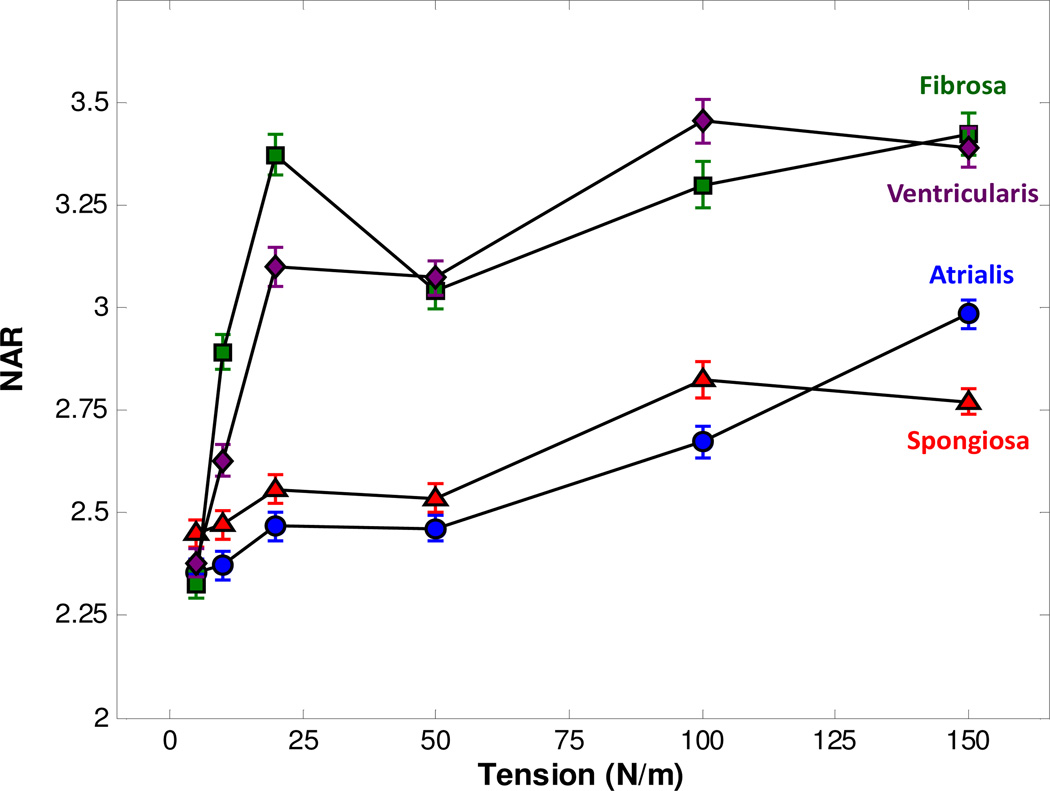
The MVICs in the fibrosa and ventricularis layers had a noticeably larger deformation than those in the atrialis and spongiosa layers, reaching a NAR of 3.3 at the maximum physiological loading (Fig. 6). The deviations for each layer were large, indicating that there was a large amount of variation in deformation that the MVICs were experiencing in each layer. This discrepancy in the magnitude of layer-specific MVIC deformations may correspond to localized cell compaction due to different mechanisms of straightening and realigning of collagen and elastin fiber networks in each of the four layers, which ceased at the tension level of 25–30 N/m (Carruthers et al., 2012b). We also found that MVICs have an intrinsic ellipsoidal configuration with a NAR of ~2.5 at the unloaded state (T = 0 N/m).

Figure 6.

MVAL layer-specific MVIC NAR as a function of applied biaxial tension, derived from MPM analysis.

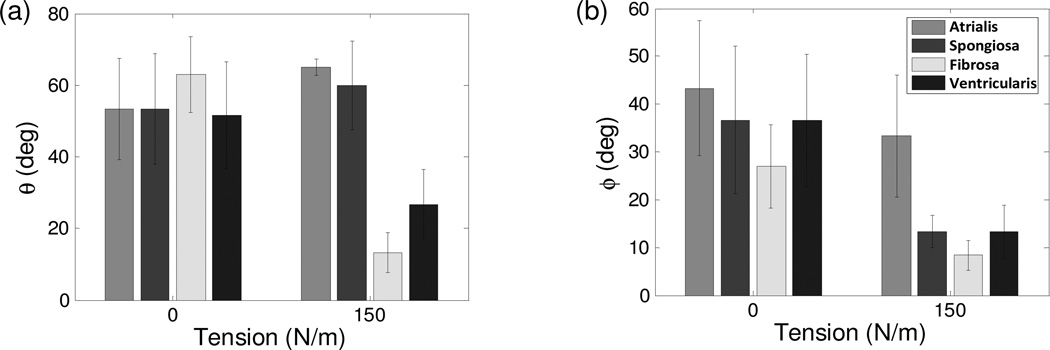
By comparing layer-specific MVIC orientation as a function of tension, we observed that reorientation occurs as a function of MVAL tissue layer (Fig. 7-a,b). This layer-specific discrepancy may be due to distinct microstructural compositions, ECM architecture, and the mismatch of material properties between the ECM, and MVIC for the four MVAL layers. At the unloaded state, the MVICs were not well oriented with large standard errors. At the maximum tension, the MVICs in the fibrosa and ventricularis layers oriented towards the circumferential direction, whereas the MVICs in the atrialis and spongiosa layers re-oriented towards the radial direction. As expected, the MVIC populations tend to re-orient along the preferred fiber direction of their respective layers (Carruthers et al., 2012b). Moreover, there was also reorientation of the MVIC population in the circumferential-radial plane, also referred to as in-plane deformation, except for the MVICs in the atrialis layer. This may correspond to the opposite directions of the collagen sheet orientation for the atrialis and fibrosa layers. These findings suggest that MVIC deformation is more dependent on valvular layer structure than on the bulk tissue-level deformations.

Figure 7.

(a,b) measured layer-specific orientation angles θ and ϕ at the unloaded configuration (0 N/m tension) and at the maximum loading state (150 N/m tension).

3.2 Finite element simulation results

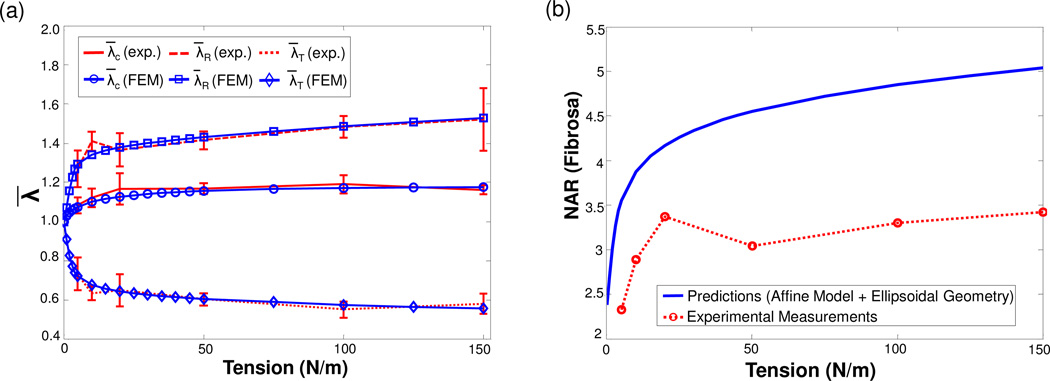
The measured tissue-level stretches in the circumferential and radial directions gradually increased with applied loading (Fig. 8-a), with the circumferential stretch remaining almost constant beyond the level of ~30 N/m tissue-level tension and the radial stretch continued to increase monotonically. Numerical predictions of the tissue-level deformations matched the experimental data very well; at 150 N/m tension the numerically predicted tissue-level stretches were ${\overline{\mathrm{\lambda }}}_{\mathrm{C}}^{\mathrm{F}\mathrm{E}\mathrm{M}}=1.177$ and ${\overline{\mathrm{\lambda }}}_{\mathrm{R}}^{\mathrm{F}\mathrm{E}\mathrm{M}}=1.528$ in the circumferential and radial directions, respectively, whereas the experimental measurements were ${\overline{\mathrm{\lambda }}}_{\mathrm{C}}^{\text{EXP}}=1.16\pm 0.04,{\overline{\mathrm{\lambda }}}_{\mathrm{R}}^{\text{EXP}}=1.52\pm 0.16$.

Figure 8.

(a) Comparison of the tissue-level deformations in terms of the three principal stretches between the experimental measurements and the FE predictions under equi-biaxial tension loading (r² = 0.9896), and (b) comparison of the fibrosa-layer MVIC NAR as a function of tissue-level tension between the experimental measurement and the calculation based on a simple affine model and an assumed ellipsoidal cellular geometry, indicating that local MVICs do not simply follow the deformation of the bulk MVAL tissue.

As a further exploration of the interrelationships between tissue and cellular deformations, we directly applied the measured tissue-level deformations (${\overline{\mathrm{\lambda }}}_{\mathrm{C}}^{\text{EXP}},{\overline{\mathrm{\lambda }}}_{\mathrm{R}}^{\text{EXP}},{\overline{\mathrm{\lambda }}}_{\mathrm{T}}^{\text{EXP}}$), assuming an ellipsoidal cellular geometry. In the calculation, we used this relation $\mathrm{N}\mathrm{A}{\mathrm{R}}_{\text{Tension}}^{\text{Fibrosa}}=({\overline{\mathrm{\lambda }}}_{\mathrm{C}}^{\text{EXP}}/{\overline{\mathrm{\lambda }}}_{\mathrm{T}}^{\text{EXP}})\times \mathrm{N}\mathrm{A}{\mathrm{R}}_0^{\text{Fibrosa}}$ to predict the NAR of the MVIC in the fibrosa layer. Clearly, the results from this simulation for the fibrosa layer deviated significantly from the experimental measurements (Fig. 8-b). This observation indicates that local MVIC deformations did not simply follow tissue-level deformations, although each layer was assumed to deform homogeneously with the MVAL bulk tissue. This result also reinforces the need for adopting the proposed macro-micro computational model for investigating local MVIC deformations induced from tissue-level forces.

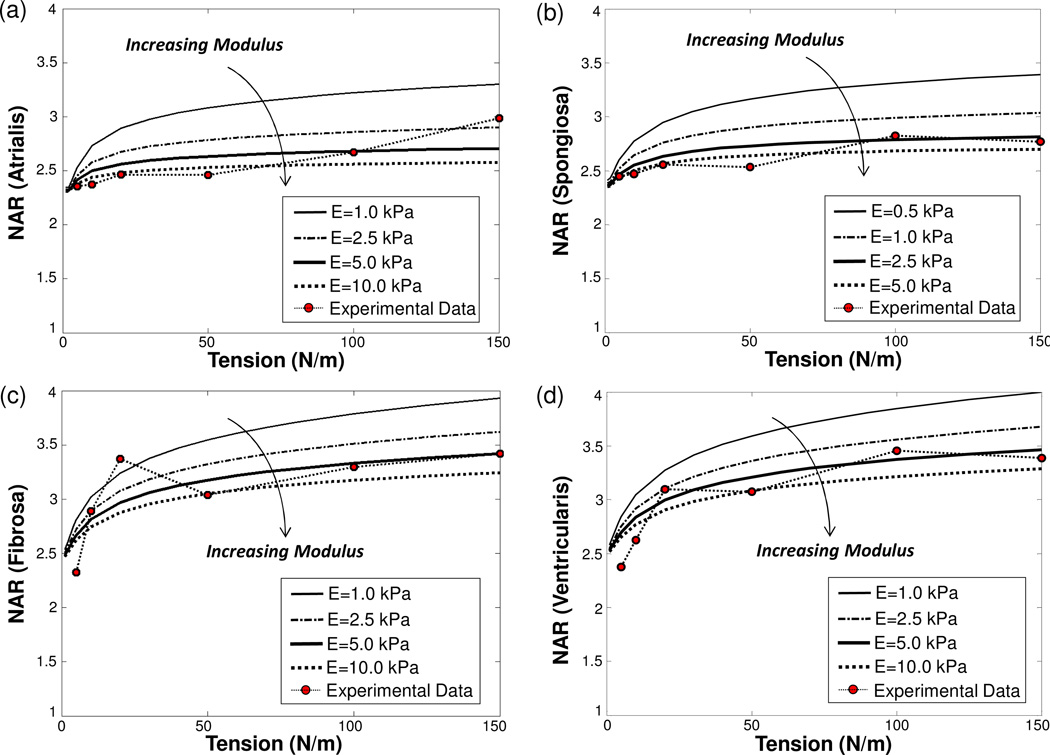
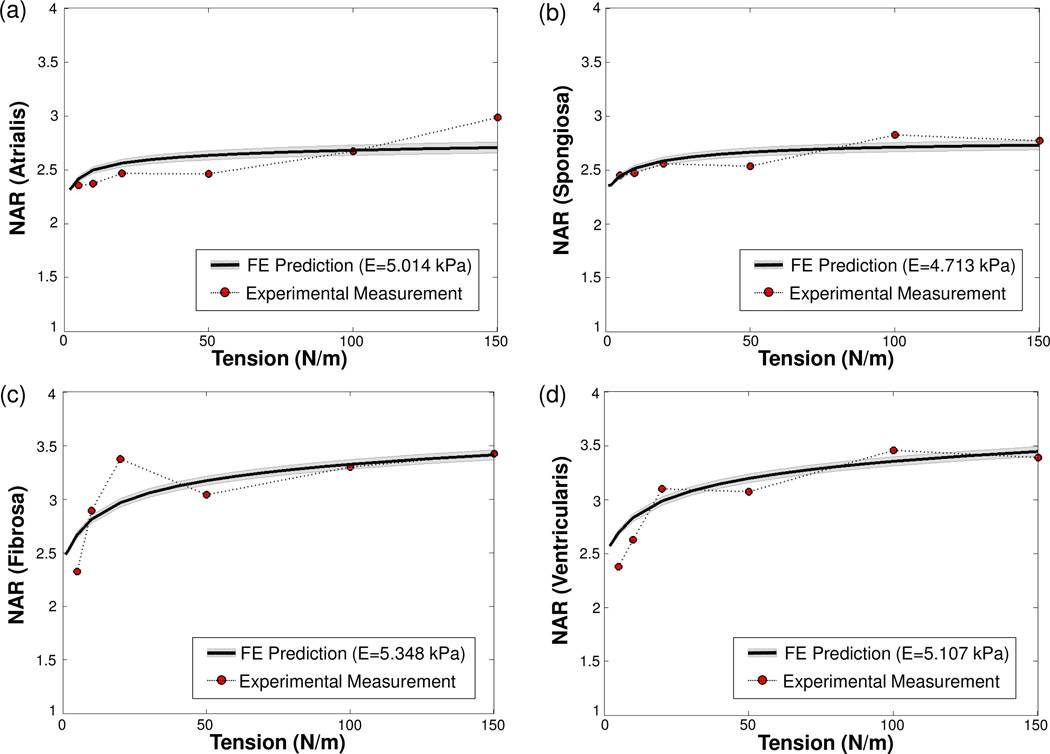
Moreover, numerically predicted NARs from the FE simulations of the MVIC microenvironment decreased as the MVIC modulus increased for the four MVAL layers (Fig. 9a–d). This increase in MVIC modulus produced anisotropic changes in the MVIC deformations, i.e., five times larger of the MVIC modulus resulted in ~3% decrease in the circumferential stretch, ~12% decrease of the radial stretch, and ~16% increase of the transmural stretch at the maximum physiological loading of 150 N/m, leading to the observed reduction of the predicted NARs. The MVIC moduli for the four layers were characterized by matching the NAR-tension curves to the experimental measurements, and they were reported as follows: E^Atrialis=5.014 kPa, E^Spongiosa =4.713 kPa, E^Fibrosa=5.348 kPa, and E^{Ventricularis}=5.167 kPa (Fig. 10a–d). These findings suggest that the MVICs may be phenotypically and biomechanically similar throughout the leaflet and more importantly that layer-specific local MVIC deformations in response to tissue-level mechanical stimuli are primarily controlled by each layer’s respective structure and mechanical behavior rather than the intrinsic MVIC stiffness.

Figure 9.

Studies on the effect of the MVIC modulus on the predicted NARs: (a) atrialis layer, (b) spongiosa layer, (c) fibrosa layer, and (d) ventricularis layer.

Figure 10.

Comparisons of the experimentally measured and numerically predicted NARs as a function of tissue-level tension (grey shaded area showing the standard deviation of the computed NARs over the 37 MVIC ellipsoidal inclusions): (a) atrialis layer (r² = 0.8403), (b) spongiosa layer (r² = 0.9166), (c) fibrosa layer (r² = 0.8906), and (d) ventricularis layer (r² = 0.9373).

4. Discussion

4.1 Main findings

As in all soft tissues, the valvular ECM is a dynamic environment composed mainly of fibrous proteins that are continuously degraded and replaced. Perturbations to this system have been shown to be associated with aging and disease (Aikawa et al., 2006; Rabkin-Aikawa et al., 2004; Rabkin et al., 2001; Stephens et al., 2011; Stephens et al., 2010b). In order to better understand the mechanical behavior and remodeling of the MV, it is necessary to gain insight into MVIC mechanobiology, particularly on how MVIC biosynthesis is modulated by organ-level mechanical stimuli. Moreover, there is still a lack of understanding of how local forces are transduced to MVICs from tissue-level mechanical loading. Using MPM imaging and 3D image reconstruction, we demonstrated in this study that MVICs experience layer-specific deformations under controlled physiological biaxial tension loading. We also found that the MVICs in the fibrosa and ventricularis layers undergo larger deformations than the MVICs in the atrialis and spongiosa layers. Moreover, the MVICs in the atrialis layer are more likely to re-orient towards the radial direction in parallel to the collagen fibers in that layer, whereas the MVICs in the fibrosa layer tend to re-orient towards the circumferential direction in accordance with the collagen fiber direction in that layer.

These experimental observations were simulated in a macro-micro computational modeling framework that allowed linking tissue-level mechanical responses to the MVIC-ECM microenvironment. In general, the FE simulated MVIC NARs under tissue-level loading for four different layers were in fairly good agreement with the experimental measurements (Fig. 10a–d). On the other hand, the estimated MVIC NAR-tension response based on a simple affine transformation model and an ellipsoidal cellular geometry deviated significantly from the experimental data. The discrepancies were found to be due to the inability of this simple affine deformation model to capture the local MVIC behaviors. Thus, one important finding in the present study is that the MVICs act as distinct inclusions and do not simply deform convectively with the bulk tissue. Another important observation is that the MVIC moduli for all four layers were all within the range of 4.71–5.35 kPa. This suggests that layer-specific MVIC responses are primarily governed by layer-specific mechanical behaviors, which are a function of their microstructural compositions, level of anisotropy, and fiber architecture. The estimated MVIC moduli in this work also agreed reasonably with previous experimental measurements of heart valve interstitial cell stiffness, such as 0.3–0.5 kPa for fully deactivated VICs via the micropipette aspiration technique (Merryman et al., 2006b) and 50–60 kPa for highly activated VICs via atomic force microscope (Merryman et al., 2007).

Both experimental measurements and numerical simulation results presented in this study indicate that MVIC deformation is dominated by layer-specific anisotropy and preferred fiber direction. This highlights the connection between organ-level loads and cellular deformations as a function of ECM fiber (mainly collagen and elastin) networks. In addition, from the parametric study of the effect of MVIC stiffness on the predicted NAR-tension response, we found that an increase in MVIC modulus leads to a relatively smaller decrease in MVIC stretches in both circumferential and radial directions compared to the larger decrease in the transmural stretch. As a result, the NAR-tension profile acquired from tissue-level responses becomes closer to the experimentally measured MVIC deformations (Fig. 9a–d). This suggests that the mechanical properties of both MVAL tissue and MVICs play an important role in accurate numerical modeling of the MVIC microenvironment in response to tissue-level mechanical stimuli.

4.2 Implications and comparisons with relevant research

As alluded to previously, it is essential to incorporate cell-level phenomena, such as protein biosynthesis and enzymatic degradation that affect tissue mechanical behaviors, into organ-level computation models for accurate simulations of the time course changes in heart valve function. It is also necessary to link cellular phenotypic and biophysical state to MV pathologies in order to fully understand how alterations in valve leaflet regional stresses and the induced mechanical stimuli lead to local changes in cellular mechanotransduction and mechanobiology and how those changes at the microscopic level, in turn, affect the subsequent adaption of tissue layer compositions and maintenance of overall tissue homeostasis. Although existing MV constitutive models (May-Newman and Yin, 1998; Prot et al., 2007; Sun and Sacks, 2005; Weinberg and Kaazempur-Mofrad, 2006; Weinberg and Kaazempur Mofrad, 2007) provide a rational basis for finite element simulations of MV mechanics, the underlying physiological changes that occur at the cellular level in response to tissue-level mechanical stimuli have not yet been included. Therefore, the present work is the first of its kind for investigating cellular behaviors in the MV leaflet tissues as a function of ECM architecture by considering the driving forces associated with layer-specific microstructural constituents, fiber architecture, and material anisotropy. In addition, the proposed integrated computational-experimental framework is applicable to other heart valves and can be implemented by incorporating appropriate leaflet tissue properties and utilizing the proposed real-time imaging technique to monitor VIC deformations under controlled physiological loading. These studies will also provide guidance for the design of the surgical repair procedures, through emulation of the biosynthetic and remodeling processes of the native, healthy heart valves.

The current findings show that although MVICs may be phenotypically similar in each layer, they experience different mechanical stimulatory inputs due to distinct ECM architecture and microstructure of the four MVAL tissue layers and may, as a result, secrete different ECM components. This further suggests a way to regulate tissue layer compositions by the VICs for achieving overall tissue homeostasis. In an earlier study on the aortic valve, serial histological section images were used to measure VIC deformations (Huang et al., 2007). A 2D representative volume area model of one homogeneous single fibrosa layer and a single aortic valve interstitial cell (AVIC) was developed. However, layer-specific microstructural compositions, fiber architecture and material anisotropy were not incorporated in the numerical modeling. Moreover, the predicted local AVIC and overall tissue peak stretches were 1.053/1.014 in the circumferential direction and 1.655/1.500 in the radial direction, showing that the AVIC almost follows tissue deformations; however, the MVIC and tissue-level peak stretches our model predicted were 1.126/1.188 in the circumferential direction and 1.127/1.422 in the radial direction, indicating that the MVIC are significantly different from the tissue-level deformations. Moreover, it was also found in the previous study on the semilunar heart valves (Carruthers et al., 2012a) that the NAR of the aortic VICs in the fibrosa layer reached a saturated value of 5.95 at the maximum transvalvular pressure, whereas the pulmonary VICs in the fibrosa layer underwent significantly greater changes in cellular deformation and reached a NAR of 9.66 at the maximum transvalvular pressure. While the underlying mechanobiology has not been fully understood, this observation along with the findings from this study suggest that the microenvironment of the fibrosa layer provides additional stress shielding for the VICs under high tissue stresses in the MV leaflets compared to those VICs in the semilunar heart valves.

Related ideas have been explored by other groups in the dynamic fluid-structure interaction simulations for studying aortic valve biomechanics (Weinberg and Mofrad, 2007; Weinberg and Kaazempur Mofrad, 2008; Weinberg et al., 2010). However, layer-specific microstructural compositions, fiber architecture, and material anisotropy were not fully considered in their tissue-level simulations, and the numerically predicted layer-specific VIC deformations were not validated with experimental data. Clearly, there still remains a need for quantitative data of layer-specific biosynthetic changes that occur in the MVIC microenvironment to be integrated into the development of a bi-directional, multi-scale finite element computational framework towards physiologically realistic modeling of MV function and pathophysiology.

4.3 FE model for the MVIC microenvironment

We further examined the appropriateness of the proposed FE model by comparing the predicted NARs of the MVICs residing in the fibrosa layer: (i) between a Saint-Venant Kirchhoff material as shown in Eq. (4) and a more commonly adopted neo-Hookean material in biomechanics research, S_MVIC=μ(I−C₃₃C⁻¹), for the MVIC regions, and (ii) between 37 populated MVICs and a single MVIC (Table 3).

Table 3.

Comparisons of the MVIC NAR-tension responses in the fibrosa layer between the experimental data and numerical predictions with various considerations of the finite element model setup

Interstitial Cell Representation		37 Uniformly Distributed MVICsa		Single MVIC with the Same Cell Volume Fraction	Experimental Measurements
Material Model for MVIC Regions		Saint-Venant Kirchhoff (E = 5.348 kPa)	Neo-Hookean (μ = 1.783 kPa)	Saint-Venant Kirchhoff (E = 5.348 kPa)
Tension (N/m)	5	2.661±0.031	4.299±0.088	2.718	2.325±0.0319
	10	2.804±0.038	4.671±0.101	2.831	2.891±0.0424
	20	2.999±0.041	5.038±0.103	2.963	3.372±0.0503
	50	3.156±0.042	5.579±0.105	3.146	3.039±0.0421
	75	3.243±0.043	5.863±0.109	3.227	–
	100	3.305±0.044	6.093±0.116	3.285	3.298±0.0568
	125	3.352±0.045	6.291±0.124	3.328	–
	150	3.391±0.046	6.469±0.132	3.363	3.422±0.0512

^aThe mean NAR and its standard deviation were obtained from the deformation states of the 37 populated cells.

First, we noted in particular that the neo-Hookean material model even with a nonphysical value for μ of 2,000 kPa was not able to capture accurate MVIC mechanical response. The discrepancy in different material model forms could be explained by the nature of the stress-strain behaviors of these two material models, i.e., linearly increasing stress-strain curves for the Saint-Venant Kirchhoff material and concave stress-strain curves for the neo-Hookean material, under substantially large strain of ~15% for the MVICs. In addition, we observed from our numerical results that the 2D plane-stress formulation with the incompressibility condition automatically enforced is able to accurately predict both in-plane deformations (λ_T and λ_R) and the compaction in the transmural direction (λ_T), which faithfully mimics the real 3D ellipsoidal geometry and deformation of the MVICs. Furthermore, we also found in our numerical studies that the aligned angle of the cells and its in-plane rotation did not play a significant role in capturing the overall behavior of the MVICs, suggesting that the assumption of perfectly aligned ellipsoidal inclusions within the RAE model was a reasonable approximation in our FE simulations. Finally, the numerical predictions from the RAE model with 37 cells and from the model with a single cell at the center were not significantly different, since the cell volume fractions in both RAE models and the inclusion geometry and orientation are the same, leading to the same homogenized or effective RAE behaviors and properties, which are the averaged cell deformations in our case (Mura, 1987), based on the micromechanics theory as well as its extension for nonlinear materials and finite-strain regime using second-order homogenization techniques (Lopez-Pamies and Castaneda, 2004; Ponte Castaneda, 2002).

4.4 Relation to other tissues and VIC mechanotransduction

The ECM not only provides the tissue with its structural integrity, but it also influences cellular processes via three different mechanisms: (i) matricellular, in which the ECM signals through adhesion receptors, (ii) matricrine, which regulates the growth factor and cytokine expression in cells, and (iii) mechanical, which can be characterized as matrix elasticity or external forces (Chen and Simmons, 2011). The link between tissue-level mechanical responses, cellular deformations, and ECM remodeling is essential in understanding MV diseases and pathologies. A normal mechanical environment results in constant tissue structural integrity, whereas altered loading conditions may lead to dysfunction and disease. In cardiac muscle, cardiomyocytes have the ability to sense mechanical stimuli and convert themselves into intracellular growth signals, leading to hypertrophy (Sadoshima and Izumo, 1997). Similarly, the MV compensates for the ventricular remodeling, which typically occurs after left ventricular infarction, and becomes regurgitant (Dal-Bianco et al., 2009), while the MVICs have increased the α-SMA levels, indicating cellular activation.

The fundamental relationship between tissue- and cellular deformations has been investigated in other tissues, such as tendon, ligament, bone and cartilage repair. Soslowsky studied tendons at both tissue and cellular levels (Dunkman et al., 2013a; Dunkman et al., 2013b) and demonstrated that aged patellar tendons result in changes in the functional activity, tissue architecture, tenocyte shape, and collagen fiber alignment. These changes were found to be regulated by ECM proteoglycans (PGs), decorin and biglycan, which have a decreased expression in aged tendons (Robinson et al., 2004; Robinson et al., 2005). Similarly, mechanical stimuli were found to alter the homeostatic balance between collagen biosynthesis and catabolism. Guilak investigated the effects of static and dynamic compression on the meniscal cell gene expression and found that types I and II collagen fibers as well as decorin are regulated by common mechanical stimuli (Upton et al., 2003).

VICs sense and transduce extracellular mechanical stimuli, such as stretch, shear stress and pressure, into intracellular biomechanical signals directly and indirectly through several mechanisms that include receptors, ion channels, caveolin, G proteins, cell cytoskeleton, kinases, and transcriptional factors (Li and Xu, 2000). These signals are processed and sorted by molecules on the cell surface, resulting in the cell response by a network of intracellular signaling pathways. Mechanical stimuli were found to activate the mitogen-activated-protein (MAP) kinase pathway, which controls gene expression (Schmidt et al., 1998). Integrins, which are the signal receptors that physically link the cell surface to the surrounding ECM, play an important role in cellular mechanotransduction, particularly in response to physiological and pathophysiological signals.

Mechanical forces modulate cell physiology and affect the biosynthetic activities of cells in the tissue. In many valve pathologies, significantly altered profiles of ECM components accompany the alterations in the mechanical strains within the tissues (Grande-Allen et al., 2003; Quick et al., 1997; Stephens et al., 2008). These measured differences initiated numerous in-vitro studies to fully characterize and link tissue-level deformation to cellular response. Static and cyclic tissue strains can profoundly influence the phenotypic and biosynthetic responses of VICs in vitro and modulate cell function through the biosynthesis of glycosaminoglycans and proteoglycans (Gupta and Grande-Allen, 2006; Gupta et al., 2009), an increase in α-SMA expression and non-muscle embryonic myosin (Lacerda et al., 2012), and the degradation of extracellular matrix components by proteolytic enzymes, matrix metalloproteases (MMP), tissue inhibitors of MMPs, and cathepsins. These changes indicate an enhancement of the activated and contractile phenotype of VICs (Balachandran et al., 2009a; Balachandran et al., 2006a) and can further lead to cellular proliferation and apoptosis that are typically responsible for valve degeneration and disease.

Collectively, these studies suggest the substantial effect of tissue-induced cellular deformations on the regulation of VIC mechano-biological responses. Moreover, excessive tissue stresses caused by surgical repair of the MV can lead to microstructural and cellular changes that in turn, affect the long-term durability of valve repair (Gillinov et al., 2001). There is thus a need to fully understand and link organ-level deformations to the biosynthetic changes that occur at the cellular level. This will enable the development of multi-scale approaches to tissue modeling for better understanding of the relation between MVIC deformation and biosynthetic state that is important in maintaining overall tissue homeostasis. Understanding this functional relation will be helpful for elucidating valvular pathologies, and will eventually lead to a more reasonable basis for the design of improved surgical repair procedures.

4.5 Limitations

The performed FE simulations were based on experimental data collected in viable valve tissues. While we have shown that our hypothermosol preparation maintains cell viability (Merryman et al., 2004; Merryman et al., 2009; Merryman et al., 2006c), the present technique required fixation of the tissue at various loaded states. It is possible that during this process some additional deformation occurred, although no detectable changes in specimen dimensions were observed in the experiments. Regardless, such additional deformations if they exist, would be systematic and would not appreciably affect the present results.

Next, it was assumed in the FE simulations of the MVIC microenvironment that the MVAL ECM region was modeled using a similar constitutive model form to the one for the MVAL tissues with considerations of the known preferred fiber directions, mass fractions of ECM and fibers, and the measured level of fiber alignment in each of the four layers. A more realistic layer-specific constitutive model may be adopted as future extensions once the data of the mechanical responses of each separated layer for the MV leaflet tissues, similar to the work for the aortic valve tissue (Stella and Sacks, 2007), becomes available. Moreover, the stress-strain behavior was simplified by using an effective fiber representation in the structural constitutive model. Further information may be incorporated to develop a full-blown structural constitutive model, which accounts for the contributions of elastin fibers and collagen fibers separately. Nevertheless, adopting the current structural constitutive model for the MVAL ECM yielded good predictions of local MVIC deformations compared to our measurements for all four layers, indicating that the above assumptions in the FE simulations served as a reasonable approximation.

Finally, the structural model can provides valuable insight into tissue function by integrating the microscopic fiber structure, kinematics, and structural adaptions into the stress-strain behaviors. This stands in contrast to conventional invariant-based constitutive models (May-Newman and Yin, 1998; Prot et al., 2007) and Fung-type constitutive models (Fung, 1993), which are phenomenological models whose parameters lack physical meanings. Despite these advantages, issues associated with efficient numerical integration of the fiber-splay in Eq. (1) still remains and may limit its applications to large-scale modeling of soft tissue and related tissue biomaterials. To address this in the present work, we constructed a global array at the pre-calculation stage in ABAQUS UMAT which stores all necessary information about the numerical integration, including fiber angle θ_j, integration weight w_j, and its respective values of fiber angular distribution function Γ(θ_j), and trigonometric functions for computing N vector and N⊗N matrix for all 100 Gauss quadrature points between −π/2 and π/2. The CPU time for simulating the MVIC microenvironment using this implementation was significantly reduced by ~30% compared to the direct implementation, which computes those values for each Gauss quadrature point at runtime. The computational efficiency can be further improved by carrying out the close-form expression for the integral in Eq. (1) similar to the previous work for the π-periodic von Mises fiber distribution (Raghupathy and Barocas, 2009). However, such extensions are limited to simple forms and cannot account for the increasing complex microstructures currently being developed in our lab that will be presented in the forthcoming publications.

4.6 Summary

In the present study, we employed an integrated computational-experimental approach to quantify and simulate layer-specific cellular deformations across the MV anterior leaflet tissue under controlled physiological tension loading. The similarity of predicted MVIC mechanical properties suggests a similar phenotypic state for the VICs regardless of layer location, and potentially a similar homeostatic state for all layers as well. These results underscore the essential role played by layer-specific microstructural compositions and fiber architecture in the underlying MVIC deformations. This work can be utilized to provide insightful information about MV function and behavior across multiple length scales in response to mechanical stimuli, specifically, the stress overload induced by mitral valve disease and surgical repair, and eventually to investigate the effect of cellular deformations on collagen biosynthesis. This important piece of information can in turn, be used to establish the interrelationship between cellular deformations and tissue-level mechanical behaviors that maintains the homeostasis of the functioning MV. The proposed macro-micro computational framework will be beneficial in the future when integrated with organ-level, structurally accurate finite element models to investigate MV pathophysiology and disease progression as a function of MVIC mechanobiology and ECM architecture, and ultimately to improve MV surgical repair procedures by enhancing the long-term durability.

Highlights.

• Layer-specific local MVICs do not simply follow MVAL bulk tissue deformations

• Cellular deformations are a function of the ECM collagen and elastin fiber networks

• ECM & MVIC properties are critical for accurate modeling the MVIC microenvironment