Normalization of RNA-seq data using factor analysis of control genes or samples

Abstract

Normalization of RNA-seq data has proven essential to ensure accurate inference of expression levels. Here we show that usual normalization approaches mostly account for sequencing depth and fail to correct for library preparation and other more-complex unwanted effects. We evaluate the performance of the External RNA Control Consortium (ERCC) spike-in controls and investigate the possibility of using them directly for normalization. We show that the spike-ins are not reliable enough to be used in standard global-scaling or regression-based normalization procedures. We propose a normalization strategy, remove unwanted variation (RUV), that adjusts for nuisance technical effects by performing factor analysis on suitable sets of control genes (e.g., ERCC spike-ins) or samples (e.g., replicate libraries). Our approach leads to more-accurate estimates of expression fold-changes and tests of differential expression compared to state-of-the-art normalization methods. In particular, RUV promises to be valuable for large collaborative projects involving multiple labs, technicians, and/or platforms.

Normalization is a crucial step in the analysis of RNA-seq data, having a strong impact on the detection of differentially expressed (DE) genes ^1–3. In the last few years, several normalization strategies have been proposed to correct for between-sample distributional differences in read counts, such as differences in total counts, i.e., sequencing depths ^1,4, and within-sample gene-specific effects, such as gene length or GC-content effects ^2,5. Although there have been efforts to systematically compare normalization methods ^1,3,6, this important aspect of RNA-seq analysis is still not fully investigated or resolved. In particular, when data arise from complex experiments, involving, for instance, cell sorting, low-input RNA or different batches (e.g., multiple sequencing centers or different read lengths), there may be more to correct for than simply differences in sequencing depths; we refer to such typically unknown nuisance effects as unwanted variation.

One largely unexplored direction is the inclusion of spike-in controls in the normalization procedure. Controls have been successfully employed in microarray normalization, for mRNA arrays ^7,8 and, more recently, microRNA arrays ⁹. One of the advantages of using negative controls in the normalization procedure is the possibility of relaxing the common assumption that the majority of the genes are not DE between the conditions under study. This assumption can be violated when a global shift in expression occurs between conditions ^9–11; in this case, control-based normalization may be the only option.

Recently, the ERCC developed a set of RNA standards for RNA-seq ^12,13. This set consists of 92 polyadenylated transcripts that mimic natural eukaryotic mRNAs. They are designed to have a wide range of lengths (250–2,000 nucleotides) and GC-contents (5–51%) and can be spiked into RNA samples prior to library preparation at various concentrations (10⁶-fold range). We refer to these standards as ERCC spike-in controls.

Lovén et al. ¹¹ make use of the ERCC spike-in controls in their normalization approach in the context of a global expression shift. Their procedure may be summarized as follows: (i) count the number of cells in each sample; (ii) add the ERCC spike-in sequences to each sample in proportion to the number of cells; (iii) normalize read counts based on cyclic loess regression ¹⁴ on the spike-in counts. Although their approach does not make any assumptions concerning differences in gene expression between samples, it relies on another equally important assumption: technical effects should affect the spike-ins in the same way as the genes. If, for instance, some library preparation step affects spike-in and gene counts differently, then normalization based on the spike-ins may incorrectly adjust the expression measures for the bulk of the genes. Unfortunately, the dataset used by the authors to illustrate their approach lacks both technical and biological replication, making it impossible to quantify the extent of variation of the spike-ins and its relation to gene variation ¹¹.

Recently, Qing et al. ¹⁵ showed that the percentage of RNA-seq reads mapping to the ERCC spike-ins varies substantially between technical replicate samples and can be markedly different from the nominal value. Moreover, the dependence of spike-in read counts on the poly(A) selection protocol (polyA+ vs. RiboZero) suggests that poly(A) selection may play a role in spike-in detection. Given the growing interest in the ERCC spike-in standards, it is essential to evaluate their performance, with particular focus on their inclusion in normalization procedures.

In this paper, our aim is two-fold. We propose a normalization strategy for RNA-seq, remove unwanted variation (RUV), that uses factor analysis to adjust for nuisance technical effects, based on counts (or residuals counts) for either negative control genes or negative control samples, i.e., genes or samples that are not expected to be influenced by the biological covariates of interest. We also evaluate the behavior of the ERCC spike-in controls in two very different datasets, involving different organisms and designs, and explore the possibility of using them as controls for normalization. We show that the spike-ins are not reliable enough to be used in standard global- scaling or regression-based normalization procedures. We further demonstrate that RUV, whether based on controls or not, generally outperforms state-of-the-art normalization approaches in context of differential expression inference. In particular, it improves upon other control-based methods and is thus promising when relying on controls is the only option (e.g., in case of global expression shift).

Results

Datasets

To evaluate the performance of the ERCC spike-in controls and to validate our RUV normalization strategy, we consider two very different datasets (see Methods). The first dataset is part of a benchmarking study by the SEquencing Quality Control (SEQC) consortium ¹⁶ and compares two commercial RNA samples, Stratagene's universal human reference RNA (Sample A) and Ambion's human brain reference RNA (Sample B). This dataset is valuable for assessing normalization methods, as there are several technical replicates for each of Sample A and B, both at the library preparation and sequencing levels, and one can rely on external controls from qRT-PCR ¹⁷. However, the absence of biological replication and the extreme difference between Sample A and Sample B make the data rather artificial and a more realistic and biologically meaningful dataset is required to confirm our findings. To this end, we use data from our recently published experiment ¹⁸. Briefly, RNA-seq was performed on three treated and three control zebrafish samples, each corresponding to a single FACS (fluorescence activated cell sorting) run on pools of cells from different fish. Here, cell sorting and library preparation effects are confounded with biological variability between pools of fish cells.

Unwanted variation in RNA-seq data

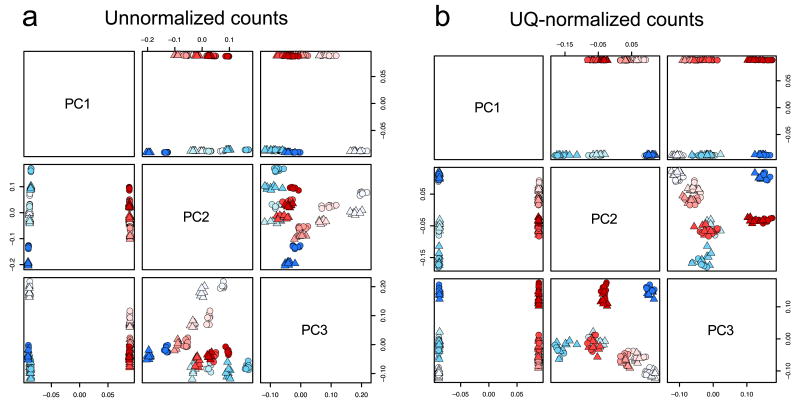
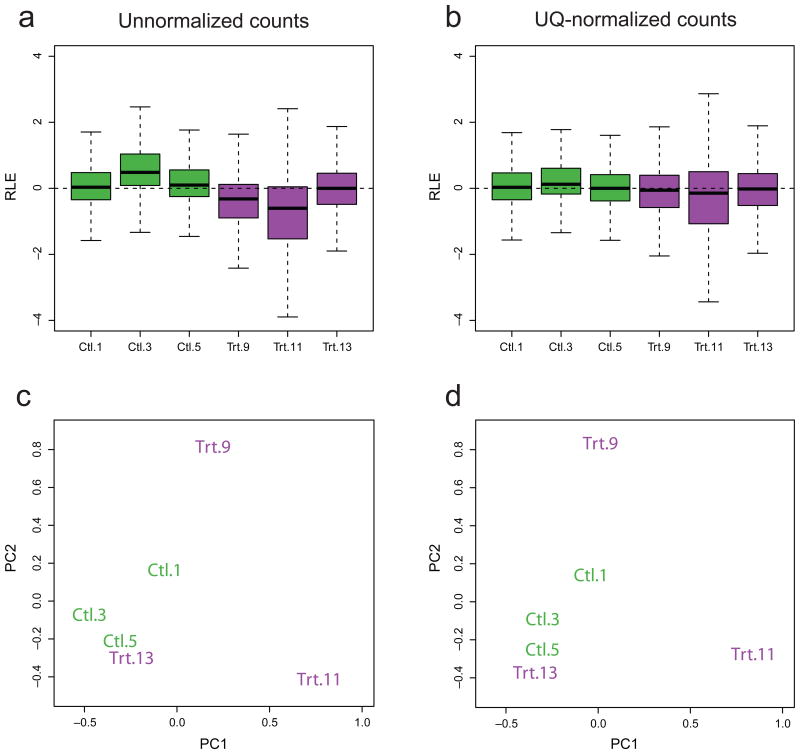
For both datasets, existing methods do not lead to satisfactory normalization of read counts (Figs. 1, 2). In particular, for the SEQC dataset, although the huge biological difference between Sample A and Sample B is captured by the first principal component (PC), residual library preparation and flow-cell effects are revealed by the second and third PCs (Fig. 1a). Upper-quartile (UQ) normalization successfully adjusts for flow-cell effects (cf. sequencing depth), but not library preparation effects (Fig. 1b). Figure 2 reveals similar findings for the Zebrafish dataset and a clear need for normalization. The boxplots of unnormalized relative log expression (RLE) show large distributional differences between replicate libraries (Fig. 2a). As for the SEQC dataset, UQ normalization is not fully satisfactory and, in particular, fails to capture the excessive variability of Library 11 (Fig. 2b). Moreover, libraries fail to cluster by treatment in the first two PCs, both when considering unnormalized counts (Fig. 2c) and UQ-normalized counts (Fig. 2d).

Figure 1.

Unwanted variation in S E Q C RNA-seq dataset. (a) Scatterplot matrix of first three principal components (PC) for unnormalized counts (log scale, centered). The PCs are orthogonal linear combinations of the original 21,559-dimensional gene expression profiles, with successively maximal variance across the 128 samples, i.e., the first PC is the weighted average of the 21,559 gene expression measures that provides the most separation between the 128 samples. Each point corresponds to one of the 128 samples. The four Sample A and the four Sample B libraries are represented by shades of blue and red, respectively (16 replicates per library). Circles and triangles represent samples sequenced in the first and second flow-cells, respectively. As expected for the SEQC dataset, the first PC is driven by the extreme biological difference between Sample A and Sample B. The second and third PCs clearly show library preparation effects (the samples cluster by shade) and, to a lesser extent, flow-cell effects reflecting differences in sequencing depths (within each shade, the samples cluster by shape). (b) Same as a, for upper quartile(UQ)–normalized counts. UQ normalization removes flow-cell effects (the circles and triangles now cluster together), but not library preparation effects. All other normalization procedures but RUV behave similarly as UQ (Supplementary Fig. 1).

Figure 2.

Unwanted variation in Zebrafish RNA-seq dataset. (a) Boxplots of relative log expression (RLE) for unnormalized counts. Purple, treated libraries (Trt); green, control libraries (Ctl). We expect RLE distributions to be centered around zero and as similar as possible to each other. The RLE boxplots clearly show the need for normalization. (b) Same as a, for UQnormalized counts. UQ normalization centers RLE around zero, but fails to remove the excessive variability of Library 11. (c) Scatterplot of first two PCs for unnormalized counts (log scale, centered). Libraries do not cluster as expected according to treatment. (d) Same as c, for UQ-normalized counts. UQ normalization does not lead to better clustering of the samples. All other normalization procedures but RUV behave similarly as UQ (Supplementary Figs. 2 and 3).

We compared other state-of-the-art normalization methods (see Methods) and found that none lead to satisfying results in terms of the removal of library preparation effects for the SEQC dataset and clustering of samples by treatment for the Zebrafish dataset (Supplementary Figs. 1–3).

Removing unwanted variation through normalization

Building on a previously described method for normalizing microarray data^19,20, we developed a normalization strategy for RNA-seq, coined RUV for remove unwanted variation. Briefly, RUV works as follows. Consider a generalized linear model (GLM), where the observed RNA-seq read counts are regressed on both the known covariates of interest (e.g., treatment status) and unknown nuisance variables, i.e., factors of unwanted variation (e.g., library preparation). RUV makes use of a subset of the data to estimate the factors of unwanted variation and adjusts for these in the model for differential expression analysis (see Methods for details).

We propose three alternative approaches for estimating the factors of unwanted variation: (i) RUVg uses negative control genes, assumed not to be DE with respect to the covariates of interest (e.g., ERCC spike-ins); (ii) RUVs uses negative control samples for which the covariates of interest are constant (e.g., centered counts for technical replicates of Sample A and of Sample B in the SEQC dataset); (iii) RUVr uses residuals from a first-pass GLM regression of the unnormalized counts on the covariates of interest.

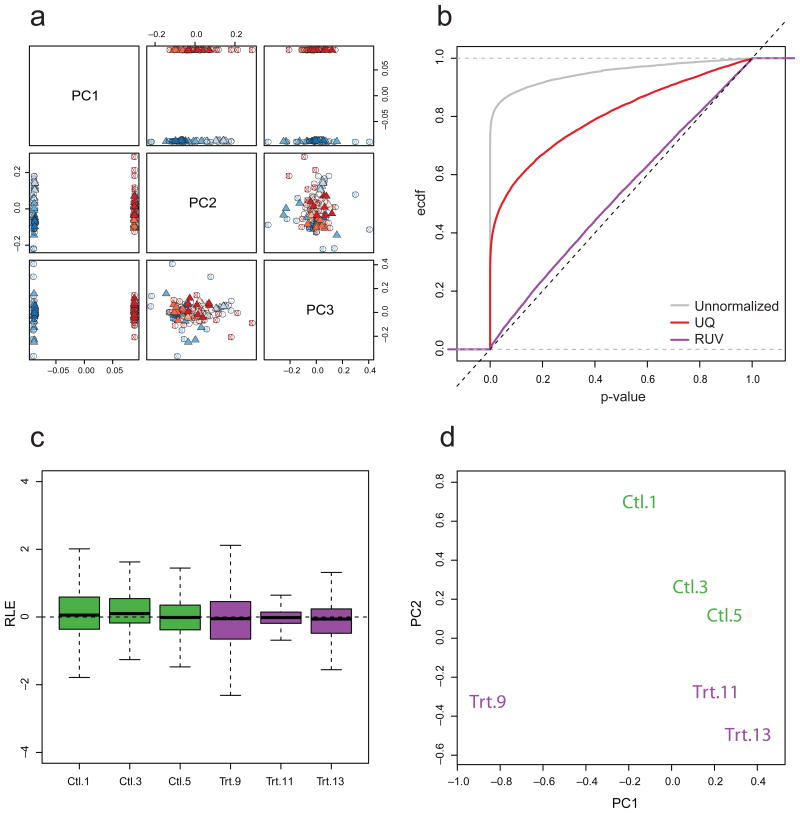
We first applied RUVg to the SEQC and Zebrafish datasets using a set of “in silico” empirical control genes (see Methods) (Fig. 3); RUVr and RUVs perform similarly (Supplementary Figs. 4–6). RUVg effectively reduces library preparation effects for the SEQC dataset without weakening the Sample A vs. B effect (Fig. 3a). We also performed differential expression analysis between technical replicates for each of Sample A (Fig. 3b) and Sample B (Supplementary Fig. 7) (see Methods for details). The p-value distribution should be as close as possible to the uniform distribution (identity line for the empirical cumulative distribution function in Fig. 3b). There are substantial library preparation effects for unnormalized counts. These are only attenuated (and not fully removed) by UQ normalization. By contrast, RUVg fully adjusts for library preparation effects. For the Zebrafish dataset, RUVg down-weights the effect of outlying Library 11 on subsequent analyses (e.g., differential expression), by shifting its read counts towards the median counts across samples, as shown in the RLE boxplots of Figure 3c, thus leading to more robust DE results (see Impact on differential expression analysis). More importantly, RUVg leads to better separation between treated and control samples (Fig. 3d).

Figure 3.

RUVg normalization using in silico empirical control genes. (a) For SEQC dataset, scatterplot matrix of first three PCs after RUVg normalization (log scale, centered). RUVg adjusts for library preparation effects (cf. Fig. 1), while retaining the Sample A vs. B difference. (b) For SEQC dataset, empirical cumulative distribution function (ECDF) of p-values for tests of DE between Sample A replicates (given a value x, the ECDF at x is simply defined as the proportion of p-values less than or equal to x). We expect no DE and p-values to follow a uniform distribution, with ECDF as close as possible to the identity line. This is clearly not the case for unnormalized (gray line) and UQ-normalized (red) counts; only with RUVg (purple) do p-values behave as expected. (c) For Zebrafish dataset, boxplots of RLE for RUVg-normalized counts. RUVg shrinks the expression measures for Library 11 towards the median across libraries, suggesting robustness against outliers. (d) For Zebrafish dataset, scatterplot of first two PCs for RUVg-normalized counts (log scale, centered). Libraries cluster as expected by treatment.

Behavior of the ERCC spike-in controls

The main assumption of RUVg is that one can identify a set of negative control genes, i.e., genes whose expression is not influenced by the biological covariates of interest. Although using a set of in - silico empirical controls works well in practice (Fig. 3), an obvious strategy is to design synthetic negative controls, known a priori not to be influenced by the biological covariates under study. To this end, we explore the possibility of using the recently proposed ERCC spike-in controls in the normalization procedure.

In order for the spike-ins to be trusted for normalization, two conditions must be satisfied: (i) spike-in read counts are not affected by the biological covariates of interest and (ii) the unwanted variation affects spike-in and gene read counts similarly. Note that these assumptions are not limited to our normalization approach and are needed also by other control-based methods ¹¹ (see Methods); hence, careful exploration of the behavior of the ERCC spike-ins is essential prior to applying any normalization method that makes use of them.

First, we consider the relationship between the ERCC spike-in counts and their nominal concentrations. Although there is a good linear relationship between log-read count and log-concentration ¹³ (Supplementary Figs. 8 and 9), strong library preparation effects are observed. We use a Poisson GLM to regress the spike-in counts on the nominal concentrations. Figure 4a displays the estimates of the regression coefficients for each of the 128 SEQC samples (see Supplementary Fig. 10 for the Zebrafish dataset). Ideally, the coefficients should be as close as possible to one. Replicate samples cluster by library (Fig. 4a), suggesting library preparation effects on the spike-in counts.

Figure 4.

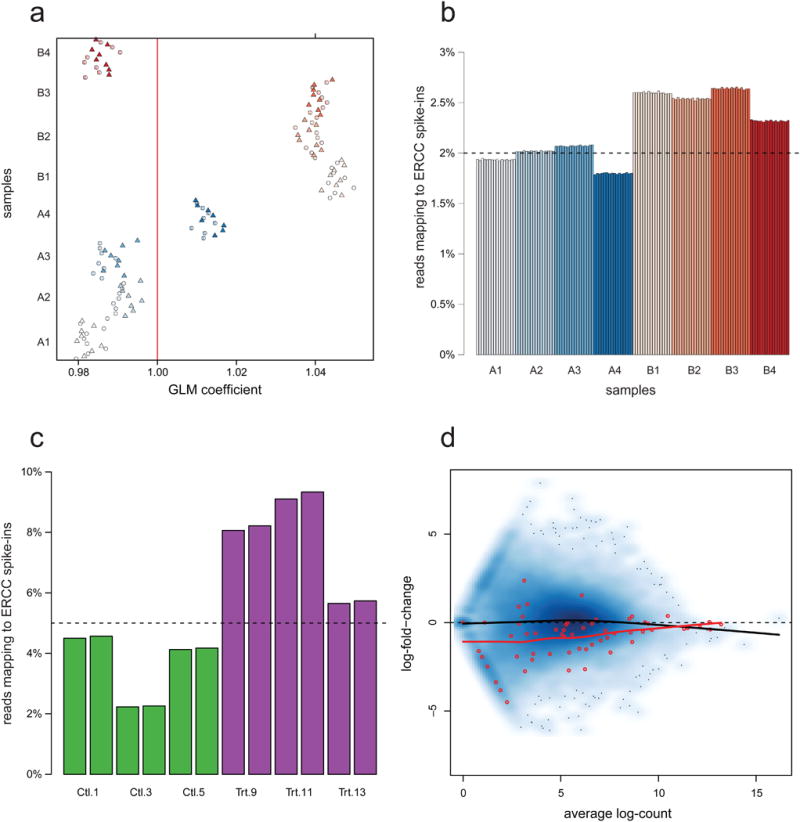
Behavior of the ERCC spike-in controls. (a) For SEQC dataset, generalized linear model (GLM) regression coefficients of spike-in read counts on nominal concentrations. Each point corresponds to one of the 128 samples. The four Sample A and the four Sample B libraries are represented by shades of blue and red, respectively (16 replicates per library). Circles and triangles represent samples sequenced in the first and second flow-cells, respectively. There are evident library preparation effects. (b) For SEQC dataset, proportion of reads mapping to spike-ins deviates markedly from nominal value (dashed line). There are library preparation effects and troubling Sample A vs. B effects which may bias the inference of DE. (c) For Zebrafish dataset, proportion of reads mapping to spike-ins deviates markedly from nominal value (dashed line). Again, there are library preparation and treatment effects (control: Ctl, green; treated: Trt, purple). (d) For Zebrafish dataset, mean-difference plot (MD-plot) of unnormalized counts (log scale) for two control samples (Library 5 vs. Library 1). The blue shading represents point density and spike-ins are plotted using red points. The lines are the lowess fits for genes (black) and spike-ins (red). As expected, log-fold-changes are scattered around the horizontal zero line, indicating that most genes are equally expressed in the two control samples. The negative slope of the black line suggests the need for normalization. The difference between the two lowess fits indicates that, disturbingly, the spike-ins do not behave as the bulk of the genes.

The proportion of reads mapping to the ERCC spike-ins is highly variable between samples and deviates markedly from the nominal value (Fig. 4b,c). In addition to the already observed library preparation effects, spike-in counts disturbingly seem to be affected by the biological factor of interest. In particular, for the SEQC dataset, spike-ins consistently receive a greater proportion of reads in Sample B than in Sample A (Fig. 4b). This is true for all the sequencing centers (Supplementary Fig. 11). Similar patterns are observed for the Zebrafish dataset (Fig. 4c): the proportion of reads mapping to the spike-ins is stable between sequencing runs of the same library, but is very variable between libraries and exhibits a strong treatment effect (being consistently higher in treated than in control samples). These distributional properties of the spike-ins have important implications for inferring differential gene expression. For the Zebrafish dataset, the mean-difference plot (MD-plot) in Figure 4d contrasts read counts for two control fish libraries, for which there is no treatment effect and for which the spike-ins are expected to have log-fold-changes of zero. The distribution of log-fold-changes for the spike-ins is markedly different from that of the genes. Using a loess fit on the spike-ins to normalize this pair of samples, in a procedure similar to that of Lovén et al. ¹¹, would result in wrongly shifting the gene log-fold-changes upward (Fig. 5). Indeed, because we are comparing two control samples, we do not expect this global shift in expression to be real.

Figure 5.

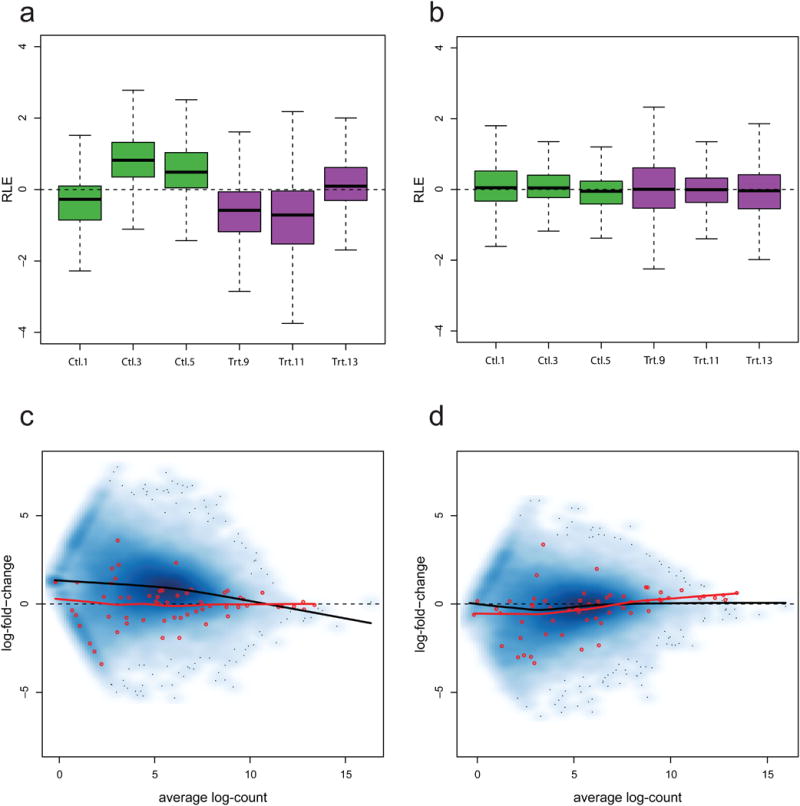
Using the ERCC spike-in controls for normalization, Zebrafish dataset. (a) Boxplots of RLE for cyclic-loess(CL)-normalized counts for control (Ctl, green) and treated (Trt, purple) samples. The expression measures are clearly not comparable across replicate libraries and CL based on the spike-ins is not effective at normalizing the counts. (b) Boxplots of RLE for RUVgnormalized counts. RUVg based on the spike-ins leads to much more reasonable RLE distributions, similar to those obtained using a set of empirical controls (Fig. 3c). (c) MD-plot for CL-normalized counts (log scale) for the same control samples as in Figure 4c. By shifting the spike-in log-fold-changes towards zero, CL normalization leads to a global shift of the gene log-fold-changes away from zero. For control samples, with no expected DE, CL normalization is likely to bias expression measures. (d) MD-plot for RUVg-normalized counts (log scale) for the same control samples as in Figure 4c. Log-fold-changes for both the spike-ins and the genes are scattered around the zero line, yielding more realistic expression measures than CL normalization.

Using the ERCC spike-in controls for normalization

Properly behaved spike-ins could be a valuable resource for normalization: by design, their read counts are expected to be constant (or to have known fold-changes) between samples and hence any deviations from nominal fold-changes should reflect nuisance technical effects. One could therefore use functions of the spike-in counts to scale gene-level read counts, using existing procedures such as UQ or TMM ⁴ normalization (see Methods). Unfortunately, given the troubling behavior of the ERCC spike-ins in our two datasets (Fig. 4), global-scaling normalization factors based on these are unrealistic and lead to poorly normalized counts (Supplementary Fig. 3). Note that similar findings were reported for TMM normalization using a different set of spike-ins ⁴. Cyclic loess (CL) normalization based on the spike-ins (see Methods) leads to similarly poor results (Fig. 5a). By contrast, RUVg normalization leads to reasonable results when based on the spike-ins (Fig. 5b). In particular, CL unrealistically shifts log-fold-changes upward in the comparison between two control libraries (cf. Fig. 4d and 5c), while both spike-in and gene expression log-fold-changes are centered around zero with RUVg (Fig. 5d).

The good performance of RUVg compared to global-scaling and regression-based normalization can be explained by the different assumptions underlying each approach (see Methods for details). Global-scaling and regression-based normalization methods assume that unwanted technical effects (i.e., between-sample differences excluding biological effects of interest) are roughly the same for genes and spike-ins and are captured by either a single parameter per sample or a regression function between pairs of samples. Such assumptions are clearly violated for our datasets (e.g., Fig. 4d). RUVg, on the other hand, only assumes that the factors of unwanted variation estimated from the spike-ins span the same linear space as the factors of unwanted variation W for all of the genes. The effects of the unwanted factors on the counts (i.e., the nuisance parameter α) are gene-specific and re-estimated for all of the genes in Step 4 of RUVg (see RUVg and Equation (1) in Methods). These different and more general assumptions seem reasonable for our datasets (Supplementary Fig. 12). However, the estimation of W is problematic when based on such a small set of negative controls (only 59 spike-ins). This explains the better performance of RUVg when it is based on a larger set of empirical controls (Fig. 6, Supplementary Figs. 12 and 13).

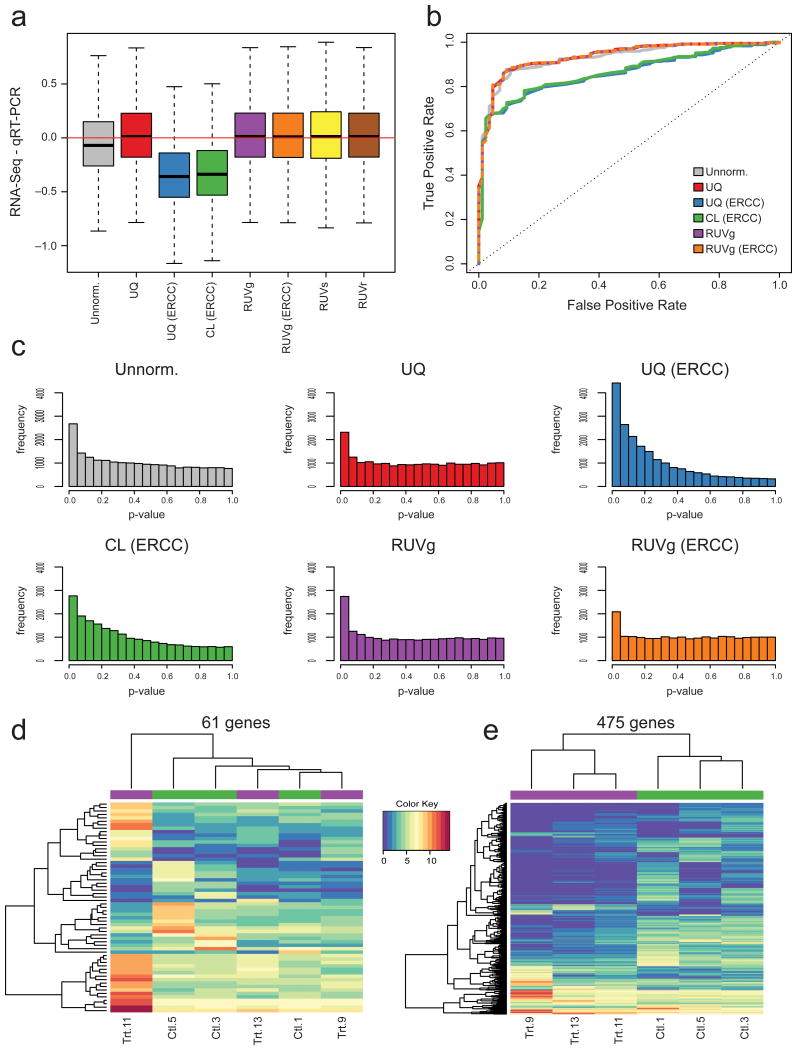
Figure 6.

Impact of normalization on differential expression analysis. (a) For SEQC dataset, difference between RNA-seq and qRT-PCR estimates of Sample A/Sample B log-fold-changes, i.e., bias in RNA-seq when viewing qRT-PCR as gold standard. All RUV versions lead to unbiased log-fold-change estimates; CL based on ERCC spike-ins leads to severe bias. (b) For SEQC dataset, receiver operating characteristic (ROC) curves using a set of 370 positive and 86 negative qRT-PCR controls as gold standard. RUVg (based on either empirical or spike-in controls) and UQ normalization perform slightly better than no normalization. UQ based on spike-ins performs similarly to no normalization and CL based on spike-ins performs the worst. (c) For Zebrafish dataset, distribution of edgeR p-values for tests of DE between treated and control samples. UQ and CL normalization based on spike-ins lead to distributions far from the expected uniform. (d) For Zebrafish dataset, heatmap of expression measures for the 61 genes found DE between control (Ctl) and treated (Trt) samples after UQ but not after RUVg normalization. Clustering of samples is driven by outlying Library 11. (e) Heatmap of expression measures for the 475 genes found DE after RUVg but not after UQ normalization. Samples cluster as expected by treatment.

Impact on differential expression analysis

One of the most important applications of RNA-seq is the study of differential gene expression between two or more biological conditions (e.g., treated vs. control samples in the Zebrafish dataset or Sample A vs. B in the SEQC dataset). Normalization has been shown to have a strong impact on the inference of DE ^1–3. To compare RUV to other normalization methods in terms of DE results, we exploit the availability of external qRT-PCR controls for the SEQC dataset (see Methods). By viewing qRT-PCR as a gold standard, one can estimate the bias in RNA-seq Sample A/Sample B expression log-fold-changes by the differences between the RNA-seq and corresponding qRT-PCR estimates (see Methods).

For the SEQC dataset, we observed a slight bias in the unnormalized Sample B vs. A log-fold-changes (Fig. 6a), which suggests the need for normalization, although the balanced design, the large number of technical replicates and the extreme differences between Samples A and B somewhat alleviate the impact of technical effects on DE measures. UQ normalization based on all genes leads to unbiased estimates of log-fold-changes. However, using the ERCC spike-ins for UQ or CL normalization leads to biased estimates. All versions of RUV (with empirical or spike-in controls) yield unbiased estimates. The receiver operating characteristic (ROC) curves lead to similar conclusions (Fig. 6b), although the extreme power of the DE tests (resulting from the large sample sizes and extreme differences between Samples A and B) makes it difficult to distinguish between methods. Indeed, even unnormalized counts lead to a reasonable ROC curve, d e spite their biased fold-change estimates (Fig. 6a).

In the absence of a gold standard for the Zebrafish dataset, one can nonetheless examine the distribution of p-values for tests of differential expression between treated and control samples (see Methods). Ideally, one expects a uniform distribution for the bulk of non-DE genes, with a spike at zero corresponding to a few DE genes. This is indeed the case for UQ normalization based on all genes and all RUV versions (Fig. 6c). However, UQ and CL based on the ERCC spike-ins lead to a distribution of p-values very far from uniform. Finally, the heatmaps of Figures 6d and 6e confirm the robust nature of RUVg (cf. Fig. 3c). The 61 genes identified as DE by UQ but not by RUVg are driven solely by the extreme expression of Library 11, as indicated by the hierarchical clustering (Fig. 6d). On the other hand, the 475 genes identified as DE by RUVg but not by UQ yield a more balanced clustering, reflecting the treatment effect (Fig. 6e). These heatmaps and the scatterplot of the first two PCs in Figure 3d suggest that RUVg leads to a more realistic and robust list of differentially expressed genes.

Discussion

Normalization is an essential, yet often overlooked, aspect of RNA-seq data analysis. As RNA-seq has become the assay of choice for measuring gene expression levels, the availability of data from large collaborative projects (such as The Cancer Genome Atlas ²¹ and ENCODE ²²) has grown exponentially in the last few years. With such projects employing multiple library preparation protocols (e.g., poly(A)+, total RNA) and platforms, and with the sequencing technology evolving quickly (cf. read length, paired- vs. single-end reads), many sources of unwanted variation can affect read counts. Normalization procedures must therefore be able to adjust for often unknown and more complex effects than simple differences in sequencing depths.

We have used the two very different SEQC and Zebrafish datasets to illustrate the misbehavior of the ERCC spike-in controls. Disturbingly, individual spike-in read counts are highly variable compared to their nominal concentrations (Supplementary Figs. 14 and 15), the overall proportion of reads mapping to the spike-ins is also highly variable and deviates markedly from the nominal proportion ¹⁵ (Fig. 4b,c), and technical effects (e.g., library preparation effects) are different for the spike-ins than for the bulk of the genes (Fig. 4d). We have also demonstrated the need for careful normalization and proposed a novel normalization strategy, remove unwanted variation, which adjusts for nuisance technical effects by performing factor analysis on counts (or residual counts) for suitable sets of control genes or samples. The different RUV versions generally outperformed state-of-the-art normalization approaches and led to more accurate estimates of expression fold-changes and tests of differential expression (Fig. 6). For the SEQC dataset, UQ leads to good DE results (Figs. 6a–b), even though it fails to adjust for library preparation effects (Fig. 1b). This property is due to the extreme difference between Sample A and Sample B and is not generalizable to more biologically relevant datasets, where the effects of interest are more subtle and comparable in magnitude to the unwanted technical effects. This is confirmed by the Zebrafish dataset, where RUV leads to better results than UQ in terms of clustering and DE gene lists (Figs. 3d, 6e). Although it performs more robustly when applied to a set of empirical control genes or, when feasible, a set of replicate samples, only RUV gave reasonable results when using the ERCC spike-ins (Fig. 5).

In this study, our three proposed RUV approaches performed equally well. However, they rely on different assumptions and the validity of these assumptions for the data at hand should guide the choice of method (see Methods and Supplementary Table 1). RUVg assumes that one can identify a set of negative control genes (e.g., housekeeping genes or spike-ins) that are not affected by the biological covariates of interest and are affected by the factors of unwanted variation in the same way as the rest of the genes. This is essentially the discrete version of RUV-2 (refs. 19, 20). RUVr, similarly to previously proposed microarray methods ²³, does not make this assumption; in fact, one can use all of the genes to normalize the data with this version. RUVs stands in the middle. Formally, one still needs a set of negative control genes for the estimation of the unwanted factors, but this version is much less sensitive to poorly chosen controls than RUVg (see Methods for details). Indeed, we found that in practice it works well when using all genes as negative controls. However, both RUVr and RUVs assume that the unwanted factors are not correlated with the covariates of interest. This assumption is usually reasonable, but it is not met when, for example, all treated samples are in one batch and all control samples in another. In this case, RUVr and RUVs will not remove the unwanted variation, while RUVg should still work, provided it is based on a reliable set of control genes^19,20. Although RUVs on all genes should perform well if the unwanted factors are not too correlated with the covariates of interest, it can only account for variation that occurs within replicate groups, e.g., it can capture library preparation effects only if the replicate groups include multiple libraries. This has implications on experimental design: technical replication at the library preparation level can facilitate normalization and is a good investment in large sequencing projects, especially when multiple centers or platforms are involved ²⁴. Although we have focused on normalization in the context of differential expression, the RUV approach can be adapted to other settings such as cluster analysis ²⁵.

Internal and external controls are essential for the analysis of high-throughput data and spike-in sequences have the potential to help researchers better adjust for unwanted technical factors. With the advent of single-cell sequencing ²⁶, the role of spike-in standards should become even more important, both to account for technical variability ²⁷ and to allow the move from relative to absolute RNA expression quantification. It is therefore essential to ensure that spike-in standards behave as expected and to develop a set of controls that are stable enough across replicate libraries and robust to both differences in library composition and library preparation protocols.

Methods

Datasets

Zebrafish dataset

Olfactory sensory neurons were isolated from three pairs of gallein-treated and control embryonic zebrafish pools and purified by fluorescence activated cell sorting (FACS) ¹⁸. Each RNA sample was enriched in poly(A)+ RNA from 10–30 ng total RNA and 1 μL (1:1000 dilution) of Ambion ERCC ExFold RNA Spike-in Control Mix 1 was added to 30 ng of total RNA before mRNA isolation. cDNA libraries were prepared according to manufacturer's protocol. The six libraries were sequenced in two multiplex runs on an Illumina HiSeq2000 sequencer, yielding approximately 50 million 100bp paired-end reads per library. We considered for mapping a custom reference sequence, defined as the union of the zebrafish reference genome (Zv9, downloaded from Ensembl ²⁸, v. 67) and the ERCC spike-in sequences (http://tools.invitrogen.com/downloads/ERCC92.fa). Reads were mapped with TopHat ²⁹ (v. 2.0.4, default parameters and supplying the Ensembl GTF annotation through the -G option). Gene-level read counts were obtained using the htseq-count python script (http://www-huber.embl.de/users/anders/HTSeq/) in the “union” mode and Ensembl (v. 67) gene annotation. After verifying that there were no run-specific biases (data not shown), we used the sums of the counts of the two runs as the expression measures for each library. Genes/Spike-ins with more than five reads in at least two libraries were retained, resulting in a total of 20,806 (out of 32,561) expressed genes and 59 (out of 92) “present” spike-ins. The FASTQ files containing the raw data are publicly available in GEO with the accession number GSE53334.

SEQC dataset

The third phase of the MicroArray Quality Control (MAQC) Project, also known as SEquencing Quality Control ¹⁶ (SEQC) Project, aims to assess the technical performance of high-throughput sequencing platforms by generating benchmarking datasets. The design includes four different sample types, namely Samples A, B, C, and D. Sample A is Stratagene's universal human reference (UHR) RNA; Sample B is Ambion's human brain reference RNA; Samples C and D are mixes of Samples A and B, in a 3:1 and 1:3 ratio, respectively. The four reference samples were sent to several sequencing centers around the world and sequenced using different platforms. We focus on the Illumina HiSeq2000 data. Each center prepared 4 libraries for each sample type and multiplex pools of the resulting 8 barcoded libraries were sequenced in 8 lanes of 2 flow-cells, yielding a total of 16 (technical) replicates per library and 64 replicates per sample type. Prior to library preparation, Ambion ERCC ExFold RNA Spike-in Control Mix 1 and Mix 2 were added to Sample A and Sample B RNA, respectively, in a proportion of 50 μL per 2,500 μL of total RNA. Here, we consider only Sample A and Sample B sequenced at the Australian Genome Research Facility (AGRF).

The data consist of an average of 10 million 100bp paired-end reads per sample. We considered for mapping a custom reference sequence, defined as the union of the human reference genome (GRCh37, downloaded from Ensembl, v. 69) and the ERCC spike-in sequences. Reads were mapped with TopHat (v. 2.0.6, default parameters and supplying the Ensembl GTF annotation through the -G option). Gene-level read counts were obtained using the htseq-count python script in the “union” mode and Ensembl (v. 69) gene annotation. Genes/Spike-ins with more than five reads in at least ten samples were retained, resulting in a total of 21,559 (out of 55,933) expressed genes and 59 (out of 92) present spike-ins. The FASTQ files containing the raw data are publicly available in GEO with the accession number ***

In addition to the internal ERCC spike-in positive and negative controls, we use external qRT-PCR positive and negative controls from the original MAQC study ¹⁷. As in our previous work ^1,2, among the genes assayed by qRT-PCR, we consider only those that match a unique Ensembl gene, are called present in at least three out of each of the 4 Sample A and Sample B qRT-PCR runs, and have standard errors across the 8 runs not exceeding 0.25. We found 698 qRT-PCR genes in common with the RNA-seq filtered genes and use this subset to compare expression measures between the two assays. The Sample A/Sample B expression log-fold-change of a gene is estimated by the log-ratio between the average of the 4 qRT-PCR measures of Sample A and the average of the 4 measures of Sample B.

ERCC spike-in controls

The External RNA Control Consortium ¹² (ERCC) developed a set of 92 polyadenylated transcripts that mimic natural eukaryotic mRNAs. Ambion commercializes two ERCC spike-in mixes, ERCC ExFold RNA Spike-in Control Mix 1 and Mix 2. The two mixes contain the same set of 92 spike-in standards, but at different concentrations. This allows the design of experiments in which the spike-ins can be used both as positive and negative controls. In particular, the spike-ins are divided into four groups of 23 transcripts each, spanning a 10⁶-fold concentration range, with approximately the same transcript size and GC-content distributions. The first group has an expected fold-change of 4:1 between the two mixes (Mix 1:Mix2); the second group has an expected fold-change of 1:1 (negative controls); the third and fourth groups have expected fold-changes of 2:3 and 1:2, respectively. (See the white paper at http://tools.invitrogen.com/content/sfs/manuals/cms_086340.pdf for additional details.)

In the Zebrafish dataset, Mix 1 was used for all samples, so that all spike-ins can be used as negative controls. In the SEQC dataset, Mix 1 was added to Sample A and Mix 2 to Sample B, so that 23 spike-ins can be used as negative controls and 69 as positive controls (23 over-represented and 46 under-represented in Sample A).

Remove unwanted variation normalization

Gagnon-Bartsch et al. ^19,20 developed a method for normalizing (continuous) microarray data coined RUV-2, for remove unwanted variation in 2 steps. Here, we propose the following extensions of the remove unwanted variation (RUV) approach to normalize discrete RNA-seq data. For n samples and J genes, consider the log-linear regression model

$$logE[Y|W,X,O]=W\alpha +X\beta +O$$ (1)

where Y is an n × J matrix containing the observed gene-level read counts, X is an n × p matrix corresponding to the p covariates of interest/factors of “wanted variation” (e.g., treatment status) and β its associated p × J matrix of parameters of interest, W is an n × k matrix corresponding to hidden factors of “unwanted variation” and α its associated k × J matrix of nuisance parameters, and O is an n × J matrix of offsets that can either be set to zero or estimated with some other normalization procedure (such as upper-quartile normalization). The matrix X is a random variable, assumed to be known a priori. For instance, in the usual two-class comparison setting (e.g., treated vs. control samples), X is an n × 2 design matrix with a column of ones corresponding to an intercept and a column of indicator variables for the class of each sample (e.g., 0 for control and 1 for treated) ³⁰. The matrix W is an unobserved random variable and α, β, and k are unknown parameters. The simultaneous estimation of W, α, β, and k is infeasible. For a given k, we consider instead the three approaches below to estimate the factors of unwanted variation W.

Unlike previously-proposed normalization procedures, RUV can be used to simultaneously normalize read counts (Wα term in Equation (1)) and infer differential expression (Xβ term), using standard techniques for GLM regression. Normalized counts can also be obtained separately as the residuals from regression of the original counts on the unwanted factors. Note, however, that removing Wα from the original counts bears the risk of removing part of the effect of X (ref. 20).

RUVg – RUV with negative control genes

1. Assume one can identify a set of J_c negative control genes, i.e., non-DE genes, for which β_c = 0 and logE[Y_c|W,X,O] = Wα_c + O_C, where the subscript c denotes the restriction of matrices to the set of J_c control genes.

2. Define Z = logY − O and Z* as the column-centered version of Z (i.e., the columns of Z* have zero mean).

3. Perform the singular value decomposition (SVD) of $Z_c^{\ast }$ that is, $Z_c^{\ast }$ = U Λ V^T, where U is an n × n orthogonal matrix with columns the left singular vectors of $Z_c^{\ast }$, V is a J_c × J_c orthogonal matrix with columns the right singular vectors, and Λ an n × J_c rectangular diagonal matrix of singular values (at most min(n,J_c) distinct non-zero singular values). For a given k, estimate Wα_c by $\widehat{{W\alpha }_c}$ = U Λ_k V^T and W by Ŵ = U Λ_k, where Λ_k is the n × J_c rectangular diagonal matrix obtained from Λ by retaining only the k largest singular values and setting other diagonal entries to zero (drop null columns to obtain Ŵ)

4. Substitute Ŵ into Equation (1) for the full set of J genes and estimate both α and β by GLM regression.

5. (Optionally) Define normalized read counts as the residuals from ordinary least squares (OLS) regression of Z on Ŵ

This is essentially the discrete version of RUV-2 (refs. 19,20). The key assumption is that one can identify a set of negative control genes, as detailed below. However, RUV-2 has been found to be quite sensitive to the choice of control genes ^19,20,25. We therefore consider the following two adaptations, that either do not require negative control genes (RUVr) or are more robust to the choice of controls (RUVs).

RUVr – RUV with residuals

1. Compute an n × J matrix of residuals E from a first-pass GLM regression of the counts Y on the covariates of interest X (model in Equation (1) without Wα term), e.g., deviance residuals. The counts may be either unnormalized or normalized with a method such as upper-quartile (UQ) normalization.

2. Perform the singular value decomposition of the residual matrix, E = U Λ V^T, and estimate the unwanted factors W by the n × k matrix Ŵ = UΛ_k. Proceed as in Steps 4 and 5 of the control gene version of RUV.

RUVs – RUV with replicate/negative control samples

1. Assume one has replicate samples for which the biological covariates of interest are constant. Then, their count differences behave like those of negative control samples, as they contain no effects of interest. Let r(i) ∈ {1, …, R } denote the replicate group to which sample i belongs; if i does not belong to any replicate group, set r(i) = 0. For example, for the SEQC dataset, the 64 (= 4 libraries × 2 flow-cells × 8 lanes) replicates of Sample A and of Sample B each form a replicate group.

2. Column-center the counts within each set of replicate samples, i.e., replace the original counts Y_i,j by Y_i,j − Ȳ_r(i),j, where Ȳ_r(i),j = Σ_iI(r(i) = r) Y_i,j/Σ_iI(r(i) = r) Let Y_d denote the resulting n_d × J matrix of column-centered counts for the n_d = Σ_iI(r(i) ≠ 0) replicate samples. Then logE[Y_d | W, X, 0] = W_dα + O_d, where W_d is n_d × k, α is k × J, and O_d is n_d ×J.

3. Perform the singular value decomposition $Z_d^{\ast }$ = U Λ V^T (where $Z_d^{\ast }$ is defined as in Step 2 of RUVg) and estimate the nuisance parameter α by the k × J matrix αˆ = Λ_kV^T obtained by retaining only the k largest singular values. Here, k ≤ min(n_d,J), the upper-bound for the number of distinct non-zero singular values.

4. Estimate the unwanted factors W by OLS regression of Z_c, for all n original samples and a set of J_c negative control genes, on ${\widehat{a}}_c,\widehat{W}=Z_c{\widehat{a}}_c^T{({\widehat{a}}_c{\widehat{a}}_c^T)}^{-1}$. Proceed as in Steps 4 and 5 of the control gene version of RUV.

RUV assumptions and scope

Here, we detail the main assumptions and scope of the three proposed RUV approaches. This information is summarized in Supplementary Table 1.

1. Negative control genes with common unwanted factors RUVg and RUVs. There exists a set of negative control genes (e.g., empirical or spike-in controls, chosen as indicated below) whose read counts are not influenced by the covariates of interest (β_c = 0) and for which the estimated factors of unwanted variation span the same linear space as the factors of unwanted variation for all of the genes (logE[Y_c | W,X,O] = Wα_c + O_c).

   Interpretation. By modeling the unwanted variation as in Equation (1) with the term Wα and re-estimating α in Step 4 using all the genes, RUVg allows gene-specific nuisance effects α. The RUVg assumption is therefore different and more general than the assumptions of global-scaling and regression-based normalization methods, that require unwanted technical effects to be roughly the same for the controls and for the rest of the genes and to be captured by either a single parameter per sample or a regression function between pairs of samples. This is particularly relevant when using the ERCC spike-in controls for normalization purposes.

   Robustness. In practice, this assumption can be relaxed for RUVs, as the method performs well even when its Step 4 is based on all genes, provided that the unwanted factors W are not too correlated with the factors of interest X (ref. 25).

2. Replicate/negative control samples: RUVs. There exists a set of negative control samples, i.e., samples whose read counts are not influenced by the biological covariates of interest. Such a set can be created easily by computing differences between (technical) replicate samples for which the biological covariates of interest are constant.

   Interpretation. RUVs can only account for variation that occurs within replicate groups, e.g., it can capture library preparation effects only if the replicate groups include multiple libraries.

3. Known matrix X: RUVg(empirical controls) and RUVr.

   Interpretation. This assumption is essential for RUVr in order to compute residuals from a first-pass GLM regression of the counts on the covariates of interest. It is needed for RUVg only when there are no a priori known negative control genes and one relies on empirical controls from a first-pass DE analysis. The main consequence of this assumption is that RUVg(empirical controls) and RUVr are applicable only to classical DE settings (e.g., treatment vs. control comparison) and not to clustering (where X is unknown) or time-course (where X is only partially known and model selection may be involved) problems.

4. Unwanted factors uncorrelated with covariates of interest: RUVg, RUVr, and RUVs.

   The unwanted factors W are uncorrelated with the covariates of interest X.

   Interpretation. This assumption is natural for any regression-based method and is mainly needed for RUVr and RUVs.

   Robustness. In practice, both RUVr and RUVs perform well with modest correlation between W and X.

The residual version RUVr does not need the negative control gene assumption and is suited to situations where the effects of interest are much larger than the unwanted variation (e.g., SEQC dataset, see Fig. 1). It is similar to previously-presented microarray methods ^23,31. The replicate sample version RUVs is adapted to the SEQC dataset, with large library preparation effects and replicate libraries for each biological condition, and, to a lesser extent, to the Zebrafish dataset, where one has three libraries per biological condition.

Choice of negative control genes

The main assumption of RUVg is that one can identify a set of negative control genes. Several types of negative controls could be used, including housekeeping genes, spike-in sequences (e.g., ERCC), or “in silico” empirical controls such as the J_c least significantly DE genes based on a first-pass DE analysis performed prior to RUVg normalization.

Interestingly, one can relax the negative control gene assumption by requiring instead the identification of a set of J_c positive or negative controls, for which the value of β_C is known a priori but need not be zero. Then, Xβ_C is known and one can perform the singular value decomposition of logY_C − Xβ_C − O_C to estimate W as in Step 3 of RUVg above. Steps 4 and 5 remain the same. This allows us to make full use of all 92 ERCC spike-in controls for the SEQC dataset.

In this study, we consider two different sets of controls for both datasets: (i) a set of empirical controls, defined as all but the top 5,000 DE genes, as ranked by edgeR p-values for UQ-normalized data (15,839 genes for the Zebrafish dataset and 16,500 genes for the SEQC dataset); (ii) the 59 ERCC spike-in controls called present. Supplementary Figures 16 and 17 show that RUVg is robust to the set of empirical control genes.

Choice of number of factors of unwanted variation

The main tuning parameter of RUV is the number of factors of unwanted variation, k. The choice of k should be guided by considerations that include sample size, extent of technical effects captured by the first k factors, and extent of differential expression ^19,20.

For instance, the small sample size (n = 6) for the Zebrafish dataset only allows the estimation of one or two factors of unwanted variation. Here, we set k = 1. The SEQC dataset has a much greater sample size (n = 128) and more factors can be considered. Here, we set k = 6; for the RUVg version, we drop the first unwanted factor, as it captures the biological factor of interest, and retain the next k = 6 factors. Supplementary Figure 18 shows that RUV is robust to the choice of k.

Linear model version of RUV

Although GLM are a natural choice for count data and have been successfully applied to address a broad range of questions in RNA-seq ^32,33, a simpler alternative is to consider a linear model (LM) for some suitable transformation of the read counts (e.g., logarithmic transformation). Such an LM-based version of RUVg reduces to RUV-2 (refs. 19,20). Additionally, using a linear model allows approaches such as RUV-4 and RUV-inv (ref. 20).

Supplementary Figures 19 and 20 show that LM-based RUVg on log counts does not perform as well as our proposed GLM-based RUVg. In particular, although LM-based RUVg seems effective at removing the unwanted variation (cf. uniform distribution of p-values in Supplementary Fig. 19), it does not yield enough power to detect any DE genes, neither when using a standard t-test nor when using an empirical Bayes moderated t-test (limma ³⁴).

Other normalization methods

We compare our novel RUV approach to the following normalization procedures.

Global-scaling normalization scales gene-level counts by a single factor per sample, such as, the per-sample total read count (TC), a.k.a., Reads Per Kilobase of exon model per Million mapped reads or RPKM ³⁵, a housekeeping gene count (e.g., POLR2A), a quantile of the per-sample count distribution ¹ (e.g., upper-quartile, UQ), or other robust summaries obtained by relating each sample to a reference sample (e.g., the Trimmed Mean of M values (TMM) ⁴ and the approach of Anders and Huber (AH) ³³).

In full-quantile normalization (FQ) ^1,14, all quantiles of the gene count distributions are matched between samples. Specifically, for each sample, the distribution of sorted read counts is matched to a reference distribution defined in terms of a function of the sorted counts (e.g., median) across samples.

In loess normalization ^7,11, loess fits are performed for mean-difference plots of log counts for pairs of samples, e.g., all possible pairs as in cyclic loess (CL) or each sample paired with a synthetic reference obtained by averaging counts across samples.

When a reasonable number of negative controls are available and behave as desired across samples, these could be used directly as part of the normalization procedure, e.g., scaling counts by the upper-quartile of the ERCC spike-in counts or fitting a loess regression only on the spike-ins.

In the main comparison, we focus on four RUV procedures (RUVg using empirical control genes or the ERCC spike-ins and RUVr and RUVs using all genes), UQ normalization (using all genes or only the spike-ins), and CL normalization (using only the spike-ins). All other methods lead to very similar results as UQ normalization, as shown in Supplementary Figures 1–3.

Evaluation criteria

Relative log expression

A particularly useful transformation of read counts is their relative log expression (RLE), defined, for each gene, as the log-ratio of a read count to the median count across samples. Comparable samples should have similar RLE distributions, that are centered around zero. Unusual RLE distributions could reveal suspicious samples (e.g., problematic library preparation) or batch effects.

Differential expression analysis

To compare normalization procedures in terms of their impact on differential expression results, we consider the negative binomial GLM of edgeR ³², with tag-wise dispersion. UQ normalization is performed through an offset using the calcNormFactors function. RUV normalization is performed by including the estimated W matrix in the GLM. CL and UQ normalization using the ERCC spike-ins are performed by directly providing the offset argument to the glmFit function. DE genes are identified by likelihood ratio tests for the effects of interest; for the Zebrafish dataset, treatment effect, and for the SEQC dataset, Sample A vs. B effect and library preparation effect in the null experiment of Figure 3b. A gene is declared DE if the associated null hypothesis is rejected at a false discovery rate (FDR) ³⁶ of 0.05.

Bias

In order to evaluate bias in log-fold-change estimation, one needs to know the true value of the expression fold-change. For the SEQC dataset, one can use the estimate of the Sample A/Sample B fold-change from qRT-PCR as the true value, since qRT-PCR is often considered as a gold standard for producing accurate estimates of expression levels. The RNA-seq estimated fold-change is the ratio of the average of the normalized counts for the 64 Sample A replicates to the average of the normalized counts for the 64 Sample B replicates. For a given gene, bias is then estimated as the difference between the estimated log-fold-changes from the two technologies.

Receiver operating characteristic curves

For the SEQC dataset, the qRT-PCR measures are used as gold standard to determine “true” differential expression and derive receiver operating characteristic (ROC) curves for the various normalization methods. As in previous work ¹, we divide the genes assayed by qRT-PCR into three sets, “non-DE”, “DE”, and “no-call”, based on whether their absolute expression log-fold-change is less than 0.2, greater than 1, or falls within the interval [0.2, 1], respectively. We ignore the “no-call” genes when determining true/false positives/negatives. False positives (FP) are defined as genes declared DE by RNA-seq (edgeR FDR adjusted p-value less than 0.05) but not by qRT-PCR. True negatives (TN) are defined as genes declared non-DE by both RNA-seq and qRT-PCR. True positives (TP) are declared DE by both RNA-seq and qRT-PCR. The true positive rate (TPR) is then defined as the number of TP divided by the number of DE genes according to qRT-PCR. The false positive rate (FPR) is computed analogously as the ratio of the number of FP to the number of non-DE genes according to qRT-PCR.

Software implementation

RUV is implemented in the open-source R package RUVSeq, freely available through the Bioconductor Project³⁷ (http://www.bioconductor.org/RUVSeq) and as Supplementary Software.