Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Mar 3;119(13):4601–4607. doi: 10.1021/acs.jpcb.5b00289

Membrane Environment Modulates the pKa Values of Transmembrane Helices

Afra Panahi †, Charles L Brooks III †,‡,*
PMCID: PMC4404502  NIHMSID: NIHMS678868  PMID: 25734901

Abstract

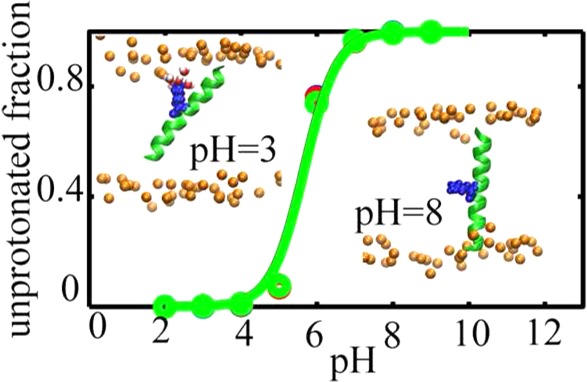
graphic file with name jp-2015-002892_0005.jpg

In this work, we apply the recently developed constant pH molecular dynamics technique to study protonation equilibria of titratable side chains in the context of simple transmembrane (TM) helices and explore the effect of pH on their configurations in membrane bilayers. We observe that, despite a significant shift toward neutral states, considerable population of different side chains stay in the charged state that give rise to pKa values around 9.6 for Asp and Glu and 4.5 to 6 for His and Lys side chains, respectively. These charged states are highly stabilized by favorable interactions between head groups, water molecules, and the charged side chains that are facilitated by substantial changes in the configuration of the peptides. The pH dependent configurations and the measured pKa values are in good agreement with relatively recent solid state NMR measurements. Our results presented here demonstrate that all-atom constant pH molecular dynamics can be applied to membrane proteins and peptides to obtain reliable pKa values and pH dependent behavior for these systems.

Introduction

Membrane proteins play a significant role in myriad biological processes and account for ∼30% of all proteins in the cell.1−3 The transmembrane (TM) segments of these proteins are usually composed of hydrophobic helices whose sequence determines their orientation and position of in membranes.4−6 Despite the hydrophobic nature of the TM segments, occurrences of charged residues are believed to be important for the function of membrane proteins. In integrins, for instance, basic amino acid side chains that are buried in the membrane regulate transmembrane signaling,7 and the ion selectivity of nicotinic-type receptors is determined by the presence or absence of a pore facing carboxylate ring in the membrane bilayer.8,9 Recent studies suggest that the microenvironment of these buried residues, for example, lipids and phosphate head groups, has a profound effect on their charged states, which would influence the orientation of the titratable side chains and their helical configurations in the membrane.6,8,10−12 Therefore, detailed information about the pKa values of buried residues in hydrophobic environments can shed light on the extent of microenvironment effects on the population of the charged and neutral states and, thus, pH-modulated biological function of membrane proteins.

The role of buried ionizable residues in determining helix orientation and the effect of the membrane bilayers in modulating their pKa values have been investigated by solid state NMR (SSNMR) in simple model peptides such as the WALP13 and GWALP14 series using quadrupolar splitting of labeled Ala residues. These TM peptides have provided the opportunity to capture peptide–membrane interactions in great detail and predict possible scenarios for protein–membrane interactions in more complicated systems.10,11,15−18 Vostrikov and Sansom et al. have shown that buried Arg residues at different positions in the GWALP23 peptides gives rise to different peptide behavior in membrane bilayers. The GWALP23 peptide with an Arg in position 14 has an average tilt angle of 16.2° which is almost 10° greater than the GWALP23. In addition, the GWALP23 peptides with one Arg in position 12 tend to exit the lipid bilayer and do not form stable TM orientations in the membrane.11 Using the same peptide models, Koeppe et al. revealed that Arg maintains its positive charge in the membrane bilayer while Lys containing peptides titrate and change their tilt angles. For instance, the pKa of a Lys residue in the 14th position of Lys-containing GWALP23 peptides is shifted down by ∼4 pH units (6.2 at 323 K and an estimated value of 6.8 at 298 K) compared to the standard pKa of Lys in aqueous solution (10.4). These peptides also adopt a tilt angle of 15°, which is ∼10° larger than the tilt angle of the GWALP23 peptide.10 Similar to Arg-containing peptides,11 the GWALP23 with Lys in the 12th position shows a smaller tendency to remain in a single membrane bound configuration, which makes it difficult to determine the pKa of this residue.10

These examples and several more8,19−22 are strong evidence of the effect of the microenvironment on the protonation equilibria of protein side chains. Thus, along with experimental techniques such as NMR, several computational methods have been developed to calculate the pKa values of titratable residues in different environments. Among these techniques, constant pH molecular dynamics (CPHMD) approaches are particularly devised to study pH dependent behavior of proteins for which little information about the charged states of the key residues are available. Unlike Poisson–Boltzmann based approaches,23 in the CPHMD methods, protonation states of a side chain are coupled with the protein dynamics and are allowed to propagate with time following degrees of freedom in the system. There are two distinct CPHMD approaches that are in use. In discrete CPHMD methods, first developed by van Gunsteren et al.,24−26 the charge states of titratable residues are determined by performing Monte Carlo (MC) steps at specific intervals of regular molecular dynamics simulations. In this approach, the abrupt change in the protonation states of the residues (and overall charge of the system) can lead to discontinuity of the potential energy and possible side effects after MC moves along the titration coordinate. This issue is alleviated in the continuous CPHMD methods pioneered by Brooks et al. In this category of CPHMD techniques, the titration coordinates propagate in time using a λ dynamics approach,27−29 which provides a continuous switch between different protonation states and prevents sudden jumps in the potential energy and its derivatives. We note that λ dynamics is related in its underlying formulation to techniques devised by Pettitt and co-workers for the addition and deletion of particles within a grand canonical ensemble to achieve constant chemical potential.30,31

First implemented in an implicit solvent framework32 and later improved to include proton tautomerism, continuous CPHMD33 has been shown to be successful in calculating the pKa values of titratable residues for a diverse set of proteins.33−38 In spite of numerous successes, this method suffers from the well-known disadvantages of the generalized Born implicit solvent models. For instance, the overestimation of the desolvation energy for the buried charges in the protein core,39,40 or the compactness of the protein structures,38,41 can induce systematic errors in pKa calculations. More significant errors can occur for membrane proteins with buried charge residues as a result of assumptions used in the implicit membrane models, such as the rigid nature of the membrane bilayer,42−44 the insertion of a charged residue in the hydrophobic core of the membrane requires complete loss of its solvation shell. However, as evidenced in detailed explicit membrane/solvent simulations, charged residues in the membrane are surrounded by a few water molecules and possibly phosphate head groups.45,46 Partial solvation of the charged residues helps to compensate for the low dielectric environment of the membrane and significantly reduces the insertion energy, while total loss of the solvation shell in implicit membrane models leads to systematic overestimation of side chain pKa’s.47,48 Recently, Brooks and co-workers developed a novel explicit solvent CPHMD approach based on a new multisite λ dynamics framework (CPHMDMSλD)49,50 and applied it to study the pH-dependent dynamics of several RNA51,52 and protein53 systems. In addition, to address the convergence problems of earlier CPHMD variants,51,54 pH-based replica exchange may be employed to enhance the sampling of the spatial and titration coordinates.52

Inspired by the recent pKa measurements of the buried Lys residues in 1,2-di(9Z-octadecenoyl)-sn-glycero-3-phosphocholine (DOPC) bilayers,10 we were motivated to utilize the CPHMDMSλD method on several TM-GWALP23 peptides containing titratable residues at position 12 or 14 to examine the influence of the membrane on the structure and pKa of the ionizable residues in these peptides. Our results indicate that the CPHMDMSλD method reproduces the pKa’s of Lys residues in the Lys-containing GWALP23 peptides inserted in the membrane bilayer, in good accord with the pKa measurements from quadrupolar splitting (QS) of deuterated Ala residues.10 In addition, we observe that the peptide tilt angle is affected by the protonation state of the titratable residues: for example, the peptides are significantly more tilted in charged states, and this general trend of the tilt angle variation is in agreement with the SSNMR data. In addition, we directly predict the pKa variations of His in an ether-linked DOPC bilayer and Glu and Asp in an ether-linked 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC) in the context of TM-GWALP23 peptides. Overall, our results indicate that both protonation states and tilt angles in the peptides containing titratable residues are considerably influenced by their surrounding environment.

Methods

The list of the peptides simulated in this paper along with their sequence and the membrane they are inserted in are provided in Table 1. Insertion of the peptides along with the equilibration steps are described in more detail in the Supporting Information.

Table 1. Sequences, Lipid Bilayer Composition, Number of Replicas, pH range, and Calculated and Experimental Values for Each Simulated TM Peptide.

name sequence membrane no. of replicas (pH range) pKa
K12 acetyl-GGALY(LA)3K(AL)3WLAGA-amide DOPC 8(2–9) 5.7 ± 0.2(<7)b
K14 acetyl-GGALY(LA)4K(AL)2WLAGA-amide DOPC 8(2–9) 5.6 ± 0.2(6.8)b
H12 acetyl-GGALY(LA)3H(AL)3WLAGA-amide DOPCa 9(0–8) 4.0 ± 0.1
H14 acetyl-GGALY(LA)4H(AL)2WLAGA-amide DOPCa 9(0–8) 4.5 ± 0.3
E12 acetyl-GGALY(LA)3E(AL)3WLAGA-amide DLPCa 9(5–13) 9.8 ± 0.1
E14 acetyl-GGALY(LA)4E(AL)2WLAGA-amide DLPCa 9(5–13) 9.7 ± 0.1
D12 acetyl-GGALY(LA)3D(AL)3WLAGA-amide DLPCa 9(5–13) 9.4 ± 0.2
D14 acetyl-GGALY(LA)4D(AL)2WLAGA-amide DLPCa 9(5–13) 9.4 ± 0.2
Open in a new tab
a

Carboxyl group is substituted with ether.

b

Experimental values in parentheses taken from ref (10).

The pH-replica exchange simulations (pH-REX) on the membrane-inserted peptides were performed in the following manner. The structures obtained from the equilibration runs of protonated and unprotonated side chains were used as the initial structures of the pH-REX calculations with each equilibrated structure used as alternative replicas. The number of replicas and the pH range for each system is listed in Table 1. Replica exchange in the pH variable has previously been shown to improve the convergence of pKa calculations.55 All simulations were performed using CPHMDMSλD with the BLOCK facility and the λN exp functional form with a coefficient of 5.5.53 Expressing λ in this particular form in terms of virtual particles that propagate through the course of the simulation (θα) has been shown to increase energy stability. More detailed discussion on the effect of functional form of λ versus θα is provided in ref.49 All nonbonded energy terms were linearly scaled by λ while all bond, angle and dihedral terms were unscaled. λ values were saved every 10 steps. A nonbonded cutoff of 12 Å was used with an electrostatic force-shifting function and a van der Waals switching function. A fictitious mass of 12 amu·Å2 was assigned to all θα. In the pH-REX simulations, exchange attempts were made every 1 ps. Each pH-REX simulation was repeated 3 times for 5 ns per replica, from which the last 3 ns was used for analysis. The average pKa’s are reported in Table 1. All parameters for the pH-Rex simulations were kept as default values as listed in ref (53).

The fraction of unprotonated state at each pH (Sunprot) was determined from the total population of the unprotonated (Nunprot) and protonated states (Nprot) states.

graphic file with name jp-2015-002892_m001.jpg 1

These populations are defined as the total number of times in the trajectory that the condition λ > 0.8 for eitnher the unprotonated or protonated state is satisfied.

To obtain the pKa of the system of interest, Sunprot is fitted versus pH using the Henderson–Hasselbalch equation.

graphic file with name jp-2015-002892_m002.jpg 2

The configuration of the peptides at different pH values was also examined. The tilt angle of the peptides was measured as the angle between the membrane normal (z-axis) and the peptide axis, which was defined as the vector connecting the Cα atoms. The rotation angle is defined as the angle between the vector that connects the helical axis to the Cα atom of residue Leu 14 and is perpendicular to the helix axis, and the projection vector of the z-axis onto the plane made by the second and third principal axes. For a more detailed definition of the tilt and rotation angles, please see ref (56).

Results and Discussion

We have simulated eight TM peptides, each having one titratable residue (i.e., K, H, E, or D) at position 12 or 14 in the peptide. The purpose of this study is to investigate the effect of the membrane bilayers on the pKa values of these residues, as well as to examine the pH-dependent variation of the peptide configurations in the membranes. In addition, we compare the pKa values obtained from the CPHMDMSλD simulations with those of Lys containing residues from the SSNMR measurements10 and make direct predictions for the other titratable side chains.

The pKa values for different side chains, averaged over three runs, are listed in Table 1. The corresponding titration curves are displayed in Figure 1. Our results show that the Lys residue in the K14 peptide has a pKa of 5.6 ± 0.2, in good agreement with the estimated experimental value of 6.8 at 300 K10 and within the error bars observed for insertion free energies of different side chains in membrane bilayers.57 The difference we see here may be due to the steep gradient of the membrane dielectric across its normal. Small changes in the position of the side chain across the membrane normal is accompanied by large variation in the apparent dielectric constant of the membrane, which can cause significant changes in the side chains pKa.42,58 The QS measurements of Ala residues for the K12 peptide only determined an upper bound of 7 for the pKa value of the Lys side chain.10 Our calculated pKa of 5.7 ± 0.2 is consistent with this bound. Thus, we find that, consistent with the SSNMR experiment, the pKa of Lys residues at the 12th or 14th position of GWALP peptides are shifted by ∼4.4 pH units. Interestingly, similar pKa shifts were previously observed for Lys residues in engineered mutants of staphylococcal nuclease.21 Among 25 single mutations, 4 mutants with Lys residues located in the inner core of the protein showed depressed pKa values between 5.3 and 6.5,21 which were accompanied by partial or global unfolding of the protein at low pH values.

Figure 1.

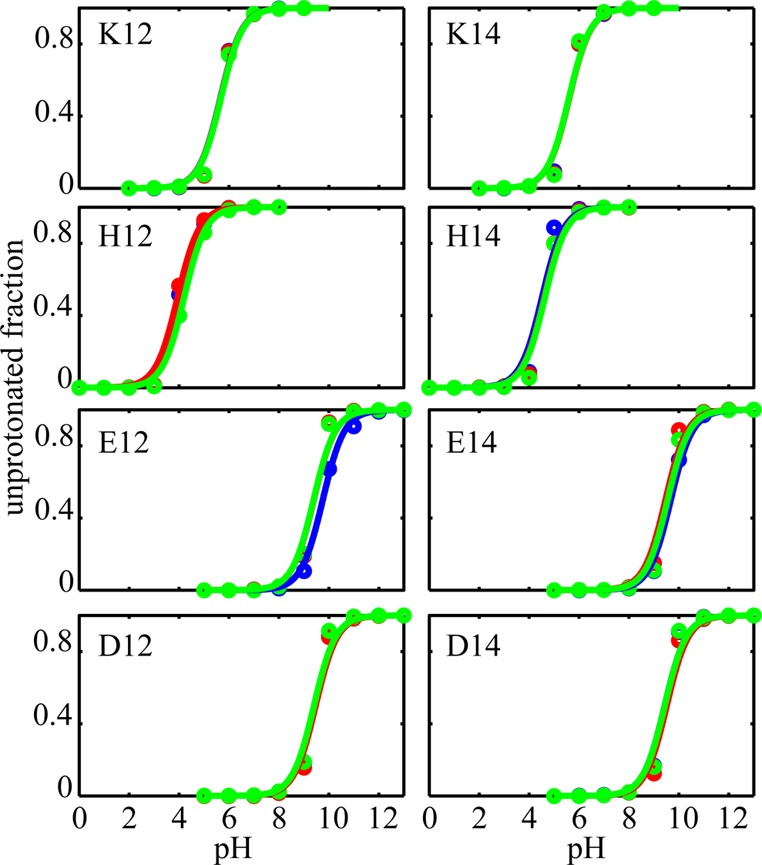
Figure 1

Open in a new tab

Titration curves for three trials of pH-REX for different peptides listed in Table 1. The unprotonated fractions obtained from pH-REX are shown with circles, and the lines represent the Henderson–Hasselbach fit. In some panels, due to overlap of the curves and data points, only two out of three colors are visible.

Since no measurements yet exist for substitutions of His, Asp, or Glu at these same positions in the GWALP peptides, we decided to make direct predictions of the pKa values and the corresponding peptide configurations. For all substituted residues, significant pKa shifts with respect to the standard reference pKa values are observed. In the case of the His-containing peptides, H12 and H14 in Table 1, pKa shifts of ∼2 and ∼1.5 units toward the neutral form are observed, respectively. Glu residues at these positions (E12 and E14) yield calculated pKa values of 9.8 ± 0.1 and 9.7 ± 0.1. For the Asp residue at position 12 (D12) and 14 (D14), pKa values of 9.4 ± 0.2 are obtained. We note that in a different study using fluorescence emission of a Trp residue, a pKa of 8.7 was reported for an Asp residue in the transmembrane helix formed by the peptide K2GL7DLWL9K2A (termed pL(D11)) indicating a ∼4.7 pH unit shift in favor of the neutral state in a DOPC bilayer.12 While, due to different peptide sequences and membrane compositions, direct comparison between this value and the pKa observed in our simulations is difficult, the difference can be attributed to the interfacial orientation of the peptide that is suggested to be adopted in the latter study.12 The significant shift of the pKa values of E and D at positions 12 and 14 suggest that the ratio of protonated versus unprotonated side chains in membranes is severely shifted toward the latter and, perhaps, in the absence of any other stabilizing interactions (e.g., salt bridges with neighboring residues), these side chains tend to stay protonated in the membrane within the biologically relevant pH ranges.

In order to investigate the effect of pH on the charge state and eventually the configurations of these peptides in membrane bilayers, we examined the tilt and rotation angles of the peptides at different pH values. The potential of mean forces (PMF) for basic (K and H) and acidic (E and D) side chains along their tilt and rotation angles were calculated and are shown in Figures 2 and 3, and the dominant structures extracted from the replicas with specified pH values are depicted in Figures 4 and 5, respectively. For positively charged side chains, depicted in the left column of Figure 2, the peptides adopt tilt angles between 30° and 50°, and rotation angles between 20° and 100°. The neutral peptides, which are populated at high pH values, on the other hand adopt smaller tilt angles roughly form 5° to 25° with rotation angles that are not significantly affected (Figure 2 right column). The experimental values for the K14 peptide at high and low pH values and for K12 at high pH obtained from the QS of deuterated Ala residues10 are marked in the figure with red circles. Due to complexity of the QS data for K12 at low pH, no tilt and rotation angles were reported. It can be seen that the tilt and rotation angles obtained experimentally for K12 and K14 at high pH values are part of diverse ensembles that are sampled by these peptides in our simulations. For positively charged K14, on the other hand, the tilt and rotation angles that are adopted by the peptide in our simulations are significantly larger.

Figure 2.

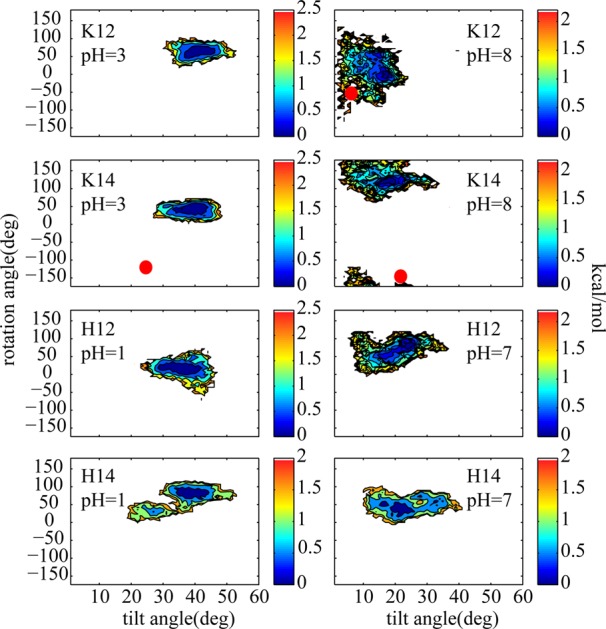
Figure 2

Open in a new tab

2D PMFs of rotation angle vs tilt angle for TM helices containing K and H side chains for low and high pH values where the titratable side chains are predominantly protonated (positively charged) and unprotonated (neutral), respectively. The experimental values are marked with red circles.10 The color bars are in kcal/mol.

Figure 3.

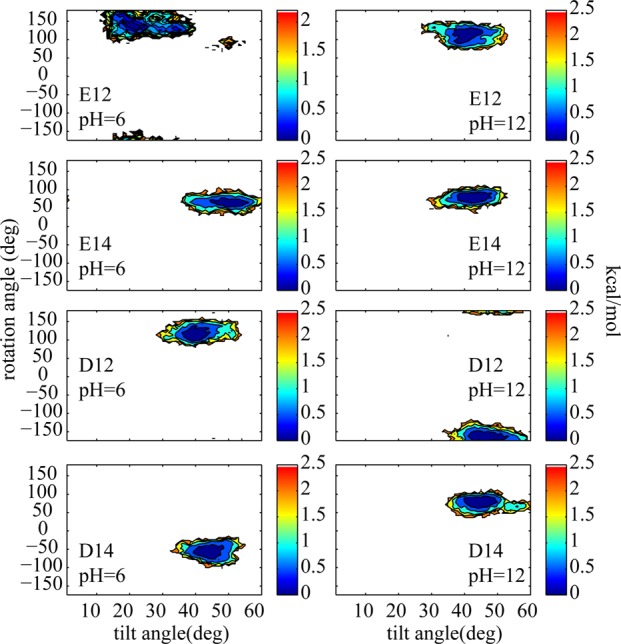
Figure 3

Open in a new tab

2D PMFs of rotation angle vs tilt angle for TM helices containing E and D side chains for low and high pH values where the titratable side chains are predominantly protonated (neutral) and unprotonated (negatively charged) respectively. The color bars are in kcal/mol.

Figure 4.

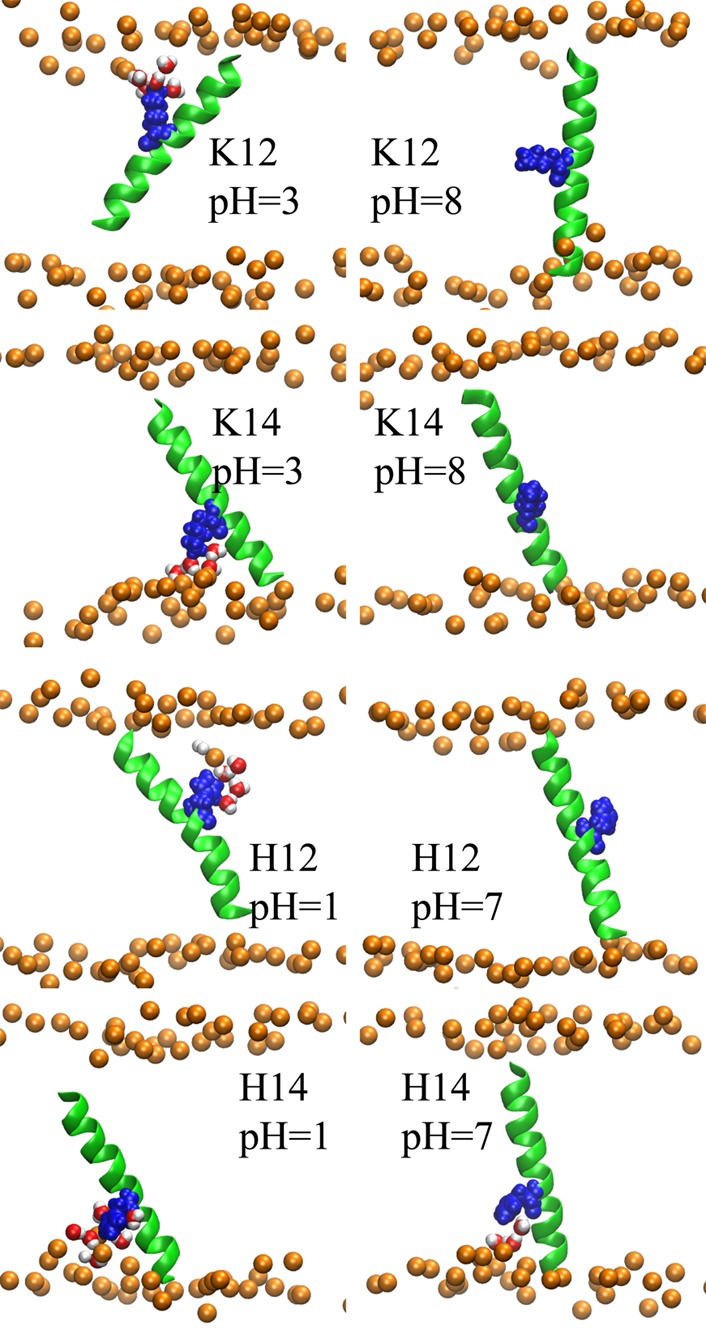
Figure 4

Open in a new tab

Representative structures of TM peptides containing one basic side chain obtained from the replica with specified pH value. The structures were rendered using VMD.63 The peptide backbone is depicted with green cartoon representation, while the titratable side chains are shown with blue van der Waals representations. The bilayer phosphate head groups are shown with orange spheres. The lipid tails are not shown to avoid complexity. Water molecules whose center of masses are within 5 Å of the side chains are illustrated with van der Waals spheres and red color.

Figure 5.

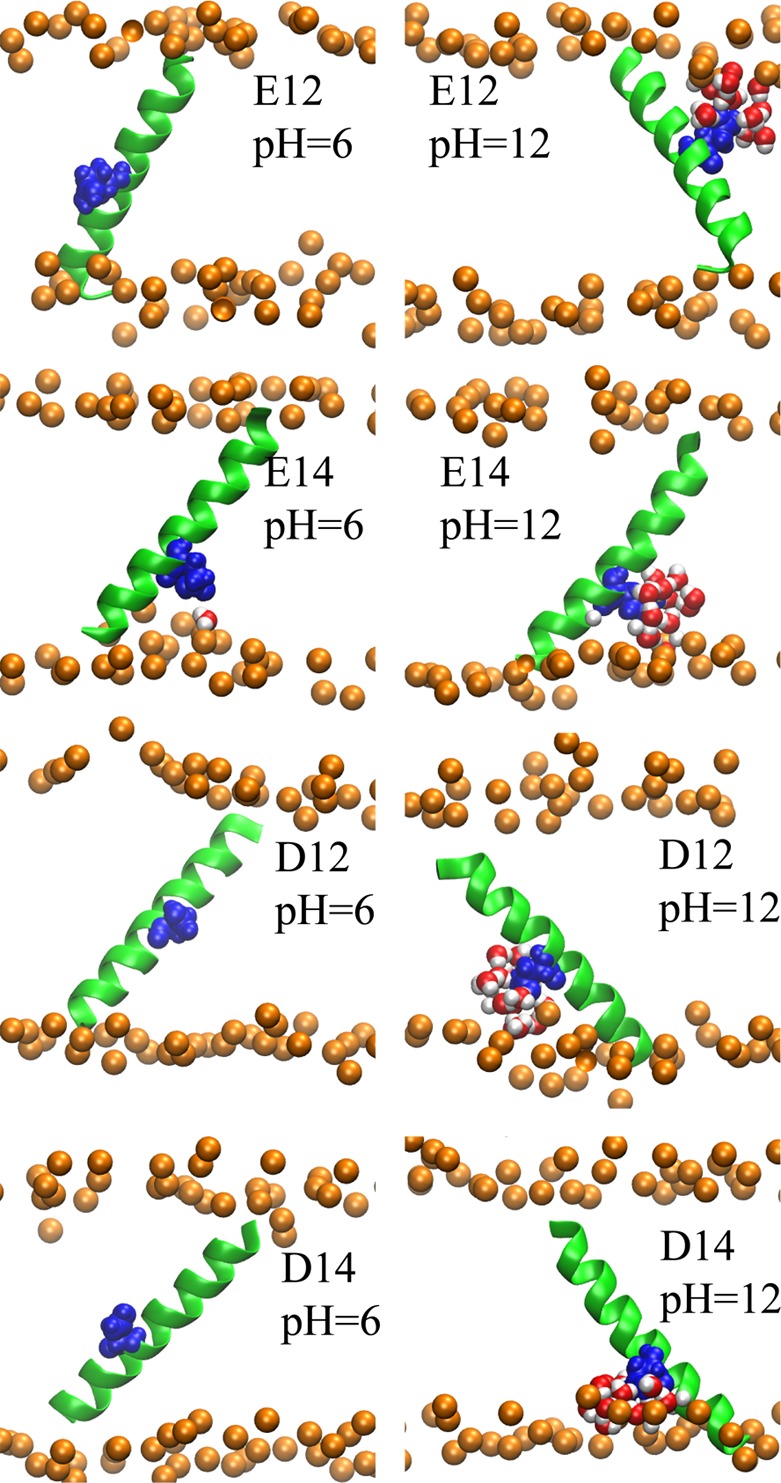
Figure 5

Open in a new tab

Representative structures of peptides obtained from the replica with the specified pH. The color coding and representation is the same as described in Figure 4. The structures were rendered using VMD.63

We also examined the distribution of tilt and rotation angles for the acidic side chains at both high and low pH (see Figure 3). At low pH, where the side chains are protonated and neutral (Figure 3 left column), the peptides tend to have smaller tilt and rotation angles compared to high pH (Figure 3 right column), where the side chains are negatively charged.

While the pH dependent variations of the tilt and rotation angles of K12 and K14 agree well with the experimental values, the values we observe are larger than those reported from the experimental measurements. Similar apparent disagreements between tilt and rotation angles obtained from molecular dynamics simulations and the values calculated from SSNMR observables have been noticed before for several TM peptides including the WALP series.17,18,43,59 These discrepancies are believed to stem from orientational fluctuations of the peptides in membrane bilayers. Recently, extensive attempts have been made to capture the complex motions of TM helices in different models in order to extract more representative tilt and rotation angles from SSNMR QS measurements. However, SSNMR observables are time and ensemble averaged data, which may not fully represent a single helix orientation. Therefore, more complicated methods are needed to obtain the tilt and rotation angles from these measurements.60

Finally, the effect of pH on the orientation of the peptides and the structure of the membrane aqueous interface can be highlighted with further details by looking at representative structures from our simulations. The dominant structures of each peptide at high and low pH values were selected as noted in the computational methodology and the results for positive and negative side chains are depicted in Figures 4 and 5, respectively. For the basic side chains, as illustrated in Figure 4, at low pH (left column), the peptides tend to have highly tilted structures with more interfacial exposure of the side chain. The tilting of the peptides accompanied by the deformation of the bilayer, which allows solvation of the charged state with water molecules and head-groups, leads to considerable stabilization of the charged states.45,46 However, increasing the pH (Figure 4 right column) causes the solvation shell to be lost and the tilt angle to decrease. The same effect can be observed in Figure 5 for acidic side chains. At low pH values, the peptides tend to have smaller tilt angles while at high pH the tilt angles are increased and the solvation shell around the side chains is formed (compare left and right columns of Figure 5). In addition to the improved charge solvation provided by helix tilting, the enhanced tilting of the peptide in the presence of the charged side chain can also be explained by the effect of partial solvation on the membrane thickness. The water molecules and head groups in the solvation shell that surround the charged side chain and penetrate into the hydrophobic core of the membrane, cause the local membrane thickness around the side chain to decrease. The thinning of the membrane causes the helix to tilt to maximize the interactions between membrane core and the hydrophobic peptide. In addition, tilting of the helix when the side chain is charged provides more exposure of the side chain to the membrane exterior where it incurs a lesser desolvation penalty. The effect of peptide sequence and membrane thickness fluctuation on the peptide tilt angle have been discussed in more detail in the following references: (45, 47, 48, and 61) and the references therein.

Our simulations suggest that the observed pKa values are tightly coupled to the conformation of the peptide and membrane/water interface. Detailed explicit solvent simulations of insertion of proteins and small molecules into lipid bilayer57,62 have revealed that these fluctuations are typically kinetically hindered and long time scale simulations (possibly ms) may be required to ensure convergence of the thermodynamics properties. This may be reflected in the pKa values reported here. In principle, CPHMDMSλD simulations can be combined with umbrella sampling along rotation and tilt angles of the peptide or advanced enhanced sampling techniques such as the ensemble dynamics approach56,60 to strengthen the sampling along these two reaction coordinates. However, our generally good agreement with experiment in the case of the lysine based peptides and the similar charge-state dependence of the peptide orientation and membrane interface structure for both basic and acidic peptides suggest that our findings are at least semiquantitatively reasonable.

Conclusions

In this study, we have applied for the first time constant pH molecular dynamics techniques to calculate the pKa values of titratable side chains in the context of TM helices and investigated the effect of pH on the configuration of the studied peptides. Our calculated pKa values for the Lys-containing peptides and the values previously obtained using SSNMR QS of deutrated Ala residues10 are in good agreement. We also observed that the configuration of the various peptides and the arrangement of the lipid molecules in the vicinity of the side chains are coupled to the external pH. At pH values where the population of the charged states dominates, the peptides tend to have more tilted structures with notable membrane deformation. On the other hand, when the pH is such that the population of the neutral side chains is pronounced, the tilt angles are decreased and the membrane deformation is less significant.

The overall good agreement between the calculated pKa values and the experimental values especially for the case of Lys containing peptides10 and the variation of the peptide conformation with pH suggest that the CPHMDMSλD captures the essence of pH dependency of peptide membrane interactions.

Acknowledgments

Support from the NIH through GM107233 is acknowledged.

Supporting Information Available

Detailed steps of system preparation and equilibration. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

C.L.B. designed the research, A.P. performed the simulations and the analysis, and C.L.B and A.P. wrote the paper.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jp5b00289_si_001.pdf (110.8KB, pdf)

References

  1. Von Heijne G. The Membrane Protein Universe: What’s out There and Why Bother?. J. Intern. Med. 2007, 261, 543–557. [DOI] [PubMed] [Google Scholar]
  2. Wallin E.; Heijne G. Von. Genome-Wide Analysis of Integral Membrane Proteins from Eubacterial, Archaean, and Eukaryotic Organisms. Protein Sci. 1998, 7, 1029–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boyd D.; Schierle C.; Beckwith J. How Many Membrane Proteins Are There?. Protein Sci. 1998, 7, 201–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Landolt-Marticorena C.; Williams K. A.; Deber C. M.; Reithmeier R. A. F. Non-Random Distribution of Amino Acids in the Transmembrane Segments of Human Type I Single Span Membrane Proteins. J. Mol. Biol. 1993, 229, 602–608. [DOI] [PubMed] [Google Scholar]
  5. Gratkowski H.; Lear J. D.; DeGrado W. F. Polar Side Chains Drive the Association of Model Transmembrane Peptides. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 880–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Caputo G. A.; London E. Cumulative Effects of Amino Acid Substitutions and Hydrophobic Mismatch upon the Transmembrane Stability and Conformation of Hydrophobic A-Helices. Biochemistry 2003, 42, 3275–3285. [DOI] [PubMed] [Google Scholar]
  7. Kim C.; Schmidt T.; Cho E.-G.; Ye F.; Ulmer T. S.; Ginsberg M. H. Basic Amino-Acid Side Chains Regulate Transmembrane Integrin Signalling. Nature 2012, 481, 209–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cymes G. D.; Grosman C. Tunable pKa Values and the Basis of Opposite Charge Selectivities in Nicotinic-Type Receptors. Nature 2011, 474, 526–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Galzi J. L.; Devillers-Thiéry A.; Hussy N.; Bertrand S.; Changeux J. P.; Bertrand D. Mutations in the Channel Domain of a Neuronal Nicotinic Receptor Convert Ion Selectivity from Cationic to Anionic. Nature 1992, 359, 500–505. [DOI] [PubMed] [Google Scholar]
  10. Gleason N. J.; Vostrikov V. V.; Greathouse D. V.; Koeppe R. E. Buried Lysine, but Not Arginine, Titrates and Alters Transmembrane Helix Tilt. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 1692–1695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Vostrikov V. V.; Hall B. A.; Greathouse D. V.; Koeppe R. E.; Sansom M. S. P. Changes in Transmembrane Helix Alignment by Arginine Residues Revealed by Solid-State NMR Experiments and Coarse-Grained MD Simulations. J. Am. Chem. Soc. 2010, 132, 5803–5811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Caputo G. A.; London E. Position and Ionization State of Asp in the Core of Membrane-Inserted Alpha Helices Control Both the Equilibrium between Transmembrane and Nontransmembrane Helix Topography and Transmembrane Helix Positioning. Biochemistry 2004, 43, 8794–8806. [DOI] [PubMed] [Google Scholar]
  13. Killian J. A.; Salemink I.; de Planque M. R.; Lindblom G.; Koeppe R. E.; Greathouse D. V. Induction of Nonbilayer Structures in Diacylphosphatidylcholine Model Membranes by Transmembrane Alpha-Helical Peptides: Importance of Hydrophobic Mismatch and Proposed Role of Tryptophans. Biochemistry 1996, 35, 1037–1045. [DOI] [PubMed] [Google Scholar]
  14. Vostrikov V. V.; Grant C. V.; Daily A. E.; Opella S. J.; Koeppe R. E. Comparison of “Polarization Inversion with Spin Exchange at Magic Angle” and “Geometric Analysis of Labeled Alanines” Methods for Transmembrane Helix Alignment. J. Am. Chem. Soc. 2008, 130, 12584–12585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Killian J. A.; Nyholm T. K. M. Peptides in Lipid Bilayers: The Power of Simple Models. Curr. Opin. Struct. Biol. 2006, 16, 473–479. [DOI] [PubMed] [Google Scholar]
  16. Killian J. A. Synthetic Peptides as Models for Intrinsic Membrane Proteins. FEBS Lett. 2003, 555, 134–138. [DOI] [PubMed] [Google Scholar]
  17. Strandberg E.; Ozdirekcan S.; Rijkers D. T. S.; van der Wel P. C. A.; Koeppe R. E.; Liskamp R. M. J.; Killian J. A. Tilt Angles of Transmembrane Model Peptides in Oriented and Non-Oriented Lipid Bilayers as Determined by 2H Solid-State NMR. Biophys. J. 2004, 86, 3709–3721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ozdirekcan S.; Etchebest C.; Killian J. A.; Fuchs P. F. J. On the Orientation of a Designed Transmembrane Peptide: Toward the Right Tilt Angle?. J. Am. Chem. Soc. 2007, 129, 15174–15181. [DOI] [PubMed] [Google Scholar]
  19. Hristova K.; Wimley W. C. A Look at Arginine in Membranes. J. Membr. Biol. 2011, 239, 49–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Moon C. P.; Fleming K. G. Side-Chain Hydrophobicity Scale Derived from Transmembrane Protein Folding into Lipid Bilayers. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10174–10177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Isom D. G.; Castañeda C. A.; Cannon B. R.; García-Moreno B. Large Shifts in pKa Values of Lysine Residues Buried inside a Protein. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 5260–5265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Isom D. G.; Cannon B. R.; Castañeda C. A.; Robinson A.; García-Moreno B. High Tolerance for Ionizable Residues in the Hydrophobic Interior of Proteins. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 17784–17788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Bashford D. Macroscopic Electrostatic Models for Protonation States in Proteins. Front. Biosci. 2004, 9, 1082. [DOI] [PubMed] [Google Scholar]
  24. Bürgi R.; Kollman P. A.; Van Gunsteren W. F. Simulating Proteins at Constant pH: An Approach Combining Molecular Dynamics and Monte Carlo Simulation. Proteins: Struct., Funct., Bioinf. 2002, 47, 469–480. [DOI] [PubMed] [Google Scholar]
  25. Mongan J.; Case D. A.; McCammon J. A. Constant pH Molecular Dynamics in Generalized Born Implicit Solvent. J. Comput. Chem. 2004, 25, 2038–2048. [DOI] [PubMed] [Google Scholar]
  26. Baptista A. M.; Teixeira V. H.; Soares C. M. Constant-pH Molecular Dynamics Using Stochastic Titration. J. Chem. Phys. 2002, 117, 4184. [Google Scholar]
  27. Kong X.; Brooks C. L. III. λ-Dynamics: A New Approach to Free Energy Calculations. J. Chem. Phys. 1996, 105, 2414. [Google Scholar]
  28. Guo Z.; Brooks C. L. III; Kong X. Efficient and Flexible Algorithm for Free Energy Calculations Using the Λ-Dynamics Approach. J. Phys. Chem. B 1998, 102, 2032–2036. [Google Scholar]
  29. Knight J. L.; Brooks C. L. III. Lambda-Dynamics Free Energy Simulation Methods. J. Comput. Chem. 2009, 30, 1692–1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lynch G. C.; Pettitt B. M. Grand Canonical Ensemble Molecular Dynamics Simulations: Reformulation of Extended System Dynamics Approaches. J. Chem. Phys. 1997, 107, 8594. [Google Scholar]
  31. Çağin T.; Pettitt B. M. Molecular Dynamics with a Variable Number of Molecules. Mol. Phys. 1991, 72, 169–175. [Google Scholar]
  32. Lee M. S.; Salsbury F. R.; Brooks C. L. III. Constant-pH Molecular Dynamics Using Continuous Titration Coordinates. Proteins: Struct., Funct., Bioinf. 2004, 56, 738–752. [DOI] [PubMed] [Google Scholar]
  33. Khandogin J.; Brooks C. L. III. Constant pH Molecular Dynamics with Proton Tautomerism. Biophys. J. 2005, 89, 141–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Law S. M.; Zhang B. W.; Brooks C. L. III. pH-Sensitive Residues in the p19 RNA Silencing Suppressor Protein from Carnation Italian Ringspot Virus Affect siRNA Binding Stability. Protein Sci. 2013, 22, 595–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Zhang B. W.; Brunetti L.; Brooks C. L. III. Probing pH-Dependent Dissociation of HdeA Dimers. J. Am. Chem. Soc. 2011, 133, 19393–19398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Khandogin J.; Brooks C. L. III. Linking Folding with Aggregation in Alzheimer’s Beta-Amyloid Peptides. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 16880–16885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wallace J. A.; Shen J. K. Unraveling A Trap-and-Trigger Mechanism in the pH-Sensitive Self-Assembly of Spider Silk Proteins. J. Phys. Chem. Lett. 2012, 3, 658–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shen J. K. Uncovering Specific Electrostatic Interactions in the Denatured States of Proteins. Biophys. J. 2010, 99, 924–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Khandogin J.; Brooks C. L. III. Toward the Accurate First-Principles Prediction of Ionization Equilibria in Proteins. Biochemistry 2006, 45, 9363–9373. [DOI] [PubMed] [Google Scholar]
  40. Arthur E. J.; Yesselman J. D.; Brooks C. L. III. Predicting Extreme pKa Shifts in Staphylococcal Nuclease Mutants with Constant pH Molecular Dynamics. Proteins: Struct., Funct., Bioinf. 2011, 79, 3276–3286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wallace J. A.; Shen J. K. Continuous Constant pH Molecular Dynamics in Explicit Solvent with pH-Based Replica Exchange. J. Chem. Theory Comput. 2011, 7, 2617–2629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Tanizaki S.; Feig M. A Generalized Born Formalism for Heterogeneous Dielectric Environments: Application to the Implicit Modeling of Biological Membranes. J. Chem. Phys. 2005, 122, 124706. [DOI] [PubMed] [Google Scholar]
  43. Im W.; Feig M.; Brooks C. L. III. An Implicit Membrane Generalized Born Theory for the Study of Structure, Stability, and Interactions of Membrane Proteins. Biophys. J. 2003, 85, 2900–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Spassov V. Z.; Yan L.; Szalma S. Introducing an Implicit Membrane in Generalized Born/Solvent Accessibility Continuum Solvent Models. J. Phys. Chem. B 2002, 106, 8726–8738. [Google Scholar]
  45. Dorairaj S.; Allen T. W. On the Thermodynamic Stability of a Charged Arginine Side Chain in a Transmembrane Helix. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 4943–4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. MacCallum J. L.; Bennett W. F. D.; Tieleman D. P. Partitioning of Amino Acid Side Chains into Lipid Bilayers: Results from Computer Simulations and Comparison to Experiment. J. Gen. Physiol. 2007, 129, 371–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Choe S.; Hecht K. A.; Grabe M. A Continuum Method for Determining Membrane Protein Insertion Energies and the Problem of Charged Residues. J. Gen. Physiol. 2008, 131, 563–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Panahi A.; Feig M. Dynamic Heterogeneous Dielectric Generalized Born (DHDGB): An Implicit Membrane Model with a Dynamically Varying Bilayer Thickness. J. Chem. Theory Comput. 2013, 9, 1709–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Knight J. L.; Brooks C. L. III. Applying Efficient Implicit Nongeometric Constraints in Alchemical Free Energy Simulations. J. Comput. Chem. 2011, 32, 3423–3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Knight J. L.; Brooks C. L. III. Multi-Site Λ-Dynamics for Simulated Structure-Activity Relationship Studies. J. Chem. Theory Comput. 2011, 7, 2728–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Goh G. B.; Knight J. L.; Brooks C. L. III. Constant pH Molecular Dynamics Simulations of Nucleic Acids in Explicit Solvent. J. Chem. Theory Comput. 2012, 8, 36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Goh G. B.; Knight J. L.; Brooks C. L. III. pH-Dependent Dynamics of Complex RNA Macromolecules. J. Chem. Theory Comput. 2013, 9, 935–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Goh G. B.; Hulbert B. S.; Zhou H.; Brooks C. L. III. Constant pH Molecular Dynamics of Proteins in Explicit Solvent with Proton Tautomerism. Proteins 2014, 82, 1319–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Donnini S.; Tegeler F.; Groenhof G.; Grubmüller H. Constant pH Molecular Dynamics in Explicit Solvent with Λ-Dynamics. J. Chem. Theory Comput. 2011, 7, 1962–1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Goh G. B.; Laricheva E. N.; Brooks C. L. III. Uncovering pH-Dependent Transient States of Proteins with Buried Ionizable Residues. J. Am. Chem. Soc. 2014, 136, 8496–8499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Kim T.; Im W. Revisiting Hydrophobic Mismatch with Free Energy Simulation Studies of Transmembrane Helix Tilt and Rotation. Biophys. J. 2010, 99, 175–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Neale C.; Bennett W. F. D.; Tieleman D. P.; Pomès R. Statistical Convergence of Equilibrium Properties in Simulations of Molecular Solutes Embedded in Lipid Bilayers. J. Chem. Theory Comput. 2011, 7, 4175–4188. [DOI] [PubMed] [Google Scholar]
  58. MacCallum J. L.; Bennett W. F. D.; Tieleman D. P. Distribution of Amino Acids in a Lipid Bilayer from Computer Simulations. Biophys. J. 2008, 94, 3393–3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Monticelli L.; Tieleman D. P.; Fuchs P. F. J. Interpretation of 2H-NMR Experiments on the Orientation of the Transmembrane Helix WALP23 by Computer Simulations. Biophys. J. 2010, 99, 1455–1464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Im W.; Jo S.; Kim T. An Ensemble Dynamics Approach to Decipher Solid-State NMR Observables of Membrane Proteins. Biochim. Biophys. Acta 2012, 1818, 252–262. [DOI] [PubMed] [Google Scholar]
  61. Li L.; Vorobyov I.; Allen T. W. Potential of Mean Force and pKa Profile Calculation for a Lipid Membrane-Exposed Arginine Side Chain. J. Phys. Chem. B 2008, 112, 9574–9587. [DOI] [PubMed] [Google Scholar]
  62. Neale C.; Hsu J. C. Y.; Yip C. M.; Pomès R. Indolicidin Binding Induces Thinning of a Lipid Bilayer. Biophys. J. 2014, 106, L29–L31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Humphrey W.; Dalke A.; Schulten K. {VMD}—{V}isual {M}olecular {D}ynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp5b00289_si_001.pdf (110.8KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES