Mean Remaining Lifespan: A new clinically relevant parameter to assess the quality of transfused red blood cells

Abstract

Background

Quality of transfused red blood cells (RBC) to treat anemia depends on its potential for oxygen delivery, governed by two properties: 1) initial post transfusion recovery (PTR₂₄); and 2) lifespan of initially surviving RBCs. The latter property is poorly evaluated by the traditional mean potential lifespan (MPL) or mean cell age (MA), because these parameters do not evaluate how long transfused RBCs remain in circulation. Furthermore, evaluation of MPL is based on two problematic assumptions regarding transfused RBCs: 1) they were produced at a constant steady state rate; 2) they have similar storage lifespans.

Study design and methods

This work introduces a new parameter, the mean remaining lifespan (MRL) to quantify transfused RBC survival (TRCS) and presents a simple algorithm for its evaluation. The MRL was calculated for four adult subjects with sickle cell disease and four adult diabetic and non-diabetic subjects using RBC survival data sets with existing TRCS parameters.

Results

The RBC survival curves in the sickle cell subjects were non-linear with rapid decline in survival within the first 5 d. The MRL was approximately 4.6 d. Thus, the MRL was indicative of the survival of all transfused RBCs. For the diabetic and non-diabetic subjects, the RBC disappearance curves did not deviate substantially from a linear decline. Thus, the estimates for MRL ranging from 39-51 d are similar to the MA previously computed.

Conclusion

MRL overcomes limitations of previously proposed TRCS parameters, is simpler to calculate, and is physiologically and clinically more appropriate.

INTRODUCTION

The goal of administering RBC transfusions is to increase the circulating blood oxygen content in anemic individuals to improve tissue oxygenation. Regulatory licensing dealing with the short-term quality of transfused RBCs has focused on the proportion of viable post-transfusion RBCs recovered at 24 h (PTR₂₄).^1-3 Labeling is used to evaluate red cell survival (RCS) of transfused RBCs. FDA regulatory standards for RBC products specify that: “Recovery of greater than 75 percent of radiolabeled RBC 24 h after infusion into autologous donors.”^4,5

In addition to PTR₂₄, other long-term RBC kinetic parameters most commonly used to characterize RCS include half-life (T₅₀), mean potential lifespan (MPL) and mean cell age (MA). The T₅₀ is defined as the time post transfusion when 50 percent of the transfused RBCs remain in the circulation. The RBC mean age (MA) represents the mean age of RBCs at time of transfusion and is derived from the mathematical relationship between the age distribution of the RBCs and their disappearance rate.⁶ If all the cells had the same age, then the death rate (i.e., same as survival function) takes the form of a straight line.⁷ The mean red-cell lifespan as defined by the International Committee for Standardization in Hematology is the mean survival time of all circulating RBCs irrespective of their destruction mechanism, i.e., random destructions vs. senescence.⁸ If the transfused donor RBCs were produced under steady-state conditions of erythropoiesis and have the same survival properties, i.e., the same intrinsic lifespan, then the RCS curve exhibits a linear decline typically quantified by linear least square regression. The MPL is then obtained by simple linear extrapolation to intersection with the time axis.⁹

This linear extrapolation time point used to evaluate MPL represents the time when the “youngest” of the RBCs transfused is removed from the circulation and thus is a poor overall representation of red cell survival. A MPL value of 120 d evaluated by the extrapolation method does not indicate that transfused RBCs remain, on average, in circulation in the recipient for 120 d. Instead, MPL indicates the time when the youngest, most viable RBCs at the time of RBC labeling were removed from the circulation. Such cells normally represent only a small fraction of the transfused RBCs. Thus, MPL is not an adequate representation of the overall survival of the transfused RBCs. Normally transfused RBCs have ages ranging from zero to the maximum lifespan. This is consistent with the fact that the quantity of transfused RBCs immediately declines after transfusion and continues to do so until those cells that were the youngest at the time of labeling are removed from the circulation, i.e., at the MPL time point.

Clearly, the quantity of transfused RBCs in terms of oxygen delivery capacity is poorly quantified by the MPL parameter. Logically, a parameter quantifying the duration that donor RBCs remain in the recipient's circulation would be a better choice. In this communication the mean remaining lifespan (MRL) parameter is proposed as such a parameter.

The objectives of this analysis are to: 1) introduce the MRL parameter to quantify TRCS and present a simple algorithm for its evaluation; 2) discuss the merits of MRL relative to MPL and other parameters for quantifying TRCS; and 3) demonstrate the evaluation of MRL in various clinical scenarios with the purpose of providing examples of evaluations for discussing conceptual differences relative to other parameters for TRCS.

METHODS

Age, remaining lifespan and total lifespan of RBCs

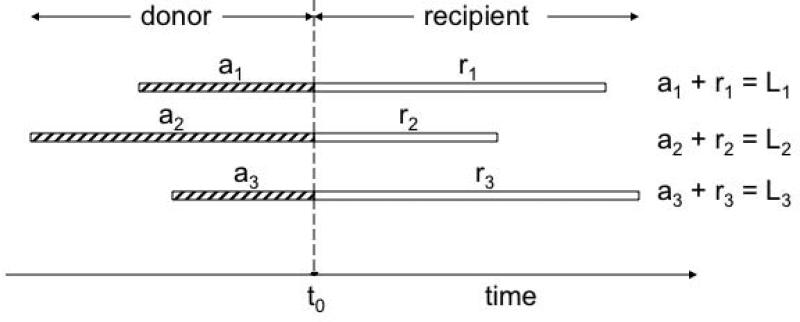
To illustrate the rationale for proposing MRL as a parameter for quantifying TRCS, it is useful to consider a hypothetical example of three individual RBCs that are transfused at arbitrary time, t₀ (Figure 1). The ages of the three RBCs at the time (t₀) of the transfusion are denoted a₁, a₂ and a₃. After transfusion, the three RBCs exhibit a remaining lifespan of r₁, r₂ and r₃. The total lifespan of each RBC is the sum of the age at time of transfusion plus the remaining lifespan, e.g. L₁ = a₁ + r_1. By summing the total RBC lifespan and averaging these, it becomes clear that: mean RBC age at time of transfusion + MRL = mean total lifespan.

Figure 1. Relationship between MPL, MRL and MA.

Three RBCs are transfused to a recipient at time t₀. The mean of a₁, a₂ and a₃ represents the MA of the transfused RBCs. Mean of L₁, L₂ and L₃ represents the MPL of the transfused RBCs. The mean of r₁, r₂ and r₃ represents the MRL, i.e., the mean time the cells will remain in the circulation relative to time t₀, the time of transfusion.

Of the three mean parameters, the MRL is the only parameter that quantifies how long, overall, the transfused RBCs remain in circulation in the recipient and is the most suitable parameter to quantify TRCS.

MRL calculation

The MRL parameter, which is analogous to the mean residence time (MRT) that has been extensively discussed in a pharmacokinetic context^10,11, is calculated as the area under the curve of the fraction (F(t)) of the transfused RBCs remaining in circulation versus time:

$$MRL={\int }_0^{\infty }F\left(t\right)dt$$ (1)

For practicality reasons, it may be more suitable to deal with the MRL representing 95 percent of the transfused RBCs. The reason for this modification is the fact that it is practically impossible to follow the disappearance until all the transfused RBCs have been taken out of circulation. Accordingly, a more practical MRT parameter is evaluated by the following expression

$$MR{L}_{0.95}={\int }_0^{t_{0.95}}F\left(t\right)dt$$ (2)

where t_0.95 is the time when 95 percent of the transfused cells have disappeared from the circulation. This parameter is derived by interpolation of the fraction of RBCs remaining versus time curve.

Consideration of all transfused RBCs instead of those RBCs recovered at 24 h (PTR₂₄)

The fraction remaining, F(t), may be defined in either of two ways depending on whether the interest is in evaluating all transfused RBCs or just those initially surviving, e.g., cells still present 24 h post-transfusion.

F(t) defined for all transfused RBCs is the ratio of quantity of cells remaining at time t and the quantity transfused, while F(t) for RBCs initially surviving after 24 h is the ratio between the quantity at time t and the quantity initially surviving.

If F_PTR24 defines the fraction of transfused RBCs initially surviving post-transfusion, then the relationship between the total MRL for all transfused cells (MRL_ALL) and MRL for the cells initially surviving 24 h is:

$$MR{L}_{ALL}=FPT{R}_{24}\cdot MR{L}_{24}$$ (3)

MRL_ALL is a valuable parameter because it is more comprehensive than MRL₂₄ in the way that it includes all transfused RBCs in the calculation of the mean remaining lifespan parameter. Equation 4 is derived considering the RBCs initially removed to have a MRL of zero. Thus, the total mean remaining lifespan considering all cells is the weighted (according to proportions) average of the two averages, i.e.,

$${\mathrm{MRL}}_{\mathrm{ALL}}=(1-{\mathrm{FPTR}}_{24})\cdot 0+{\mathrm{FPTR}}_{24}\cdot {\mathrm{MRL}}_{24}={\mathrm{FPTR}}_{24}\cdot {\mathrm{MRL}}_{24}.$$ (4)

Importantly, MRL_ALL incorporates both the property of initially survival and the survival property (MRL) of the surviving cells.

Relationship of MRL to T_max and T₅₀

In addition to MPL, two parameters T_max and T₅₀ have been recommended to quantify the survival of transfused RBCs.¹²T_max is defined as the longest time a transfused RBC will remain in circulation after transfusion, while T₅₀ denotes the time when 50 percent of transfused RBCs remain in circulation.

In a rare, hypothetical case, MRL relates in a simple way to these two parameters:

$$MRL=\frac{T_{\max }}{2}=T_{50}$$ (5)

This case (Equation 4) requires two assumptions: 1) all transfused RBCs have identical survival in the donor, during storage and while circulating in recipient; 2) transfused RBCs were produced at a constant, steady state rate for as long as their lifespan in the donor.

Example Illustrations with Subject Data

Two RBC survival data sets were selected from previous publications to illustrate the calculation of MRL.^6,13.

Example 1 (Figure 2) illustrates biotin labeled RBC non-fetal cell (F cell) survival curves in four adult study subjects with sickle cell disease.¹³ In this study, 10 ml of autologous sickle cells were labeled with biotin and reinfused.¹³ The labeled RBCs were identified by flow cytometry. The percentage of F-cells was determined as a function of time after reinfusion using a 2 color flow cytometric analysis.¹³

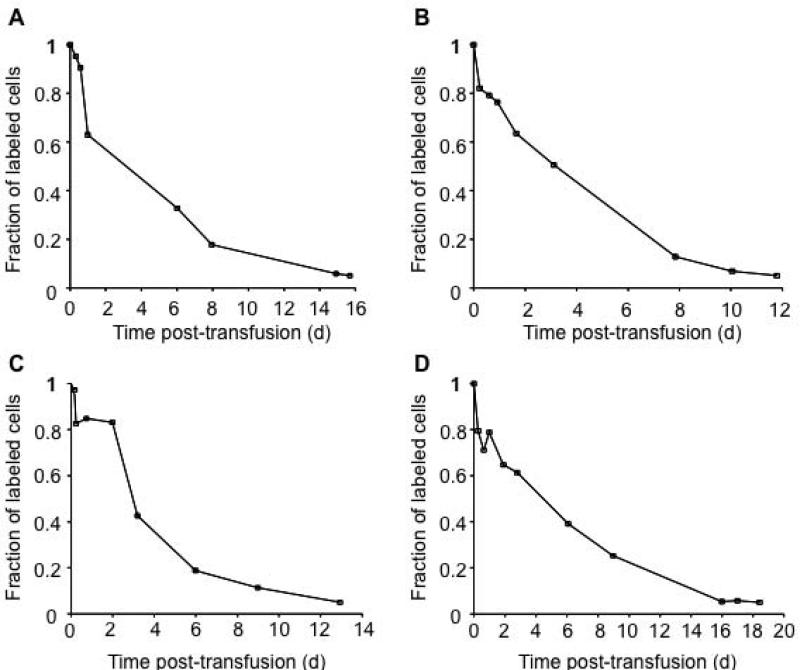
Figure 2. Mean remaining lifespan from survival curves of non-F cells.

Panels A, B, C and D illustrate the survival of biotin labeled non-F cells for four study subjects with sickle cell disease.¹³ The last data point in the graphs is calculated by linear interpolation and represents the time at which only 5 percent of the labeled cells remain in circulation. The mean remaining lifespan (MRL_0.95) is calculated from the RCS curve by computing the area under the curve until 95 percent of the labeled cells are removed from circulation. All survival data points below 5 percent are omitted, as they are not used in MRL_0.95 calculations.

Example 2 (Figure 3) illustrates the RBC lifespan using a biotin label in diabetic and non-diabetic adult subjects.⁶ Both Type 1 and Type 2 diabetic subjects were selected based on age greater than or equal to 14 y and stable diabetic control.⁶ Non-diabetic subjects who were hematologically normal were recruited from the general population.⁶Ex vivo biotinylation with flow cytometric analysis was used to determine the survival of autologous RBCs. Up to 10 ml of RBCs were labeled with biotin under sterile conditions and re-infused. Initial post-infusion blood samples were obtained after 10 min, 20 min, 2 h, and 24 h.⁶ Additional blood samples, were taken after 2 d, one wk, 2 wk, and at subsequent 2-wk intervals until the fraction of biotinylated cells fell below 5 percent of the initial percentage of biotin labeled RBCs.⁶

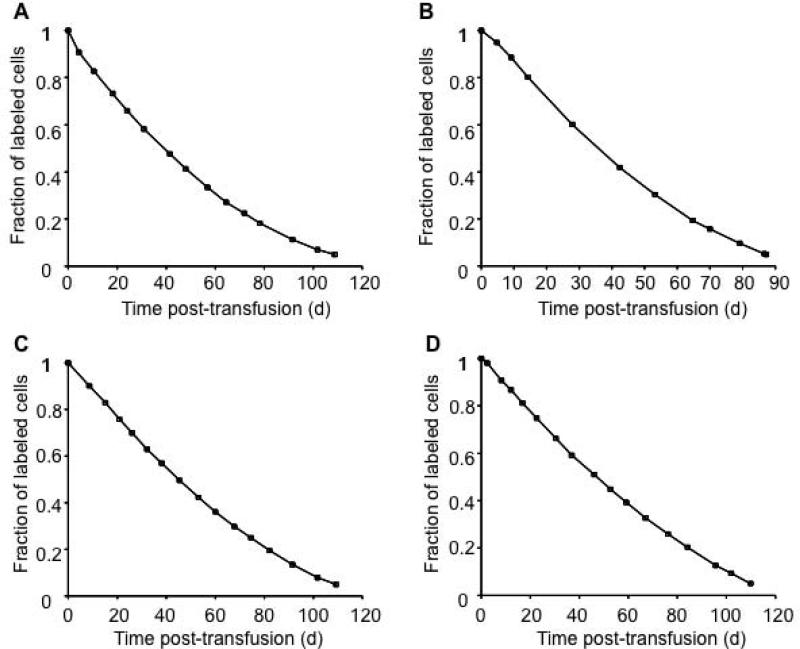
Figure 3. Mean remaining lifespan from RBC survival of diabetic and non-diabetic subjects.

Panels A - D illustrate the survival of RBCs in diabetic (A, C) and non-diabetic (B, D) subjects. The mean remaining lifespan (MRL_0.95) is calculated from the RBC survival curve by computing the area under the curve until 95 percent of the labeled cells are removed from circulation.

RESULTS

Example 1. Survival of non-F cells in sickle cell disease subjects (Figure 2)

The MRL_0.95 calculated for the four study subjects in Example 1 are shown in Table 1. Based on the survival curves for four study subjects with sickle cell disease, it is clear that the RBCs from individuals with sickle cell disease undergo rapid clearance during the first few days post-transfusion.

Table 1.

Mean remaining lifespan (MRL_0.95) for each study subject in Example 1

Subject ID	Figure	MRL0.95, days
A	Figure 2 A	4.62
B	Figure 2 B	3.92
C	Figure 2 C	4.08
D	Figure 2 D	5.78

The RBC survival data from the published paper by Franco et al.¹³

As illustrated in Figure 2, the RBCs are removed rapidly from circulation under disease conditions leading to a largely convex elimination versus time profile. Under these circumstances, it is difficult to estimate the MPL. Even if MPL was estimated using non-linear extrapolation, it would not provide a meaningful estimate for the survival of transfused RBCs. To illustrate this point, in Figure 2A, it can be observed that the percent survival of labeled RBCs drops down close to zero percent at ~20 d. This indicates that the youngest labeled RBCs are cleared from the circulation at ~20 d. The MRL_0.95 estimate for the same subject provides a value of only 4.6 d. If Figure 2A is used as a reference, one observes that less than 20 percent of the labeled RBCs remain in the circulation 8 d post-transfusion. Therefore, a lifespan estimate of 20 d is misleading as an estimate for the overall survival of the transfused RBCs and thus not useful as a clinical evaluation of the potential oxygen carrying capacity of the transfused cells. A similar analysis can be done with Figures 2B, 2C and 2D. In every case, it is observed that the survival curves are non-linear with rapid decline in survival (to less than 50 percent of labeled cells) within the first 5 d. Thus, any parameter used to describe RCS should be able to capture this rapid decline. The mean MRL_0.95 for the four subjects is ~4.6 d. Clearly, the MRL_0.95 provides a more meaningful evaluation of the survival of the transfused RBCs.

Example 2. Survival of RBCs in diabetic and non-diabetic study subjects (Figure 3)

The RBC disappearance curves (Figure 3) in diabetic and non-diabetic subjects further illustrate the advantage of MRL.⁶ Again, because of the curvature of the four RBC disappearance curves in these examples, it is not meaningful to use linear extrapolation of all the data points to determine the RBC lifespan. Linear extrapolation of the first few points of the disappearance curve would underestimate of the true mean RBC lifespan while a linear extrapolation of the final few points would overestimate the true mean RBC lifespan of transfused RBCs. Moreover, it does not provide information regarding how the older RBCs behave in the circulation. The MRL_0.95 for each of the four subject's RBC disappearance curves were computed and compared to the mean cell age computed previously (Table 2).

Table 2.

Mean remaining lifespan (MRL_0.95) for each study subject in Example 2

Subject ID	Figure	RBC MA*, (d)	MRL0.95, (d)
A (DM 3)	Figure 3 A	45.4	44.3
B (NDM 3)	Figure 3 B	38.4	39.4
C (DM 5)	Figure 3 C	49.3	49.1
D (NDM 4)	Figure 3 D	51.6	50.9

^*The RBC mean cell age data from the published paper by Cohen et al.⁶ The method used for mean cell age calculation was adapted from previous published literature.⁷

The MA estimates used for comparison to the MRL estimates were calculated by the method described previously by Cohen et al.⁶ Briefly, the maximum survival time was computed by extrapolation of the final two points of the curve to the time axis.⁶ This was followed by fitting cubic equations to the survival data.⁶ The first derivative of the survival curve generates the death rate as a function of time, which was used to determine the initial cell age distribution.⁶ The mean age at any postinfusion time t was then computed from the recalculated death rate function and age distribution at each time t.⁶ Additional details on the derivation of the MA parameter are provided by Lindsell et al.⁷

DISCUSSION

The present study demonstrates that applying mean remaining lifespan is simpler to calculate as compared to previously proposed parameters used to characterize the survival of transfused RBCs and that doing so also overcomes their limitations. In addition, MRL is a physiologically and clinically relevant parameter for quantifying the survival of transfused RBCs. The relative merits of the MRL parameter are illustrated in the two clinical examples provided: 1) among individuals with markedly shortened red cell survival as a result of sickle cell disease; and 2) among individuals with diabetes mellitus who demonstrated subject to subject variability in RBC survival.

Ambiguity in the Lifespan Notation

Intrinsically the total lifespan of an individual RBC encompasses the time from when the RBC enters the donor bloodstream from the marrow until the time it is cleared from the circulation in the donor or the transfused recipient. The notation “total lifespan” above is consistent with this intrinsic definition of a lifespan. Accordingly, “lifespan in recipient” or “lifespan of transfused RBC” are confusing terms that should be avoided. This is particularly relevant if the rate of RBC aging truly is different in the donor and recipient, a situation quite likely to be present when donors and recipients are fundamentally different, e.g., an adult donor and a newborn infant recipient.

The term “remaining lifespan” avoids such confusion by being more clearly defined. It also provides a clinically more meaningful parameter for the oxygenation potential of transfused RBCs. Furthermore the evaluation of the MRL does not depend on a steady state assumption for the production of the transfused RBCs. In contrast, the MPL parameter, unfortunately, has the above ambiguity associated with lifespan. For the casual reader, MPL may incorrectly be interpreted in several different ways: e.g., as the mean lifespan of donor RBCs in the donor, as the mean lifespan of fresh new donor cells in the recipient, or as the mean remaining lifespan of transfused cells. None of these interpretations would be correct.

MRL as an alternative to MA

The estimates for the RBC MA and MRL were similar in Table 2 because the RBC disappearance curves for the four study subjects do not deviate substantially from a linear decline (Figure 3). For RBCs produced under steady state conditions with similar lifespan, the MA will be equal to the MRL. However, this equality will not be true under non-steady state production of RBCs. Also, the MA relates to the mean age of the cells at the time the cells enter the recipient circulation, i.e., the time spent in the donor prior to transfusion to the recipient (Figure 1), which is far from as relevant as the time spend in the recipient, and thus can be misleading. Also, the MA cannot be directly calculated from the RCS curve post-transfusion in the recipient. In contrast, the MRL is directly calculated from the RBC post-transfusion disappearance curve and relates directly to the time the transfused cells spend in the recipient, not the donor.

MRL as an alternative to MPL

The mean remaining lifespan (MRL) indicates the mean in vivo survival of all the RBCs that are transfused to the recipient. If all transfused RBCs have same fixed lifespan, then the MRL will be equal to the T₅₀ if produced under steady state conditions. Thus, T₅₀ is not as useful a parameter because this parameter is only an accurate estimate of MRL for situations in which the steady state production of the transfused RBCs also exhibits a fixed lifespan. Since the older RBCs are cleared earlier from the circulation than the younger RBCs, MRL is less than MPL. In contrast, MRL accurately accounts for the reduced lifespan in the recipient of the older transfused cells. The MRL represents a true mean survival of the cells in the recipient even when the transfused RBCs have been produced under non-steady state conditions.

While it may be tempting to assume that MPL represents the survival of RBCs in the donor as well as in the recipient, this assumption is not valid when “environmental effects” altering RBC survival are considered. The RBC membrane is composed of 39.5 percent proteins and 35.1 percent lipids, both of which are susceptible to oxidative modifications.¹⁴ RBCs have high content of oxygen and hemoglobin, making them susceptible to oxidative damage.¹⁵ Mature RBCs are more susceptible to oxidative damage than other cells due to their inability to synthesize new proteins or overcome damage to cellular components.¹⁶ These factors indicate that mature RBCs are more prone to damage than newly produced cells. In contrast to MPL, the MRL does not have this limitation to its interpretation since the MRL parameter, as its name clearly indicates, only pertains to survival of the transfused RBCs in the recipients, and thus inherently considers the environmental effects.

The MRL as an accurate estimate of the potential oxygen delivery assumes that independent of their age and their remaining lifespan, transfused RBCs deliver the same amount of oxygen to tissues irrespective of their age. This assumption may not be valid if the affinity of oxygen to hemoglobin changes with the age of the transfused RBCs. With prolonged ex- vivo storage of RBCs, there is a reduction in 2,3-diphosphoglycerate (2,3-DPG), a major allosteric modifier of the hemoglobin (Hb) oxygen affinity.¹⁷ Further work needs to be done to account for the changes in oxygen delivery potential of transfused RBCs that occur with age.

In conclusion, the mean remaining lifespan has been proposed as a more clinically relevant parameter for predicting the quality of stored RBCs used for transfusion. Relative to mean potential lifespan and mean age, estimation of MRL requires fewer assumptions and is more meaningful in the evaluation of red cell survival in the recipient and the potential oxygen delivery of the transfused RBCs. In contrast to MPL, MRL is easily estimated under non-steady state conditions. This makes it more universally applicable than MPL or MA for quantifying the quality of transfused RBCs.